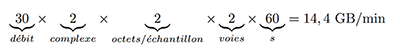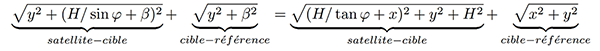RADAR passif bistatique au moyen d’une Raspberry Pi 4, d’une radio logicielle et du satellite Sentinel-1

Le détournement de signaux radiofréquences à des fins autres que ceux pour lesquels ils sont initialement prévus (un hack dans le sens le plus noble du terme) a récemment été diffusé dans l’« actualité » avec l’utilisation de la constellation de satellites en orbite basse Starlink pour la géolocalisation. Malheureusement, cette prouesse technique est associée à deux drames pour la science : la diffusion du résultat technique au travers d’un communiqué de presse aussi concis que dénué de contenu scientifique rigoureux [1], et sa reprise par des journalistes que certains n’hésiteraient pas à qualifier d’aussi incompétents que stupides [2] puisque capables d’affubler la prouesse technique d’adjectifs tels que « piratage » et « absence de gain financier pour Starlink » alors que la constellation n’avait jamais été conçue pour la géolocalisation. On ne pourra que regretter que le compte rendu technique ne soit pas librement disponible [3], mais seul un résumé de quelques lignes qui nous donne l’envie de découvrir les techniques mises en œuvre : patientons un peu le temps que l’article soit libéré des éditeurs commerciaux [4]. Nous allons ici aborder le « piratage » – ou en termes plus nuancés l’exploitation passive de signaux radiofréquences issus de RADAR spatioportés – pour une détection de position de réflecteurs au sol en exploitant le signal brut (analogique) reçu directement du satellite et après réflexion par des cibles au sol. Cette application est surprenamment peu commune puisque nous avons trouvé une unique référence bibliographique [5] abordant ce problème.

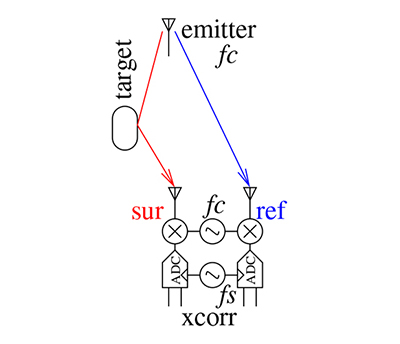
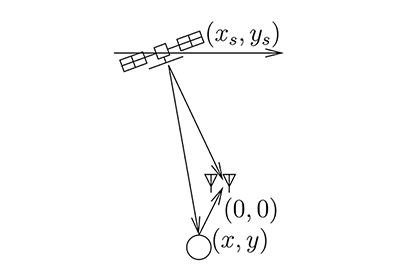
Nous avons décrit dans ces pages la « bonne » façon de développer sur Raspberry Pi 4 et en particulier des applications gourmandes en ressources telles que le traitement logiciel de signaux radiofréquences grâce à Buildroot [6] qui permet de ciseler l’exécutable aux ressources disponibles. Nous avons décrit dans ces pages comment Sentinel-1 [7], RADAR spatioporté de l’ESA, observe la surface de la Terre en l’illuminant autour de 5,405 GHz et comment ces données sont mises à disposition pour en tirer le meilleur parti, éventuellement au-delà des applications initialement prévues. Nous avions déjà abordé les préceptes du RADAR bistatique passif (Fig. 1) dans lequel un émetteur non coopératif, généralement émettant un signal bien plus puissant que ce que le civil amateur moyen aurait le droit de diffuser, est observé sur une voie dite de référence tandis qu’une seconde voie de mesure radiofréquence dite de surveillance observe les réflexions retardées dans le temps (distance) et décalées en fréquence par effet Doppler (vitesse) des cibles. Nous allons fusionner l’ensemble de ces connaissances en exploitant une Raspberry Pi 4 pour enregistrer les signaux radiofréquences d’un récepteur de radio logicielle à deux voies cohérentes (cadencées par le même oscillateur fc pour garantir la même phase et donc fréquence) afin de traiter les signaux bruts de Sentinel-1 pour une application de RADAR passif (Fig 1).

Il est en effet tout à fait fascinant de non seulement constater qu’il est relativement « simple » de capter un signal venant de l’espace de satellites à plus de 700 km de distance – nous l’avions déjà largement discuté avec les satellites météorologiques [8, 9] et d’autres auteurs dépassent les 300 millions de kilomètres dans les conditions idéales de propagation en espace libre [10] – mais en plus d’observer les réflexions de ces signaux au sol à une distance de plusieurs kilomètres du récepteur. Bien entendu, l’ESA met à disposition les mesures de Sentinel-1 et l’exercice peut sembler futile – pourquoi détourner des signaux radiofréquences alors que les « vraies » mesures reçues par le satellite sont librement accessibles – mais nous considérons cet exercice comme valable pour tous les RADAR spatioportés, une faune en pleine expansion si l’on en croit [11] qui nous informe que « Since 2018, the number of civil and commercial SAR satellites in orbit has more than doubled. And at least a dozen more are set to launch this year, which would bring the total to more than 60. » que nous confirme notamment l’annonce du lancement de NISAR, le projet indo-américain qui semble s’aligner sur la distribution libre des données acquises [12].

1. Objectifs de l’acquisition de données

Sentinel-1 émet en bande C, et en attendant le lancement de NISAR (prévu 2023) ou Sentinel-12 (peut-être en 2027) qui émettront en bande L en deçà de 2 GHz, il faut utiliser un récepteur fonctionnant au-dessus de 5 GHz pour recevoir ses signaux analogiques. Pour le moment, seuls les récepteurs de radio logicielle équipés de détecteur (frontend) Analog Devices AD936x et dont les deux voies sont câblées seront utilisables : nous exploiterons le récepteur Ettus Research B210 [13, 14] à ces fins, même si l’E312 plus cher a aussi été démontré fonctionnel dans de telles applications [15], tandis que la PlutoSDR de Analog Devices ne proposant qu’une unique voie ne peut être utilisée, et les récepteurs à base de Lime Microsystems LMS7002 étant limités à 3 GHz ne seront pas utilisables pour l’application qui nous intéressera ici. Par ailleurs, les signaux de Sentinel-1 occupent une bande passante de 100 MHz, imposant d’échantillonner les signaux au maximum de la bande passante disponible sur le récepteur de radio logicielle. Une bande passante de 100 MHz suppose un bus de communication de plus de 400 Mb/s en continu si toute la résolution (deux octets) des deux voies doit être conservée. Peu d’interfaces embarquées permettent un tel débit – embarquées, car nous verrons que les sites intéressants de réception sont souvent isolés et sans infrastructure pour l’alimentation d’un poste fixe – et nous choisissons le port USB 3 de la Raspberry Pi 4 pour atteindre le maximum de la bande passante de la B210 de 30 Méchantillons/s.

Le scénario est donc ficelé : acquérir aussi rapidement que possible un flux de données de deux voies d’une radio logicielle B210 au moyen d’un ordinateur Raspberry Pi 4 en vue de transférer les données vers un ordinateur portable pour du post-traitement visant à identifier les cibles illuminées par Sentinel-1 lors de son survol. Notons que l’heureux possesseur d’un ordinateur portable équipé d’un port USB 3 pourra s’affranchir de l’intermédiaire de la Raspberry Pi 4, mais 1) ce n’est pas le cas de notre Panasonic CF19 qui n’est équipé que de ports USB 2 et 2) il est intéressant d’appliquer les préceptes du développement de systèmes embarqués à ce projet, ne serait-ce que dans un objectif de mesure long terme autonome en énergie sur un site isolé. En effet, la Raspberry Pi 4 et la B210 consomment à pleine vitesse de 1,55 GHz globalement 1,55 A sous 5 V, tandis qu’une acquisition dure 1 minute : il est donc envisageable d’effectuer environ 85 mesures sur une batterie de capacité 2200 mA h telle que nous avons utilisée ici, excluant le traitement embarqué ou le stockage.

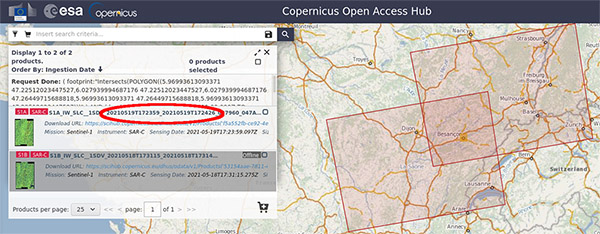
Les deux satellites Sentinel-1 survolent tout point de la Terre selon la même orbite tous les 12 jours, mais dans la pratique aux latitudes de la France métropolitaine, nous pouvons espérer observer un passage tous les jours ou tous les deux jours, selon des orbites et donc une élévation différentes. Alors que Heavens Above (https://www.heavens-above.com) nous informe qu’un passage de Sentinel-1 d’horizon à horizon dure 9 minutes, l’observation des signaux radiofréquences démontre que Sentinel-1 n’illumine un point donné de la surface de la Terre que pendant quelques secondes, et son mode de balayage de faisceau (swath) séquencé en impulsions successives (burst) ne fournira finalement que des séquences d’une fraction de seconde exploitables. Une différence majeure entre les observations systématiques de Sentinel-1 et les mesures ponctuelles de RADARSAT canadien, TerraSAR-X allemand ou ALOS-2 japonais est que le lieu et la date de passage sont prédictibles et se déduisent des observations publiées 12 jours auparavant. Nous pouvons donc connaître à la seconde près (Fig. 2) la date de début et de fin du passage du satellite au-dessus d’une zone géographique donnée : cette information est fortement dépendante de la localisation du récepteur et doit être répétée pour chaque nouveau site d’écoute. Ainsi, la nomenclature des fichiers bruts obtenus sur le site Copernicus Hub de l’ESA est de la forme S1A_IW_RAW__0SDV_20210519T172356_20210519T172429_037960_047AF4_8DCD pour le fichier brut de niveau 0 qui indique une acquisition le 19 mai 2021 de 17:23:56 à 17:24:29 UTC donc une durée de 33 s, ou le fichier traité de niveau 1 IW SLC (Interferometric Wide – Single Look Complex) S1B_IW_SLC__1SDV_20210705T173118_20210705T173144_027662_034D27_3FBE indique une acquisition plus ciblée le 7 mai 2021 de 17:31:18 à 17:31:44, soit une durée de 16 s. Cependant, compte tenu de l’incertitude sur l’exactitude de l’horloge locale et la durée du lancement de l’acquisition, il est prudent d’acquérir une minute de données et d’extraire les informations utiles a posteriori. Au débit de 30 Méchantillons/s complexes sur deux voies, des données sur 16 bits occupent :

Ayant acquis des Raspberry Pi 4 munies de 8 GB de RAM et désirant stocker les mesures en RAMdisk pour éviter d’être handicapés par le débit de communication avec la carte SD, nous choisissons de tronquer la taille des données transmises par la B210 vers la Raspberry Pi 4, ayant par ailleurs constaté que le débit maximal de 30 Méchantillons/s ne pourrait être atteint en transférant 16 bits/échantillons : la bibliothèque UHD qui contrôle le transfert de données des plateformes de radio logicielle Ettus permet de définir le format de données transmises over the wire (otw) et de le réduire à 8 bits. De ce fait, il nous reste à stocker 7.2 GB, qui rentrent dans les 8 GB de la Raspberry Pi 4 appropriée en laissant un peu de mémoire pour le système d’exploitation et les applications.

2. Raspberry Pi 4 pour acquisition « rapide »

Ettus Research propose, sur le dépôt de la bibliothèque UHD https://github.com/EttusResearch/uhd/tree/master/host/examples, des programmes d’exemple et notamment rx_multi_samples.cpp qui ne travaille cependant que sur une voie et transfère des données sur 16 bits. Ainsi partant de cet exemple, nous dupliquons toutes les définitions des propriétés des canaux pour passer d’une à deux voies, et indiquons à UHD de transmettre des données en format complexe 8 bits par :

Ainsi que de communiquer les informations en flux tendu et non sous forme d’un unique paquet de données :

Ainsi, nous recevrons deux flux de données que nous stockons aussi vite que possible dans deux fichiers qui seront traités comme les deux voies d’observation synchrones puisque les convertisseurs analogiques numériques sont cadencés par la même horloge f_s (Fig. 1), l’une issue d’une antenne pointée vers le ciel qui fournit le signal de référence illuminant la scène observée à la surface de la Terre, et la seconde pointant vers cette scène pour observer les cibles réfléchissant les signaux radiofréquences. Nous gagnerons en rapport signal à bruit en nous efforçant d’isoler l’antenne de mesure du signal de référence selon le montage proposé en Fig. 3 où le plan de masse de l’antenne hélicoïdale observant le signal de référence cache autant que possible l’antenne de mesure du signal direct. L’implémentation finale est disponible à https://github.com/jmfriedt/sentinel1_pbr/blob/main/b210_to_file/rx_multi_samples.cpp.

On pensera à passer la Raspberry Pi 4 en mode performance pour fournir la puissance de calcul nécessaire à l’acquisition de données :

Buildroot plaçant par défaut le processeur en économie d’énergie en le cadençant à 800 MHz au lieu des 1500 MHz du mode performance. Une fois assemblé, le système est transportable et prêt pour l’acquisition de données (Fig. 3).

3. Traitement sur une antenne unique : taux de répétition des impulsions

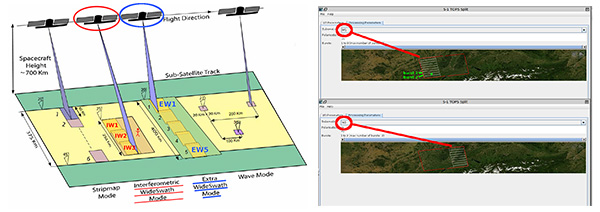
Une scène illuminée au sol peut recevoir des signaux de diverses natures puisque Sentinel-1 balaie trois faisceaux (swath) en mode IW (Interferometric Wide) utilisé aux latitudes moyennes et cinq faisceaux en mode EW (Extra Wide) utilisé aux latitudes élevées et au-dessus des océans, un cas qui nous intéresse lors de l’utilisation de ce système au Spitzberg (79°N) où les satellites en orbite polaire sont visibles deux fois chaque jour, augmentant les chances de mesures répétées (Fig. 4). Ces divers faisceaux ne sont pas caractérisés par les mêmes paramètres d’émission et en particulier le taux de répétition des impulsions radiofréquences émises par le RADAR : PRI pour Pulse Repetition Interval.

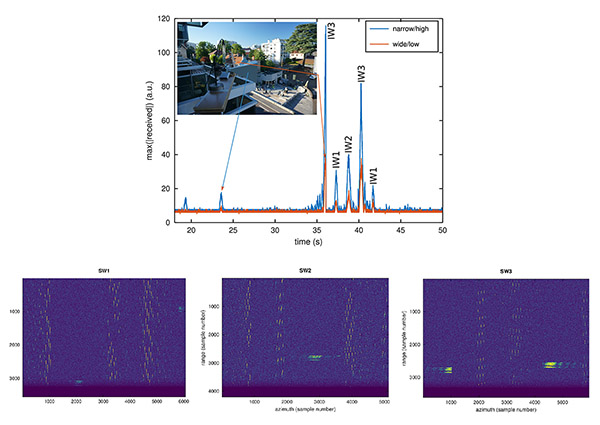
Alors que le décodage des signaux de niveau 0 fournis par l’ESA [20] nous informe des diverses valeurs possibles de PRI, nous ne savons pas a priori quel faisceau illumine l’antenne au sol à un instant donné. Soit nous testons tous les cas possibles (Fig. 5), soit une autocorrélation du signal directement reçu depuis le satellite (dit de référence) nous fournira cette information qui sera nécessaire pour découper la séquence continue de mesure dans le temps en échos observés suite à chaque illumination. Heureusement, les PRI associés à chaque swath restent constants d’un survol à l’autre et il n’est pas nécessaire de systématiquement décoder tous les fichiers de niveau 0 pour trouver cette information : nous avons retrouvé les mêmes paramètres au cours de tous les survols étudiés dans ce document, avec un PRI de 22777 pour swath 14 (EW1), 19355 pour swath 15 (EW2), 22779 pour swath 16 (EW3), 19777 pour swath 17 (EW4) et 23018 pour swath 18 (EW5), ou encore 21859 pour IW1, 25857 pour IW2 et 22265 pour IW3 (ces paramètres doivent être divisés par la fréquence de référence de 37.53472224 MHz pour être convertis en intervalle temporel, par exemple 1647.9 Hz pour EW1). Ainsi, connaissant la fréquence d’échantillonnage f_s, nous découperons le signal temporel acquis par chaque canal en matrice de M=f_s× PRI points par ligne et autant de colonnes que le permet la durée de la mesure. Cette matrice contiendra donc l’information temporelle selon l’abscisse qui se répète le long des colonnes alors que le satellite avance sur son orbite. Nous avons largement discuté dans ces pages que la corrélation le long de l’abscisse permettra de retrouver la distance aux cibles et se nomme la compression en distance (range compression) tandis que la mesure alors que le satellite avance le long de son orbite simule une antenne synthétique de dimensions égales à la longueur parcourue et l’analyse du signal le long des colonnes, qui s’avère être une transformée de Fourier inverse, se nomme la compression en azimut (azimuth compression). Nous reprendrons ces points dans la section suivante.

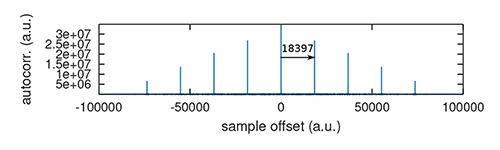
Une alternative à l’analyse le long de l’azimut des mesures alignées en distance (range) consiste à considérer l’autocorrélation du signal de référence. L’impulsion émise périodiquement ne se ressemble à elle-même que sur une période égale au PRI. La Fig. 6 illustre une telle analyse et son interprétation. Ici encore, l’analyse des données de niveau 0 informant de PRI (en bits, normalisé par rapport à la fréquence de référence f_ref=37.53472224 MHz) que nous avions entreprise auparavant, couplée à l’acquisition à une fréquence d’échantillonnage connue de 30 MHz, nous permet de trouver la période T des pics de corrélation et donc le swath, que ce soit en mode IW ou EW. Dans cet exemple, la mesure au cours d’un passage au-dessus du Spitzberg en mode EW du satellite indique une autocorrélation tous les 18397 échantillons acquis à 30 Méchantillons/s soit par rapport à f_ref un PRI de 23018 qui s’avère égal à la valeur de la télémétrie du faisceau EW5 que nous avons décodé sur S1B_EW_RAW__0SDH_20210925T063129_20210925T063237_028851_037165_3786.SAFE du 25 septembre 2021.

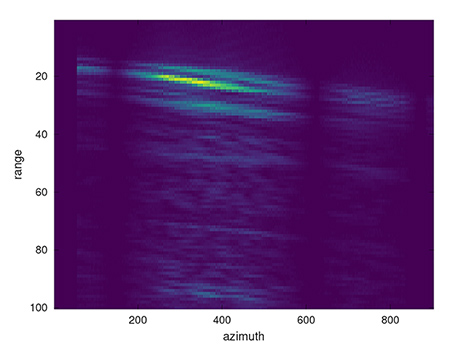
Nous pourrions déduire de cette analyse que connaissant les paramètres des impulsions émises par le satellite depuis l’espace tel que documenté dans les télémesures de niveau 0, nous pourrions exploiter les mesures acquises par une unique antenne visant les cibles et qu’il serait inutile de recevoir le signal de référence. Ce faisant, nous diminuerions d’un facteur deux les contraintes de bande passante, d’espace de stockage et multiplierions le nombre de plateformes de radio logicielles compatibles avec cette analyse. Malheureusement, il n’en est rien : l’analyse fine des mesures acquises sur une unique voie et alignées selon le PRI théorique démontre une dérive excessive alors que le satellite avance le long de son orbite. En effet, le déplacement est tellement rapide (7,5 km/s) que pendant le temps d’acquisition, même si nous n’exploitons que 200 ms du fichier acquis, le satellite s’est déplacé de 1,5 km, loin d’être négligeable devant la distance des cibles que nous visons (Fig. 7). Il faut donc absolument acquérir sur une seconde voie le signal de référence émis par le satellite pour s’affranchir de l’impact de la distance variable entre le satellite et la cible et ainsi permettre à tous les échos réfléchis par une même cible d’être alignés sur la même ordonnée de la Fig. 7, condition nécessaire à la compression en azimut.

L’acquisition de la seconde voie de référence abaisse le débit maximum de données que peut transmettre la B210 de 56 Méchantillons/s (simple voie) à 30 Méchantillons/s (doubles voies), fournissant tout de même une résolution en distance de 5 m.

4. Traitement des signaux acquis sur deux antennes...

4.1 ... dans un référentiel arbitraire

Nous avions développé, avec quelques erreurs à la relecture, le modèle classique de RADAR à antenne synthétique dans lequel l’émetteur et le récepteur sont colocalisés et se déplacent tous deux linéairement, ou dans le cas qui nous avait intéressés où l’émetteur restait fixe et le récepteur de déplaçait linéairement pour simuler une antenne de dimensions égales au chemin parcouru par le récepteur et ainsi présentant une résolution angulaire nettement améliorée par rapport à l’antenne réceptrice elle-même. On rappelle en effet que l’ouverture angulaire d’une antenne de dimensions d est de l’ordre de acos(λ/d) et que la résolution azimutale d’un RADAR est donc directement liée à la taille d’antenne d, dans la limite de ce qu’il est raisonnablement réalisable mécaniquement (Fig. 8). Pour d trop grand, l’antenne ne devient plus réalisable, mais le concept d’ouverture synthétique consiste à considérer qu’en déplaçant l’antenne le long d’un chemin de longueur d, il est possible de recombiner les signaux acquis successivement le long de ce parcours pour former une antenne équivalente de taille d. Dans le cas de Sentinel-1 dont les paramètres orbitaux (TLE pour Two Line Element) diffusés par le NORAD américain indiquent qu’il parcourt 14.592 orbites autour de la Terre chaque jour à une altitude de 700 km, la vitesse linéaire est donc de (40000+700× 2π)× 14.592/24=27000 km/h en considérant la circonférence de la Terre égale à 40000 km, soit 7,5 km/s. Cette vitesse, qui pourrait sembler incroyable au sol, permet de déduire qu’entre deux impulsions émises au rythme d’environ 1900 Hz, le satellite parcourt environ 4 m. Cette source qui se déplace à 700 km d’altitude est reçue par notre montage de RADAR bistatique passif au sol pour observer des cibles à une distance que nous prendrons à environ 7 km au maximum du récepteur, donc par le théorème de Thalès le satellite se comporte comme une source mobile s’avançant de 4 cm – le rapport des 7 km à la cible aux 700 km à la source – vérifiant les contraintes de l’équivalent spatial du théorème d’échantillonnage pour ne pas présenter d’incertitude de repliement spectral lors de l’acquisition des données. Cette différence de géométrie – une source très loin des récepteurs de référence et de surveillance ainsi que des cibles illuminées – nous impose de développer un nouveau modèle de propagation des signaux qui justifiera de la transformée de Fourier inverse pour la compression en azimut, mais qui fournira les constantes nécessaires à graduer les axes en distance connue et non en unités arbitraires.

La démonstration se développe comme suit :

• la compression en distance se déduit d’une corrélation entre le signal de référence ref et le signal de surveillance sur le long de l’axe temporel de la matrice que nous avons formé en alignant f_s× PRI échantillons les uns après les autres, et la corrélation xcorr se calcule dans le domaine de Fourier tel que le démontre le théorème de convolution par FFT(xcorr(ref,sur))=FFT(ref)· FFT*(sur) avec FFT la transformée de Fourier rapide de complexité algorithmique Nlog(N) lors du traitement de N points et non N² comme le ferait une transformée de Fourier classique, avec * le complexe conjugué ;
• la compression en azimut se déduit d’une transformée de Fourier inverse le long de la colonne où le signal se répète puisque nous savons [17] que la transformée de Fourier d’un signal de la forme exp(j2π k_x·x)exp(j2π k_y·y) se comprime en un Dirac en (x,y) par transformée de Fourier. Dans cette expression, k_x et k_y sont les grandeurs duales de x et y que les physiciens nomment habituellement vecteur d’onde. La question est donc de savoir si nous sommes capables d’exprimer le signal reçu et contenu dans la matrice (échantillon(t),position satellite) sous une forme qui sépare explicitement k_x et k_y : si c’est le cas, alors une transformée de Fourier inverse bidimensionnelle après avoir effectué la transformée de Fourier selon l’axe du temps doit fournir l’image dans le domaine spatial (x,y) qui s’apparentera à la géographie des cibles ;
• supposons (Fig. 8) le satellite en position (x_s,y_s) se déplaçant le long de l’axe x, les récepteurs à l’origine (0, 0), et une cible en (x,y) ;
• nous pouvons exprimer la distance entre le satellite et les récepteurs comme R₁=√(x_s)²+(y_s)²≃ y_s+1/2(x_s)²/y_s puisque y_s≫ x_s qui permet d’exploiter le développement limité de √u²+v² avec u≪ v qui s’écrit v√1+(u/v)²≃ v(1+1/2(u/v)²)=v+u²/(2v) ;
• de la même façon, la distance entre le satellite et une cible au sol s’exprime par R₂=√(x_s−x)²+(y_s−y)²≃ y_s−y+1/2(x_s−x)²/y_s−y≃ y_s−y+1/2(x_s−x)²/y_s selon le même argumentaire ;
• enfin, la distance entre la cible et les récepteurs est R₃=√x²+y² sans approximation, mais qu’on notera être indépendant de x_s ;
• un signal de bande relativement étroite est impacté lors de sa propagation par un déphasage qui s’exprime soit en fonction du temps τ t soit de la distance parcourue R à vitesse c comme ϕ=2π fτ=2π/λR puisque τ=R/c ;
• finalement, la différence de chemin entre le signal arrivant directement au récepteur de référence et le signal qui a rebondi sur une cible avant d’atteindre le récepteur de surveillance s’exprime comme R₃+R₂−R₁ qui induit donc un déphasage :

Qui sépare bien la distance et l’azimut et justifie la compression d’impulsion par transformée de Fourier inverse le long de f et x_s avec l’expression des grandeurs duales pour retrouver une graduation quantitative.

Ce calcul ne nécessite en aucun cas la connaissance précise des paramètres orbitaux du satellite ou sa position dans l’espace : seule sa vitesse et donc l’intervalle entre deux mesures est nécessaire, qui se déduit d’une analyse simple des fichiers TLE (nombre de rotations autour de la Terre par jour) et de la connaissance de l’altitude à laquelle il survole la Terre, en plus de PRI. La seule hypothèse que nous avons faite pour autoriser le développement limité qui sépare les variables est que la distance satellite-sol est très grande devant la distance cibles-récepteur. Ainsi, le traitement se réduit à une transformée de Fourier inverse en deux dimensions, dans l’axe de la distance sur le produit des transformées de Fourier qui permet de produire une intercorrélation, et selon l’axe de l’azimut pour la compression tel que le démontre l’application de ce traitement sur le tout premier jeu de données acquis et présenté sur la Fig. 9.

Bien que la présence de motifs géométriques sur cette image soit plus qu’encourageante et prouve que nous sommes sur la bonne voie, une analyse détaillée notamment juste à gauche de la flèche qui pointe vers le nord laisse présager d’un problème lorsque nous plaquons nos mesures sur un fond de carte : les motifs géométriques sont proches, mais ne se superposent pas avec la carte, avec un écart d’autant plus grand que l’on s’écarte de l’axe de visée de l’antenne de surveillance. Il faut donc améliorer le modèle de projection.

4.2 ... en coordonnées géographiques

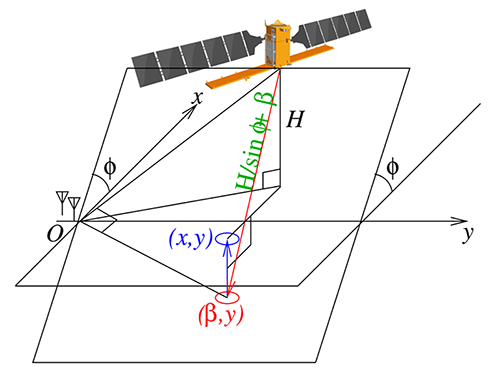
La dernière subtilité est que ce calcul de compression en distance et azimutale se fait dans le plan contenant la trajectoire du satellite et les récepteurs au sol, alors que nous voudrions une projection dans le plan tangent à la surface de la Terre qui permettrait de se raccorder à un système de coordonnées géographiques (Fig. 10). Connaissant l’altitude de vol du satellite et l’angle d’illumination, il est possible de migrer chaque pixel du premier plan vers le second, une opération un peu longue en calcul qui nécessite de trouver une solution numérique pour chaque point, mais qui permettra ci-dessous de fournir des images dans un format compatible avec un outil de Système d’Information Géographique (SIG) tel que QGIS sans aucun degré de liberté autre que la rotation des images. S’agissant de géométrie en trois dimensions, la représentation graphique sur une feuille en deux dimensions n’est pas aisée et nous laisserons le lecteur se convaincre que connaissant l’altitude H=693 km du satellite et l’angle d’illumination ϕ≃ 45° dont la valeur est fournie avec précision pour chaque survol par le site web Heavens Above, alors la condition d’égalité de la somme des temps de vol satellite-cible et cible-récepteur dans le plan trajectoire-récepteur (α,β) dans le premier cas, et le plan tangent à la surface de la Terre (x,y) dans le second membre, s’exprime par :

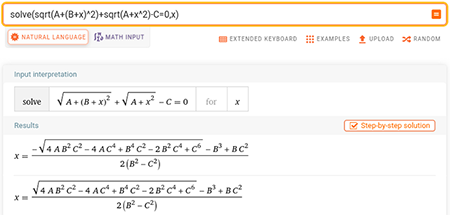
En choisissant arbitrairement α=y (ne connaissant pas la position du satellite le long de sa trajectoire, cela suppose « simplement » que l’origine de la carte que nous traçons est centrée sur les récepteurs au sol... dont nous connaissons la position et qui impose donc l’emplacement de la carte sur un système de projection géographique) et en éliminant à droite et à gauche le terme commun de temps de vol du satellite à l’antenne de référence. Cette équation impose donc de trouver β du plan de départ qui vérifie pour chaque point (x,y) du plan d’arrivée l’égalité : après avoir cherché maintes approximations et solutions numériques (par exemple par méthode de Newton [21]... qui diverge ici compte tenu du très grand écart des valeurs numériques des différents termes) qui ont échoué, Wolfram Alpha (https://www.wolframalpha.com/) nous informe à notre plus grande surprise qu’il existe une solution analytique. En effet, en réduisant l’égalité à √A+(B+β)²+√A+β²−C=0 avec A, B et C des termes dépendant de x, y, H et ϕ uniquement et donc de valeur numérique constante pour chaque itération, il est possible de trouver la solution β par une équation certes longue, mais simple à implémenter dans un langage tel que GNU/Octave ou Python (Fig. 11).

5. Résultats

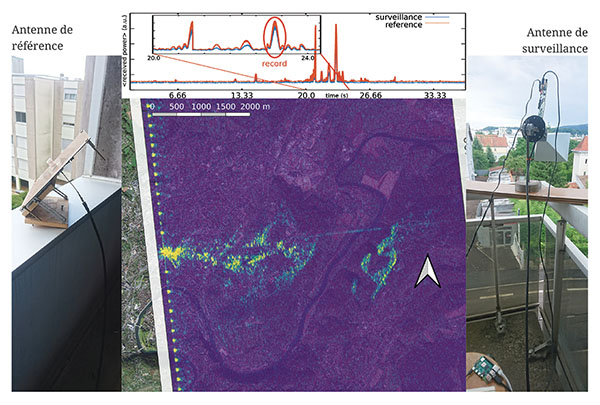
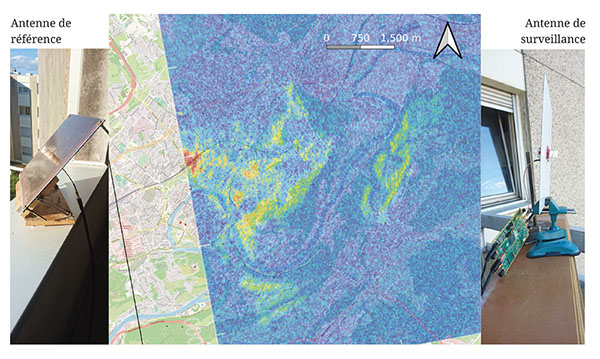
Nos premiers essais avec une architecture à deux antennes sont illustrés en Fig. 9 et 12 pour mettre en évidence les erreurs de débutant. Dans ce montage, deux antennes sont utilisées, l’une visant le satellite (référence, gauche) et l’autre les cibles (surveillance, droite). Inquiet de ne pas avoir assez de gain du signal rétrodiffusé par les cibles tout en considérant le signal venant du satellite puissant, nous avions sélectionné une antenne cornet (horn antenna) de fort gain (20 dB) A-Infomw LB-159-20-C-SF comme antenne de surveillance et une antenne hélicoïdale comme antenne de référence. Ces deux choix sont erronés : alors que le signal direct du satellite ne sera reçu que pendant un temps très court et donc dans une ouverture angulaire étroite compatible avec l’antenne cornet – le satellite parcourt en 5 secondes une distance de 37,5 km qui à une distance de 700/cos(45°)=980 km se traduit par une ouverture angulaire de 2,2°, bien moins que les 16 à 18° de l’antenne cornet de 20 dB de gain – il est souhaitable de recevoir les signaux réfléchis par les cibles dans une couverture angulaire aussi large que possible. Par ailleurs, la qualité du signal de référence détermine directement le rapport signal à bruit sur la détection des cibles, une autre bonne raison pour sélectionner l’antenne cornet comme antenne de référence et non de surveillance. Malgré ces erreurs, les structures géographiques des environs de Besançon illuminées par Sentinel-1 restent identifiables sur l’image (Fig. 9 et 12, milieu). On notera que la distance d’une quinzaine de mètres entre le balcon qui supporte l’antenne de surveillance (droite) et la cage d’escalier dans laquelle se trouve l’antenne de référence (gauche) ne pourra être couvert à 5,405 GHz par un câble coaxial de qualité médiocre aux fréquences micro-ondes tel que RG-58 (plus de 30 dB de pertes), mais qu’un câble de bonne qualité tel que LMR-400 (moins de 6 dB de pertes sur cette longueur) utilisé ici sera indispensable.

Dans ce premier exemple de la Fig. 9, non seulement la géométrie des antennes choisies est peu judicieuse, mais en plus l’image obtenue par transformée de Fourier inverse a « simplement » été déformée par homothétie en abscisse et ordonnée – en l’absence de coordonnées géographiques avant projection sur le plan tangent à la surface de la Terre, tel qu'expliqué en section 5.1 – et tournée en imposant la localisation des récepteurs sur le balcon de l’appartement de l’auteur.

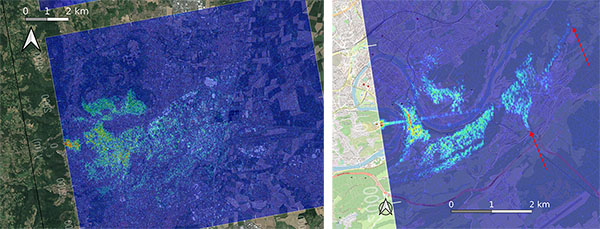
Les mesures ont été répétées depuis divers sites, toujours en nous positionnant en altitude afin de limiter l’impact d’obstacles entre les cibles et le récepteur, sans pour autant tenir compte de cette différence d’élévation dans le modèle de projection : Fig. 13 illustre le cas de Clermont-Ferrand et le point de vue de la Pierre Carrée qui surplombe la ville, ainsi que le Fort Chaudanne qui surplombe Besançon. L’acquisition depuis le point de vue à proximité du mont Valérien à l’ouest de Paris (Fig. 14), au cours d’un passage ascendant pendant lequel Sentinel-1 illumine vers l’est, nous permet d’observer les réflecteurs majeurs dans une circonférence de quelques kilomètres autour des récepteurs, sans pour autant atteindre la butte de Montmartre et le Sacré-Cœur, probablement trop éloignés. La tour Eiffel, une masse imposante de métal est clairement observable, comme un réflecteur à sa position nominale, et nos hypothèses [18] sur un effet de layover [19] dans lequel le sommet de la tour réfléchit le signal électromagnétique avant sa base, 360 m plus bas, était erronées et uniquement attribuables à une erreur dans le calcul de la migration des données lors de la projection sur le plan tangentiel à la surface de la Terre.

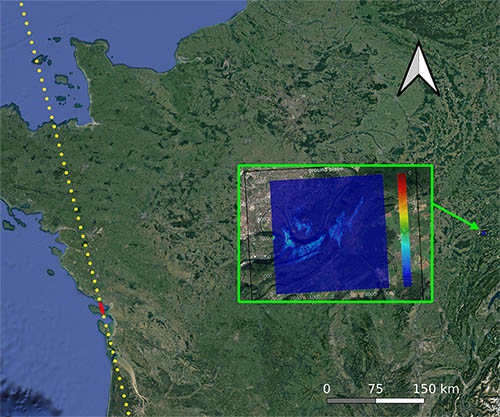
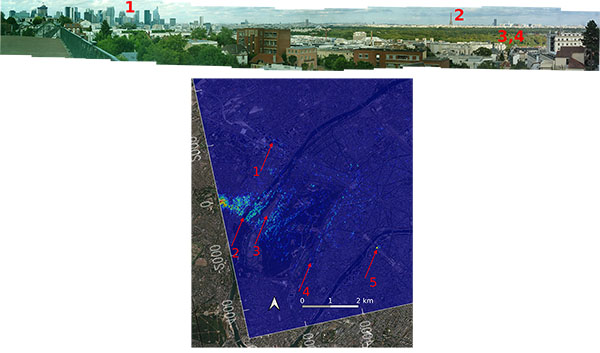
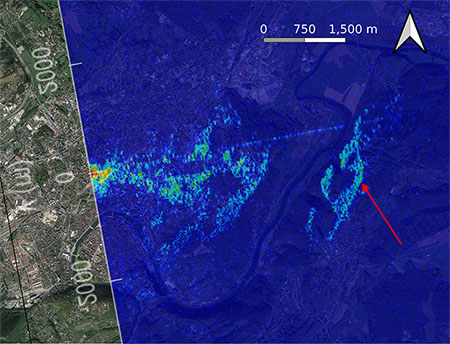
Pour conclure cette série de démonstrations expérimentales, la portabilité et l’efficacité du système sont validées au Spitzberg, dans un environnement où le poids et le volume des bagages sont contraints. Le montage tient dans un sac à dos et se déploie en quelques minutes sur site (Fig. 15, haut) pour un résultat de mesure passive par RADAR bistatique tout à fait en accord avec le signal obtenu par Sentinel-1 lors de son survol du site d’observation (Fig. 15, bas). Sur cette image, l’arrière-plan fournit le contexte géographique de Google Earth, l’image en tons de gris est la carte de réflectivité des cibles obtenue par Sentinel-1, et la couleur indique les réflecteurs détectés par le RADAR passif. Les montagnes imposantes visibles sur Fig. 15, en haut à droite, sont clairement visibles sur la mesure par RADAR passif à un emplacement en accord avec la mesure de Sentinel-1.

Conclusion

Nous nous sommes efforcés de démontrer une implémentation à coût réduit – B210 et Raspberry Pi 4 avec une antenne réalisée sur un support de teflon aisément récupérable – d’un récepteur de radio logicielle exploité pour une application de RADAR passif bistatique. Le coût réduit ne retire rien à la subtilité du traitement du signal mis en œuvre, dont la validité est mise en évidence par la cohérence des cartes de réflecteurs superposées sur des images aériennes des sites observés (Fig. 16). Ainsi, l’application pédagogique est avérée sur une expérience accessible aux expérimentateurs intéressés par ce sujet.

On pourra s’interroger pourquoi tous les exemples illustrant les traitements sont orientés vers l’est : simplement les passages ascendants de Sentinel-1 au-dessus de la France se déroulent en fin d’après-midi, bien plus simples à acquérir depuis des sites distants que les passages descendants illuminant vers l’ouest qui se déroulent tôt le matin.

Une zone dégagée est nécessaire pour obtenir des échos réfléchis par les cibles au sol sans avoir été atténués par des obstacles à proximité des récepteurs, d’où la recherche de points élevés (point de vue de Clermont-Ferrand, Mont Valérien à Paris, colline de Planoise ou Chaudanne à Besançon) lors de ces mesures. Le système est suffisamment léger et peu gourmand en ressources pour être emmené par drone : cette perspective n’a pas (encore) été mise en œuvre, mais semble envisageable pour s’affranchir de la contrainte sur le site d’observation, le vecteur de vol ne devant rester stationnaire en altitude que quelques secondes.

L’ensemble des logiciels et scripts de traitement décrits dans ce document est disponible à https://github.com/jmfriedt/sentinel1_pbr.

Remerciements

Les recherches bibliographiques pour nos activités de développement ne sauraient aboutir sans Library Genesis [4], une ressource incontournable. L’acquisition du matériel ayant permis ce projet a été en partie financée par le Centre National d’Études Spatiales (CNES) au travers du projet R-S18/LN-0001-036 tandis que le voyage au Spitzberg a été financé par l’Institut polaire Paul Émile Victor (IPEV) dans le cadre du projet PRISM.

Références

[1] L. Arenschield, SpaceX satellite signals used like GPS to pinpoint location on Earth (22/09/2021) à https://news.osu.edu/spacex-satellite-signals-used-like-gps-to-pinpoint-location-on-earth

[2] C. Deluzarche, « Des chercheurs créent leur propre système de GPS en piratant des satellites » (07/10/2021) à https://www.futura-sciences.com/tech/actualites/piratage-chercheurs-creent-leur-propre-systeme-gps-piratant-satellites-93962/

[3] M. Neinavaie & al., Exploiting Starlink Signals for Navigation: First Results, Proc. ION GNSS (2021) à https://www.ion.org/publications/abstract.cfm?articleID=18122

[4] Library Genesis à gen.lib.rus.ec

[5] A. Anghel & al., Bistatic SAR imaging with Sentinel-1 operating in TOPSAR mode, 2017 IEEE Radar Conference.

[6] G. Goavec-Merou, J.-M Friedt, « On ne compile jamais sur la cible embarquée » : Buildroot propose GNU Radio sur Raspberry Pi (et autres), Hackable n°37 (avril-mai-juin 2021)
https://connect.ed-diamond.com/hackable/hk-037/on-ne-compile-jamais-sur-la-cible-embarquee-buildroot-propose-gnu-radio-sur-raspberry-pi-et-autres

[7] J.-M Friedt, P. Abbé, Parler à un RADAR spatioporté : traitement et analyse des données de Sentinel-1, GNU/Linux Magazine France n°246 (mars 2021) https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-246/parler-a-un-radar-spatioporte-traitement-et-analyse-des-donnees-de-sentinel-1

[8] S. Guinot, J.-M Friedt, La réception d’images météorologiques issues de satellites : utilisation d’un système embarqué, GNU/Linux Magazine France Hors Série n°24 (2006).

[9] J.-M. Friedt, Décodage d’images numériques issues de satellites météorologiques en orbite basse : le protocole LRPT de Meteor-M2, GNU Linux Magazine France (2019), en 3 parties.

[10] D. Estevez, Decoding Interplanetary Spacecraft, tutoriel GNU Radio Conference (2019) à https://www.youtube.com/watch?v=RDbs6l4rMhs

[11] J. Rosen, Shifting ground, Science 371 (6532), pp. 876-880 (2021) annonce plus de 60 RADAR spatioportés dans les années à venir.

[12] J. Blumenfeld, Getting Ready for NISAR - and for Managing Big Data using the Commercial Cloud (2 oct. 2017) à https://earthdata.nasa.gov/learn/articles/tools-and-technology-articles/getting-ready-for-nisar

[13] S. Prager & al., Ultrawideband Synthesis for High-Range-Resolution Software-Defined Radar, IEEE Trans. Instrum. Meas. 69 3789–3803 (2020).

[14] O. Toker & al., A Synthetic Wide-Bandwidth Radar System Using Software Defined Radios, 7th International Electronic Conference on Sensors and Applications (15-30 November 2020).

[15] S.T. Peters & al., In Situ Demonstration of a Passive Radio Sounding Approach Using the Sun for Echo Detection, IEEE Trans. Geosci. and Remote Sensing 56 (12) 7338 (Dec. 2018).

[16] C.A. Balanis, Antenna Theory – Analysis and design, 3rd Ed., Wiley Interscience (2005).

[17] https://hforsten.com/synthetic-aperture-radar-imaging.html

[18] J.-M Friedt, W. Feng, Passive bistatic RADAR using spaceborne Sentinel-1 non-cooperative source, a B210 and a Raspberry Pi 4, GNU Radio Conference (2021) à https://youtu.be/BaRgx5ehdOw?t=7960

[19] Remote sensing and SAR radar images processing – Physics of radar, p.40, ESA/CNES à https://earth.esa.int/c/document_library/get_file?folderId=226458&name=DLFE-2127.pdf

[20] https://github.com/jmfriedt/sentinel1_level0

[21] J.-M Friedt, Arithmétique sur divers systèmes embarqués aux ressources contraintes : les nombres à virgule fixe, GNU/Linux Magazine France Hors Série n°113 (mars 2021)
https://connect.ed-diamond.com/GNU-Linux-Magazine/glmfhs-113/arithmetique-sur-divers-systemes-embarques-aux-ressources-contraintes-les-nombres-a-virgule-fixe

[22] G. Charvat, The Range Migration Algorithm (RMA), section 4.2 de Small and Short-Range Radar Systems, CRC Press (2014).