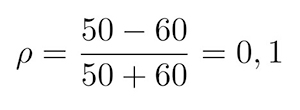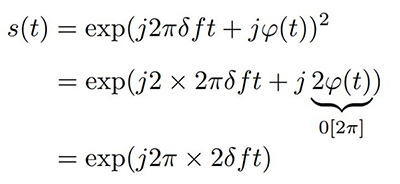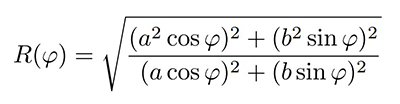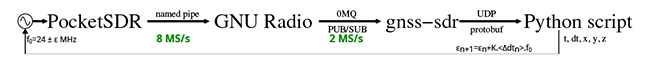Depuis que Tomoji Takasu, auteur de RTKLib, a publié à https://github.com/tomojitakasu/PocketSDR son récepteur de radio logicielle dédié aux constellations de navigation par satellite, nous rêvions d’en obtenir une copie. Indisponible commercialement, nous avons donc décidé d’en produire une déclinaison nous-mêmes, en respectant les préceptes de n’utiliser que des outils libres. Nous profiterons de cette nouvelle plateforme de travail pour étudier quelques aspects d’exploitation des signaux de navigation par satellite, de la détection de leurrage à l’asservissement d’un oscillateur à quartz sur la référence de temps produite par les horloges atomiques à bord des satellites, et ce, en tirant parti des connaissances acquises sur la programmation des interfaces USB, et des communications entre logiciels de PocketSDR, GNU Radio et gnss-sdr.
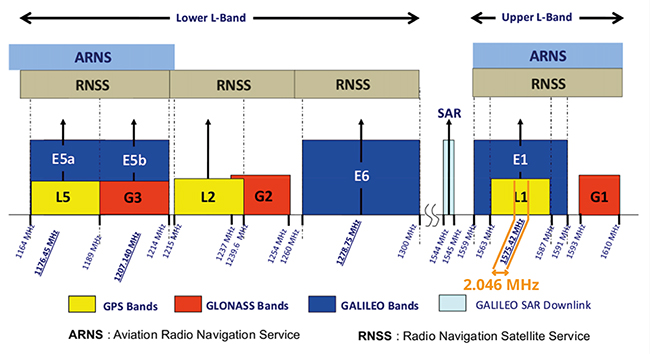
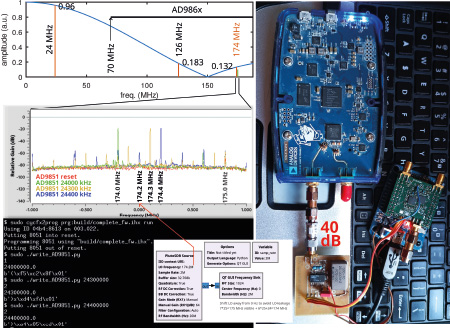
Nous poursuivons [1] notre exploration de la programmation efficace du bus USB sous GNU/Linux, en particulier pour la réception de signaux de navigation par satellite en général (GNSS), et de GPS en particulier. Cette étude fournit les outils pour s’approprier les concepts, quelque peu abstraits en l’absence de données concrètes à traiter, du traitement par radio logicielle des signaux GNSS initié avec la lecture de [2] et remis récemment à jour dans [3], qui étend les analyses à toutes les constellations désormais disponibles. La nécessité de maîtriser les techniques de communication permettant d’atteindre plusieurs dizaines de MB/s est justifiée par la multiplication des signaux de navigation par satellite occupant des bandes passantes de plus en plus importantes pour fournir une résolution qui ne cesse de s’améliorer (Fig. 1).
Nous avions mentionné dans le premier numéro de cette série que l’EZ-USB FX2LP peut être obtenu assemblé et prêt à l’emploi pour un peu moins de 5 euros sur AliExpress, quand le composant chargé de l’interface USB coûte seul près de 20 euros chez Farnell (code commande 1269134). Nous avons fait le choix de redessiner le circuit imprimé de la PocketSDR de Tomoji Takasu, cette fois comme carte fille de https://fr.aliexpress.com/item/1005006134347046.html et nous libérer de la contrainte de n’utiliser qu’une seule antenne pour alimenter les deux récepteurs tel qu’imposé dans le circuit original, afin de laisser la liberté d’effectuer du contrôle de diagramme de rayonnement en vue d’annuler une source de leurrage ou de brouillage de GNSS [4], en bénéficiant de la diversité spatiale de deux antennes distinctes pour produire les signaux des deux interfaces d’acquisition Maxim IC MAX2771.
1. Conception du circuit imprimé
Alors que PocketSDR n’est pas commercialement disponible, tous ses schémas et routage le sont sur le dépôt GitHub donc la fabrication n’est qu’« une » question financière de faire sous-traiter la réalisation des circuits imprimés (à moins d’avoir chez soi les moyens de réaliser un circuit 4 couches avec trous métallisés). On notera que d’autres initiatives, même libres, existent, en particulier https://github.com/WKyleGilbertson/MAX2769FT2232H qui propose librement les schémas et routage d’une carte à base de MAX2769 limité à la bande L supérieure entre 1550 et 1610 MHz, qu’il commercialise pour la modique somme de 500 euros sur https://www.navstargps.us/. Cependant, l’utilisation du FT2232 de FTDI à la place du FX2LP retire l’accès à un microcontrôleur embarqué programmable et réduit un peu la portée du développement. Nous nous sommes donc efforcés d’adapter le schéma et circuit routé de la PocketSDR à la carte de développement commercialement disponible munie du FX2LP (Fig. 2).
PocketSDR est conçue comme un circuit 4 couches. On pourrait penser qu’avec un peu d’efforts, les deux MAX2771 et l’interface FX2LP pourraient être routées sur un double couche. Cependant, un point clé en manipulant des signaux autour de 1,5 GHz est l’adaptation d’impédance de la piste portant les signaux radiofréquences. Un petit calcul rapide avec KiCAD permet de se convaincre que seule une solution à 4 couches permet une adaptation à 50 Ω – l’impédance standard des lignes de transmission radiofréquences adaptées à leurs charges – avec une largeur de piste compatible avec l’espacement des broches sur un circuit intégré monté en surface, et que cette adaptation est impossible sur un substrat FR4 de 1,6 mm d’épaisseur. Le calculateur de KiCAD se charge automatiquement avec les paramètres du substrat FR4, à savoir une permittivité relative de εr≃ 4,5 et des pertes exprimées comme tan δ≃ 0,02 (Fig. 3). Si avec un substrat d’épaisseur H=1,6 mm nous adaptons une ligne de transmission « coplanar wave guide with ground plane » avec un espacement conducteur-plan de masse de 0,2 mm, alors la ligne doit faire 1,08 mm de large pour présenter une impédance de 50 Ω, et forcément se rétrécir en atteignant le composant dont les pattes sont séparées de 0,4 mm et sont de 0,2 mm de large (boîtier QFN à 28 broches), créant une rupture d’impédance et donc une réflexion d’une partie du signal incident. Mettre plus d’espace entre la piste et le plan de masse empire la situation, avec une piste de 1,94 mm de large si nous laissons 0,5 mm entre elle et le plan de masse. La seule chance d’atteindre 50 Ω avec une piste de 200 µm de large est de réduire l’épaisseur H du substrat diélectrique séparant la piste de plan de masse enterré. Avec une épaisseur H=0,2 mm que nous trouvons comme épaisseur de couche externe chez la majorité des fabricants de circuits imprimés d’épaisseur totale 1,6 mm, alors une piste de 0,34 mm de large sera adaptée à 50 Ω avec une séparation de 0,2 mm au plan de masse, ou comme le propose PocketSDR avec une isolation (distance ligne de transmission au plan de masse) de 0,1524 mm, alors le conducteur fera idéalement 0,315 mm. Tomoji Takasu fait réaliser ses circuits imprimés chez JLCPCB chez qui la couche interne fait 0,2104 mm d’épaisseur (https://jlcpcb.com/impedance) avec un substrat de permittivité relative de 4,1 donc une piste de largeur 0,3556 mm qui correspond bien à la valeur vue sur le routage de la PocketSDR. Chez Eurocircuits, le substrat « FR4 Improved » est de permittivité relative 3,9 mais d’épaisseur 0,36 mm, de sorte que la piste de 0,3556 mm de large et séparée du plan de masse de 0,1524 mm présente une impédance de 60 Ω. Nous aurions peut-être dû refaire le calcul avant de faire sous-traiter la fabrication chez Eurocircuits et augmenter la largeur de piste à 0,515 mm ! Malgré ce défaut de conception, le coefficient de réflexion en tension est :
donc la conservation d’énergie indique que ce qui n’est pas réfléchi est transmis 1−(0,1)2=0,992 soit 0,04 dB de pertes par désadaptation d’impédance.
Le circuit résultant du routage occupe 35×31 mm, principalement contraint par l’espacement entre les deux connecteurs de la carte de développement du FX2LP, et la fabrication des 4 couches coûte 5 euros/circuit imprimé pour 50 circuits chez Eurocircuits ou 1,6 euro/circuit chez Seeed Studio – qui n’accepte cependant pas les bons de commande – pour le même volume.
Nous avons passé le premier épisode de cette série d’articles à nous familiariser avec la carte de développement faible coût comprenant un FX2LP et les périphériques nécessaires, en argumentant notamment que la carte complète venant de Singapour coûte moins cher que le composant seul acheté localement. Par conséquent, partant du schéma et routage de PocketSDR, nous éliminons du circuit original toute la partie concernant la communication numérique pour ne router vers des borniers à l’espacement de 2,54 mm que les signaux pertinents que sont les signaux IQ et l’horloge qui cadence leur mise à jour, les signaux du bus SPI dont les deux activations CS#, et une paire de signaux de statut des récepteurs radiofréquences (Fig. 4).
Journaux à kits électroniques japonais
Le Japon a une culture du développement de circuits électroniques que la France ne connaît que de façon marginale – au moins grâce à la présente publication – en particulier avec la diffusion des journaux par CQ Publishing (https://www.cqpub.co.jp/) incluant Transistor Gijutsu et FPGA Magazine et divers ouvrages portant sur les microcontrôleurs et autres circuits numériques embarqués. Même si le quartier d’Akihabara à Tokyo a perdu de sa splendeur des années 1990 en passant de la vente de composants électroniques vers les mangas et produits dérivés de dessins animés, quelques enseignes telles qu’Akizuki Denshi (https://akizukidenshi.com, littéralement « magasin d’électronique d’Akizuki ») continuent à survivre et fournissent des kits sous forme de petits sacs contenant le circuit imprimé et les composants à assembler soi-même. Dans cette lignée, des ouvrages contenant un kit et la description des expériences associées, pour une trentaine d’euros (3000 yens), sont accessibles dans nombre de librairies. À titre d’illustration, un des ouvrages acquis en 2018 sur l’ARM Cortex M3 LPC1343 (gauche) avec son kit et CD contenant les logiciels – malheureusement exclusivement MS Windows (milieu) – et un exemple de page descriptive de périphérique, suivie des exemples de codes (droite).
Le lien étroit entre les auteurs de CQ Publications et Akizuki Denshi est mis en évidence dans l’introduction de l’article portant sur l’utilisation d’un processeur ARM comme source de radio logicielle à https://toragi.cqpub.co.jp/Portals/0/backnumber/2021/01/p115.pdf qui commence par « Circuits de cet article assemblés avec des composants disponibles chez Akizuki ». Une telle synergie aura du mal à exister en France où les magasins d’électronique se contentent de vendre des pinces ampèremétriques et des circuits intégrés au format DIL, quand ce ne sont pas des guirlandes de LED. Le circuit présenté dans cet article aurait sûrement pu faire l’objet d’un tel format de kit associé au texte, mais l’investissement financier et l’incertitude sur le volume de vente rendent la démarche incertaine.
Les lecteurs désireux de reproduire le circuit décrit dans ces pages peuvent contacter l’auteur, puisqu’un certain nombre de circuits imprimés (non peuplés de leurs composants) sont disponibles.
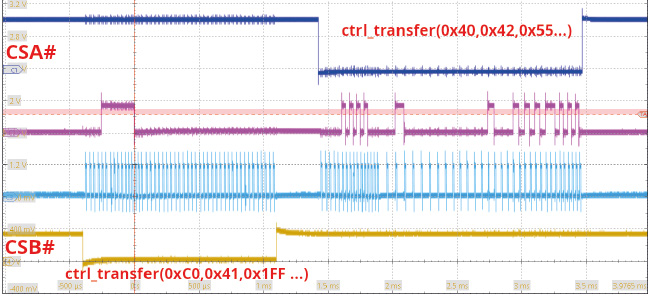
Par rapport à la carte d’évaluation du MAX2771 de Maxim IC qui ne propose qu’une unique interface d’acquisition, nous avons maintenant à notre disposition deux MAX2771 qui sont distingués, lors de leur configuration par le bus synchrone s’apparentant au SPI, par le signal d’activation CS#. Il faut donc vérifier que l’octet de poids fort du Vendor Request USB est bien interprété comme le numéro du composant avec lequel communiquer (Fig. 5) lors des transactions pour configurer les MAX2771.
Nous nous convainquons de bien comprendre l’interprétation des Vendor Requests avec la séquence suivante :
1. Partant d’un FX2LP flashé avec le contenu de FX2LP/complete_fw/build/complete_fw.ihx issu de la compilation de l’archive https://github.com/jmfriedt/max2771_fx2lp/, nous configurons les deux MAX2771 au moyen de PocketSDR avec sudo app/pocket_conf/pocket_conf pocket_L1L2_8MHz.conf et validons que le débit de communication est 8 MS/s avec sudo app/pocket_dump/pocket_dump -t 1 1.bin 2.bin qui indique :
et pocket_conf sans argument indique :
2. Nous modifions uniquement les bits 29 à 31 REFDIV du registre numéro 3 (PLL Configuration) du premier MAX2771 – horloge maîtresse qui cadence le second MAX2771 – pour passer de 8 à 16 MS/s en multipliant par deux la fréquence d’horloge cadençant l’ADC au moyen du script Python :
qui commence par identifier le périphérique par son Vendor ID = 0x04B4 et Product ID = 0x1004 tel qu’indiqué par lsusb | grep ypress, puis lit (Vendor Request de type 0x0C) le résultat de la transaction SPI initiée par le 8051 du FX2LP (commande 0x41) adressant le registre 0x03 pour mettre le résultat dans msg. L’octet de poids le plus fort (le premier du tableau) est masqué avec 0x1F pour conserver tous les bits sauf les 3 bits de poids les plus forts imposés à 0, déterminant donc REFDIV=0 pour « XTAL frequency x2 » (au lieu de x1 initialement avec 0x03). Cette approche est plus élégante qu’imposer tous les bits (en commentaire), ce qui risquerait d’écraser des configurations prises en charge par pocket_conf que nous ne voudrions peut-être pas modifier en ne voulant imposer qu’une nouvelle fréquence d’échantillonnage. Ce nouveau registre est écrit (Vendor Request de type 0x40) dans le registre 0x03, puis relu (Vendor Request de type 0xC0) pour validation avec un affichage selon un autre mode de conversion qu’utilisé auparavant. Le résultat de cette séquence est :
3. Après la reconfiguration, relancer pocket_dump comme auparavant indique désormais :
donc la configuration a bien été prise en compte avec cette fois 16 MS/s.
4. Enfin, pour accéder à un registre du second MAX2771, le numéro de registre fourni en troisième argument de ctrl_transfer devient 0x103 au lieu de 0x03, pour indiquer que c’est le second CS# et non le premier qui est activé.
2. Exploitation pour la réception de signaux GPS
Le bénéfice de placer deux récepteurs en parallèle est soit d’acquérir simultanément les signaux transmis dans deux bandes de fréquences loin l’une de l’autre, par exemple L1 et L5 (partie supérieure et inférieure de la bande L), et ainsi viser le positionnement centimétrique en s’affranchissant de la contribution de l’ionosphère sur le délai de propagation de l’onde électromagnétique en profitant de sa relation de dispersion, soit de configurer les deux antennes sur la même bande de fréquences et analyser la direction d’arrivée des signaux en vue de détecter un leurrage. En effet, si une source radiofréquence produit un signal représentatif du codage et des messages de GPS en vue de leurrer le récepteur, il est fort probable que cette source soit unique et ainsi que tous les signaux des satellites semblent venir d’une même direction, impossible avec une vraie constellation dont les satellites sont distribués sur la sphère céleste. Ainsi, une phase identique entre les signaux acquis par deux antennes pour tous les satellites est une forte suspicion de leurrage, et au contraire, compte tenu de la difficulté à synchroniser les émetteurs pour une attaque distribuée, une phase différente pour les signaux reçus des divers satellites est une indication que le signal reçu est réel. Cette analyse n’est cependant valable que si les signaux acquis par les deux MAX2771 sont synchrones, ce que normalement la configuration de l’horloge de l’ADC du second MAX2771 comme esclave du premier doit garantir, mais il reste à le démontrer.
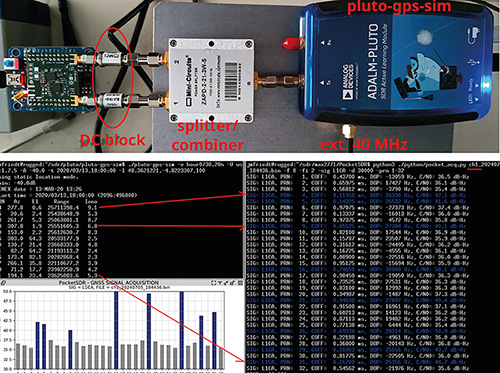
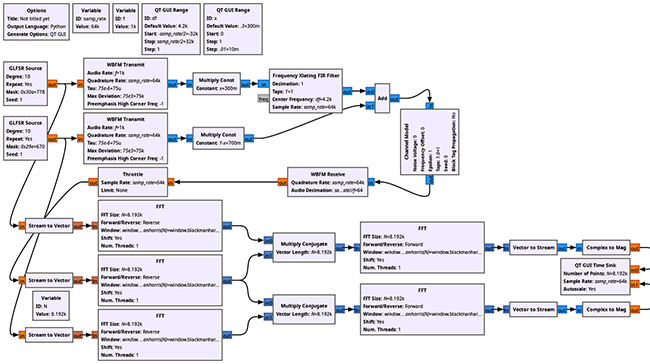
Dans un premier temps, nous validons la capacité d’une PlutoSDR à produire un signal représentatif de GPS et qui pourra être acquis et décodé par notre version de la PocketSDR. Pour ce faire, PlutoSDR émet le signal produit par pluto-gps-sim de https://github.com/Mictronics/pluto-gps-sim. Pour ce faire, il suffit d’obtenir sur le Web un fichier de navigation auprès de https://cddis.nasa.gov/archive/gnss/data/daily/ (qui impose de fournir une adresse e-mail pour s’enregistrer) permettant de positionner les satellites dans l’espace, et un signal, somme des signaux produits par tous les satellites, est généré par logiciel et émis par la PlutoSDR. Ce signal est divisé en deux par un splitter Mini-Circuits ZAPD-2-21-3W-S pour être injecté sur les deux entrées des deux MAX2771 : tous ces signaux seront vus avec la même phase par les deux récepteurs, puisque l’unique splitter introduit une unique phase entre ses deux voies. Noter l’utilisation de DC blockers (filtres passe-haut, ici Mini-Circuits MCL BLK-18-S, qui coupe la composante continue, mais laisse passer un signal jusqu’à 18 GHz) entre la sortie de la PlutoSDR et les entrées de la PocketSDR (Fig. 6, haut) : en effet, nous avons muni la PocketSDR des T de polarisation pour alimenter des antennes actives, et la PlutoSDR se comporte comme un court-circuit à la masse pour ces alimentations si nous n’y prenons garde (transformateurs de type balun qui se comportent comme des courts-circuits pour la composante continue).
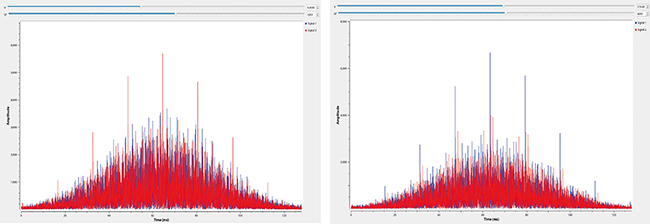
Lorsque nous émettons un signal représentatif de GPS et l’acquérons par PocketSDR, nous constatons (Fig. 6) la cohérence entre les signaux émis (gauche) et ceux décodés (droite et bas), indiquant que le leurrage fonctionne bien. La puissance du signal émis par la PlutoSDR est ajustable et peut se situer au-dessus du bruit thermique pour faciliter le déverminage du circuit de la PocketSDR en cas de dysfonctionnement.
Si cette acquisition est reproduite en branchant deux antennes actives sur les deux entrées de la PocketSDR, nous observons les vrais signaux de la constellation GPS distribuée sur la sphère céleste et donc introduisant des phases arbitraires entre les deux antennes. Les signaux GPS sont modulés en phase binaire (BPSK), donc une phase ϕ(t) qui porte l’information qui ne peut valoir que 0 ou π selon que le bit transmis soit 0 ou 1 (ou le contraire). Le rythme auquel ϕ(t) est modifié pour porter le code unique à chaque satellite est 1,023 Mb/s, donc l’étalement spectral de ce signal est de l’ordre de 2 MHz, et la puissance émise se distribue dans cette gamme spectrale : la densité de signal (puissance par unité spectrale, donc mW/Hz ou plus classiquement dBm/Hz) est très faible compte tenu du dénominateur de 2·106 Hz, et même en dessous de la densité spectrale du bruit thermique de −174 dBm/Hz. L’astuce classique de détection de signaux BPSK est de calculer le carré du signal s(t)=exp(j2πδ f t+jϕ(t)) avec δ f un écart de fréquence à la porteuse nominale introduit à la fois par décalage Doppler et imperfection de l’oscillateur local :
et nous constatons que toute l’énergie distribuée dans les 2 MHz de bande passante s’est accumulée dans une porteuse pure à la fréquence 2δ f puisque la modulation de phase 2ϕ a été annulée, valant 0 modulo 2π lors de la mise au carré du signal qui produit le double de l’argument. La transformée de Fourier de ce signal sera donc une série de raies spectrales, une pour chaque satellite visible, à une fréquence de Fourier de 2δ f et par conservation de l’énergie, une puissance qui maintenant dépasse le bruit thermique et devient visible sur le spectre. La différence des phases des raies spectrales à la même fréquence de Fourier entre les deux antennes est représentative de la direction d’arrivée du signal puisque l’onde plane de longueur d’onde λ atteignant les deux antennes séparées d’une distance d avec un angle ϑ induit une différence de phase (2π/λ)dsinϑ. Nous constatons (Fig. 7) que les phases sont uniformément distribuées pour la vraie constellation GPS (gauche), mais qu’elles valent toutes la même valeur (droite) dans le cas du leurrage.
Leurrage de signaux modulés en fréquence ou en phase
GPS en particulier, et GNSS en général, utilisent une modulation de phase, et compte tenu du faible rapport signal à bruit, en exploitant peu de symboles en BPSK où la phase ne prend que deux états, 0 ou π pour coder un état de bit ou l’autre.
Alors qu’on pourrait croire l’analyse de la puissance du signal reçu comme indicateur de leurrage quelque peu naïve, en argumentant qu’un signal convenablement leurré peut atteindre le récepteur avec une puissance représentative de celle d’un satellite, cette évaluation n’est pas dénuée de sens si l’antenne du récepteur est par ailleurs exposée aux vrais signaux en même temps qu’à ceux de leurrage. En effet, la question revient à savoir de combien il faut augmenter la puissance de la source de leurrage pour éblouir le récepteur qui voit par ailleurs le vrai signal, et ainsi lui faire croire qu’il est au mauvais emplacement à la mauvaise date.
Commençons par reprendre le cas de la modulation en fréquence (FM), bien connue pour son capture effect [5] tel que présenté par Tom Rondeau [6], dans lequel un signal interférant à peine plus puissant que le vrai signal va accrocher la boucle à verrouillage de phase du démodulateur FM qui ne sortira qu’une information, celle de l’interférant, au détriment du vrai signal qui a disparu de la sortie.
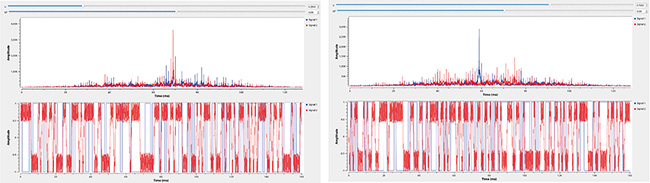
Afin de démontrer ce concept, deux codes pseudoaléatoires sont émis. Ces codes sont dits orthogonaux au sens que l’intercorrélation de l’un avec l’autre donne un résultat nul (au bruit près) tandis que l’autocorrélation du code avec lui-même produit un fort pic de corrélation à chaque période de répétition (longueur de la séquence). La corrélation est calculée dans GNU Radio comme transformée de Fourier inverse iFT du produit des complexes conjugués des transformées de Fourier FT des signaux : xcorr(u,v)=iFT(FT(u)· FT*(v)) avec * le complexe conjugué. En effet, nous constatons ci-dessous que si un signal est à peine plus fort que l’autre (curseur en haut des graphiques), alors seuls ses pics de corrélation (rouge à gauche, bleu à droite) ressortent du bruit. En effet, la boucle à verrouillage de phase (PLL) qui fait office de convertisseur fréquence-tension dans le démodulateur FM ne s’accroche que sur le signal puissant et filtre les autres.
Au contraire, dans le cas de la modulation de phase BPSK illustrée ci-dessous, la boucle de Costas qui reproduit la porteuse du signal incident pour permettre l’extraction de la phase est perturbée si le signal à décoder n’est pas suffisamment puissant. Lorsque la somme de deux signaux modulés en phase atteint une boucle de Costas, aucune sortie exploitable n’est produite si le rapport signal à bruit d’un des signaux par rapport à l’autre n’est pas suffisant :
On notera sur ces deux exemples qu’alors que pour un signal FM, il suffit qu’un des deux signaux soit à peine plus puissant que l’autre pour que la PLL fournisse en sortie un signal uniquement associé au code pseudoaléatoire modulé sur le signal le plus puissant, dans le cas de la modulation de phase le rapport signal à bruit du signal alimentant la boucle de Costas doit être beaucoup plus élevé pour permettre la démodulation du code pseudoaléatoire le plus puissant. Sans cette condition sur un rapport signal à bruit suffisant, la boucle de Costas fournit un signal inexploitable ne contenant ni l’un ni l’autre des codes modulés.
Ainsi, éblouir un récepteur GNSS implique de le soumettre à un signal de leurrage significativement plus important que le signal original, saut de puissance qui serait une signature probable d’attaque, tel que nous en informe U-blox dans la notice de son récepteur ZED-F9P en affirmant « A detection is successful when a signal is observed to transition from an initially genuine one to a spoofed version. Hence detection is not possible if the receiver is started under spoofing conditions. »
3. Utilisation d’une source de fréquence programmable
GPS est avant tout une constellation d’horloges atomiques en orbite autour de la Terre dont les informations transmises au sol doivent permettre de reproduire la stabilité des horloges embarquées. Comme l’oscillateur à quartz qui cadence le circuit électronique de réception de radio logicielle n’a aucune raison d’être stable ou exact, nous devons le remplacer par une source programmable afin de corriger la fréquence avec les informations issues du récepteur GNSS par logiciel. En effet, gnss-sdr fournit l’information d’écart de temps entre le signal GPS et l’oscillateur local, même si cette information est un peu cachée et peu exposée à l’utilisateur. L’objectif de ce paragraphe est donc de remplacer l’oscillateur 24 MHz fixe qui cadence les MAX2771 par une source de fréquence programmable, et ce avec une granularité suffisamment fine pour corriger les dérives de l’oscillateur par rapport à GPS. Le résultat est un GPS Disciplined Oscillator ou GPSDO, largement disponible commercialement, mais qui est réalisé ici avec le bénéfice des deux récepteurs en parallèle, donc capable de détecter un leurrage, voire de tenter d’annuler la source d’interférence en créant une interférence destructive dans la direction ϑ en introduisant une phase opposée à celle détectée auparavant [7].
Notre choix de source de fréquence se porte sur le vénérable synthétiseur numérique (Direct Digital Synthesizer – DDS) d’Analog Devices AD9851 (Fig. 8). Ce composant, très simple d’emploi et d’implémentation, propose une configuration de son mot de fréquence FTW sur 32 bits, offrant donc une résolution relative de 1/232=2·10−10 ou avec une horloge de référence de 25×6=150 MHz, une résolution de 35 mHz, qui sans être exceptionnelle en termes de stabilité d’oscillateur, reste au moins trois ordres de grandeur meilleure que les quelques ppm (parties par million) de variation d’un oscillateur à quartz avec son vieillissement et les fluctuations de température ambiante. Nous apprenons de la documentation technique que AD9851 se programme avec un mot de 40 bits formé de 32 bits de fréquence suivis de 8 bits de contrôle et de phase, bit de poids faible en premier, selon un protocole synchrone que l’on pourrait abusivement associer à SPI, mais qui n’en a que les apparences. En effet, au lieu d’activer le composant par un CS#, AD9851 décale toujours son registre à décalage sur chaque coup d’horloge du bus synchrone, et transfère le résultat aux registres de configuration correspondants sur le front montant d’une impulsion d’une broche nommée FQ_UD. Le problème avec cette approche est que le registre à décalage ne cesse d’être modifié même si nous discutons avec les MAX2771, et se retrouve dans un état incertain au moment de discuter avec AD9851. Le palliatif que nous avons trouvé à cet état instable est de réinitialiser le registre à décalage par une impulsion sur FQ_UD juste avant de communiquer, envoyer les 40 bits et les valider par une nouvelle impulsion FQ_UD, étant certain qu’aucune autre transaction n’a eu lieu sur le bus SPI entre temps (par conception du programme sur le 8051).
Nous avions affirmé dans le premier épisode comprendre comment fonctionnent les Vendor Requests : communiquer avec AD9851 est l’occasion de le prouver en ajoutant une nouvelle commande pour communiquer avec ce périphérique. En passant, nous devrons ajouter quelques fonctions pour manipuler FQ_UD que nous avons branché sur PA7.
Le nouveau Vendor Request est ajouté au firmware du FX2LP dans :
qui fait appel aux fonctions de communication avec AD9851 :
qui tout comme le write_reg() original de Tomoji Takasu émule par logiciel la communication synchrone, mais cette fois en activant la broche PA7 et surtout en communiquant le bit de poids faible en premier (et non le bit de poids fort en premier, comme le demande le MAX2771). Comme l’horloge et le bus de données sont communs à tous les composants, nous exploitons la fonction write_sdata() d’origine. Finalement, nous configurons dès l’initialisation du 8051 l’AD9851 pour émettre un signal à 24 MHz avec :
Affirmer que cela fonctionne serait bien prétentieux sans une vérification du spectre du signal produit par l’AD9851. Au lieu d’utiliser l’artillerie lourde d’un analyseur de spectre professionnel, nous désirons utiliser du matériel couramment disponible, par exemple une PlutoSDR. Cependant, nous produisons un signal à 24 MHz, alors que la PlutoSDR est équipée d’un AD9363 qui peut être reconfiguré pour apparaître comme un AD9364 dont la fréquence minimum de mesure est 70 MHz. Nous devons donc faire appel à une astuce pour valider le bon fonctionnement du programme Python qui programme l’AD9851 au moyen de :
en produisant le Vendor Request numéro 0x50 (en accord avec la définition de VR_AD9851 dans le firmware) suivi des 5 octets de msg contenant la fréquence ftw suivie du mot de contrôle.
L’astuce consiste à tirer profit de l’échantillonnage en temps discret de la sortie du DDS, dont la documentation technique explique très bien la forme du spectre sous forme d’une raie à la fréquence voulue f, deux raies de part et d’autre de l’horloge fCK qui cadence le DDS à fCK± f, et copie de ce signal pour toutes les harmoniques de la fréquence d’horloge. La puissance de ces raies est pondérée par une enveloppe de sinus cardinal sinc(x)=sin(π x)/(π x) qui s’annule pour les valeurs entières de x que l’on prendra égales à la fréquence normalisée par la fréquence d’échantillonnage. Ainsi, en choisissant de cadencer l’AD9851 par un oscillateur à 25 MHz et de tirer profit de son multiplieur interne de fréquence par 6, le DDS est cadencé à fCK=150 MHz, et produit un signal de sortie à 24 MHz qui se traduit par deux raies spectrales à 150± 24 MHz donc 126 MHz et 174 MHz, toutes deux dans la gamme de mesure de PlutoSDR. Nous nous focalisons sur la seconde, proche de l’harmonique 7 de l’oscillateur 25 MHz qui ne manquera pas d’être visible sur le spectre, et servira de référence pour vérifier le bon fonctionnement de la PlutoSDR, même si le programme de configuration de l’AD9851 échoue. Après quelques séances de déverminage, en particulier sur l’endianness du mot transmis par le PC vers le FX2LP [1], nous obtenons la mesure présentée en Fig. 9 qui nous convainc de la bonne communication entre le programme Python émettant les ordres de programmation de fréquence de sortie de l’AD9851 et les spectres observés.
3.1 Mesure en boucle ouverte
Afin de corriger un oscillateur, il faut déjà le mesurer. Dans cette application, l’oscillateur 25 MHz cadence l’AD9851 qui produit le 24 MHz qui cadence le convertisseur analogique/numérique du MAX2771 et donc horodate implicitement chacun de ses échantillons, sous réserve qu’aucun ne soit perdu. Ainsi, lorsque gnss-sdr traite le flux de données, quelles que soient les latences ou les tailles de tampon introduites par la communication USB, il est capable de retrouver la date à laquelle chaque échantillon a été acquis. Comme le flux de données IQ décodé porte l’information de temps de la constellation GPS, gnss-sdr peut comparer l’évolution de son horloge locale, matérialisée par le 24 MHz qui cadence le MAX2771 (il est important de noter que seule l’horloge qui cadence le convertisseur analogique/numérique importe, quelle que soit la fréquence des oscillateurs qui cadencent USB ou le processeur de traitement en aval de l’acquisition [8]) avec le temps GPS supposé parfait, puisque produit par des horloges atomiques périodiquement comparées aux références primaires de l’USNO à Washington. Même si les manipulations du temps ne sont pas documentées par l’USNO sur le système à finalités militaires qu’est GPS, il est peu probable aujourd’hui, avec l’omniprésence de GPS et le nombre d’utilisateurs qui en observent les performances, que ce temps dévie significativement d’UTC, aux secondes intercalaires près pour conserver la cohérence historique avec le temps astronomique.
Nous avons donc d’une part app/pocket_dump/pocket_dump de PocketSDR qui peut acquérir sur bus USB et envoyer le flux I(Q) dans un fichier, et d’autre part gnss-sdr qui peut lire un flux de données et le traiter. Cependant, si nous demandons à pocket_dump d’écrire dans un pipe nommé créé par mkfifo /tmp/fifo1in, alors soit gnss-sdr se plaint en ouvrant un tel fichier qu’il ne peut en déterminer la taille, soit s’il s’agit d’une interface FIFO que cette dernière veut absolument un flux complexe et ne sait traiter un flux réel sans partie imaginaire. En effet, afin de nous affranchir du bruit introduit par les divers circuits numériques dans la bande de base, nous avons configuré le MAX2771 pour acquérir avec une fréquence intermédiaire de 2 MHz au rythme de 8 MS/s un flux réel. De cette façon, les sources de bruit en bande de base sont rejetées après numérisation des signaux par une transposition logicielle pour éliminer la fréquence intermédiaire, permettant par la même occasion de filtrer les bruits rejetés hors bande.
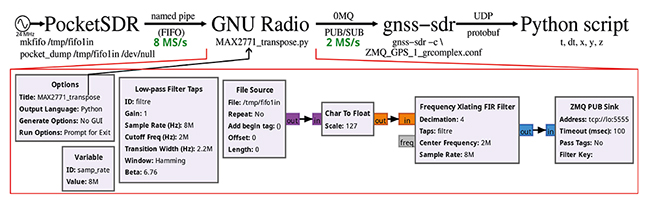
Ainsi, entre l’acquisition par pocket_dump d’un flux réel transposé en fréquence intermédiaire et le décodage par GNSS-SDR, il faut convertir en un flux complexe compensé de sa fréquence intermédiaire et décimé. Ce sera GNU Radio qui se chargera de cette transposition (Fig. 10) : une chaîne de traitement triviale se contente de lire dans le pseudofichier qu’est la FIFO alimentée par pocket_dump, de convertir les entiers codés sur 8 bits en flottants, de transposer en fréquence par le Xlating FIR Filter aussi chargé de filtrer et décimer, avant d’exporter son flux de données en sortie. Nous avons tenté d’écrire dans une autre FIFO en sortie pour communiquer avec gnss-sdr, mais le résultat fut décevant donc nous nous sommes rabattus sur une sortie de type UDP en interface ZeroMQ Publish que gnss-sdr reconnaît comme une entrée ZeroMQ Subscribe [9]. Ainsi, gnss-sdr est capable de produire une solution en position, vitesse et temps (PVT) et de l’afficher à l’écran [1]. Cependant, seule la date de l’acquisition est fournie sur l’interface utilisateur, tandis que l’écart entre le temps local du logiciel de traitement et le temps GPS reste caché dans les fonctions de résolution PVT. Par le passé [8], nous avions modifié le solveur PVT pour extraire cette information et l’utiliser pour commander un oscillateur externe asservi sur GPS, mais cela nécessite de patcher chaque nouvelle version de gnss-sdr qui bien entendu change d’organisation et nécessite d’insérer les fonctions à la main. Heureusement depuis une paire d’années, gnss-sdr prévoit d’exporter l’état de ses variables internes aux logiciels désireux de les exploiter, et ce par une liaison UDP. Soit nous pouvons exporter l’état de tous les canaux de traitement des fonctions de traitement PVT – bloc de traitement Monitor décrit à https://gnss-sdr.org/docs/sp-blocks/monitor/ – mais ce qui nous intéresse vraiment est la synthèse de la solution PVT, pas le décalage Doppler ou la pseudodistance du récepteur à chaque satellite (forts intéressants, par ailleurs). Ainsi, ce qui nous intéresse n’est pas d’ajouter les instructions Monitor.enable_monitor=true dans le fichier de configuration de gnss-sdr, mais plutôt d’ajouter l’affichage de la solution du traitement PVT, selon les consignes tout en bas de https://github.com/acebrianjuan/gnss-sdr-pvt-monitoring-client, à l’exception de la dernière ligne (celle concernant Protobuf), par :
Ainsi, un flux de données en UDP sort d’un serveur fourni par gnss-sdr et peut être lu par un client. Maintenant que nous avons appris à communiquer avec l’AD9851 en Python, nous voudrions ne pas utiliser l’exemple de client juste cité en C++, mais lire ces informations depuis Python afin d’utiliser un langage unique pour toutes les opérations. Il faut donc lire les données UDP depuis Python (client sur une socket UDP/IP bien connu) et interpréter chaque champ pour retrouver les informations qui nous intéressent. La documentation https://gnss-sdr.org/docs/sp-blocks/pvt/ nous enseigne que les données transmises sur UDP sont sérialisées par un protocole proposé par Google nommé Protobuf. Nous découvrons que ce protocole s’appuie sur un générateur de code à destination d’une multitude de langages à partir d’un fichier de configuration des champs, leur taille et leur emplacement dans le flux de données. Cette description des champs se trouve dans gnss-sdr/docs/protobuf dans le fichier monitor_pvt.proto. Nous trouvons en effet au début de ce fichier des informations du type :
qui commence bien puisque tow_at_current_symbol_ms est la date, en millisecondes, du symbole analysé, et user_clk_offset l’information d’écart de temps entre l'horloge GPS et notre horloge locale qui cadence le convertisseur analogique/numérique. Moins intéressant, mais toujours utile pour vérifier le bon fonctionnement, les champs pos_x, pos_y et pos_z donnent la position du récepteur en format ECEF, donc en mètres depuis le centre de la Terre. Ainsi, une classe Python est automagiquement produite depuis cette description par :
dans le fichier monitor_pvt_pb2.py qui est exploitée, sous réserve d’avoir installé sous Debian GNU/Linux le paquet python3-protobuf, par le programme :
avec MonitorPvt le mot clé vu dans la définition du protocole au début de monitor_pvt.proto. En lançant ce programme Python, une fois que gnss-sdr a identifié une solution PVT acceptable, nous obtenons :
dont nous avons enlevé quelques décimales trop optimistes sur la position par souci de compacité. Nous nous rassurons que √(x2+y2+z2)=6367011 m ou 6367 km qui est bien le rayon de la Terre par une latitude de 47°N : notre récepteur se trouve bien à sa surface !
Rayon de la Terre
Historiquement, le mètre était défini comme la dix millionième partie du quart de la circonférence de la Terre, ou en d’autres termes le quarante millionième de la circonférence de la Terre, soit pour une Terre sphérique un rayon terrestre de 6366,2 m puisque la longueur de l’équateur était alors 40000 km. Cependant, la Terre n’est pas une sphère (sans pour autant être plate) et son rayon dépend de la latitude : en première approximation de sphère aplatie (ellipsoïde), le rayon à la latitude ϕ est d’après Wikipédia (démonstration à https://fr.planetcalc.com/7721/)
avec a=6378,14 km et b=6356,75 km (convention WGS84). Ainsi, R(47∘)=6366.7 km qui n’est pas si loin de la valeur observée, surtout si l’on considère que notre antenne est positionnée à une altitude de 357,379 m (solution PPP sur 24 h d’acquisition), et met en évidence le problème de la définition du géoïde de référence lors de la définition des altitudes, bien plus difficile que la latitude ou la longitude. Nous reviendrons sur ce point dans un article ultérieur.
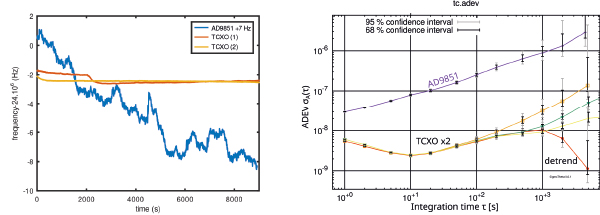
Plus intéressant cependant, le tracé de dt écart de temps GPS au temps local qui semble une droite, qu’un ajustement linéaire indique de pente 4·10−7 ou 400 ns/s. Cet écart, qui peut sembler important (Fig. 11, haut), n’est cependant que 0,4 ppm, tout à fait raisonnable pour un oscillateur à quartz faible coût qui n’a pas de prétention d’exactitude ou de stabilité meilleure que quelques ppm.
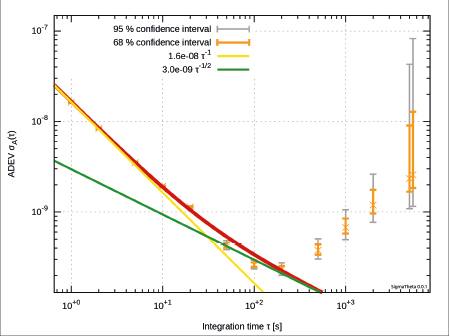
Si nous retranchons numériquement la dérive linéaire (écart de fréquence du quartz à la valeur nominale), il nous reste les coefficients polynomiaux d’ordres plus élevés, dont la variance d’Allan fournit la stabilité en fonction du temps d’intégration. Cette variance d’Allan, calculée avec ses barres d’erreur grâce à SigmaTheta de nos collègues du laboratoire du temps-fréquence de Besançon disponible à https://gitlab.com/sigmatheta1, nécessite de convertir les écarts entre date GPS et date de l’oscillateur local en différence d’écarts de temps, puis de calculer la variance d’Allan. En supposant les écarts de temps GPS à horloge locale stockés en ASCII dans le fichier df, alors X2Y df produit df.ykt différence des df successifs, et SigmaTheta df.ykt produit le graphique de la Fig. 12. Nous constatons que les courbes sur ce graphique présentent un minimum à 200 secondes, après quoi la variance remonte en l’absence de correction et à cause des fluctuations thermiques : il s’agit de la constante de temps avec laquelle programmer l’AD9851 pour tirer le meilleur parti de la stabilité court terme de l’oscillateur à quartz et la stabilité long terme de GPS.
Stabilité des oscillateurs
Tous les oscillateurs ne sont pas égaux devant le dieu de la stabilité. Nous avons initié cette étude en cadençant les MAX2771 avec un oscillateur à 24 MHz en format CMS qui ne délivre que quelques centaines de mV d’amplitude, suffisant pour le MAX2771, mais pas pour l’AD9851 qui attend une tension compatible TTL. Ressortant un antique oscillateur en boîtier métallique répondant à ces exigences (Fig. 8), force est de constater que quelques décennies de développement sur les oscillateurs ont considérablement amélioré leur stabilité, tel que l’illustre la figure ci-dessous à gauche. Un estimateur pour quantifier la stabilité d’une grandeur en fonction du temps d’intégration est la variance d’Allan, qui observe l’écart type de moyennes glissantes sur diverses durées τ fournies en abscisse. Un oscillateur qui dérive verra toujours sa variance d’Allan augmenter puisque, quel que soit le temps d’intégration, les mesures pour de grands τ seront loin de la valeur moyenne. Au contraire, un oscillateur stable qui fluctue autour d’une valeur moyenne verra sa variance d’Allan décroître puisque moyenner réduit le bruit. De très nombreuses études analysent la nature du bruit en fonction de la pente à laquelle la variance d’Allan croît ou décroît et la cause physique associée à ces bruits. Le calcul de variance d’Allan est loin d’être trivial, et plutôt qu’utiliser les codes Python d’allantools d’Anders Wallin et ses collègues à https://github.com/aewallin/allantools, nous nous appuyons sur la suite de logiciels bisontine à https://gitlab.com/sigmatheta1/ pour tracer les courbes présentées dans cet article (figure ci-dessous, droite).
Nous constatons que retrancher la tendance linéaire (detrend) n’impacte que sur le comportement long terme, mais que le comportement court terme est indépendant de cette tendance lente. Notez que pour atteindre ce résultat, il faut absolument sauver les données prétraitées par GNU Octave sous forme de save -text qui conserve toutes les décimales, puisque la notation scientifique de save -ascii ne conserve que 6 décimales, insuffisantes pour étudier des stabilités relatives de quelque 10−8 à la seconde. La courbe notée « AD9851 » réfère à l’oscillateur métallique visible à droite de la Fig. 8, tandis que « TCXOx2 » réfère aux deux mesures de l’oscillateur CMS dont nous avons équipé nos cartes de développement pour MAX2771, référence Epson TG2520SMN 24.0000M-MCGNNM3.
Sachant que nous obtenons une estimation de l’erreur de temps chaque seconde et que la constante de temps optimale est de 200 s, nous serions tentés de ne traiter qu’un point tous les 200, ce qui serait évidemment stupide en se privant de la capacité de moyenner 200 observations successives avant d’appliquer une correction. Un filtre récursif de réponse impulsionnelle infinie de la forme yn+1=a·xn+b·yn, donc une nouvelle sortie comme somme pondérée des anciennes entrées xn et sorties yn, peut avoir diverses formes en fonction des coefficients a et b. Ainsi, https://tomroelandts.com/articles/low-pass-single-pole-iir-filter enseigne qu’un filtre de la forme :
quand l’opérateur += existe (prendre l’ancienne valeur de la variable et lui assigner la somme avec la différence entre la nouvelle entrée et son ancienne valeur, pondérée du coefficient c), alors la constante de temps τ est déterminée par d=1−c tel que τ=−1/ln(d) ou d=exp(−1/τ). Si τ=200 s, alors d=0,995 et c=5·10−3.
Puisque nous avons un processus en Python séparé de l’acquisition et traitement des données capable de mesurer les grandeurs que sont l’écart de temps et de fréquence issus de gnss-sdr, et par ailleurs sommes capables en Python de programmer l’AD9851 en émettant des Vendor Requests au FX2LP, il ne reste plus qu’à insérer la loi de commande que nous venons de déterminer pour corriger périodiquement l’oscillateur et l’amener à sa valeur nominale visant à corriger le biais de fréquence (Fig. 13).
Au cours de ces mesures prolongées, nous avons découvert une anomalie sur la datation extraite des messages de navigation GPS chaque samedi soir : il s’agit de la fin de la semaine GPS [10] et le passage à la nouvelle semaine, transition que gnss-sdr ne semble pas gérer correctement. Carles Fernández-Prades, auteur de gnss-sdr, a noté ce dysfonctionnement comme un bug dans le rapport d’erreur de GitHub à https://github.com/gnss-sdr/gnss-sdr/issues/787, mais le solveur PVT de gnss-sdr est un morceau complexe de logiciel qui ne sera certainement pas simple à corriger. Par ailleurs, gnss-sdr est censé fournir dans la variable TOW (Time of Week), en millisecondes, le numéro du symbole pour lequel le retard a été observé. Les symboles des messages de navigation de GPS L1 C/A se succèdent toutes les 20 ms et le retard user_clk_offset n’est compris qu’entre 0 et 20 ms : il faut donc connaître à quel symbole correspond le retard pour lever l’ambiguïté modulo 20 ms. Avec un temps qui dérive au rythme de 400 ns chaque seconde (0,4 ppm), nous nous attendons à changer d’indice de symbole toutes les 20·10−3/400·10−9=50000 s ou environ 14 h, mais il n’en est rien. En effet, lors d’acquisitions bien plus longues que 14 h, l’indice du symbole reste obstinément le même. Ce comportement ne semble pas normal.
3.2 Asservissement de la fréquence
Notre objectif est bien de produire un vrai oscillateur stabilisé (et sécurisé par la détection potentielle de leurrage), et donc de commander l’AD9851 cadençant le MAX2771. Cette tâche apparemment triviale – retirer l’oscillateur 24 MHz pour le remplacer par la sortie de l’AD9851 – s’est avérée bien plus ardue que prévu, puisque le MAX2771 produisait bien les signaux d’horloge et IQ vers le FX2LP, mais aucune communication USB n’arrivait au PC. Après avoir exploré la puissance du signal de référence – la documentation technique du MAX2771 parle d’une sinusoïde 0,5 Vpp comme « reference input level » alors que l’AD9851 produit péniblement 0 dBm donc 0,6 Vpp, mais nous avons vérifié que le cadencement est fonctionnel avec −20 dBm – il s’avère que la solution tient en une subtile combinaison de démarrer l’AD9851 tôt dans la séquence d’initialisation du FX2LP et de filtrer les signaux parasites qui nous ont justement permis de vérifier le bon fonctionnement de l’AD9851 avec la PlutoSDR. Le moment de démarrage de l’oscillateur cadençant le MAX2771 reste un mystère. Par contre pour ce qui est de filtrer, plutôt que se battre avec des inductances et condensateurs qui ne se comportent jamais comme prévu aux fréquences radio, nous allons détourner un résonateur à quartz pour nous en servir non pas comme d’un élément sélectif en fréquence dans une boucle d’oscillation comme il est d’habitude utilisé, mais comme filtre en transmission. Il se trouve qu’un résonateur à 24 MHz traînait dans nos réserves de composants, permettant de facilement tester ce principe (Fig. 14).
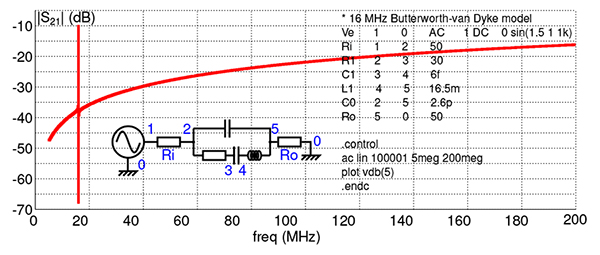
Le résonateur à onde de volume est une lame de quartz plaquée sur ses deux faces planes par des électrodes : le potentiel électrique appliqué au dipôle se traduit par un déplacement dans la maille cristalline du quartz par effet piézoélectrique inverse, et ce déplacement se traduit par une contrainte dans le matériau qui génère des charges et donc un courant par effet piézoélectrique direct. Ainsi du point de vue de l’électronicien, un résonateur à quartz est un dipôle présentant une résonance d’autant plus fine que les pertes dans le matériau sont faibles, à une fréquence de résonance déterminée par l’épaisseur de la lame de quartz. Ces deux électrodes de part et d’autre du diélectrique qu’est le quartz forment un condensateur parasite en parallèle de la résonance mécanique qui peut se modéliser, comme toute résonance, par un circuit RLC série. Ce condensateur parasite explique que la capacité de filtrage du résonateur se dégrade à haute fréquence (Fig. 15), mais nous avons constaté que la réjection des composantes spectrales qui perturbent le MAX2771 est suffisante pour permettre son bon fonctionnement.
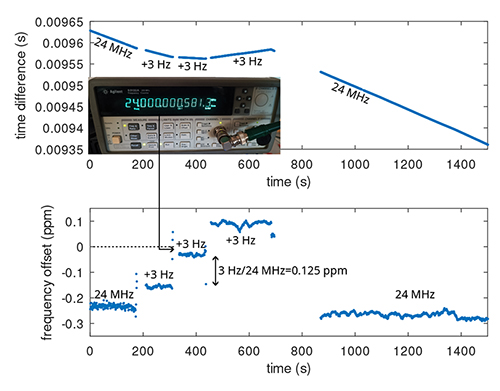
Une fois que le MAX2771 accepte d’être cadencé par l’AD9851 et communique ses mesures, nous assemblons l’ensemble du système avec l’acquisition des données et leur transmission par USB pour être réceptionnées par app/pocket_dump/pocket_dump de PocketSDR vers la FIFO, GNU Radio qui effectue la transposition de fréquence pour retirer la fréquence intermédiaire de 2 MHz et décimer pour produire 2 MS/s sur son port ZeroMQ Publish, et gnss-sdr qui produit la solution en position et en temps transmise sur port UDP et lue par le script Python implémentant Protobuf. Les informations d’écart de temps et de fréquence entre l’oscillateur local – donc cette fois la sortie de l’AD9851 – et les horloges GPS sont lues : dans un premier temps, nous reprogrammons l’AD9851 afin de vérifier son impact sur les informations issues de gnss-sdr. Déjà, il faut éviter de modifier la fréquence trop brutalement, sinon les boucles d’asservissement de gnss-sdr décrochent et le temps de retrouver les signaux des satellites peut être long. Dans l’exemple de la Fig. 16, nous avons commencé avec une fréquence nominale de 24 MHz produite par l’AD9851 – qui n’est bien entendu pas 24 MHz exacts puisque l’AD9851 est cadencé par un oscillateur à quartz lui-même inexact – puis nous incrémentons de 3 Hz toutes les 200 secondes environ. Nous constatons (Fig. 16, haut) que gnss-sdr détecte bien les variations de fréquence de cadencement des MAX2771, visibles sous la forme de la pente de l’écart de temps au 1-PPS GPS (1-impulsion par seconde représentant le temps GPS), et que l’ajout de 6 Hz a presque annulé la dérive de temps. Dans la seconde moitié de l’expérience, après la date 800 s, nous avons brutalement retranché 9 Hz pour revenir à 24 MHz nominaux, illustrant le décrochage des boucles d’asservissement et le temps nécessaire à gnss-sdr pour retrouver les informations de la constellation GPS. En bas, l’écart de fréquence à la valeur nominale suit la même tendance, puisque la fréquence est la dérivée de la phase et le temps s’apparente à une phase, donc chaque pente sur la dérive du temps (haut) se traduit par des paliers à des niveaux différents d’écart de fréquence. GPS étant cadencé par des horloges atomiques, nous pouvons faire confiance que l’annulation de cet écart de fréquence permet d’obtenir un signal à une fréquence exacte cette fois, tel que nous le constatons en mesurant la fréquence de sortie du DDS sur un compteur référencé sur un maser à hydrogène considéré comme exact (Fig. 16, insert).
Le code final de commande se résume en une initialisation des divers modules Python pour les communications avec les périphériques et des constantes d’asservissements :
suivie de l’ouverture de l’interface de communication par USB et UDP :
La boucle d’asservissement à proprement parler est un contrôleur proportionnel intégral classique, que nous prendrons simplement soin de réinitialiser après une absence prolongée de messages de gnss-sdr qui aura permis à l’oscillateur libre de trop dériver (variable m) :
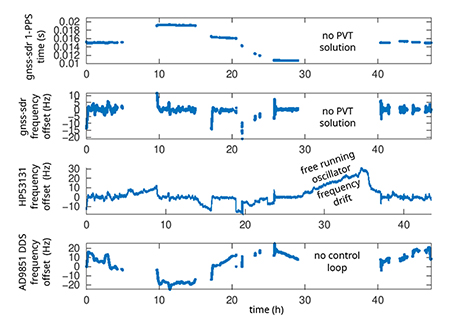
Le résultat sur deux jours est présenté en Fig. 17 sur lequel nous constatons dans un premier temps les amnésies de gnss-sdr qui peine parfois à trouver une solution (trois grandes absences autour de 7 h, 15 h et de 30 à 40 h) : il s’agit des trous dans les deux courbes du haut pendant lesquels gnss-sdr n’a pas d’information à fournir. Pendant ce temps, l’oscillateur qui cadence le MAX2771 est libre de dériver à sa guise, tel que nous l’observons sur la 3e courbe à partir du haut, acquise par un compteur de fréquence externe HP53131A. Lorsque la solution est retrouvée, la commande ramène bien l’oscillateur sur la valeur nominale de fréquence de 24 MHz. Finalement en bas, la fréquence de commande de l’AD9851 qui vise à absorber les fluctuations de l’environnement en maintenant sa sortie sur la valeur nominale de 24 MHz par rapport au signal GPS : ici encore, en l’absence de mesure par gnss-sdr, aucune commande n’est produite et la courbe présente des trous pendant ces phases d’amnésie.
Ce problème de dérive de l’oscillateur en l’absence de signal de référence sur lequel s’asservir est un problème classique nommé holdover que tout relais de téléphonie mobile (Fig. 18), par exemple, doit pouvoir gérer, justifiant de « bons » oscillateurs à côté du récepteur GPS équipant ces stations de base. Par ailleurs, nous constatons que notre correction ne mesure et n’agit que sur la fréquence et laisse donc une erreur statique sur le temps qu’il faudra encore corriger afin que les paliers visibles sur la courbe du haut de Fig. 17 soient alignés sur la même valeur de consigne. C’est ce point que nous allons maintenant aborder.
3.3 Asservissement du temps (de la phase)
Nous avons réussi à corriger la fréquence de l’oscillateur à quartz lorsque gnss-sdr a identifié les signaux de la constellation GPS, et rattraper la dérive entre temps. Cela répond déjà à un certain nombre de besoins pour les récepteurs radiofréquences qui ne s’intéressent qu’à la fréquence de l’oscillateur local et pas au temps. Cependant, nombre d’applications s’intéressent non seulement à syntoniser les oscillateurs (même fréquence), mais aussi les synchroniser (même phase). Phase ϕ et temps τ sont intimement liés au travers de la fréquence de la porteuse ν du signal radiofréquence puisque ϕ=2πντ, mais surtout la fréquence est donc la dérivée de la phase ν=1/(2π)·dϕ/dt. L’asservissement est donc passablement plus compliqué puisque cette fois le système ne commande plus une fréquence (DDS) pour corriger une fréquence – avec donc un gain unitaire entre les deux grandeurs – mais la phase (le temps) : ainsi, l’intégrale de la fréquence accumule les erreurs. Idéalement, nous aurions deux commandes, une de retard pour corriger la phase et une de fréquence, mais ce n’est pas le cas, donc nous devons compter sur l’unique degré de liberté qu’est la fréquence qui commande le MAX2771, issue de l’AD9851 pour d’abord amener la phase (le temps) sur sa valeur de consigne, puis l’empêcher de dériver en maintenant l’oscillateur sur sa fréquence nominale par rapport à la fréquence fournie par GPS, et le tout avec un oscillateur à quartz qui dérive avec les conditions environnementales.
La limitation de ne commander que la fréquence du DDS se heurte à une contrainte additionnelle : il ne faut pas trop s’éloigner de la valeur nominale des 24 MHz sous peine de ne plus permettre à gnss-sdr de compenser le décalage Doppler. Bien que de valeur nominale ± 5 kHz, la configuration de gnss-sdr permet d’étendre la gamme de recherche de l’écart de fréquence pour compenser l’inexactitude de l’oscillateur local, mais plus nous étendons cette gamme et plus les ressources de calcul sont importantes. Enfin, il ne faut pas trop perturber l’oscillateur qui cadence le MAX2771 sous peine de faire décrocher les boucles d’asservissements en fréquence et en retard de gnss-sdr qui devra donc retrouver sa solution (acquisition) avant de propager à nouveau une solution (tracking). De ces deux conditions, nous déduisons une phase d’initialisation en boucle ouverte visant à atteindre grossièrement le point de consigne, comme suit :
- En configurant l’oscillateur à 24 MHz nominaux, sans en connaître l’exactitude, nous laissons gnss-sdr trouver le signal GPS en espérant que l’oscillateur local n’est pas « trop faux » pour que le signal décalé du Doppler lié aux mouvements du satellite ainsi que le décalage de l’oscillateur reste dans la gamme que nous avons définie dans Acquisition_1C.doppler_max du fichier de configuration de gnss-sdr.
- Une fois la constellation acquise, gnss-sdr fournit d’une part une estimate de l’écart de fréquence entre l’oscillateur local et la fréquence exacte attendue, et d’autre part l’écart de temps entre l’horloge locale et le temps GPS. En fonction du signe de cet écart de temps par rapport à la consigne du milieu d’un symbole de durée 20 ms, donc consigne à 10 ms, nous décalons la fréquence de l’oscillateur local de +300 Hz si le retard est inférieur à 10 ms, ou de −300 Hz par rapport aux 24 MHz nominaux si le retard est supérieur. Ce faisant, nous laissons volontairement le temps de l’horloge locale dériver par rapport au temps GPS au rythme de 300/24·106=12,5 µs/s. Ainsi, il faudra au plus 10·10−3/12,5·10−6=800 s pour atteindre la valeur de consigne dans le cas le plus défavorable où le point initial était à 10 ms de la consigne.
- Cependant, en décalant l’oscillateur à 24 MHz de 300 Hz, cela revient à décaler à la porteuse L1 GPS de 1575,42 MHz de 300/24× 1575,42≃ 19 kHz, donc bien plus que les ± 5 kHz introduits par le mouvement des satellites. Il faut donc bien penser à ajuster Acquisition_1C.doppler_max à plus de 25 kHz pour retrouver les satellites lors de la dérive de l’horloge locale.
- Une fois la consigne atteinte, l’oscillateur local est reprogrammé aux 24 MHz nominaux que nous savons atteindre en ayant reçu l’information de gnss-sdr de l’écart de l’oscillateur local à la fréquence nominale, incluant les ± 300 Hz que nous avons introduits. On notera que ce faisant, nous ennuyons pour la seconde fois gnss-sdr qui déteste ces changements soudains de fréquence de cadencement du convertisseur analogique/numérique qui fait décrocher ses boucles à verrouillage de fréquence et de phase. Le mieux que nous puissions espérer est que la constellation est suffisamment favorable pour que gnss-sdr retrouve tous les satellites avant que le temps n’ait trop dérivé, d’autant plus que l’oscillateur étant à sa valeur exacte, la dérive a été réduite au minimum en boucle ouverte.
- Une fois la constellation retrouvée, sachant que le retard est proche de sa valeur de consigne, nous engageons l’asservissement PI avec des gains très importants : en effet par rapport à l’asservissement sur la fréquence, puisque temps t et fréquence f sont reliés par f=1/t donc df/f=−dt/t et f=24·106 tandis que l’intervalle de temps entre deux mesures de retard est t=1 s donc df=dt·24·106 qui ferait décrocher les boucles d’asservissement si nous tentions d’appliquer de tels gains lors de la phase d’initialisation, qu’il faut de toute façon saturer pour ne pas perdre les signaux des satellites. Nous avons constaté que limiter le saut de fréquence à df=0,2 Hz chaque seconde permet à gnss-sdr de maintenir les boucles d’asservissements sans décrocher de la phase et la fréquence des signaux, et permet tout de même d’incrémenter la fréquence de l’oscillateur local de 2 Hz en 10 s donc de rattraper les dérives de l’environnement.
Tout ça, c’est la théorie...
Dans la pratique, nous avons implémenté la loi de commande cn par son équation de récurrence qui partant de l’erreur à la date n à la consigne εn produit un terme proportionnel Kpεn et un terme intégral :
qui indique donc que cn+1−cn=Kp(εn+1−εn)+Kiεn+1 et alors que nous pensions nous affranchir du terme intégral puisque le système est lui-même intégrateur, nous constatons que si l’erreur n’évolue plus alors la consigne n’évolue plus en ne conservant que le terme proportionnel, mais sans garantie que l’erreur est annulée, simplement maintenue constante. Donc, même avec le comportement intégrateur du système, nous conservons le terme intégral pour annuler l’erreur statique.
Un des gros soucis que nous rencontrons, et qui devient d’autant plus dramatique que la phase accumule l’erreur pendant les phases de perte de signal GPS de holdover, est que gnss-sdr décide d’invalider les solutions PVT alors que plus de 4 satellites sont visibles. Cela est très ennuyeux, surtout que nous ne nous intéressons pas du tout à la position mais uniquement au temps, même si toutes ces grandeurs sont intimement imbriquées. La solution PVT produit deux informations que sont la dilution de la solution en position :
somme des variances des positions, et la dilution de la solution géométrique :
qui est la somme des variances en position ainsi qu’en temps. Nous avons utilisé la convention de la littérature de noter σt, mais on notera que par homogénéités des grandeurs, c’est en réalité c·t qui est exprimé avec c la vitesse de la lumière pour transformer le retard en distance. Ainsi, nous constatons évidemment que la fluctuation en temps σt2=GDOP2−PDOP2 qui s’appelle TDOP2, mais qui n’intéresse personne puisque tout le monde utilise GPS pour se positionner : cet estimateur n’est donc pas produit par gnss-sdr, mais il faut le calculer soi-même. Si nous visons un asservissement sur la centaine de nanosecondes (10−7 de stabilité relative), alors le TDOP de 3·108×10−7=30 reste acceptable même si c’est la limite que s’impose gnss-sdr sur GDOP pour invalider les solutions PVT dont nous constatons qu’en pratique, c’est souvent la position qui handicape le résultat. Le problème est connu puisque https://rtklibexplorer.wordpress.com/2019/05/18/a-few-simple-debugging-tips-for-rtklib/ indique « I have found that the chi square threshold can be too strict in some cases,so in the demo5 code I have changed the error to a warning ».
Conclusion
Nous avons conclu cette exploration de la programmation efficace du bus USB sous GNU/Linux avec le développement d’une carte dédiée à la réception de signaux de navigation par satellite en bande L, munie de plusieurs récepteurs synchrones permettant, par exemple, une mesure de direction d’arrivée du signal. Le bon fonctionnement du système a été démontré en décodant la position du récepteur.
Plus intéressant, l’erreur entre l’horloge locale et l’horloge distante a été mesurée puis corrigée, et ce, par une mesure long terme en temps réel en respectant les préceptes d’Unix, à savoir un outil efficace dédié à chaque opération. Pour ce faire, PocketSDR a acquis les échantillons, GNU Radio a lu sur une FIFO pour transposer la fréquence et émettre le résultat sur une socket ZeroMQ, afin que gnss-sdr puisse en décoder le contenu et diffuser le résultat de ses calculs sur une socket UDP. On notera que cette approche, ici mise en œuvre sur un unique ordinateur, est parfaitement appropriée pour être distribuée sur plusieurs plateformes de calcul, sous réserve d’un débit de communication suffisant. Sans forcément le savoir, la synchronisation du temps par signaux GNSS est omniprésente (Fig. 18), et les enjeux sont tels que fournir un signal sécurisé, ou tout au moins couper ce signal si une source de leurrage est identifiée, a été abordé avec l’analyse de direction d’arrivée du signal sur deux antennes spatialement séparées.
Toutes nos discussions ont porté sur GPS L1 C/A, car c’est le seul signal pour lequel nous avons la puissance de calcul nécessaire pour traiter en temps réel par gnss-sdr, condition nécessaire à la mise en place des asservissements. Nous avons validé le bon fonctionnement du décodage de L5, E1 ou E5 en post-traitement, mais le temps de calcul est là largement plus long que le temps d’acquisition, d’une part du fait du débit de données plus important, et d’autre part de complexités algorithmiques beaucoup plus gourmandes en ressources de calcul.
L’affirmation d’un récepteur générique en bande L est quelque peu abusive puisque les oscillateurs commandés en tension (VCO) qui équipent chaque MAX2771 ne peuvent couvrir l’intégralité de la bande 1–2 GHz, mais avec l’ajout d’un premier oscillateur local et mélangeur pour amener le signal d’intérêt dans les fréquences accessibles aux VCO, les 44 MS/s de bande passante de mesure restent très attractifs. Mentionnons en ce sens Inmarsat qui communique avec les terminaux au sol entre 1525 et 1646,5 MHz, tandis que les téléphones par satellite Thuraya (projet OsmocomGMR) exploitent les fréquences entre 1525 et 1661 MHz, toutes accessibles, au moins en partie, au MAX2771. Cependant, les liaisons des satellites météorologiques communiquant par HRPT à 1700 MHz avec une bande passante de 3 MHz sont au-delà des capacités du MAX2771.
Finalement, ces circuits sont l’opportunité de découvrir les spécificités du monde fascinant des convertisseurs analogiques/numériques de faible résolution mais rapides, aux propriétés statistiques quelque peu différentes des convertisseurs à haute résolution. En effet, [11] répète plusieurs fois « when the quantization grain size q is fine enough, (i. e., equal to one standard deviation or less), ... » comme hypothèse à ses analyses des propriétés statistiques de la quantification des signaux échantillonnés, p. ex. « ... the PDF, CF, and moments of the quantization noise are almost indistinguishable from those of uniformly distributed noise. To see differences from the uniform case, the quantization must be extremely rough. » Et donc probablement invalides pour les convertisseurs codés sur 2 ou 3 bits seulement, puisque la quantification grossière dont il est fait mention est exactement le cas exposé ici.
Les codes sources, fichiers de configuration et plans des circuits imprimés sont disponibles à https://github.com/jmfriedt/max2771_fx2lp.
Remerciements
Claudio Calosso, du laboratoire de métrologie italien INRIM (Turin), a présenté la conception du filtre passe-bas sous forme de filtre à réponse impulsionnelle infinie (IIR) et proposé diverses analyses sur les données collectées au cours de cette étude. Tous les ouvrages de la bibliographie ont été obtenus sur Library Genesis.
Ces développements ont été menés dans le cadre du Master ELISE de l’Université de Franche-Comté à Besançon pour l’enseignement de l’électronique embarquée au moyen de logiciels libres (http://electronique.univ-fcomte.fr/elise.php).
Références
[1] J.-M Friedt, « Programmation USB sous GNU/Linux : application du FX2LP pour un récepteur de radio logicielle dédié aux signaux de navigation par satellite (1/2) », Hackable 57 pp. 88–130 (nov.-déc. 2024) - https://connect.ed-diamond.com/hackable/hk-057/programmation-usb-sous-gnu-linux-application-du-fx2lp-pour-un-recepteur-de-radio-logicielle-dedie-aux-signaux-de-navigation-par-satellite-1-2
[2] K. Borre, M. D.M. Akos, N. Bertelsen, P. Rinder, S.H. Jensen, A software-defined GPS and Galileo receiver: a single-frequency approach, Springer (2007)
[3] K. Borre, I. Fernández-Hernández, J.A. López-Salcedo, M.Z.H. Bhuiyan, GNSS software receivers, Cambridge University Press (2023)
[4] J.-M. Friedt, W. Feng, « Anti-leurrage et anti-brouillage de GPS par réseau d’antennes », MISC 110 (juillet-août 2020) - https://connect.ed-diamond.com/MISC/misc-110/anti-leurrage-et-anti-brouillage-de-gps-par-reseau-d-antennes
[5] J.- M Friedt, « La peinture sur spectre radiofréquence, et l’effet capture de la modulation en fréquence – ou pourquoi les avions communiquent encore en AM », GNU/Linux Magazine France 216 (juin 2018) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-216/la-peinture-sur-spectre-radiofrequence-et-l-effet-capture-de-la-modulation-en-frequence-ou-pourquoi-les-avions-communiquent-encore-en-am
[6] Tom Rondeau, GNU Radio for Exploring Signals, FOSDEM (2016) à https://archive.fosdem.org/2016/schedule/event/gnu_radio/
[7] D.S. De Lorenzo & al. GPS receiver architecture effects on controlled reception pattern antennas for JPALS, Proc. 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2004) 2010–2020 discute de l’annulation de leurrage et brouillage avec des récepteurs munis de convertisseurs analogiques/numériques à peu de bits, rendant difficile l’extraction du vrai signal quand le signal interférant est puissant.
[8] D. Rabus & al., Generating A timing information (1-PPS) from A software defined radio decoding of GPS signals, Proc. joint EFTF/IFCS (2021)
[9] J.-M Friedt, « Échanges de données pour un traitement distribué : communication par réseau ou entre langages », GNU/Linux Magazine France 267 (janv.-févr. 2024) - https://connect.ed-diamond.com/gnu-linux-magazine/glmf-267/echanges-de-donnees-pour-un-traitement-distribue-communication-par-reseau-ou-entre-langages
[10] Il se trouve que la semaine GPS a commencé dans la nuit du 5 au 6 janvier 1980, entre un samedi soir et un dimanche matin, d’après https://www.cnmoc.usff.navy.mil/Our-Commands/United-States-Naval-Observatory/Precise-Time-Department/Global-Positioning-System/GPS-Information-SA-DGPS-Leap-Seconds-etc/GPS-Week-Number-Rollover/. Le problème de gnss-sdr est plus ennuyeux que les récepteurs qui ne savent pas gérer le fait que la semaine GPS n’est codée que sur 10 bits et se réinitialisent tous les 20 ans environ.
[11] B. Widrow, I. Kollár, Quantization Noise – Roundoff Error in Digital Computation, Cambridge University Press (2008)
Correctif : couplage entre fils adjacents
Nous avions conclu l’article précédent sur le prototypage avec le FX2LP pour contrôler la carte d’évaluation du MAX2771 par une estimation du couplage, par analyseur de réseau, de fils adjacents portant des signaux rapides (quelques MHz), en argumentant de la nécessité de router un circuit imprimé pour éviter ces couplages induisant les corruptions de données. Pour rappel, un analyseur de réseau émet un signal à une fréquence et observe, sous forme du ratio de l’amplitude du signal reçu à l’amplitude du signal émis, la tension réfléchie et transmise. Les indications sous forme de coefficients de diffraction (scattering parameters) notés Sij sont fournies en décibels. Comme le décibel est un rapport de puissances, alors que la mesure de paramètres S est un rapport de tensions, le passage de l’un à l’autre s’obtient par SdB=20log10(Sij). Dans notre analyse précédente, nous avons converti les mesures en dB en rapport d’amplitudes de façon erronée, tel que nous l’a fait remarquer un lecteur, Yves Barbin, qui est remercié pour ses corrections.
Nous reprenons donc l’illustration du coupage entre fils adjacents, pour corriger les valeurs numériques fournies précédemment et compléter les mesures par analyseur de réseau par une mesure temporelle par oscilloscope. Dans cette démonstration, un générateur de signal carré à 8 MHz polarise un fil de 21 cm relié à la masse par une résistance de 50 Ω, tandis qu’un second fil parallèle de la même longueur relie l’entrée d’un oscilloscope radiofréquence (impédance 50 Ω) à la masse via une résistance de 50 Ω, les deux fils étant parallèles et séparés de quelques millimètres.
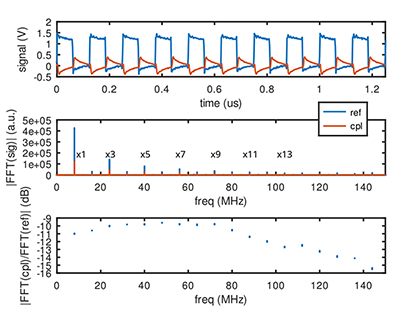
En haut de ce graphique, le signal émis en bleu, et le signal induit (couplé) en rouge, dont l’amplitude significative est la source de bits erronés transmis. Au milieu, la transformée de Fourier du signal émis (bleu) et induit (rouge), avec majoritairement les harmoniques impaires dont l’amplitude (et non la puissance comme nous l’avions indiqué) décroît comme le numéro de l’harmonique (série de Fourier du créneau). En bas, le ratio de l’amplitude du signal induit au signal émis (Vo/Vi), converti en décibels par 20log10(·) pour tenir compte du carré reliant amplitude et puissance.
Dans le tableau de l’article précédent, il fallait donc lire, en convertissant dB en échelle linéaire de ratio de tensions par 10 dB/20 :
08 MHz : -24,9 dB=0,06
12 MHz : -21,7 dB=0,08
24 MHz : -16,4 dB=0,15
48 MHz : -12,1 dB=0,25
en bien meilleur accord avec les observations dans le domaine temporel ci-dessus que celles déduites auparavant des mesures dans le domaine spectral.