Nous déployons notre propre serveur NTRIP fournissant les informations de référence pour le positionnement centimétrique par trilatération de signaux de navigation par satellite, avant de nous interroger sur la définition de l’altitude et en particulier de « au-dessus du niveau moyen de la mer ».
Nous avions présenté [1] comment utiliser les services de Centipède ou d’IGN pour compenser les retards de propagation des ondes électromagnétiques utilisées pour le positionnement par trilatération de signaux de navigation par satellite, et en particulier en utilisant la bibliothèque RTKLib et le récepteur u-blox ZED-F9P comme source de données.
Ces solutions étaient sympathiques tant que nous nous limitions au territoire français, mais que faire en zone qui n’est pas couverte par Centipède/IGN au cours d’une campagne temporaire de mesure ? En effet, une station de référence provisoire n’est pas admise (à juste titre) par Centipède qui exige que les stations de référence soient fonctionnelles 365 jours/an. Ainsi, notre objectif ici est de :
- fournir un service de correction de signaux GNSS (Global Navigation Satellite Systems) autonome ;
- permettre une mesure centimétrique sur ordinateur, mais aussi sur téléphone mobile récent sous Android, et en particulier en exploitant la capacité du ZED-F9P à produire le signal corrigé et pas uniquement les signaux bruts d’observation en vue d’alimenter RTKLib.
Ces expériences amèneront une nouvelle surprise, à savoir définir ce qu’est le concept d’altitude, et notamment par rapport à quelle référence. En effet, alors que les systèmes de gestion d’informations spatialisées tels que QGIS savent très bien gérer les transformations de coordonnées entre projections sphériques et planes, la troisième dimension n’est qu’un attribut arbitraire qui n’est pas manipulé par ces transformations. L’altitude n’est pas un problème qui semble beaucoup intéresser les géographes puisqu’il n’en est jamais fait mention dans [2] (Fig. 1). Le problème est significatif du point de vue de l’ingénierie cependant, tel que le rappelle [3], p.169, en mentionnant « On se souvient que Picard, chargé de l’alimentation en eau du château de Versailles, avait choisi comme origine le rez-de-chaussée du château. Cassini avait adopté le niveau de la mer dans la région de Perpignan. Le choix de la Méditerranée où les marées sont très faibles est assez logique. Cela n’empêchera pas l’ingénieur Collin de proposer le point situé à 100 mètres en dessous de la cour de l’Observatoire de Paris. [...] Il faut attendre une décision ministérielle de 1860 fixant l’origine des altitudes au niveau moyen de la Méditerranée à Marseille, défini par le trait 0,40 mètre de l’échelle de marée de Fort Saint-Jean, pour qu’enfin le réseau français de nivellement soit rattaché à une origine unique. »
Le problème sera d’autant plus ardu que nous prétendrons mesurer une altitude avec une précision et une exactitude centimétrique...
1. Casters NTRIP
Le principe de la mesure différentielle, et en particulier RTK (Real Time Kinematic), est de supposer qu’une station de référence est placée à une position connue. Si l’information brute venant des satellites est acquise – les pseudoranges comme temps de vol des ondes électromagnétiques des satellites au récepteur – et que les positions des satellites et du récepteur sont connues, alors il est possible d’en déduire les retards de propagation introduits par l’ionosphère et la troposphère [4]. Sous réserve que le récepteur mobile, dont la solution doit être corrigée, soit « proche » de la station de référence, alors ces mêmes corrections sont valables et peuvent être compensées lors de la recherche de la solution de sa position.
Les transparents de [5] montrent bien comment d’une part la qualité de la correction se dégrade avec une longueur de plus en plus importante entre la station de référence et la station de mesure, pour devenir inopérante au-delà de quelques dizaines de kilomètres [5], page 26, aussi mentionné [4], page 12. Par ailleurs, alors que l’utilisation de la corrélation sur le code du signal de navigation permet une précision métrique grâce au bénéfice du rapport signal à bruit de la compression d’impulsion qui ramène les 300 mètres de résolution du code qui défile chaque microseconde, il faut absolument exploiter la phase de la porteuse pour prétendre atteindre le centimètre. En effet, la longueur d’onde d’un signal de navigation est de l’ordre de 300/1575,42=19 cm et cette mesure permet de prétendre, après correction des retards corrélés entre référence et mesure, d’atteindre une position avec une résolution centimétrique.
Un protocole réduisant la taille des messages pour informer un récepteur GNSS des corrections se nomme RTCM pour Radio Technical Commission for Maritime services (puisque comme pour les trames NMEA, acronyme de National Marine Electronics Association, ce sont avant tout les marins qui étaient intéressés de se positionner), et la diffusion de ces trames sur réseau informatique suit la norme NTRIP pour Networked Transport of RTCM via Internet Protocol. Dans une architecture NTRIP, qui n’est pas sans rappeler MQTT, un serveur centralise les informations des stations de base qui fournissent les corrections, et accepte les connexions des récepteurs mobiles (rovers) qui ont besoin de ces corrections. Cette architecture en étoile centralisée sur un nœud vulnérable qui concentre les échanges semble antagoniste aux principes de distribution qui régissent Internet, mais c’est ainsi ! Si nous voulons connecter une station de base de position connue qui distribue les corrections aux pseudoranges observés vers des récepteurs mobiles qui veulent se positionner au centimètre près, il faut un serveur NTRIP, ou dans le jargon un NTRIP caster.
Le serveur http://caster.centipede.fr fournit un tel service, mais uniquement si la station est pérenne et validée par ses administrateurs. En l’absence de garantie de ce service, ou parce que notre station de référence se trouve derrière un firewall qui bloque le port 2101 utilisé par défaut, il nous faut fournir notre propre service. Sans réfléchir, une solution gratuite mais propriétaire se trouve dans yccaster de https://yccaster.com/. C’est la solution que nous avons adoptée dans l’urgence en allant expérimenter au Spitzberg pour positionner des balises sur un glacier dont nous voulons cartographier le champ de déplacement. Ce n’est pas malin, car pour autant que nous le sachions, nous avons peut-être participé à un botnet en installant un serveur dont nous n’avons pas consulté les sources, mais la précipitation est toujours source d’imprudence. La solution libre sera décrite plus bas.
Le programme yccaster, fourni comme une grosse archive, s’exécute sans surprise sur un système Debian/GNU Linux stable, se place dans /var/caster et se configure par un fichier YAML dans /var/caster/caster.yml auquel la seule modification que nous apportons est :
pour lancer le service sur le port 443 à l’écoute de toute requête entrante, le port 2101 étant bloqué du côté de la station de base par les administrateurs de l’Alfred Wegner Institute (AWI) allemand qui gère le réseau informatique de la station Rabot à Ny-Ålesund.
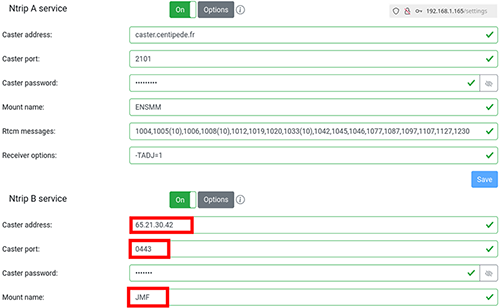
La station de base est formée d’un récepteur u-blox ZED-F9P connecté à une Raspberry Pi (3) exécutant l’image fournie par Centipède (https://docs.centipede.fr/docs/base/Installation.html) puisque ce projet autorise à configurer sa station de base pour émettre des trames de correction RTCM vers tout serveur NTRIP et pas uniquement caster.centipede.fr (Fig. 2), voire de dupliquer les échanges en proposant deux configurations de casters NTRIP. Côté serveur, l’exploitation du port 443 interdit bien entendu qu’un serveur web (Apache) s’exécute en même temps. Le mot de passe n’est pas pris en compte et n’importe quelle chaîne de caractères (non vide) conviendra.
Cette solution est fonctionnelle, mais ne respecte pas le précepte de n’utiliser que des logiciels libres dont nous pouvons consulter les sources pour en valider la sécurité et en corriger les dysfonctionnements. Une alternative à yccaster est le vénérable https://github.com/goblimey/ntripcaster et en particulier https://github.com/goblimey/ntripcaster/tree/master/ntripcaster qui, bien qu’écrit en 2008, fournit un service similaire. Ce programme fournit les services de NTRIP1 (et non de NTRIP2 [6]), largement suffisants pour nos objectifs. Nous n’avons pas réellement cherché à comprendre comment fonctionne son système de configuration puisque l’entête des paramètres par défaut est limpide avec src/ntripcaster.h qui contient :
donc le port par défaut du serveur (tant pour les services de corrections que pour les récepteurs mobiles) et un mot de passe à fournir dans l’interface de la station de base Centipède pour que la connexion soit effective. Contrairement à yccaster, ce programme ntripcaster veut absolument que la station de référence s’authentifie avec DEFAULT_ENCODER_PASSWORD, tandis que le mot de passe sera omis pour les stations mobiles. Si nous conservons les paramètres par défaut, alors la station Centipède se configure avec :
dont les deux dernières lignes restent inchangées par rapport à leur valeur par défaut, et nous validons que la station de base communique ses corrections au serveur NTRIP qui les renvoie aux clients au moyen du programme fourni par RTKLib exécuté comme :
que le lecteur pourra reproduire sur les services de Centipède avec :
pour permettre un post-traitement en cas de perte de connexion internet sur le terrain.
Si tout se passe bien, cette commande affichera des séquences binaires que sont les messages de correction RTCM, qui sont utilisés pour corriger la position de l’antenne mobile (rover) recevant les signaux bruts (UBX -> RAWX) d’un ZED-F9P connecté par USB au PC qui exécute depuis RTKLib :
Par ailleurs, nous pouvons nous convaincre que nous recevons des flux de données du port série /dev/ttyACM0 auquel est connecté le récepteur ZED-F9P ainsi que depuis le serveur NTRIP par connexion internet au moyen de la commande stream de rtkrcv :
et finalement la solution fournie par RTKLib, de type FIX indiquant que la solution RTK a été obtenue avec une résolution centimétrique :
Pour atteindre ces résultats, nous avons exploité le fichier de configuration RTKlib_NTRIP.conf qui contient comme seules lignes importantes :
Le fichier sortie.txt qui contient la solution indique lui aussi, dans un format un peu différent de rtkrcv qui fournissait des latitudes/longitudes/altitude, une solution de la forme :
donc une solution FIX (type 1 en 6e colonne) de résolution centimétrique (colonnes 8 à 10) pour une position par rapport au centre de la Terre de x=4313726.9632 m, y=452872.5077 m et z=4661056.3621 en exploitant la position de 28 satellites (champ ns) qui transmettent leur position au travers de codes pseudo-aléatoires orthogonaux. Nous reviendrons plus bas sur ce référentiel de coordonnées cartésien (x,y,z) nommé ECEF (section 3) qui a été choisi en fournissant le Fmt=xyz dans la configuration de RTKLib. Cette origine pour le calcul semble naturelle, puisque les satellites de navigation gravitent autour de la Terre, approximée comme une masse ponctuelle en son barycentre.
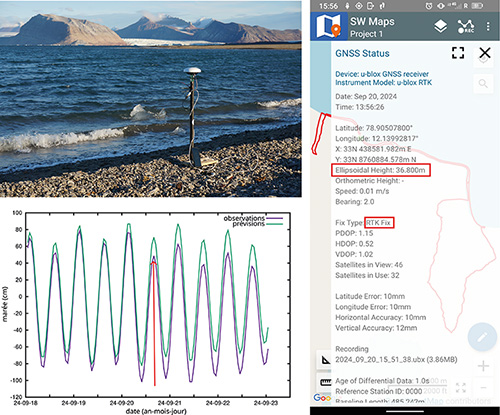
Lors de nos mesures sur le terrain, nous avons toujours pris soin de laisser tourner une instance de str2str -in ntrip://65.21.30.42:443/JMF -out file://sortie.bin pour conserver une trace des messages de correction et potentiellement les appliquer en post-traitement. En effet, alors que Ny-Ålesund vient d’installer récemment une station de base 4G [7] sub-GHz pour limiter les interférences avec les radiotélescopes permettant de communiquer de la donnée dans un rayon d’une dizaine de kilomètres, la couverture dans un cirque de glacier est incertaine, et sans signal de correction, point de mesure centimétrique. Cependant, une application telle que SW Maps sous Android (propriétaire mais gratuite) sauve un fichier contenant les données brutes venant d’un récepteur ZED-F9P en plus de se connecter au serveur NTRIP pour communiquer les informations de correction : en l’absence de connexion informatique, il sera toujours possible de post-traiter les deux jeux de données pour appliquer les corrections, avec le risque d’une solution qui ne converge pas si la qualité de l’enregistrement est insuffisante. C’est là le principal bénéfice de la solution RTK en temps réel : savoir si la solution centimétrique a été atteinte ou s’il faut attendre pour améliorer la convergence de la solution.
Configuration de SW Maps sous Android pour l’application de corrections RTK en temps réel
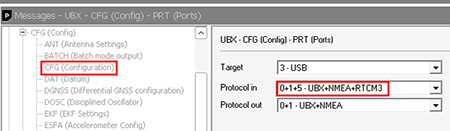
Nous avions auparavant [1] plébiscité la version de RTKLib pour Android comme solution pour recevoir deux flux de données – de correction par un serveur NTRIP et un récepteur u-blox ZED-F9P – afin d’appliquer les corrections et fournir la solution centimétrique. Force est de constater que RTKLib ne fonctionne plus sous Android 12, et qu’une alternative doit être trouvée pour poursuivre les mesures avec un téléphone mobile récent. Pour ce faire, nous tirons profit de la capacité d’un ZED-F9P d’exploiter un flux RTCM pour appliquer les corrections et fournir lui-même une solution centimétrique. Malgré la boîte noire que constitue la solution RTK du ZED-F9P, c’est une solution fonctionnelle largement adoptée. Pour ce faire, nous configurons le ZED-F9P pour recevoir les corrections RTCM sur port USB (figure ci-dessous) en vérifiant que cette fonctionnalité est activée au moyen du logiciel u-center, https://www.u-blox.com/en/product/u-center, qui fonctionne néanmoins sous Wine.
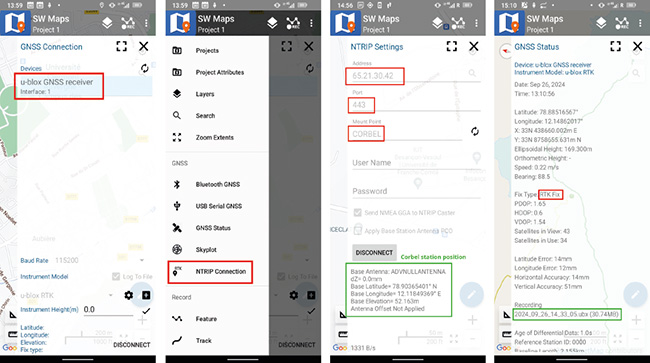
Par ailleurs, nous avons besoin d’un logiciel capable de recevoir les trames RTCM du serveur NTRIP, les communiquer au ZED-F9P, et recevoir la solution résultante. La seule solution gratuite, à défaut d’être libre, que nous ayons identifiée est SW Maps. Avec ce logiciel, connecter un ZED-F9P au port USB du téléphone portable se traduit par l’activation du menu USB Serial GNSS. Ayant sélectionné et activé la communication entre le ZED-F9P et le téléphone par interface USB, un nouveau menu s’active sous forme de NTRIP Settings. Nous y renseignons dans Address l’adresse IP de notre serveur NTRIP, sous Port le port (443) que nous avons choisi, sous Mount Point le nom de la station de référence renseignée dans l’interface Centipède, et si tout se passe bien avec une connexion fonctionnelle, nous sommes informés du transfert de données de quelques kilo-octets/seconde et des paramètres de la station de référence.
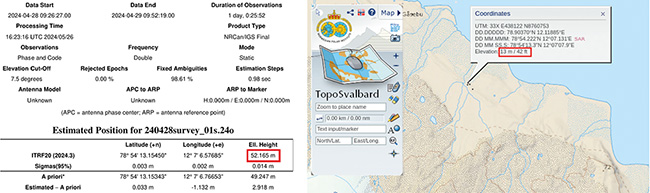
Lors de l’installation de la station de base, nous devons commencer par la position avec précision et exactitude. Pour ce faire, Centipède préconise d’enregistrer les données brutes (pseudoranges en code et en phase) observées par le récepteur de la station de base pendant 24 h, et calculer la solution précise PPP en exploitant les informations précises de position des satellites dans le ciel et de leur horloge, publiées par l’IGS, l’International GNSS Service dont les produits sont disponibles à https://cddis.nasa.gov/archive/gnss/products/ sous réserve de dévoiler son identité en fournissant une adresse e-mail. Alors que RTKLib sait effectuer ce calcul, une solution en ligne proposée par Centipède est d’utiliser le service de l’IGN qui ne fonctionne que sur le territoire français, et sinon le service canadien du NRCAN (Natural Resource of CANada) à https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php. Ici aussi, il faut dévoiler son e-mail pour accéder au service, qui demande un fichier RINEX d’observations toutes les 30 secondes : ce fichier est par exemple produit depuis le fichier UBX sauvé par un récepteur u-blox ZED-F9P par convbin -t 30 fichier.ubx pour produire le fichier d’observations .obs requis. Le traitement se fera en mode statique, la station de base n’étant pas mobile, et nous voyons apparaître le problème qui va se poser dans la suite quand nous devons remplir les champs concernant le référentiel avec soit NAD83, soit ITRF, et si le second choix est sélectionné alors « Vertical datum » impose CGVD2013. Afin d’exploiter convenablement les informations fournies par le récepteur mobile qui se référencera par rapport au récepteur fixe, nous devons comprendre le sens de ces acronymes. « ITRF » est International Terrestrial Reference system and Frame qui définit notamment la position de la Terre dans l’espace et sa forme, tandis que NAD83 est la même définition, mais pour l’Amérique du Nord. Comme nous travaillons en Europe, le choix d’ITRF semble naturel. Ensuite, CGVD2013 pour Canadian Geodetic Vertical Datum of 2013 propose la définition de l’altitude pour le Canada. Lorsque nous obtenons la solution du NRCAN sur la position de la station de référence, calculée une quinzaine de jours après la mesure pour exploiter les solutions les plus précises publiées par IGS, nous sommes informés de la solution en Fig. 3, entourée en rouge pour indiquer 52,165 m. Cela semble excessivement élevé, surtout que le site norvégien Toposvalbard à https://toposvalbard.npolar.no/ indique une élévation de 13 m. Quelle est la source de l’erreur ? Est-ce le fait d’utiliser un référentiel canadien en Europe ? Cela pose la question de la définition de l’altitude. Alors que nous avons l’habitude d’utiliser QGIS pour convertir d’un mode de projection horizontal vers un autre – par exemple de coordonnées sphériques vers un plan tangent local – ce logiciel ne nous sera pas d’une grande aide pour convertir des altitudes.
Centipède annonce la publication le 26 février 2025 de son caster libre Millipede disponible à https://github.com/pbeyssac/millipede-caster/ et accessible à crtk.net:2101 pour diffuser des messages au format NTRIP v1 ou v2.
2. Exploitation des résultats : qu’est-ce que l’altitude ?
Lors des mesures sur le terrain de positions de cibles approximativement connues, mais affinées par cette solution centimétrique, l’emplacement dans le plan XY était excellent, mais une interrogation se posait sur l’altitude Z. En effet, Fig. 4 montre comment un récepteur placé sur une plage au niveau de la mer indique une altitude de 36,8 m. Une telle altitude dans un référentiel arbitraire n’aurait rien de choquant, mais il est certain qu’elle ne qualifie pas d’« au-dessus du niveau moyen de la mer » (above mean sea level). Quel est donc ce référentiel, et comment se relie-t-il au niveau de la mer ?
Les satellites, et en particulier ceux des constellations en orbite moyenne qui transmettent les signaux permettant le positionnement par trilatération, n’ont que faire de la position d’une masse d’eau, et les coordonnées qui sont solution de la mesure du temps de vol des ondes électromagnétiques issues de ces satellites sont fournies par rapport au centre de la Terre (ECEF pour systèmes de coordonnées Earth Centered, Earth Fixed). Ce système cartésien est centré sur le barycentre de la Terre et orienté par rapport aux astres célestes supposés suffisamment loin pour ne pas se déplacer significativement lorsqu’observés depuis la Terre, par des radiotélescopes par exemple.
Comme le positionnement par rapport au centre de la Terre n’est pas très pratique au quotidien, les coordonnées cartésiennes sont projetées sur un ellipsoïde qui tente de plaquer au plus près au patatoïde que forme la surface de la Terre, et en particulier son aplatissement aux pôles dû à la force centrifuge induite par la rotation. Ici encore, le niveau d’un liquide que sont les océans et les mers n’a aucune importance, l’ellipsoïde est uniquement défini arbitrairement pour ne pas trop diverger des masses continentales. Un exemple de tel ellipsoïde est WGS84 – World Geodetic System de 1984 – défini par un demi-grand axe de 6378,137 km, et un aplatissement de 1/298,257223563. L’intersection de la ligne allant du centre de la Terre avec cet ellipsoïde indique la latitude et la longitude, et la distance de la coordonnée cartésienne à la surface de l’ellipsoïde détermine l’altitude. On sent donc bien que la différence entre l’altitude du NRCAN – par rapport à un ellipsoïde – et Toposvalbard vient d’une référence différente d’altitude, ce dernier se référant au niveau de la mer puisqu’interroger sur l’altitude au bord de l’eau indique « 1 m ».
La définition de « niveau de la mer » fournie par [9] ainsi que [3], p.237, est intéressante : il s’agit d’une distribution d’eau selon une équipotentielle du champ de gravité terrestre « In the absence of dynamics or other external forcing, the surface of the ocean should lie on an equipotential of the Earth’s gravity field, called the geoid. » En effet, si le champ de gravité présentait un gradient, alors l’eau s’y écoulerait pour équilibrer le gradient. Nous voyons donc une définition de la surface de l’eau indépendante de considérations célestes nécessaires à définir l’ellipsoïde, mais qui dépend de la distribution de masses sur et dans la planète, sans relation évidente avec la topographie de surface. Ces surfaces diffèrent selon le point de référence choisi, et chaque continent ou zone de surface émergée pourra choisir son point de référence, tel que nous l’avons vu en introduction avec le choix d’un niveau de marégraphe à Marseille pour la France. La relation entre un ellipsoïde et le niveau de l’eau sur une zone géographique émergée n’a aucune raison d’être simple ou rationnelle et ne fait qu’épouser la forme de l’isopotentiel du champ de gravité : la relation entre les deux grandeurs est une carte en deux dimensions associant pour chaque latitude et longitude une différence d’altitude entre niveau de la mer et ellipsoïde.
Même si QGIS ne sait pas convertir des altitudes, il reste une source d’informations utiles. Si nous chargeons des positions référencées en coordonnées sphériques WGS84 (EPSG:4326), nous pouvons les convertir (bouton de droite de la souris sur la couche à convertir et Export -> Save Feature As... pour choisir le nouveau CRS) en ITRF2020 (EPSG:9989) comme l’indique le rapport de mesure de NRCAN (Fig. 3), et le résultat contient des coordonnées identiques dans les trois axes. Nous apprenons par ailleurs qu’il existe un « European Vertical Reference Frame 2000 » nommé EPSG:5129, mais QGIS ne le connaît pas. Par contre, QGIS connaît CGVD2013 (EPSG:6649) que nous avions rencontré auparavant sur le site du NRCAN et lorsque nous tentons de sauver une couche en CRS ITRF2020 vers CGVD2013, QGIS nous fournit l’information fort utile que « This grid is available for download from https://cdn.proj.org/ca_nrc_CGG2013n83.tif. » Ainsi, QGIS nous propose de télécharger ce fichier et le placer dans $HOME/.local/share/QGIS/QGIS3/profiles/default/proj afin de connaître la relation entre altitude de l’ellipsoïde et le géoïde. De façon générale, ces cartes sont disponibles au format GeoTIFF à https://cdn.proj.org/ pour indiquer la différence d’altitude entre ellipsoïde et les géoïdes choisis par les divers continents, et pas uniquement pour le Canada comme nous venons de le faire. Les mers et océans ne sont pas couverts, car que veut dire « au-dessus du niveau de la mer » au milieu du Pacifique quand le mouvement de la Lune et du Soleil font varier de plusieurs mètres chaque jour le niveau du liquide, et en l’absence d’un référentiel fixe qu’est une masse de terre émergée ? Pourtant, ces hauteurs sont bien mesurées par satellite en orbite basse, que ce soient les missions TOPEX/Poseidon de la NASA et du CNES d’altimétrie par RADAR, puis les Jason qui en sont à leur troisième itération, et maintenant Sentinel-6. Par ailleurs, les satellites GRACE observent les variations du champ de gravité en mesurant finement la distance qui les sépare l’un de l’autre alors qu’ils parcourent la même orbite polaire basse.
Maintenant que nous savons comment identifier l’écart entre l’ellipsoïde WGS84 dans lequel un récepteur de navigation par satellite fournit sa solution, et le niveau moyen de la mer, nous pouvons tracer ces cartes et observer leur évolution (Fig. 5). Cette distribution des altitudes est décrite par l’institut géographique norvégien [10] Kartverket en expliquant dans la section Vertical Datums de leur site fournissant le niveau des marées que « To determine heights and depths we need knowledge about the different vertical datums, and the relationship between them. The relationship between the different datums vary from place to place. These levels are important for different utilizations and it is therefore possible to hide or show some types of datums in the list below. » – le terme datum faisant référence au choix d’une origine.
Tracé d’un champ de potentiel sur une sphère, et l’avenir du géoïde
Programme GNU/Octave pour produire la Fig. 5 (droite) : la lecture d’un fichier GeoTIFF contenant des valeurs représentées en nombres à virgule flottante nécessite d’utiliser la boîte à outils mapping et sa fonction rasterread(), puisque imread() de GNU/Octave interprète les valeurs des pixels comme des entiers codés sur 16 bits.
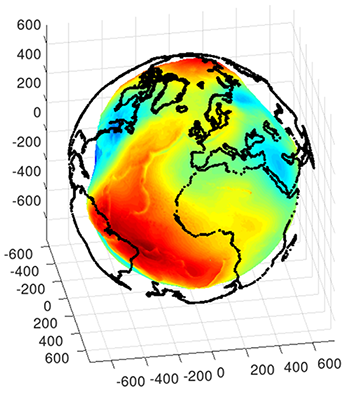
Nous avons tous vu ces superbes représentations de la distribution d’un champ sur le globe, que ce soit l’intensité du champ magnétique ou ici le champ de gravitation à la surface de la Terre [3], p. 240. Le résultat est surprenamment facile à atteindre en s’inspirant de sphere.m fourni par GNU/Octave dans /usr/share/octave/9.2.0/m/plot/draw/, en ajoutant le concept de rayon (puisque sphere trace une sphère de rayon constant) sous forme de la variable R ci-dessus, et en modifiant la couleur pour non plus dépendre de l’ordonnée (z), mais de la distance au centre de la sphère (variable C ci-dessus). Le programme ci-dessus atteint ce résultat pour la hauteur du niveau moyen de la mer sur le globe terrestre, en amplifiant d’un facteur 104 puisque le rayon moyen ajouté est de 640 m au lieu des 6400 km du rayon de la Terre.
Alors que nous assistions à la présentation de P. Tavella, responsable du temps et fréquence au Bureau International des Poids et Mesures (BIPM), dans laquelle cette illustration apparut, notre attention fut attirée sur le fait que les horloges deviennent si précises que la correction du décalage gravitationnel (gravitationnal redshift) décrit par la relativité générale devient nécessaire pour permettre leur comparaison. En effet, avec des horloges annoncées avec des stabilités relatives meilleures que 10−16, la variation du champ de gravité Δ U induit une variation de fréquence Δ U/c2 avec c la vitesse de la lumière. À la surface de la Terre, Δ U est déterminée par la constante (locale) de gravitation g=9,81 m.s−2 multipliée par la variation de hauteur, de telle sorte que Δ U/c2≃ 9/(3·108)2=10−16/m. Ainsi, déplacer une horloge verticalement de 1 m se traduit par une variation détectable de sa fréquence, induisant la proposition de non plus définir le géoïde sur des considérations astronomiques et géographiques, mais sur des considérations atomiques, tout comme la fréquence a perdu en 1967 sa relation à l’astronomie avec la définition sur une transition micro-onde de l’atome de césium. Nous avons profité de cette illustration des transparents de P. Tavella pour ajouter le profil des continents tel que le contenait sa présentation (voir ci-dessous). Les points représentant les limites des continents sont disponibles au format Shapefile à : https://www.naturalearthdata.com/downloads/10m-physical-vectors/ et en particulier : https://www.naturalearthdata.com/http//www.naturalearthdata.com/download/10m/physical/
ne_10m_land.zip. La boîte à outils mapping de GNU/Octave permet de lire ce format de fichiers.
Complément au programme GNU/Octave pour lire le contenu d’un fichier au format Shapefile classiquement utilisé par les systèmes de gestion d’informations spatialisées (GIS), extraction des coordonnées, et tracé au-dessus de la surface du potentiel gravitationnel sous forme de points individuels.
Noter que la NSF américaine propose une jolie version analogique de ce globe à https://web.archive.org/web/20240621165530/https://www.nsf.gov/news/classroom/images/Gravity.pdf
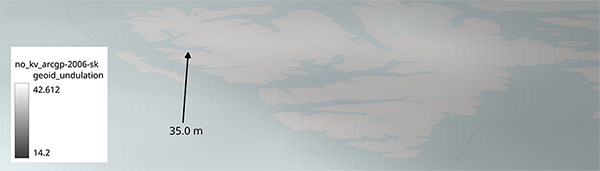
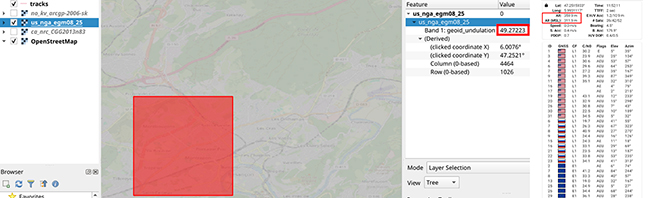
Ainsi, en prenant la carte des différences de hauteurs entre ellipsoïde et géoïde pour la zone où la photographie de la Fig. 4 a été prise, no_kv_arcgp-2006-sk.tif (Fig. 6), et en interrogeant QGIS sur la valeur de la table attributaire dans la zone de prise de vue, nous constatons que l’écart est de 35 m, ramenant bien l’altitude fournie par le récepteur de navigation par satellite à un niveau proche de 0, l’incertitude résiduelle étant attribuée à la marée au moment de la prise de vue et aux 79 cm de mât qui supportent l’antenne de réception GNSS.
Le même exercice pour Besançon indique que pour la France, l’écart entre l’ellipsoïde et le géoïde est de l’ordre de 50 m, ce que sait l’application GPSTest sous Android en indiquant Alt (par rapport à l’ellipsoïde WGS84) et Alt (MSL) (par rapport au géoïde Mean Sea Level) tel qu’affiché en Fig. 7.
Le système japonais MADOCA/CLAS
MADOCA [11], Multi-GNSS Advanced Demonstration tool for Orbit and Clock Analysis (https://ssl.tksc.jaxa.jp/madoca/public/public_index_en.html)/CLAS (Centimeter Level Augmentation Service) est un système développé au Japon pour propager des informations de correction des signaux de navigation par satellite pour atteindre la résolution centimétrique en observant sur un réseau dense de stations de référence l’impact de l’environnement dans lequel se propagent les ondes électromagnétiques. Ces informations sont relayées par les satellites géosynchrones QZSS (Michibiki ![]() [12]) conçus pour améliorer la performance du positionnement par les satellites en orbite moyenne. Tomoji Takasu, auteur de RTKLib et de la PocketSDR, a co-rédigé un ouvrage décrivant l’exploitation de la bibliothèque qu’il a développée sur ce sujet (droite). Son analyse s’appuie sur une plateforme d’acquisition et de traitement Mosaic-CLAS produite par Septentrio. L’identifiant des trames RTCM en fonction de la constellation considérée est mentionné succinctement en page 12 de cet ouvrage.
[12]) conçus pour améliorer la performance du positionnement par les satellites en orbite moyenne. Tomoji Takasu, auteur de RTKLib et de la PocketSDR, a co-rédigé un ouvrage décrivant l’exploitation de la bibliothèque qu’il a développée sur ce sujet (droite). Son analyse s’appuie sur une plateforme d’acquisition et de traitement Mosaic-CLAS produite par Septentrio. L’identifiant des trames RTCM en fonction de la constellation considérée est mentionné succinctement en page 12 de cet ouvrage.
Conclusion
Installer une station de référence pour le positionnement centimétrique en analysant les perturbations induisant un retard dans la propagation des ondes électromagnétiques et en les corrigeant au niveau du récepteur mobile a été l’occasion de s’interroger sur la nature des solutions fournies et leur interprétation. L’accès à la mesure centimétrique pour un coût modique – la carte d’évaluation de Mikroe est disponible pour 220 euros, mais une antenne de bonne qualité coûte rapidement quelques milliers d’euros ! – va démocratiser l’accès à ces informations et ouvrir de nouvelles perspectives dont l’agriculture de précision est un des exemples qui motive Centipède. Alors qu’un agriculteur n’a probablement que peu d’intérêt pour l’information d’altitude tant que les roues de son tracteur touchent la surface du champ, nombre de sols se déplacent de plusieurs centimètres par an, que ce soit par la fonte des glaciers ou le pompage excessif des nappes phréatiques qui ne portent plus les sols, voir le rebond isostatique induit par le recul des glaces lors de la dernière ère glaciaire. Même en latitude/longitude, le positionnement centimétrique implique de nouvelles problématiques, avec par exemple le continent australien qui dérive de 7 cm/an vers le nord-est ! Au-delà de la position, l’obtention des informations brutes issues des signaux de navigation – les pseudoranges transmis par les serveurs NTRIP – permet de remonter à des mesures aussi fascinantes que le délai troposphérique incluant la quantité d’eau dans l’atmosphère [13].
Alors que nous cherchions à identifier les spécifications de NTRIP et en particulier du serveur rédigé par l’institut géographique allemand BKR (Bundesamt für Kartographie und Geodäsie), nous avons découvert à https://igs.bkg.bund.de/ntrip un réseau de services incluant des stations de référence à Besançon et sur notre site d’études au Spitzberg ! (Fig. 8). Les casters NTRIP sont accessibles sur une adresse de la forme euref-ip.net:2101/MOUNT ou igs-ip.net:2101/MOUNT avec la source des signaux de référence MOUNT visible à http://igs-ip.net:2101/ par exemple, mais les requêtes à str2str -in ntrip://login:passwd@euref-ip.net:2101/NYA200NOR0 se soldent par :
en l’absence d’authentification. Une fois autorisé par les administrateurs de https://register.rtcm-ntrip.org/cgi-bin/registration.cgi à utiliser le service [14] (la réponse vient d’un humain donc une adresse non professionnelle en .free.fr par exemple suffit, mais on évitera une adresse fournie par Guerilla Mail) et le flux redirigé (-out file://fichier.rtcm3) vers un fichier de sortie d’extension .rtcm3, nous constatons par convbin fichier.rtcm3 que seul le fichier RINEX d’observations .obs correspondant est produit, et aucun fichier de navigation qui permettrait de placer les satellites dans l’espace, connaissance nécessaire pour placer la station de référence au sol. En téléchargeant un fichier de navigation produit en temps réel sur https://cddis.nasa.gov/archive/gnss/data/daily/2024/289/24n/brdc2890.24n.gz pour l’instant de cette observation, nous pouvons calculer la position de la station de référence avec RTKLib par rnx2rtkp -p 0 fichier.obs brdc2890.24n et constater que la solution 78.93033°N, 11.85861°E et une altitude de 79 m correspond bien au site de Kartverket qui porte les antennes de réception de signaux satellitaires. Cependant, l’autorisation d’accès fut accompagnée de la recommandation « Note that data is made available primarily for demonstration and evaluation purposes. The BKG aims to provide an uninterrupted service. In spite of all efforts downtimes cannot be totally avoided. It is important to understand that streams may be interrupted or become unavailable at any time without prior notice. » donc la contribution à Centipède en installant une station de référence que nous maîtrisons ne semble pas totalement inutile. La solution pour euref-ip.net:2101/BSCN00FRA0 de 47.246888°N, 5.989391°E est clairement à l’observatoire de Besançon, comme la Fig. 8 ne le montre pas.
Remerciements
Les missions de terrain au Spitzberg ainsi que les antennes de réception des signaux de navigation par satellite ont été financées par l’Institut polaire Paul-Émile Victor (IPEV). La participation au séminaire à l’Observatoire Royal de la Marine espagnole à laquelle les transparents de P. Tavella furent présentés a été financée par EURAMET, le réseau européen des instituts de métrologie.
Références
[1] J.-M Friedt, « Exploitation des signaux de référence de navigation par satellite pour un positionnement centimétrique : RTKLib fait appel à Centipède et l’IGN pour afficher dans QGIS », Hackable 48 (mai/juin 2023) - https://connect.ed-diamond.com/hackable/hk-048/exploitation-des-signaux-de-reference-de-navigation-par-satellite-pour-un-positionnement-centimetrique-rtklib-fait-appel-a-centipede-et-l-ign-pour-afficher-dans-qgis
[2] J.-P. Snyder, Flattening the Earth: two thousand years of map projections, Univ. of Chicago Press (1997)
[3] J. Lefort, L’aventure cartographique Belin/Pour la Science (2004)
[4] C.C.J.M. Tiberius, Recursive data processing for kinematic GPS surveying, Netherlands Geodetic Commission (1998)
[5] N. Kubo, GNSS Precise Positioning and RTKLIB (2018) à https://www.unoosa.org/documents/pdf/icg/2018/ait-gnss/15a_PPP_RTKLIB.pdf
[6] Le site https://www.use-snip.com/kb/knowledge-base/ntrip-rev1-versus-rev2-formats/ détaille les différences entre NTRIP 1 et 2. On notera que SNIP est une alternative à yccaster et n’est pas plus libre : nous ne l’avons pas testé au cours de cette étude.
[7] T. Nilsen, World’s northernmost research settlement gets mobile phone service, The Barents Observer (27 nov. 2023) à https://www.thebarentsobserver.com/arctic/worlds-northernmost-research-settlement-gets-mobile-phone-service/118555
[8] Mikroe RTK Click à https://www.mikroe.com/gnss-rtk-click est disponible chez Mouser pour 220 euros.
[9] Mark E. Tamisiea & al., Sea level: measuring the bounding surfaces of the ocean, Phil. Trans. of the Royal Society A 372(2025) 20130336 (2014)
[10] Defining Sea Level and Understanding its Causes à https://kartverket.no/en/at-sea/se-havniva/sea-level/defining-sea-level-and-understanding-its-causes
[11] K. Kawate & al., MADOCA: Japanese precise orbit and clock determination tool for GNSS, Advances in Space Research 71(10) 3927–3950 (2023)
[12] Les hiraganas ne sont pas utiles, mais sont juste inclus pour démontrer la supériorité de LaTeX sur les éditeurs de texte WYSIWYG. Chaque caractère japonais est inclus par \newcommand\mi{\textup{\usefont{U}{min}{m}{n}\symbol{'177}}} pour le « mi » par exemple, avec \DeclareFontFamily{U}{min}{}\DeclareFontShape{U}{min}{m}{n}{<-> udmj30}{}.
[13] P. Bosser & al., Water vapour monitoring over France using the low-cost GNSS collaborative network Centipede, European Geoscience Union (2023)
[14] G. Weber & al., Networked Transport of RTCM via Internet Protocol (NTRIP), dans « A Window on the Future, Proceedings of the IAG General Assembly », Sapporo, Japan, 2003, Springer Verlag, Symposia Series, 128 60–64 (2005)



 Ajouter à une liste de lecture
Ajouter à une liste de lecture