Tracer les fractales de Mandelbrot ou de Newton sur de petits microcontrôleurs 8 bits ou 32 bits nous donne l’opportunité d’appréhender la représentation des nombres en virgule fixe pour une implémentation efficace de l’arithmétique – même sur des nombres complexes – sur systèmes embarqués à ressources réduites. Pouvoir tester le même code sur une multitude de plateformes impose de structurer son code pour séparer la partie algorithmique et l’accès aux ressources matérielles : nous allons proposer une architecture de code et de Makefile compatible à la fois avec des tests sur PC et sur diverses architectures de microcontrôleurs, en faisant appel aux stubs.
Bien que le développement sur Raspberry Pi, BeagleBone ou Red Pitaya soit actuellement qualifié d’embarqué, la majorité des systèmes faibles coûts, mais surtout faible consommation restent architecturés autour de processeurs aux performances bien plus modestes, ne serait-ce que comme gestionnaire d’énergie et de périphériques [1]. Nombre de ces processeurs ne sont pas équipés de périphériques de calcul matériel sur des nombres à virgule flottante, dont les opérations doivent être émulées par logiciel. Cette représentation des nombres n’est pas naturelle pour une unité de calcul logique et arithmétique (ALU) qui est optimisée pour traiter des nombres entiers. La majorité des problèmes physiques permettent d’ajuster les unités pour manipuler des valeurs du même ordre de grandeur, qu’une simple homothétie permet de considérer comme des entiers. Il s’agit de l’arithmétique des nombres à virgule fixe. Cependant, contrairement à l’arithmétique des nombres entiers qui est exacte, l’arithmétique des nombres à virgule fixe va souffrir d’inexactitudes liées aux pertes des bits de poids faibles lors de certaines opérations.
Rappel : Nombre à virgule flottante
L’Unité Arithmétique et Logique (ALU) d’un processeur sait naturellement exprimer des opérations logiques ou arithmétiques sur des nombres entiers, positifs ou éventuellement négatifs dans une représentation binaire en complément à deux. Dans cette représentation, les valeurs codées sur N bits sont restreintes à [0:2N-1] en non signé ou [-2N-1:2N-1-1] en signé. La représentation en virgule flottante [2] vise à représenter une gamme plus vaste de valeurs, au détriment de l’exactitude des calculs. Ainsi, les N bits d’un entier sont découpés en deux segments que sont, dans une notation scientifique de la forme M x 2E, une mantisse M<1 et un exposant E. Si, comme c’est le cas en simple précision, un bit est dédié au signe, 8 bits à l’exposant et 23 bits à la mantisse, alors des grandeurs comprises entre 2-128 à 2127 peuvent être représentées (en réalité -126 et non -128), les fameux 1038. Les 11 bits d’exposant en double précision sont plus faciles à interpréter, puisque :
Malgré cette grande dynamique de représentation, les opérations sur les nombres à virgule flottante impliquent d’aligner la virgule – comme nous le ferions en posant une addition à la main – avec une perte de précision résultant du nombre fini de bits pour représenter la mantisse. Les exemples d’imprécisions des calculs en virgule flottante sont bien connus, mais apparaissent dans des cas aussi simples que :
Ce code répond : 109.998894 110.000000 0.001106262, soit une différence de 10-3 sur les mêmes calculs effectués en simple ou double précision (qui donne la bonne solution ici). L’erreur sera d’autant plus grande que les ordres de grandeur manipulés sont importants, un cas classique de la moyenne glissante qui commence par sommer des termes du même ordre de grandeur, mais finit avec un accumulateur important auquel on ajoute une petite valeur en fin de calcul. Ces problèmes deviennent dramatiques pour les systèmes chaotiques que nous avons volontairement proposés d’illustrer ici – le chaos étant défini par un système dans lequel les erreurs initiales croissent exponentiellement lors des itérations de calculs.
Nous allons aborder ces considérations pour traiter sur microcontrôleurs 8 bits et 32 bits le problème bien connu de la convergence de suites complexes qui donnent naissance aux fractales de Mandelbrot et de Newton. Dans le premier cas, la question est de savoir pour quelle condition sur c∈ℂ la suite zn+1 = zn2+c converge, ou dans le cas de divergence, quelle est la vitesse de divergence (c.-à-d. au bout de combien de temps le module de la suite dépasse-t-il un seuil prédéfini). Dans le second cas, la question est de savoir vers laquelle des 3 racines possibles la méthode de Newton résolvant z3-1 converge en fonction de sa condition initiale (la méthode de Newton et la suite résultante seront explicitées en temps voulu). Le premier problème fait intervenir des sommes et produits de complexes sur des nombres de l’ordre de -1 à 1 avec une résolution de l’ordre de 10-2. Le second problème sera à peine plus compliqué, car il fera intervenir une division (complexe).
1. Architecture du programme
Notre objectif sera de comparer un même algorithme sur une multitude de plateformes, donc nous pouvons réfléchir dès le début à architecturer le programme pour séparer la partie algorithmique, indépendante du matériel et le cœur de notre analyse, de l’initialisation et de l’accès aux ressources de communication spécifiques à chaque plateforme (stdout sous UNIX, port série compatible RS232 pour processeurs ARM, USB pour processeur Atmel/Microchip). Nous choisissons donc de n’avoir qu’un unique code source contenant l’algorithme avec des stubs vers l’implémentation des initialisations et fonctions de communication dépendantes de chaque architecture (figure 1).
Ces stubs exposent les mêmes prototypes (arguments et résultat retourné par la fonction), mais implémentent la fonction recherchée différemment selon l’architecture visée, par exemple par une fonction vide telle que ce sera le cas sous UNIX pour l’initialisation des horloges. Séparer l’algorithme des accès bas niveau est une bonne pratique pour garantir la pérennité du cœur de compétence – l’algorithme – sans devenir dépendante d’une plateforme matérielle qui deviendra rapidement obsolète [3]. Nous lierons les stubs appropriés en sélectionnant le fichier contenant les codes sources associés à une architecture donnée lors de l’édition de liens par Makefile.
Nous allons manipuler des complexes formés d’une partie réelle et d’une partie imaginaire, donc il semble évident de définir une structure struct complexe {montype re; montype im;}; et puisque nous allons tantôt travailler sur des entiers représentant les nombres à virgule fixe par homothétie, tantôt des nombres à virgule flottante, nous proposons une définition conditionnelle :
De cette façon, nous passerons dans Makefile en incluant le drapeau -Dfl pour l’activation ou non des nombres à virgule flottante, et faisons le choix d’utiliser la nomenclature des types étendus des entiers du C fournis dans stdint.h, puisque la taille de l’int n’est pas normalisée et dépend de l’architecture sur laquelle s’exécute le code [4].
Architecture du Makefile
Reléguer au Makefile le passage de paramètres de configuration est aisé, mais se pose la question des diverses architectures possibles de Makefile permettant de compiler un même code à destination de diverses cibles, donc en précisant quelle déclinaison de gcc utiliser (pour quelle cible) et quelles options de compilation utiliser :
- la solution la plus stupide que nous proposons par simplicité sur le dépôt GitHub qui accompagne cet article : un fichier de configuration Makefile.xxx avec xxx la cible, et exécution par make -f Makefile.xxx. Ce faisant, nous ne profitons pas du dénominateur commun des divers Makefile, mais nous nous contentons de copier-coller un motif de départ pour le décliner vers les diverses cibles, avec la nécessité de corriger tous les Makefile si une erreur est découverte ultérieurement ;
- un unique Makefile qui reçoit ses arguments du Shell en ligne de commande. Ainsi, si nous définissons non pas le compilateur par CC=avr-gcc dans le Makefile, mais par CC?=avr-gcc, alors l’affectation ne sera effective que si CC n’est pas défini comme variable d’environnement. Ainsi, exécuter CC=arm-none-abi-gcc make écrasera la valeur par défaut de CC avec le nouveau compilateur et le binaire généré sera à destination d’un processeur ARM et non AVR. Cependant, cette méthode nécessite d’écraser toutes les variables que sont les drapeaux de compilation CFLAGS et d’édition de liens LDFLAGS, générant des lignes de commande relativement longues et fastidieuses à taper. C’est toutefois l’approche utilisée par Buildroot pour compiler un même code source à destination d’une multitude de cibles. On prendra cependant soin dans ce cas d’éviter la nomenclature de certaines constantes qui ont des valeurs prédéfinies, si elles ne sont pas fournies en ligne de commande : c’est le cas de CC (qui vaut cc donc le compilateur à destination de l’hôte, CFLAGS, LDFLAGS ou CXX selon la liste fournie sur https://www.gnu.org/software/make/manual/html_node/Implicit-Variables.html#Implicit-Variables) ;
- l’inclusion de Makefile.inc dépendant de la cible définie en ligne de commande. Ainsi, à coups de ifdef XXX ... else ... endif de make dépendants de la définition de la constante XXX, voire de la génération dynamique du nom du greffon inclus include Makefile.$(XXX), il sera possible de dynamiquement modifier la définition du compilateur et de ses options de compilation, en fonction de la cible choisie. Nous pouvons nous convaincre de cette approche par le Makefile contenant include Makefile.$(XXX) qui peut appeler Makefile.1 ou Makefile.2 selon la valeur assignée à XXX lors de l’exécution en Shell de XXX=1 make. Si nous définissons Makefile.1 par (noter que @ évite d’afficher la commande exécutée) :
- et Makefile.2 avec le même contenu en remplaçant le symbole affiché par la règle all, alors nousobtenons comme prévu :
2. Principe du nombre à virgule fixe
Travailler en nombre à virgule fixe tient simplement en l’idée d’effectuer une homothétie adéquate du problème pour le transformer en nombres entiers. Si un calcul se doit de fournir une température avec une résolution en 0,1 K, alors nous exprimons le problème sur 10 fois la température et nous manipulerons des entiers. Cependant, contrairement à l’arithmétique sur les nombres entiers, exacte, car conservant les bits de poids faible au risque du dépassement de capacité sur les bits de poids fort, l’arithmétique en virgule fixe maintient constant le nombre de décimales après la virgule. Cela n’impacte pas la somme : la somme de deux nombres plaçant la virgule à une position connue de la représentation fournit un résultat avec la virgule à la même position. Donc, si deux nombres a et b en virgule fixe ont effectué (en base 10 pour simplifier) une homothétie de 10N, la somme s suit simplement s=a+b en gardant ce facteur d’homothétie 10N (273,1 K+0,7 K=273,8 K et nous gardons toujours une décimale). Le produit est moins intuitif pour le physicien puisque l’unité de la grandeur manipulée n’est pas conservée (le produit de deux températures en K est exprimé en K2), mais d’un point de vue arithmétique, l’opération diffère du calcul sur les entiers en ce que cette fois des bits de poids faible seront éliminés afin de conserver le même nombre de chiffres après la virgule, tronquant ainsi la précision du calcul. Par exemple 1,1 x 2,3 = 2,53 qui s’exprime comme 2,5 en ne conservant qu’une décimale : si les deux arguments du produit ont subi la même homothétie, le résultat du calcul doit être divisé par ce facteur. Dans notre expression en nombres entiers, 11 x 23 = 253 et il faut diviser (partie entière) par 10 pour ne conserver que la partie respectant notre représentation.
Nous concluons donc par deux fonctions d’addition et de multiplication que sont :
Ici, SCALE est une constante définie dans les conditions #ifdef vues plus haut à 1.0 si fl est actif, et au facteur d’homothétie sinon. Nous avons ici manipulé des divisions, mais il est évidemment avantageux de remplacer par des décalages en choisissant des facteurs d’homothétie puissance de 2 au lieu de 10 (multiplier par 128 au lieu de 100 ou 1024 au lieu de 1000 ne changera pas grand-chose à la formulation du problème). Nous en avons profité pour glisser le calcul du module au carré du nombre complexe dont nous aurons besoin, et qui renvoie un type montype selon la nature des types manipulés.
3. La fractale de Mandelbrot
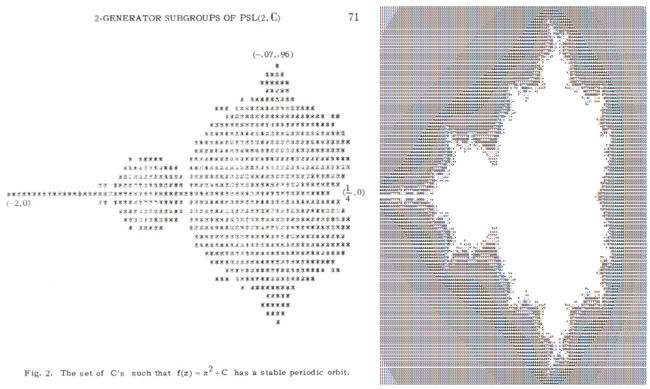
Fort de ces définitions et de ces trois fonctions, efforçons-nous de tracer la fractale [5, 6] de Mandelbrot sur microcontrôleur. La fractale de Mandelbrot est une structure géométrique dans le plan complexe issue de l’analyse de la suite zn+1 = zn2+c pour chaque point c∈ℂ du plan complexe en initialisant z1=c. Chaque point c est représenté par deux symboles, selon que la suite converge ou diverge, et en cas de divergence, nous indiquerons au bout de combien d’itérations la condition de divergence a été atteinte – en pratique, un module de zn qui dépasse un seuil.
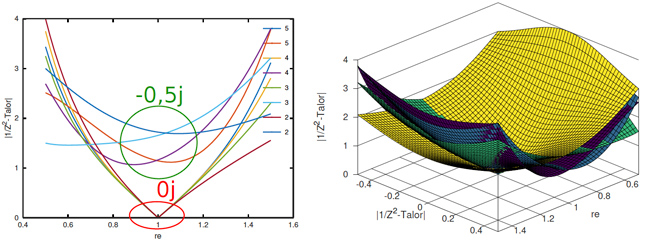
Nous nous inspirons, par souci de rigueur scientifique, des bornes exploitées dans [7] (figure 2, gauche), même s’il suffit de passer quelques minutes sur XaoS [8] (figure 2) pour identifier les bornes intéressantes dans le plan complexe du tracé de la publication [7], qui se focalise sur l’intervalle réel [-2;0,25] et l’intervalle imaginaire [-0,96;0,96] pour rechercher des orbites périodiques. Ici, nous allons nous intéresser à un ensemble un peu plus large avec une condition de divergence en établissant que si au bout de 16 itérations, le carré du module de |zn| n’a pas dépassé 10, alors la suite converge probablement et nous afficherons le premier symbole. Dans le cas contraire, si le module dépasse ce seuil avant 16 itérations, nous afficherons le nombre d’itérations qu’il a fallu pour atteindre le seuil. L’objectif est de cartographier les valeurs de c pour lesquelles la suite converge et diverge : un terminal de 80 caractères de large nécessitera donc un calcul par pas de 0,0285 que nous arrondirons à 0,025=1/40. Il devient donc évident qu’une homothétie naturelle est de multiplier toutes les données du problème par 40 pour ne manipuler que des entiers.
3.1 Code générique
La partie algorithmique du code se résume à itérer la suite zn2+c en faisant trivialement appel aux deux fonctions que nous avons créées pour additionner et multiplier deux complexes, et de tester le carré du module pour vérifier si le seuil de divergence est atteint. Ce code se résume aux quelques lignes suivantes :
Ces lignes font appel aux trois stubs que sont clock_setup() et usart_setup() ainsi que mon_putchar() dont les prototypes sont définis dans uart.h : ces fonctions seront spécifiques à chaque plateforme sur laquelle sera exécuté le code. Dans tous les cas, nous obtiendrons la figure 2 (droite).
3.2 Cas du PC
Un ordinateur exécutant GNU/Linux n’a pas besoin d’initialiser l’horloge ou l’interface de communication, puisque le système d’exploitation s’est chargé d’initialiser stdout : ainsi, les fonctions clock_setup() et usart_setup() sont vides et mon_putchar(char c) se résume à {printf("%c",c);} qui aura nécessité d’inclure #include <stdio.h> pour éviter les avertissements de gcc. Nous pouvons ainsi rapidement tester le bon fonctionnement de l’implémentation de l’arithmétique en virgule fixe, sans mettre en doute l’implémentation sur microcontrôleur.
3.3 Cas du STM32F1
Le travail sur STM32 s’appuie sur la bibliothèque libre libopencm3 de https://github.com/libopencm3/libopencm3 et le compilateur arm-none-eabi-gcc disponible en paquet binaire dans Debian/GNU Linux sous le nom de gcc-arm-none-eabi. Une fois ces dépendances installées, les stubs sont implémentés par :
3.4 Cas du STM32F4
Le Cortex-M4 du STM32F4 est équipé d’une unité matérielle de traitement des nombres à virgule flottante (FPU) et ne devrait donc pas souffrir des mêmes pertes de performance lors du passage de la représentation en virgule fixe vers la représentation en virgule flottante. Malheureusement, libopencm3 ne propose pas l’unité de fonctions entre Cortex-M3 et Cortex-M4 et les fonctions d’initialisation doivent être reprises pour cette nouvelle architecture :
3.5 Cas de l’Atmega32U4/simavr
L’assembleur ARM est presque aussi obscur que l’assembleur x86 en mode protégé et l’analyse du code ne permet pas de facilement mettre en évidence les incroyables optimisations amenées par gcc. Au contraire, l’assembleur du petit cœur 8 bits d’Atmel est limpide et compatible avec une analyse des performances au niveau de l’instruction exécutée par l’ALU et donc, au cycle d’horloge près. En particulier, l’analyse du code assembleur va nous permettre d’appréhender les opérations prises en charge par le préprocesseur afin de libérer les ressources du processeur au moment de l’exécution.
Les premières lignes de code initialisent simavr en l’absence de matériel sur lequel exécuter le code, mais ne seront pas inclus dans le firmware transféré au microcontrôleur si ce matériel est disponible. L’exécution dans simavr [9] s’effectue par simavr -f 16000000 -m atmega32u4 executable.elf avec la génération d’une trace contenant l’évolution du registre de communication sur le port série UDR1, si nous désirons analyser les temps d’exécution. L’initialisation de l’horloge est détournée pour initialiser au plus tôt les fonctionnalités de l’Atmega32U4 fourni en sortie d’usine en mode DFU, à savoir désactiver rapidement le chien de garde et désactiver la division par 8 de la fréquence de cadencement du cœur de processeur (faute de quoi, les temps d’exécution ne seront pas en accord avec simavr configuré pour simuler un cœur à 16 MHz). Dans le mode AVR109 compatible avec la bibliothèque Arduino, on prendra soin de désactiver l’interruption liée à la communication sur bus USB, même si ici les interruptions ne sont pas utilisées.
Nous pouvons nous interroger sur la pertinence d’utiliser des float dans la définition des bornes des boucles sur une architecture ne contenant pas de FPU. Nous allons constater que gcc est malin et précalcule toutes les constantes, même faisant intervenir les flottants, et n’inclut pas l’émulation du calcul sur nombre à virgule flottante si toutes les constantes (entières) peuvent être précalculées. Même en l’absence d’optimisation du code (option -O0 de avr-gcc), nous constatons (option -g3 pour avoir tous les symboles de déverminage lors de l’affichage du l’assembleur par avr-objdump -dSt executable.elf) que les bornes de la boucle ont été précalculées, ici dans le cas SCALE valant 1000 :
Les bornes de la boucle ont bien été précalculées puisque -2000 s’exprime en représentation en complément à deux comme 0xFFFFF830 (lignes 3ca à 3d0) et l’itération incrémentant zr est implémentée comme un décrément de -20 (lignes 4e2 à 4e8) !
3.6 Temps d’exécution
Tous les temps d’exécution s’obtiennent en prenant soin d’éliminer toute communication – excessivement lente – et répéter chaque calcul itérations fois pour obtenir des temps d’exécution en secondes facilement mesurables. Compte tenu de la vaste différence de puissance de calcul des cœurs de processeurs considérés, le nombre de calculs de la fractale de Mandelbrot a été ajusté comme indiqué en deuxième ligne du tableau de la figure 4.
On notera que dans le code de la section 3.1, nous avons préfixé les déclarations de variables du mot clé volatile pour interdire à gcc d’optimiser le code associé à ces variables et éliminer le code mort en l’absence d’affichage. En effet, avr-gcc élimine (option -Os) purement et simplement tout le code si nous ne prenions pas ce soin, et une incertitude subsiste sur l’interdiction d’optimisation sur volatile montype zr,zi,seuil; puisque le temps d’exécution diffère si ces variables, pourtant au cœur de l’algorithme, ne sont pas déclarées en volatile (colonne simavr, gauche). Le compromis entre optimiser sans éliminer abusivement le code utile reste donc subtil : à trop vouloir éliminer de code considéré comme inutile, gcc rend le code excessivement rapide, mais incapable d’aboutir au résultat escompté !
Nous constatons que :
- l’utilisation de la représentation en virgule flottante, émulée en logiciel sur le Cortex-M3 sur STM32F1, induit une augmentation dramatique du temps d’exécution en l’absence de FPU ;
- flottant ou virgule fixe n’a qu’un impact marginal sur le temps d’exécution sur le Cortex-M4 du STM32F4 avec un léger gain pour les entiers ;
- le calcul flottant est plus rapide que le calcul sur 32 bits pour un Atmega32U4 émulé par simavr, une affirmation corroborée sur divers forums, puisque ces deux modes de calcul doivent être émulés par logiciel sur le petit cœur 8 bits d’Atmel/Microchip. Les mesures sur simavr, en analysant la trace résultante de la simulation (figure 5) et sur microcontrôleur (allumage/extinction d’une LED en début et fin de calcul) ont été effectuées indépendamment, corroborant l’excellent respect du timing de simavr, avec ici les valeurs numériques pour un cadencement à 16 MHz ;
- alors que les cœurs ARM ne bénéficient pas significativement de remplacer la division par 1000 lorsque 3 décimales sont utilisées par rapport à un décalage logique de 10 bits à droite (≫10), le gain en performance dans simavr est significatif.
4. La fractale de Newton
Le cas de la fractale de Newton est l’opportunité d’appréhender le cas de la division en virgule fixe. La méthode de Newton permet d’efficacement trouver la solution d’une fonction dérivable f(x) = 0 en itérant la suite xn+1 = xn-f(xn)/f’(xn) selon le principe de rechercher à chaque fois l’intersection de la dérivée avec l’axe des abscisses et ainsi converger petit à petit vers la solution. Cette méthode de résolution s’applique au cas f(x)∈ℂ. L’étude de la solution vers laquelle converge la suite en fonction du point de départ x0∈ℂ a donné lieu à la découverte de la fractale de Newton [5].
Nous allons nous intéresser au cas le plus simple de f(x) = x3-1, x∈ℂ et tracer la racine vers laquelle la suite converge en fonction de la valeur initiale de x0 dans le plan complexe compris entre [-1,4;1,44] pour la partie réelle et [-0,8;0,8] pour la partie imaginaire par pas de 0,02. Les racines de x3-1 sont évidemment exp(j2π/n), n∈[0..2] qui se distingueront pour la racine réelle par une partie réelle positive (+1) tandis que les deux racines complexes (-1±√3)/2 présentent une partie réelle négative, mais une partie imaginaire positive ou négative, fournissant des critères simples de discrimination. La dérivée de z3-1 est 3z2, donc la suite est z→z-(z3-1)/(3z2)=(3z3-z3+1)/(3z2)=(2z3+1)/(3z2). Le facteur d’homothétie est à peine plus subtil à sélectionner ici que dans le cas de la fractale de Mandelbrot, puisque le numérateur est mis au cube, amplifiant les risques de dépassement de capacité de l’entier qui contient z si nous n’y prenons garde avec SCALE trop important.
La fonction qui nous manque dans la bibliothèque de calcul sur les nombres complexes implémentée auparavant est le quotient de deux nombres complexes. L’approche classique pour éliminer la partie imaginaire du dénominateur est de multiplier numérateur et dénominateur par le complexe conjugué * du dénominateur, sachant que z x z* = |z|2 ∈ ℝ. Le dernier point concerne le facteur d’homothétie : de même que le résultat du produit devait être tronqué des décimales ajoutées par la multiplication, nous devons ici d’abord multiplier le numérateur du facteur d’homothétie pour ne pas perdre de résolution lors du quotient. Le résultat est :
Le bon fonctionnement de cette fonction est validé sur PC par :
Ceci confirme que (1+8j)/(-2-j) = -2-3j et (1+6j)/(-1-j) = -3,5-2,5j.
La convergence sera déterminée par un module suffisamment proche de 1, condition vérifiée par les trois racines.
Le résultat obtenu par calcul sur nombres à virgule flottante est illustré en figure 6, qui se compare favorablement au calcul sur des entiers, avec un facteur d’homothétie pour éviter les risques de dépassement de capacité de stockage d’un entier codé sur 32 bits, tel qu’affiché sur la figure 7.
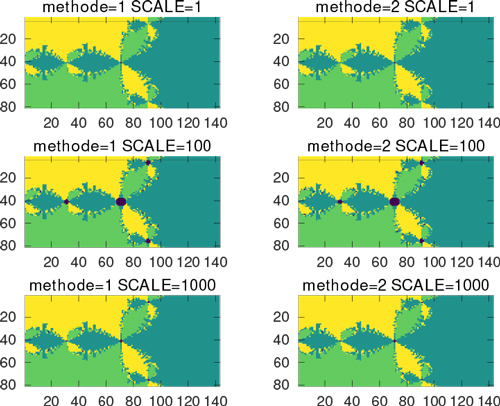
Nous avons vu que le calcul du cube présente un réel risque de dépassement de capacité : à titre d’exemple, avec trois décimales significatives, ma multiplication par 1000 des réels pour exprimer les entiers se traduit par 10003 = 109 qui nous rapproche dangereusement des 2,14 x 109 d’un entier 32 bits signé. Nous pouvons nous interroger sur la différence entre une expression de la suite de Newton comme zn+1 = (2zn3+1)/(3zn2) ou zn+1 = 2/3zn+1/(3zn2) pour éviter le calcul du cube. Ce type de prototypage est bien plus simple à mettre en œuvre sous GNU/Octave, version libre de Matlab, comme proposé ci-dessous où les deux fonctions de multiplication et division en virgule fixe sont réimplémentées en profitant de ce que GNU/Octave connaît la notion de complexe (j2 = -1), tandis que le cas SC=1 implémente le calcul flottant et SC>1 la notation en virgule fixe, l’addition étant toujours faite avec les décimales, car sans grande importance dans cette suite. Le programme ci-dessous itère sur la résolution (boucle sur SC et sur l’expression de la suite (boucle sur methode)) :
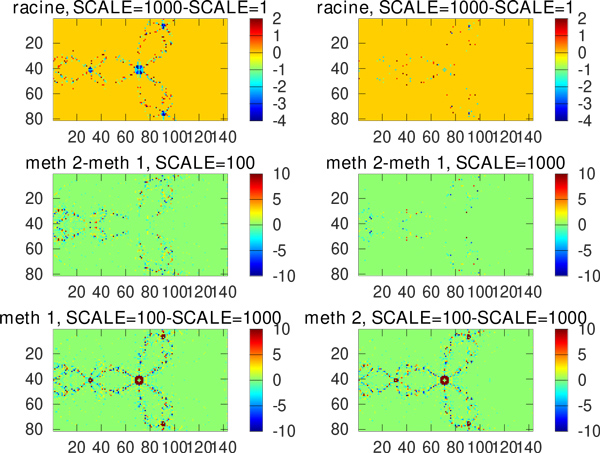
Nous omettons la figure qui compare les deux méthodes dans le cas de l’implémentation en virgule flottante : la racine sur laquelle les deux expressions de la suite et le nombre d’itérations pour converger sont strictement identiques dans les deux cas. Cependant, nous constatons en figures 8 et 9 une différence sur la racine identifiée ou le nombre d’itérations nécessaires pour converger selon la résolution de l’expression en virgule fixe et la méthode sélectionnée.
Développement de 1/z2 en série de Taylor
Quitte à effectuer des calculs un peu faux, pourquoi ne pas tenter une solution complètement fausse visant à éliminer le calcul de l’inverse 1/z2 proche de la racine z ≈ 1. En effet, nous savons que 1/(1 − x)2 s’exprime autour de x → 0 comme un développement de Taylor de la forme 1 + 2x + 3x2 + ... = Σn n · xn−1. Donc en posant z = 1-x nous avons une solution proche de z → 1. Le calcul de la suite devient donc, sous GNU/Octave, de la forme :
avec l’ajout dans denum des termes polynomiaux des plus élevés vers les plus faibles – ici, nous avons volontairement commenté les termes d’ordre 4 et 5. Malheureusement, cette solution diverge trop rapidement quand z s’éloigne de 1 et ne permet pas à la suite de converger vers une racine. Les figures suivantes présentent l’erreur entre le module de la série de Taylor aux 2, 3 et 4e ordre, en 3D dans le plan complexe et en 2D selon l’axe réel (partie imaginaire nulle avec une solution exacte en 1 + 0j) et pour le cas extrême d’une partie imaginaire de −0, 5j (tracé toujours selon l’axe réel).
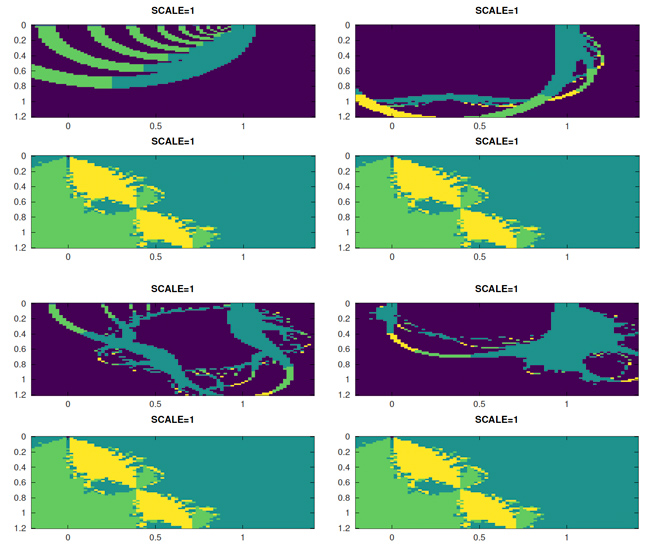
Les motifs restent néanmoins élégants et évoluent en fonction du nombre de termes du polynôme inclus dans la suite, pour toujours donner une solution autour de 1, mais diverger plus ou moins rapidement en s’éloignant de 1 – ci-après la carte de la racine atteinte pour les ordres 2 à 5, avec bleu foncé indiquant l’absence de convergence et bleu clair la racine 1 + 0j. Pour toutes ces figures, l’axe réel va de -0,2 à 1,4 et l’axe imaginaire de 0 à 1,2 :
À chaque fois, la figure du haut est la solution atteinte avec le développement de Taylor et en bas, la solution recherchée avec l’expression complète de la suite.
Conclusion
Nous avons proposé une architecture de programme facilement portable d’une architecture à une autre par l’utilisation de stubs implémentant les particularités de l’accès au matériel dans un fichier séparé du programme, contenant la partie algorithmique qui reste portable. Nous sélectionnons l’implémentation appropriée lors de l’édition de liens par le Makefile. Ce faisant, nous avons proposé le calcul des fractales de Mandelbrot et de Newton sur architecture 8 bits Atmel/Microchip et sur architectures 32 bits ARM pour une comparaison des performances de calcul entre les implémentations des opérations arithmétiques en virgule fixe et en virgule flottante. Alors que la première solution est fondamentale pour tirer le meilleur parti des microcontrôleurs aux ressources les plus réduites, l’avènement d’unités de calcul flottant même dans des architectures modestes rend le choix délicat, compte tenu du compromis entre le temps de développement, les risques de dépassement de capacité, le temps d’exécution et le coût unitaire du composant.
Les codes sources proposés dans cet article sont disponibles sur https://github.com/jmfriedt/arithmetique.
Remerciements
Les ouvrages de la bibliographie qui ne sont pas librement disponibles sur le Web ont été acquis auprès de Library Genesis à gen.lib.rus.ec, une ressource indispensable à nos activités de recherche et développement.
Références
[1] « Global 8 bits microcontroller Market », 2020, mentionné sur :
https://www.mordorintelligence.com/industry-reports/8-bit-microcontroller-market-industry
[2] Projet Arénaire, « Floating-Point Arithmetic », LIP/ENS Lyon, 2009 :
https://perso.ens-lyon.fr/jean-michel.muller/chapitre1.pdf
[3] J.S. VETTER et al, « Striving for Performance Portability of Software Radio Software in the Era of Heterogeneous SoCs », Free Software Radio Devroom, FOSDEM, 2020 : https://archive.fosdem.org/2020/schedule/event/fsr_striving_for_performance_portability/
[4] International Standard, « Programming languages - C », ISO/IECISO/IEC 9899:201x, 2011 :
http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1570.pdf annonce au sujet des tailles d’entiers en section 5.2.4.2.1 que « Their implementation-defined values shall be equal or greater in magnitude to those shown ».
[5] H.-O. PEITGEN, H. JÜRGENS, D. SAUPE, « Chaos and Fractals: New Frontiers of Science », Springer, 1992.
[6] B. MANDELBROT, « The Fractal Geometry of Nature », Times Books, 1982.
[7] R. BROOKS & P. MATELSKI, « The dynamics of 2-generator subgroups of PSL(2,C) », in Irwin Kra (ed.). Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference.
[8] Site du projet XaoS : https://xaos-project.github.io/
[9] J. FRIEDT, « Émulation d’un circuit comportant un processeur Atmel avec simavr », Hackable no34, juillet-septembre 2020 :
https://connect.ed-diamond.com/Hackable/HK-034/Emulation-d-un-circuit-comportant-un-processeur-Atmel-avec-simavr



 Ajouter à une liste de lecture
Ajouter à une liste de lecture