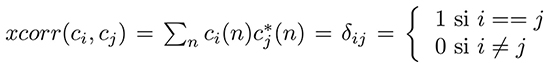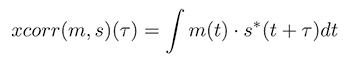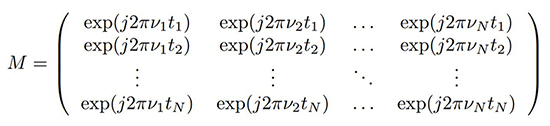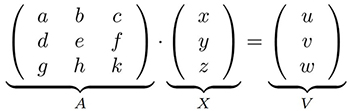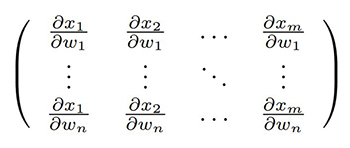L’algèbre linéaire est habituellement introduite comme un formalisme abstrait d’opérations matricielles. Nous proposons quelques applications concrètes de cette algèbre dans le cas du traitement de signaux radiofréquences, ainsi que des mises en œuvre sur processeur généraliste (CPU) et graphique (GPU) en vue de passer d’un post-traitement de signaux enregistrés à un traitement en temps réel. Nous survolerons ainsi quelques fonctions des principales bibliothèques de calcul linéaire pour proposer des implémentations de corrélation ou d’optimisation aux moindres carrés.
1. Introduction : algèbre linéaire et calcul matriciel
Nous avons abordé le traitement du signal sur systèmes embarqués aux ressources réduites [1] et avons vu qu’avec même peu de mémoire, il est possible de traiter des petits vecteurs de signaux. De façon générale, le traitement du signal se cantonne communément aux fonctions linéaires f vérifiant, par définition, f(ax+by)=af(x)+bf(y). En effet, depuis Fourier, nous avons appris la puissance de décomposer tout signal arbitraire x comme somme de fonctions trigonométriques pondérées X, et par conséquent de bénéficier de la connaissance du comportement à chaque fréquence ν du système étudié S(ν) pour en déduire son comportement en présence d’un signal quelconque ∑n cn·X(νn) puisque la linéarité indique alors une réponse de la forme S(∑n cn X(νn))=cn∑n S(X(νn)). En particulier, lorsque le système physique répond selon des équations dérivées, la décomposition en fonctions trigonométriques s(t)=exp(jω t) permet de remplacer la dérivée première ds/dt par jωs et la dérivée seconde d2s/dt2 par −ω2s, avec ω=2π ν, donnant ainsi l’opportunité d’atteindre une solution aux équations différentielles, sans devoir passer par une résolution potentiellement pénible et instable dans le domaine temporel.
Toute opération linéaire se formalise dans une expression de produit matriciel, dans lequel les divers termes de l’équation sont fournis comme vecteurs et matrices. À titre d’exemple, le carré de la norme d’un vecteur ![]() que l’on sait être x2+y2+z2 s’exprime matriciellement comme
que l’on sait être x2+y2+z2 s’exprime matriciellement comme ![]() avec ′ la transposée, potentiellement avec un complexe conjugué si v est complexe (au sens de posséder une partie imaginaire). Des langages tels que Matlab et sa version libre GNU Octave tirent pleinement profit de cette expression compacte pour implémenter en quelques lignes des algorithmes potentiellement complexes, mais au détriment des performances d’un langage interprété. Ainsi dans GNU Octave, le calcul mentionné ci-dessus s’implémente comme :
avec ′ la transposée, potentiellement avec un complexe conjugué si v est complexe (au sens de posséder une partie imaginaire). Des langages tels que Matlab et sa version libre GNU Octave tirent pleinement profit de cette expression compacte pour implémenter en quelques lignes des algorithmes potentiellement complexes, mais au détriment des performances d’un langage interprété. Ainsi dans GNU Octave, le calcul mentionné ci-dessus s’implémente comme :
qui donne 14, la norme au carré obtenue par 1+4+9. Notez que .' dans GNU Octave prend la transposée des termes, complexes ou non, tandis que ' (sans le point) prend le complexe conjugué de l’argument s’il est complexe. Ainsi :
répond 17 qui est la bonne réponse, tandis que v.'*v répond 11 + 12i qui n’a pas de sens pour calculer une longueur.
Les variables i et j dans Octave
Alors qu’il est courant dans nombre de langages d’appeler les indices i et j, ces noms sont absolument à proscrire dans Matlab et GNU Octave, car représentent la partie imaginaire définie comme i2=j2=−1. Définir une variable du nom de i ou j en écrasera le contenu et rendra tout calcul sur des nombres complexes erroné. Selon les domaines liés à la physique ou à l’ingénierie, le complexe se nomme i ou j, mais tous deux représentent la même grandeur.
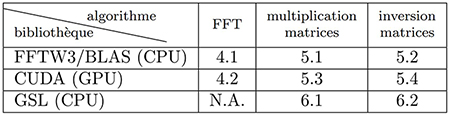
L’algèbre linéaire est tellement commune pour résoudre des problèmes de physique ou d’ingénierie que nombre de bibliothèques ont été rédigées pour optimiser ces calculs (Fig. 1). Mentionnons sans ordre particulier les classiques BLAS (Basic Linear Algebra Subprograms) et LAPACK (Linear Algebra Package), GSL (GNU Scientific Library) et, pour la transformée de Fourier, FFT3W pour les processeurs généralistes, ainsi que VOLK pour tirer le meilleur parti des instructions SIMD (Single Instruction, Multiple Data pour répéter la même opération en parallèle sur plusieurs données) et finalement, ce qui nous intéressera ici, CUBLAS et CUFFT les implémentations des algorithmes d’algèbre linéaire et de passage dans le domaine de Fourier pour CUDA, l’environnement propriétaire des processeurs graphiques (GPU) de NVIDIA. Ces fonctions seront peut-être bientôt intégrées dans les normes officielles du C++ (https://isocpp.org/files/papers/P1673R13.html), mais on n’en est pas encore là et l’utilisation de bibliothèques externes reste nécessaire pour ces fonctionnalités.
En effet, sans complaisance pour l’absence d’infrastructure libre pour exploiter les GPU NVIDIA, force sera de constater que ces processeurs vont très, très vite. Nous avons été exposés malgré nous à un code CUDA pour identifier par corrélation des temps de communication par satellite, et devions en comprendre le fonctionnement pour les exploiter en post-traitement sur processeur généraliste. L’histoire que nous allons raconter ici relate les explorations pour traduire du code CUDA en C++, tester le code CUDA après avoir découvert être en possession d’un GPU compatible CUDA, et comparer les performances. Sans prétention de benchmark détaillé toujours sujet à controverses, nous nous contenterons de valider la cohérence des résultats lors des calculs et de mesurer le temps d’exécution sur des applications bien particulières faisant appel à l’algèbre linéaire, sans prétention de comparaison quantitative ou rigoureuse de ces temps d’exécution.
Quelques concepts de CUDA et des GPU
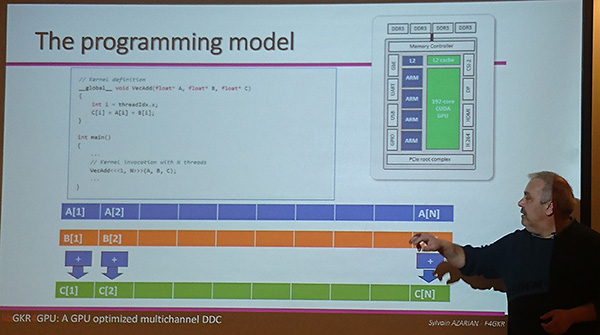
NVIDIA a produit une multitude de GPU avec des fonctionnalités croissantes : les performances de calcul scientifique des GPU sont qualifiées par leur CUDA Capability. Il s’agit d’un nombre majeur et un nombre mineur qui peut être identifié, comme nombre d’autres paramètres, par deviceQuery fourni dans https://github.com/NVIDIA/cuda-samples sous Samples/1_Utilities/deviceQuery. Sur notre carte vidéo T400 équipant un ordinateur DELL récent, nous apprenons que CUDA Capability: 7.5 (« Turing ») et Maximum number of threads per block: 1024 ou Max dimension size of a thread block (x,y,z): (1024, 1024, 64) qui définira le nombre maximum de threads exécutés en parallèle sur le GPU. Afin de bénéficier des performances d’une certaine génération de GPU, nous compilerons en passant à nvcc – le compilateur C de NVIDIA fourni par CUDA – l’argument -arch=sm_xy avec x le major number de la génération de GPU et y le minor, dans notre cas -arch=sm_75.
Comme tout traitement sur système hétérogène, le cœur du problème est de transférer les données de la mémoire d’une zone de calcul à une autre en l’absence de mémoire partagée, et de les y laisser le plus longtemps possible. Dans un contexte de traitement de signaux de radio logicielle, les informations proviennent forcément d’un périphérique du CPU (Ethernet, USB) et se trouvent dans la mémoire du processeur. Effectuer le traitement sur GPU nécessite de transférer les mesures de la mémoire CPU vers la mémoire GPU cudaMemcpy(dev_mem, host_mem, sizeof(cuDoubleComplex) * taille,cudaMemcpyHostToDevice); avec la convention que l’hôte est le CPU et le périphérique device est le GPU. Cette opération est gourmande en temps et impose donc que le traitement massivement parallèle sur GPU justifie du temps de transfert, et qu’ensuite tout traitement ultérieur reste sur le GPU aussi longtemps que possible. Nous ne nous intéresserons pas ici à l’implémentation sur GPU de traitements généralistes, un sujet abordé il y a longtemps dans [2, 3, 4], mais nous contenterons d’exploiter les bibliothèques fournies par CUFFT et CUBLAS en respectant les préceptes de conserver les données dans la mémoire de l’hôte ou de la cible le plus longtemps possible.
Dans les pages qui vont suivre, nous allons nous intéresser à trois applications de complexité croissante – la transformée de Fourier, le produit matriciel, et l’inversion de matrices rectangulaires pour fournir la solution optimale aux moindres carrés lorsqu’il y a plus d’observations que de variables – sur trois infrastructures de calcul que sont BLAS, GSL et CUDA. Afin d’introduire ces concepts, nous les mettrons dans un premier temps en œuvre dans GNU Octave, version libre de Matlab particulièrement adéquate pour exprimer un problème d’algèbre linéaire sous forme d’expressions matricielles.
2. Application dans le contexte de la radio logicielle
Une acquisition par un récepteur radiofréquence échantillonnée en temps discret peut être considérée comme un vecteur avec des échantillons successifs xn indexés par n∈ℕ, et l’analyse dans le domaine spectral impose de supposer l’intervalle de temps entre deux échantillons constant et égal à la période d’échantillonnage Te. Sous réserve de ne perdre aucun échantillon lors des transferts, la connaissance de l’indice n de chaque point permet de remonter à sa date d’acquisition n·Te quelle que soit la latence de transfert des données lors de la communication ou le traitement. Nous voici déjà munis des vecteurs que nous avons introduits ci-dessus.
Le GPU pour le calcul de filtres
Une des opérations les plus classiques en radio logicielle est la transposition de fréquence pour centrer une sous-porteuse vers 0 Hz, suivie d’un filtrage et d’une décimation (DDC ou Digital Down Converter). Nous n’aborderons pas ces calculs qui imposent un kernel dédié alors que nous nous focalisons ici sur les traitements d’algèbre linéaire par opérations matricielles et transformées de Fourier, mais Sylvain Azarian aborde en détail ce problème dans [5], y compris le partage de mémoire entre CPU et GPU et les options de compilation pour paralléliser effectivement les calculs sur GPU.
Nombre de traitements assemblent des copies de ces vecteurs accolés les uns à côté des autres pour former des matrices. Mentionnons deux cas concrets :
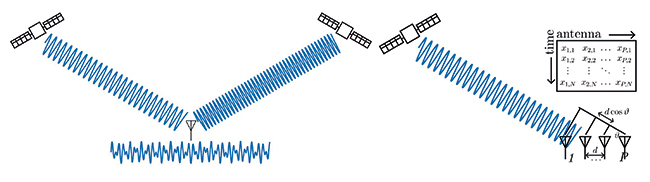
- l’acquisition de signaux radiofréquences par plusieurs antennes spatialement distribuées, ou acquis successivement par une même antenne qui se déplace, en supposant la scène illuminée par un émetteur statique pendant le mouvement de l’antenne. Ce cas des RADAR MISO ou MIMO (Multiple Input et Multiple ou Single Output) forme naturellement une matrice avec chaque colonne représentant une position d’antenne et chaque ligne une date d’échantillonnage. Si en plus les antennes sont alignées et équidistantes (ULA pour Uniform Linear Array), les analyses deviennent très sympathiques, car à une vitesse de la lumière près, les échantillons sont périodiques le long des colonnes et le long des lignes ;
- un même signal temporel décalé dans le temps en vue de trouver les copies d’un signal connu retardé dans une mesure bruitée : chaque colonne contient alors xn−pτ avec n l’indice du temps le long des colonnes et pτ un retard qui s’incrémente le long des colonnes d’indice p. Nous verrons que ce type de matrice sera utile pour trouver et éliminer des copies retardées dans le temps d’un signal connu, par exemple lors de l’enregistrement du signal rétrodiffusé par des cibles illuminées par une source radiofréquence à des distances différentes du récepteur.
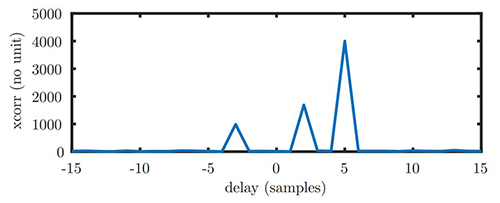
Afin de fournir quelques cas concrets d’utilisation d’algèbre linéaire en liaisons radiofréquences, considérons le cas d’une multitude d’émetteurs communiquant avec un même récepteur (au hasard, un relais de téléphonie mobile). L’antenne réceptrice reçoit la somme vectorielle des champs électriques incidents, et l’objectif du traitement par radio logicielle est de décoder les contributions individuelles de chaque émetteur. Ainsi, une première question est de savoir si un interlocuteur est présent dans le fouillis des communications. Dans une différentiation des émetteurs par codes orthogonaux de type CDMA – Code Division Multiple Access tel qu’utilisé par les constellations de navigation par satellite (GPS, Galileo, Beidou) où les émissions se font sur la même fréquence porteuse et il faut distinguer les émetteurs dans l’espace, ou la téléphonie mobile 3G – chaque bit de message est porté par une séquence pseudoaléatoire cn, et la recherche de la présence de cette séquence dans le signal bruité sn s’obtient par intercorrélation xcorr(), tel que nous le verrons ci-dessous. La définition de l’orthogonalité de deux codes indique que
nous allons voir que plusieurs approches sont disponibles pour calculer la corrélation dans le domaine spectral et le domaine temporel, et la méthode la plus rapide n’est pas toujours celle qu’on pourrait croire. De la même façon dans les mesures de distance de cibles par RADAR, un signal émis connu est réfléchi par plusieurs cibles statiques et un récepteur reçoit la somme de ces contributions noyées dans le bruit en retour : le signal rétrodiffusé par chaque cible est identifié par intercorrélation du signal reçu avec le motif émis.
Bases orthogonales
Rappelons la définition d’orthogonalité de la base des codes (vecteurs de longueur N) ci sur laquelle décomposer un signal quelconque de longueur N comme x=∑N-1n=0 ai·ci(n) : la base des ci est dite orthogonale si la corrélation de ci avec cj est nulle si i≠ j et non nulle uniquement si i==j. La base est dite orthonormale si la corrélation d’un code avec lui-même donne 1, et dans ce cas les poids ai s’obtiennent chacun par corrélation du signal x(n) avec ci(n). Un cas particulier de la transformée de Fourier est cν(t)=exp(j2π ν t), mais de façon générale toute séquence pseudoaléatoire de longueur maximale pourra convenir. Ce type de code est utilisé dans les communications multiplexées par code, CDMA.
Une fois que nous avons connaissance de la présence d’un signal connu dans la somme des signaux reçus, il peut être souhaitable de retrancher ce signal devenu indésirable pour analyser les autres composantes plus faibles : en RADAR, cela s’appelle Direct Signal Interference (DSI) removal puisque le chemin direct de l’émetteur au récepteur – dont la puissance décroît comme l’inverse du carré de la distance – est beaucoup plus faible que le signal réfléchi par des cibles dont la puissance rétrodiffusée décroît comme la puissance quatrième de la distance, ou Successive Interference Cancellation (SIC) en communication numérique (Fig. 2) [6].
Ainsi, nous désirons optimiser la vitesse de calcul de trois algorithmes de traitement linéaire du signal en tirant le meilleur parti des périphériques matériels à notre disposition :
- Le passage du domaine temporel au domaine spectral par transformée de Fourier, et comparaison de FFT3W avec CUFFT, en particulier dans le contexte du calcul de corrélations.
- Le calcul de corrélations dans le domaine temporel par produit matriciel quand le retard est connu comme étant faible, par exemple dans le cas d’une boucle d’asservissement de retard (Delayed Locked Loop ou DLL).
- L’identification du retard de signaux polluants – leurrage ou brouillage – dans un signal recherché par calcul de la pseudo-inverse, une méthode pour identifier la pondération optimale d’un polluant dans un signal, au détriment de fortes ressources de calcul (par rapport à la descente de gradient stochastique, par exemple).
Nous conclurons avec une extension vers les réseaux de neurones, domaine à la mode qui semble contribuer à la popularité des GPU NVIDIA, si l’on en croit la presse (https://www.bbc.com/news/business-66601716).
Comme dans toute bonne série, mieux vaut commencer par le dernier épisode pour s’assurer que la fin de l’histoire mérite à être connue, avant de revenir vers les premiers épisodes pour comprendre comment nous en sommes arrivés à cette conclusion. Ainsi, posons dans un premier temps quelques bases de problèmes d’algèbre linéaire rencontrés en traitement de signaux acquis par radio logicielle, justifiant notre recherche de performance de calcul. En effet, un récepteur de radio logicielle acquiert aisément quelques mégaéchantillons à quelques dizaines de mégaéchantillons par seconde, et analyser ces signaux requiert souvent des produits matriciels ou transformées de Fourier sur des vecteurs de telles longueurs.
3. Corrélations dans le domaine spectral et temporel, et optimisation aux moindres carrés : principes sous GNU Octave
Nous avons abordé à de multiples occasions le problème de la corrélation [8] qui consiste à rechercher un motif supposé connu m(t) en fonction du temps (ou de l’espace en traitement d’images) t dans un signal bruité s(t), avec potentiellement plusieurs motifs présents successivement dans s pour divers retards τ.
L’estimateur naturel pour identifier m dans s avec un retard τ inconnu est l’intercorrélation :
ou dans sa version discrétisée qui remplace le temps continu t par un indice k et le retard continu τ par un indice n :
Cet algorithme est de complexité N2 si m et s contiennent N échantillons, puisque pour chaque somme il faut N multiplications, que nous répétons pour tout n∈[0:N−1]. Grâce au théorème de convolution, nous pouvons passer dans le domaine de Fourier par la transformée de Fourier notée FT tel que M(f)=FT(m)=∫m(t)exp(j2π ft)dt et ainsi :
avec * le complexe conjugué ; cette expression se retrouve dans le code source de GNU Octave dans la fonction /usr/share/octave/packages/signal-1.4.5/xcorr.m lorsque :
qui bénéficie de l’implémentation de la transformée de Fourier rapide FFT de Gauss qui profite de la symétrie des fonctions trigonométriques pour implémenter cet algorithme en N·log2(N) au lieu de N2.
Nous en concluons donc que la corrélation doit toujours se calculer dans le domaine de Fourier pour être efficace... ou pas. En effet, dans xcorr() de GNU Octave, un dernier argument est Maxlag le retard maximum envisagé entre m et s. Si nous pouvons faire une hypothèse sur τ le retard maximum de m dans s, il n’est peut être pas utile de rechercher de façon exhaustive tous les N cas possibles alors que nous savons que n≤ Maxlag. Or, chaque recherche pour un n donné ne prend que N multiplications, donc si Maxlag est suffisamment petit, peut-être que l’approche temporelle devient plus rapide que l’approche spectrale. Ceci est d’autant plus vrai dans le cas d’une boucle à verrouillage de phase ou de retard (Phase Locked Loop ou PLL, et DLL) dans laquelle les paramètres sont recalculés à chaque itération en vue de maintenir n proche de 0 : c’est le cas, dans le traitement des signaux satellitaires de navigation, lorsque la phase d’acquisition grossière est achevée (qui nécessite une recherche exhaustive sur les N retards possibles) et que la phase de tracking fait l’hypothèse qu’entre deux mesures les satellites sont dans des conditions relativement proches.
Le bénéfice de l’approche temporelle ou spectrale se fait en comparant la complexité du premier en N2 par rapport au second Nlog2(N) donc la question se pose lorsque Maxlag devient petit face à log2(N) : dans ce cas, l’approche temporelle pourrait devenir plus rapide que l’approche spectrale. Ainsi, sans hypothèse sur le retard du motif dans le signal, il faut calculer tous les cas de Nlag∈[−N/2:N/2−1] et l’algorithme est de complexité N2 dans le domaine temporel pour devenir Nlog2(N) en passant dans le domaine de Fourier et en profitant de la transformée de Fourier rapide. Si cependant Nlag est limité à quelques valeurs proches de 0, c.-à-d. |MaxLag|≪ log2(N), alors il vaut mieux une implémentation dans le domaine temporel que nous allons implémenter comme produit matriciel.
Afin de calculer une corrélation pour divers retards Nlag dans le domaine temporel, nous devons effectuer xcorr(m,s)(Nlag)=∑mn×sn+Nlag et cela peut s’exprimer naturellement sous forme de matrice par s×M avec M une matrice contenant dans chacune de ses colonnes la copie de s retardé d’un nombre d’échantillons égal à l’indice de la colonne. On notera que la convolution ou la corrélation bénéficient des instructions SIMD, car chaque produit des deux éléments des deux vecteurs d’entrée est indépendant de ses voisins, et seule l’accumulation finale a besoin de tous les résultats intermédiaires calculés en parallèle pour achever l’intégrale, tel que le montre src/algorithms/tracking/libs/cpu_multicorrelator.cc de gnss-sdr à https://github.com/gnss-sdr/gnss-sdr.
En considérant un vecteur de mesures s dans lequel nous désirons rechercher le motif m connu, nous exprimons dans GNU Octave :
et la matrice contenant les copies retardées de Nlag de m se construit comme :
Grâce à cette matrice et le vecteur de mesures, la corrélation devient dans le domaine temporel :
qui se compare avantageusement au calcul dans le domaine spectral par :
Ce calcul, que nous retrouverons dans https://github.com/jmfriedt/learning_blas sous octave/demo_xcorr.m, est itéré pour deux cas de Nlag petit et grand :
et le temps de calcul est obtenu en préfixant le produit matriciel et la fonction xcorr() de tic et une instruction toc en fin de la séquence à horodater. GNU Octave répond :
et le verdict est sans appel : le produit matriciel prend toujours à peu près le même temps quel que soit Maxlag, tandis que la méthode temporelle est beaucoup plus rapide pour Maxlag petit, mais beaucoup plus lente pour Maxlag grand devant log2(N)≃ 10.
Notre premier objectif dans la prose qui va suivre sera donc de calculer les corrélations dans le domaine temporel, sous forme de produit matriciel, et le domaine spectral, par transformée de Fourier rapide, et de comparer les temps d’exécution des diverses infrastructures de calcul envisagées.
Savoir qu’un motif m se trouve dans un signal s est bien, mais parfois nous voudrions savoir quelle est sa pondération, à savoir quelle amplitude (et phase si m et s sont des nombres complexes) caractérise la contribution à m dans s. Ce problème se retrouve dans nombre de configurations, qu’il s’agisse d’un émetteur puissant dont la contribution couvre celle d’un autre émetteur moins puissant dont la somme des contributions est reçue sur un récepteur, et ce, par exemple dans le cas de RADAR monostatiques où une séquence émise est reçue par le récepteur bien plus fort que les échos rétrodiffusés par les cibles (problème d’éliminer le signal direct DSI). Un autre cas pratique est le brouillage et le leurrage de signaux, par exemple de signaux de navigation par satellite, que nous avons abordés dans ces pages [9] : si deux antennes reçoivent des signaux supposés venir de satellites dispersés sur la sphère céleste, alors une source de brouillage ou de leurrage apparaîtra avec des contributions (poids, phase) identiques pour tous les satellites, une solution impossible pour le vrai signal venant d’une multitude de directions différentes. Si maintenant nous voulons retrouver le vrai signal en éliminant la source de brouillage ou de leurrage, nous devons estimer finement la pondération de m dans s afin de le retrancher et faire ressortir les signaux d’origine.
S’il y a autant d’échantillons dans m que de poids à rechercher, le problème est simple puisque nous l’avons déjà illustré en introduisant le produit matriciel et l’inverse de matrice pour résoudre un système linéaire d’équations : les copies de m dans s sont pondérées par des poids p (potentiellement complexes) et si une matrice M formée des copies retardées de τ dans le temps m(t−τ) est formée, alors s contient M× p et les pondérations p se trouvent simplement comme solution de M−1× s, comme nous venons de le voir.
Cependant, M−1 n’existe que si M est carrée, donc contient autant de lignes que de colonnes. Cette situation simple n’est pas utile en pratique, car les retards τ sont souvent peu nombreux, typiquement quelques échantillons de retard lors de l’éblouissement à courte portée d’un récepteur RADAR par son émetteur proche en configuration monostatique, ou quelques échantillons de retard dans un asservissement de DLL comme nous l’avons mentionné en communication numérique. Par contre, s est bruité et trouver m dans s peut nécessiter nombre de moyennages pour abaisser le bruit et faire ressortir la contribution du signal interférent dans ce bruit. Il est donc judicieux d’avoir de très nombreuses observations – autant que possible tant que la scène reste stationnaire (afin que les poids p restent constants pendant cette analyse), pour trouver les quelques coefficients de p avec autant de précision que possible.
Dans ce contexte, la matrice M des copies retardées de Nlag de m n’est plus du tout carrée, puisqu’elle contient autant de lignes que d’échantillons de s sur lesquels se calcule l’intégrale, alors que nous avons relativement peu de colonnes le long de l’axe des retards. Comment inverser une matrice rectangulaire qui contient beaucoup de lignes et peu de colonnes pour trouver une solution optimale de p ?
Roger Penrose, et d’autres avant lui identifient le calcul de la pseudo-inverse de A rectangulaire définie comme :
pinv(A)=(A′·A)−1·A′
avec ′ la transposée de la matrice, en prenant le complexe conjugué si ses termes sont complexes. La fonction pinv() de GNU Octave effectue cette opération. Par exemple :
montre bien comment plusieurs observations (ici, 5) de mêmes variables (ici, tous les p sont supposés valoir idéalement 1) vont permettre d’atténuer l’effet du bruit rand(5,1)-0.5 sur les observations et de trouver une solution à peu près correcte – tous les pinv(A)*B valent à peu près 1, d’autant meilleure que les observations sont nombreuses, mais nécessitant de manipuler des vecteurs et matrices d’autant plus grands et donc des calculs d’autant plus longs.
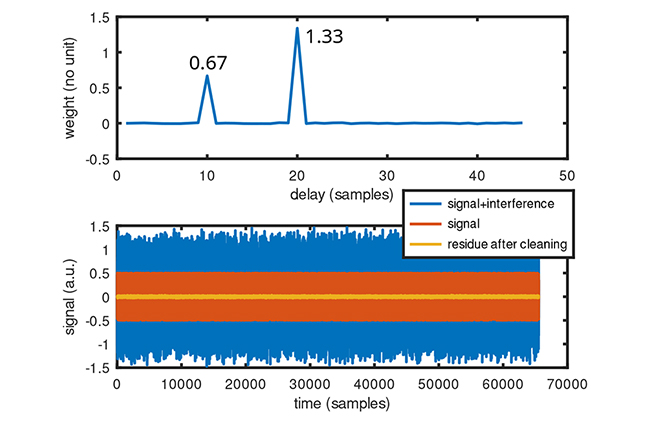
Mettons ces concepts quelque peu abstraits en pratique sur un cas concret d’un signal x reçu par une antenne, mais pollué par un interférent signal supposé connu, par exemple parce que détecté par une seconde antenne – cas du CRPA (Controlled Radiation Pattern Antenna) de l’anti-leurrage et anti-brouillage des signaux de navigation par satellite :
Afin d’illustrer l’identification des retards et les pondérations associées de l’interférent dans un signal bruité, le code ci-dessus propose d’étudier un signal x que nous sauvons avant de le polluer dans xavant. Ce vecteur x est sommé avec des copies décalées dans le temps, ici de 10 et 20 échantillons, d’un interférent signal que nous désirons éliminer. Pour ce faire, la matrice matrice est formée des copies retardées dans le temps de signal : cette matrice possède bien plus de lignes (le nombre de mesures, ou longueur de x) que de colonnes (le nombre de retards considérés, supposé réduit compte tenu de la géométrie entre émetteur, récepteur et réflecteurs).
La question est donc de trouver une matrice P de poids qui, multipliée par la matrice des signaux retardés matrice, que nous noterons M, donnera une représentation fidèle des copies de signal dans x sachant que nous n’avons connaissance que de x et de signal au travers de ses copies retardées dans M. Ainsi, si P· M≃ x, alors une bonne estimation de P est x· M−1. Cependant, M est rectangulaire et son inverse n’est à priori pas définie : nous allons donc utiliser sa pseudo-inverse pinv(M)=M·(M· M′)−1.
Transposition de produit de matrices
On rappelle que (A· B)′=B′· A′ qui permet d’identifier (pinv(M))′=((M·M′)−1·M′)′=M·(M·M′)−1 donc M·(M·M′)−1 et (M· M′)−1·M′ sont deux expressions équivalentes de la pseudo-inverse à une transposée près.
Ici, M·M′ a autant de lignes et de colonnes que de retards, ainsi que son inverse. Par conséquent, (M·M′)−1·M′ a autant de colonnes que de retards et autant de lignes que de mesures, de façon à ce que sa multiplication par x, qui est un vecteur du nombre de mesures, résulte en un vecteur d’autant d’éléments que de retards, et donc chaque valeur est une estimation de la pondération de signal dans x. Une fois que nous connaissons ce vecteur de poids, multiplier P par M fournit une estimation de la somme des copies de signal dans x, et nous traçons (Fig. 3) en bleu x pollué, x avant pollution (rouge), et le résidu en jaune de cette estimation soustraite du vrai x avant pollution, qui serait idéalement nulle si l’estimation des poids avait été parfaite.
Maintenant que le décor est posé – nous désirons détecter la présence d’un motif connu dans un signal bruité pour des retards longs ou faibles selon une approche spectrale ou temporelle, puis identifier la pondération de ces interférents en vue de les retrancher – comment implémenter efficacement ces concepts d’algèbre linéaire avec les outils logiciels et matériels à notre disposition ?
Nous allons explorer trois cas sur CPU : les classiques BLAS et LAPACK en C ou C++ (pour manipuler des grandeurs complexes), et la GSL qui encapsule quelques-uns des reliquats des origines en FORTRAN (FORmula TRANslator) – langage utilisé historiquement pour implémenter nombre de bibliothèques de calcul scientifique – des deux premières bibliothèques. Fort des connaissances acquises sur CPU, nous allons conclure par l’utilisation des GPU pour effectuer ces opérations en bénéficiant des implémentations tirant parti de l’architecture massivement parallèle de ces fonctions dans CUDA.
4. Transformée de Fourier : FFTW3 sur processeur
4.1 FFTW3 sur processeur généraliste CPU
Un calcul courant, gourmand en ressources, que ce soit pour une exploration des propriétés spectrales d’un signal, pour un calcul de corrélation ou pour une interpolation (0-padding), est le passage du domaine temporel au domaine spectral par transformée de Fourier, qui correspond à projeter le signal x sur la base orthogonale des fonctions trigonométriques exp(j2πν t). La notion de projection passe par le produit scalaire de xn par exp(j2πνn) qui s’écrit souvent ⟨xn,exp(j2πν n)⟩=∑n xn× exp(j2πν n) et la notion d’orthogonalité ramène au fait que le produit scalaire de deux fonctions trigonométriques est nul, sauf si elles sont de pulsation égale : ⟨exp(j2πν n),exp(j2πν′ n)⟩=δ(ν,ν′). Ainsi, une transformée de Fourier discrète
est une combinaison linéaire des échantillons x acquis en temps continu x(t) ou discret xn avec les fonctions trigonométriques aux diverses pulsations ω=2π ν qui peut donc s’exprimer sous forme matricielle [10]. Cette expression a surtout un intérêt si on considère une distribution non uniforme de ω puisque les divers termes de la matrice sont définis individuellement.
Cette expression, somme des produits de coefficients constants avec des mesures x, est une expression parfaitement exprimée comme produit matriciel x· M avec la matrice M les termes trigonométriques :
Cette expression matricielle est intéressante, car elle permet de calculer une transformée de Fourier quels que soient les instants de mesure (supposés connus néanmoins) tn et les fréquences de Fourier recherchées νn, n∈ℕ. En l’absence de symétrie dans ces coefficients, le calcul est de complexité N2 puisque chacun des N coefficients nécessite N multiplications.
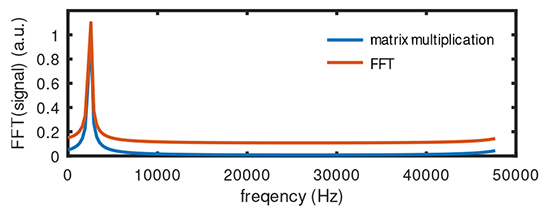
La transformée de Fourier rapide bénéficie de l’hypothèse que les intervalles de temps sont constants ainsi que les intervalles de fréquences. Dans ces conditions, le calcul se décompose comme un arbre binaire profitant des calculs adjacents, et devient un algorithme de complexité Nlog2(N). Nous pouvons nous convaincre de l’égalité des deux approches en exécutant dans GNU Octave :
qui donnera le résultat de la Fig. 4 qui compare le module de resmat et resfft qui sont bien entendu strictement identiques. Cependant, en encadrant les lignes de calcul de chacun de ces vecteurs des instructions tic et toc pour en estimer la durée d’exécution, nous constatons que pour N=1500 l’approche matricielle prend, sur un ordinateur portable CF-19 muni d’un processeur i5 cadencé à 2,70 GHz, de l’ordre de 4 ms quand la durée d’exécution de la FFT se compte en quelques dizaines de microsecondes, ou un ratio d’une centaine qu’est le log2(1500). Le bénéfice de la FFT devient d’autant plus évident que le vecteur analysé est long.
Le cas pratique le plus courant étant une période d’échantillonnage constante, intéressons-nous au cas de la FFT. La bibliothèque classique pour ce calcul en C, ou en C++ si des grandeurs complexes sont analysées puisque seul C++ propose ce type de données avec une partie imaginaire, est FFTW3, décrite à https://www.fftw.org/. On prendra soin de noter que cette bibliothèque ne supporte pas « simplement » les applications possédant plusieurs threads et qu’un soin particulier doit être pris quand plusieurs FFT doivent être calculées en parallèle (https://www.fftw.org/fftw3_doc/Thread-safety.html). Au contraire, FFTW3 sait distribuer son travail sur plusieurs processeurs ou plusieurs cœurs.
L’exemple ci-dessous aborde tout de suite le cas des nombres complexes <complex.h> de type std::complex<double> contenant deux méthodes, .real() et .imag(). Nous commençons par allouer une zone mémoire suffisamment grande pour contenir nobs complexes, puis remplissons le tableau avec un signal de la forme exp(j2π f/fs×t) avec f=440 Hz la fréquence du signal et fs=48000 Hz la fréquence d’échantillonnage :
On note que comme il est classiquement connu que les fonctions trigonométriques deviennent instables lorsque leurs arguments croissent vers l’infini (cas de t qui devient grand), nous travaillons sur la phase ph en la ramenant toujours dans l’intervalle [0:2π] où les fonctions trigonométriques sont précises, sans perte de généralité puisque de toute façon les fonctions trigonométriques sont définies modulo 2π.
Nous planifions les deux opérations de transformée de Fourier directe puis inverse (qui doit nous ramener au signal d’origine) en réinterprétant le contenu des tableaux complexes comme types attendus par fftw_plan_dft_1d, puis effectuons les opérations en affichant les premiers termes du résultat à chaque fois. Nous vérifions d’une part que le tableau mem après la première transformée de Fourier directe propose des termes presque tous nuls, sauf le 10e puisque la composante spectrale de 440 Hz échantillonnés à 48 kHz sur 1000 échantillons se trouve à l’indice 440/48000× 1000≃ 9 (les indices commencent à 0, donc il s’agit du 10e point), et que le tableau mem contient les mêmes éléments au début du programme lors de son initialisation et en fin de programme après transformée de Fourier directe puis inverse.
4.2 CUFFT sur processeur graphique GPU
Maintenant que nous savons effectuer une FFT sur CPU, pouvons-nous en faire autant sur GPU ? Accéder aux ressources de calcul des GPU NVIDIA impose d’installer leur compilateur propriétaire nvcc et la collection de bibliothèques qui va avec. Sous Debian/GNU Linux, le paquet correspondant est nvidia-cuda-toolkit : en effet au moins avec Debian/Sid, un conflit de dépendance semble interdire d’installer la dernière version en date disponible sur le site NVIDIA. Une fois le compilateur disponible, nous compilerons les programmes en C/C++ d’extension .cu comme nous le ferions avec GCC, mais en nous liant aux bibliothèques CUDA de la forme -lcufft pour CUFFT (la FFT sous CUDA) ou ci-dessous -lcublas -lcusolver pour les algorithmes de calculs matriciels.
Abordons donc le même programme que ci-dessus, mais sur GPU : nous passons sous silence l’initialisation du tableau entrant host_mem selon le même principe qui a servi à remplir mem auparavant, le préfixe host_ référant ici à une allocation en mémoire du CPU. Nous prendrons soin de transférer en mémoire sur la cible qu’est le GPU avant d’y effectuer les calculs :
Cette fois, un tableau additionnel est créé en mémoire GPU au moyen de cudaMalloc() qui prend en argument un pointeur de pointeur, ici vers dev_mem le pendant en mémoire GPU de host_mem en mémoire CPU, tous deux de longueur nobs. Un point fondamental est le transfert de données depuis la mémoire du processeur vers la mémoire du GPU : cudaMemcpy(dev_mem, host_mem, taille, cudaMemcpyHostToDevice); avec taille de chaque élément multiplié par le nombre d’éléments. Réciproquement, accéder aux résultats des calculs nécessite absolument de cudaMemcpy(host_mem, dev_mem, taille, cudaMemcpyDeviceToHost); sous peine sinon d’obtenir une erreur de segmentation en accédant à une plage mémoire qui n’est pas allouée au processeur. Une fois les données initialisées en mémoire CPU transférées en mémoire GPU, la séquence est très proche de celle vue avec FFTW3 avec la planification des FFT, directe ou inverse, en mémoire GPU par cufftPlan1d() et l’exécution de ces noyaux de calcul par cufftExecZ2Z() avant de libérer les ressources par cufftDestroy(). Nous constatons, heureusement, que le résultat du calcul de la FFT par CUDA ou par FFTW3 est strictement identique, et ici encore, la transformée de Fourier inverse de la transformée de Fourier renvoie le même résultat que le tableau d’entrée lors de son initialisation avec la sinusoïde à 440 Hz échantillonnée à 48 kHz.
Nous savons donc effectuer des FFT sur CPU et sur GPU, mais la FFT n’est qu’une étape intermédiaire pour ensuite effectuer une corrélation selon une opération s’apparentant à un produit matriciel. Abordons donc désormais les opérations sur des matrices, sur CPU puis sur GPU.
5. BLAS et LAPACK
5.1 Mise en œuvre sur processeur généraliste : produits de matrices
BLAS et LAPACK sont deux bibliothèques compatibles avec les langages C et C++ dans leur implémentation sous forme de paquets libclblas et liblapacke sous Debian GNU/Linux. Issues d’une longue lignée de développements en FORTRAN, elles en gardent certaines séquelles que nous devrons appréhender, et en particulier l’organisation des données en mémoire. En effet, le langage C ne connaît que les pointeurs, donc l’adresse en mémoire d’un tas d’octets, et comment les données sont organisées dans ce tas d’octets est laissé au soin du développeur (avec la beauté du void* quand on veut procrastiner cette décision). Nous pourrons choisir de plaquer l’emplacement des données contenues dans une matrice, mais il y aura plein de façons possibles d’accumuler les nombres contenus dans une matrice dans une zone mémoire dédiée.
Organisation de la mémoire et relation à l’organisation des matrices
Il est bien connu que les tableaux n’existent pas en C, mais qu’un pointeur indique un emplacement en mémoire à partir duquel des valeurs sont stockées selon une organisation laissée libre à l’utilisateur. Que ces valeurs s’interprètent comme un tableau unidirectionnel (vecteur) ou un tableau bidirectionnel (matrice) dépend du saut que nous faisons sur l’indice en mémoire pour chercher ladite valeur. L’organisation en ligne ou en colonne est donc déterminée selon que les indices adjacents dans le tableau représentent les éléments adjacents le long des lignes ou le long des colonnes ; il s’agit du problème de https://en.wikipedia.org/wiki/Row-_and_column-major_order :
Bien que nous ne manipulerons que des pointeurs et donc des vecteurs (matrices à une dimension) pour interpréter la position d’éléments matriciels par leur ordonnée multipliée par le nombre d’éléments par ligne auquel s’ajoute l’abscisse, il est bon de vérifier la relation entre les indices bidirectionnels de C et l’organisation en mémoire. Ainsi :
démontre que tab2d[l][m+1] est juste après tab2d[l][m] donc le second indice indique les termes adjacents en mémoire. Le problème avec gemm est que les erreurs peuvent se compenser aux transposées près entre une erreur de représentation et une transposition des arguments : il est donc fondamental de s’assurer de bien comprendre l’organisation des données et surtout des dimensions du résultat du calcul qui contraint l’ordre des arguments en entrée. On pourra pour cela lire aussi https://petewarden.com/2015/10/25/an-engineers-guide-to-gemm/.
Savoir que le C ne manipule que des tableaux à un indice unique – l’indice i quand on écrit tab[i] défini comme int tab[N] impliquant i∈[0:N−1] – et que le double indice est traduit en indice simple par :
indice=colonne × éléments par ligne + ligne
ne dit pas si le second indice est une ligne ou une colonne, et encore moins si BLAS respecte la convention du C ou une autre (du FORTRAN au hasard – voir « Organisation de la mémoire et relation à l’organisation des matrices »). Prenons donc le premier exemple de multiplication matricielle et éliminons le problème de savoir quelle est la taille des lignes ou des colonnes en considérant une matrice carrée, donc nobs=nlag=2 puisque tout au long de cette présentation, nobs le nombre d’observations détermine le nombre de lignes de la matrice d’entrée et nlag le nombre de colonnes. BLAS et LAPACK étant des bibliothèques de C(++), les variables matricielles et vectorielles sont définies comme des pointeurs dont l’espace mémoire est alloué dynamiquement par malloc() : float *mat; mat=(float*)malloc(sizeof(float)*nobs*nlag); dont le contenu est rempli par int m,l;for (m=0;m<nobs;m++) for (l=0;l<nlag;l++) mat[m*nlag+l]=(double)(2*m-l);.
La première fonction BLAS que nous rencontrons est sûrement la plus complexe : cblas_sgemm(). Toutes les fonctions commencent par cblas, suivi de gemm comme « multiplication de matrices généralisées », et s référant à des opérations sur des nombres à virgule flottante (réels) codés en simple précision donc sur 32 bits. Alternativement, d réfère aux réels en double précision (64 bits), et c et z aux complexes simples et doubles précisions respectivement. Cette fonction prend en argument trois pointeurs vers l’espace mémoire contenant des matrices, deux en entrée et une en sortie, et il est à la charge du programmeur de s’assurer de la cohérence des opérations, à savoir si le produit matriciel existe, et si les dimensions sont cohérentes. Dans l’expression :
cblas_sgemm(CblasColMajor,CblasNoTrans,CblasTrans,m,n,k,a,A,u,B,v,beta,C,w);
nous apprenons que l’opération effectuée est C=a × op(A) × op(B) + b × C avec A et B les matrices en entrée comme 8e et 10e argument, les coefficients multiplicatifs a et b fournis en 7e et 12e argument, et C la matrice résultante. L’instruction op(·), quelque peu surprenante à première lecture de la documentation, réfère à l’absence de transposition (CblasNoTrans), transposition (CblasTrans) ou transposée conjuguée (CblasConjTrans) de A et B selon les 2e et 3e arguments.
La rigueur est nécessaire pour définir m, n, k et le reliquat de FORTRAN se trouve dans la définition manuelle de u, v et w qui pourrait être (et sera plus loin, voir section 6.1) automatisée. La documentation explique que C est de dimensions m× n, que op(A) est de dimensions m× k et que op(B) est de dimensions k×n. Si nous savons comment C doit être organisée – par exemple un vecteur de solutions avec une dimension selon la ligne ou la colonne – les autres paramètres se déduisent pour distribuer m, n et k comme dimensions communes à C et A ou C et B respectivement. La documentation explique que le dernier argument w vaut m (pourquoi le demander, alors ?), donc ce point est clair. Cependant, nous apprenons que u vaut m si A n’est pas transposée, mais u vaut k si A est transposée, tandis que v vaut k si B n’est pas transposée, mais v vaut n si B est transposée. Avec un peu d’exercice, nous comprenons que c’est la direction de la matrice selon laquelle la somme est effectuée lors du produit matriciel, mais pourquoi ne pas automatiser une démarche rationnelle qui ne laisse aucun degré de liberté au programmeur ?
Ainsi, pour bien remplir u et v, il faut comprendre comment sont organisées les lignes et colonnes dans BLAS, et comme rien n’est simple, cette organisation dépend du premier argument CblasColMajor ou CblasRowMajor qui indique si les pointeurs visent des zones mémoires où les matrices sont organisées en ligne ou en colonne. Seule de l’expérimentation va permettre de se familiariser avec la multitude de cas possibles pour ne pas se tromper.
Afin de limiter les erreurs de segmentation, que BLAS intercepte avec des messages cryptiques de la forme ** On entry to ZGEMM parameter number 13 had an illegal value qui signifie qu’un des paramètres u, v ou w est nul ou négatif, mais en pratique indique que la mémoire a été corrompue par un accès invalide en mémoire lors de la requête d’un pointeur, évoluons étape par étape avec des matrices carrées (donc m=n=k=u=v=w), des matrices rectangulaires avec C carrée (donc m=n=w), et finalement des matrices de tailles quelconques. Pour reprendre le cas ci-dessus, nous choisissons donc nlag=nobs=2 :
avec la fonction d’affichage du contenu d’une matrice :
Ici, nous ne nous sommes pas fatigués à identifier m, n, k, u, v et w puisque tous valent la même valeur choisie comme nlag. Nous voyons déjà le problème apparaître dans affiche_matrice() : il faut faire attention à quel indice saute de la longueur des lignes ou des colonnes selon que l’organisation est ColMajor ou RowMajor, et toute erreur sur l’affichage du contenu des matrices se traduit par une erreur sur l’analyse du comportement des fonctions BLAS ! Nous obtenons :
et
Comment vérifier cela avec GNU Octave ? Une matrice a est définie comme a=[0 -1 ; 2 1] dans lequel nous notons que les données adjacentes dans le tableau en C (0.00 2.00 -1.00 1.00) se suivent le long des colonnes de la matrice dans Octave, et a*a répond :
tandis que a*a’ donne :
Ces résultats sont cohérents. Le point important de cette démonstration est que les éléments contigus en mémoire du programme C (mat[l*x+m]) se suivent selon les colonnes, c.-à-d. les deux premiers éléments de mat sont 0 et 2 qui sont le contenu de la première colonne sous Octave dont les éléments sont séparés dans leur définition par le nombre d’éléments dans chaque ligne. Ces essais se généralisent pour toutes les transpositions possibles de A et B et pour le cas CblasRowMajor – en prenant soin d’adapter la fonction d’affichage en conséquence – pour se convaincre de la bonne compréhension de l’organisation de la mémoire manipulée par BLAS et la cohérence avec les résultats fournis par Octave dans https://github.com/jmfriedt/learning_blas/blob/main/blas/demo1_matrix_square.c. Se tromper entre CblasRowMajor et CblasColMajor conduit à une transposition des matrices et donc a*a et a’*a’ seront identiques, mais a’*a et a*a’ seront inversées en se rappelant la relation d’algèbre matricielle (A× B)′=B′× A′.
Nous laissons le lecteur s’entraîner avec les cas des matrices rectangulaires A, d’abord pour produire un résultat carré en calculant A′× A ou A× A′ (exemples 2 à 5 de https://github.com/jmfriedt/learning_blas/blob/main/blas/ avec progressivement les matrices réelles puis complexes, puisque BLAS sait manipuler le type complexe de C++ défini dans <complex> comme std::complex<double>, organisées en ligne et colonne) pour finalement arriver au cas quelconque nécessaire à la corrélation dans le domaine temporel. On notera qu’une erreur double sur l’organisation ligne/colonne de la mémoire et de la fonction d’affichage qui intervertirait ces deux arguments est indétectable sur une matrice réelle puisque A′× A est une matrice symétrique, et seul le passage aux complexes permet de lever l’ambiguïté, puisque dans ce cas les termes antisymétriques sont complexes conjugués (matrice hermitienne).
Après cette longue introduction aux structures de données manipulées, voyons comment implémenter dans le domaine matriciel la corrélation, comme nous le proposons dans l’exemple https://github.com/jmfriedt/learning_blas/blob/main/blas/demo6_matrix_xcorr.cpp. Nous désirons trouver m (code) dans s (val) avec des retards allant de −lag à +lag selon l’hypothèse que dans une boucle d’asservissement, nous pouvons nous retrouver un peu en retard ou un peu en avance (donc lag positif ou négatif) sur le motif recherché dans le signal, mais pas trop (nlag petit devant nobs). Les signaux sont donc définis par :
et les copies retardées du code interférent sont introduites par :
avec des pondérations de 0,5, 1,2 et 0,3 pour des retards positifs de 2 et 5 échantillons et une avance de 3 échantillons respectivement.
Ainsi, la corrélation sous forme M×s requiert M une copie de m retardée, donc :
qui concrètement est formée comme :
qui commence par mettre tous les éléments de M nommée mem à 0 puis écrase les éléments pertinents avec le motif supposé être contenu dans code. Si cette matrice est multipliée par le signal bruité contenant des copies du code val, alors le résultat de :
qui s’obtient aussi par transposée (même résultat à une transposition près puisque cette fois m× n est devenu (2*nlag+1)× 1 au lieu de 1× 2*nlag+1 auparavant), avec :
et peut même s’optimiser en explicitant qu’un des arguments est un vecteur et non une matrice générale, en utilisant cblas_zgemv() au lieu de cblas_zgemm, avec :
Le résultat de toutes ces options pour obtenir le même résultat est illustré, en affichant graphiquement le module de res, en Fig. 5, avec un résultat en accord avec nos attentes puisque les pics de corrélations apparaissent pour les retards que nous avons introduits dans le signal synthétique avec des pondérations d’autant plus importantes que le motif est puissant dans le signal bruité. Cependant, nous ne sommes pas capables de retrouver dans ce calcul les pondérations de chaque contribution du motif dans le signal pour éventuellement le retrancher, et ce calcul nécessite une pseudo-inverse.
5.2 Inverse et pseudo-inverse de matrices
Le cas de la pseudo-inverse est intéressant, car il fait appel aux fonctionnalités d’inversions de matrices carrées de BLAS. Commençons donc déjà par le calcul de la matrice inverse d’une matrice carrée, puisque si nous savons effectuer cette opération, il suffira de fabriquer son argument carré comme produit de la matrice rectangulaire avec sa transposée.
Le calcul général d’une inverse de matrice carrée est un problème complexe, surtout si la matrice est grande. Les mots tels que comatrice et cofacteurs rappellent des souvenirs trop douloureux pour que nous désirions les développer ici et nous nous contentons de nous appuyer sur les bibliothèques de calcul numériques que nous nous sommes engagés à présenter. En effet, des gens malins ont découvert qu’en décomposant une matrice en deux sous-matrices dont les éléments diagonaux supérieurs (U) et inférieurs (L) sont non nuls, mais les autres sont tous égaux à 0, il est possible d’efficacement calculer l’inverse d’une matrice. La décomposition LU d’une matrice carrée est un prérequis au calcul de son inverse, tel qu’implémenté dans LAPACK avec zgetrf_() (toujours avec le z du début de fonction qui indique la nature des données et se décline en s, d ou c) en vue de son inversion par zgetri_().
Calcul d’inverse et décomposition LU
Une façon « simple » d’appréhender l’inversion de matrices est de se rappeler qu’écrire A· X=V avec A une matrice de n× n éléments et X et V deux vecteurs de n éléments revient à résoudre un système d’équations linéaires. Par exemple, pour n=3 nous aurions :
et nous voyons bien que nous pouvons multiplier chaque ligne par une constante ou sommer les lignes sans que cela change le résultat : (a+α d)x+(b+α e)y+(c+α f)z=(u+α v) en sommant les deux premières lignes dont la seconde a été multipliée par une constante α vérifie la même solution, mais cette fois nous pouvons choisir judicieusement α tel que (a+α d)=0 et ainsi éliminer la dépendance de la solution en x de la première ligne. De la même façon, nous pouvons combiner ce résultat avec la troisième équation pour éliminer la dépendance en y et il ne restera plus que z=... qui se résout trivialement et permet de remonter à la solution de y et donc de x. Cette méthode d’élimination successive des dépendances aux variables s’appelle le pivot de Gauss et est la base de l’inversion de matrice. Ainsi, A est décomposée en une partie inférieure L dont les éléments de la diagonale sont unitaires et seuls les éléments inférieurs sont non nuls, et une partie supérieure U dont seuls les éléments supérieurs sont non-nuls. Alors, si A· x=b ⇔ LU· x=b permet d’exprimer L·(UX)=b et comme L a ses éléments supérieurs nuls, la résolution successive de UX=b s’obtient itérativement et comme U a tous ses éléments inférieurs nuls, la relation entre UX et X se retrouve simplement toujours de façon itérative. La décomposition LU est donc au cœur des inversions de matrice et nécessite de propager les pivots, c.-à-d. les valeurs de α pour chaque ligne qui ajoute un terme nul après combinaison [11].
Seule subtilité pour ces calculs sur des matrices complexes, nous devons explicitement caster les complexes en préfixant les arguments de reinterpret_cast <__complex__ double*>(matrice) pour satisfaire C++. L’implémentation détaillée de l’inverse est proposée dans https://github.com/jmfriedt/learning_blas/blob/main/blas/demo7_matrix_inv.cpp avec une matrice carrée dont le résultat se compare favorablement avec la sortie de GNU Octave en respectant l’organisation lignes/colonnes, et s’étend finalement au cas de la pseudo-inverse dans https://github.com/jmfriedt/learning_blas/blob/main/blas/demo8_matrix_pinv.cpp quand l’argument de l’inversion, initialement une matrice rectangulaire A, devient carrée par AtA et finit par fournir le résultat attendu, à savoir le retard de chaque motif connu dans le signal bruité et sa pondération, éventuellement complexe avec un module et une phase et donc une direction d’arrivée.
Dans l’exemple qui va suivre, la fonction d’affichage de matrice est légèrement modifiée par rapport au cas précédent pour s’accommoder d’arguments complexes et devient ainsi :
toujours en format column major. Les fichiers d’entête, qui déclarent les fonctions qui seront accessibles en se liant à la bibliothèque openblas par l’option -lopenblas de g++ (au lieu de GCC à cause des complexes), sont :
Afin de se familiariser avec les étapes « simples » de l’inversion de matrice en passant par la décomposition LU, nous proposons de remplir la matrice carrée (nlag=nobs) nommée mem de valeurs aléatoires, d’en afficher le contenu, de calculer les pivots pour transformer cette matrice en une partie supérieure U et une partie inférieure L par zgetrf_(), puis de bénéficier de cette transformation pour calculer l’inverse par zgetri_() qui trouve Q tel que Q· L· U=I avec I la matrice identité.
Nous laisserons le soin au lecteur de copier dans GNU Octave la matrice b affichée par ce programme et de comparer l’affichage de BLAS avec la solution d’Octave obtenue par inv(b) pour constater qu’elles sont identiques. Ainsi, nous savons inverser une matrice carrée.
Le cas de la pseudo-inverse se résume donc à former, à partir de la matrice rectangulaire M, une matrice carrée comme M′· M, d’en calculer l’inverse comme nous venons de le faire, et ensuite d’effectuer M′· (M′· M)−1 donc deux appels à la multiplication de matrice généralisée zgemm avant et après la séquence que nous venons de voir. Cela se résume par :
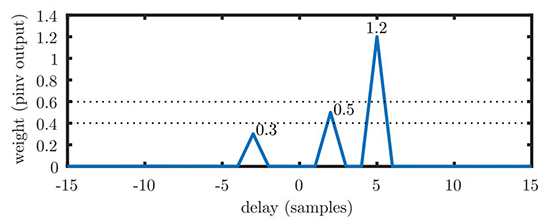
en notant que chaque résultat intermédiaire est stocké dans une nouvelle matrice, sans tenter de réutiliser la mémoire. Cela peut sembler trivial, mais a été la cause de quelques déboires dans la suite, CUDA expliquant explicitement que la mémoire contenant la sortie du calcul ne doit pas se superposer avec la mémoire contenant une des matrices fournies en argument d’entrée. De toute façon, vu les dimensions des matrices mises en jeu qui changent à chaque étape, nous n’avions aucune chance de sauver de la mémoire en réutilisant un tableau. Nous nous convainquons en observant le module de final de la cohérence du résultat (Fig. 6) avec des valeurs non nulles de la contribution du signal interférent à des retards de −3, +2 et +5 pour des pondérations respectives de 0,3, 0,5 et 1,2 tel qu’utilisé dans la définition de val.
5.3 CUBLAS sur processeur graphique : multiplication de matrices
Tout cela marche fort bien sur processeur généraliste : saurons-nous porter ces connaissances au GPU en nous appuyant sur CUBLAS, la version CUDA de BLAS ? Pour utiliser cette bibliothèque, nous compilerons avec le compilateur nvcc en faisant appel à -lcublas et en insérant les entêtes :
Afin de nous entraîner au cas simple du produit scalaire, mais surtout du transfert de données entre mémoire de l’hôte (CPU) et mémoire du périphérique (GPU donc device), nous reprenons la démarche vue auparavant pour la FFT, à savoir remplir les complexes en espace CPU, transférer en mémoire GPU, effectuer les opérations et récupérer le résultat :
qui est en accord avec le calcul sous GNU Octave de la norme au carré de host_mem obtenu comme a=mod([0:99],8)+j*mod([0:99],9); et (a*a')^2 répond bien 3938.
Plus intéressant, le cas du produit matriciel vu ci-dessus pour calculer la corrélation. La génération des vecteurs signal host_val et de l’interférent host_code reste identique aux exemples précédents, le préfixe host_ indiquant que ces opérations sont effectuées sur des complexes en C++ dans la mémoire du processeur, donc avec des arguments de type .real() et .imag(). Le cast vers les structures de données manipulées par CUBLAS, pour qui la partie réelle s’appelle .x et la partie imaginaire .y, n’aura pas besoin d’être explicité ici, si ce n’est dans la définition de α et β utilisée par zgemm :
Nous suivons les préconisations de CUBLAS en utilisant cublasSetMatrix() et cublasGetMatrix() au lieu de cudaMemcpy(...,cudaMemcpyHostToDevice); et cudaMemcpy(...,cudaMemcpyDeviceToHost); mais le résultat est strictement identique. Dans cet exemple, nous perdons beaucoup de temps à transférer le résultat du calcul de corrélation de la mémoire GPU vers la mémoire CPU pour affichage : si tout ce qui nous intéresse est l’indice de la position du maximum de corrélation, alors nous pourrions faire appel depuis le GPU à cublasIdamax(handle, 2*nlag+1, dev_res, 1, &idx); qui renverrait dans idx la position du maximum dans la convention du FORTRAN – « Notice that the last equation reflects 1-based indexing used for compatibility with Fortran » à https://docs.nvidia.com/cuda/cublas/index.html – donc avec un indice commençant à 1 et non à 0. L’utilisation en C nécessite donc de retrancher une unité par idx-=1; pour être cohérent.
5.4 Inversion de matrices sous CUBLAS sur processeur graphique
Pour effectuer la démonstration de la pseudo-inverse, nous allons avoir besoin de deux nouveaux éléments dans CUBLAS :
- l’ajout de l’extension CUSOLVER pour effectuer la décomposition LU de la matrice à inverser ;
- la définition d’une matrice identité I, car CUSOLVER ne fournit pas le cas particulier de A× M=I qu’était zgetri_(), mais uniquement le cas général de A× M=B implémenté comme cusolverDnZgetrs() que nous utiliserons avec le cas particulier de B=I. Cette construction de la matrice identité sera l’occasion de reprendre la structure d’une fonction dédiée (kernel) exécutée en parallèle sur les cœurs du GPU.
Ce kernel exploite trois variables implicites que sont blockIdx.x, blockDim.x et threadIdx.x qui indiquent quel thread s’exécute sur quel cœur de calcul du GPU, et permet d’accéder à un emplacement de la mémoire GPU en fonction de cet indice, parallélisant donc le calcul. Le nombre de threads est défini lors de l’appel à la fonction de la forme initIdentityGPU<<<128, 128>>>(dev_Id,N); dans la séquence qui suit :
nobs, dev_Id, 2*nlag+1, &beta, dev_mem_out, nobs);
not allowed", "C must not overlap")
dev_mem_out, nobs, &beta, dev_res, 1);
Nous découvrons cudaDeviceSynchronize(); pour attendre que le GPU achève son calcul avant d’aller chercher le résultat pour le transférer en mémoire CPU. Par ailleurs, l’entrée et la sortie de cusolverDnZgetrs() sont de même taille (l’inverse de la matrice carrée est carrée) et il était tentant de sauver le résultat dans l’emplacement mémoire d’entrée... et cela est strictement interdit, sous réserve d’obtenir un résultat nul si 2×nlag+1 est supérieur à 32. La documentation CUBLAS le dit bien à https://docs.nvidia.com/cuda/cublas/ puisque « This function is a short cut of cublas<t>getrfBatched plus cublas<t>getriBatched. However it doesn’t work if n is greater than 32. If not, the user has to go through cublas<t>getrfBatched and cublas<t>getriBatched », et cela est certainement lié à l’argument dont la taille doit être inférieure à 32 de gesvdjBatched(), mais bien entendu, nous ne lisons la documentation qu’en dernier recours quand toute autre approche empirique échoue.
Le passage de la FFT vers le calcul matriciel avait été introduit par le désir de combiner la sortie de deux FFT – le code et le signal bruité – par le produit de l’un par le complexe conjugué de l’autre, avant de revenir dans le domaine temporel par FFT inverse. Il semble cependant qu’il n’y ait pas de méthode efficace dans (CU)BLAS pour effectuer un produit terme à terme entre deux vecteurs, et nous reprenons la définition d’un kernel dédié comme nous venons de le voir, de la forme :
qui s’appelle par mul<<<nobs/1024,1024>>>(nobs, dev_mem, dev_code, dev_res);. Finalement, après FFT inverse, nous évitons le long transfert depuis mémoire GPU vers CPU en effectuant la recherche du maximum de la corrélation dans le GPU par cublasIdamax(handle, nobs, res, 1, &index); tel que mentionné auparavant.
5.5 Profilage du code
Tout comme le classique gprof de GCC qui permet d’estimer le temps passé à exécuter chaque fonction d’un programme sur CPU lorsque compilé par gcc -pg, CUDA propose son outil de profilage du temps d’exécution des diverses fonctions sur GPU, d’autant plus important que nous faisons appel à des bibliothèques complexes dont nous n’avons aucune idée du temps d’exécution. Ainsi, pour reprendre le cas de la FFT sur 108 points, l’exécution de :
édité par souci de compacité du résultat indique que les calculs dominent le temps d’exécution, mais que le temps de transfert entre les mémoires CPU et GPU est loin d’être négligeable. Ce classement se maintient sur des vecteurs de taille plus réduite. Notez par ailleurs que le temps indiqué lors de l’exécution du programme inclut les transferts entre zones mémoires en plus du calcul, et que la seconde FFT inverse ne subit pas le transfert CPU-GPU puisqu’est effectuée sur des données déjà en mémoire GPU. Dans ce cas, nous constatons que déporter le calcul sur GPU réduit d’un facteur deux le temps de calcul, en plus de libérer le CPU et ses 36 cœurs (Xeon W-2295 cadencé à 3,00 GHz) pendant ce temps.
6. GNU Scientific Library – GSL
Nous avons découvert BLAS et LAPACK et les subtilités de leur organisation de la mémoire ou de l’excès d’arguments aux fonctions hérité du FORTRAN. La bibliothèque de calcul scientifique GNU nommée GSL, décrite à https://www.gnu.org/software/gsl/doc/latex/gsl-ref.pdf, fournit un certain nombre d’outils pour le calcul matriciel, y compris le support des fonctions BLAS, avec des fonctions rationalisées, mais au détriment de structures de données quelque peu étranges à prendre en main.
Pour les points positifs : les dimensions des matrices et des vecteurs sont clairement spécifiées à leur création et ne laissent pas de doute sur leur manipulation. Par ailleurs, les bornes des tableaux sont vérifiées lors des accès mémoire et une erreur est produite si nous sortons du segment alloué. Point négatif : le remplissage des matrices et vecteurs ne se fait pas par une simple égalité que permettrait la surcharge des opérateurs du C++, mais par des fonctions du C.
Fort des connaissances acquises sur BLAS, la prise en main de GSL est relativement indolore une fois que nous comprenons :
- comment remplir les vecteurs et matrices de complexes ;
- comment extraire des sous-ensembles des vecteurs et colonnes et l’organisation des structures de données correspondantes.
6.1 Prise en main de GSL : produit matrice-vecteur
Reprenons point par point l’exemple de la corrélation par produit matriciel, mais en GSL, pour explorer ces difficultés. La définition des entêtes et constantes du programme ne pose pas de problème :
ni l’allocation des ressources pour définir des vecteurs :
mais le remplissage du vecteur par des nombres complexes nécessite une boucle itérant les indices pour définir par les macros GSL_REAL() et GSL_IMAG() les parties réelle et imaginaire d’une variable complexe intermédiaire qui se voit ensuite assignée (gsl_vector_complex_set()) à une position i du vecteur. C’est fastidieux, mais ça marche et nous n’avons pas trouvé mieux.
Une fois le vecteur rempli, les opérations d’algèbre linéaire reprennent les noms de fonctions de BLAS préfixées de gsl_, mais simplifiées. Ainsi, alors que le produit scalaire (dot product) de BLAS nécessitait zdotc (N, ZX, INCX, ZY, INCY) le nombre d'éléments, les deux vecteurs du produit scalaire ∑n xn*·yn et l’incrément le long des vecteurs x et y, ici nous avons juste les deux vecteurs (leur longueur est déjà connue de GSL) et le pointeur vers la variable contenant le résultat. Par ailleurs, GSL fournit des fonctions toutes faites pour afficher le contenu des matrices et vecteurs telle que gsl_vector_complex_fprintf() même si la mise en forme des matrices est discutable. Après avoir vérifié que le résultat est cohérent avec le résultat fourni par GNU Octave, nous libérons les ressources.
Convaincus que nous maîtrisons l’API de GSL, abordons la corrélation. Pour ce faire, nous fabriquons le vecteur du signal val et le vecteur de l’interférent code dont nous voudrons fabriquer une matrice avec ses sous-ensembles décalés dans le temps. La notion de sous-ensemble fait intervenir la structure de données XXX_view de GSL, avec XXX égal à vector ou matrix. Nous commençons donc par remplir les deux vecteurs val et code de séquences aléatoires (afin que leur corrélation soit un unique pic de Dirac) :
puis allons ajouter au signal les copies retardées de l’interférent. Un sous-ensemble de vecteur s’obtient par gsl_vector_complex_subvector() qui prend en argument le vecteur source, l’indice de départ et la longueur. GSL nous insultera si la fin de cette séquence dépasse la longueur du vecteur fourni. Le résultat n’est pas une nouvelle allocation en mémoire, mais un pointeur vers le vecteur initial : ce point est important, car toute manipulation du sous-vecteur impactera le vecteur d’origine si nous ne prenons garde de le dupliquer. Ainsi dans cet exemple, l’élément .vector de la structure gsl_vector_complex_view va subir une homothétie par gsl_vector_complex_scale(), mais si nous ne prenons pas soin de copier le contenu du vecteur initial, les homothéties successives vont s’appliquer les unes sur les autres au lieu de toutes s’appliquer au vecteur initial. Aussi, nous contenter de :
se traduirait par un contenu de tmp_vector_view2 qui aurait été modifié par la multiplication de tous ses termes par 0,3, et la prochaine copie du vecteur n’affecterait pas tmp_vector_view2, mais 0.3*tmp_vector_view2 qui n’est pas le but recherché. L’addition de la copie décalée dans le temps de code à val passe donc par une fonction qui duplique en mémoire chaque structure de données pour ne pas en écraser le contenu :
Ainsi, le pointeur inout fourni en argument de la fonction se voit assigné à tmp1 lors du gsl_vector_complex_subvector() et son contenu est implicitement modifié lors de gsl_vector_complex_add(&tmp1.vector,tmp); qui en réalité agit sur le contenu de inout. Afin de ne pas modifier le contenu de l’emplacement mémoire pointé par *code, nous dupliquons son contenu par gsl_vector_complex_memcpy() avant d’effectuer l’homothétie par gsl_vector_complex_scale() dont le résultat sera ajouté au sous-ensemble de inout contenu dans tmp1 sous la dénomination de son élément .vector dont on prendra soin de fournir le pointeur en argument (&). Cette fonction gère par ailleurs le cas des retards positifs (off>=0) quand nous ne conservons qu’un sous-ensemble de l’interférent, ou des retards négatifs (off<0) quand nous ne considérons qu’un sous-ensemble du signal. De toute façon, les longueurs de tmp1 et tmp2 doivent être les mêmes (len-abs(off)) sinon GSL nous insulte lors degsl_vector_complex_add(). Nous finissons par poliment restituer les ressources allouées lors de l’appel à cette fonction par gsl_vector_complex_free(). Grâce à cette fonction, quatre copies retardées de l’interférent sont ajoutées au signal par :
avec des pondérations respectives de 0,3, 1,3, 0,8 et 1. Maintenant que le signal à analyser est formé, il reste à fabriquer la matrice des copies retardées dans le temps de l’interférent, toujours en utilisant le sous-ensemble de code au moyen de gsl_vector_complex_subvector et en prenant connaissance du pendant de cette fonction pour une colonne de matrice qu’est gsl_matrix_complex_subcolumn. Comme ce sont de nouveau des XXX_view, nous manipulerons les éléments .vector et .matrix de ces structures de données :
Maintenant que le vecteur val et la matrice mem sont formés, il reste à effectuer le produit matriciel au moyen de zgem et nous utiliserons sa version vectorielle zgemv puisque GSL distingue vecteur et matrice et interdit de fournir un vecteur comme argument de zgemm. Cependant, nous voulions absolument prendre le complexe conjugué d’un des arguments, et avions pris auparavant le conjugué du vecteur. Qu’à cela ne tienne, puisque a′· b′=(b· a)′ il suffit d’intervertir les arguments et prendre le conjugué de la matrice pour obtenir le même résultat, à une transposition près :
dont on peut se convaincre de l’exactitude du résultat en affichant le module de res le résultat du produit matrice-vecteur y=α· op(A)· x + y avec α, β∈ℂ et op l’identité, la transposition ou la transposée avec complexe conjugué.
6.2 Inversion de matrice avec GSL
Nous nous inspirons de http://theochem.mercer.edu/pipermail/csc335/2013-November/000101.html pour apprendre comment inverser une matrice, toujours en passant par la décomposition LU. Pour ce faire, nous ajoutons aux entêtes #include <gsl/gsl_linalg.h>, mais sinon le reste du programme initial reste le même jusqu’à la définition du vecteur val et de la matrice des copies retardées dans le temps de l’interférent code. Cette fois, nous fabriquons la matrice carrée issue du produit de la matrice rectangulaire mem contenant autant de colonnes que de retards et autant de lignes que d’échantillons en effectuant le produit mem′· mem avec ′ la transposée-conjuguée (CblasConjTrans), puis effectuons la décomposition LU du résultat res en fournissant le tableau contenant les pivots p, pour finalement inverser res par gsl_linalg_complex_LU_invert() que nous multiplions par la matrice initiale afin d’effectuer ![]() qui est placé dans out.
qui est placé dans out.
Le produit de la pseudo-inverse de mem par val donne le vecteur des poids de l’interférent dans le signal que nous traçons dans GNU Octave en copiant la sortie de l’exécution de ce programme pour définir final puis plot([-nlag:nlag],abs(final(:,1)+j*final(:,2))).
7. Cas des réseaux de neurones
Toute cette algèbre linéaire peut paraître bien désuète en cette période d’intelligence artificielle et de deep learning. En fait, sous ces termes à la mode se cache simplement une extension du traitement linéaire du signal à une cascade de filtres de convolution, avec insertion d’une fonction non linéaire entre chaque combinaison linéaire des entrées de ce que nous nommerons neurone.
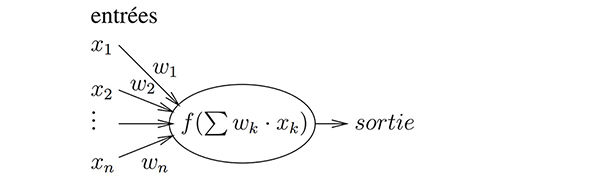
Concrètement, un « neurone » est une opération qui calcule la somme pondérée de ses entrées (Fig. 7), et effectue une opération non linéaire sur le résultat pour en fournir une sortie. La réelle innovation des « réseaux de neurones artificiels » tient aux algorithmes d’identification des poids appliqués à chaque terme en entrée, obtenus au moyen d’un algorithme de backpropagation. Cet algorithme consiste à estimer la dépendance de chaque neurone aux poids de ses entrées et de ses prédécesseurs, et à effectuer une descente de gradient pour minimiser cette fonction de coût en vue d’atteindre un objectif donné, à savoir une ressemblance maximale entre la sortie du réseau de neurones et une solution connue lors de la phase dite d’apprentissage.
Cependant, indiquer que la sortie d’un neurone est l’application d’une fonction non linéaire f de la somme des produits des poids w des entrées par les observations x s’exprime matriciellement comme sortie=f(∑wk xk) et nous savons maintenant que l’argument de f s’obtient par produit matriciel. Moins intuitif, la backpropagation fait intervenir la dépendance de chaque sortie avec les poids en entrée [12], et cette dépendance s’exprime comme la dérivée de la sortie par chaque paramètre d’entrée donc ∂ sortie/∂ wk et comme la sortie a fait intervenir f, nous verrons apparaître la dérivée de f (ou son gradient selon la direction k), d’où la nécessité de choisir intelligemment f pour que son gradient ne soit pas trop compliqué à calculer. Quoi qu’il en soit, nous allons voir apparaître une matrice dite jacobienne avec toutes les dérivées partielles des sorties en fonction de tous les poids, qui peut devenir très volumineuse s’il y a beaucoup d’entrées, par exemple dans le cas du traitement d’images. Ainsi, pour m « neurones » de sortie alimentés par n « neurones » d’une couche intermédiaire dans une architecture dense (où toutes les sorties d’une couche sont connectées aux entrées de la suivante), nous avons m× n connexions dont les dépendances s’expriment par la matrice de m× n éléments de la forme :
Nous avons pu constater, au cours d’un récent voyage en Chine, combien la reconnaissance de motifs dans des images est devenue omniprésente dans un pays qui a décidé d’appuyer toute sa surveillance sur le traitement d’images. En se promenant de quelques centaines de mètres à Chongqing, nous avons abandonné de compter les caméras qui observaient nos mouvements à 200, ayant perdu le décompte tellement les caméras étaient nombreuses à observer la circulation, les plaques minéralogiques aux entrées des parkings ou les piétons sur les trottoirs. Le traitement du signal et le calcul efficace d’opérations matricielles ont donc bien un impact au quotidien bien plus significatif qu’on pourrait le croire au premier abord (Fig. 8).
Conclusion
Nous avons commencé cet exposé en introduisant les calculs d’algèbre linéaire et de manipulation de matrices au moyen de GNU Octave, langage interprété permettant un prototypage rapide, mais reconnu pour sa lenteur face aux solutions compilées. Pourtant, GNU Octave fait appel à des bibliothèques dynamiques pour nombre de ses calculs d’algèbre linéaire, bibliothèques qui peuvent être détournées pour faire appel à leur implémentation sur GPU : c’est ce que propose NVBLAS. Si les fonctions de la bibliothèque dynamique implémentant BLAS sont proposées avec les mêmes prototypes, mais pour GPU, il doit être possible d’intercepter les appels vers la bibliothèque proposée habituellement pour CPU et faire appel à la version GPU sans recompiler l’exécutable : ce point est décrit en détail à https://developer.nvidia.com/blog/drop-in-acceleration-gnu-octave/ qui se contente de redéfinir l’emplacement de la bibliothèque dynamique sans modifier le binaire d’Octave fourni par Debian. Ainsi :
avec les messages d’avertissements qui nous convainquent que la bibliothèque GPU est bien utilisée lors des tests et effectue correctement ses opérations, mais surtout qui achève de nous convaincre que notre GPU n’est probablement pas à la hauteur du processeur Intel Xeon W-2295 à 3,00 GHz et ses 36 cœurs, compte tenu d’une multiplication par 100 du temps d’exécution en passant par le GPU au lieu du CPU. Il est néanmoins satisfaisant de constater que le détournement de la bibliothèque dynamique fournissant les fonctions appelées par Octave fonctionne. Le facteur 100 chute à 3 si au lieu de multiplier deux matrices de 512× 512 éléments, nous travaillons sur des matrices de 8192× 8192 flottants en simple précision. On aura quand même la satisfaction de conclure par une mesure du temps d’exécution sur les 4 cœurs du processeur Intel i5-3610ME cadencé à 2,70 GHz d’un portable Panasonic CF-19 pour constater que le temps d’exécution est plus de 15 fois plus long que le GPU dans le cas des matrices 8192× 8192.
Et Python ?
Tout comme Octave qui peut accélérer des calculs matriciels en bénéficiant du GPU, Python permet d’accélérer les calculs de numpy et scipy par cette approche hétérogène du calcul. La bibliothèque CuPy de https://cupy.dev/ annonce atteindre ce résultat, mais nous ne l’avons pas explorée.
Ainsi, nous nous sommes efforcés de démontrer l’importance du calcul matriciel dans le traitement du signal « classique » linéaire, qu’il s’agisse dans le domaine temporel ou dans le domaine spectral après transformée de Fourier, et surtout l’utilisation de diverses bibliothèques de calcul scientifique implémentant efficacement des opérations, telles que produits matriciels, décomposition LU et inversion de matrices. Ces quelques exemples de base ne sont que les introductions à des applications bien plus ambitieuses et utiles qui pourront s’appuyer sur ces connaissances.
Nous avons illustré le calcul sur GPU en abordant exclusivement les coprocesseurs NVIDIA s’appuyant sur CUDA, avec les déboires de temps de transfert excessifs entre CPU et GPU qui nécessitent un réel bénéfice en termes de vitesse de calcul pour être compensés. Il serait probablement utile de considérer des architectures alternatives aux GPU NVIDIA qui seraient susceptibles de partager de la mémoire avec le processeur généraliste, et ainsi aborder Vulkan ou SYCL – une extension du C++ visant les architectures hétérogènes capables de produire du code à destination de CPU, GPU ou FPGA – les concurrents de CUDA chez AMD, qui notamment devraient permettre l’exploitation du GPU de la Raspberry Pi 5, si on en croît la publicité.
Nous avons compté 53 caméras sur les trois photographies de la figure 8, incluant celles qui surveillent les entrées de parking et les trottoirs. Cela fait beaucoup de GPU au kilomètre !
Tous les exemples proposés dans cet article sont disponibles à https://github.com/jmfriedt/learning_blas/.
Remerciements
Weike Feng (Air Force Engineering University, Xi’an, Chine) nous a présenté l’utilisation de la pseudo-inverse comme solution optimale aux moindres carrés de l’identification des poids d’un interférent dans un signal, concept utilisé à maintes reprises dans les domaines liés aux traitements de signaux RADAR ou de leurrage et brouillage de signaux de navigation par satellite. Toutes les références bibliographiques ont été obtenues sur Library Genesis et Sci Hub, sur les divers sites accessibles selon les indications de http://vertsluisants.fr/index.php?article4/where-scihub-libgen-server-down.
Références
[1] J.-M Friedt, Du domaine temporel au domaine spectral dans 2,5 kB de mémoire : transformée de Fourier rapide sur Atmega32U4 et quelques subtilités du C, Hackable 49 (juillet-août 2023) -
https://connect.ed-diamond.com/hackable/hk-049/du-domaine-temporel-au-domaine-spectral-dans-25-kb-de-memoire-transformee-de-fourier-rapide-sur-atmega32u4-et-quelques-subtilites-du-c
[2] G. Saupin, Programmation GPU nVidia : Le CUDA sans peine, GNU/Linux Magazine 135 (2011) à
https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-135/programmation-gpu-nvidia-le-cuda-sans-peine
[3] G. Saupin, Le CUDA sans peine : produire un code efficace, GNU/Linux Magazine 137 (2011) à
https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-137/le-cuda-sans-peine-produire-un-code-efficace
[4] G. Saupin, Le CUDA sans peine 3, GNU/Linux Magazine 140 (2011) à
https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-140/le-cuda-sans-peine-3
[5] S. Azarian, Using GPU for real-time SDR Signal processing, FOSDEM (2024) à
https://fosdem.org/2024/schedule/event/fosdem-2024-1643-using-gpu-for-real-time-sdr-signal-processing/
[6] S. Hong, J. Brand, J.I. Choi, & al., Applications of self-interference cancellation in 5G and beyond, IEEE Communications Magazine 52 (2), pp. 114–121 (2014).
[7] W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in C++: The Art of Scientific Computing, 2nd Ed., Cambridge University Press (2002).
[8] J.-M Friedt, Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées, GNU/Linux Magazine France 139 (juin 2011) -
https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-139/auto-et-intercorrelation-recherche-de-ressemblance-dans-les-signaux-application-a-l-identification-d-images-floutees
[9] J.-M. Friedt, W. Feng, Anti-leurrage et anti-brouillage de GPS par réseau d’antennes, MISC 110 (juillet-août 2020).
[10] Chap 2: The Discrete Fourier Transform dans K. R. Rao & P.C. Yip., The Transform and Data Compression Handbook, CRC Press (2001).
[11] T.H. Cormen, C.E. Leiserson, R.L. Rivest & C. Stein, Introduction to Algorithms, MIT Press (2001).
[12] I. Goodfellow, Y. Bengio & A. Courville, Deep learning, MIT Press (2016), section 6.5.2, p.199.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture