Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées

1. Introduction

Par exemple, une équipe anglaise a ainsi identifié au moyen d’un accès gratuit aux images satellites de résolution médiocres (preview [1]) la localisation de toutes les colonies de manchots en Antarctique, tâche impossible à réaliser (ou financer) par un mode d’observation dédié à cet objectif [2]. Une des approches les plus intuitives est la recherche de l’occurrence (ou absence) d’une information dans cette masse de données. Pour appliquer plus précisément ce concept aux images, il s’agit de rechercher l’occurrence d’un motif. Nous proposons donc ici une présentation d’un outil classique de recherche de ressemblances entre motifs : la corrélation. Concrètement, après une brève introduction théorique, nous appliquerons ce concept aux images (rechercher l’occurrence d’un motif) et étude dans des séquences temporelles d’images de déplacement de motifs (champ de déplacements), qui serviront de mise en place des outils en vue du cœur du sujet, la recherche de zones floutées dans les images. Enfin, nous conclurons sur un cas particulier où l’utilisateur choisit le signal sonde qui va servir à détecter une cible, et montrerons comment un choix judicieux des propriétés statistiques permet de maximiser les chances d’identifier l’écho et sa localisation.

L’ensemble des expérimentations de traitement statistique du signal se fera au moyen de GNU/Octave (www.gnu.org/software/octave) [3], un port open source de l’outil propriétaire Matlab de Mathworks totalement fonctionnel depuis l’implémentation de la majorité des toolbox, et notamment signal processing toolbox dans le cas qui nous intéressera ici. L’objectif de cette étude, au-delà d’acquérir quelques connaissances utiles pour extraire toute l’information de la masse de données accessibles sur le Web, est d’être conscient des risques associés à ces données, notamment par une analyse systématique de la statistique du signal. Par exemple, il est bien connu qu’une analyse du flux de données fournit une information en cryptographie sans nécessairement permettre l’identification de l’information elle-même : il est peu judicieux de ne crypter par PGP que les messages à vocation de secret, messages qui ressortiront trivialement lors d’une analyse de flux [4]. Une extrapolation audacieuse qui conclura notre étude est que de la même façon, il est peu judicieux de manuellement modifier les propriétés statistiques (flouter), les zones considérées comme sensibles sur les images aériennes, la signature associée à cette opération étant identifiable.

2. L’intercorrélation : quelques notions de base

Le concept que nous proposons de mettre en œuvre au cours de cet exposé est l’intercorrélation entre deux signaux. Ce concept vise à extraire le « taux de ressemblance » entre deux signaux unidimensionnels (signaux temporels, par exemple) ou bidimensionnels (images). La définition mathématique de ce concept, que nous nous efforcerons d’intuiter par la suite, est que l’intercorrélation entre deux signaux, supposés unidimensionnels dans un premier temps, de moyenne nulle, s(t) et s′(t) est :

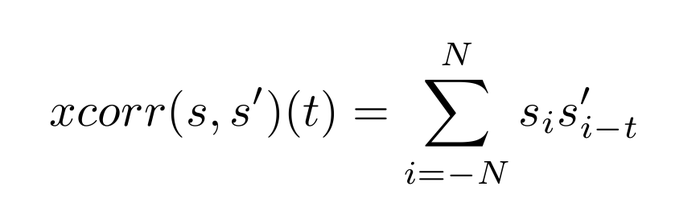
Le lecteur qui ne désire pas entrer en détail dans la compréhension de cette formule – et par là esquiver toute chance de comprendre le sens du concept – pourra se contenter d’expérimenter avec les fonctions xcorr() et xcorr2() (pour la version 2D applicable en imagerie) de GNU/Octave. La philosophie de l’intercorrélation est de rechercher le retard (ou translation t) qui permet de maximiser la ressemblance entre s et s′. En effet, ce n’est que pour un retard t qui maximise la ressemblance que la somme s’effectue de façon cohérente avec des produits si et s'i−t tous positifs (de l’ordre de si2). Dans le cas contraire, le produit des valeurs de si se fait avec un signal s′ de valeur moyenne nulle qui a toutes les chances de fournir un résultat proche de 0. Ainsi, nous allons rechercher t qui maximise la somme des éléments du produit s(i)xs′(i-t) lorsque le retard t permet à s de ressembler au mieux à s′ décalé de t.

On notera la forte ressemblance entre la définition de la corrélation xcorr(s,s′)(t) et la convolution définie par :

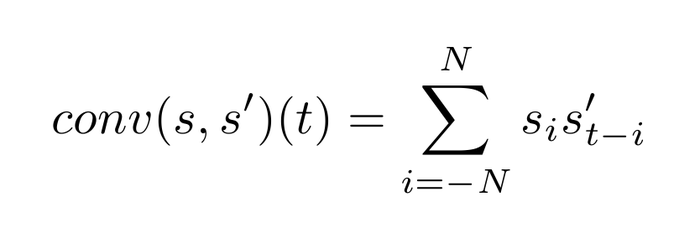
Dans ce cas, le produit dans l’intégrale se fait en balayant s selon un axe du temps i croissant, tandis que le second signal s′ est décalé d’un retard t mais balaie le temps à l’envers (-i). Cette opération reflète l’application du filtre défini par s′ au signal s. Cette digression est nécessaire pour entrer dans les détails pratiques de la mise en œuvre de l’intercorrélation : par souci d’efficacité, il nous faut impérativement passer par le domaine spectral (transformée de Fourier). En effet, une relation fondamentale [5] pour la mise en place d’un calcul d’intercorrélation est le fait que la transformée de Fourier (TF) de la convolution de deux signaux est le produit des transformées de Fourier de chaque signal :

TF(conv(s,s′))=TF(s′)× TF(s)

Cette affirmation, apparemment anodine, permet de passer d’un nombre de multiplications de l’ordre de N2 (avec N le nombre d’éléments du vecteur à analyser) vers N.ln N grâce à l’algorithme de transformée rapide de Fourier (Fast Fourier Transform – FFT) [6]. Une subtilité subsiste : nous nous proposons de travailler sur la corrélation, alors que nous énonçons un théorème sur la convolution. On aura remarqué, par rapport à la définition de la corrélation, l’inversion du signe sur le terme de la variable d’intégration : dans un cas, la variable glisse le long de l’axe du temps (s′(i-t)), dans l’autre cas, elle glisse dans le sens opposé (s′(t-i)). Le passage de la convolution à la corrélation va donc soit s’obtenir par inversion de l’axe du temps dans le domaine temporel (rotation de 180° du motif s′) [7], soit dans le domaine spectral en prenant le complexe conjugué de la transformée de Fourier. On pourra se convaincre que cette dernière opération inverse la direction du temps en considérant que le complexe conjugué de exp(i× ω t) est exp(-i× ω t) (avec t le temps, ω une pulsation et i2=-1).

Appliquons ces concepts quelque peu abstraits en l’état au cas particulier de la recherche de l’occurrence d’une lettre dans un texte. Si la corrélation est un estimateur capable d’identifier le taux de ressemblance entre deux motifs, alors en prenant un texte (Fig. 2, en haut à gauche) dont on extrait une lettre (Fig. 2, en haut à droite), nous devons être capables de retrouver la position de toutes les occurrences de ces lettres dans le texte. Au-delà des points déjà mentionnés sur le retournement de l’axe des temps de s′, le dernier point fondamental à ne pas oublier est que s et s′ doivent être de moyenne nulle : on prendra soin de toujours retrancher la valeur moyenne de s et s′ avant tout calcul (fonction mean() dans GNU/Octave). Afin d’illustrer les deux modes de calcul cités auparavant, nous pouvons dans un premier temps appliquer la convolution en deux dimensions (fonction conv2() de GNU/Octave) :

Ce programme charge le texte (supposé contenu dans l’image texte.ppm) et le motif (la lettre « a » dans a.ppm). Puis il effectue la convolution 2D sur une rotation de 180 degrés (fonction rot90()) appliquée sur un des motifs d’une part, et l’autre motif d’autre part. Finalement, nous seuillons à 70 % du maximum de l’intercorrélation pour bien faire ressortir l’identification des positions des maxima (Fig. 2, en bas à gauche : les deux points blancs sur les lettres ’a’ en haut à gauche de l’image et en bas à droite sont l’identification des positions de maxima).

Nous pouvons nous convaincre de la validité de l’approche en passant par le domaine spectral :

Nous effectuons la transformée de Fourier (fonction fft2() de GNU/Octave pour l’application sur une image bidimensionnelle) du texte (par défaut, GNU/Octave génère une matrice de mêmes dimensions que le motif original, ici 619×232 pixels), et la transformée de Fourier du motif en précisant la taille de la matrice résultante. Une fois ces deux matrices obtenues (dans le domaine spectral), le produit terme à terme (opposé au produit matriciel du symbole *) s’obtient par p=conj(tfa_z).*tftexte_z, avec conj() le complexe conjugué (donc inversion de l’axe temporel pour la variable qui lui est associée). Finalement, nous retournons dans le domaine spatial par transformée de Fourier inverse (ifft2()) et affichage comme précédemment. Cette fois (Fig. 2, en bas à droite) les maxima sont légèrement décalés par rapport aux lettres « a », pour cause de convention sur la position de l’origine de la transformée de Fourier.

Notons, pour le lecteur désireux d’expérimenter avec des images couleurs au lieu d’images noir et blanc, qu’il faut absolument réduire l’espace des couleurs (RGB) à un scalaire (tons de gris), puisque les opérations de traitement d’images de GNU/Octave ne s’appliquent que sur des matrices. On pourra soit choisir de ne conserver qu’un des canaux de couleurs, soit de convertir l’image couleur lue dans un fichier en tons de gris par rgb2gray().

3. L’intercorrélation : recherche de ressemblances dans des séquences temporelles

Au-delà des concepts nécessaires à une mise en œuvre efficace de l’intercorrélation, le point le plus important pour exploiter cet estimateur est de concevoir qu’il s’agit d’une recherche de maximum de ressemblances du motif s′ dans la séquence s.

Après l’application simple de recherche de toutes les occurrences d’un motif pioché dans une image, le premier exemple concret qui va nous intéresser concerne le calcul du champ de déplacement d’un objet observé par une séquence d’images. Considérons un flux vidéo de cadence connue – dans notre cas des séquences de photographies haute résolution de glacier acquises plusieurs fois par jour – que nous désirons exploiter pour calculer le champ de déplacement [8]. Ce champ de déplacement, une fois divisé par l’intervalle de temps entre deux photographies, fournit le champ de vitesse et donc la dynamique de l’objet considéré.

Le principe de l’intercorrélation consiste à rechercher, dans des segments de deux images d’un même objet, les vecteurs de translation qui permettent de retrouver le maximum de similarités entre les deux photos. Dans le formalisme proposé dans le chapitre précédent, il s’agit de trouver le retard t pour lequel l’intercorrélation xcorr(t) est maximale. Si nous supposons que le champ de déplacement n’est pas homogène, i.e. que l’objet s’est déformé au cours de son déplacement, une unique recherche sur l’ensemble des pixels de l’image de départ et de fin n’a pas de sens. Il nous faut travailler sur des vignettes contenant des sous-ensembles de l’image : chaque vignette doit être aussi petite que possible pour maximiser la résolution spatiale du résultat, tout en étant suffisamment grande pour garantir la présence d’une fraction suffisante d’un motif entre les images de début et de fin pour permettre à l’algorithme de reconnaître un déplacement. Si tous les motifs sont sortis de la fenêtre analysée dans l’intervalle de temps séparant les deux photos, il sera impossible de trouver t qui maximise l’intercorrélation xcorr(t). Le résultat de l’implémentation de ces concepts :

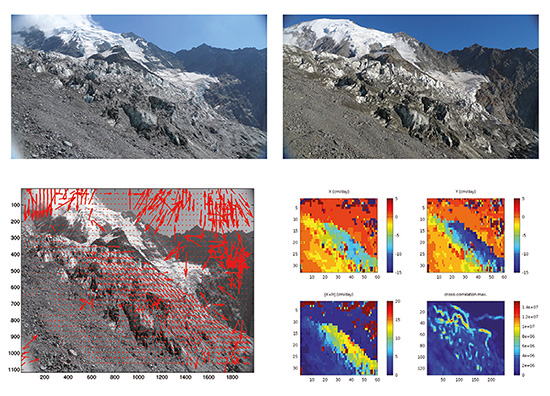
est l’application de l’intercorrélation sur des vignettes de 32×32 pixels entre deux images séparées d’environ une semaine d’images du glacier de Bionassay dans le massif du Mont Blanc, afin de fournir le résultat de la figure 3. Plus le paramètre de taille des images est grand (ici 32), plus le temps de calcul est long, et plus le champ de déplacement lisse des phénomènes potentiellement locaux. Il est donc judicieux de rechercher la plus petite fenêtre qui contient les motifs pertinents sur toute l’image. On notera par ailleurs l’utilisation de la fonction xcorr2(), qui est simplement l’appel à la fonction conv2() suivant les concepts que nous avons explicités plus haut, et une mise en forme (normalisation) appropriée des données.

La figure 3 mérite une description détaillée :

• Bien que le champ de déplacement soit relativement homogène sur le glacier, nous distinguons bien les zones englacées (en mouvement) du premier plan constitué du socle rocheux (immobile).
• Les montagnes en arrière-plan ne bougent pas.
• Le ciel présente des vecteurs de déplacement aberrants, que nous aurions pu éliminer en seuillant sur le maximum d’intercorrélation (vignette en bas à droite dans la série de 4 figures de droite). En effet, le ciel ne présente pas de motif représentatif d’un déplacement (soit le ciel est vierge de nuages et il n’y a pas moyen d’identifier les déplacements, soit comme ici, les motifs de nuages sur un intervalle de 1 semaine sont incohérents). Cette notion de qualité de l’intercorrélation est importante, car elle permet de quantifier la validité du champ de déplacement observé [9].
• La représentation des vecteurs de déplacement se fait soit sous forme de flèches (fonction quiver() de GNU/Octave) dont la direction donne l’orientation du mouvement, et la longueur la magnitude du déplacement, ou (vignettes de droite, en haut) nous pouvons fournir individuellement les contributions en abscisse et ordonnée (variables cx et cy), puis la norme du vecteur déplacement (vignette en bas à gauche) qui démontre à l’évidence le mouvement du glacier. Connaissant la géométrie de l’installation (ouverture angulaire de l’appareil photo, distance de l’appareil aux différents plans de la scène), il est possible de remonter à un déplacement quantitatif en fonction de chaque saison.

Un point fondamental de la méthode d’intercorrélation pour identifier le déplacement est la disponibilité de points de repère. Dans le cas des glaciers, seuls les blocs de roche, crevasses ou bandes de Forbes permettent l’application de l’intercorrélation. Le lecteur désireux d’expérimenter ce concept par lui-même sur la Mer de Glace est encouragé à récupérer les photographies numériques disponibles par exemple à http://www.compagniedumontblanc.fr/webcam/CMM1MERDEGLACE.jpg, tout en étant conscient que le format de compression avec pertes JPEG et la faible résolution des images ne permettent pas un traitement automatique sur des intervalles de temps courts. Une base de données sur plus de 2 ans de ces images, acquise sur le Web 4 fois par jour, est disponible auprès de l’auteur sur demande.

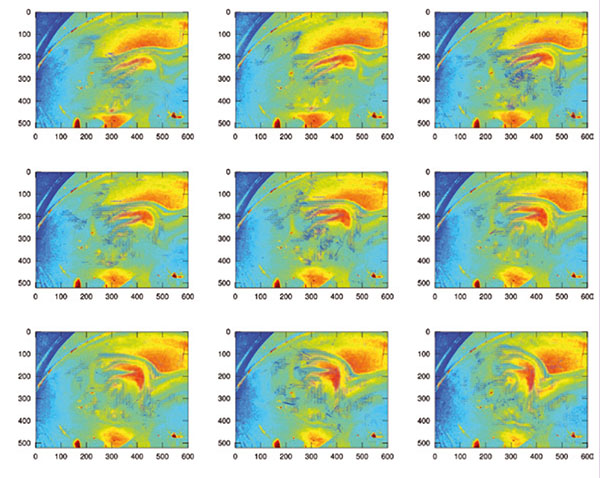
Parmi les utilisateurs de l’intercorrélation, la communauté de la mécanique des fluides est constamment à la recherche de méthodes d’identification du champ de déplacement des fluides. Normalement, les structures visibles sont injectées sous forme de particules ou fluorophore afin de créer les marqueurs représentatifs du mouvement du fluide. Nous allons illustrer cette méthode de mesure sur une bulle de savon [10, 11], dont il est bien connu que les motifs colorés sont représentatifs de l’épaisseur de liquide inclus entre les deux couches de surfactant qui définissent la surface de la bulle. L’hypothèse est donc que l’épaisseur de la bulle est représentative des mouvements de liquides qui s’y déroulent [12] et que l’on peut y appliquer les règles de description eulérienne du fluide [13, p.99] dans laquelle un observateur fixe regarde passer des particules mobiles de fluide et en étudie la statistique en un point donné (Fig. 4).

Une fois le champ de vitesse calculé, la porte est ouverte à une exploitation quantitative des séquences d’images, notamment pour un calcul de l’évolution de la vorticité sur ces fluides [13, p.127] : pour un champ de vitesse bidimensionnel v→, le calcul du rotationnel R→=∇→∧v→ ne fournit qu'une composante normale au plan de l’écoulement Rz=∂ vy/∂ x−∂ vx/∂ y. Ce calcul est effectué, depuis la version 3.4 de GNU/Octave (qui n’est pas encore disponible en paquet Debian à la date de rédaction de ce document), par la fonction curl(cx,cy), dont une illustration est proposée en figure 5. Une extension de ce calcul est la validation expérimentale du théorème de Stokes [14, p.200], qui affirme que l’intégrale sur une surface fermée A de la vorticité doit être égale à l’intégrale de la composante du champ de vitesse le long du contour l définissant cette surface : A Rz dA=∫l v→.dl→.

Une autre application pratique de ces concepts est la proposition d’encodage dans un certain nombre de versions récentes de MPEG : au-delà du codage des différences entre images JPEG successives (cas du MPEG1), l’objectif serait de coder les déplacements de zones d’images, sans recoder les parties statiques de l’image qui sont redondantes dans un flux vidéo ni recoder l’objet lui-même (MPEG4). Nous avons cependant vu que la puissance de calcul pour appliquer ces méthodes est considérable, surtout pour une application en temps réel pour la transmission d’un flux vidéo.

4. L’autocorrélation

Un cas particulier qui va nous amener au cœur du sujet de cet exposé est le cas de l’intercorrélation pour des signaux s et s′ identiques. On parle alors d’autocorrélation, dont nous allons voir la puissance dans l’exemple qui suit.

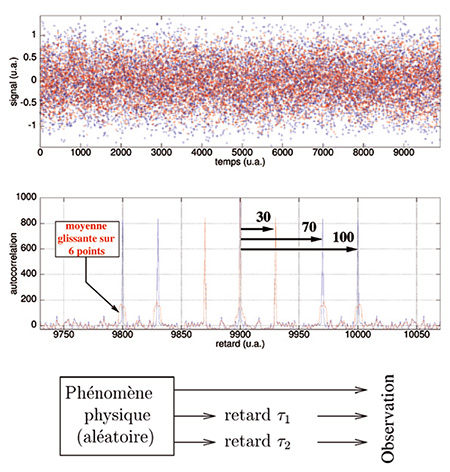
Une approche intuitive des performances de l’autocorrélation est proposée en figure 6. Dans cet exemple, un phénomène physique supposé aléatoire subit deux retards avant d’être observé par l’opérateur. Notre objectif est d’identifier ces retards et donc les constantes de temps des réservoirs affectant la propagation du signal. La figure 6 (haut) propose un signal aléatoire décalé de 30 et 100 unités arbitraire généré par :

Ce signal apparaît, pour l’observateur non averti, aléatoire. Cependant, un calcul d’autocorrélation tel que proposé sur la figure 6 (bas) démontre la présence de 3 maxima locaux de chaque côté du maximum correspondant au décalage nul (abscisse 900, le signal se ressemble à lui-même en l’absence de translation). Ces maxima sont situés en abscisse ±30 et ±100 (retard que nous avons choisi pour synthétiser ce signal), et un troisième maximum en 70 correspond à la ressemblance entre les deux signaux retardés de τ1=30 et τ2=100. Ainsi, la recherche d’une ressemblance au sein du signal permet de retrouver les retards qui se superposent au signal original. Cependant, au-delà de l’aspect purement retard (présence ou absence de pic d’autocorrélation en dehors du retard nul), l’aspect de l’autocorrélation va nous indiquer si un retard est aussi associé à une « dilution » du signal (si par exemple le signal initial est non seulement retardé mais aussi emmagasiné avant restitution).

L’objectif de cette section est de démontrer l’inutilité – voire le danger – de vouloir changer les propriétés statistiques du signal dans l’objectif naïf d’en cacher le contenu. Tenter de soustraire des informations par le secret fournit au lecteur susceptible d’une recherche statistique sur la masse de données d’identifier une rupture des propriétés moyennes de la scène observée, et donc de focaliser son attention sur les quelques zones qui ont été suffisamment dignes d’intérêt pour mériter une manipulation manuelle. Nous allons en particulier démontrer la recherche des sites floutés sur Google Maps sur le territoire français [15, 16].

4.1 Obtention des données

Notre objectif est de traiter les images disponibles sur Google Maps en vue d’y rechercher les sites floutés. La licence d’exploitation de la base de données des cartes Google interdit de récupérer ces photos sans les afficher sur une carte (http://code.google.com/apis/maps/documentation/geocoding/), donc nous allons rechercher sur le serveur de Google une photo du puzzle, l’afficher, la traiter puis l’effacer.

Afin d’automatiser ce processus, il nous faut connaître l’URL pour recherche une pièce du puzzle par une requête HTTP contenant les coordonnées de l’image à obtenir. En allant sur maps.google.com et en visualisant la région qui nous intéresse au zoom approprié, nous pouvons connaître l’URL de chaque pièce composant une page web de la façon suivante :

• sous iceweasel : Tools / Page Info / Media. Nous obtenons alors une série d’URL de la forme http://khm1.google.com/kh/v=81&x=66377&s=&y=45087&z=17&s=Ga que nous tronquons en http://khm1.google.com/kh/v=81&x=66377&s=&y=45087&z=17. L’obtention des images s’obtient alors trivialement par une boucle sur x et y et une requête par wget. Chaque image contient 256×256 pixels et couvre une surface dépendant du facteur de grossissement (argument z=).
• sous Google Chrome, nous exploitons parmi les menus accessibles au moyen de l’icône de la feuille cornée en haut à droite (Control the current page) / Developer / Developer Tools, qui propose d’afficher toutes les ressources, incluant les URL des images affichées.

Ayant identifié les chemins, nous fabriquons les URL au moyen d’un script shell qui incrémente les valeurs de x et y, obtenons les images par wget pour un traitement immédiat sans stockage local, limité à 2500 pièces par jour et par adresse IP pour interdire à tout contrevenant d’abuser du service fourni par Google.

4.2 Traitement des données

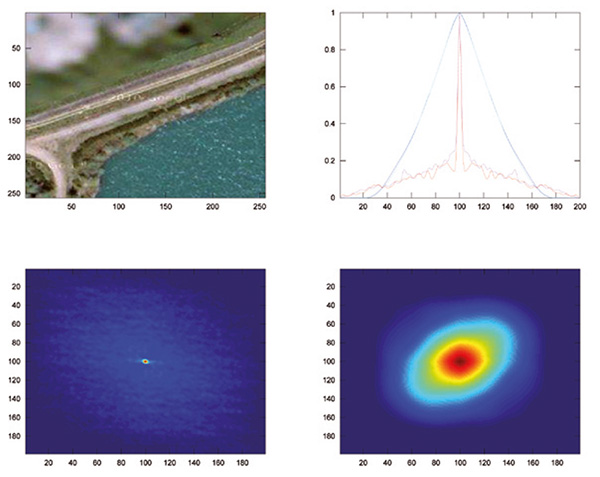
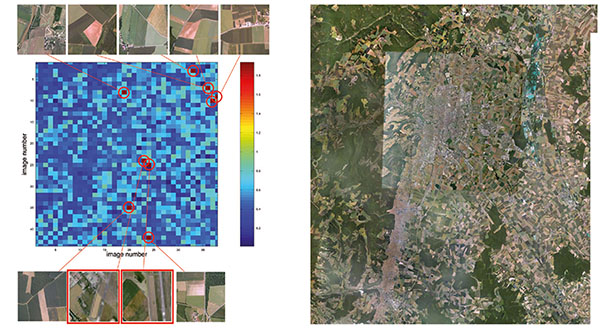
Prenons l’exemple d’une des pièces du puzzle obtenu au niveau de la base militaire aérienne de Luxeuil. Une analyse statistique d’une région floutée (en haut à gauche de l’image) et d’une région nette (en bas à droite) est proposée sur la Figure 7. Pour chacune de ces régions, nous proposons l’affichage de l’autocorrélation (en bas à gauche pour la zone floutée, en bas à droite pour la zone nette, sur des images de 100×100 pixels dans les deux cas) définie comme l’intercorrélation d’un signal avec lui-même.

Tout comme l’intercorrélation, l’autocorrélation recherche le taux de ressemblance entre une image, et cette même image déplacée d’un vecteur t dans le plan. On peut se demander quel est l’intérêt de rechercher la ressemblance d’un signal avec lui-même : le résultat d’une autocorrélation en fonction du décalage est évidemment maximal pour un retard nul, puisqu'un signal se ressemble au mieux avec lui-même. Cependant, les points en dehors du décalage nul présentent un intérêt que nous allons exploiter ici : plus une image est floue, plus les translatées de cette image sont proches de l’original. Au contraire, une image nette et contenant beaucoup de détails ne se ressemblera pas après translation de quelques pixels. Ce constat est visuellement illustré sur les deux graphiques en bas de la figure 7 : la zone floue présente une décroissance lente de l’autocorrélation autour du vecteur de déplacement nul situé en (100, 100), tandis que l’autocorrélation de la région nette présente une distribution étroite qui chute rapidement dès que nous nous éloignons du vecteur de translation nulle. En prenant une coupe de ces distributions selon l’ordonnée 100 (en haut à droite) et en normalisant par le maximum de l’autocorrélation, nous voyons apparaître un critère simple de sélection d’une zone floutée ou non. La hauteur de l’autocorrélation à une position décalée du retard nul est d’autant plus importante que l’image est floue (ici, le retard nul se trouve en abscisse 100). Pour chaque image, nous allons sélectionner des sous-ensembles de quelques dizaines de pixels de côté (afin d’accélérer le calcul et pouvoir identifier des régions floutées au sein d’une image de 256×256 pixels obtenue sur le serveur de Google), et tracer la valeur de l’autocorrélation en des points situés à côté du maximum (translation nulle). Le choix de l’abscisse peut varier selon le rapport signal à bruit recherché, et nous avons constaté qu’il est peu judicieux d’aller trop loin sur les parties les plus faibles de la distribution. Nous nous sommes focalisés sur la mesure de la valeur de l’autocorrélation normalisée à des distances de 2 à 5 % de la position du maximum (i.e. abscisse 95 ou 98 dans l’exemple de la figure 7 en haut à droite). En pratique, le script GNU/Octave rapatriant les images, affichant chaque pièce du puzzle avant d’en effacer la copie locale, puis traitement, ressemble à :

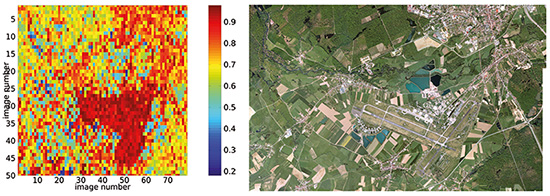
Une application systématique de cet algorithme sur l’ensemble des images proposées par le serveur Google au grossissement z=18 fournit le résultat de la figure 8. L’aéroport flouté ressort en rouge sur un fond bruité mais de valeur nettement moindre de l’autocorrélation.

Le principe de fonctionnement de l’algorithme semble donc acquis, mais son exploitation au delà d’une base aérienne pour l’appliquer, avec un tel facteur grossissement, à une région plus large est impossible. En effet, couvrir une surface intéressante nécessiterait trop de requêtes à Google Maps pour permettre un résultat probant (ce qui ne veut pas dire qu’un organisme suffisamment motivé, avec suffisamment d’adresses IP à sa disposition, ne puisse pas mettre en œuvre une telle stratégie). Nous estimons à 110 m×110 m la surface couverte par une image acquise sur le serveur Google au zoom 18. Ainsi, pour couvrir la majorité de la France par une analyse sur une surface de 800 km×800 km, il faudrait effectuer 64 millions de requêtes, soit 70 ans au rythme de 2500 images/jour (en supposant que l’accès ne soit pas bloqué avant !). Nous allons donc considérer le travail sur un grossissement plus faible, au détriment des performances, puisque l’effet de flouter l’image devient moins évident.

Le second exemple qui va nous intéresser concerne donc l’exploitation de cet algorithme à grossissement moindre, où la notion de flouté devient moins claire, induisant par conséquent plus de faux positifs et un réglage plus fin de paramètres de seuillage en vue d’une identification automatique des régions floutées. Nous nous sommes proposés de travailler à zoom 15, soit sur une région où une même image de 256×256 pixels couvre une superficie 8×8 fois plus importante.

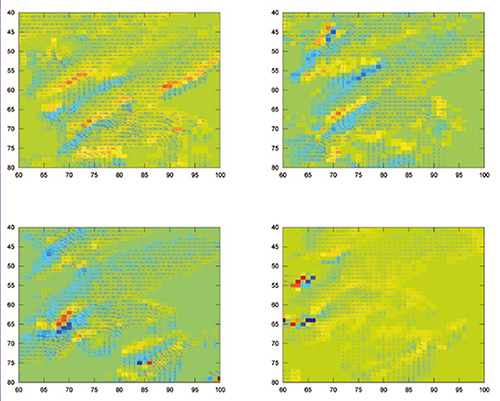
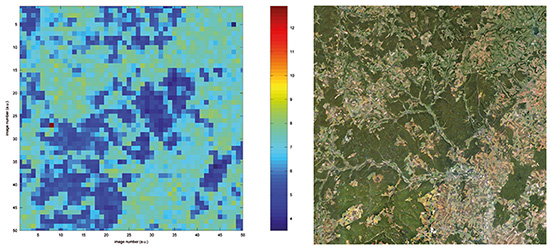
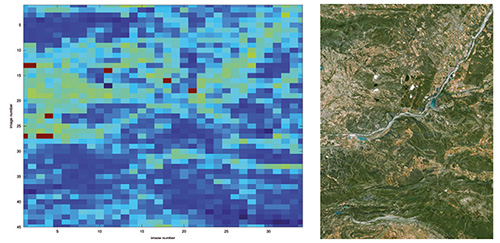
Le problème d’une analyse sur une zone plus vaste (zoom 8 fois plus faible, en passant du grossissement 18 à 15) est le mauvais rapport signal à bruit associé à l’identification de zones faiblement contrastées (étendues d’eau, champs) comme des régions floutées. Nous pouvons néanmoins traiter rapidement des zones de 40 km×40 km (région autour du centre de Valduc du CEA, au nord-ouest de Dijon, Fig. 9) avec un taux de faux positifs de l’ordre de 0,5 %. Le site flouté est bien identifié par un unique pixel représentatif d’un taux d’autocorrélation anormalement élevé, abscisse 7 et ordonnée 27. On notera sur cette même figure qu'au-delà de la recherche des régions floutées, l’analyse par autocorrélation est un bon indicateur, au-delà des analyses colorimétriques classiques, de la nature du terrain. Le pic d’autocorrélation s’avère fin dans les régions boisées présentant un fort contraste, tandis qu’il s’élargit dans les régions cultivées où le faible contraste des champs peut aller jusqu’à s’apparenter à une image floue. Un cas intermédiaire présentant un taux de faux positifs important est autour de l’aéroport de Longvic à Dijon : bien que la zone floutée soit bien identifiée au centre de la région analysée (abscisses 23 et 24 de la figure 10), plusieurs champs mal résolus sont identifiés comme floutés par le simple seuillage que nous appliquons.

Cette conclusion est encore plus évidente autour du site de Cadarache du CEA (Fig. 11), où la région floutée recherchée n’est pas identifiée par un traitement automatique du fait de nombreuses zones de faible contraste – notamment lacs et rivière, ainsi qu’une paire de nuages que Google n’a pas pu éliminer par l’exploitation d’une image de meilleure qualité. Ces zones de faible contraste augmentent artificiellement le seuil de détection des régions floutées, qui devient insuffisant pour identifier le centre de Cadarache.

Il est surprenant de constater que l’application de cet algorithme sur un rayon d’environ 50 km autour de Paris ne permette pas d’identifier une seule zone floutée, et une vérification manuelle sur un certain nombre de sites que l’on pourrait considérer comme sensibles valide effectivement la netteté des images dans toutes ces régions.

Nous nous sommes jusqu’ici contentés d’appliquer des outils de traitement du signal – auto et intercorrélation – sur des données qui nous sont imposées, avec leur dynamique et leur qualité intrinsèque. Cependant, il existe de nombreux cas – dont les RADAR et le SONAR sont les plus connus – où l’utilisateur sonde son environnement avec un signal dont il choisit les propriétés statistiques. Pouvons-nous alors améliorer les performances de la détection en choisissant un signal sonde optimisé en ce sens ?

5. La compression d’impulsion

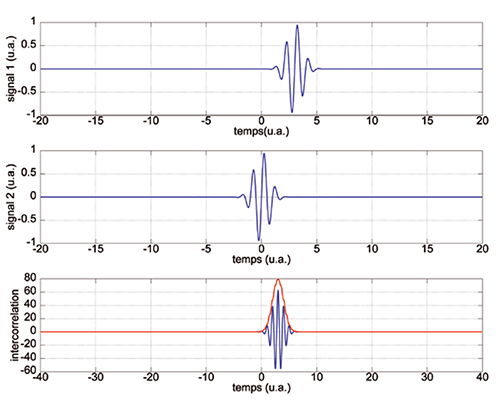
L’intercorrélation est un estimateur classiquement utilisé pour retrouver le signal émis par un RADAR ou un SONAR dans le signal bruité enregistré par le système de réception (Fig. 1). Au-delà de la détection de l’écho, ces dispositifs s’intéressent à la localisation de la cible, qui pour la direction radiale s’obtient par une estimation du temps de vol.

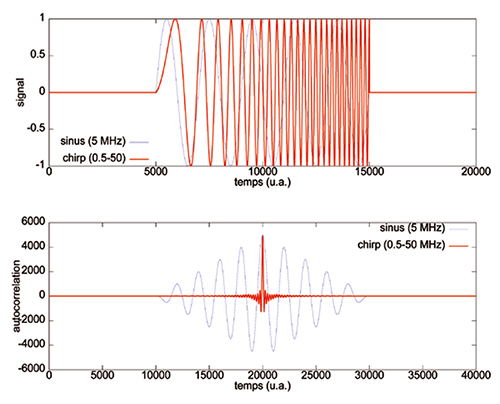
Le problème de l’application d’une intercorrélation sur une impulsion délimitant une oscillation périodique est que rien ne ressemble plus à une période de sinusoïde qu’une autre période de sinusoiïde (Fig. 12). Par ailleurs, en cas de décalage Doppler par une cible mobile, l’intercorrélation ne somme pas de façon cohérente le signal d'écoute au signal émis du fait du changement de fréquence lors de la réflexion de l’impulsion sur la cible mobile.

Afin de pallier ces deux problèmes, et nous nous focaliserons sur le premier, il est d’usage de remplacer la sinusoïde formant la porteuse de l’impulsion par un signal dont la fréquence évolue dans le temps, pour générer un signal nommé le chirp. De cette façon, une période du signal ressemble moins à ses voisines, et l’intercorrélation saura déterminer au mieux la date de coïncidence des signaux émis retardés et du signal retour. Nous pouvons intuiter que plus la variation de fréquence est rapide et dans une large plage, plus cette stratégie est efficace. Pour un balayage de la fréquence dans une bande de B Hz pendant une durée τ (secondes), nous définissons le facteur de compression comme le produit sans dimension B× τ.

Concrètement, un chirp a pour équation :

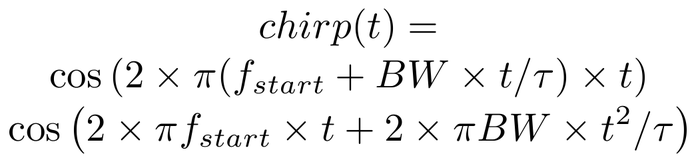
/div>

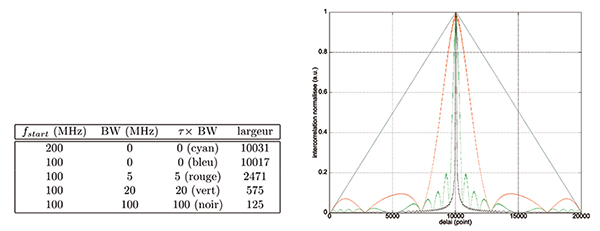
avec BW l’excursion de la fréquence de début fstart à la fréquence de fin du chirp pendant une durée τ. Il s’agit donc d’un balayage linéaire de la fréquence fstart (date 0) pour atteindre la fréquence fstart+BW à la date τ. Si ce signal nous est retourné inchangé par la cible, alors l’intercorrélation du signal reçu avec le signal émis est d’autant plus fine et importante que BW est grand (Fig. 13). La notion de compression d’impulsion ne se comprend donc que sur la chaîne de mesure complète, incluant le traitement du signal acquis, et pas juste sur le chirp lui-même.

Sous GNU/Octave, la démonstration de ces concepts se fait par :

t=[0:0.1e-9:1e-6];                     % duree de 1 us par pas de 100 ps

l=100;                                 % taille de la fenetre pour filtre passe bas

s=chirp(t,100e6,t(end),105e6);         % chirp de 100 a 105 MHz

r=conv(abs(xcorr(s,s)),ones(l,1)/l);   % convolution + passe bas

plot(r/max(r),'r');

k=find((r/max(r))>0.5);(k(1))-(k(end)) % largeur a mi-hauteur

Figure 13 : Gauche : autocorrélation de chirps de bande passante variable. Le tableau indique la largeur à mi-hauteur des diverses courbes d’intercorrélation, démontrant l’efficacité de la compression d’impulsion en réduisant la largeur du pic d’un facteur bande passante × durée du chirp (et donc à énergie constante, en augmentant d’autant la hauteur du pic).

Conclusion

Nous nous sommes efforcés de démontrer qu’une maîtrise de quelques outils simples de traitement du signal permet d’extraire un maximum d’informations disponibles, librement ou non, sur le Web. Nous avons illustré ces idées dans un premier temps avec de la reconnaissance de position de motifs dans une image, avant de passer au calcul d’un champ de déplacement entre deux images d’un même site prises avec un intervalle de temps de l’ordre de la semaine. Après avoir exploité l’intercorrélation, nous avons démontré la richesse d’un estimateur moins courant, l’autocorrélation, pour la recherche de zones floutées sur des images aériennes. Enfin, nous avons montré comment un choix judicieux du signal sonde, lorsque l’utilisateur a la liberté de le synthétiser avec les propriétés statistiques requises, permet de considérablement améliorer le rapport signal à bruit et la localisation du signal émis dans un enregistrement bruité d’un récepteur.

Tous ces concepts méritent à être approfondis afin d’extraire le maximum d’informations de la masse de données disparates disponibles sur le Web, et ainsi être maître de l’information plutôt qu'esclave d’un flot continu de données au rapport signal à bruit souvent bien faible. Seul expérimenter sur ses propres problèmes permet de s’approprier les concepts présentés dans ce document : le traitement du signal ne nécessite aucun autre investissement que de la motivation et du temps.

Remerciements

Luc Moreau (www.moreauluc.com), glaciologue indépendant rattaché au laboratoire EDYTEM de Chambéry, a fourni les images du glacier de Bionassay pour leur traitement, ainsi qu’une motivation à ce travail en installant des appareils photo automatisés dans divers sites du massif du Mont Blanc. Les discussions avec D. Laffly (Univ. Toulouse 2) ont été l’origine du premier exemple sur la localisation de lettres dans un texte. C. Marlin (Univ. Paris 11) a proposé l’identification par autocorrélation des délais du signal retardé.

Références

[1] l’accès aux previews des satellites dont les images sont commercialisées en pleine résolution par DigitalGlobe est disponible à http://browse.digitalglobe.com/imagefinder/main.jsp

[2] P.T. Fretwell & P.N. Trathan, Penguins from space: faecal stains reveal the location of emperor penguin colonies, Global Ecol. Biogeogr. 18, 543-552 (2009)

[3] J.-M Friedt, Affichage et traitement de données au moyen de logiciels libres, GNU/Linux Magazine France 111 (Déc. 2008)

[4] D. Kahn, The codebreakers – the story of secret writing, The MacMillan Company (1973)

[5] F. Roddier, Distributions and transformation de Fourier, Edisciences International, Paris (1978) [chapitre 11]

[6] un point de vue historique sur les performances d’un ordinateur nécessaires à ces calcluls : Y. Granclaude & J.Y. Ranchin, Corrélation et convolution par transformées entières, actes du Septième colloque sur le traitement du signal et ses applications (Nice, 1979), disponible à http://documents.irevues.inist.fr/bitstream/handle/2042/10373/AR66.pdf

[7] une autre excellente illustration des concepts présentés dans le premier chapitre de ce document : http://www.mathworks.com/help/toolbox/images/f21-17064.html

[8] J.-M Friedt, C. Ferrandez, G. Martin, L. Moreau, M. Griselin,E. Bernard, D. Laffly & C. Marlin, Automated high resolution image acquisition in polar regions, European Geosciences Union (2008), disponible à http://jmfriedt.free.fr/EGU_jmfriedt2008.pdf

[9] J. Korona, É. Berthier, M. Bernard, F. Rémy & É. Thouvenot, SPIRIT. SPOT 5 stereoscopic survey of Polar Ice: Reference Images and Topographies during the fourth International Polar Year (2007-2009), ISPRS Journal of Photogrammetry and Remote Sensing 64 204-212 (2009)

[10] Y. Couder, J.-M Chomaz & M. Rabaud, On the hydrodynamics of soap films, Physica D 37 (1989) 384-405, disponible à yakari.polytechnique.fr/people/jmarc/pdf/paru/PhyD1989Yves

[11] J.-M Chomaz & B. Cathalau, Soap films as two-dimensional classical fluids, Physical Review A 41 (4), (1990) 2243-2245, disponible à http://www.off-ladhyx.polytechnique.fr/people/jmarc/noticelp.html

[12] O. Greffier, Y. Amarouchene, & H. Kellay, Thickness Fluctuations in Turbulent Soap Films, Phys. Rev. Letters 88 (19), (2002) 194101, disponible à www.cpmoh.cnrs.fr/IMG/pdf/ThicknessPRL2002.pdf

[13] E. Guyon, J.-P. Hulin & L. Petit, Hydrodynamique physique, Interéditions/Editions du CNRS (1991)

[14] R.W. Fox & A.T. McDonald, Introduction to fluid mechanics, John Wiley & Sons (1994)

[15] http://www.wired.com/dangerroom/2008/06/every-military/

[16] http://www.gearthhacks.com/dlcat19/Airports,-Air-Force-Bases,-Space-Centers.htm comparaison avec ikonos/previews