Nous avons exploré diverses implémentations libres de transformées de Fourier discrètes rapides (FFT), mais leur occupation en mémoire reste de la dizaine de kilooctets. Que peut-on faire avec 2,5 kB de mémoire ? La vénérable note d’application 3722 de Maxim IC nous enseigne comment implémenter efficacement une FFT sur microcontrôleur 8-bits et l’arithmétique en virgule fixe, et la notation en complément à deux au passage.
La note d’application 3722 de Maxim [1] devrait être une lecture obligatoire pour tout développeur désireux d’appréhender toute la puissance des petits microcontrôleurs 8 bits (taille des données manipulées par leur unité arithmétique et logique) que nous pourrons choisir pour leur faible consommation par exemple, mais elle est malheureusement devenue introuvable sur le Web. Heureusement, nous avions archivé ce document avant que Maxim ne soit racheté par Analog Devices et le mettons à disposition, dans https://github.com/jmfriedt/l3ep, dans le répertoire FFT avec son archive associée de codes sources. Cette note d’application contient toutes les informations nécessaires pour développer efficacement de l’arithmétique sur des entiers codés en virgule fixe, en définissant le mode d’encodage des informations en format Qm.n pour attribuer m bits à la partie entière du nombre et n bits à fractionnaire, en produisant automatiquement le code effectuant la transformée de Fourier rapide (Fast Fourier Transform ou FFT), et une méthode efficace de calcul du module s’affranchissant de multiplications et de la racine carrée en passant par une table d’allocation (Look Up Table) précalculée et donc stockée en mémoire non volatile, car préfixée dans sa définition du terme const. Nous nous proposons de reprendre ce texte fondateur sur un microcontrôleur plus actuel qu’est l’Atmega32U4 avec ses 2,5 kB de RAM et 32 kB de mémoire non volatile et voir comment y porter le code pour effectuer le passage du domaine temporel au domaine spectral de mesures acquises sur le convertisseur analogique numérique.
1. Prise en main de la note d’application
La note d’application AN3722 venait avec une archive contenant le logiciel de démonstration pour compilateur propriétaire IAR visant une architecture un peu exotique nommée MAXQ2000 (https://www.analog.com/en/products/maxq2000.html) spécifiquement conçue pour commander un écran LCD. Une fois débarrassé des fichiers de l’IDE fft_r2* pour se concentrer sur les codes sources, il ne reste que l’implémentation de la FFT maxqfft.c et les prototypes de fonctions associées maxqfft.h, le fichier iomaxq200x.h étant spécifique au microcontrôleur qui sert de prétexte à cette note d’application. Ce code en C devrait être portable, sauf :
qui prétend forcer les multiplieurs matériels du microcontrôleur. Ces registres n’ayant aucun sens pour l’Atmega32U4, nous nous contentons de les déclarer comme variables globales du programme pour permettre la compilation. Le sens de ce code est limpide puisque toute la FFT est implémentée sur des entiers codés sur 16 bits, dont les 8 bits de poids fort sont la partie entière de la représentation en virgule fixe et les 8 bits de poids faible sont la partie fractionnaire, avec la perte de précision lors de la multiplication associée à la perte des bits de poids faible que nous observons avec les décalages en fin d’opération. Ainsi, cette fonction se traduit trivialement par :
et le tour est joué pour compiler le code sur PC (nous verrons plus loin que ce n’est pas si simple !).
2. Premiers essais sur PC : les stubs
Développer sur microcontrôleur c’est bien, mais c’est long, fastidieux et peu d’outils de déverminage (gdb) sont disponibles. Développer sur PC, c’est mieux : comment prendre le code destiné à un microcontrôleur et le tester sur PC ? En prenant soin de séparer la partie algorithmique du code, portable, des aspects d’initialisation du matériel et de communication, par exemple : au moyen de stubs qui émuleront le fonctionnement du matériel sur le microcontrôleur lors de l’exécution sur PC. Ainsi, alors que la communication se fera de façon asynchrone par port série compatible RS232 ou USB sur le microcontrôleur, la fonction d’affichage implémentée sur PC peut se contenter d’un printf() sur la console. Le choix du stub se fait lors de la compilation, en liant l’exécutable avec la version appropriée du code. Cette approche de développement du code permet de bénéficier d’outils puissants sur PC tels que valgrind ou lint pour profiler le code afin d’identifier de potentielles sources de dysfonctionnement avant de l’exécuter sur microcontrôleur, dont l’absence de gestionnaire de mémoire (MMU) rend les dépassements de mémoire indétectables autrement que par un comportement aléatoire et inattendu du code.
Ainsi, les deux fonctions dépendantes du matériel que sont l’initialisation du port de communication et la fonction d’affichage des valeurs elle-même sont remplacées dans l’implémentation sur PC par une fonction vide pour l’initialisation et printf("%hx",val); pour la seconde, toutes les variables manipulées étant codées sur 16 bits. Plutôt que de s’attaquer tout de suite à des données expérimentales, la fonction d’acquisition est remplacée par la génération d’un signal de forme connue, par exemple sinusoïde ou créneau, dont la transformée de Fourier est connue, permettant donc de valider le bon fonctionnement de la bibliothèque.
La compilation conditionnelle exploite le drapeau __AVR_ATmega32U4__ identifié dans /lib/avr/include/avr/io.h du paquet avr-libc de Debian/GNU Linux et défini par avr-gcc lorsque l’option de compilation -mmcu=atmega32u4 est activée. En l’absence de ce drapeau, nous supposons que la compilation cible le processeur compatible Intel du PC.
Lors de l’exécution de ce code, nous constatons que tous les 256/2=128 coefficients de Fourier aux fréquences positives sont nulles lorsque les données représentent une sinusoïde, sauf le 11ème coefficient. Ce résultat est en accord avec les attentes : le signal analysé est défini comme 127×sin(i/4.) avec i l’indice du point. L’argument de la fonction trigonométrique s’exprime comme une fréquence f qui fait tourner la phase en fonction du temps t comme 2π f t qui vaut ici 1/4 donc f=1/(2π×4)≃ 0,04 et comme la transformée de Fourier couvre la gamme des fréquences allant de 0 à la fréquence d’échantillonnage sur les N=256 points considérés, l’abscisse de la composante spectrale est 0,04× 256=10,2. Le premier point étant d’indice 0 pour la composante continue du signal, le 11e point représente bien la composante spectrale 1/4 utilisée dans la définition du signal.
De la même façon, si nous décommentons la définition des échantillons en créneaux de rapport cyclique 50 % et de période 20 échantillons – représentation en complément à deux qui propage donc le bit de signe de l’octet de poids faible si celui-ci est à 1 pour indiquer un nombre négatif – nous obtenons des coefficients non nuls aux abscisses (en commençant à compter avec l’indice 0) 13, 38, 64, 90, et 115 pour des valeurs de 143, 32, 22, 16 et 16, respectivement. La transformée de Fourier discrète d’un créneau est caractérisée par une série de raies spectrales aux harmoniques impaires du mode fondamental dont l’amplitude décroît comme l’indice de l’harmonique. Les indices sont bien aux abscisses prévues, tandis que l’axe des ordonnées présente la bonne tendance sans suivre exactement la loi attendue, compte tenu de la fuite d’énergie dans les composantes spectrales adjacentes (143 est entouré de 35 et 16, 32 est suivi de 16).
3. Validation sur Atmega32U4 : la taille d’un int
Le code fonctionnel sur PC est cross-compilé pour Atmega32U4 en remplaçant gcc par avr-gcc -mmcu=atmega32u4 dans le Makefile et... l’exécution échoue lamentablement avec le renvoi exclusivement de 0 s après la FFT d’un signal qui devrait présenter une raie spectrale. La promesse de portabilité du code en C entre plateformes n’est donc pas respectée.
Dans la série des choses qui ne sont pas définies dans le langage C :
- coder un entier sur 8 bits en signé ou non signé n’est pas défini par défaut si nous omettons le préfixe signed ou unsigned. En effet, https://gcc.gnu.org/onlinedocs/gcc/C-Dialect-Options.html affirme dans la description de l’option -funsigned-char que « Each kind of machine has a default for what char should be. It is either like unsigned char by default or like signed char by default. Ideally, a portable program should always use signed char or unsigned char when it depends on the signedness of an object. But many programs have been written to use plain char and expect it to be signed, or expect it to be unsigned, depending on the machines they were written for. » tandis que l’int est toujours signé par défaut tel que l’affirme l’option -fno-unsigned-bitfields de cette même page avec « the basic integer types such as int are signed types », mais sa taille dépend de l’architecture.
- la taille de l’int utilisé tout le temps dans un code C dépend de l’architecture. En effet, int est défini comme la taille « native » de l’entier sur l’architecture ciblée, mais capable de représenter au moins 32767 donc sur 2 octets au minimum. Le seul type strictement défini en C est le short avec ses deux octets, puisque nous constatons dans /usr/include/stdint.h d’une machine sous GNU/Linux que :
- et que donc sur un PC basé sur un processeur compatible Intel 32 bits le long est codé sur 4 octets et le long long sur 8, tandis que sur une machine 64 bits les deux long et long long sont tous deux codés sur 8 octets.
- l’ordre d’analyse des arguments d’une fonction dépend du compilateur : LLVM (compilateur clang) et GCC n’interprètent pas dans le même ordre les arguments de printf("%d %d %d\n",i,f(&i),i); pour une fonction f(int *i) {(*i)++;return(*i);} qui modifie le contenu de la variable. En effet, lors de la compilation du code :
- nous obtenons un résultat différent selon le compilateur utilisé :
Le problème que nous venons de rencontrer est du deuxième type, à savoir que le calcul sur le PC est passé par un int codé sur 4 octets qui s’est réduit à deux octets sur Atmega32U4, résultant dans l’échec de la multiplication de deux nombres en virgule fixe codés sur 16 bits qui doivent absolument passer par une variable intermédiaire sur 32 bits, avant de tronquer les bits de poids faible. Le problème se résout en définissant :
afin d’imposer des opérations arithmétiques sur 32 bits et non sur les 16 bits qu’occupent A et B, et cette fois le résultat sur Atmega32U4 est strictement identique à l’exécution sur PC.
Analyse de l’occupation de la pile dans le simulateur simavr
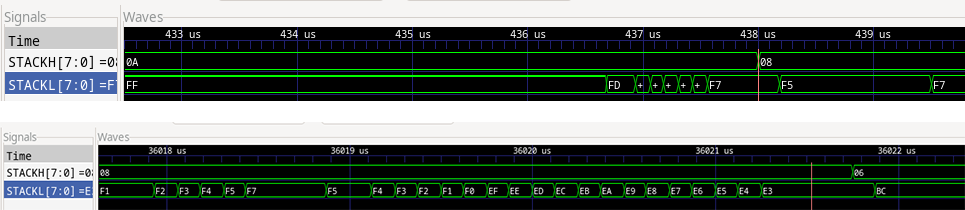
Nous avons déjà expliqué dans [2] la puissance du simulateur simavr et sa capacité à tracer l’état interne des registres pour en mémoriser les changements d’état dans un fichier VCD (Value Change Dump) lisible par gtkwave. Ici, nous avons un doute sur la capacité de l’Atmega32U4 à stocker toutes les informations utiles à une transformée de Fourier rapide sur 256 points et désirons tester l’état de la pile en cours d’exécution. L’Atmega32U4 a cette particularité que le pointeur de pile – la zone brouillon où le microcontrôleur stocke les variables temporaires en partant de l’adresse la plus élevée de la RAM – n’est pas un registre proche de l’unité arithmétique et logique, mais un registre adressable aux emplacements 0x5D et 0x5E. Nous indiquons à simavr de mémoriser l’état de ces deux registres par un entête qui ne sera pas lié au binaire flashé dans le microcontrôleur, mais uniquement comme consigne à l’émulateur :
dont l’exécution par simavr --freq 16000000 --mcu atmega32u4 fft se traduit par une trace dont l’affichage est découpé dans les zones les plus intéressantes :
qui indiquent que la pile est initialisée en 0xAFF (qui est bien l’adresse la plus haute de la RAM) pour soudainement s’effondrer à 0x8F5 soit une occupation de la pile de 522 octets, raisonnable pour un tableau de 512 octets contenant une FFT sur 256 valeurs codées sur 2 octets chacune et quelques variables additionnelles. Plus tard, la pile passe de 0x8E3 à 0x6BC, ou encore 551 octets occupés. Ces deux occupations mémoire de 1073 octets réquisitionnent une fraction significative des 2560 octets disponibles, mais le pointeur de pile ne descend jamais sous 0x6BC alors que les autres tableaux utilisés par la FFT sont préfixés de const, donc en mémoire non volatile et n’occupent pas le tas (qui serait utilisé si nous préfixions la définition de la variable de static). Ainsi, la collision entre le tas et la pile n’est pas la cause du dysfonctionnement... que nous avons identifié par ailleurs comme un cast erroné lors d’un calcul intermédiaire de produit entre deux entiers qui doit se faire sur 32 et non 16 bits pour être correct.
4. Affichage en waterfall en ASCII
Maintenant que nous avons validé le bon fonctionnement de la bibliothèque sur PC et sur Atmega32U4, il reste à analyser un vrai signal physique et pas une simple simulation. Pour ce faire, le convertisseur analogique numérique de l’Atmega32U4 est connecté à la carte son d’un PC faisant office de générateur de fonction. La carte son génère un signal centré sur 0, tantôt positif et tantôt négatif, quand le convertisseur analogique numérique ne peut que mesurer une tension entre la masse et sa tension de référence. Il faut donc introduire une tension de biais constante entre la sortie de la carte son et l’entrée du convertisseur (Fig. 1) : afin de s’affranchir de tout composant actif (p. ex. amplificateur opérationnel), la solution la plus simple est le pont de résistances pour définir la tension de biais, et un condensateur pour protéger la sortie de la carte son du potentiel constant. Ce montage nommé T de polarisation suppose de respecter deux hypothèses :
- le pont diviseur ne produit en son point milieu un potentiel pondéré par les valeurs des résistances que si le courant qui circule dans les résistances est grand devant le courant consommé par le montage connecté au point milieu. Or, le convertisseur analogique numérique présente [3, p.306] une impédance caractéristique d’une dizaine de kΩ. Le choix de résistances de quelques kΩ tout au plus permettra de vérifier la condition de fonctionnement du pont diviseur de tension ;
- le condensateur se comporte toujours comme un circuit ouvert pour la composante continue introduite par le pont de résistances, mais doit laisser passer le signal audiofréquence comme le ferait un fil. Le module de l’impédance |Z| du condensateur C traversé par un signal de fréquence f est |Z|=1/(C2π f) qui sera d’autant plus faible que f est élevé. Le problème se pose donc aux basses fréquences : notre choix d’un condensateur non polarisé de valeur arbitrairement sélectionnée à 100 nF implique une impédance de 10 kΩ ou plus lorsque la fréquence passe en dessous de 150 Hz. Lors de nos essais, nous avons par conséquent toujours mesuré des signaux audiofréquences au-dessus de 500 Hz pour limiter l’impact du condensateur sur l’amplitude du signal vu par le convertisseur analogique numérique.
Deux approches s’offrent à nous pour cadencer le convertisseur analogique numérique : soit acquérir le plus vite possible dans une boucle de N éléments en vue d’effectuer la FFT de ce tableau et déduire la fréquence d’échantillonnage, inconnue a priori, d’une mesure d’un signal à fréquence fixe, ou cadencer le convertisseur sur un timer dont l’interruption déclenche la conversion. Bien que plus lente à cause de la surcharge de gestion des interruptions, nous utilisons la seconde solution pour imposer la fréquence d’échantillonnage fs et donc l’axe des abscisses de la FFT.
Le code :
initialise le timer 4 (codé sur 10 bits) pour se déclencher tous les 200 coups d’horloge après une décimation d’un facteur 16 de l’oscillateur à 16 MHz qui cadence le microcontrôleur, résultant en une fréquence d’échantillonnage de 5 kHz puisque adc_init() déclenche la conversion en configurant ADCSRB sur le timer. La voie mesurée est définie dans ADMUX comme étant le convertisseur numéro 7... noté A0 dans la sérigraphie compatible Arduino de la carte Olimexino32U4. Chaque fois que la conversion est achevée, l’interruption liée à la fin de conversion analogique numérique ADC_vect est appelée et se charge de stocker dans le tableau des valeurs à convertir par FFT la nouvelle mesure. Lorsque le tableau est plein, la conversion est effectuée et son résultat affiché à l’écran :
en s’appuyant sur la bibliothèque LUFA et sa version allégée réduite à la communication s’apparentant au lien asynchrone compatible RS232 fournie à http://jmfriedt.free.fr/LUFA_light_EEA.tar.gz pour communiquer par USB.
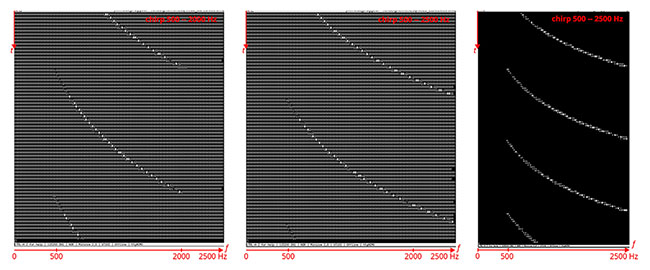
La FFT étant bijective, les N points acquis dans le temps deviennent N points dans le domaine spectral s’étendant de −fs/2 à +fs/2 donc un pas de fréquence de fs/N. Puisque le module de la FFT d’un signal réel est une fonction paire, nous nous contentons de n’afficher que les N/2 points compris entre 0 et fs/2 : avec N=256, ces 128 points tiennent dans un terminal un peu élargi par rapport aux 80 colonnes standard, et afficher successivement les FFT en codant l’amplitude de chaque raie spectrale comme un symbole différent permet d’afficher en ASCII un waterfall dans lequel l’axe des abscisses est la fréquence et l’ordonnée le temps, permettant d’observer les évolutions des composantes spectrales caractérisant un signal en fonction du temps. La Fig. 2 illustre le résultat en codant (gauche et milieu) l’intensité spectrale par la lettre « A » à laquelle s’ajoute un indice proportionnel à l’amplitude du pic, permettant de voir toute l’étendue du spectre, et à droite la solution quand le symbole de référence en l’absence d’énergie est l’espace, améliorant le contraste, mais ne permettant pas d’identifier la fréquence maximale sur l’écran. Le signal a été produit par sox comme un chirp, donc une sinusoïde de fréquence variable à gauche entre 500 et 2000 Hz, et au milieu et à droite entre 500 et 2500 Hz, par les commandes :
et :
respectivement, avec pour premier argument la durée du chirp (4 secondes) suivi de la nature du signal (une sinusoïde) et la gamme de fréquences.
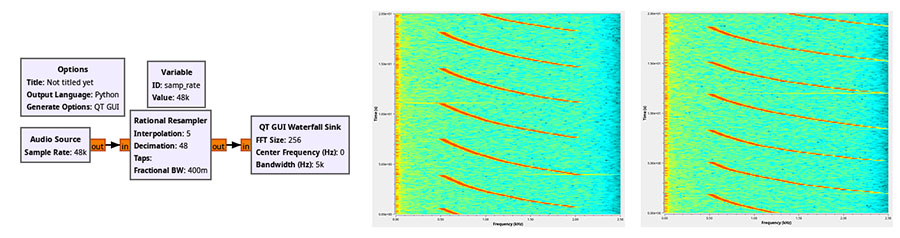
N’ayant aucune raison d’avoir confiance dans notre résultat, nous désirons le comparer à une approche indépendante du même problème, par exemple par l’implémentation du waterfall dans GNU Radio. Cette comparaison est proposée en Fig. 3 avec une chaîne d’acquisition et de traitement réduite à sa plus simple expression, avec la seule subtilité de passer de la fréquence d’acquisition imposée par la carte son du PC – 48 kS/s – à une fréquence comparable à celle utilisée sur microcontrôleur – 5 kS/s. Pour ce faire, le Rationale Resampler se charge de décimer et d’interpoler pour atteindre la fréquence d’échantillonnage requise : nous conservons les paramètres par défaut du bloc et enregistrons le flux audiofréquence sur l’entrée microphone alors que sox joue au moyen de play les chirps sur la sortie casque, l’entrée et la sortie étant reliées par un câble audio jack mâle/jack mâle.
Nous pourrions être surpris par la forme du chirp dans le waterfall : pourquoi l’évolution de la fréquence n’est-elle pas linéaire dans le temps ? La page de manuel ou les sources disponibles à https://sourceforge.net/projects/sox/ nous indiquent en lignes 81 et 262 de synth.c que :
signifiant que le symbole utilisé entre les deux fréquences balayées définit la nature du balayage : l’utilisation de « - » comme séparateur se traduit par « the tone will change by a fixed number of semitones per second. », donc une évolution exponentielle de la fréquence telle que nous l’observons.
Conclusion
Porter un code sur une architecture aux ressources contraintes est une opportunité de s’assurer de comprendre en détail le fonctionnement des outils utilisés, ici le langage C et quelques-unes de ses subtilités, afin d’utiliser aussi efficacement que possible les ressources disponibles. Ce faisant, nous avons atteint notre objectif d’implémenter une transformée de Fourier rapide – FFT – sur un microcontrôleur 8 bits ne proposant que 2,5 kB de mémoire volatile.
La disparition de Gordon Moore, fondateur d’Intel et auteur de la loi empirique qui porte son nom annonçant que le nombre de transistors double tous les deux ans, ne doit pas nous faire oublier que la consommation électrique d’un processeur croît comme le nombre de commutations des portes logiques, donc croît avec la fréquence de cadencement et le nombre de processeurs. Cependant, la vitesse n’est qu’un paramètre d’un système de calcul qui ne met en jeu que notre patience à attendre la fin du calcul. Plus dramatique est la taille de stockage : alors que nous avons commencé à programmer sur des disquettes ou cassettes d’une capacité de 360 kB, il est maintenant devenu courant d’acquérir un support de stockage qualifié en téraoctets, soit 7 ordres de grandeur en 40 ans, avec une conséquence bien plus dramatique sur notre capacité à appréhender une telle masse d’informations.
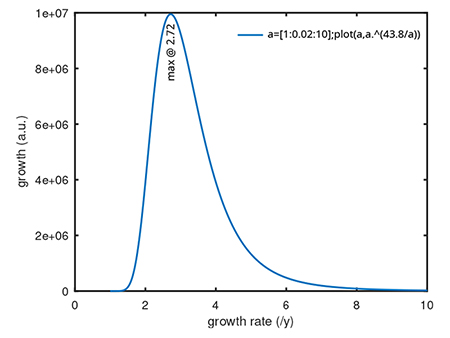
Une croissance régulière d’une propriété, par exemple d’un facteur r tous les y ans, s’exprime classiquement par une loi exponentielle de la forme f(t)=f(0)× r(t/y) avec f la grandeur analysée en fonction du temps t de valeur initiale f(0). Afin de rendre la loi plus facile à retenir, il est classique d’annoncer qu’une grandeur « multiplie sa capacité d’un facteur n tous les n ans », imposant donc que r et y soient égales : la loi devient donc n(t/n) et nous pouvons nous demander quel n induit la croissance la plus rapide, par exemple une multiplication modeste, mais rapide des capacités (n petit) ou une multiplication importante mais lente (n grand) : la figure 4 indique le facteur multiplicatif après 43,8 ans ajusté pour atteindre le facteur 107 de croissance de la capacité de stockage, qui est atteint pour une croissance d’un facteur 2,72 tous les 2,72 ans. La loi de Gordon Moore doublant la capacité tous les deux ans empiriquement observée pour le nombre de transistors dans les processeurs, donc n=2, permet dans la même durée de multiplier le nombre d’unités de calcul d’un facteur 2·106 !
Il peut avoir du bon de se rappeler ce qu’on peut faire avec 2560 octets, ou pour se laisser un peu de marge avec 8 kB pour l’incroyable Tetris de la console portable Gameboy originale [5] ! Les codes décrits dans ce document sont disponibles à https://github.com/jmfriedt/l3ep dans le sous-répertoire FFT.
Références
[1] Maxim IC, Developing FFT Applications with Low-Power Microcontrollers, Application note 3722 (2006).
[2] J.-M Friedt, Développer sur microcontrôleur sans microcontrôleur : les émulateurs, GNU/Linux Magazine France HS 103 (2019) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmfhs-103/developper-sur-microcontroleur-sans-microcontroleur-les-emulateurs
[3] Microchip, Datasheet ATmega16U4/ATmega32U4 version “Atmel-7766J-USB-ATmega16U4/32U4-Datasheet_04/2016” (2016).
[4] R.E. Fontana Jr, G.M. Decad, Moore’s law realities for recording systems and memory storage components: HDD, tape, NAND, and optical, AIP Advances 8(5) 056506 (2018).
[5] Film Tetris (2023).



 Ajouter à une liste de lecture
Ajouter à une liste de lecture