http://www.cbp.ens-lyon.fr/emmanuel.quemener/dokuwiki/doku.php?id=sagemath4debian
1. Introduction
Sorti pour la première fois en 2005, Sage est un ensemble d'outils mathématiques articulés autour d'un environnement en Python. L'idée du projet est d'incorporer les bibliothèques mathématiques existantes quand cela est possible au sein d'une interface unifiée, ce qui en fait un ensemble modulaire. Son ambition est de proposer une alternative aux solutions propriétaires comme Maple, Magma ou Mathematica. Il est disponible sous Mac, Linux et en machine virtuelle sous Windows.
2. Installation
Étant une collection de nombreux outils mathématiques différents, la compilation de Sage est apparemment épineuse au point qu'il n'y ait d'après le site du projet qu'un paquet binaire pour la distribution Ubuntu, disponible via un PPA. En console, en root, on tape :
apt-add-repository -y ppa:aims/sagemath
apt-get update
apt-get install sagemath-upstream-binary
Sous Debian, plutôt que de tenter l'utilisation du PPA ci-dessus, on peut se tourner vers la compilation des sources. Attention néanmoins : cette étape peut prendre plusieurs heures en fonction de votre processeur et du nombre de cœurs que vous dédiez à la tâche (testé sur une nuit sur un Core 2 Duo avec deux cœurs utilisés).
Pour commencer, on installe les outils nécessaires à la compilation et à l'utilisation de toutes les fonctionnalités de Sage. Dans une console, en root :
apt-get install -y build-essential m4 gfortran readline-common libreadline-dev texlive xpdf evince tk-dev tcl-dev
On se place dans le répertoire voulu pour télécharger les sources :
cd /dossier/de/téléchargement
wget http://www-ftp.lip6.fr/pub/math/sagemath/src/sage-5.3.tar
On se déplace ensuite dans le dossier où l'on souhaite installer Sage et on décompresse l'archive :
cd /dossier/installation
tar xvf /root/sage-5.3.tar
Passons à la compilation :
ln -sf sage-5.3 sage
cd sage
export SAGE_MATPLOTLIB_GUI='yes'
export MAKE="make -j2"
export SAGE_CHECK="yes"
make
Les utilisateurs d'Arch Linux sont assez bien lotis pour installer Sage sur leur système : un paquet compilé à partir des sources de la version 5.3 existe dans le dépôt Community. Dans une console, il suffit de taper la commande magique :
sudo pacman -S sage-mathematics
et de laisser travailler Pacman, qui installera les dépendances nécessaires. Prévoyez 2 Go d'espace libre pour l'installation. Un paquet est également disponible sous Mandriva.
3. Les interfaces
3.1 Le shell
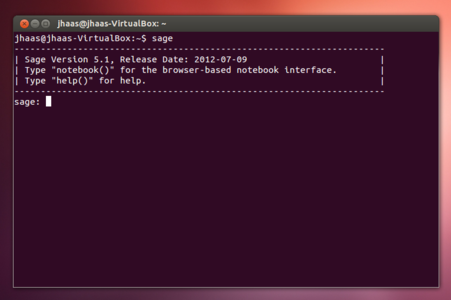
C'est l'usage le plus simple de Sage. Il suffit de taper la commande sage pour lancer le programme en console (Fig. 1). Le programme ouvre un navigateur Internet pour le rendu des graphiques.
Fig 1 : Sage peut s'utiliser simplement en ligne de commandes... En tout cas, tant qu'il n'y a rien à représenter graphiquement...
3.2 Le navigateur
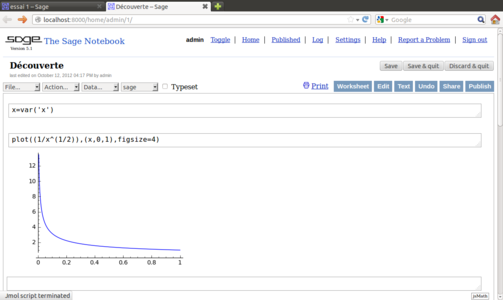
Une option plus confortable. Sur Ubuntu, il suffit de taper « Sage » dans la barre de recherche globale, puis de cliquer sur le bouton du binaire. Autre solution : dans une console, lancez sage, puis tapez la commande notebook() et validez. Le navigateur Internet s'ouvre alors (Fig. 2). Cliquez sur New Worksheet pour démarrer dans un nouveau fichier.
Fig 2 : L'interface principale de Sage s'affiche dans votre navigateur Internet préféré. La représentation des fonctions et diagrammes repose sur Java.
3.3 Cantor
Cette application du projet KDE Edu peut servir d'interface à de nombreux programmes mathématiques, dont Sage. Il suffit de l'installer et d'ajouter un binaire spécifique. Sous Ubuntu, en root :
apt-get install cantor cantor-backend-sage
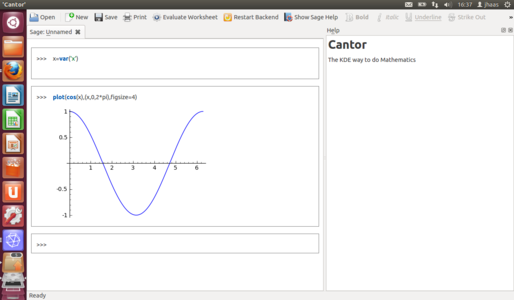
Le résultat est une interface proche de celle du navigateur (Fig. 3), mais mieux intégrée à un environnement de bureau, avec plus de menus et des volets ré-arrangeables. Pour valider une ligne dans le fichier, on appuie sur [Shift]+[Entrée].
Fig 3 : Cantor sert d'interface à de nombreux logiciels scientifiques, dont Sage, à l'aide des bibliothèques spécifiques à KDE.
Les modules
Sage inclut près d'une centaine de paquets mathématiques au rôle spécifique. Parmi les plus connus, on citera Maxima et Singular pour l'algèbre, PARI/GP pour la théorie des nombres, ATLAS pour l'algèbre linéaire, GAP pour l'algorithmique algébrique, ou encore R pour l'analyse statistique.
Pour afficher les listes des paquets standards ou optionnels installés ou non, on tapera respectivement en console (et non dans Sage en console) :
sage --standard
ou
sage --optional
Si l'on a besoin d'un module non encore installé sur le système, on tape dans une nouvelle console :
sage -i paquet
4. Fonctions de base
4.1 Calcul
Un calcul classique s'écrit de manière normale, comme sur les autres logiciels du genre ou sur les calculatrices scolaires, puis on appuie sur la touche [Entrée] :
2+2
4
À noter que comme dans la plupart des logiciels de mathématiques (et scientifiques de manière plus large), la virgule est symbolisée par un point :
4.2/9.76
0.430327868852459
Pour calculer les 100 premières décimales de Pi, une petite formule s'impose :
N(pi, digits=100)
4.2 Fonctions et équations
Pour effectuer des opérations sur les fonctions, on définit d'abord une variable symbolique :
x = var('x')
Puis on entre la fonction et l'opération voulues, par exemple intégrer la fonction racine de x :
integrate(sqrt(x),x)
2/3*x^(3/2)
Pour résoudre une équation simple, on utilise la fonction solve. Dans Sage, le symbole de l'égalité est représenté par == :
solve(x^2+x==1,x)
nous donne les solutions :
[x == -1/2*sqrt(5) - 1/2, x == 1/2*sqrt(5) - 1/2]
À noter que les retours du logiciel peuvent comporter des espaces entre les différents composants d'une expression ; vous pouvez faire de même dans vos expressions pour faciliter la lecture de votre feuille de calcul.
4.3 Matrices
La création de matrices et les opérations sur celles-ci sont aisées à réaliser. Le signe = est utilisé pour assigner une lettre à une expression. Pour définir une matrice, on écrira par exemple :
A = matrix([[1,2,3],[3,2,1],[1,1,1]])
Pour un vecteur, on utilise la même syntaxe :
w = vector([1,1,-4])
Il suffit alors d'utiliser les noms donnés à chaque élément pour réaliser une opération :
w*A
(0, 0, 0)
sage: A*w
(-9, 1, -2)
4.4 Dessin 2D
Dans l'interface navigateur, Sage peut tracer des lignes, des cercles, des polygones, mais aussi tout type de fonctions. Par exemple :
circle((0,0), 1)
produit un cercle de rayon 1, centré sur l'origine.
On peut par exemple changer la couleur du trait :
rgbcolor=(1,1,0)
donne du jaune.
Pour dessiner une figure pleine, on ajoutera l'option et la valeur fill=True.
Une fonction de base se modélise ainsi :
x = var('x')
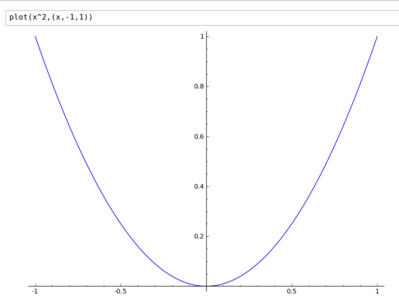
plot(x^2, (x,-1,1))
On demande ainsi le rendu de la fonction carrée de x, pour x allant de -1 à 1.
Fig 4 : Exemple de rendu graphique d'une fonction dans Sage.
4.5 Dessin 3D
La commande plot a sa contrepartie en relief, plot3d. Voyons un exemple de tracé.
On définit deux variables, x et y :
x = var('x')
y = var('y')
Puis, on crée une fonction :
def f(x,y): return sin(x-y)*y*cos(x)
Enfin, on trace notre fonction en relief :
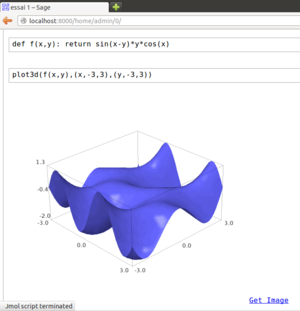
plot3d(f(x,y),(x,-3,3),(y,-3,3))
Fig 5 : On peut faire pivoter une figure en relief en maintenant appuyé le bouton gauche de la souris.
Il est possible d'agir sur les figures tracées directement avec la souris (glisser-déposer avec le bouton gauche). Le clic droit donne accès à quantité d'options : couleur, axe de vue, zoom, rotation... En bas à droite de la modélisation, Get Image permet de réaliser une capture de la figure pour l'utiliser ailleurs.
Partage des feuilles
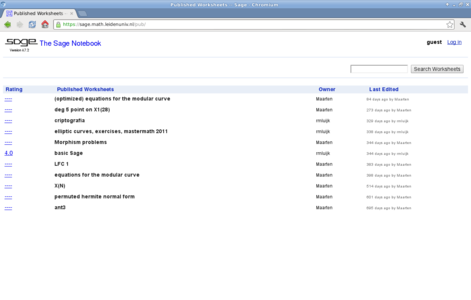
Quand vous êtes dans l'interface navigateur, vous pouvez enregistrer votre feuille de travail en cliquant sur Save. Pour partager vos travaux, l'onglet Publish vous y aide. Il vous propose une URL que vous pouvez communiquer à vos collaborateurs. Par défaut, les feuilles de travail sont stockées en local.
Les feuilles de travail sous Sage, une fois enregistrées, peuvent être partagées en ligne. Un exemple ici avec l'université de Leiden.
4.6 Obtenir de l'aide
Pour obtenir des informations sur une fonction dans Sage, on tape le nom de la fonction suivi d'un point d'interrogation :
tan?
Cette commande vous affiche le nom de la fonction (ici tangente), les fichiers rattachés à cette fonction, ou encore des exemples d'utilisation.
Le logiciel gère aussi l'auto-complétion. Écrivez les premières lettres de votre fonction, puis tapez la touche [Tab], qui vous affichera une liste des commandes possibles.
Pour plus de détails, en haut du notebook, l'onglet Help amène une page avec des liens vers des documents d'aide.
Conclusion
Nous n'avons fait que gratter la surface de Sage. En tant qu'alternative aux Maple et autre Mathematica, Sage remplit certainement son pari, avec un fonctionnement similaire à ces solutions. En termes de performances, le projet n'a rien à leur envier, selon ses concepteurs (voir Pour aller plus loin). On regrettera cependant que l'installation de la suite logicielle peut s'avérer difficile pour les distributions non dotées d'un paquet binaire dans leurs dépôts.
Pour aller plus loin
Le site du projet Sage. On y trouve des supports de présentation de Sage, les sources et les indications d'installation selon la plateforme, ou encore des cartes de référence rapide pour divers usages.
http://www.cbp.ens-lyon.fr/emmanuel.quemener/dokuwiki/doku.php?id=sagemath4debian
Quelques précisions supplémentaires pour l'installation de Sage à partir des sources sur Debian Squeeze.
http://www.sagemath.org/doc/tutorial/index.html
Un tutoriel pas-à-pas pour Sage. Divers usages avancés y sont décrits.
http://www.sagemath.org/links-components.html
Le détail des paquets contenus dans Sage, avec un lien de référence pour chacun.
Le site de l'application Cantor, pour en savoir plus sur les autres logiciels mathématiques supportés et des fonctionnalités avancées.
http://www.sagemath.org/tour-benchmarks.html
Des tests de performance sur la version 4 de Sage.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture