1. Une nouvelle menace ?

À l'origine théorisée en 1989 [1], la confidentialité persistante revient depuis ces dernières années comme une caractéristique essentielle des outils de communication électronique à destination du grand public. En trouver les raisons n'est pas difficile : les compromissions très fréquentes des clefs (stockage en clair, vol, clef faible), l'encadrement législatif relativement récent de l'usage de la cryptographie (qui impose notamment en France la remise des clefs de chiffrement sous certaines conditions), et désormais la surveillance effectuée par de nombreuses agences de renseignement qui peuvent potentiellement enregistrer tout ce qui est relatif au trafic chiffré pour, dans l'hypothèse où la clef de chiffrement serait obtenue, déchiffrer l'ensemble des flux ainsi conservés. Ce cas de figure s'est avéré, au moins outre-Atlantique, dans le cas de la demande de remise de clef effectuée par le FBI auprès de Lavabit dans le cadre des révélations d'Edward Snowden [2].

2. Confidentialité persistante : une affaire de longue durée

La confidentialité persistante a été initialement définie comme le fait qu'« un échange de clef authentifié fournit une confidentialité persistante si la découverte de la clef secrète longue durée ne compromet pas la confidentialité des clefs échangées précédemment ». La notion d'échange de clef authentifié se réfère bien entendu à la génération d'un secret partagé éphémère entre deux parties dont l'objet sera, dans de nombreux cas, le chiffrement d'une partie de la communication. On peut nommer cette dernière clef « clef de session », une session étant ici un concept abstrait se référant seulement à une durée finie (liée par exemple à l'envoi d'un message dans un système de messagerie instantanée, ou encore la durée d'une connexion TCP, ou une période fixe d'une semaine par exemple). Concernant la clef secrète longue durée, cette notion se réfère au secret partagé au préalable par les deux parties (dans le cas d'un système symétrique) ou alors à la clef privée RSA de chacune des parties. Bien que l'usage de cette clef ne soit pas spécifié dans la définition originale, elle peut, et cela dépend bien entendu des spécifications utilisées, servir pour l'authentification ou le chiffrement au début de l'échange. Un échange de clef naïf tel la génération d'une chaîne aléatoire et son chiffrement avec la clef longue durée puis son envoi n'offre donc pas, au regard de cette première définition, une confidentialité persistante. Cette définition de base ne couvrant pas l'ensemble des problèmes potentiellement rencontrés (on ne parle ici que de la découverte du secret longue durée), voyons plus en détail les notions utilisées à l'heure actuelle.

2.1 Définitions

D'un côté, nous avons la Forward Secrecy : un échange de clef authentifié fournit la Forward Secrecy si la découverte de la clef secrète longue durée (telle celle d'un certificat X509) ne compromet pas la confidentialité des messages chiffrés passés. C'est-à-dire que la clef utilisée pour chiffrer l'échange (clef de session) est indépendante de la clef secrète longue durée. D'un autre côté, la Perfect Forward Secrecy conserve également la confidentialité des messages chiffrés passés même en cas de compromission de la clef de session. En d'autres termes, connaissant la clef de la session courante, il est impossible de retrouver les clefs générées précédemment qui permettraient de déchiffrer les sessions passées. Une autre définition assez récente concerne la compromission des futures sessions. Dans le cas de la PFS (et de la FS), nous ne pouvons en rien affirmer que les futures sessions ne seront pas compromises dans le cas du vol d'une clef de session. Imaginons par exemple un protocole qui dériverait la clef de la session n+1 en utilisant un procédé déterministe, une fonction de hachage disons, sur la clef de la session n : ce protocole assure bien la confidentialité des messages passés en cas de découverte de la clef de session courante (fonction de hachage non inversible), mais un attaquant ayant réussi à obtenir la clef de session courante pourrait alors la dériver (application de la fonction de hachage) et obtenir ainsi la clef de session suivante. Le fait que la découverte de la clef de session ne compromet pas la confidentialité des messages futurs a été élégamment nommée Future Secrecy. En définitive, l'ensemble de ces propriétés (Forward Secrecy, Perfect Forward Secrecy et Future Secrecy) implique de bien distinguer chaque cas de compromission de clef possible.

2.2 Primitives cryptographiques

Afin de fournir de telles propriétés, il est nécessaire de générer des clefs éphémères. Le protocole de mise en accord de clef Diffie-Hellman étant la référence actuelle, décrivons brièvement son fonctionnement ainsi que les différents usages qui lui sont associés. Nous verrons également par la suite qu'il existe plusieurs méthodes permettant de dériver des clefs tout au long d'une communication offrant une confidentialité persistante. Du côté des primitives nécessaires, ces différentes méthodes (connues sous le nom de ratchet) n'utilisent guère plus qu'une fonction de hachage ou (de nouveau) un échange Diffie-Hellman pour l'obtention d'une nouvelle clef.

2.2.1 Le protocole Diffie-Hellman

Sans prétendre détailler l'ensemble du cadre de la théorie des nombres sur lequel repose ce protocole, celui-ci permet à deux entités de générer un secret partagé au travers d'un canal public sans qu'il soit possible pour un adversaire passif de retrouver le secret, même en ayant enregistré l'intégralité de l'échange. Voici, dans sa version simplifiée, l'échange de clef : Alice et Bob choisissent ensemble les paramètres p et g. Le premier étant un nombre premier de grande taille et le second un générateur du sous-groupe Z/pZ. S'ensuit l'échange suivant (l'ensemble des opérations est effectué modulo p) :

- Alice génère localement un nombre aléatoire a puis envoie g^a ;

- Bob génère localement un nombre aléatoire b puis envoie g^b ;

- Alice et Bob génèrent localement le (même !) secret partagé (g^a)^b et (g^b)^a.

La difficulté pour un adversaire passif va être le calcul de : a (ou b) connaissant g^a (ou g^b). C'est un problème bien connu et qui résiste depuis des années : le calcul du logarithme discret. Un clin d’œil à l'actualité où une publication de recherche de début d'année propose un algorithme de calcul du logarithme discret en temps quasi polynomial [3].

On trouvera également des variantes de ce protocole, notamment celles utilisant les courbes elliptiques, permettant l'utilisation de clefs plus petites avec un niveau de sécurité aussi élevé. Pour comparaison, selon les recommandations de l'ANSSI [4], une courbe elliptique utilisant une clef de 256 bits est évaluée comme étant aussi solide qu'une clef RSA de 3072 bits. Celle-ci repose également sur le problème du logarithme discret (mais sur courbe elliptique) et se retrouve pour le protocole d'échange de clef Diffie-Hellman sous l'acronyme d'ECDH, pour Elliptic Curve Diffie Hellman.

2.2.2 Usages de Diffie-Hellman pour la confidentialité persistante

L'élément essentiel dans le fait de fournir les propriétés liées à la confidentialité persistante va résider dans le changement fréquent de la clef de session (donc l'usage de Diffie-Hellman), ainsi que l'indépendance de cette clef vis-à-vis de l'ensemble des autres clefs (passées, futures et longue durée). Prenons un exemple concret utilisé massivement à l'heure actuelle : TLS pour le transport sécurisé de HTTP. Synthétiquement, une poignée de main TLS sans PFS présente côté client les primitives disponibles puis, côté serveur, les primitives supportées et le certificat X509 contenant la clef publique du serveur afin d'en effectuer l'authentification (seul le serveur est authentifié). Enfin, une clef de session est alors générée par le client, chiffrée avec la clef publique du serveur puis envoyée à celui-ci. Cette dernière clef sera utilisée comme clef de chiffrement durant toute la durée de la session TLS. Ce type d'échange ne permet en rien d'assurer la confidentialité persistante : si la clef privée associée au certificat du serveur est corrompue, alors la clef de session pourra être déchiffrée. TLS permet, afin d'offrir la PFS, l'utilisation d'un échange Diffie-Hellman éphémère, c'est-à-dire qui sera effectué en début de chaque session. Une clef unique sera utilisée comme clef de session et le certificat permettra uniquement l'authentification du serveur. Détail d'importance, car l'échange de clef Diffie-Hellman nécessite en effet de se prémunir d'attaque MITM. On retrouvera ces primitives sous les noms ECDHE et DHE (le dernier E étant ici pour ephemeral). TLS n'est qu'un exemple particulier dans l'ensemble des contextes possibles dans lequel Diffie-Hellman peut être utilisé. La notion de session étant ici utilisée dans un contexte synchrone et de courte durée, une clef de chiffrement éphémère est tout à fait appropriée au chiffrement de chaque message envoyé durant cette session. Si l'on se place dans un cadre asynchrone avec des sessions très longues, alors il convient de chiffrer chaque message durant cette session avec une clef différente (décrit par la suite avec l'exemple de Pond).

2.2.3 Usage d'une fonction de hachage pour la confidentialité persistante

Un autre exemple est celui de SCIMP [5] (Silent Circle Instant Message Protocol), un protocole dont le but est de fournir une communication de type « messagerie instantanée » sécurisée en utilisant XMPP. Après la génération d'un secret partagé par l'usage de Diffie-Hellman, la clef est dérivée par l'usage d'une fonction de hachage afin de produire une clef différente pour chaque message envoyé. Un des points faibles de ce type de ratcheting est que la compromission de la clef de chiffrement en un point de la communication compromet l'ensemble des clefs suivantes. Cette méthode d'offre donc pas la  Future Secrecy.

2.3 Limites

Un des problèmes majeurs qui n'a été que partiellement formulé dans l'ensemble des paragraphes précédents reste celui de l'authentification. Une attaque par « l'homme du milieu » (man in the middle) est toujours possible sur un échange de clef Diffie-Hellman, il faut donc que ce dernier soit authentifié. C'est de ce problème que découle une des limites de la confidentialité persistante, qui est que la clef permettant l'authentification peut également être découverte. Ainsi, la combinaison d'une attaque MITM avec l'usage de la clef permettant l'authentification (on notera également qu'une attaque plus triviale peut même utiliser une autre clef si l'utilisateur n'effectue pas de vérification sur cette dernière) engendre la perte totale de la confidentialité des messages, présents et futurs. Si la PFS est par exemple fournie au-dessus d'un protocole tel que Jabber (qui fournit le chiffrement entre le client et le serveur seulement), la compromission du serveur offre alors une attaque efficace contre la PFS.

En plus de cet aspect important, il convient de rappeler que la PFS repose sur des primitives cryptographiques qui pourront un jour être rendues obsolètes par l'arrivée de puissances de calcul plus grandes (telles celles promises par l'informatique quantique) ou tout simplement, car une solution au problème a été trouvée (décomposition en facteurs premiers et calcul du logarithme discret en un temps raisonnable). On pourra également mentionner l'usage de paramètres dégradés pour Diffie-Hellman ou de nouveaux types d'attaque concernant la cryptographie à base de courbe elliptique.

Enfin, en termes d'implémentation dans des applications pour la vie de tous les jours, la confidentialité persistante reste difficile à utiliser avec plus de deux entités comme un canal de discussion public, ainsi que dans un contexte de communication asynchrone (tel le courrier électronique). Ces derniers problèmes seront détaillés par des exemples pratiques dans la suite de l'article.

2.4 Quelques exemples concrets

Pour le cas déjà cité de HTTPS avec l'utilisation des primitives ECDHE ou DHE, relevons que Google propose l'usage de ces primitives depuis fin 2011 et Twitter depuis fin 2013, et que selon le projet SSL Pulse, qui établit des statistiques sur 200 000 sites utilisant SSL/TLS, environ 50 % d'entre eux permettent l'usage de primitives offrant la PFS. De nombreux autres protocoles font de même, tels que SSH, IPSec ou encore WPA2. Aussi quelques protocoles ont-ils été entièrement élaborés autour de la confidentialité persistante, et pour n'en nommer qu'un : Off-the-record messaging. Ce dernier sera décrit dans le contexte dans lequel il a été élaboré (la messagerie instantanée), dans un contexte asynchrone (Pond) et enfin, sera discuté brièvement les problèmes que pose l'usage d'un tel protocole dans un cadre de discussion en groupe.

3. Messagerie instantanée : Off-the-record messaging

Le protocole OTR a été élaboré autour d'une idée simple : fournir à l'utilisateur final les propriétés d'une discussion informelle de la vie quotidienne. La première publication concernant la normalisation d'OTR [6] (sous-titrée « Why Not To Use PGP ») présente les motivations de l'écriture d'OTR : des outils tels que PGP n'offrent en rien des communications sécurisées pour les usages d'un utilisateur lambda : l'authentification produite avec les signatures offre par là même une preuve à quiconque voudra démontrer que son auteur a bien écrit les propos signés (non-répudiation) ; si la clef est compromise dans le futur, alors la conversation tenue pourra être intégralement déchiffrée et le système de gestion de clef est tout simplement inaccessible à un utilisateur non initié. Tant dans les propriétés que dans l'usage couvert, PGP n'est pas une solution idéale pour celui qui voudrait protéger ses discussions informelles électroniques de la vie quotidienne.

Le protocole OTR s'est élaboré autour de ces propriétés : authentification mutuelle des participants, messages authentifiés, déniabilité, confidentialité persistante. Il s'est également conçu dans un souci de permettre un usage facile, notamment dans la gestion des clefs : Trust On First Use et Socialist Millionaire Protocol (qui permet à deux entités de s'authentifier sur la base d'un secret partagé sans relever d'information relative à ce secret). Même s'il est impossible de délier l'une de ces propriétés des autres, nous allons nous attacher à décrire comment la PFS est implémentée.

3.1 OTR et la PFS : three-step ratchet

Tout d'abord, la communication s'établit après un échange de clef authentifié (AKE). Cette première étape est dérivée du protocole SIGMA, dont l'objectif est d'effectuer un échange Diffie-Hellman non authentifié, puis d'effectuer une authentification mutuelle (en même temps qu'un nouvel échange Diffie-Hellman) à l'intérieur du canal chiffré ainsi créé, ceci afin notamment de se prémunir d'attaques du type identity misbinding (auquel OTR est vulnérable dans sa première version [7]). S'ensuit alors l'échange des messages entre les utilisateurs où, pour chaque message, une clef sera fournie afin d'établir un potentiel secret partagé pour le message suivant. De manière très simplifiée :

- Alice génère a puis envoie (g^a) avec le message ;

- Bob génère b puis envoie (g^b) avec message ;

- Alice utilise le nouveau secret ainsi généré ((g^a)^b) pour chiffrer un futur message.

Sachant bien entendu que le message courant est chiffré par la clef précédemment générée. Il en ira de même pour tous les messages suivants envoyés : une clef sera fournie dans chaque message afin de proposer la génération d'un nouveau secret partagé. Notons que tant que l'échange ne s'est pas effectué au complet, Bob et Alice doivent avoir proposé une clef, la clef de chiffrement ne change pas (plusieurs messages envoyés successivement par la même partie sans réponse utiliseront donc la même clef de chiffrement).

4. Implémentation asynchrone expérimentale : Pond

4.1 Introduction

Pond [8] est une application client/serveur expérimentale publiée fin 2012 qui a pour objectif de fournir un service d'échange de message avec comme propriété principale la confidentialité persistante. Développé sur la base d'OTR pour le chiffrement des messages, Pond a divergé de ce dernier protocole pour tenter d'offrir un service qui divulgue le moins d'information possible sur les échanges effectués et ceci, dans un cadre asynchrone. L'ensemble des choix techniques en est largement impacté notamment en ce qui concerne l'échange de clef initial entre deux clients ainsi que le mécanisme d'envoi de message. Une des caractéristiques qui distinguent Pond de l'e-mail ne se situe pas dans son intégration par défaut de mécanisme de sécurisation, mais dans le fait que c'est un système fermé, on ne peut envoyer un message à une adresse pond spécifique sans avoir établi un contact a priori. La raison principale de ce choix est simplement d'empêcher le spam. Par ailleurs, il n'existe pas d'adresse pond publique, il existe un nom dans un client (choisi arbitrairement par l'utilisateur) attaché à un contact (une clef publique et une identité publique sur un serveur). Pond se base sur le réseau Tor (notamment pour empêcher un attaquant de connaître le serveur auquel se connecte un client), utilise des messages de tailles fixes afin d'obtenir un profil de trafic constant et des délais d'envois et réceptions de messages exponentiellement distribués. Ainsi, le trafic d'un utilisateur sera composé de messages chiffrés de 16KB (la taille actuelle des messages de pond). On ne pourra ni dire si ce sont des messages envoyés ou reçus, ni de quel client ils ont été envoyés (si le profil du trafic n'était pas constant, il pourrait être aisé d'identifier l'expéditeur d'un message). Un modèle de menace détaillé [9] a d'ores et déjà été établit où l'on retrouve notamment le Global passive adversary, qui peut au mieux localiser les utilisateurs de pond. La conservation des messages étant d'une durée fixée à une semaine par défaut, il est à noter que rien n'empêche un utilisateur de les conserver. Enfin, les primitives cryptographiques utilisées correspondent à l'état de l'art actuel et ne sont pas forcément recommandées par les grands organismes pour le moment, à savoir : curve25519, Ed25519, salsa20, poly1305, HMAC-SHA256, les signatures BBS et Rijndael sur des blocs de 256 bits (nécessaire pour PANDA).

4.2 Les protocoles

4.2.1 BBS group signature

Un des choix découlant du fait de la restriction d'envoi de message à une adresse est celui de l'usage du schéma de signature BBS group signature [10] (pour les anciens, on ne parle pas de Bulletin Board Systems mais de Boneh-Boyen-Shacham signatures). Ce schéma permet de vérifier que l'utilisateur désirant vous envoyer un message fait bien partie de votre groupe de contacts autorisé sans pour autant avoir à divulguer son identité. Cette méthode repose sur une preuve à divulgation nulle de connaissance (Zero-Knowledge Proof of Knowledge) : elle consiste en une clef publique de groupe permettant de vérifier, du côté du serveur d'un utilisateur, que la signature d'un message envoyé a bien été effectuée par un utilisateur autorisé (c'est-à-dire signé avec une clef privée associée à ce groupe, qui est distribuée durant la phase initiale du premier échange de clef avec PANDA). La vérification de la signature n'offrant aucune information sur quel membre du groupe l'a effectuée.

4.2.2 SIGMA : « SIGn-and-MAc » pour authentifier Diffie-Hellman

À l'instar d'OTR, Pond utilise un dérivé du protocole SIGMA [11] pour établir un échange de clef Diffie-Hellman authentifié avec dissimulation des identités. En effet, la signature des paramètres d'un échange de clef Diffie-Hellman ne permet pas de se prémunir d'une attaque du type « identity-misbinding attack » (décrit dans le document décrivant SIGMA) et encore moins de masquer l'identité (certificat X.509 par exemple) des participants. L'échange de clef proposée par SIGMA s'effectue de la façon suivante :

- Alice génère a puis envoie (g^a) ;

- Bob génère b puis envoie (g^b), {Bob, SIG_Bob(g^b, g^a), MAC_km(B)) }_Ke ;

- Alice envoie {Alice, SIG_Alice(g^a, g^b), MAC_km(A)) }_Ke.

Où Km (utilisée pour effectuer une MAC) et Ke (utilisée pour chiffrer le message) correspondent à deux clefs distinctes dérivées de (g^a)^b. Cet échange permet de se protéger d'attaques actives (impossibilité de modifier les paramètres de l'échange) par l'utilisation de signatures, mais offre également une protection contre l'attaque « identity-misbinding attack » par l'usage de MAC (Message Authentication Code) sur l'identité de l'expéditeur. L'identité de l'initiateur (ici Alice) sera cachée d'un attaquant actif (impossibilité de dévoiler l'identité d'Alice même en intervenant durant l'échange), et celle de Bob d'un attaquant passif (impossibilité de dévoiler l'identité de Bob par simple lecture du trafic), mais pas d'un attaquant actif. Il est important de noter que Pond n'a intégré aucune méthode afin de vérifier l'identité du serveur (sa clef longue durée dans le cas présent) et que cette tâche est laissée à l'utilisateur.

4.2.3 PANDA : Phrase Automated Nym Discovery Authentication

La première étape nécessaire pour utiliser Pond va être l'ajout d'un contact. Ceci peut se faire par un échange de clef sur un canal extérieur (envoi d'un fichier PEM avec PGP ou OTR par exemple) ou par l'usage de PANDA (qui se fera également sur un canal extérieur). Ce dernier permet un échange de clef sur la seule et unique base d'un secret partagé, dans le but d'accepter des messages de la part d'un nouveau contact (qui possède également ce fameux secret partagé). Le problème va être d'effectuer un échange de clef authentifié par mot de passe (PAKE, Password Authenticated Key Exchange) dans un contexte asynchrone où l'on souhaite donc avoir un seul message envoyé par les deux parties (pas d'attente de réception de réponse ou d'établissement de rôle). Pour les détails de ce protocole, conçu en partie pour Pond, se référer à sa documentation [12].

4.3 La PFS en mode asynchrone : Axololt

Le mécanisme pour générer des clefs de sessions pour chaque message est dérivé de celui d'OTR, en omettant l'ensemble des informations pouvant indiquer le nombre de messages échangés (identifiant de clef, compteurs). Cette méthode de ratcheting, Axololt, part de plusieurs constats : la PFS fournie par un système de ratchet en trois étapes n'est pas optimale et un système à base de clef dérivée avec une fonction de hachage de manière itérative (tel que SCIMP) n'offre pas la Future Secrecy. Les deux ont également des avantages notables l'un sur l'autre : l'utilisation d'une clef dérivée ne nécessite aucun échange pour produire la nouvelle clef, et le système en trois étapes à base de Diffie-Hellman offre la Future Secrecy. Aussi, OTR étant à la base élaboré dans un cadre parfaitement synchrone (les messages arrivent dans l'ordre et ont une réponse, sauf déconnexion de l'utilisateur), Axololt a été étudié de manière à simplifier la gestion des clefs temporaires (ne pas devoir stocker une grande quantité de clefs et d'identifiants de clefs) ainsi qu'à permettre le déchiffrement de messages arrivés dans le désordre avec un impact minimal sur la PFS. Le concept derrière ce système est un usage combiné des deux méthodes présentées (pour plus de détail, voir les spécifications [9]), pour en définitive arriver à un format de message simplifié (un identifiant de clef contre quatre avec OTR), une grande simplification de la gestion des clefs et donc un usage adapté à un cadre asynchrone.

4.4 Exemple d'utilisation de Pond

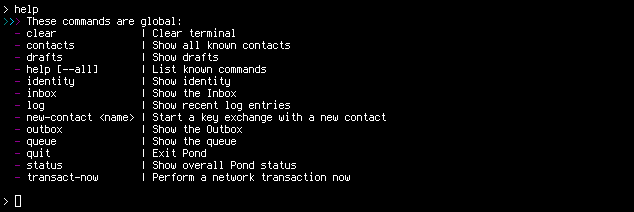
Au lancement de Pond (vous avez le choix entre un client en ligne de commandes, avec l'option -cli, ou un GUI par défaut), vous est demandé un mot de passe afin de protéger le fichier qui va stocker l'ensemble des informations de Pond (messages, contacts). Ensuite, on vous propose également l'usage d'un TPM (si vous en avez un), la sélection d'un serveur (par défaut, celui de https://hoi-polloi.org) pour enfin arriver au prompt (je n'utiliserai que la ligne de commandes). Une série de commandes simples est disponible :

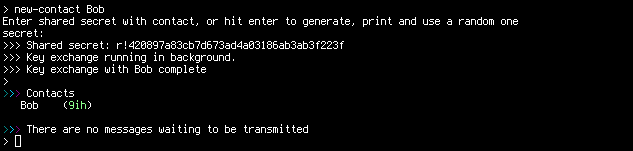
Le contenu du client est composé d'éléments listés par chaque appui sur la touche entrée (sans commande spécifiée). Après l'ajout d'un contact (en utilisant PANDA, avec comme « meeting place » codé en dur https://panda-key-exchange.appspot.com) :

On peut accéder à un contact et montrer les attributs qui le compose (un élément est accessible en spécifiant son identifiant, ici qnr) :

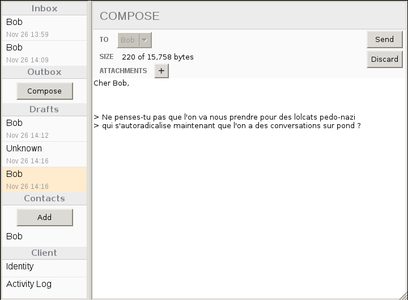
On peut également (pour un autre contact ici), composer un message (dans vim, ou dans le GUI) puis l'envoyer :

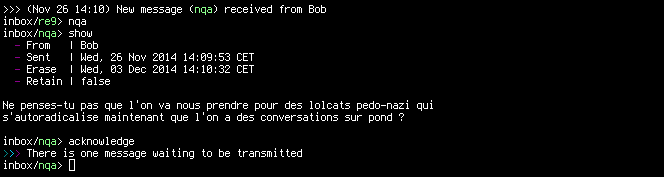
On peut noter l'ajout d'un message dans une file d'attente (les « transactions », réceptions et envois de messages, sont exponentiellement distribués dans le temps) ainsi que la taille du message (qui sera donc rempli jusqu'à obtenir les fameux 16KB). Le même message, reçu cette fois-ci :

On relèvera le bon usage qui consiste à acquitter systématiquement les messages permettant ainsi d'optimiser le mécanisme de ratcheting pour la PFS (mais aussi simplement d'être informé de la bonne réception du message), Pond offre ainsi une commande pour acquitter rapidement un message comme utilisé sur la précédente figure.

5. Et à plusieurs ? mpOTR

Une des problématiques centrales de la PFS, et notamment des protocoles tels qu'OTR, est son intégration à un contexte de communication en groupe. Une première étude [14], bien qu'incomplète, jette les bases du protocole OTR pour son usage « multi-partie ». Une des questions fondamentales est le protocole de mise en accord de clef entre tous les participants. En effet, la méthode proposée devient extrêmement complexe et coûteuse en nombre d'opérations nécessaires dès que l'on dépasse un petit nombre d'entités. Aussi, du fait du nombre d'échanges nécessaires au préalable afin d'établir une communication, un cadre asynchrone est tout simplement inenvisageable. Des travaux sont en cours [15] et une seconde version des spécifications devrait bientôt voir le jour. Trouvera-t-on aussi des implémentations déjà existantes de la PFS dans un tel cadre avec un protocole spécifique comme le mode de discussion en groupe de Textsecure (qui nécessite notamment la création préalable d'un groupe statique).

Remerciements

Quand bien même ce n'est pas d'usage de remercier le correcteur, de sincères remerciements à Aurélien.

Références

[1] http://link.springer.com/chapter/10.1007%2F3-540-46885-4_5?LI=true

[2] http://www.thoughtcrime.org/blog/lavabit-critique/

[3] http://eprint.iacr.org/2013/400.pdf

[4] http://www.keylength.com/en/5/

[5] https://silentcircle.com/scimp-protocol

[6 ] https://otr.cypherpunks.ca/otr-wpes-present.pdf

[7] https://www.dmi.unict.it/diraimondo/web/wp-content/uploads/papers/otr.pdf

[8] https://pond.imperialviolet.org/

[9] https://pond.imperialviolet.org/threat.html

[10] http://www.robotics.stanford.edu/~xb/crypto04a/groupsigs.pdf

[11] http://webee.technion.ac.il/~hugo/sigma-pdf.pdf

[12] https://github.com/agl/pond/tree/master/papers/panda

[13] https://github.com/trevp/axolotl/wiki

[14] http://www.cypherpunks.ca/~iang/pubs/mpotr.pdf

[15] https://blog.crypto.cat/2014/01/mpotr-project-plan/