Décodage par radio logicielle du VOR pour le positionnement sans GPS

Au cours d’un voyage en Norvège, nous nous sommes vus imposer une quarantaine de dix jours (une dizaine ?) à proximité de l’aéroport international d’Oslo à Gardermoen. Dire à un utilisateur GNU Radio qu’il est mis en quarantaine à côté d’une piste d’aéroport, c’est un peu comme dire à un renard qu’il séjournera en vacances dans un poulailler. Ce ne sont pas les activités qui vont manquer. Les sanglots longs des messages ACARS de l’aéroport, d’une langueur monotone n’étant que d’un intérêt limité, et l’absence de vols rendant l’analyse d’ADS-B peu passionnante, nous jetons notre dévolu sur l’infrastructure au sol qu’est VOR, le Very High Frequency Omnidirectional Ranging équipant souvent les aéroports les plus importants pour une assistance de navigation aux instruments. VOR, déployé pour mailler le territoire de « phares aéronautiques », est en particulier utilisé pour orienter les avions le long des routes aériennes au cours de leurs trajets.

Nous avons discuté comment la couche logicielle/protocolaire des systèmes satellitaires de navigation (GNSS) peut être leurrée [2], alors que la physique ne peut être leurrée. VOR (Fig. 1) est basé sur la transmission d’informations de direction d’arrivée du signal, mais encodée dans diverses modulations [3, 4] que nous allons expliciter ci-dessous, et non sur une mesure physique de direction d’arrivée du signal (Direction of Arrival, DoA). Ainsi, VOR pourra être leurré tout comme GPS : il est cependant quelque peu surprenant de constater que peu de littérature aborde ce sujet, probablement du fait de la nécessité d’assembler du matériel avec des conditions de synchronisation qui ne sont pas complètement triviales à respecter [5]. Une fois de plus, l’approche logicielle du traitement numérique de signaux radiofréquences amène un nouveau point de vue, ne serait-ce qu’en excitant la curiosité de la communauté informatique plus entraînée aux problématiques de sécurité que les radioamateurs. C’est en tous cas l’argumentaire développé dans [6] qui met en avant les bénéfices de la radio logicielle pour rapidement prototyper des attaques contre les protocoles radiofréquences les plus anciens, VOR ayant commencé à être déployé juste après la Seconde Guerre mondiale (https://www.icao.int/EURNAT/Pages/HISTORY/history_1954_upto.aspx). Contentons-nous ici d’explorer le fonctionnement de ce mode de communication avec un récepteur de télévision numérique terrestre équipé d’un détecteur radiofréquence R820T2 et d’un convertisseur analogique/numérique 8 bits RTL2832U.

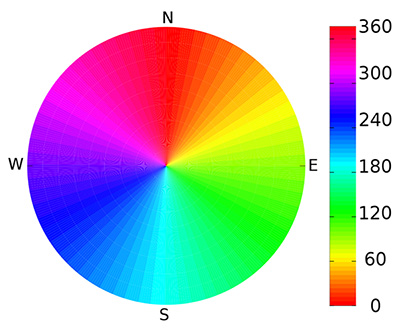
VOR est basé sur la transmission de deux signaux, l’un omnidirectionnel de référence, et l’autre directif portant une phase représentative de l’azimut par rapport au nord magnétique. Ces deux signaux sont démodulés sous forme de sinusoïdes à 30 Hz : la sinusoïde de référence est issue de la démodulation en amplitude (AM) de l’information transmise par la porteuse, et l’autre sinusoïde (mesure) issue de la démodulation en fréquence (FM) de l’information transportée à 9,96 kHz de la porteuse. Cette seconde sinusoïde présente une phase par rapport à la première sinusoïde qui représente l’angle azimutal par rapport au nord magnétique. Si les deux sinusoïdes sont en phase, nous sommes au nord de l’émetteur VOR, 90° pour un récepteur situé à l’est, 180° au sud et 270° pour l’ouest (Fig. 2). Le mode de production de ce second signal par commutation rapide d’antennes est très bien expliqué dans [5], avec une démonstration expérimentale quelque peu restreinte de 4 antennes, contre les 48 antennes qui équipent un émetteur VOR d’aéroport, synthétisant la sinusoïde transmise en modulation FM comme 48 segments successifs. Par ailleurs, VOR porte un identifiant de la station émettrice soit en audio, soit en Morse, avec une modulation en amplitude à environ 1 kHz (Fig. 3).

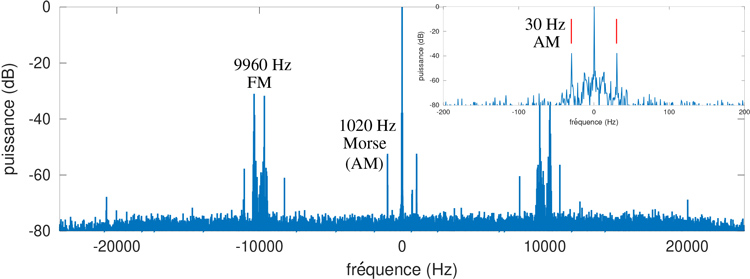
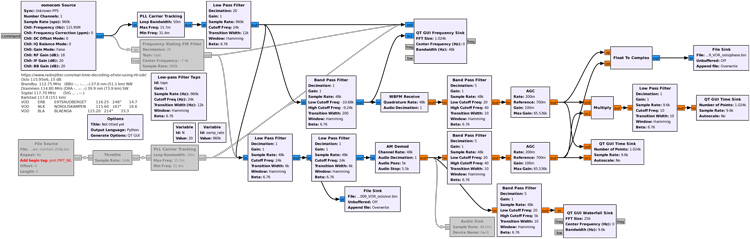
1. Acquisition et traitement par GNU Radio

L’acquisition se fait dans la bande 108-118 MHz aéronautique en alimentant le récepteur R820T2 par le signal issu d’une antenne monopôle télescopique – dans le cas particulier d’Oslo, https://ourairports.com/navaids/GRM/Gardermoen_VOR-DME_NO/ nous informe que l’émission est sur 115,95 MHz. La longueur idéale du monopôle serait de l’ordre du quart de la longueur d’onde ou 60 cm, mais en l’absence d’un plan de masse de dimensions raisonnables face à la longueur d’onde, toute adaptation empirique pour maximiser le signal fera l’affaire. Nous travaillerons en polarisation verticale (condition de fonctionnement d’un monopôle) ou oblique en penchant l’ordinateur qui fait office de plan de masse, une condition loin d’être idéale pour recevoir le signal normalement polarisé horizontalement, mais qui conviendra pour les mesures lorsque l’émetteur est proche. Le signal reçu occupe une dizaine de kHz de part et d’autre de la porteuse. Le signal Morse modulé en AM à environ 1 kHz (1020 Hz pour être exact) est immédiatement audible et indique le bon fonctionnement de la réception. Nous devons donc implémenter deux chaînes de traitement, une démodulation AM et une démodulation FM pour obtenir les deux sinusoïdes de référence et de mesure à 30 Hz et en déduire notre position.

La démodulation AM se limite classiquement en un redressement pour détecter les variations d’amplitude de l’enveloppe de la porteuse, et d’un filtre passe-bas de fréquence de coupure inférieure à l’écart potentiel entre la fréquence de l’oscillateur local du récepteur par rapport à l’émetteur. Ici, nous désirons détecter un signal modulé à 30 Hz de telle sorte que ce filtre sera complexe à concevoir, et nous allons donc utiliser une identification de la porteuse émise en vue de corriger l’oscillateur local pour s’asservir sur la porteuse du signal reçu. Ce rôle est pris en charge par la boucle à verrouillage de phase (Phase Locked Loop, PLL) qui compare la fréquence de l’oscillateur local du récepteur avec la fréquence porteuse reçue, et décale un signal par rapport à l’autre pour que leur phase s’annule, garantissant ainsi l’égalité des deux fréquences. En sortie de la PLL, nous obtenons le signal reçu, mais corrigé de l’écart à la fréquence de l’oscillateur local, donc avec une porteuse centrée sur 0 après transposition de la bande radiofréquence à la bande de base. Ce faisant, le redressement présentera deux raies latérales symétriques à ± 30 Hz pour la sinusoïde portant la phase de référence, et un peu plus loin pour la modulation Morse qui elle aurait pu se contenter d’un simple redressement tellement elle est loin de la porteuse (Fig. 3, insert en haut à droite).

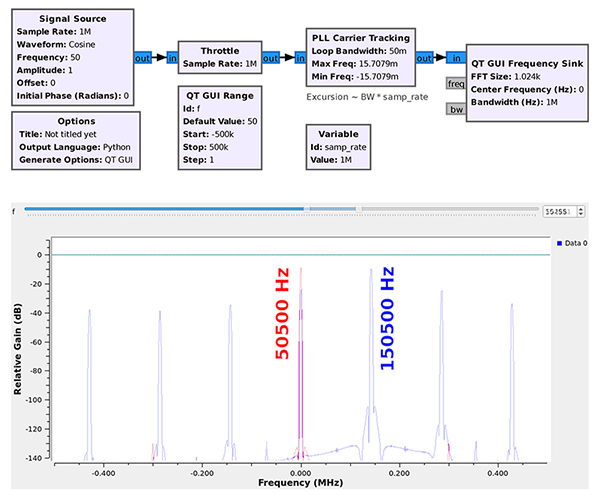
Bien que la PLL soit utile pour compenser tout écart entre les oscillateurs locaux de l’émetteur du signal modulé en amplitude et le récepteur, son réglage doit être minutieux, en particulier pour éviter le risque de s’accrocher involontairement sur toute porteuse puissante dans la bande reçue, même loin du signal recherché. La Fig. 4 propose un petit schéma simple de test pour se familiariser avec les paramètres, et en particulier se convaincre que la Loop Bandwidth n’est pas une bande passante en Hz (qui n’a pas de sens pour un signal échantillonné en temps discret), mais une fraction de la fréquence d’échantillonnage. Dans notre exemple, une bande passante de 0,05 avec une fréquence d’échantillonnage de 1 Méchantillons/s permet de rattraper un écart entre oscillateurs de l’émetteur et du récepteur jusqu’à une cinquantaine de kilohertz (empiriquement, on arrive à une 70aine de kHz). Plus la bande est grande, plus l’excursion en fréquence peut être importante, mais plus le risque de s’accrocher sur un mauvais signal est important, et nous avions vu [1] le danger de s’accrocher sur le signal le plus puissant dans l’effet de FM-capture.

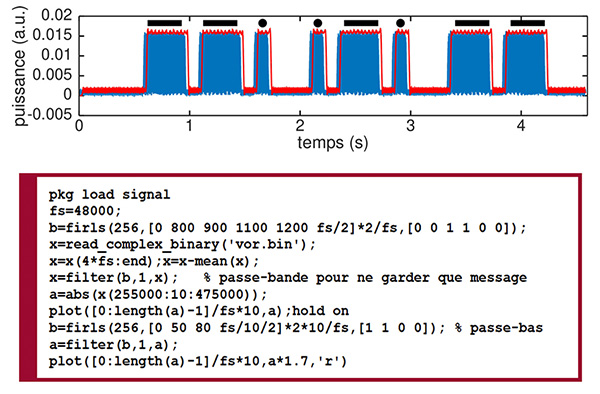
Comme nous avons déjà vu la capacité de démoduler la voix, nous ne développons pas en détail le décodage du code Morse qui s’observe aisément après redressement et filtrage (Fig. 5), ici illustré au moyen d’un script GNU/Octave exécuté en post-traitement au lieu d’une analyse en temps réel par GNU Radio. Le résultat est en accord avec les informations fournies à https://ourairports.com/navaids/GRM/Gardermoen_VOR-DME_NO/.

La démodulation FM porte sur deux signaux décalés de la porteuse de ± 9600 Hz. Nous sélectionnons un de ces signaux de modulation en fréquence et devons le ramener en bande de base (autour de 0 Hz) pour en analyser le contenu. Nous proposons dans la chaîne de traitement un simple filtre passe-bande autour de -9960 Hz, la transposition en fréquence vers 0 Hz n’étant pas nécessaire puisqu’un écart en fréquence se traduit uniquement par un biais (offset) en sortie de la démodulation FM, mais n’impacte pas la capacité de démodulation. Ce signal filtré alimente un démodulateur FM WBFM pour en extraire l’information contenant la seconde sinusoïde à 30 Hz dont la phase encode l’azimut. Ces étapes sont résumées dans la Fig. 6, dans lequel nous avons commenté une alternative à la PLL qu’est la transposition de fréquence par mélange du Xlating FIR Filter (transposition statique au lieu de dynamique comme le propose la PLL) et en bas à gauche, la séquence de blocs permettant de relire un fichier enregistré au lieu de ne traiter qu’en temps réel un flux reçu par récepteur de télévision numérique terrestre exploité comme source de radio logicielle, une étape bien pratique lors du développement et du déverminage de la séquence de traitements. Lors de l’activation de la lecture d’un fichier, on pensera à toujours insérer le bloc Throttle qui tente de cadencer la lecture proche du débit nominal et évite de saturer les processeurs comme le fait l’ordonnanceur GNU Radio, si une temporisation ne lui est pas imposée.

Nous avons deux sinusoïdes, il reste à en déduire la phase. Nombre de méthodes existent pour aboutir à cette grandeur. L’approche analogique classique consiste à multiplier (mélanger) les deux signaux A₁cos(ω t+ϕ) et A₂cos(ω t) avec ici ω=2π× 30 rad/s la pulsation angulaire de la sinusoïde à 30 Hz, et ϕ la phase recherchée. Le produit de ces deux termes est A₁A₂cos(ϕ) après passage dans un filtre passe-bas qui coupe le terme 2ω=2π× 2× 30 Hz. Noter que ce filtre passe-bas nécessite de l’ordre de 9600/60=160 coefficients lorsque la fréquence d’échantillonnage des sinusoïdes à 30 Hz est de 9600 Hz (décimation d’un facteur 5 du flux de données à 48 kHz), donc une puissance de calcul qui n’est pas négligeable, puisque chaque échantillon de sortie nécessite 160 multiplications. Nous notons la dépendance de ce produit avec A₁A₂ le produit des amplitudes des signaux incidents, de telle sorte que ϕ issue de arccos du produit des deux sinusoïdes dépendra de la puissance du signal reçu et pas seulement de la phase. Pour pallier ce problème, il est classique soit de saturer les signaux, soit d’insérer un contrôle de gain automatique (AGC) tel que nous l’avons fait ici (Fig. 6, droite) pour stabiliser A₁ et A₂ à des valeurs unitaires. L’inconvénient de cette approche est que arccos présente une incertitude de π qui nécessite l’étude du signal avant multiplication pour être levée.

Nous choisirons donc la solution bien plus lourde en ressources de calcul – sans importance dans les étapes de post-traitement qui vont nous concerner – de calculer la transformée de Hilbert [7] de chaque signal, transformant ainsi le signal réel en signal complexe dont la phase évolue dans le temps pour respecter les conditions de causalité, et la différence des phases des signaux (ou la phase du quotient des deux signaux complexes) fournit une estimation de ϕ qui s’affranchit de l’incertitude de π.

2. Évolution de la phase avec l’azimut

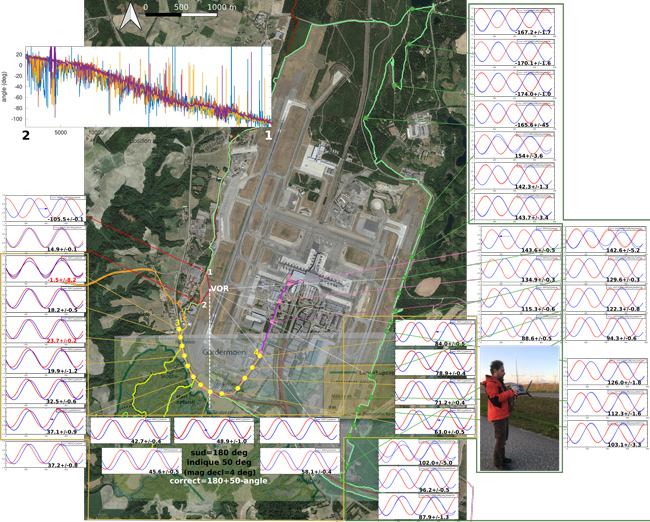
Ayant obtenu deux sinusoïdes à la fréquence recherchée de 30 Hz qui présentent un déphasage, nous nous interrogeons sur l’évolution de ce déphasage avec l’azimut. Étant localisés à proximité de l’antenne émettrice VOR, nous pouvons tourner autour de ce signal et valider la dépendance de la phase avec l’azimut (Fig. 7, insert en haut à gauche). L’aéroport d’Oslo est suffisamment petit et entouré d’un chemin pour que nous puissions parcourir la circonférence en moins d’une journée, tel qu’illustré sur la Fig.7. La mesure a par ailleurs été répétée à plusieurs jours d’intervalle pour en analyser la reproductibilité. Focalisons-nous dans un premier temps sur les graphiques les plus proches de la carte, avec la courbe bleue la sinusoïde de référence et la courbe rouge la sinusoïde dont la phase représente l’azimut.

Nous constatons sur les graphiques en bas de Fig. 7 que le sud (normalement azimut 180°, ou 176° si l’on tient compte des 4° d’écart entre le nord géographique et le nord magnétique à Oslo) est associé à une phase d’environ 50°. En prenant cette mesure comme étalonnage, nous transposons tous les angles de angle_vrai=180+50−angle_mesure pour nous ramener à des azimuts cohérents avec la représentation géographique.

Cependant, nous pouvons nous interroger sur la cause de cet écart entre phase nominale et phase mesurée. La phase est un concept qui n’a de sens que relativement à une référence : le signal FM présente une phase par rapport au signal AM. Or, les chaînes de démodulation AM et FM sont significativement différentes. Une démodulation numérique FM se limite à l’arctangente du produit entre l’échantillon courant et l’échantillon précédent [8], tandis que la démodulation AM est un redressement (valeur absolue en numérique) suivi d’un filtre passe-bas, donc un filtre à réponse impulsionnelle finie avec un nombre de coefficients de l’ordre de la fréquence d’échantillonnage en entrée de ce bloc divisé par la bande de transition. Ces coefficients induisent un retard qui n’a aucune raison d’être le même que celui introduit par la séquence de démodulation FM. Or, une phase peut aussi être interprétée dans le domaine temporel comme un retard, avec un retard d’une période égale à une rotation de phase de 2π. À 9600 Hz, les oscillations à 30 Hz sont représentées par 320 échantillons et une rotation de phase de 50° est introduite par 56 retards de plus dans une chaîne de traitement (démodulation AM ou FM) que dans l’autre, facilement introduits par un filtre FIR dans une branche. Nous pourrions compenser ce retard par un bloc delay de GNU Radio après étalonnage ou analyse fine des latences introduites par le traitement. Ce phénomène est exactement le même, en version échantillonnée en temps discret, du retard de groupe introduit par les filtres analogiques.

3. Évolution de la phase avec le gain de réception

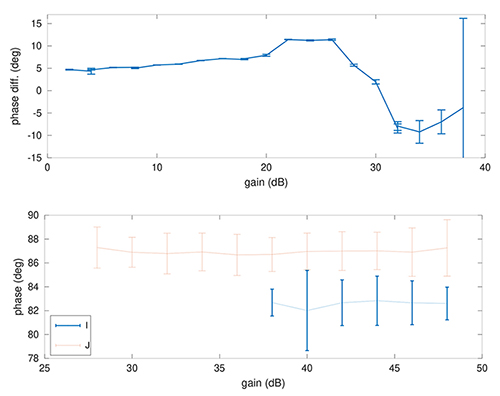
Nous constatons sur la Fig. 7 des incohérences sur les mesures au sud-est acquises deux jours différents. Alors que les mesures au nord-est et est sont cohérentes entre mesures acquises à plusieurs jours d’intervalle, le sud-est présente des différences significatives. La différence entre ces deux jeux de mesures consiste en la séquence d’acquisitions : les premières mesures ont été faites d’ouest en est, en partant de la proximité de l’émetteur VOR et en s’en éloignant, donc avec un gain manuel de réception faible. Au contraire, le second jeu de mesures est acquis du nord vers le sud, donc du signal le plus faible vers le plus fort, avec par conséquent un gain sélectionné presque au maximum (48 dB). Nous attribuons donc la différence des mesures au gain qui doit déformer le signal et biaiser les mesures de phase entre démodulations de phase et d’amplitude. Cette hypothèse est validée par des mesures depuis un même site, avec des gains croissants, et une analyse identique sur tous les jeux de données. La dépendance de la valeur moyenne, mais aussi de la qualité (écart type visible sous forme de barre d’erreur) indique qu’il est peu judicieux de maximiser le gain, au risque de saturer l’étage radiofréquence avant numérisation (Fig. 8).

4. Triangulation de la position

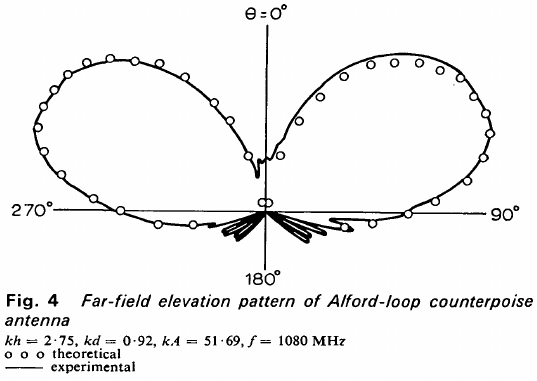
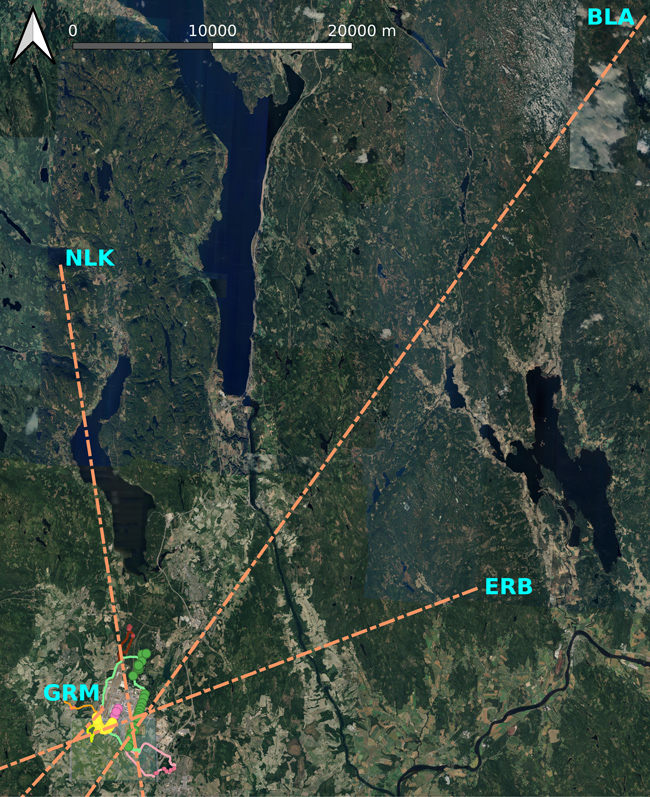
Forts du constat que la phase tourne de façon cohérente avec la position du récepteur par rapport à l’émetteur, nous désirons tenter de trianguler notre position par la réception de plusieurs émetteurs distants. Notre désillusion fut grande en l’absence de toute réception aux fréquences des émetteurs les plus proches, situés à seulement une vingtaine de kilomètres du récepteur : Ertsrudberget à 14,7 km (116,25 MHz), Nordliskampen à 16,6 km (115,60 MHz) ou Blåenga à 33,3 km (115,20 MHz). On notera que toutes ces fréquences sont comprises dans une bande de moins de 2 MHz de large et sont donc toutes accessibles simultanément avec un récepteur de télévision numérique terrestre R820T2. Bien que A. Blais nous fasse remarquer que notre réception par un monopôle vertical soit inadéquate pour recevoir les signaux VOR émis en polarisation horizontale, l’utilisation d’un dipôle horizontal qui avait pourtant permis de recevoir les signaux de Meteor M2N [10], satellite à plus de 800 km d’altitude et émettant une puissance plus faible que VOR, n’a pas donné de meilleurs résultats, même depuis le Bois de Boulogne où les émetteurs parisiens sont plus proches (Le Bourget, Roissy, Orly, Toussus-le-Noble, Rambouillet). La combinaison de l’effet du sol (zone de Fresnel dans laquelle la propagation est atténuée par les diélectriques présents à proximité du chemin de propagation de l’onde) et du diagramme de rayonnement, volontairement orienté vers le ciel (Fig. 9) [11, 12, 13] en vue de minimiser la propagation vers le sol et ainsi éviter les interférences de multi-chemin, rend les signaux distants inexploitables. En effet, [12] justifie le diagramme de rayonnement par « ... use with a conventional very high frequency omnidirectional radio range (VOR) to minimize propagation towards the ground, and thereby reduce siting effects due to multipath reflections. » Les mesures présentées dans ce document seront donc difficiles à reproduire sans se placer à proximité d’un aéroport, ou sans faire voler un drone à une altitude largement au-dessus du plafond légal de vol.

Nous nous intéressons néanmoins à la méthode de traitement que nous aurions mise en œuvre sous QGIS – logiciel libre de gestion d’informations spatialisées (GIS) – si nous avions acquis de telles mesures. Nous nous inspirons des émetteurs VOR environnant l’aéroport d’Oslo-Gardermoen tel que décrit à https://skyvector.com/airport/ENGM/Oslo-Gardermoen-Airport qui fournit en particulier les angles auxquels les signaux doivent être reçus. Une version graphique de ces émetteurs est illustrée dans la description de l’aide au vol par instruments de https://skyvector.com/?ll=60.202777778,11.083888889&chart=302&zoom=3.

La triangulation s’obtient sous QGIS en plaçant un point à l’origine située au niveau de l’émetteur distant, et en traçant un segment de droite de longueur L à partir de ce point. Si tout se passe bien, les segments de droite doivent s’intersecter au niveau du récepteur. Sous QGIS, la console Python est accessible dans le menu sous les Plugins. Nous fournissons le code suivant pour tracer un segment depuis 11,54750°E, 60,28250°N et d’azimut 248°. Évidemment, QGIS travaille en radians, donc nous prendrons soin de la conversion au moment de tracer le segment. La même opération est effectuée pour tous les VOR environnants.

Le résultat est visible sur la Fig. 10 qui, sans fournir une intersection parfaite, réduit la zone où se trouve le récepteur, ici le VOR d’Oslo-Gardermoen.

Conclusion

La souplesse de la radio logicielle est démontrée avec l’analyse des signaux de navigation aéronautiques VOR : partant pour une quarantaine à proximité d’un aéroport avec une clé de réception de télévision numérique terrestre comme seule occupation, nous avons pu aborder les divers modes de modulation et de décodage de ce protocole pour en explorer les fonctionnalités exclusivement par traitement de radio logicielle.

Cette étude a montré comment plusieurs signaux peuvent être transportés sur une même porteuse par utilisation de modulations différentes – ici, en amplitude et en fréquence. Fort de cette analyse, nous avons obtenu deux sinusoïdes dont la phase relative représente l’angle azimutal au nord magnétique. Nous avons vérifié que ces deux grandeurs varient de façon cohérente, pour finalement rencontrer l’obstacle d’utilisation à longue portée depuis le sol qu’est un diagramme de rayonnement exclusivement orienté vers le ciel et évitant toute propagation vers le sol.

Remerciements

A. Blais (ENAC, Toulouse) a initié cette étude par sa présentation pédagogique sur VOR aux European GNU Radio Days 2019 [3], et a patiemment répondu à nos interrogations sur l’absence de signal reçu à longue portée. Le déplacement en Norvège a été financé par l’Institut Paul-Émile Victor (IPEV) et le Centre National de la Recherche Scientifique (CNRS). Toutes les références bibliographiques qui ne sont pas librement disponibles sur le Web ont été obtenues auprès de Library Genesis à https://gen.lib.rus.ec.

Références

[1] J.- M Friedt, La peinture sur spectre radiofréquence, et l’effet capture de la modulation en fréquence – ou pourquoi les avions communiquent encore en AM, GNU/Linux Magazine France n^o216 (juin 2018), disponible à https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-216/La-peinture-sur-spectre-radiofrequence-et-l-effet-capture-de-la-modulation-en-frequence-ou-pourquoi-les-avions-communiquent-encore-en-AM.

[2] G. Goavec-Merou, J.-M Friedt, F. Meyer, Leurrage du GPS par radio logicielle, MISC HS n^o19 (février 2019).

[3] A. Blais, C. Morlaas, Using GNU Radio Companion to improve student understanding of signal processing theory through VHF Omni-Directional Range (VOR) signal demodulation, European GNU Radio Days (2019) disponible à https://hal.archives-ouvertes.fr/hal-02194172 et la vidéo de la présentation à 2 h 30 de https://www.youtube.com/watch?v=BWyeOBH3gwc.

[4] Real Time Decoding of VOR using RTL-SDR à https://www.radiojitter.com/real-time-decoding-of-vor-using-rtl-sdr/ (accédé octobre 2020).

[5] B. Seeber, DUFF DUFF – SDR Direction Finding, GNU Radio Conference 2012 à https://www.youtube.com/watch?v=F2wX6gou8ic à 4 minutes.

[6] H. Sathaye, D. Schepers, A. Ranganathan, and G. Noubir, Wireless Attacks on Aircraft Instrument Landing Systems, 28th USENIX Security Symposium (2019) à https://www.usenix.org/system/files/sec19-sathaye.pdf.

[7] J.-M Friedt, Quelques éléments de traitement de signaux échantillonnés en temps discret avec GNU Radio, GNU/Linux Magazine n^o221 (décembre 2018) à https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-221/Quelques-elements-de-traitement-de-signaux-echantillonnes-en-temps-discret-avec-GNU-Radio.

[8] D. Bederov, Arithmetic based implementation of a quadrature FM Demodulator, FOSDEM (2015) avec le transparent 7 pour la démonstration de la quadrature FM-demod de GNU Radio.

[9] D.L. Sengupta, Theory of VOR antenna radiation patterns, Electronics Letters 7 (15) 418–420 (1971).

[10] J.-M Friedt, Décodage d’images numériques issues de satellites météorologiques en orbite basse : le protocole LRPT de Meteor-M2 (en 3 parties), GNU/Linux Magazine France nos226–228 (mai à août 2019) :
https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-226/Decodage-d-images-numeriques-issues-de-satellites-meteorologiques-en-orbite-basse-le-protocole-LRPT-de-Meteor-M2-partie-1-3,
https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-227/Decodage-d-images-numeriques-issues-de-satellites-meteorologiques-en-orbite-basse-le-protocole-LRPT-de-Meteor-M2-partie-2-3,
https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-228/Decodage-d-images-numeriques-issues-de-satellites-meteorologiques-en-orbite-basse-le-protocole-LRPT-de-Meteor-M2-partie-3-3.

[11] S.R. Anderson, VHF omnirange accuracy improvements, IEEE Trans. Aerospace and Navigational Electronics 12 (1), pp. 26–35 (1965).

[12] J.G. Dong, Evaluation of Thomson/CSF Five-Day VOR Antenna, US Department of Transportation (1977).

[13] L. Fei, Y. Hu, Y. Li, Research on Height and Diameter of Doppler VHF Omnidirectional Beacon in Complex Environment, IOP Conference Series: Materials Science and Engineering 608 (1) (2019).