De nombreux signaux radiofréquences acquis au moyen de montages rudimentaires sont réels (en opposition à complexes). La propriété de parité de la transformée de Fourier des signaux réels rend leur traitement quelque peu délicat, avec le risque d’injecter dans la bande d’analyse des composantes spectrales non voulues. Nous allons analyser une transformée classique – la transformée de Hilbert – qui à partir d’un signal réel introduit une composante complexe conçue pour éliminer la partie des fréquences négatives du spectre et ainsi faciliter le traitement des signaux acquis.
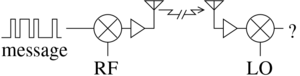
Un signal radiofréquence a été transposé en fréquence, à l’émission, pour permettre un partage de la ressource du spectre électromagnétique entre divers utilisateurs, et éventuellement pour permettre une émission efficace avec une antenne de dimensions commensurables avec l’objet contenant l’émetteur – pour rappel, la dimension caractéristique d’une antenne est la demi-longueur d’onde λ/2, avec λ=300/f lorsque le signal est émis à f MHz. Lors de sa réception, le signal doit être ramené de sa bande radiofréquence – autour d’une porteuse – vers la bande de base autour de 0 Hz pour permettre son traitement (voir figure 1). Une façon simple de transposer en fréquence est de multiplier dans le domaine temporel : un signal s(t)=e(jωt) est ramené dans la bande d’analyse du récepteur échantillonnant à fs si le mélange avec un oscillateur local de pulsation ωLO selon s(t)·e(-jωLOt)=e(j(ω-ωLO)t) vérifie |ω-ωLO| ≤ π·fs. Une fois cette transposition effectuée, la conversion analogique numérique fournit un flux de données qui peut être encore une fois transposé en fréquence, numériquement cette fois, par une nouvelle multiplication par e(-jω'LOt) avec cette fois t un temps discret synthétisé par pas de 1/fs, soit en syntaxe Matlab t=[0:length(s)-1]/fs;.
Fig. 1 : Transmettre un message sur une porteuse radiofréquence RF vise à partager le spectre entre divers interlocuteurs et rendre la taille d’antenne compatible avec l’application envisagée. Cependant, l’oscillateur local du récepteur LO ne sera pas synchrone avec l’émetteur : diverses stratégies de recalage seront nécessaires (démodulation) pour décoder le message à la réception.
Jusqu’ici, nous avons pris un cas idéal où les signaux sont complexes, simplifiant l’analyse spectrale puisque e(jωt) ne présente qu’une unique raie à ω. Cependant, une antenne reçoit une tension, qui est un signal réel, et un synthétiseur de signaux radiofréquences génère une tension, elle aussi réelle. Un signal réel présente deux composantes spectrales à +ω et -ω puisque c(ωt)=(1/2)(e(jωt)+e(-jωt)). Même sans passer par le mélange pour transposer la fréquence [1], connecter une antenne sur une carte son par exemple permet d’échantillonner une tension, toujours réelle. Le concept de partie imaginaire est généré par l’introduction d’une seconde composante en quadrature, selon la notation e(x)=c(x)+js(x) qui vérifie bien une partie réelle (c) et imaginaire (s) en quadrature (c(x)=s(x+π/2)). Nombreux sont les récepteurs qui ne mesurent qu’une tension, et non pas deux composantes en quadrature telles que fournies par un détecteur I/Q. Nous avions mentionné la carte son exploitée comme récepteur très basse fréquence (VLF [2]), mais c’est le cas des mesures sismiques ou en RADARs (aériens ou de sol [3]), ou de tout récepteur qui se contente d’un unique mélangeur pour effectuer la transposition de fréquence, voire qui échantillonne directement en bande radiofréquence.
Le problème de l’acquisition d’un signal réel est que la partie imaginaire du spectre est, en module, égale à la partie réelle (voir figure 2). Toutes les composantes spectrales visibles dans la partie des fréquences positives du spectre se retrouvent dans la partie de fréquences négatives. Cela devient ennuyeux lorsque le traitement numérique du signal sur le flux de données réelles vise à transposer en fréquence – par multiplication numérique du signal – vers une bande de fréquence plus basse. En effet dans cette opération, tout le spectre est transposé selon l’axe des abscisses, sous condition de périodicité du spectre échantillonné en temps discret : tout signal qui passe en deçà de -fs/2 revient de l’autre côté en +fs/2 et réciproquement : c’est le principe du repliement spectral, qui peut être utilisé à bon escient lorsque le spectre est bien maîtrisé, mais qui sera ici considéré comme un inconvénient.
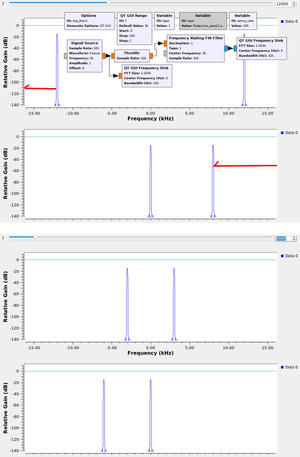
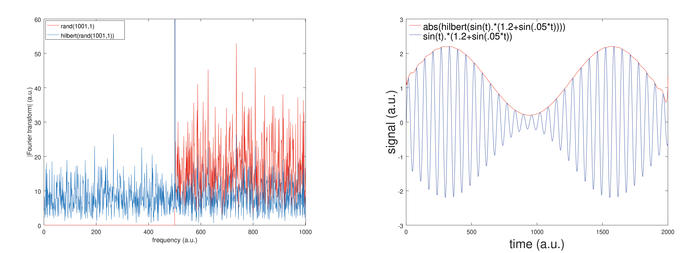
Fig. 2 : Impact de la transposition en fréquence d’un signal réel : en bas, la transposition d’un signal de fréquence 3 kHz échantillonné à 32 kHz garde la composante à la fréquence négative dans la gamme [-16:0] kHz, il n’y a pas de repliement, le filtrage de la composante négative sera aisé. En haut : un signal à 12 kHz, respectant le théorème d’échantillonnage, voit sa composante de fréquence négative transposée dans la bande de fréquences positives par périodicité du spectre du signal échantillonné en temps discret, puisque 2 x (-12) kHz < -32/2 kHz. Cette composante de fréquence positive peut venir jusqu’à la fréquence nulle, introduisant du bruit lors du traitement du signal en bande de base.
1. Impact de la transformée de Hilbert dans le domaine spectral
Ainsi, nous avons vu qu’un signal périodique réel de la forme c(ωt) s’écrit comme somme de deux exponentielles complexes e(jωt)=c(ωt)+js(ωt) tel que nous le démontrons simplement en nous rappelant que sin(-ωt)=-s(ωt) : c(ωt)=(1/2)(e(jωt)+e(-jωt)), démontrant bien qu’un signal périodique réel présente deux composantes spectrales en +ω et -ω. Par ailleurs, l’expression de e(jωt) qui ne contient qu’une composante spectrale en +ω nous montre la voie à suivre, à une fréquence donnée, pour éliminer la composante spectrale de fréquence négative : ajouter une composante imaginaire au signal en quadrature avec la partie réelle. Par linéarité de la transformée de Fourier, tout signal se décompose comme somme de signaux de diverses composantes spectrales, et cette opération peut être effectuée pour chacune des composantes spectrales, généralisant donc le concept à tout signal réel acquis. Cette opération mathématique consistant à introduire une composante imaginaire visant à éliminer la composante de fréquence négative du spectre s’appelle la transformée de Hilbert.
Concrètement, la lecture du code source de l’implémentation de hilbert.m dans la Signal Processing Toolbox de GNU/Octave nous montre que la mise en pratique ne s’épuise pas avec une considération d’identification de composantes en quadrature du signal. La transformée de Fourier du signal réel est calculée, sa partie de fréquence négative définie comme nulle, et la transformée de Fourier inverse est calculée, générant par définition une partie imaginaire en quadrature de la partie réelle telle que nous l’avons vue auparavant :
f=fft(f);
f=[f(1,:);
2*f(2:(N+1)/2,:);
zeros((N-1)/2,W)];
f=ifft(f);
Au contraire, GNU Radio propose dans github.com/gnuradio/gnuradio/blob/master/gr-filter/lib/hilbert_fc_impl.cc une implémentation de la transformée de Hilbert comme un filtre à réponse impulsionnelle finie (Finite Impulse Response filter – FIR) selon les préceptes décrits par exemple dans [4], puisque les coefficients du filtre sont définis par firdes::hilbert(d_ntaps, window, beta);. Nous retrouvons bien dans github.com/gnuradio/gnuradio/blob/master/gr-filter/lib/firdes.cc le filtre qui approxime la réponse h(t) ∝ 1/t puisque float x = 1/(float)i; avec i l’indice de l’élément dans le filtre. Les détails du filtre passe-bande permettant de s’affranchir des effets indésirables de la bande passante finie du filtre liée au nombre de coefficients sont décrits en détail dans [5, section3.37, pp.168–177].
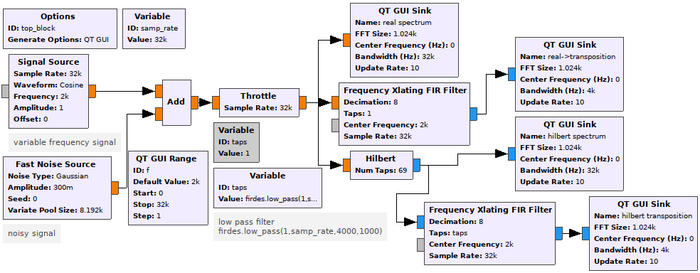
Nous expérimentons avec ces concepts sous GNU Radio (voir figure 3) en analysant le spectre du signal avant et après transposition en fréquence et décimation pour zoomer sur la zone intéressante autour de la bande de base et éliminer les parties hautes du spectre qui ne nous intéressent plus, et ce avec ou sans transformée de Hilbert (voir figure 4). Nous constatons bien que la raie parasite a été éliminée dans le second cas.
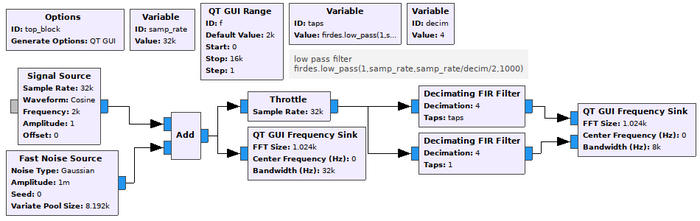
Fig. 3 : Analyse de l’impact de la transformée de Hilbert sur un signal transposé en fréquence et décimé, réduisant par la seconde opération la bande passante d’analyse et augmentant donc les risques de repliement spectral.
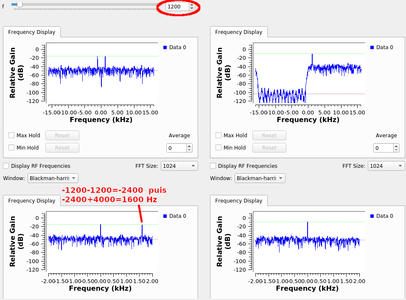
Fig. 4: En haut à gauche le signal réel, et en bas à gauche le signal transposé et décimé, faisant apparaître une composante spectrale polluant le spectre à droite. En effet, la raie à -1200 Hz (fréquence du signal émis) est transposée à -2400 Hz par le Xlating FIR Filter, puis la décimation d’un facteur 8 qui réduit la plage de fréquences de -2000 à 2000 Hz ramène la raie à -2400 Hz à +1600 Hz par addition d’un nombre entier de périodes d’échantillonnage (hypothèse de périodicité du spectre expliquant le repliement spectral). En haut à droite : la transformée de Hilbert a été appliquée au signal réel, éliminant la composante de fréquence négative du spectre, qui ne se retrouve donc plus dans la bande d’analyse après transposition et décimation (en bas à droite).
2. Impact de la transformée de Hilbert dans le domaine temporel
La transformée de Hilbert est utilisée en RADAR comme détecteur d’enveloppe lors du calcul de son module (voir figure 5). En effet, alors que le signal A(t)·c(ωt) présente une composante périodique de pulsation ω, l’introduction de la composante imaginaire jA(t)·s(ωt) produit A(t)·(c(ωt)+js(ωt))=A(t)e(jωt) dont le module est |A(t)| puisque |e(jωt)|=1 ∀t. De la même façon, la phase du signal ainsi généré est représentative du retard du signal.
Fig. 5 : Sous GNU/Octave, la fonction hilbert.m effectue la même opération que vue précédemment, en éliminant la composante de fréquence négative du spectre du signal réel (gauche) ou en permettant l’extraction de l’enveloppe du signal en éliminant la porteuse (droite).
Comme la plupart du temps en traitement du signal, on prendra soin de retrancher la valeur moyenne du signal réel avant de lui appliquer la transformée de Hilbert.
3. Transposition et décimation, et la nécessité de filtrer
Nous venons de parler de décimer le flux de données. Dans une chaîne de traitement de signaux radiofréquences, la quantité d’information ne peut que réduire, jamais augmenter en étant créée dans la chaîne de traitement. Nous commençons par échantillonner une large bande spectrale contenant toutes les raies spectrales intéressantes, puis démodulons pour extraire le contenu informatif, puis analysons le contenu du message en bande de base pour former les lettres (bits), puis les mots (octets), puis les phrases (code correcteur d’erreur, checksum)... chacune de ces opérations nécessite un peu moins de bande passante.
Le spectre d’un signal acquis à la fréquence d’échantillonnage fs s’étale de -fs/2 à +fs/2. Par ailleurs, le processeur doit traiter les données au rythme de fs échantillons/seconde. Si fs est grand, seules des opérations simples pourront être appliquées sur le flux de données sans risque de perdre des échantillons, faute de puissance de calcul. Cependant, rapidement après les premiers traitements (transposition en fréquence et filtrage, comme nous le verrons ci-dessous), le spectre est trop large et une partie des composantes spectrales n’est plus nécessaire. Comment ne garder qu’une partie du spectre ? Dans le domaine temporel, en ne gardant qu’un point tous les N. Ce faisant – opération de décimation – nous réduisons le flux de données et donc le nombre d’échantillons à traiter par seconde : à puissance de calcul donnée, nous pouvons effectuer des opérations plus complexes (e.g. démodulation FM, boucle de Costas). Le pendant dans le domaine spectral est de proposer un spectre s’étalant de -fs/(2N) à +fs/(2N) : nous ne nous concentrons que sur la partie centrale du spectre et éliminons les parties de fs/(2N) à fs/2.
Cependant, que se passe-t-il si une composante spectrale se trouve dans la bande fs/(2N) à fs/2 au moment de la décimation ? Elle sera ramenée dans la bande d’analyse [-fs/(2N),+fs/(2N)] par repliement spectral. Si nous ne voulons pas volontairement profiter de cet effet, nous devons penser à filtrer le signal initial avant de décimer, avec une fréquence de coupure du filtre autour de fs/(2N) (voir figure 6). Comme ce filtre est centré sur 0 Hz, il s’agit d’un filtre passe-bas, qui coupera automatiquement à -fs/(2N). Sous GNU/Octave, la décimation s’obtient en ne gardant qu’un point sur N selon la notation x(1:N:end), tandis que le filtrage s’obtient en appliquant les coefficients de pondération b d’un filtre passe-bas (filter(b,1,x);) identifié par b=firls(M,[0 fs/2/N fs/2/N*1.1 fs/2]*2/fs,[1 1 0 0]);. Nous laissons comme exercice au lecteur la compréhension de cette définition de filtre qui propose une bande de transition de l’ordre de 10% de la fréquence d’échantillonnage, avec un nombre M de coefficient sélectionné autour de quelques dizaines. La résolution spectrale d’une transformée de Fourier sur M points étant fs/M, il faut choisir M suffisamment grand pour résoudre la transition de fs/(2M) à fs/(2M) x 1,1 sans nécessiter un volume excessif de calculs. Le résultat est l’élimination de la raie repliée lors de la décimation, et qui risquerait d’atteindre la bande de base si nous n’y prenons garde (voir figure 7).
Fig. 6 : Flux de traitement pour illustrer l’impact du filtrage sur la décimation. Noter que la décimation du haut exploite un filtre passe-bas défini par taps dont l’expression est donnée en commentaire sous le bloc de la variable, tandis que la chaîne du bas effectue la même opération sans filtrage (taps=1 signifie que yn=xn soit une sortie identique à l’entrée).
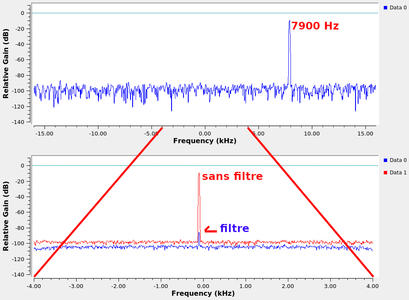
Fig. 7 : Résultat de la décimation d’un signal complexe à 7900 Hz, échantillonné à 32 kHz et décimé par 4, replié proche de la bande de base si aucun filtrage n’est implémenté (rouge). Le filtrage (bleu) évite de tels problèmes, qui s’étendent du cas particulier de la raie discrète au fond continu du bruit du récepteur en pratique. La fréquence de transposition est nulle, donc le Xlating FIR filter n’est ici pas utilisé, mais il permet de combiner transposition et décimation pour se familiariser avec l’impact du filtrage lors de ces deux traitements.
4. De la simulation aux vrais signaux
4.1 PlutoSDR pour écouter 8 stations FM
Nous concluons ce survol de GNU Radio Companion et du traitement de signaux échantillonnés en temps discret en remplaçant les sources de signaux synthétiques par de « vrais » signaux. Pour nous changer des récepteurs DVB-T, nous démontrons ici la réception de plusieurs stations FM simultanément (voir figure 8) en traitant les signaux issus de la PlutoSDR de Analog Devices (85 euros chez Mouser, référence 584-ADALM-PLUTO).
Bien que nous ayons déjà décrit une telle application dans [6], nous profitons de l’opportunité d’une nouvelle plateforme SDR à moins de 100 euros pour étendre nos horizons sur une bande passante accrue. En effet, la Pluto fournit plus de 10 MHz de bande passante (voire 50 MHz en configurant le récepteur radiofréquence comme version haut de gamme AD9364, même si ce n’est pas le composant équipant la carte [7]) et s’intègre parfaitement dans GNU Radio avec un flux continu de données sur le bus USB pour une fréquence d’échantillonnage de 3,5 Méchantillons/s. Pour ce faire, compiler libad9361-iio (github.com/analogdevicesinc/libad9361-iio.git) puis gr-iio (github.com/analogdevicesinc/gr-iio.git) et utiliser dans GNU Radio Companion la source nouvelle créée PlutoSDR Source. On pensera à ajouter l’utilisateur au groupe plugdev dans /etc/group si la règle udev fournie est utilisée.
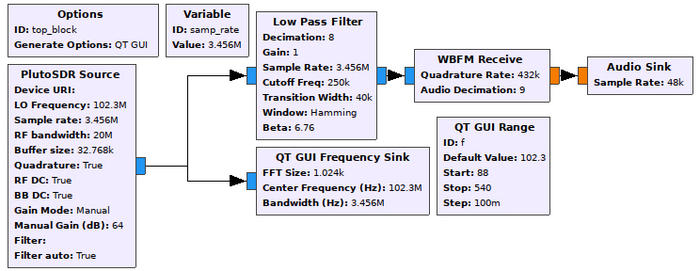
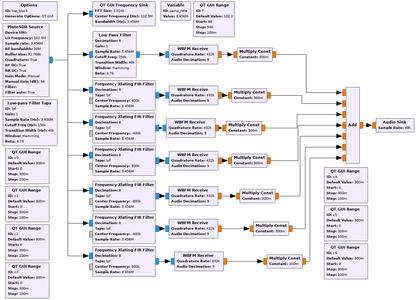
Fig. 8 : Flux de traitement pour écouter une station de la bande FM au moyen de la Pluto de Analog Devices. Noter que les sources de signaux synthétiques ont été remplacées par une source physique de données, imposant donc l’élimination du bloc de cadencement throttle.
Une bande passante de 3,5 MHz est suffisante pour capter 8 stations de la bande FM commerciale, puisque l’espacement entre deux stations est de 400 kHz. Nous désirons donc écouter simultanément ces stations, non pour rapporter à la SACEM les émissions musicales [8], mais pour simplement démontrer la capacité à traiter l’ensemble des informations de la bande analysée. Écouter une simple station FM est le premier exercice de toute implémentation SDR et se fait trivialement au moyen de la chaîne de traitement de la figure 8 qui permet de vérifier le bon fonctionnement de la source PlutoSDR. Cette étape validée, nous copions une transposition de fréquence par Xlating FIR filter dans lequel le filtre passe-bas a été « judicieusement » conçu avec une bande de transition suffisamment large pour induire peu de coefficients tout en rejetant les stations adjacentes. Nous avons pour cela utilisé un filtre (Low Pass Filter Taps) de 150 kHz de bande de transition, soit environ 3500/150=24 coefficients. La puissance de calcul requise pour implémenter la convolution avec aussi peu de coefficients est suffisamment faible pour qu’un processeur puisse traiter plusieurs stations radio : un processeur Intel i5-3320M cadencé à 2,60GHz tel que fourni par un ordinateur Panasonic CF-19 suffit à traiter simultanément les 8 stations présentes dans la bande passante. L’exécution du flux de traitement présenté en figure 9 donne le résultat de la figure 10 audible sur jmfriedt.free.fr/fmpluto.ogv. Dans cette vidéo, nous avons volontairement initialement sélectionné un filtre avec une transition trop étroite pour induire un nombre excessif de coefficients, dépassant la puissance de calcul disponible sur l’ordinateur pour traiter en continu le flux de données des 8 stations. Élargir la bande de transition résout le problème en réduisant le nombre de coefficients.
Fig. 9 : Flux de traitement pour écouter plusieurs stations de la bande FM simultanément.
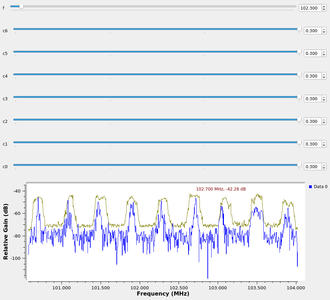
Fig. 10: Résultat de l’exécution de la chaîne de traitement de la figure 9. Une vidéo présentant dynamiquement ce résultat est disponible sur jmfriedt.free.fr/fmpluto.ogv.
La multitude de curseurs sert à ajuster le niveau audio de chaque station et donc de sélectionner l’une ou l’autre des émissions en sortie sur la carte son.
4.2 Exploitation de la bande WiFi 2,4 GHz pour application RADAR
Un second cas d’application de transposition de fréquence nécessitant une transformée de Hilbert est l’acquisition d’un signal pour une mesure RADAR. Le Wi-Fi fait partie des signaux dans lesquels nous baignons constamment : une mesure du signal direct et du signal réfléchi, voire décalé en fréquence par effet Doppler, permet de détecter des cibles dans l’environnement de l’émetteur [9]. Le signal Wi-Fi n’occupe qu’une quinzaine de MHz (IEEE 802.11g) autour de la porteuse, par exemple 2,422 GHz pour le canal 3. Alors qu’une PlutoSDR fournit le signal complexe issu d’un mélange avec l’oscillateur local et sa copie en quadrature (détecteur I/Q), ce type de montage devient d’autant plus complexe que la fréquence est élevée et les imperfections (I/Q imbalance, à savoir gain différent sur les voies identité et quadrature, et phase différente des 90° idéaux entre les deux voies) plus flagrantes. Par ailleurs, si nous voulons acquérir les signaux avec un oscilloscope, nombre de ces instruments ne comportent que deux voies et non quatre tel que nécessaire pour acquérir les deux voies complexes des deux récepteurs radiofréquence que sont la voie de référence et la voie de surveillance nécessaires dans une application de RADAR passif [10].
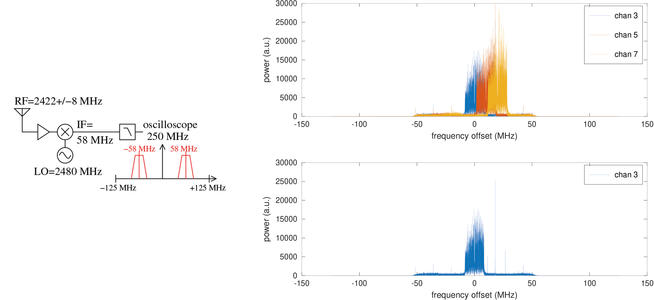
Une alternative au détecteur I/Q est l’utilisation d’un simple mélangeur suivi d’un filtre passe-bas (en pratique, la bande passante finie de l’oscilloscope suffit comme filtre passe-bas) pour acquérir une copie réelle (en opposition à complexe) du signal radiofréquence transposé proche de la bande de base (voir figure 11). Cependant, nous avons vu que la transformée de Fourier d’un signal réel est paire : amener le signal Wi-Fi directement en bande de base mélangera les composantes de fréquences négatives et positives du spectre introduites par la transposition en fréquence, et l’incapacité après acquisition de les séparer par filtrage. L’alternative est donc de travailler avec une fréquence intermédiaire IF inférieure à la moitié de la bande passante de l’oscilloscope. Dans ces conditions, une première transposition analogique est effectuée par le mélangeur – éliminant tout problème de défaut de détecteur I/Q – puis une seconde étape de transposition numérique est effectuée après numérisation du signal : l’expression mathématique e(-jωIFt) garantit la quadrature entre les termes en cosinus et sinus et le gain unitaire. Le passage à une transposition complexe numérique garantit le comportement idéal de cet étage de transposition. Cependant, nous avons vu que si nous décalons de -ωIFla composante spectrale se trouvant à +ωIF nous amenons le signal d’intérêt en bande de base, mais du fait du signal réel acquis nous nous retrouvons avec une seconde composante de pulsation négative -2ωIF qui pourrait bien, si on n’y prend garde, se retrouver dans une plage de fréquence que nous désirons exploiter par repliement spectral. Ainsi, la transformée de Hilbert avant transposition numérique garantit l’élimination de cette composante et résout le problème. Cette approche a été mise en œuvre dans [11]et [12].
Fig. 11 : Droite : acquisition de signaux dans 3 bandes de fréquence WiFi adjacentes, combinées par somme des spectres calculés par transformées de Fourier des spectres et transposées en bande de base numériquement (haut), et même opération (bas) sur une bande WiFi (canal 3 centré sur 2,422 GHz).
4.3 Récepteur Airspy
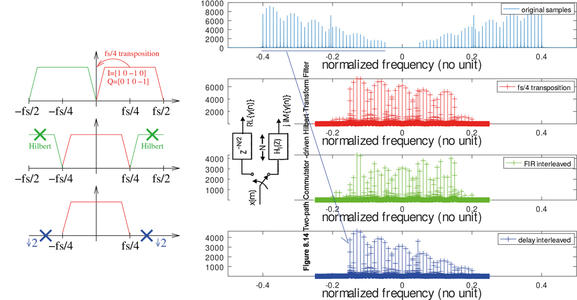
Cette technique de traitement est a priori utilisée dans le récepteur Airspy (airspy.com) qui acquiert depuis un circuit radiofréquence Rafael R820T(2) un signal transféré avec une fréquence intermédiaire égale au quart de la fréquence d’échantillonnage, avant d’effectuer la transformée de Hilbert, filtrage et décimation sur l’ordinateur hôte [13] (figure 12, gauche). Malgré l’analyse de la séquence globale de traitement (figure 12, droite) en alimentant la chaîne par un signal synthétique s’étendant de 0,05 fois la fréquence d’échantillonnage à 0,4 fois la fréquence d’échantillonnage (tenant compte du fait que la fréquence intermédiaire est de 0,25 fois la fréquence d’échantillonnage) qui démontre bien le bon fonctionnement de l’ensemble de l’algorithme, nous n’avons pas été capables d’identifier chaque étape individuelle de cette séquence à la lecture des codes sources, trop optimisés pour isoler chaque filtre, mais qui semble néanmoins suivre la suite d’opérations décrites dans [14, pp. 210-214] : tel qu’observé dans filters.h de airspy, les coefficients pairs (réels) du filtre sont tous nuls sauf le coefficient central (nommé hbc dans airspy pour normaliser le gain des deux branches), et les coefficients impairs représentent la réponse impulsionnelle de la transformée de Hilbert implémentée sous forme de filtre centré de demi-bande (Half Band Centered). On retrouve aussi dans cette référence l’argumentaire justifiant de n’appliquer les coefficients du filtre qu’aux termes d’indices impairs de la mesure [14, figure 8-14].
Comme la séquence d’analyses mise en œuvre ne semble pas explicitement documentée actuellement, nous avons testé le code en remplaçant le contenu de airspy.c disponible sur github.com/airspy/airspyone_host/tree/master/libairspy/src par :
#include <stdio.h>
#include <math.h>
#include "iqconverter_float.h"
#include "filters.h"
#define N (256*64)
void affiche(float *d)
{int c;for (c=0;c<N;c++) printf("%f \n",d[c]);}
int main()
{int c;
float output_buffer[N],freq;
iqconverter_float_t *cnv_f;
cnv_f=iqconverter_float_create(HB_KERNEL_FLOAT,HB_KERNEL_FLOAT_LEN);
iqconverter_float_reset(cnv_f);
for (c=0;c<N;c++) // signaux de synthese ...
output_buffer[sample_count]=cos(2*M_PI*0.205*(float)c);
for (freq=0.05;freq<0.4;freq=freq+0.01) // ... somme de sinusoides
for (c=0;c<N;c++)
output_buffer[c]+= (freq*3.)*cos(2*M_PI*freq*(float)c);
affiche(output_buffer); // affiche valeurs initiales
iqconverter_float_process(cnv_f, (float *)output_buffer, N);
sample_count /= 2;
affiche(output_buffer); // ... et apres traitement
return(0);
}
Ceci afin d’alimenter la chaîne de traitement par nos propres signaux de caractéristiques spectrales connues. Il est par ailleurs intéressant d’afficher les étapes intermédiaires du calcul visibles dans la fonction translate_fs_4() de iqconverter_float.c (figure 12, droite), en se rappelant que la première étape du calcul qui multiplie les données réelles par les vecteurs {1, 0, -1, 0} et {0, 1, 0, -1} correspond à la transposition du quart de la fréquence d’échantillonnage, tranformant les valeurs réelles en complexes.
Fig. 12 : Gauche : principe de l’acquisition du signal avec une fréquence intermédiaire du quart de la fréquence d’échantillonnage, suivi de la transposition en fréquence pour amener le signal en bande de base et décimation pour éliminer la partie inutile du spectre. Droite : analyse de l’implémentation dans la couche hôte de airspy exécutée sur ordinateur. Noter que la partie aux fréquences positives du spectre (ou négatives, car contenant la même information puisque le spectre d’un signal réel est pair), centrée sur le quart de la fréquence d’échantillonnage (haut) se retrouve bien autour de la bande de base (bas) après traitement. La légende de chaque graphique correspond au nom de la fonction dans le code source de la couche hôte de airspy. En insert, l’extrait de ce qui semble décrire la séquence de traitements.
Conclusion
Ces quelques petits exercices exploitant GNURadio Companion permettent de mettre en pratique des concepts quelque peu arides de traitement numérique de signaux échantillonnés en temps discret si l’on se restreint aux aspects formels du traitement mathématique. Nous avons vu pourquoi les signaux radiofréquences sont complexes, comment créer la partie complexe si l’échantillonnage de signaux ne fournit que la partie réelle, et comment cette partie imaginaire simplifie le traitement ultérieur, qu’il s’agisse de transposition ou décimation, en éliminant la partie de fréquences négatives du spectre dès le début de la chaîne de traitement. La transformée de Hilbert, puisque c’est de cette opération qu’il s’agit, est cependant gourmande en ressources de calculs, puisque nécessite une transformée de Fourier puis une transformée de Fourier inverse sur le flux de signaux acquis.
Suite à l’engouement pour la radio logicielle et afin de promouvoir la PlutoSDR, Analog Devices propose sur son site un excellent ouvrage alliant théorie, mise en pratique sur signaux synthétiques sous Matlab (donc GNU/Octave) et sur signaux expérimentaux qui mérite d'être consulté pour approfondir cette introduction.
Remerciements
Le contenu de cette présentation a été assemblé pour la séance de travaux pratiques des First French GNU Radio days (gnuradio-fr-18.sciencesconf.org). Y. Touil a orienté les études sur le code gérant le traitement des signaux issus de Airspy par l’hôte. Les ouvrages qui ne sont pas librement disponibles sur Internet ont été obtenus auprès de Library Genesis sur gen.lib.rus.ec, une source documentaire inestimable pour nos recherches.
Références et notes
[1] La multiplication dans le domaine temporel revient à une addition dans le domaine spectral, puisque e(jω1t) x e(jω2t) = e(j(ω1+ω2)t).
[2] J.-M FRIEDT etal., « Software defined radio decoding of DCF77: time and frequency dissemination with a sound card », Radio Science 53 (1), 48–61, janvier 2018.
[3]M.T. TANER, F. KOEHLER & R.E. SHERIFF, « Complex seismic trace analysis », Geophysics 44 (6), 1041–1063, 1979.
[4]Hilbert Transform Design Example : http://www.dsprelated.com/freebooks/sasp/Hilbert_Transform_Design_Example.html
[5]L.R. RABINERet B. GOLD, « Theory and application of digital signal processing », Prentice-Hall, 1975.
[6] J.-M FRIEDT, « La réception de signaux venus de l’espace par récepteur de télévision numérique terrestre », OpenSilicium n°13, décembre 2014/janvier/février 2015 : http://jmfriedt.free.fr/sdr2.pdf
[7] La procédure est officiellement décrite sur le site d’Analog Devices sur http://wiki.analog.com/university/tools/pluto/users/customizing.
[8]B. HAPPI TIETCHE, « Proposition d’architectures radio logicielles FPGA pour démoduler simultanément et intégralement les bandes radio commerciales, en vue d’une indexation audio », Doctorat Université Pierre et Marie Curie – Paris VI, 2014, dans le cadre du projet SurfOnHertz.
[9] H. GUO et al., « Passive radar detection using wireless networks, International IET Conference on Radar Systems », 2007, ou K. CHETTY et al., « Through-the-Wall Sensing of Personnel Using Passive Bistatic WiFi Radar at Standoff Distances », IEEE Trans. Geoscience & Remote Sensing, 2012.
[10] J.-M FRIEDT, « RADAR passif par intercorrélation de signaux acquis par deux récepteurs de télévision numérique terrestre », GNU/Linux Magazine n°212, février 2018 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-212/RADAR-passif-par-intercorrelation-de-signaux-acquis-par-deux-recepteurs-de-television-numerique-terrestre
[11] J.-M. FRIEDT, G. GOAVEC-MEROU, G. MARTIN, W. FENGet M. SATO, « Passive RADAR acoustic delay line sensor measurement: demonstration using a WiFi (2.4 GHz) emitter and WAIC-band (4.3 GHz) », Proc. WiSEE, 2018 : http://jmfriedt.free.fr/wisee2018.pdf
[12]W. FENG, J.-M FRIEDT, G. GOAVEC-MEROU, M. SATO, « Passive radar delay and angle of arrival measurements of multiple acoustic delay lines used as passive sensors », IEEE Sensors, 2018.
[13]opensourceradiotelescopes.org/pipermail/members_opensourceradiotelescopes.org/2018-April/000271.html
[14]F.J. HARRIS, « Multirate signal processing for communication systems », Prentice-Hall, 2004, ou N. ROBERTSON, « Simplest Calculation of Half-band Filter Coefficients », 2017 : http://www.dsprelated.com/showarticle/1113.php
[15]T.F. COLLINS, R. GETZ, D. PUet A.M. WYGLINSKI, « Software-Defined Radio for Engineers », Artech House, 2018 : http://www.analog.com/media/en/training-seminars/design-handbooks/Software-Defined-Radio-for-Engineers-2018/SDR4Engineers.pdf