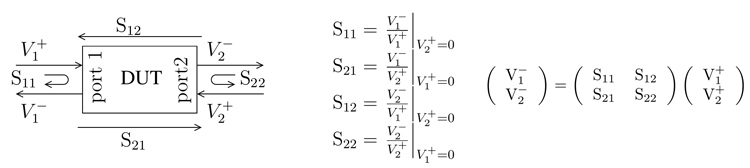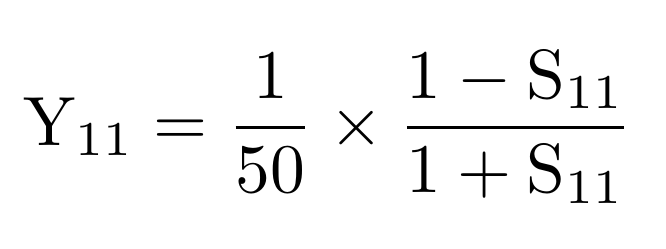L’analyseur de réseau est l’outil incontournable de tout développeur de systèmes radiofréquences, au même titre que le multimètre pour les développements en électronique analogique ou GDB en logiciel. Alors qu’un analyseur de réseau était (et peut encore être) un outil coûteux à plusieurs dizaines de milliers d’euros, inaccessible à la plupart des amateurs, l’avènement de composants radiofréquences intégrés contenant émetteur et récepteur agiles en fréquence offrent la possibilité de réaliser des analyseurs de réseau à moindre coût - certes aux performances réduites, mais suffisantes pour bien des applications, voire irremplaçables face aux offres commerciales lorsque l’instrument open source permet de l’adapter au mieux à ses besoins.
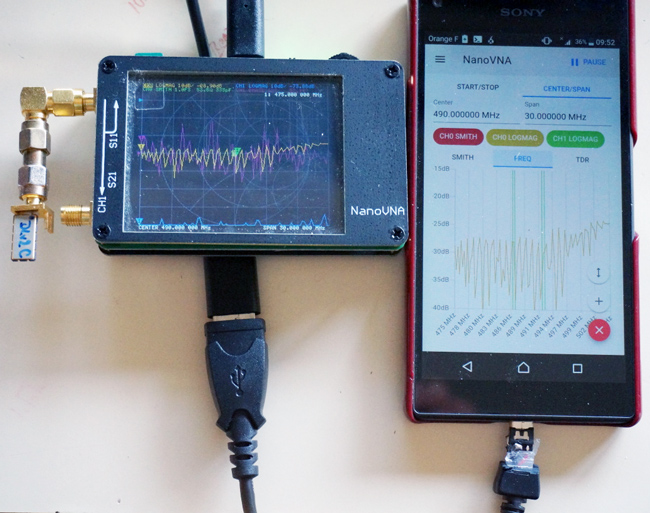
Nous allons illustrer ces principes sur le NanoVNA [1], un petit analyseur de réseau vectoriel disponible pour une cinquantaine d’euros (Fig. 1).
1. Introduction : paramètres de diffraction
Un analyseur de réseau vectoriel [2] a pour vocation de fournir l’évolution des caractéristiques d’un dipôle ou d’un quadripôle en fonction de la fréquence. Il s’agit d’un instrument qui contient un oscillateur de fréquence ajustable qui excite le dispositif à caractériser à la fréquence f et, sous hypothèse de linéarité de ce dispositif 1, permet d’observer la phase et le module de la réponse du composant testé que nous nommerons DUT (Device Under Test) pour respecter la nomenclature anglo-saxonne habituellement utilisée.
Distinguons dès l’introduction l’analyseur de réseau, qui sollicite activement le DUT par un signal généré par l’instrument de l’analyseur de spectre, qui observe passivement les composantes spectrales émises par un dispositif actif, ou évidemment l’oscilloscope, qui observe passivement l’évolution temporelle du signal émis par un dispositif actif (la distinction entre ces deux derniers instruments devenant de plus en plus floue avec l’avènement des oscilloscopes numériques qui proposent le passage dans le domaine spectral par transformée de Fourier). Ces trois instruments font partie de la panoplie de l’expérimentateur en dispositifs radiofréquences, mais avec des fonctions très différentes.
Un dipôle se caractérise par une unique mesure qu’est la fraction du signal incident réfléchi par le DUT (Fig. 2). Plus le DUT absorbe de puissance, moins la puissance détectée par l’instrument est importante (par conservation de l’énergie). Ce coefficient de réflexion que nous nommerons S11 (prononcer « S un un », S étant la première lettre de scattering ou diffraction en français) est une grandeur complexe qui indique le déphasage et module du signal réfléchi : S11=|S11|exp(jϕ(S11)). La définition de S11 est le rapport de la tension (complexe, donc en module et phase) réfléchie à la tension (complexe) incidente. Il s’agit donc de propriétés liées aux propagations d’ondes incidentes et réfléchies, que nous verrons comment convertir en admittance, qui est la caractéristique du circuit équivalent induisant la réflexion et la transmission de ces ondes.
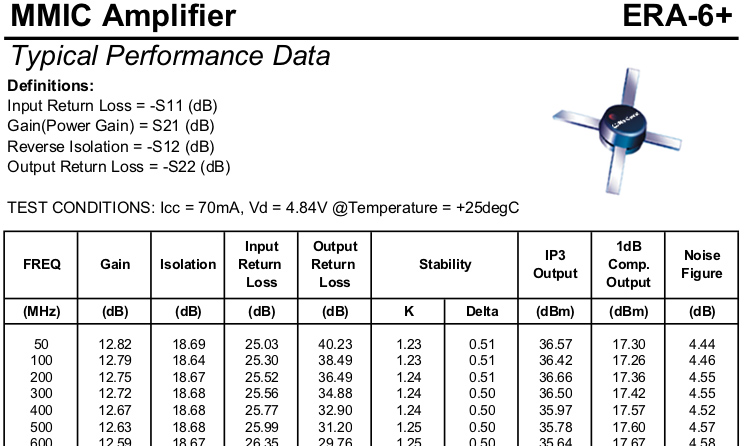
Ce principe se généralise au quadripôle qui ne se définit plus par une unique grandeur, mais par quatre grandeurs que sont les coefficients de réflexion aux deux ports (entrée et sortie) et coefficients de transmission (de l’entrée à la sortie et de la sortie à l’entrée). La nomenclature se généralise donc à S11 et S22 pour les coefficients de réflexion et S21 et S12 pour les coefficients de transmission. Dans ce cas, S21 est défini comme le ratio de la tension (complexe) sortant sur le port 2 à la tension (complexe) injectée sur le port 1, sous hypothèse d’absence de réflexion. Dans ce dernier cas, le deuxième chiffre de l’indice indique le port d’émission du signal d’excitation et le premier chiffre le port en entrée. Ce point est important dans le cas des composants actifs - par exemple amplificateur - dans lequel exciter le DUT par son port de sortie peut l’endommager, si la puissance injectée est trop puissante. Pour un amplificateur, |S21| sera son gain tandis que |S12| sera son isolation. Un exemple de documentation technique obtenue sur https://www.minicircuits.com/WebStore/dashboard.html?model=ERA-6%2B (onglet View Data) est fourni en Fig. 3. La situation est plus simple dans les dispositifs passifs isotropes réciproques où S21=S12 : c’est le cas des filtres, atténuateurs ou diviseurs de puissance, par exemple. De façon générale, nous pouvons considérer la matrice de passage de N ports en entrée vers N ports en sortie (par exemple, un circulateur avec ses 3 ports).
On notera que le S21 d’un dispositif passif (en dB) est nécessairement négatif (c.-à-d. inférieur à 1 en module) puisque forcément dissipatif et donc incapable de créer de l’énergie. Au contraire, un amplificateur aura un gain (en dB) positif s’il fonctionne convenablement (Fig. 3, deuxième colonne). Par ailleurs, les coefficients S étant des rapports de tensions représentatives de la propagation d’ondes électromagnétiques, la conservation de l’énergie ne s’applique pas à S, mais à son carré, la puissance étant proportionnelle au carré de la tension [3] : |S21|=√1−|S11|2 dans un dispositif sans pertes.
2. Principe de l’analyseur de réseau vectoriel
L’architecture interne d’un analyseur de réseau s’apparente au récepteur classique de radio logicielle : un oscillateur ajustable excite le dispositif à f, et des mélangeurs dont l’oscillateur de référence est lui aussi à f (habituellement une copie par coupleur du signal d’excitation pour garantir la cohérence en phase) amènent le signal radiofréquence réfléchi et transmis en bande de base. La phase et l’amplitude de ce signal proche de 0 Hz sont mesurées dans une bande passante nommée IF BW pour Intermediate Frequency Band Width pour un analyseur de réseau vectoriel, au contraire de l’analyseur de réseau scalaire qui se contente de mesurer le module et omet la phase2. Cette bande passante détermine la puissance de bruit introduite dans la mesure, puisque plus la bande passante est grande, plus la puissance du bruit additif est importante, mais aussi la durée de la mesure. En effet, la mesure pour chaque fréquence f nécessite une durée proportionnelle à (IF BW)−1. Les bandes passantes de mesure sont typiquement de la centaine de Hz à la dizaine de kHz, soit une durée de mesure de 10 ms à 100 µs par point. Pour une mesure sur 3000 points, cela se traduit par une durée de la mesure de 30 s à 0,3 s. Le choix de cette largeur de bande passante a donc un impact déterminant sur la qualité et la durée de la mesure.
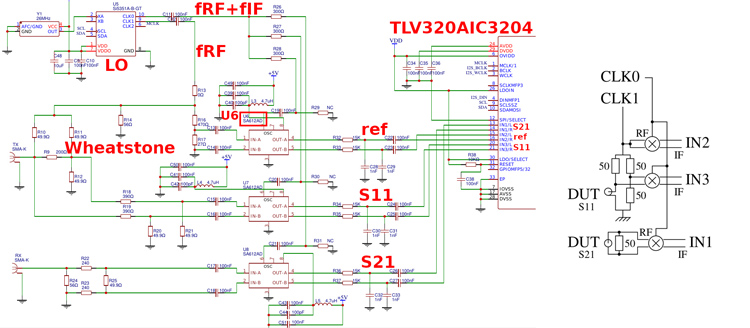
Le schéma du circuit électronique du NanoVNA, disponible à https://raw.githubusercontent.com/hugen79/NanoVNA-H/master/doc/Schematic_nanovna-H_REV3_4_2.pdf, est limpide (Fig. 4). Un générateur de signal radiofréquence Si5351, commandé en I2C pour configurer sa fréquence de sortie, alimente trois mélangeurs dont les sorties sont mesurées par le codec audio TLV320AIC3204 (trois convertisseurs analogiques numériques). La première voie acquière le signal direct alimentant le premier mélangeur U6 pour évaluer le signal de référence, le second mélangeur est placé en entrée du DUT, mais après les résistances de 50 Ω de référence dans le pont réfléctométrique dont le principe s’apparente au pont de Wheatstone. Dans cette mise en œuvre en haute fréquence du pont de Wheatstone, nous ne plaçons pas un galvanomètre en sortie, mais des mélangeurs ramenant le signal issu de l’impédance inconnue référencée à la résistance de 50 Ω en bande de base. Ces mesures de tensions (complexes) permettent de déduire le coefficient de réflexion, et à la sortie du troisième mélangeur placé après le second port, le coefficient de transmission.
On comprend ainsi qu’avec cette architecture, cet instrument ne peut pas mesurer S22 ni S12 - tout comme l’analyseur de réseau vectoriel faible coût Siglent SVA1015X qui présente les mêmes limitations (pour un coût 30 fois plus élevé, tout de même). La sortie du codec audio alimente un STM32F072 qui se charge des traitements et de l’affichage avec un logiciel s’appuyant sur l’environnement exécutif ChibiOS.
L’extraction des composantes complexes S11 et S21 passe par une fréquence intermédiaire : les sorties de CLK0 et CLK1 diffèrent légèrement d’une fréquence de battement audiofréquence fIF qui permettra, après numérisation, de multiplier par exp(j2π fIFt) pour ramener la raie à fIF vers 0, repousser la raie à −fIF vers −2fIF et rejeter cette seconde composante spectrale indésirable par filtrage passe-bas.
Il est intéressant de s’appuyer sur le code source du logiciel contrôlant le NanoVNA, disponible à https://github.com/ttrftech/NanoVNA, pour en comprendre le fonctionnement et l’interaction intime du logiciel et du matériel au travers du traitement du signal, et éventuellement en modifier les fonctionnalités. En effet, nous constatons à la lecture des codes sources que (main.c) static int32_t frequency_offset = 5000; est la fréquence intermédiaire échantillonnée par le codec audio, avec (si5351.c) CLK0: frequency + offset et CLK1: frequency lors de l’appel à si5351_set_frequency_with_offset(uint32_t freq, int offset, uint8_t drive_strength). La vidéo https://www.youtube.com/watch?v=cU05VVFl0N0 résume les grandes lignes de ce fonctionnement ainsi que l’utilisation des harmoniques du synthétiseur direct de fréquence qui impose d’augmenter la puissance au-delà de sa fréquence de cadencement (paramètre drive_strength). Dans ces conditions, le choix des auteurs d’échantillonner à 48 kHz est discutable, car impose de définir une vraie table de sinus et cosinus (sincos_tbl[48][2] dans dsp.c). En choisissant une fréquence intermédiaire du quart de la fréquence d’échantillonnage, cette table se serait résumée à [1, j, -1, -j], au lieu des 48 coefficients nécessaires pour représenter un nombre entier de périodes d’un signal à 5 kHz lors d’un échantillonnage à 48 kHz (avec la surcharge de calcul visible dans dsp_process() de dsp.c).
Cette architecture se distingue, par sa simplicité, du montage classique chez les radioamateurs pour la mesure du coefficient de réflexion s’appuyant sur le pont réflectométrique. Ce montage, qui s’apparente à la version radiofréquence du pont de Wheatstone, permet d’observer le signal retourné par le DUT lorsqu’il est excité à f, de nouveau pour alimenter le mélangeur en phase (identité I) et quadrature (Q) pour retrouver phase (arctan(Q/I)) et module (√I2+Q2), mais en prenant un grand soin à convenablement équilibrer la branche opposée au DUT. La qualité du pont réflectométrique, et notamment son équilibrage qui détermine sa directivité (isolation de l’entrée aux variations d’impédance de la sortie), détermine la qualité de la mesure du coefficient de réflexion, et en particulier la plus petite variation détectable.
3. Exemple de mesure
Ces principes de mesure étant acquis, passons à la pratique avec d’une part la présentation d’une implémentation faible coût de l’analyseur de réseau - le NanoVNA - et un exemple de mesure. Plutôt que de mesurer des objets relativement peu intéressants que sont les circuits passifs (R, L ou C) ou difficilement reproductibles (antennes), nous allons illustrer l’utilisation d’un analyseur de réseau sur des dispositifs de traitement de signaux radiofréquences que sont les filtres à ondes élastiques de surface.
Dispositifs à ondes élastiques
Une onde électromagnétique se propage à la vitesse de c=300 m/µs en espace libre. La longueur d’onde λ est la vitesse de l’onde c divisée par sa fréquence f : il est classique en radiofréquence de considérer λ=300/f pour une longueur d’onde en mètres et une fréquence en mégahertz (MHz). Ainsi la bande FM autour de 100 MHz est portée par des ondes de longueur typiquement de 3 m.
Un instrument de traitement du signal - antenne, filtre, guide d’onde - a des dimensions caractéristiques inférieures de l’ordre de la longueur d’onde. Ainsi, si nous voulions filtrer la bande FM sur notre récepteur portable, il faudrait une cavité de dimensions typiques de quelques décimètres, solution ni compacte ni transportable. La solution identifiée depuis la Seconde Guerre mondiale pour les résonateurs et depuis 1969 pour dispositifs à ondes de surface, pour rendre ces filtres compacts, est de convertir l’onde électromagnétique en onde élastique (propagation d’une onde mécanique dans un solide) : les ondes élastiques se propagent à des vitesses de l’ordre de 3000 m/s. Ce ralentissement d’un facteur 105 de la vitesse de l’onde se traduit immédiatement par une réduction des dimensions du filtre du même facteur. La cavité qui faisait 1 m ne fait maintenant plus que 10 µm. Chaque utilisateur de téléphone portable possède une dizaine de filtres à ondes élastiques de surface pour sélectionner les multiples bandes de fréquences traitées (FM, GSM, UMTS, GPS, Wi-Fi/Bluetooth...). Ce nombre est déjà à 60 dans l’actuelle génération des téléphones 4G [5] et continuera à croître dans la prochaine génération de protocoles compatibles avec la 5G et la prolifération des bandes radiofréquences accessibles. Le principe de génération de ces ondes élastiques repose sur la piézoélectricité, propriété de certains matériaux d’induire un déplacement mécanique, lorsque soumis à un champ électrique, et réciproquement, de créer des charges électriques (courant) lorsque soumis à une contrainte mécanique. Le matériau piézoélectrique le plus connu est le quartz (le même qui cadence les microcontrôleurs ou les montres), les filtres radiofréquences étant plus souvent réalisés en niobate ou tantalate de lithium.
Prenons par exemple un filtre passe-bande Epcos B3607 fonctionnant autour de 140± 3 MHz que nous avions acquis pour la réception d’images satellites en orbite basse (émission autour de 137 MHz) et comme transpondeur pour l’espionnage d’une liaison RS232 [6]. Ce filtre est un quadripôle qui accepte en entrée un signal large bande et ne laissera passer sur sa sortie que les composantes spectrales dans sa fonction de transfert. Il est caractérisé par des propriétés telles que les pertes d’insertion qu’il induit dans sa bande passante, sa réjection (sa capacité à atténuer les composantes spectrales en dehors de sa bande passante), les fluctuations des pertes dans la bande ou les rotations de phase qu’il induit dans sa bande (risquant de faire osciller le circuit radiofréquence si le filtre est suivi d’un amplificateur). Ce filtre se caractérise donc en transmission, ainsi qu’en réflexion pour identifier sa propension à accepter le signal incident, car un coefficient de réflexion trop important pourrait endommager le circuit qui alimente le filtre en lui renvoyant trop de puissance. En effet, en dehors de sa bande passante, le filtre se comporte comme un circuit ouvert qui renvoie l’intégralité de la puissance incidente vers le générateur.
Attention : un récepteur d’analyseur de réseau est un circuit radiofréquence délicat et sensible. On prendra soin de toujours vérifier la puissance injectée - en particulier lors de la caractérisation de composants actifs tels que les amplificateurs - pour rester en deçà de la puissance limite acceptable. Mieux vaut commencer en atténuant la puissance d’excitation en sortie de l’analyseur de réseau, quitte à retirer les atténuateurs si la qualité de la mesure est insuffisante faute de puissance.
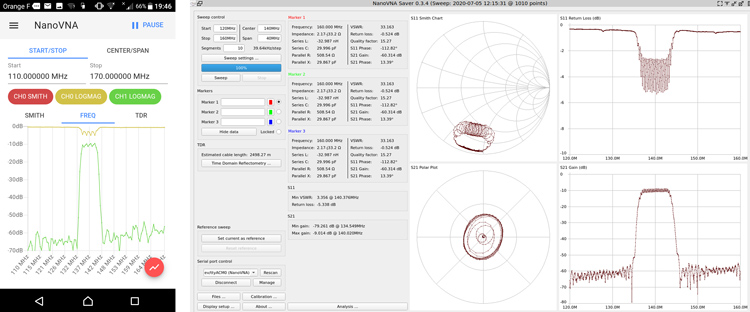
La figure 5 illustre la mesure de ce filtre par un instrument haut de gamme - Rohde & Schwarz ZNB-8 - et le NanoVNA. Nous constatons que les mesures sont cohérentes, avec une bande passante entre 137 et 143 MHz et des pertes d’une dizaine de dB, tandis que les rotations de phase dans la bande passante (bas) sont elles aussi cohérentes. On notera que la phase ϕ représente le temps τ que met une onde à se propager le long du DUT dont le chemin radiofréquence est de longueur D. En effet ϕ=−2π f τ=−2π f D/c donc dϕ/df=−2π D/c, le signe moins indiquant qu’il s’agit d’un retard. Dans le cas d’un dispositif à ondes élastiques, c n’est pas la vitesse de la lumière, mais la vitesse de l’onde élastique, que nous pouvons retrouver par ce biais.
Cette figure met par ailleurs en évidence l’importance déterminante de calibrer les composants entre l’analyseur de réseau et le composant à qualifier. Nous avions initialement associé à une mauvaise conception matérielle la faible réjection d’une vingtaine de dB entre la ligne de base en dehors de la bande passante et les pertes dans la bande passante. Il n’en est rien : une erreur dans l’étape d’étalonnage corrigée entre la version 0.2.2 et 0.3.3 de NanoVNA-Saver (voir la liste des correctifs à https://github.com/NanoVNA-Saver/nanovna-saver/releases : « Fixed through calibration » et en particulier https://github.com/NanoVNA-Saver/nanovna-saver/commit/22be293ff287aa3946758ad3c3d95e84d28f56a3 qui indique que la correction n’était pas prise en compte lors du calcul des coefficients d’étalonnage). Suite à cette correction, la correspondance entre la mesure du Rohde & Schwarz ZNB-8 et du NanoVNA est tout à fait impressionnante. Lors de cette mesure, nous avons divisé la plage de fréquences en 10 sous bandes, permettant d’acquérir un total de 1010 points et fournissant une résolution acceptable en abscisse. La limitation en nombre de points de mesures n’est donc pas problématique avec le NanoVNA.
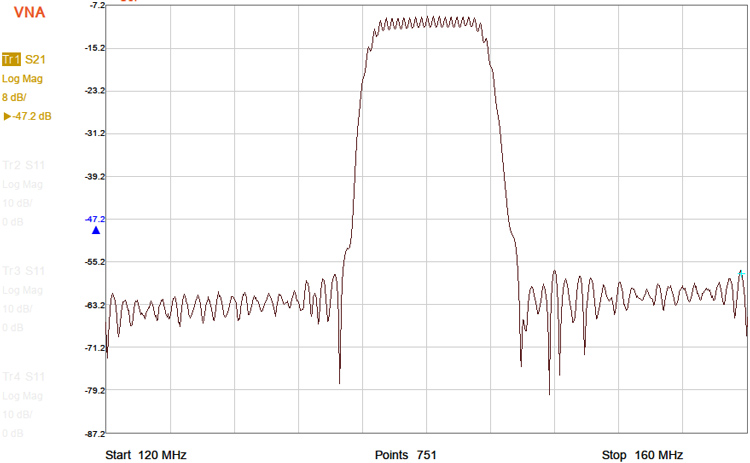
Pour comparaison, la même mesure par un instrument de coût intermédiaire entre le NanoVNA et le Rohde & Schwarz ZNB-8 - Siglent SVA1015X - est utilisée pour une mesure similaire (Fig. 6). Cet instrument est limité à 751 points de mesure, mais propose la fonction d’analyseur de spectre en plus de l’analyseur de réseau.
Bels et décibels
Il est classique de travailler en unité logarithmique lorsque nous manipulons des puissances radiofréquences, compte tenu des très grandes dynamiques mises en œuvre. Il semble en effet plus facile de dire que le signal émis à 500 MHz par un émetteur de 74 dBm est reçu avec une puissance de -26 dBm à 5 km par dilution de la puissance sur la surface de la sphère de ce rayon, plutôt que dire que le signal émis de 25 kW est reçu 2,5 µW (il s’agit du bilan de liaison entre l’émetteur de télévision qui illumine Besançon et la résidence de l’auteur). Le bel est une échelle logarithmique obtenue par le logarithme en base 10 de la grandeur, et le décibel est obtenu par 10log10() de même que le décimètre est obtenu en multipliant par 10 la longueur en mètres. L’argument d’un logarithme ne saurait avoir d’unité (dont le résultat serait un log10(W)), donc il faut normaliser l’argument : c’est le sens du « m » de dBm pour indiquer que la puissance est normalisée par 1 mW, ou dBW qui indique que la puissance est en W. Comme le décibel noté dB est un rapport de puissances et que les coefficients de diffraction sont un rapport de tensions, il existe une relation de mise en carré entre les deux (la puissance est le carré de la tension divisée par l’impédance de référence de 50 Ω, l’impédance de référence s’éliminant dans le ratio des deux tensions de sortie et d’entrée). Ainsi, l’affichage en dB des coefficients de diffraction s’obtient par 20log10(|S|) en sortant le carré comme facteur multiplicatif par 2 de la définition de 10log10().
4. Interfaces utilisateur du NanoVNA
Le NanoVNA est fourni avec un écran tactile et une molette de sélection des menus dont on conclut rapidement qu’ils sont à peu près inutilisables, même pour visualiser le signal acquis puisque l’ajustement des échelles est pratiquement impossible. Cet inconvénient est largement pallié par l’excellent logiciel Python (testé sous GNU/Linux, mais a priori fonctionnel sous MS-Windows) nanovna-saver et Android (Figs. 7 et 1) qui non seulement fournissent toutes les fonctionnalités attendues d’un analyseur de réseau vectoriel, mais surtout permettent d’ajouter les fonctionnalités manquantes du fait de la disponibilité des codes sources. Le code Python de nanovna-saver est disponible à https://github.com/mihtjel/nanovna-saver tandis que l’APK pour Android évitant de devoir s’enregistrer auprès de Google est disponible à https://github.com/cho45/NanoVNA-Web-Client/releases/tag/latest.
Ces interfaces utilisateur permettent de régler les paramètres de mesure que sont la bande de fréquence analysée, le nombre de points de mesure par bande (limité à 101), le nombre de bandes de mesure pour atteindre en fin de compte un nombre de points de mesure illimité sur l’ensemble de la bande observée, et la nature de la mesure (transmission ou réflexion).
Dans les deux cas, les fichiers peuvent être sauvés pour un post-traitement.
Le format SnP
Les mesures acquises par analyseur de réseau sont classiquement sauvées au format Touchstone noté SnP. Il s’agit d’un format standardisé qui contient en entête la nature de la mesure, son format (réel-imaginaire ou module-phase), et l’impédance de référence. La première colonne est toujours la fréquence, suivie pour les deux colonnes suivantes du coefficient de réflexion. S’il s’agit d’une mesure en transmission, elle suit dans les deux colonnes suivantes. On notera que certains analyseurs de réseau (p. ex. Siglent SVA 1015X) ne supportent pas la sauvegarde au format SnP, mais n’autorisent que le format CSV (Comma Separated Values, c.-à-d. des colonnes au format ASCII sans information de leur nature) : dans ce cas, la sauvegarde de la grandeur complexe (p. ex. S11) s’obtient souvent en passant en diagramme de Smith, représentant les parties réelles et imaginaires de la grandeur mesurée, au lieu de sauvegarder séquentiellement le module et la phase affichés à l’écran.
Une liste plus ou moins exhaustive des ressources permettant de collecter les données du NanoVNA est proposée à https://www.rudiswiki.de/wiki9/nanoVNA.
5. Étalonnage
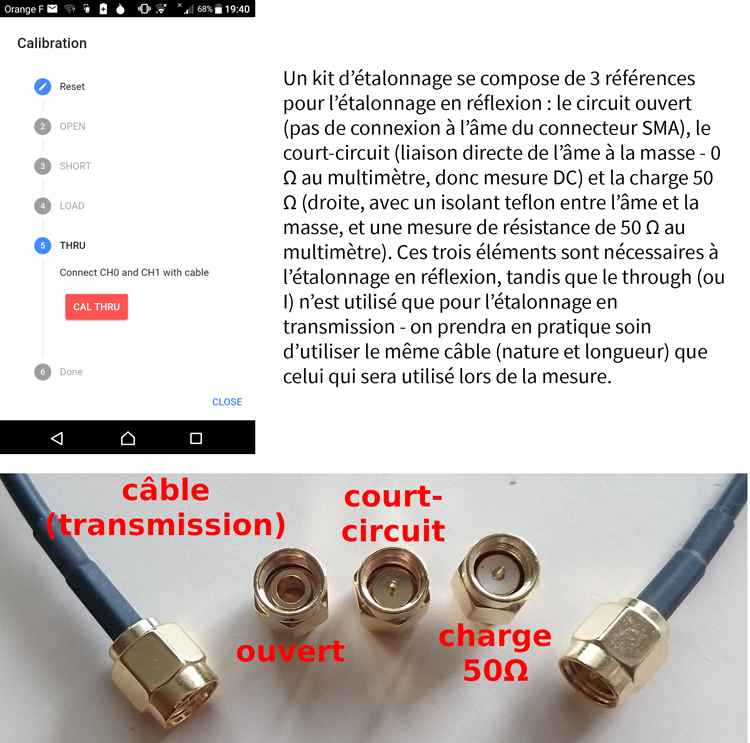
Une mesure n’a de sens que par rapport à une référence. Alors qu’en basse fréquence, cette référence peut être une résistance fixe, en radiofréquence la ligne de transmission qui relie l’instrument de mesure au DUT impacte la mesure. En effet, l’impédance vue par le port de l’analyseur de réseau inclut à la fois le DUT et le câble portant le signal radiofréquence. Étant donné que l’utilisateur désire connaître les propriétés du DUT et non son association avec le câble, il faut étalonner [7] la contribution du câble avant d’effectuer la mesure du DUT. Ce résultat s’obtient par trois mesures : extrémité ouverte, extrémité court-circuitée, et extrémité chargée par l’impédance caractéristique de l’analyseur de réseau et de son câble, à savoir 50 Ω par convention.
Il est par conséquent impératif de calibrer l’analyseur de réseau avant toute mesure, et ceci est d’autant plus fondamental pour le NanoVNA, dont les résultats sont tout bonnement aberrants en l’absence d’étalonnage. Par ailleurs, l’étalonnage de l’instrument est fondamental si les données collectées lors de la mesure des coefficients de diffraction (paramètres S) ont pour vocation d’être transformées en grandeurs physiques exploitables. En effet, S n’est qu’une matrice reliant les diverses tensions d’un DUT entre elles. Un électronicien désire manipuler des impédances ou des admittances (inverse de l’impédance) qu’il peut relier à des modèles électriques des circuits (résistance R, inductance L et condensateur C, par exemple). Les coefficients S informent sur les propriétés de propagation des ondes dans le dispositif, tandis que l’admittance informe sur les propriétés intrinsèques de ce dispositif : les deux grandeurs sont évidemment reliées, mais l’information contenue dans chaque représentation diffère. Un cas simple est le cas du coefficient de réflexion S11∈ℂ du dipôle qui se relie facilement à l’admittance (complexe) Y par :
Le cas du quadripôle (2-ports) en transmission est beaucoup plus pénible, car il nécessite la mesure du coefficient de réflexion sur le second port S22 : cette mesure n’est pas possible directement sur NanoVNA ou Siglent SVA1015X, mais nécessite une seconde mesure en retournant le DUT pour identifier les quatre paramètres S.
Un étalonnage correct (Fig. 8 sous Android) est fondamental si le coefficient de réflexion doit être transformé en admittance. De même que le module du coefficient de réflexion S11 ne peut être supérieur à 1 (ou 0 dB) pour un composant passif, la partie réelle de l’admittance ne peut être négative3.
La physique du transducteur est contenue dans l’admittance et tout calcul lié à la physique du composant (opposée à la physique de l’onde qui s’y propage) doit se faire sur Y. Ainsi, le facteur de qualité, défini comme le ratio de l’énergie emmagasinée dans le dispositif sur l’énergie dissipée par période, s’avère dans le cas d’un système harmonique être la fréquence de résonance définie comme la fréquence associée au maximum d’admittance, divisée par la largeur à mi-hauteur du pic d’admittance. Le facteur de qualité d’un circuit électronique ne se calcule jamais sur le coefficient de réflexion S11 qui n’a pas de sens physique en termes de courant et de tension dans le circuit équivalent, mais n’indique que l’adaptation du DUT à la source qui l’excite.
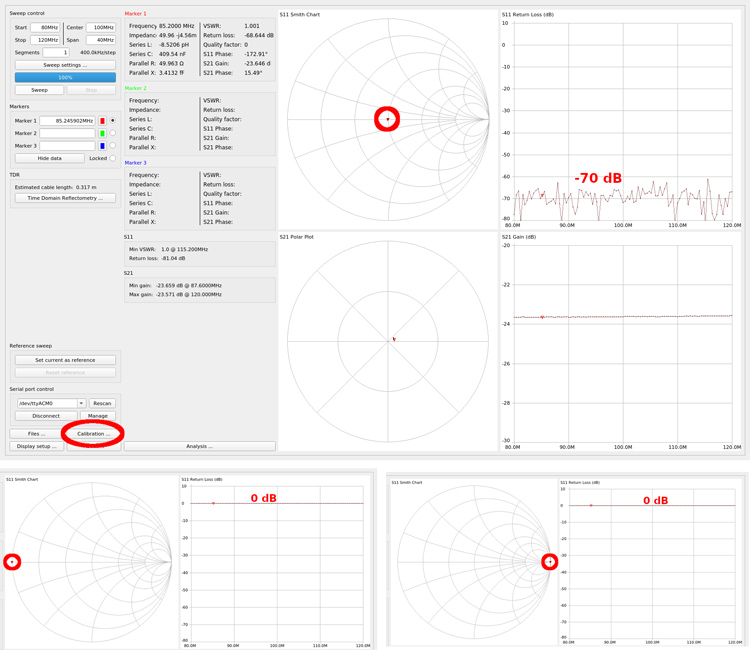
Calibrer c’est bien, mais un étalonnage faux est probablement pire que pas d’étalonnage du tout (Fig. 5). Il est donc fondamental de s’assurer après étalonnage que les charges de référence présentent bien la réponse attendue lors de leur mesure en appliquant les coefficients d’étalonnage. La charge 50 Ω doit présenter un minimum du coefficient de réflexion (typiquement -50 à -70 dB), tandis que les circuits, ouvert et fermé présentent tous deux des réflexions totales (|S11|=~ 0 dB), mais avec une phase qui tourne de 180° entre les deux mesures (réflexion en phase ou en opposition de phase selon la condition limite appliquée). Sur un abaque de Smith qui représente la partie imaginaire en fonction de la partie réelle, la charge 50 Ω se trouve au centre de l’axe des abscisses, le circuit ouvert à une extrémité et le court-circuit à l’autre extrémité, toujours sur l’axe des abscisses pour indiquer une composante purement réelle et pas de partie imaginaire (qui serait une composante inductive ou capacitive parasite). Ces points sont illustrés sur les graphiques acquis au cours de l’étalonnage d’un analyseur de réseau Rohde & Schwarz ZNB-8 (Fig. 9) et d’un NanoVNA (Fig. 10). On prendra soin de calibrer l’instrument sur la gamme de fréquences sur laquelle s’effectuera la mesure.
À titre de démonstration de ces concepts, nous allons analyser un résonateur à quartz de fréquence nominale 39 MHz. Nous pourrions croire qu’il s’agit d’une fine lame de quartz taillée pour résonner à cette fréquence en confinant une onde élastique entre les deux faces métallisées. Une onde de volume de cisaillement se propage dans le quartz autour de 5000 m/s. Les conditions limites de confinement d’une onde élastique de volume impliquent qu’un nombre impair de demi-longueurs d’onde doit tenir dans l’épaisseur du substrat. Ainsi avec une longueur d’onde de 5000/39=128 µm, il faudrait une lame de quartz de 64 µm d’épaisseur. Une telle valeur n’est pas inaccessible, mais serait difficile à manipuler et fragile à assembler. En pratique, tous les résonateurs à quartz fonctionnant au-dessus d’une vingtaine de MHz fonctionnent sur un mode harmonique, dans le cas de notre résonateur l’harmonique 3 d’un mode fondamental autour de 13 MHz, ou une lame de quartz de 192 µm d’épaisseur.
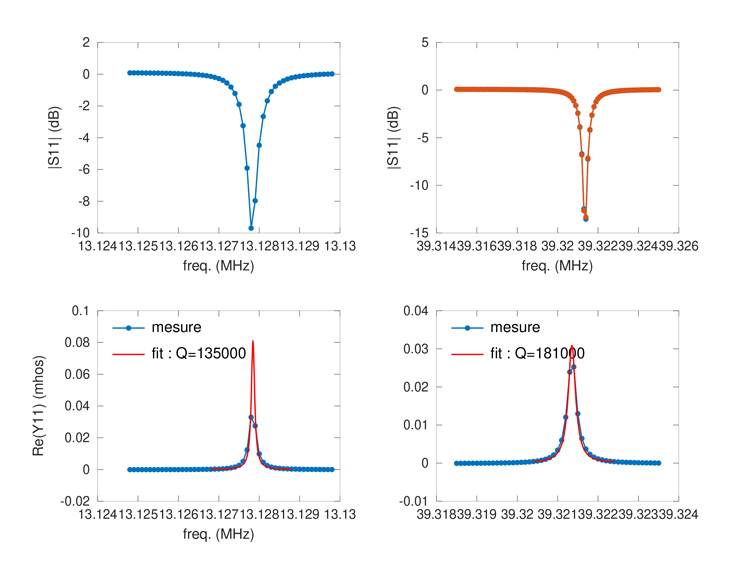
Nous observons sur la Fig. 11 le mode harmonique (droite) et fondamental (gauche) en coefficient de réflexion (haut) et admittance (bas). La partie réelle de l’admittance a été ajustée par une lorentzienne, modèle approprié pour l’admittance d’un circuit RLC série, lui-même justifié pour tout système résonant4. Le facteur de qualité Q calculé comme fréquence de maximum d’admittance divisé par largeur à mi-hauteur du pic d’admittance est indiqué en légende. Le produit Q x f=2,5 x 1012 est en accord avec la figure de mérite habituellement attribuée au quartz, qui indique que les pertes (inverse du facteur de qualité) croissent avec la fréquence de fonctionnement.
On prendra soin lors de la mesure d’un dispositif de fort facteur de qualité d’abaisser suffisamment la vitesse de balayage pour garantir l’indépendance des mesures successives lors du balayage de fréquence. En effet, un résonateur de facteur de qualité Q fonctionnant à la fréquence f présente une constante de temps de charge et de décharge de Q/(π f) : un balayage trop rapide se traduit par la fuite de l’énergie du point précédent lors de la mesure du point suivant. Cet effet s’observe comme une asymétrie de la résonance, mais surtout un S11>0 dB qui ne saurait exister physiquement sur un dispositif passif. Alors que sur un résonateur à 39 MHz un Q≃ 150000 se traduit par une constante de temps de 150000/π/39=122 µs, un diapason à quartz de facteur de qualité typique Q=60000 à f=32768 Hz présente une constante de temps de l’ordre de la demi-seconde : la caractérisation d’un tel dispositif nécessite une certaine patience pour être correcte.
Les graphiques de la figure 11 s’obtiennent par le script GNU/Octave ci-dessous qui s’appuie sur peakfit.m disponible à http://terpconnect.umd.edu/~toh/spectrum/InteractivePeakFitter.htm.
Comme dans tout ajustement paramétrique, les valeurs initiales (ainsi que le choix du modèle) sont fondamentales pour garantir la convergence. Dans le cas de la lorentzienne qui nous concerne ici pour ajuster la partie réelle de l’admittance, ces deux paramètres sont la fréquence du maximum et la largeur à mi-hauteur. Nous convertissons donc le coefficient de réflexion mesuré s11 en admittance y11 et fabriquons le vecteur contenant en première colonne la fréquence (abscisse) et en ordonnée la partie réelle de l’admittance (ordonnée) à peakfit(). Nous demandons un ajustement par une unique lorentzienne (peakfit() est capable de déconvoluer une somme de plusieurs fonctions) en lui proposant des valeurs « raisonnables » de fréquence de résonance freqreson (maximum de la partie réelle de l’admittance) et de largeur à mi-hauteur freqwidth. Par ailleurs, nous n’ajustons que le pic d’admittance en omettant la ligne de base qui pourrait perturber la convergence ((mpos-10:mpos+10,:)). Le résultat de l’ajustement permet une bien meilleure détermination de la fréquence de résonance, mais surtout du facteur de qualité défini - dans le cas d’un système résonnant du second ordre - comme la fréquence de résonance sur la largeur à mi-hauteur Q=freql/dfl. Ce paramètre clé détermine la sélectivité spectrale du résonateur ou sa stabilité aux perturbations extérieures.
6. Protocole de communication
Outre le fait que le NanoVNA soit open source et open hardware, son protocole de communication par trames ASCII est limpide et trivial à implémenter. Ainsi, compléter l’offre Python ou Android par son logiciel dédié se fait simplement en émettant sur le port série virtuel les commandes définissant la nature de la mesure, la plage de fréquence, et en lisant le résultat. À titre d’exemple en C, dont la motivation était de répéter périodiquement la mesure sur une longue durée pour observer l’impact de la dérive de l’oscillateur local lors de sa chauffe après mise sous tension de l’appareil, nous communiquons avec le NanoVNA par :
Et nous répétons cette séquence d’échanges avec les commandes lues par help depuis un terminal (minicom, screen) connecté au port série virtuel : info, trace 2 pour sélectionner la mesure en réflexion sous forme de complexe (partie réelle et imaginaire dans le diagramme de Smith), frequencies pour stocker la liste des fréquences mesurées, et nous bouclons sur la mesure par data qui renvoie autant de lignes que nous avons obtenues de fréquences, soit 101.
L’ouverture du port série s’obtient par les très habituelles commandes de gestion des terminaux :
7. Spectre de la source
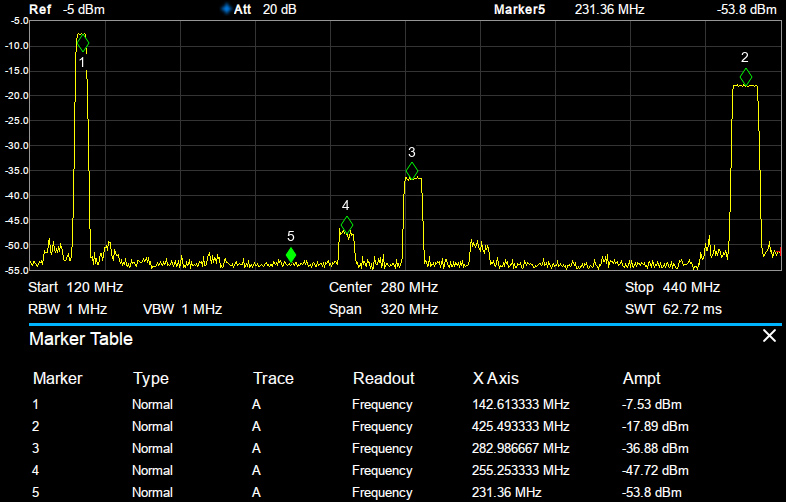
Nombre de forums discutent de la fréquence supérieure de fonctionnement du NanoVNA par l’utilisation de diverses astuces sur la source de fréquence (Fig. 12), et en particulier l’utilisation de composantes spectrales harmoniques - en supposant les mélangeurs capables de supporter de telles fréquences, les NXP SA612AD étant limités à 200 MHz pour l’oscillateur local et 500 MHz pour le signal. Le fait est que le Si5351 génère nombre de raies au-delà de la fondamentale compte tenu du signal carré généré, qui peuvent être utilisées à bon escient sous hypothèses sur le DUT. En ne connaissant rien de la fonction de transfert du DUT, l’exciter ainsi avec une multitude de raies peut fournir une réponse incohérente puisque nous ne savons pas séparer la contribution de la composante fondamentale des harmoniques, mais la majorité des DUT étant des filtres passe-bande (c’est aussi le cas des antennes) relativement étroits, focaliser la mesure sur la bande passante prévue donne généralement un résultat acceptable, sans bien entendu rivaliser avec les instruments professionnels d’excellente pureté spectrale du signal excitant le dispositif inconnu. Un exemple de spectre émis par le NanoVNA à fréquence nominale autour de 140 MHz est illustré en Fig. 13. L’harmonique 3 est particulièrement puissante, à seulement 10 dB de moins que le fondamental, une propriété regrettable, car nombre de filtres (à ondes élastiques notamment) présentent eux aussi une réponse sur leur troisième harmonique.
Ce graphique nous informe par ailleurs que la puissance qui sert à exciter le DUT est autour de −7 dBm. Cette information est importante pour ne pas endommager les composants passifs fragiles ou ne pas atteindre le point de compression d’amplificateurs lors de leur caractérisation. La puissance de sortie n’est pas paramétrable sur le Si5351 et seul l’ajout d’atténuateurs externes permet de réduire cette puissance de sortie, si besoin.
8. Application au RADAR à balayage de fréquences
Nous allons ici démontrer l’utilisation de l’analyseur de réseau vectoriel comme RADAR à balayage de fréquence par pas discret, ou Frequency Stepped Continuous Wave FSCW RADAR.
Un RADAR (RAdiofrequency Detection And Ranging) est souvent associé à un générateur d’impulsions pour émettre un signal large bande dont les échos permettront une mesure précise du temps de vol - et ce d’autant plus que la largeur de bande occupée B est importante, c.-à-d. que l’impulsion est courte. En effet, la résolution en distance (range resolution) est Δ R=c/(2B), avec c=300 m/µs la vitesse de la lumière dans le vide. Le RADAR impulsionnel souffre de nombreux défauts technologiques, incluant la difficulté à générer des impulsions brèves puissantes (par transistor à avalanche, par exemple), la faible durée pendant laquelle le signal peut être détecté interdisant tout bénéfice d’intégration (corrélation) pour réduire le bruit en le moyennant, et un mauvais contrôle de l’encombrement spectral qui dépend de l’environnement diélectrique de l’antenne émettrice.
L’impulsion n’est qu’une façon parmi de nombreuses autres de générer un signal large bande. Nous avions décrit [8] le RADAR à bruit dans lequel nous avions introduit le NanoVNA comme implémentation possible d’un RADAR à balayage de fréquence par pas discrets (FSCW - Frequency Stepped Continuous Wave). Le nombre de points acquis N (c.-à-d. le pas de fréquence B/N) détermine la distance maximale de la cible la plus lointaine N/2×Δ R tandis que l’excursion de fréquence B détermine la résolution de la mesure. Avec un NanoVNA qui peut aller de 200 à 500 MHz (gamme raisonnable pour une antenne large bande), la résolution en distance est de l’ordre de 50 cm et lors d’une mesure sur 101 points, la cible la plus lointaine doit se trouver au plus à 25 m. Comme le NanoVNA permet de concaténer des mesures sur des segments adjacents, le nombre de points peut être augmenté pour accroître la distance maximale de mesure, dans la limite de sensibilité de l’étage de réception.
Au lieu d’appliquer le NanoVNA à une mesure RADAR dans l’air, nous allons de nouveau illustrer ces concepts en remplaçant l’onde électromagnétique par une onde élastique qui permet d’introduire un retard d’une microseconde, non pas avec 100 m de câble coaxial, mais avec 1,5 mm d’un matériau piézoélectrique fortement couplé pour limiter les pertes de conversion électromécaniques : le niobate de lithium. Le dispositif à onde élastique fonctionne cette fois en réflexion et non en transmission, comme le faisait le filtre. Nous allons utiliser un dispositif réalisé spécifiquement pour cette mesure, mais le lecteur pourra reproduire les mesures avec le filtre EPOCS 140 MHz utilisé en réflexion, avec le second port déconnecté (circuit ouvert désadapté en impédance induisant donc une réflexion de l’onde élastique).
Une ligne à retard à ondes élastiques réflective (Fig. 14) [9] est un ensemble d’électrodes déposées sur un substrat piézoélectrique fortement couplé - typiquement niobate ou tantalate de lithium - avec un transducteur en forme de peigne interdigité chargé de convertir l’onde électromagnétique incidente en onde élastique par effet piézoélectrique inverse. Cette onde se propage à la surface du substrat piézoélectrique pour atteindre une nouvelle série d’électrodes judicieusement espacées pour se comporter comme des miroirs par rupture d’impédance. Finalement, l’onde élastique réfléchie revient au transducteur interdigité pour être convertie en onde électromagnétique par effet piézoélectrique direct. Compte tenu du ratio de 105 entre les vitesses des ondes électromagnétiques et élastiques, un dispositif à 100 MHz (3 m de longueur d’onde électromagnétique dans l’air) nécessite des ressources technologiques un peu complexes pour dessiner les électrodes de 30/4=7,5 µm de large espacées de 7,5 µm.
Le dispositif sondé étant défini, comment obtenir sa réponse impulsionnelle ? C’est en effet le problème que cherche à résoudre un RADAR en mesurant la distance aux cibles réfléchissant une impulsion électromagnétique incidente. Il s’agit du même problème que cherche à résoudre la TDR (Time Domain Reflectometry) qui par exemple trouve la distance aux courbures ou ruptures des câbles électriques ou fibres optiques. L’injection d’une impulsion contrôlée est souvent technologiquement complexe, et il est bien plus simple de balayer une plage de fréquence f−B/2 à f+B/2 (la fréquence centrale f est généralement imposée par des contraintes technologiques telles que la fréquence de coupure basse d’un guide d’onde, mais n’a aucune influence dans la suite du discours) qui va permettre, par transformée de Fourier inverse, de trouver la réponse impulsionnelle du système sondé avec une résolution temporelle 1/(2B) (le facteur 2 vient de l’aller-retour de l’onde) ou en terme spatial, de c/(2B) avec c la vitesse de l’onde dans le milieu dans lequel elle se propage.
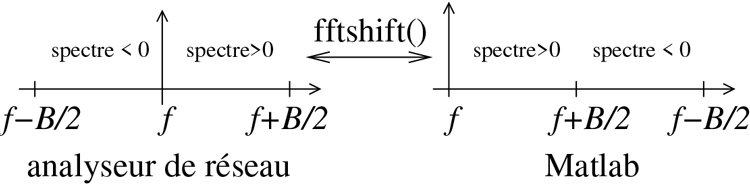
On prendra en pratique soin, lors de l’application de ce calcul, de tenir compte de la norme de Matlab (et donc de GNU/Octave) qui place la fréquence centrale f au point d’abscisse 1, la fréquence de Nyquist f+B/2 à l’indice égal à la moitié des points acquis, et son opposé f−B/2 à l’abscisse égale au nombre de points acquis (Fig. 15). Cette convention est contraire à l’affichage d’un analyseur de réseau qui place f au milieu de l’écran, f−B/2 à gauche et f+B/2 à droite (ou en bande de base après transposition de f, −B/2 à gauche, 0 au centre et B/2 à droite). Le passage de la première convention à la seconde s’obtient sous Matlab ou GNU/Octave par la fonction fftshift qui échange les quadrants de droite et de gauche pour placer f au milieu du graphique. Une fois l’axe des abscisses convenablement défini, nous pouvons tracer ifft(fftshift(s11)) en module et phase. Le module est une représentation grossière, mais absolue du temps de vol, la phase est une représentation fine, mais avec une incertitude de 2π (ou une longueur d’onde) sur la phase parcourue (la distance parcourue respectivement).
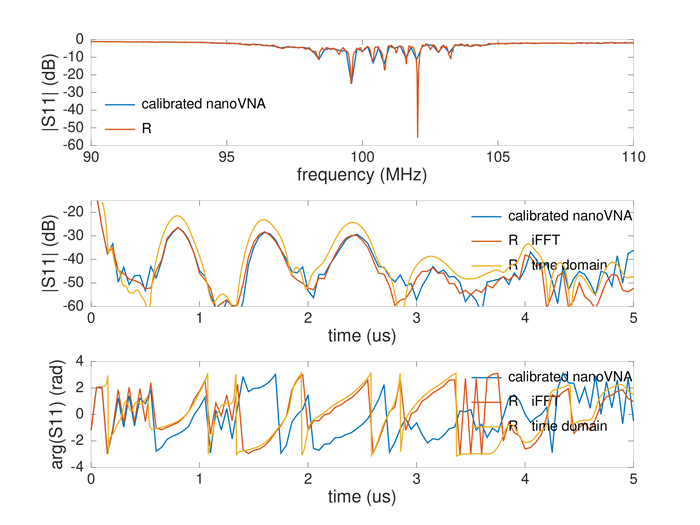
La Fig. 16 illustre l’excellente adéquation entre le NanoVNA et le Rohde & Schwarz ZNB-8, avec la plus grande différence entre le module de notre transformée de Fourier inverse des mesures dans le domaine spectral et le résultat de l’option temporelle du ZNB-8 (milieu, orange) : nous attribuons cette différence à la pondération du fenêtrage appliqué par Rohde & Schwarz sur une mesure plus large que la bande affichée, sans avoir pu vérifier cette affirmation. Concrètement, la conversion d’une mesure spectrale au format S1P en information temporelle s’obtient par :
On pourra noter qu’en réflectométrie, la corrélation dans le domaine temporel du signal (large bande, donc bruit ou chirp formé d’une sinusoïde dont la fréquence varie dans le temps) émis dans le guide d’onde à mesurer s’obtient en pratique comme la transformée de Fourier inverse (iFT) du produit de la transformée de Fourier (FT) du signal de référence r(t) par le complexe conjugué de la transformée de Fourier du signal réfléchi mesuré m(t). En clair : xcorr(r,m)=iFT(FT(r)· FT*(m)). Or, il arrive souvent que nous n’ayons accès qu’à la dépendance spectrale de r(f) et m(f) et non à leur dépendance temporelle r(t) et m(t). C’est par exemple le cas du RADAR à balayages discrets de fréquence (FSCW) qui n’est autre qu’un analyseur de réseau. Dans ce cas, seul le produit des mesures dans le domaine spectral r(f)· m(f) est utile pour effectuer la corrélation, dont le retour dans le domaine temporel s’obtient par transformée de Fourier inverse iFT(r(f)· m(f)). Un analyseur de réseau est donc bien un RADAR FSCW.
9. Stabilité de l’oscillateur local
Le dernier point sur lequel nous pouvons nous interroger est la stabilité à long terme de la référence de fréquence qu’est l’oscillateur à quartz compensé en température (Temperature Compensated Crystal Oscillator - TCXO) qui référence toute la chaîne de mesure. Alors qu’un TCXO n’a aucune prétention de stabilité long terme, le quartz étant sensible à toutes sortes de paramètres environnementaux et la température en premier lieu, l’échauffement initial de l’électronique est souvent un point clé pour savoir au bout de combien de temps la référence de fréquence est stable.
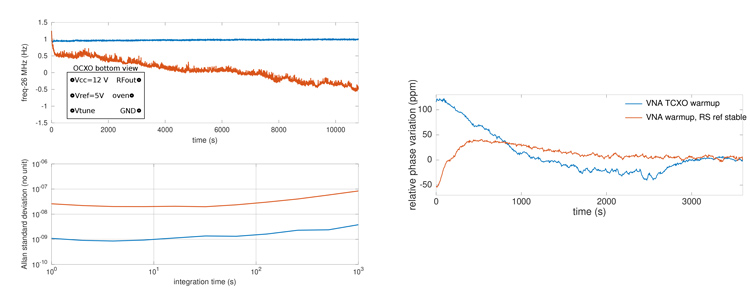
La Fig. 17 présente deux courbes de mesure de phase de la cible coopérative présentée ci-dessus, maintenue dans un environnement stable de façon à ce que son retard τ reste constant : dans ce cas, la mesure de phase ϕ=2π fτ reflète exclusivement la variation de fréquence f du signal qui sonde la réponse de la ligne à retard. Nous traçons une variation relative de phase δ ϕ/ϕ en partie par million (ppm) après avoir multiplié le résultat par 106. En considérant que la valeur après 1 h de stabilisation est correcte, nous constatons que le TCXO démarre avec un biais de 100 ppm pour se stabiliser avec une durée de l’ordre de l’heure. Si nous retirons le résonateur à quartz et le remplaçons par une source externe stable à 26 MHz (Rohde & Schwarz SMC100A stabilisé, car continuellement alimenté), seul un résidu de dérive associé à la synthèse de fréquence subsiste. Cette mesure justifie la pratique habituelle de ne jamais cesser d’alimenter les oscillateurs qui réfèrent les instruments à sortie de fréquence (compteur, analyseur de spectre ou de réseau, par exemple). Comme tout lecteur ne possède pas forcément un excellent synthétiseur tel que le Rohde & Schwarz SMC100A, nous avons aussi expérimenté avec un oscillateur contrôlé en température par un four (Oven Controlled Crystal Oscillator - OCXO) en retirant le résonateur fourni initialement et en alimentant le générateur de signaux radiofréquences du NanoVNA par la sortie d’un Tele Quarz TQOC26-01 (aussi disponible sous la référence C-Mac STP 2085B) acquis pour 12 euros sur eBay. Ce composant s’alimente en 12 V selon le schéma de la Fig. 17 (gauche) et génère un signal carré qu’il est judicieux de filtrer et d’atténuer. Le gain en stabilité court et long terme en remplaçant le TCXO par l’OCXO est dramatique, avec un gain d’un facteur 30 sur toute la plage d’intégration temporelle évaluée ici (1 à 1000 s). La mesure est effectuée par un compteur HP53131A référencé sur une source 10 MHz issue d’un maser à hydrogène distribué par White Rabbit avec un temps de porte (gate time) de 1 s.
Conclusion
L’analyseur de réseau vectoriel est un instrument fournissant une information très riche sur un composant radiofréquence - actif ou passif - ou l’environnement électromagnétique d’une antenne (RADAR). Nous n’avons pas abordé ici la caractérisation des antennes, fortement dépendante de leur environnement, et nécessitant souvent une infrastructure dédiée (chambre anéchoïque) pour une mesure pertinente. Nous nous sommes donc efforcés d’illustrer la mesure par analyseur de réseau sur les composants classiquement utilisés en traitement des signaux radiofréquences s’appuyant sur les ondes élastiques, et avons ainsi développé quelques méthodes d’exploitation des informations acquises par l’instrument dans le domaine spectral, mais aussi le passage vers le domaine temporel. La prolifération des composants radiofréquences performants à faible coût rend désormais ces instruments accessibles à l’amateur, qui n’a plus qu’à s’en approprier les principes de mesure pour en tirer le meilleur parti. Pour paraphraser la démarche pédagogique de MiniCircuits [10] qui comprend que sans une nouvelle génération d’ingénieurs compétents dans la caractérisation de dispositifs radiofréquences, leurs produits n’auront plus de débouchés : « two companies realized that there was a gap in the RF industry in how new engineers were linking the knowledge they learn in the classroom to the sophisticated equipment they were using in their respective careers ». Il nous semble que le NanoVNA remplit ce rôle.
Remerciements
Franck Daout (IUT Ville-d’Avray) m’a informé de l’existence du NanoVNA et de son utilisation dans le contexte de la caractérisation des antennes VHF en deçà de la gamme de fréquences de fonctionnement des chambres anéchoïques. Denis Bodor m’a motivé à rédiger au sujet de cet instrument. Les lignes à retard réflectives à ondes élastiques ont été conçues et réalisées par mes collègues Melvin Paquit, Lilia Arapan et David Rabus (FEMTO-ST, département temps-fréquence, Besançon). L’analyseur de réseau Siglent a été acquis par le département d’enseignement d’électronique de l’Université de Franche-Comté à Besançon. P. Stempflé (FEMTO-ST, département micro et nanosystèmes) a amélioré le manuscrit par ses relectures et corrections. Les éléments bibliographiques qui ne sont pas librement disponibles sur le web ont été acquis auprès de Library Genesis à gen.lib.rus.ec, une ressource indispensable à nos activités de recherche et d’enseignement.
Références
[1] On évitera de croire toutes les publicités plus ou moins fantaisistes proposées par les vendeurs sur Internet. Nous avons choisi au hasard https://www.amazon.fr/Slickbox-analyseur-vectorielle-Analyseur-param%C3%A8tres/dp/B07VDC4JQT/ (53 euros).
[2] Rohde & Schwarz, Fundamentals of Vector Network Analysis, version 1.1 (consulté juin 2020), à https://www.signalintegrityjournal.com/ext/resources/White-papers-App-notes/Vector-Network-Analyzer-Fundamentals-Primer.pdf pour éviter de devoir donner son mail à Rohde & Schwarz.
[3] C.H. Liang, Y. Shi & T. Su, T., S parameter theory of lossless block network, Progress In Electromagnetics Research 104 pp.253-266 (2010).
[4] J.-M Friedt, Quelques éléments de traitement de signaux échantillonnés en temps discret avec GNU Radio, GNU/Linux Magazine No 221 (déc. 2018) à https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-221/Quelques-elements-de-traitement-de-signaux-echantillonnes-en-temps-discret-avec-GNU-Radio
[5] S. Mahon, « The 5G effect on RF filter technologies », IEEE Transactions on Semiconductor Manufacturing 30(4) pp.494-499 (2017) dont les résultats sont multipliés par les 1,5 milliard de téléphones vendus chaque année pour conclure à plus de 100 milliards de filtres radiofréquences à ondes élastiques fabriqués et commercialisés chaque année pour la seule téléphonie.
[6] J.-M Friedt, Wideband measurement strategies: from RADAR to passive wireless sensors ... and how passive wireless sensors were/are used by intelligence agencies, FOSDEM 2016.
[7] Nous évitons l’anglicisme « calibrage » si courant en nous appuyant sur VIM3 : Vocabulaire international de métrologie, BIPM (2012) à https://www.bipm.org/fr/publications/guides/vim.html
[8] J.-M. Friedt, W. Feng, Analyse et réalisation d’un RADAR à bruit par radio logicielle, GNU/Linux Magazine France : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-240/Analyse-et-realisation-d-un-RADAR-a-bruit-par-radio-logicielle
[9] J.-M Friedt, S. Ballandras, E3212 : capteurs acoustoélectriques radiofréquences - modes d’interrogation, Techniques de l’Ingénieur juillet 2020, disponibles à https://www.techniques-ingenieur.fr/base-documentaire/electronique-photonique-th13/materiaux-pour-l-electronique-et-dispositifs-associes-42271210/capteurs-acousto-electriques-radiofrequences-modes-d-interrogation-e3212/
[10] Un analyseur de réseau vectoriel assemblé de composants discrets (pour la modique somme de 3000 $) : https://www.minicircuits.com/pdfs/UVNA-63.pdf
Notes
1 Qui répond par conséquent à la fréquence f.
2 Cette distinction se justifiait à l’époque des instruments analogiques, mais les analyseurs scalaires ont désormais disparu au profit des instruments vectoriels, le logiciel se chargeant d’extraire l’information complexe et donc la phase par transformée de Hilbert si nécessaire [4].
3 Voir par exemple https://www.electrical4u.com/admittance/ pour se convaincre que la partie réelle de l’admittance est proportionnelle à une résistance divisée par un module au carré d’impédance qui ne saurait être négative.
4 Nous oublierons pour cet article la capacité parallèle formée par les électrodes qui induit l’anti-résonance dans le modèle de Butterworth-Van Dyke qui dépasse ces considérations.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture