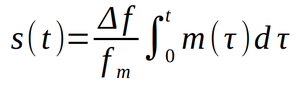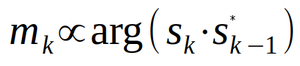Nous présentons la peinture de motifs définis dans une image matricielle (bitmap) sur le spectre radiofréquence en émettant un signal audiofréquence. Ce projet nous donne l’opportunité de redécouvrir l’effet capture de la modulation de fréquence (FM) dans lequel la station la plus puissante accroche le démodulateur, expliquant l’utilisation de la modulation d’amplitude (AM) en aéronautique où le pilote doit être informé de toute interférence possible sur ses communications. Les expériences exploitent un récepteur TNT comme source de radio logicielle traitée par GNURadio, pour un investissement matériel de moins de 20 euros.
Lors de la session 2018 du FOSDEM, deux orateurs de la session radio logicielle (SDR) ont proposé de peindre un message sur le spectre radiofréquence [1]. De cette façon, le spectre n’est plus un medium abstrait dont les composantes spectrales encodent une information transformée par le mode de modulation utilisé (amplitude, fréquence ou phase), mais chaque fréquence encode une information qui permet, lors de l’affichage du spectre, de restituer un motif dont l’assemblage, ligne par ligne, formera une image.
Cette opération pourrait se faire directement sur la porteuse, mais le problème au cœur des liaisons radiofréquences est l’absence de synchronisation entre l’oscillateur de référence de l’émetteur et celui du récepteur, par définition spatialement séparés. Nous verrons que dans le cas d’un oscillateur de stabilité médiocre, la dérive de fréquence peut être telle que le signal sort de la bande d’analyse. Cet effet est pallié par la modulation qui encode l’information selon un mécanisme qui permet d’identifier l’écart entre la porteuse de l’émetteur et l’oscillateur de référence du récepteur, qui peut alors être corrigé. Un de ces mécanismes est la modulation en fréquence (FM), dont nous allons explorer une propriété originale nommée « effet capture ».
1. La peinture sur spectre radiofréquence
En émettant un signal dont les composantes spectrales représentent l’intensité de chaque pixel, une démodulation suivie d’un affichage du spectre en fonction du temps dans une configuration de waterfall permet d’afficher le message transmis sous forme d’une image. Mathématiquement, chaque signal est simplement la transformée de Fourier inverse de la ligne de l’image transmise, puisque le waterfall se chargera d’effectuer la transformée de Fourier du signal reçu et donc de représenter chaque ligne telle que transmise. Ce concept est mis en pratique par le bloc GNURadio nommé gr-paint (https://github.com/drmpeg/gr-paint) qui se contente d’appliquer la règle que nous venons de décrire (https://github.com/drmpeg/gr-paint/blob/master/lib/paint_bc_impl.cc#L160-L166).
pixels = image_width * pixel_repeat;
volk_32f_cos_32f(angle_cos, angle_line, pixels);
volk_32f_sin_32f(angle_sin, angle_line, pixels);
volk_32f_x2_multiply_32f(angle_cos, angle_cos, magnitude_line, pixels);
volk_32f_x2_multiply_32f(angle_sin, angle_sin, magnitude_line, pixels);
volk_32f_x2_interleave_32fc(out, angle_cos, angle_sin, pixels);
out += pixels;
L’auteur de gr-paint nomme cette modulation OFDM (Orthogonal Frequency Division Multiplexing) puisque toutes les composantes spectrales du signal sont transmises simultanément. Notre intérêt pour cette forme d’expression artistique porte sur le fait que tel quel, gr-paint propose un flux de coefficients complexes I, Q qui alimentent un modulateur IQ tel que proposé dans les émetteurs de Ettus Research. En l’absence d’un tel équipement, pouvons-nous tout de même peindre sur le spectre ?
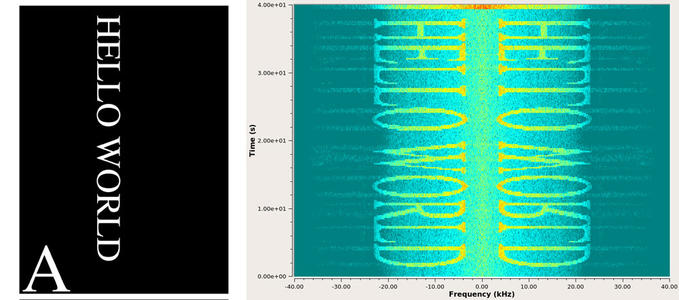
Dans un premier temps, nous pouvons analyser les paramètres qui vont déterminer les propriétés du signal transmis. La source de signaux présente une bande passante fs égale à la fréquence d’échantillonnage (la transformée de Fourier s’étendra de -fs/2 à +fs/2 pour le signal complexe émis). Cela signifie que chaque ligne de N pixels sera observée comme les composantes spectrales d’une transformée de Fourier sur N points, qui nécessite donc une durée N/fs pour être transmise. Ce temps de transmission va déterminer la vitesse à laquelle le waterfall défilera, i.e. à quelle vitesse les lignes successives vont s’afficher. À titre d’exemple, pour une carte son où fs = 192 kHz, chaque ligne d’une image de 1920 pixels de large met 10 ms pour être transmise, et une image complète de 2770 lignes mettra 27,7 secondes pour être transmise. En pratique, gr-paint exploite une variable ofdm_fft_size = 4096 qui détermine le nombre de fréquences en sortie de la transformée de Fourier en complétant la gauche et la droite de l’image par le nombre approprié de pixels à zero (zero-padding) : les 4096 échantillons mettent donc 4096/fs secondes pour être transmis, et dans notre application numérique chaque ligne met 21,3 ms pour être transmise, soit une durée totale de 1 minute pour les 2770 lignes, en parfait accord avec nos observations (voir figure 1, droite).
Fig. 1 : Gauche : image transmise par gr-paint. N’avoir conservé que la partie réelle des coefficients I, Q du modulateur nous oblige à introduire beaucoup de vide (moitié droite) dans l’image transmise afin d’éviter de perturber la démodulation à cause du repliement spectral induit par la perte de la moitié des informations. Le quart gauche (lettre « A ») ne sera pas visible compte tenu des paramètres de modulation et de démodulation. Droite : signal démodulé par détecteur FM et affichage du message sous forme de waterfall.
Nos études ont porté sur l’émission sur la carte son de la partie réelle du signal issu de la transformée de Fourier inverse de chaque ligne de l’image à transmettre, perdant ainsi la moitié des informations nécessaires. En effet, une entrée de modulation d’émetteur radiofréquence ne s’attaque qu’avec un unique signal qui ne peut donc être que la partie réelle ou imaginaire de la transformée de Fourier. L’alternative qu’est un modulateur I/Q – qui permettrait de sommer les composantes réelles et imaginaires sur deux porteuses en quadrature – n’équipe pas la majorité des émetteurs radiofréquences (figure 2). De ce fait, nous devons fournir une image dont au moins la moitié de l’information est nulle, afin d’éviter de mélanger les parties positives et négatives du spectre : ces deux moitiés du spectre sont initialement séparées par la partie imaginaire des coefficients complexes, mais se superposent quand on ne garde que la partie réelle du spectre puisque la transformée de Fourier d’un signal réel est une fonction paire (figure 3).
Fig. 2 : Émission par un synthétiseur radiofréquence modulé en FM par son entrée externe connectée à la carte son d’un PC. L’excursion FM est de quelques centaines de kHz/V. Nous verrons plus loin dans le texte comment utiliser des circuits plus accessibles au grand public.
Fig. 3 : Illustration de l’impact de ne conserver que la partie réelle de la transformée de Fourier de chaque ligne de l’image lors de la transmission : la parité du spectre dans ce cas est clairement visible sur l’image de droite, tandis que l’image de gauche dans laquelle toutes les informations ont été conservées au cours des transformations est restituée à l’identique de l’originale.
Le lecteur qui ne s’intéresse pas à la théorie sous-jacente, mais veut juste émettre un signal audiofréquence dont les composantes spectrales représentent l’intensité lumineuse de chaque pixel pourra tenter d’utiliser enscribe (http://www.coppercloudmusic.com/enscribe.html)dont nous ne nous sommes pas servis. Pour ce qui est des expériences proposées dans cet article, la chaîne de transmission et réception sous GNURadio est illustrée en figure 4.
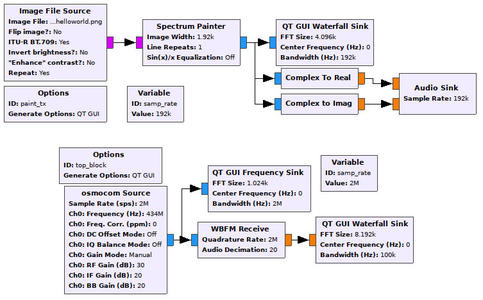
Fig. 4 : Chaîne d’émission (haut) et de réception (bas). Le signal est transmis en alimentant l’entrée de modulation externe FM d’un synthétiseur Rohde & Schwartz SMA100 par la sortie de la carte son (Fig. 2) : l’excursion de la modulation FM est de 300 à 500 kHz/V. Bas : réception par récepteur de télévision numérique terrestre utilisé comme source de radio logicielle.
En manipulant un peu les fréquences d’échantillonnage et l’amplitude du signal d’entrée, nous arrivons à un résultat relativement convaincant, tel que démontré sur la figure 1.
2. Mise en pratique
Peu de lecteurs auront accès à un synthétiseur de fréquence de compétition tel que le Rohde & Schwartz SMA100 avec son entrée de modulation en fréquence de la porteuse. Pouvons-nous démontrer le concept de peinture sur le spectre radiofréquence avec du matériel abordable financièrement ? Les deux solutions que nous proposons exploitent un modulateur FM intégré, ou un émetteur radiofréquence fourni en puce unique par Maxim IC, autour du MAX2606. La première solution démontre le concept de peinture sur spectre en alimentant l’entrée audio d’un Radiometrix TX2-433-160-5V, émetteur dans la bande ISM (Industrielle, Scientifique et Médicale) 434 MHz par la sortie d’une carte son générant les signaux issus de gr-paint (figure 5).
La seconde implémentation exploite le MAX2606, émetteur dans la bande 70-150 MHz, toujours en alimentant son entrée audiofréquence par la sortie de la carte son générant la sortie de gr-paint (figure 6).
Fig. 5 : Exploitation d’un émetteur FM commercial opérant dans la bande ISM autour de 434 MHz pour peindre sur spectre, avec réception du signal par clé DVB-T.
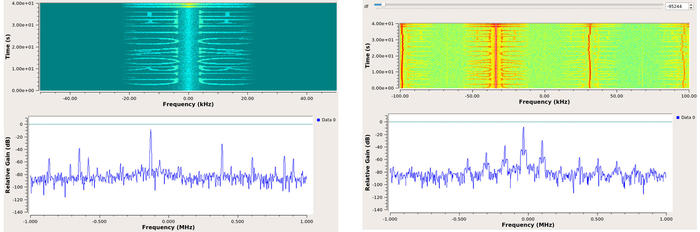
Fig. 6 : Gauche : waterfall en sortie du démodulateur WBFM de GNURadio, qui se charge de corriger tout écart entre la fréquence de porteuse de l’émetteur (Fig. 5) et de l’oscillateur local du récepteur. Droite : waterfall sur le signal modulé brut, avant traitement par le bloc WBFM de GNURadio, illustrant la redondance de l’information portée par les diverses raies de la modulation FM.
Ce composant a été sélectionné pour sa capacité à émettre dans la bande FM commerciale, et donc de valider son fonctionnement avec un récepteur FM sans nécessiter du matériel de laboratoire spécialisé (analyseur de spectre), ainsi que sa disponibilité comme échantillon gratuit auprès du fabricant [2] (figure 7). Le circuit est fortement inspiré de la note d’application associée [3], même si l’absence d’asservissement du VCO fournit une source de stabilité très médiocre. Nous avons ainsi l’opportunité d’illustrer l’intérêt de la modulation de la porteuse pour permettre la restitution, au niveau du récepteur, de l’information transmise, quel que soit l’écart entre l’oscillateur local de l’émetteur et du récepteur, dans la limite de la bande passante d’acquisition (figure 8).
Ces deux implémentations sont intéressantes, car au-delà de leur coût réduit qui permet à chacun de les reproduire, elles permettent de mettre en évidence la redondance d’informations introduite par la modulation, qui confère à la communication FM sa robustesse malgré les interférences destructives introduites par les chemins multiples (multipath) ou les perturbations locales du spectre (figure 6).
Fig. 7 : Émetteur radiofréquence autour du Maxim MAX2606 : une inductance définit la plage de fréquence d’émission dans la gamme 70-150 MHz, et la tension constante introduite par le potentiomètre au-dessus du signal audiofréquence découplée par un condensateur de 470 nF permet de finement sélectionner la fréquence de travail.
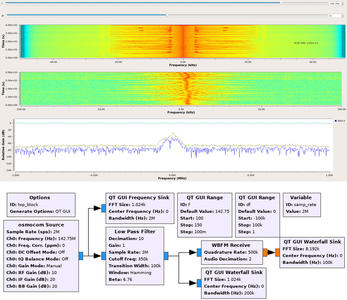
Fig. 8 : En l’absence de verrouillage de l’oscillateur sur une source stable telle qu’un oscillateur à quartz, la dérive énorme de l’oscillateur local à l’émetteur (figure 7) de piètre qualité est clairement visible sur le waterfall du milieu. Après démodulation par le bloc WBFM, le message est devenu clairement visible, de nouveau par correction de l’écart entre les fréquences de l’émetteur et du récepteur (haut). La séquence de traitement GNURadio permettant de générer la figure est fournie en bas.
3. L’effet « capture » de la modulation FM
Alors que nous observions l’impact d’un signal parasite à proximité du signal émis en modulation de fréquence, il est apparu un comportement binaire en l’absence de filtrage efficace pour rejeter ce parasite : soit le parasite présente une puissance plus faible que le signal encodant l’image dans le domaine spectral, et la réception du motif est excellente, soit le parasite présente une puissance supérieure au signal transmettant le motif, et l’image est inexistante dans la démodulation. Ce comportement binaire de la démodulation FM, sans état intermédiaire où la qualité de l’image démodulée est simplement dégradée, se nomme « l’effet capture » (capture effect) de la modulation en fréquence (figure 9). Il s’agit une fois de plus d’un effet très connu et abondamment étudié dans les années 1950 à 1980 [4], pour avoir été quelque peu oublié à notre époque obsédée par les liaisons numériques exploitant des modes de modulation excessivement performants.
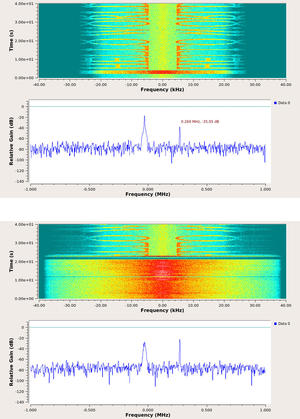
Fig. 9 : Haut : le signal transmis contenant l’image – proche de 0 Hz – est plus puissant que le parasite décalé de 300 kHz. Le message est parfaitement visible sur le waterfall. Bas : alors que le parasite est initialement faible, sa puissance est graduellement augmentée jusqu’à dépasser la puissance du signal portant l’information contenant l’image. Soudainement, l’image disparaît, le démodulateur ayant accroché le parasite dès que sa puissance a dépassé la puissance de l’information contenant l’image.
Lors de sa présentation plénière à l’édition 2016 du FOSDEM [5], Tom Rondeau concluait sur l’impact social des émetteurs pirates FM dans la région de New York, et en particulier sur la propriété d’un émetteur FM plus puissant qu’une autre émission sur la même fréquence de porteuse d’écraser cette dernière. La modulation FM a ainsi la propriété qu’un récepteur, qui reçoit deux signaux émis par deux émetteurs sur la même fréquence, amplifie le signal le plus puissant et élimine le signal le plus faible : il s’agit là du même effet de capture que nous venons de rencontrer. Nous nous proposons de profiter de GNURadio pour explorer cet effet sur des signaux synthétiques, d’en estimer les conséquences, et surtout d’en identifier la cause. Une implémentation « manuelle » de l’algorithme de démodulation sous GNU/Octave validera cette analyse.
Notons dès à présent, avant d’entrer dans l’étude détaillée du traitement du signal, que cette analyse répond enfin à une question qui nous taraudait depuis la découverte de l’utilisation de la modulation en amplitude (AM) par les bandes aéronautiques (108–137 MHz) alors que cette modulation, inefficace en terme de puissance et d’encombrement spectral, a été abandonnée par à peu près tous les autres utilisateurs du spectre radiofréquence. Pourquoi donc les communications entre aéroports et contrôleurs aériens avec les avions sont-elles modulées en amplitude et non en fréquence, plus robuste et fournissant une meilleure qualité audio ? La réponse tient en cet effet de capture de la FM : alors qu’un pilote peut entendre deux émissions simultanées sur la même porteuse et détecter la présence d’interférences, et donc tenter d’y pallier sur la même porteuse en demandant une retransmission, l’effet de capture FM atténue l’émetteur le plus faible pour rendre l’émission la plus puissante dominante. Le pilote n’est pas informé de l’interférence potentielle, et ne peut tenter de résoudre le conflit d’utilisation du spectre radiofréquence.
3.1 GNURadio
Le problème étant posé, tentons de le modéliser au moyen de GNURadio. Deux flux de traitement sont considérés : deux émetteurs transmettent deux signaux de fréquence différente, leur contribution relative est ajustable par leur gain avant sommation, et la sortie d’un démodulateur alimente un analyseur de spectre d’une part, et la carte son d’autre part. Ce flux de traitement est proposé dans le cas d’une modulation de fréquence, et dans le cas d’une modulation d’amplitude. On notera qu’il n’existe pas de bloc « modulation d’amplitude » : en effet, moduler en amplitude est obtenu par multiplication de la porteuse par le signal modulant (une sinusoïde de fréquence différente pour chaque émetteur, décalée d’un biais en tension pour ne jamais passer sous 0). Le modulateur FM est à peine plus subtil, en notant que le débit de données en sortie doit être multiple du débit des données audiofréquences en entrée.
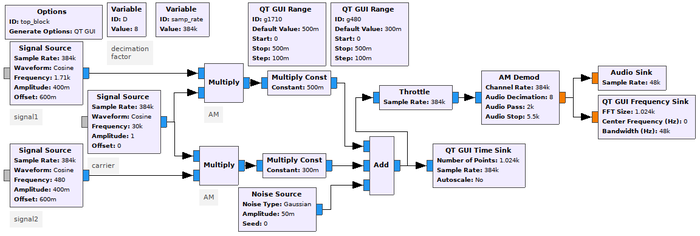
Les figures 10 et 11 proposent deux flux de traitement de signaux synthétiques dans GNURadio afin d’expérimenter avec l’effet capture de la FM, et son absence en AM. Dans les deux cas, les deux signaux d’information sont des signaux périodiques de fréquence sélectionnée arbitrairement à 480 et 1710 Hz.
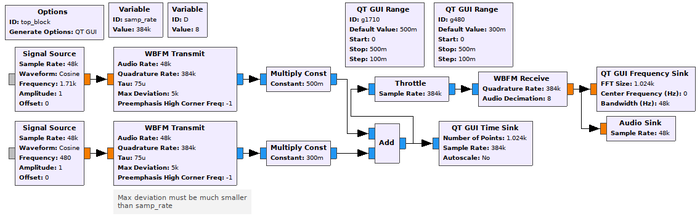
Fig. 10 : Flux de traitement GNURadio pour une modulation en FM de deux sources transmises simultanément puis démodulées par un unique bloc de traitement de signaux FM large bande (WBFM).
Fig. 11 : Même chaîne de traitement que Fig. 10, dans le cas d’une modulation en amplitude. Le modulateur en amplitude n’existe pas : une même porteuse est multipliée par l’information qui est des sinusoïdes décalées en tension pour être toujours positives.
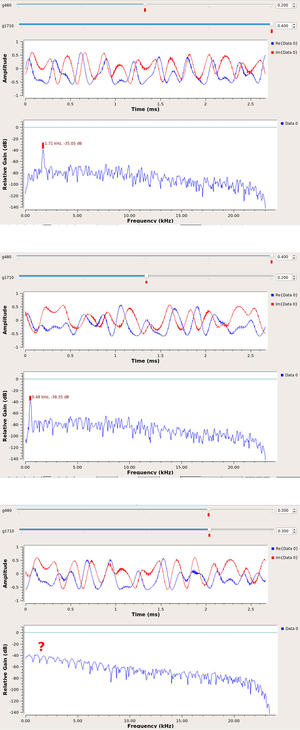
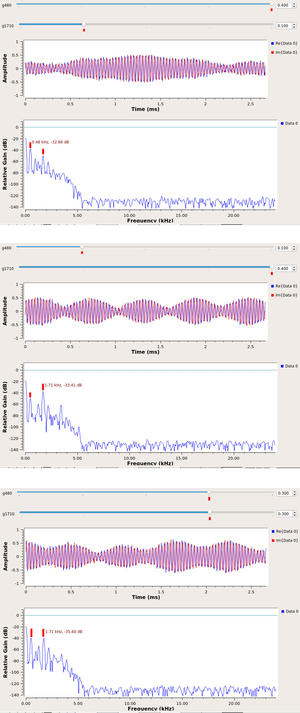
Le résultat de ces simulations, qui sera plus marquant si le lecteur reproduit ces flux de traitement et émet le signal résultant sur une carte son, est résumé en figure 12 pour la modulation FM et figure 13 pour la modulation AM. Pour aider à la lecture de ces graphiques quelque peu chargés, tous les affichages présentent en haut l’évolution du signal modulé dans le domaine temporel, et en bas le signal démodulé dans le domaine spectral. Le signal temporel n’est pas simple à analyser dans le cas de la modulation FM, mais la somme des deux composantes périodiques se voit parfaitement sur l’enveloppe de la modulation d’amplitude. Dans le domaine spectral, nous voyons bien qu’une seule composante spectrale apparaît, à 1710 ou 480 Hz, dans le cas de la modulation FM, mais jamais les deux en même temps (figure 12, graphique du bas, figures à gauche et milieu). Dans le cas d’un signal synthétique, fournir la même puissance aux deux composantes spectrales induit un échec de la démodulation (figure 12, en bas à droite, sur laquelle on note que les deux sélecteurs de puissance en haut de la figure sont au même niveau). Dans le cas de la modulation d’amplitude (figure 13), nous observons toujours les deux composantes spectrales à 1710 et 480 Hz, avec des niveaux relatifs représentatifs de la puissance injectée dans chaque composante (définie par le sélecteur en haut de chaque figure).
Alors que la démodulation AM est très simple à analyser – redresseur et filtre passe-bas mis en œuvre numériquement comme une valeur absolue et une moyenne glissante – la démodulation FM implémentée numériquement n’est pas une « simple » transposition de la boucle à verrouillage de phase analogique, mais exploite pleinement les propriétés des signaux complexes numériques. Afin de nous affranchir de la boîte noire « WBFM » de GNURadio qui ne nous apprend rien de la cause de l’effet de capture de ce mode de modulation, nous allons exposer la démodulation numérique de signaux modulés en fréquence et voir que la boucle à verrouillage de phase n’est pour rien dans l’effet capture, mais est bien une propriété intrinsèque du mode de modulation. Pour ce faire, nous allons analyser des signaux synthétiques modulés en fréquence sous GNU/Octave.
Fig. 12 : Résultat du flux de traitement pour une modulation FM. Seule la composante spectrale du signal le plus puissant (graphique bas des figures du haut et milieu) apparaît lors de la démodulation, tandis que le signal temporel (graphiqu) ne laisse pas distinguer aisément chaque composante. Si les deux signaux sont exactement de même puissance (figure du bas), le démodulateur est perdu et aucune composante spectrale représentative des signaux émis n’est visible. Les marques rouges sont ajoutées pour guider l’œil sur les points importants de chaque figure.
Fig. 13 : Résultat du flux de traitement pour une modulation AM. Les deux composantes spectrales des informations transmises apparaissent lors de la démodulation, quelle que soit leur puissance relative. Le signal temporel (haut) laisse distinguer les deux composantes du signal. Les marques rouges sont ajoutées pour guider l’œil sur les points importants de chaque figure.
3.2 GNU/Octave
Une première idée sur l’effet de capture se baserait sur l’approche classique analogique pour démoduler un signal FM qui utilise une boucle à verrouillage de phase (PLL) : un tel circuit ne peut s’accrocher que sur une fréquence, rejetant le second signal plus faible. Cette analyse ne résiste cependant pas à la lecture du code source, qui démontre que l’implémentation numérique d’un démodulateur FM n’exploite aucune rétroaction, mais se contente d’une simple opération de multiplications entre mesures successives des signaux complexes I, Q issus de la transposition en fréquence du signal incident à l’antenne.
Nous constatons en effet dans gr-analog/lib/quadrature_demod_cf_impl.cc qui est appelé par gr-analog/python/analog/wfm_rcv.py que l’implémentation du démodulateur FM dans GNURadio suit la formule proposée dans la présentation de D. Bederov sur https://archive.fosdem.org/2015/schedule/event/sdr_arithmetic/, à savoir :
volk_32fc_x2_multiply_conjugate_32fc(&tmp[0], &in[1], &in[0], noutput_items);
for(int i = 0; i < noutput_items; i++) {
out[i]=d_gain*gr::fast_atan2f(imag(tmp[i]), real(tmp[i]));
Ceci traduit le fait qu’un message m(t) de fréquence maximale fm, modulé en fréquence pour donner le signal s(t) avec une déviation de fréquence Δf, s’écrit :
Et que la démodulation de ce signal échantillonné en temps discret k.Ts, k ∈ ℕ et Ts la période d’échantillonnage, s’obtient par le calcul de :
Il n’y a dans cette formule aucun asservissement qui pourrait s’accrocher sur un signal plus puissant et rejeter une composante spectrale moins puissante. Au contraire, la démodulation AM se contente d’un redressement suivi d’un filtrage passe-bas, qui laisse passer toutes les composantes spectrales, quelle que soit leur contribution relative. Nous observons en figure 14a que la démodulation du signal FM se traduit bien par la réception du signal le plus puissant et le rejet du signal le plus faible. Cependant, le signal temporel est pollué de nombreux artefacts qui rendent la comparaison avec le signal initialement émis difficile. Nous proposons donc une analyse spectrale, plus facile à lire, dans la figure 14b. Dans ce cas, nous voyons immédiatement que seule la composante spectrale du signal le plus puissant est présente dans le spectre, complétée d’un certain nombre d’artefacts à haute fréquence qui s’atténuent d’autant plus que le second signal est faible.
kf=.0628; % Modulation index
f=100; % Carrier frequency
fs=1000; % Sample frequency
N=1000; % Number of samples
R1=.9 % ratio of one channel v.s other
R2=.6 % ratio of one channel v.s other
t=[0:1/fs:(N/fs-1/fs)];
msg1=sin(2*pi*20*t); % first signal (f=20)
msg2=sin(2*pi*5*t); % second signal (f=5)
subplot(311);plot(msg1);hold on;plot(msg2)
S1=exp(j*2*pi*(f*t+kf*cumsum(msg1))); % FM modulation
S2=exp(j*2*pi*(f*t+kf*cumsum(msg2))); % FM modulation
subplot(312);plot(real(S1+.8*S2)); % sum of FM modulated signals
S=S1+R1*S2; demod11=angle(S(2:end).*conj(S(1:end-1))); % FM demod
S=S1+R2*S2; demod12=angle(S(2:end).*conj(S(1:end-1))); % FM demod
S=R1*S1+S2; demod21=angle(S(2:end).*conj(S(1:end-1))); % FM demod
S=R2*S1+S2; demod22=angle(S(2:end).*conj(S(1:end-1))); % FM dmeod
dref1=angle(S1(2:end).*conj(S1(1:end-1))); % FM demod of signal 1 alone
dref2=angle(S2(2:end).*conj(S2(1:end-1))); % FM demod of signal 2 alone
subplot(313)
plot(demod12,'b');hold on;plot(demod22,'r') % compare outputs in the time domain
plot(dref1,'c');hold on;plot(dref2,'m') % ... with the raw signals
figure(2)
subplot(311) % same analysis, in the frequency domain ... easier to read
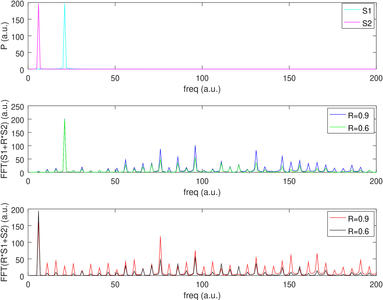
plot(abs(fft(dref1-mean(dref1))),'c');hold on;plot(abs(fft(dref2-mean(dref2))),'m')
subplot(312);plot(abs(fft(demod11-mean(demod11))),'b');
hold on ;plot(abs(fft(demod12-mean(demod12))),'g');
subplot(313);plot(abs(fft(demod21-mean(demod21))),'r')
hold on ;plot(abs(fft(demod22-mean(demod22))),'k')
Cette analyse est en excellent accord avec l’étude proposée dans [6] qui présente bien les sauts abrupts de fréquence instantanée lors de la démodulation, et va dans le sens de [7] qui argumente que l’effet capture est amplifié par la réduction de bande passante induite par le filtrage passe-bas du signal démodulé.
Intuitivement [8], argumente que la différence entre le comportement des détecteurs AM et FM vient du fait que le second se base sur une mesure de fréquence, donc de date de passage par 0 d’un signal, contrairement à AM qui se base sur une mesure d’amplitude. Un signal périodique pollué par un signal présentant une puissance faible passe toujours « à peu près » au même instant à 0, car le déphasage introduit par le second signal n’affecte que peu la date d’intersection avec l’axe des abscisses, le passage à 0 présentant la plus grande pente du potentiel avec le temps. En terme de diagramme dans le plan complexe, [9] propose une analyse dans laquelle la somme vectorielle des deux composantes complexes est effectuée, et présente bien que l’angle que fait le vecteur résultant (dont le passage par 0 définit la fréquence) ne bouge que peu avec la composante la plus faible tandis que la composante la plus puissante domine son comportement en phase.
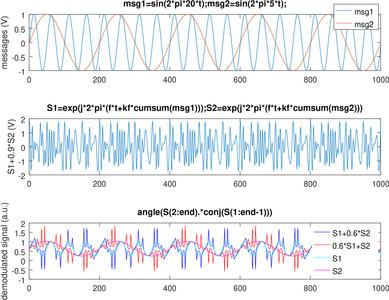
Fig. 14a : Gauche : évolution temporelle des signaux de référence (haut), des signaux modulés en fréquence dans le cas d’une contribution presque identique des deux messages (milieu), et résultat de la démodulation pour diverses pondérations des deux signaux dans le signal transmis, y compris des signaux purs.
Fig. 14b : une analyse spectrale facilite l’interprétation : nous voyons bien que si un message domine l’autre (bas, milieu), seule sa composante spectrale apparaît sur le spectre comme s’il était seul (haut), et la seconde composante a complètement disparu. Les composantes parasites (milieu, bas, moitié droite du spectre) sont les mêmes dans les deux cas.
Conclusion
En commençant par peindre sur le spectre radiofréquence des messages observables sous forme d’évolution temporelle du spectre (waterfall), nous avons rencontré le problème de l’effet capture de la modulation de fréquence si un interférant plus puissant que le signal analysé se trouve dans la bande de démodulation. Une modélisation de cet effet nous permet d’identifier la cause de la capture non au mode de démodulation du signal FM – classiquement basé sur une boucle à verrouillage de phase dans son implémentation analogique, mais qui s’en affranchit dans son implémentation numérique – mais sur la nature intrinsèque de la modulation qui encode l’information. En effet, l’encodage FM se base sur une notion de fréquence et donc de passage par 0 du signal émis, plutôt que sur une amplitude qui est, elle, immune à cet effet de capture. La nécessité de robustesse des communications aériennes, et en particulier la capacité à détecter un signal interférant au lieu de le cacher sous le signal le plus puissant, motive l’utilisation du second mode de modulation, malgré son inefficacité en terme d’exploitation de l’étage d’amplification radiofréquence de l’émetteur.
Actualité
La première journée GNURadio France est organisée les 2 et 3 juillet à l’INSA de Lyon. Elle convie les utilisateurs et développeurs autour de GNURadio à se réunir pour échanger leurs expériences et résultats, puis à participer à des cours – tutorials allant d’une introduction à GNURadio et son interface graphique GNURadio-Companion, à la réalisation de blocs et la compréhension de l’ordonnanceur cadençant le flux de données. Le site web de la conférence, incluant l’appel à contributions et les sujets abordés, se trouve sur https://gnuradio-fr-18.sciencesconf.org/.
Remerciements
Toutes les références bibliographiques qui ne sont pas librement disponibles sur internet, et en particulier les publications de IEEE, sont obtenues auprès de Library Genesis, gen.lib.rus.ec. L’analyse des modes de modulation exploités pour les communications aériennes a été motivée par le cours de radio logicielle proposé à l’IUT de Ville-d’Avray sur invitation de l’auteur par D. Lautru et F. Daout.
Références & notes
[1] GETZ R., « Stupid Pluto Tricks – Real world things you can do with a PlutoSDR », FOSDEM 2018, illustré en figure 2 de « Faut s’démener au FOSDEM ! », GNU/Linux Magazine n°213, mars 2018, et la session finale « BYOR: Bring-your-own-radio hacking session »
[2] Pour être exact, les déclinaisons de ce composant hors bande FM sont disponibles en échantillons, sinon le coût est de 1,71 euros chez Farnell
[3] AU-YEUNG T. et TANG W., « VCO Enables a Hands-Free Car Kit for Cell Phones », note d’application Maxim 5123, 18 mars 2013 : www.maximintegrated.com/en/app-notes/index.mvp/id/5123
[4] BAGHDADY E. J., « Theory of Stronger-Signal Capture in FM Reception », Proc. IRE 46 (4), 1958, p. 728 à 738
[5] RONDEAU T., « GNU Radio for Exploring Signals – Talk Hard: A technical, historical, political, and cultural look at FM », FOSDEM 2016 : archive.fosdem.org/2016/schedule/event/gnu_radio/
[6] PARK S. S., « On capture effect of FM demodulators », Master thesis, 1989 : https://calhoun.nps.edu/handle/10945/26120
[7] BRUYLAND I., « The Influence of Finite Bandwidth on the Capture Effect in FM Demodulators », IEEE Trans. on Communication COM-26 (6), 1978, p. 776 à 784
[8] https://www.radiomuseum.org/forum/fm_capture_ratio.html#post245932
[9] LEENTVAAR K. et FLINT J. H., « The capture effect in FM receivers », IEEE Trans. on Communications COM-24 (5), 1976, p. 531 à 539



 Ajouter à une liste de lecture
Ajouter à une liste de lecture