Affichage et traitement de données au moyen de logiciels libres

Cet article est rédigé à la suite d’un constat aussi surprenant qu'incompréhensible : nombre d'enseignants ou d'ingénieurs s'obstinent à utiliser un tableur pour tracer des courbes et traiter des fichiers de données. Je désire démontrer que l'utilisation d'un outil tel qu'Excel – ou ses clones gratuits tels que OpenOffice et al. – est inappropriée pour des traitements répétitifs sur des fichiers de données ou l'affichage graphique de leur contenu. Le choix des outils que nous proposons se fait selon trois critères principaux : le dynamisme du développement et la pérennité du logiciel, sa disponibilité sous GNU/Linux et autres plateformes – notamment les systèmes d'exploitation que nous haïssons tous sans les nommer, et le consensus des collègues que côtoient l'auteur sur l'efficacité des logiciels. Le second point semble important, car sans une version disponible sous Windows (je l'ai dit) des logiciels utilisés, nous n'avons aucune chance d'espérer arriver à un outil commun avec les actuels utilisateurs d'Excel, pour qui le passage à un système d'exploitation libre est inenvisageable (par ignorance ou par contraintes associées aux environnements informatiques d'entreprise). C'est suivant ce critère que nous n'avons pas retenu le par ailleurs excellent plotmtv. Ce document n'a pas la prétention d'être une présentation exhaustive des outils de traitement de données proposés – ni même une introduction, puisque de nombreux documents en ce sens sont disponibles sur le web – mais plutôt une série d'illustrations de traitements effectués quotidiennement par l'auteur sur des séries de données. L'objectif est de présenter quelques cas concrets dans lesquels les outils que nous présenterons sont efficaces, et d'ainsi convaincre le lecteur d'abandonner des outils inappropriés pour ces tâches.

1. gnuplot

La présentation commence avec l'outil présentant le moins de fonctionnalités, mais le plus souple et le plus léger pour exploiter rapidement un fichier de points : affichage graphique des données, opérations simples, sauvegarde dans des fichiers insérables dans des documents texte. Gnuplot [1] – et sa version sous Windows WGnuplot – sont excessivement simples à prendre en main, mais livrent encore des secrets insoupçonnés après des années d'utilisation.

1.1 Bases

Gnuplot sait traiter des fichiers de points séparés par des espaces ou des tabulations, quel que soit le nombre de colonnes et de lignes tant que toutes les colonnes contiennent le même nombre de points. La rapidité de Gnuplot devient particulièrement visible lorsque des fichiers de plusieurs centaines de milliers de points sont exploités. Pour un fichier contenant une unique colonne, l'instruction plot "fichier" en tracera le contenu. Lorsque plusieurs colonnes sont présentes, la ième colonne est sélectionnée par plot "fichier" using i. La superposition de plusieurs graphiques sur la même figure s'obtient en remplaçant plot par replot. Une colonne est interprétée comme une variable dans une opération en la précédent d'un $ : plot "fichier" using (sqrt($1)) trace la racine carrée de la première colonne ou, plus utile, pl "fichier" u (20*log10($1)) pour tracer (en version abrégée des commandes, u signifie par exemple using) le contenu de la première colonne en décibels. Un complexe se note {0,1} donc deux colonnes peuvent être interprétées comme la partie réelle et imaginaire d'un complexe par using ($1+{0,1}*$2) pour en extraire la phase (fonction arg()) ou le module (fonction abs()). Ces fonctions sont particulièrement utiles lors du traitement de données issues d'un instrument ou d'une simulation qui fournit des résultats complexes sous forme de partie réelle et imaginaire (voltmètre vectoriel, pour ensuite en extraire phase et magnitude par exemple, et ainsi tracer un diagramme de Bode). Les axes et titres se définissent par set xlabel, set ylabel et set title respectivement. Gnuplot accepte, par la fonction load 'fichier.pl', d'exécuter une série de commandes depuis un fichier contenant un script.

1.2 Analyse de données

Soit un fichier de points expérimentaux, stockés dans un fichier nommé mes_points, de la forme

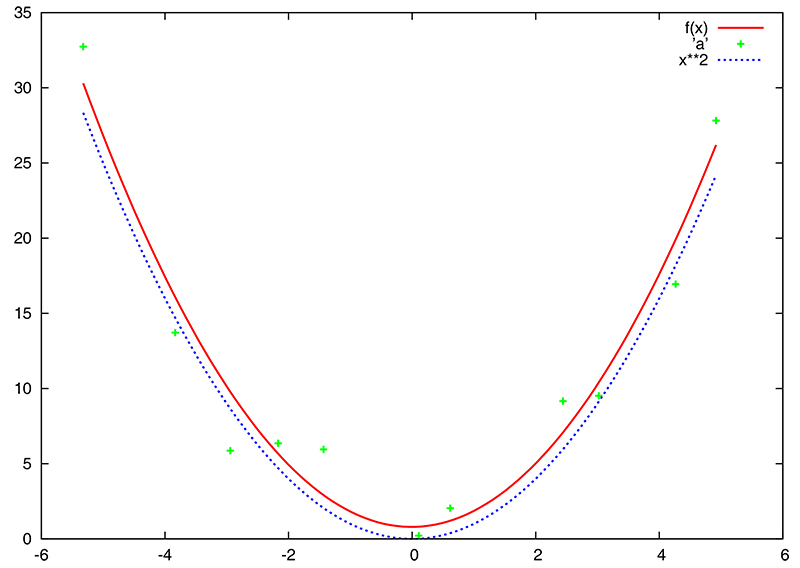
(notre fichier de points expérimentaux a en fait été généré par la procédure présentée plus loin en section 2.1, code 1). Après s'être fait une idée du comportement général des points par plot 'mes_points', nous désirons effectuer des calculs un peu plus complexes tel qu'identifier les coefficients du polynôme décrivant au mieux les points. En faisant l'hypothèse d'un comportement parabolique (définition de la fonction f(x)),

renvoie

Ces coefficients sont corrects compte tenu de notre connaissance sur le comportement de ces points, puisqu'ils ont été synthétisés en suivant une parabole bruitée y=x2. Nous constatons sur la figure 1 que les points initiaux sont fortement bruités, et observons l'écart de la loi recherchée (bleu) à la loi observée (rouge). Nous utilisons dans cet exemple la syntaxe abrégée de Gnuplot en remplaçant with point par w p ou with line par w l. De la même façon, pl est l'abréviation de plot.

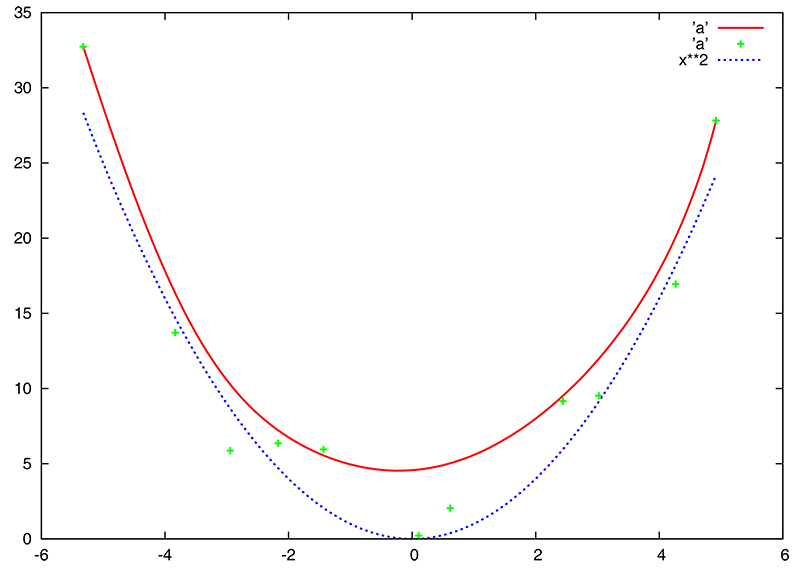
Les éventuelles barres d'erreur peuvent être incluses dans le fichier de données comme colonnes additionnelles (erreur en abscisse et en ordonnée). L'option with errorbars de plot ajoute alors les intervalles de confiance aux points tracés. Une activité courante de traitement de données bruitées est de lisser les données par une moyenne glissante. Gnuplot ne permet pas de réaliser une telle opération, et en l'absence d'un modèle approprié tel que décrit plus haut, une méthode purement graphique pour lisser des points est fournie par l'option smooth de plot. Ainsi, par exemple

La figure 2 présente une comparaison du modèle qui suivent les points bruités (verts) : la parabole bleue. Cet exemple montre clairement que malgré l'attrait visuel du lissage, la courbe ainsi fournie est grossièrement erronée et que l'a priori du modèle polynomial sous-jacent améliore considérablement la qualité de l'ajustement.

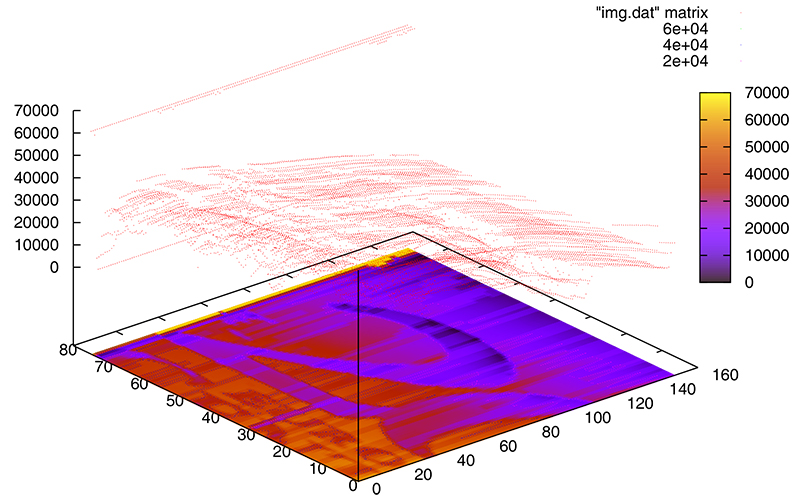
Afin de tracer des courbes en 3 dimensions, deux classes de données peuvent être générées : des fichiers contenant des triplets (X,Y,Z) qui représentent les 3 coordonnées de chaque point de la courbe ou une matrice contenant l'ensemble des altitudes d'une surface périodiquement échantillonnée dans les deux directions spatiales, comme le serait une image bitmap. Prenons comme exemple le second cas, dont les données ont été générées par un profilomètre dont la sonde s'est déplacée sur une pièce de 20 centimes [2]. Nous désirons tracer la topographie de la pièce ainsi que les lignes d'isovaleurs :

trace le contenu du fichier img.dat, qui se présente sous la forme

interprétée comme une matrice (c’est-à-dire un ensemble d'altitudes) sous forme de surface, avec projection des contours sous la surface (set contour base) et affichage en dégradé de couleurs des contours, mais pas de la surface en 3D (set pm3d at b), tel qu'illustré sur la figure 3.

La multitude d'options pour traiter les fichiers de points sous Gnuplot est illustrée de façon exhaustive dans la FAQ à http://t16web.lanl.gov/Kawano/gnuplot/index-e.html.

1.3 Génération de fichiers graphiques

Une force de Gnuplot est le très grand nombre de formats supportés : bitmap pour les utilisateurs de traitements de texte wysiwig (Word et ses clones gratuits) ou vectoriels pour les vrais traitements de texte (LATEX). Le choix du format de sortie se fait par set term suivi du nom du format de sortie et de ses options éventuelles (png pour du bimap, postscript pour du vectoriel, fig pour un fichier exploitable par xfig). Le choix du format étant effectué, le fichier de sortie est défini par set output "fichier.sortie" et le graphique y est généré par replot. Gnuplot est un outil souple et rapide capable d'exécuter des scripts pour traiter de façon automatique des fichiers de points. Cependant, il montre ses limites quand un traitement complexe devient nécessaire : calcul de transformée de Fourier, analyse statistique, gestion de fichiers ne comportant pas simplement des colonnes de points... Pour ces tâches, nous proposons un outil à peine plus complexe, mais considérablement plus puissant : Octave.

1.4 Affichage de données en cours d'acquisition

Lorsque des données sont acquises depuis un instrument, il est inutile de perdre en portabilité du logiciel d'acquisition en l'alourdissant avec une gestion de l'affichage graphique en temps réel qui ne sera de toute façon jamais aussi performant que Gnuplot. Il nous semble plus efficace de stocker les données au format ASCII dans un fichier, et de demander à Gnuplot de périodiquement rafraîchir le graphique obtenu en traçant le contenu du fichier. Ce résultat s'obtient au moyen des commandes replot (relire le fichier de points et rafraîchir le graphique) et reread (recharger le script). Ces deux opérations sont temporisées par une instruction pause : le script dynamique.gnu contient donc

et sous Gnuplot, après avoir lancé l'acquisition de données dont le contenu est placé dans le fichier donnees.dat, nous appelons

Ce script semble mal se terminer sur certaines versions de Gnuplot sous Windows, mais fonctionne parfaitement sous GNU/Linux.

1.5 Annotations diverses

Une présentation complète des options de Gnuplot a déjà été proposée dans ces pages [3]. Parmi les plus utiles, la possibilité d'annoter une courbe au moyen de flèches et de texte associé :

Une autre solution plus souple, mais nécessitant un outil additionnel, est la sauvegarde du graphique brut au format Xfig1 (set term fig color puis sauver dans le fichier figure.fig par set output "figure.fig" et replot). Le fichier vectoriel résultant peut alors être modifié au moyen de xfig pour ensuite être exporté en PDF ou EPS pour inclusion dans LATEX par exemple.

2. Octave

Octave est un projet [4] visant à fournir un environnement de travail similaire au logiciel commercial Matlab (MATrix LABoratory) sous licence GNU. Son interface graphique – par défaut basée sur Gnuplot – est encore un point faible par rapport aux excellentes sorties graphiques que fournit Matlab. L'auteur admettra sans honte effectuer tous ses traitements de données sous GNU/Octave pour finalement exécuter les scripts de traitement sous Matlab lors de la sortie finale des graphiques destinés à être insérés dans des présentations ou des articles (les traits des sorties en couleur de Gnuplot sont par défaut illisibles sur fond blanc et trop fins pour des présentations sur vidéo-projecteur). À quelques exceptions près, les scripts Octave sont directement compatibles avec Matlab (et réciproquement). Par ailleurs, la majorité des toolbox (fonctions spécifiques à un domaine particulier, telles que les réseaux de neurones, l'automatique ou le traitement d'images) – commerciales sous Matlab – ont été réimplémentées avec plus ou moins de succès sous Octave. Une richesse d'Octave, de par sa compatibilité avec Matlab, est la vaste quantité de scripts disponibles sur le web permettant de résoudre, ou tout au moins de trouver l'inspiration, pour de nombreux problèmes. Réciproquement, les utilisateurs de Matlab trouvent dans les implémentations libres des toolbox pour Octave une source de scripts qui ne sont sinon accessibles que commercialement.

2.1 Bases

La programmation sous Octave nécessite de revoir quelque peu ses habitudes de programmation séquentielle pour essayer d'exprimer autant que possible les calculs sous forme matricielle. La majorité des boucles implémentées en langages de bas niveau (assembleur, C, Fortran...) expriment en fait des opérations matricielles qui s'exécutent très efficacement sous Octave. Ce point de vue de programmeur est évidemment erroné et se focalise sur l'implémentation du code, alors que tout problème linéaire s'exprime sous forme matricielle et s'implémente donc naturellement sous Octave. Un vecteur est défini entre crochets : le vecteur v de 3 éléments se définit par v=[1 2 6]. Un matrice est définie comme une série de vecteurs, le retour à la ligne étant indiqué par ; : m=[1 2 4;8 16 32;64 128 256]. Outre les opérations matricielles classiques (somme, produit, inversion), les opérations élément par élément se font en précédent l'opération d'un point. La transposée s'obtient par l'apostrophe. Ainsi,

et

La dernière expression est probablement la plus couramment utilisée. Au-delà des opérations arithmétiques, des opérateurs de recherche de maximum (max(v)), minimum (min(v)), taille du vecteur (length(v) et size(a)) nous aideront dans nos scripts à gérer les cas de vecteurs de tailles variables. La lecture d'un fichier de point s'effectue par load('fichier'); avec fichier un fichier ASCII contenant toujours le même nombre d'éléments sur chaque ligne. Octave est beaucoup plus pointilleux que Gnuplot sur le format des fichiers : seuls l'espace et la tabulation sont acceptés comme séparateur. Charger un fichier load('f.txt') crée automatiquement la variable du nom de fichier sans son extension : ici f. La commande whos donne la liste des variables en mémoire et leur structure. Le symbole % indique que le reste de la ligne est un commentaire. Octave supporte tous les opérateurs habituels des langages évolués : boucle for ... end et while, condition if ... end et switch ... case. Dans beaucoup de cas, il est cependant peu judicieux d'utiliser ces opérations dont l'action a souvent un équivalent matriciel beaucoup plus performant. Une aide sur toute fonction – sa syntaxe et ses arguments généralement – est disponible par help fonction. Octave travaille avec des complexes et connaît la constante i tel que i2=−1 (éviter donc d'utiliser i comme variable de boucle pour ne pas avoir de mauvaise surprise), et les opérations habituelles sur les complexes (phase angle(), module abs(), opérations arithmétiques etc.). Je ne propose dans les exemples qui suivent que des applications concrètes, choix évidemment biaisé par des activités de traitement du signal triviales d'un ingénieur chargé d'analyser un grand nombre de signaux expérimentaux.

2.2 Moyenne glissante

Le premier exemple illustrant la puissance du calcul matriciel est la moyenne glissante appliquée sous forme de convolution. En langage de bas niveau, une moyenne glissante s'implémente par un tableau rotatif dont on soustrait le dernier élément obsolète et ajoute le nouvel élément de la fenêtre glissante. L'opération de convolution visant à effectuer une moyenne glissante de n points sur les données y s'exprime en termes matriciels sous la forme :

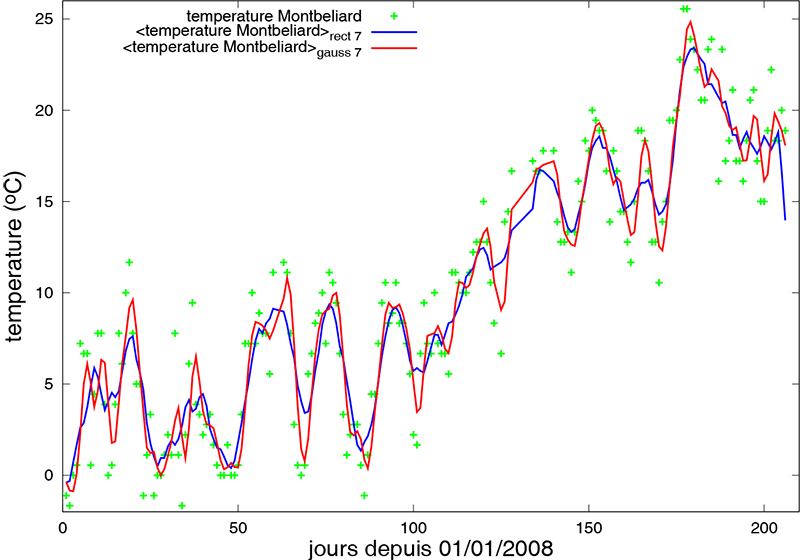
Cet exemple est le cas le plus simple, avec une fenêtre glissante rectangulaire. Il est habituellement plus intéressant d'utiliser une fenêtre « moins brutale » à ses frontières telle que la gaussienne2, en pensant toujours à conserver l'énergie : s=3;x=[-10:10];y=1/sqrt(2*pi*s*s)*exp(-x.^2/2/s^2); (on vérifie que sum(y) est égal à 1).

Un exemple de courbe brute et lissée par les deux méthodes est fourni sur la figure 4. Pour des données acquises sur le site [5] et traitées pour être compatibles avec Octave (retirer les virgules et les symboles moins grâce à sed) :

2.3 Modélisation polynomiale de données

Il est courant de vouloir ajuster des données expérimentales selon une loi polynomiale (qui, à défaut d'une justification théorique, peut toujours être invoquée comme un début de développement de Taylor de la « vraie » loi). Soit une série de données (x,y) (Tab. 1) associant une mesure y à une condition expérimentale x (par exemple la température du système au moment de la mesure) : la solution optimisant l'erreur quadratique (moindres carrés) par un polynôme de degré n s'obtient par

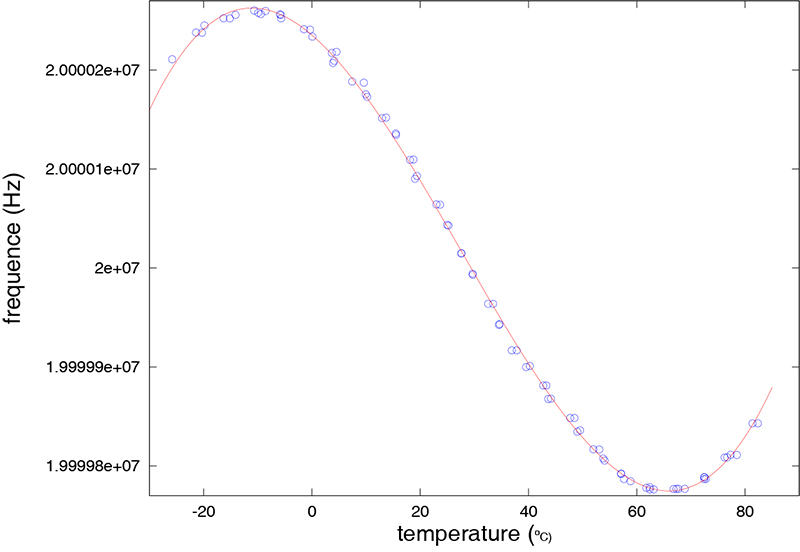
Dans cet exemple, a contient les coefficients du polynôme ajustant au mieux (au sens des moindres carrés) les données y associées aux conditions x, et yy le résultat du fit polynomial pour les mêmes abscisses que les points expérimentaux. Le résultat est le même que celui vu auparavant avec Gnuplot (Fig. 1). Un exemple concret de mesure de variation de fréquence de résonance d'un résonateur en quartz avec la température est proposé sur la figure 5. Le fichier de mesures est de la forme

Nous observons visuellement sur le tracé des données expérimentales (Fig. 5) qu'un fit parabolique des données ne sera pas approprié (la fonction n'est clairement pas paire). Donc, nous tentons un ajustement par un polynôme d'ordre 3 :

qui renvoie dans la variable p les coefficients du polynôme p = 2.1379e-03 -1.7592e-01 -4.6795e+00 2.0000e+07, du coefficient d'ordre le plus élevé vers le terme constant.

L'ajustement polynomial semble visuellement acceptable (Fig. 5).

2.4 Cas de la modélisation par une fonction quelconque

Dans le cas général, la fonction fminsearch() est fournie dans la toolbox octave-optim sous Debian. L'objectif de cet outil est l'identification de paramètres : nous allons ici prendre l'exemple de l'identification de paramètres d'un circuit RLC (résistance-inductance-condensateur séries) supposés inconnus. fminsearch accepte en premier argument le nom de la fonction simulant le comportement, en fonction des paramètres à ajuster, de la loi recherchée. Le second et troisième argument sont des options d'exécution de l'algorithme de recherche de la solution. Les arguments suivant sont des valeurs additionnelles fournies comme paramètres à la fonction modélisant le comportement du système. Dans notre cas, il s'agit de l'impédance d'un circuit RLC série, dans un fichier nommé rlc.m :

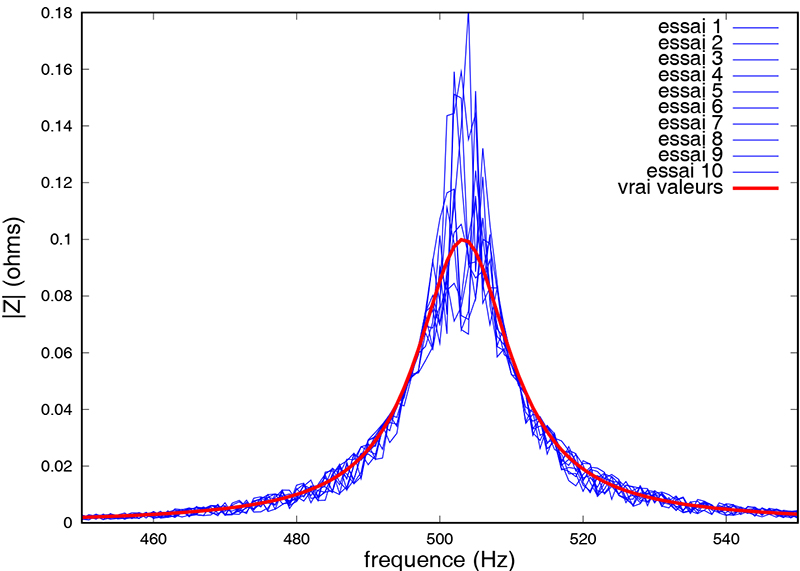
Cette fonction fournit une erreur entre des données expérimentales y acquises aux fréquences f, et la loi issue des paramètres proposés dans le vecteur p=[R L C]. Supposons que nous ayons une série expérimentale z_exp de points correspondant à la mesure sur un voltmètre vectoriel de l'impédance (complexe) d'un circuit RLC série (R=10 Ω, L=100 mH et C=1 μF) dans la gamme de fréquences f :

Nous allons alors proposer des paramètres clairement erronés (R=13 Ω, L=120 mH et C=5 μF) et demander à fminsearch() d'identifier les paramètres optimaux sur des données bruitées :

Le résultat de ce calcul

montre que, même sur des données très bruitées (Fig. 6), les paramètres sont correctement identifiés dans les 10 cas testés (pour rappel, l'objectif était de trouver 10, 0,1 et 10−6), et ce, bien que l'estimation initiale des paramètres ait été erronée de plus de 20%. Cependant, il faut toujours prendre soin de valider les solutions fournies par fminsearch, car la convergence de l'algorithme est fortement dépendante du choix des conditions initiales.

2.5 Exemple de calcul concret : interférométrie radiofréquence

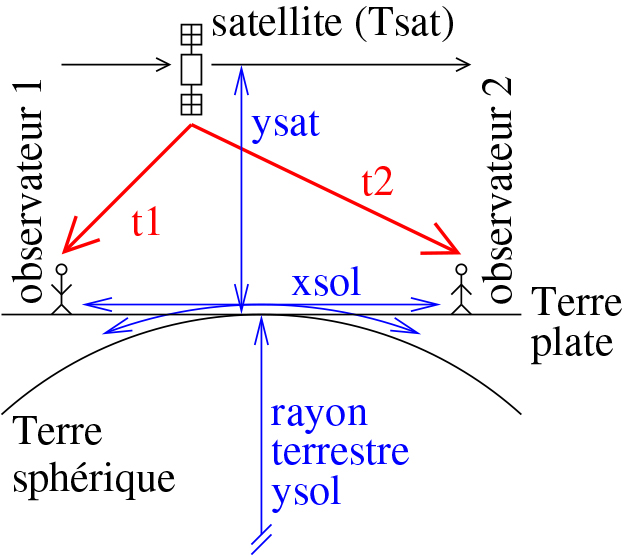
Nous voulons connaître le décalage entre les temps d'arrivées de signaux radiofréquences issus de satellites en orbite polaire autour de la Terre [6]. Nous désirons savoir si, par une acquisition échantillonnée à 11025 Hz ou 40 kHz, il nous sera possible au moyen de deux stations au sol séparées de quelques centaines de kilomètres, d'identifier l'altitude des satellites par cette mesure de temps de vol des signaux (Fig. 8). La méthode « classique » consisterait à itérer sur les paramètres de la simulation (boucle for sur les altitudes potentielles des satellites par exemple), puis d'itérer sur les dates de simulation (incrément du temps par une boucle for pour calculer la position du satellite à chaque instant). Cette méthode est très inefficace sous Octave et résulte dans des temps de calcul excessivement longs. Nous devons nous rappeler que tant que nous n'effectuons que des opérations linéaires, une boucle for se traduit par une opération matricielle, dont l'implémentation sous Octave est bien plus efficace que l'interprétation de boucles for imbriquées.

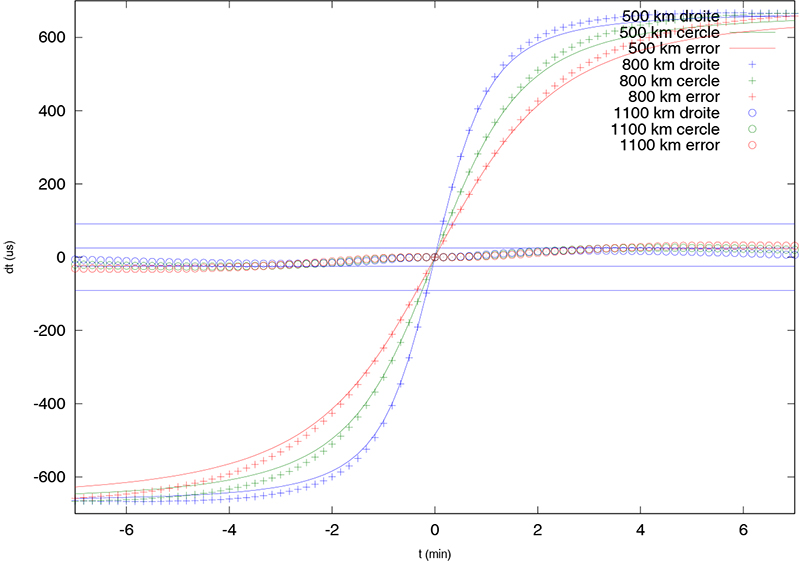
Nous proposons ainsi par exemple le code suivant pour calculer la différence de temps de vol des signaux radiofréquences pour des satellites volant à 800±300 km au-dessus de la surface de la Terre (cas des satellites en orbite basse polaire) entre deux stations au sol séparées de xsol (Fig. 7).

Après avoir défini les constantes de la simulation (rayon terrestre ysol, temps de la simulation sous forme de vecteur t), nous allons éviter d'itérer sur les altitudes du satellite ysat en remplaçant la tentation d'une boucle for par un vecteur de paramètres. Le reste du calcul se déroule naturellement comme opérations matricielles, la seule subtilité étant dans la neuvième ligne : l'addition de x (une matrice d'autant de lignes que d'étapes dans le temps, et de colonnes que de paramètres d'altitudes) avec y nécessite que cette structure de données se présente sous la forme d'une matrice du même nombre d'éléments que x. Le passage du vecteur y=ysat à une matrice de la même taille que x s'obtient par multiplication par un vecteur unitaire de la même longueur : y=ysat*ones(1,length(x));. L'instruction ones() est une fonction interne à Octave dont la description s'obtient par help ones. Le résultat de ce calcul est une matrice contenant autant de colonnes que de paramètres (ici 3) et autant de lignes que de pas de temps (ici 85). Le résultat de cette simulation est illustrée sur la figure 9. Ce graphique démontre que l'approximation d'une Terre plate (traits pleins) est valable la majorité du temps par rapport au calcul complet d'une Terre sphérique (croix). Les trois courbes proches de l'ordonnée 0 présentent l'erreur entre les deux simulations, et les deux paires de lignes horizontales présentent le pas de mesure pour une carte son échantillonnant à 11025 Hz (pas de 90 μs). Les deux lignes les plus proches de l'ordonnée nulle présentent le pas de quantification pour un échantillonnage à 40 kHz (25 μs). Dans tous les cas, la différence de temps de vol des signaux issus du satellite reçus par deux stations séparées de 200 km est facilement mesurable par carte son.

Le résultat d'un calcul s'exporte en format ASCII (facilement accessible par la suite par n'importe quel script shell ou autre logiciel traitant des fichiers textes) par save -text fichier_sortie.txt ou save -ascii fichier_sortie.txt (l'option -text a été récemment ajoutée, apparemment en remplacement de l'ancienne option -ascii).

2.6 Exemple de calcul concret : analyse temps-fréquence

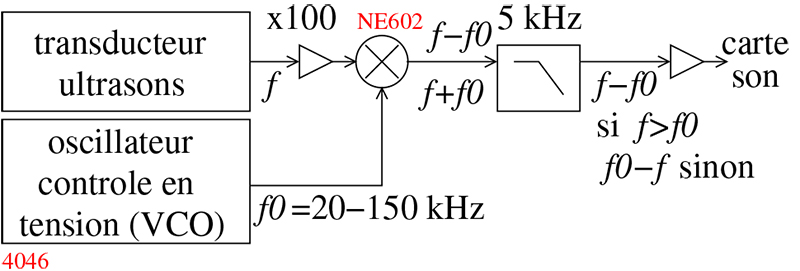
Nous nous proposons d'analyser des signaux expérimentaux de sonar de chauve-souris [7, 8]. Les signaux sont acquis sur une carte son d'Asus EEE PC 701 à une fréquence d'échantillonnage de 96 kHz, mono, 16 bits/échantillon, en sortie d'un montage électronique chargé de translater les fréquences ultrasonores dans la plage de fréquence audible [9] (Fig. 10). L'approche la plus simple pour analyser l'évolution temporelle de la distribution spectrale d'énergie dans le signal est d'effectuer une transformée de Fourier sur une fenêtre glissante :

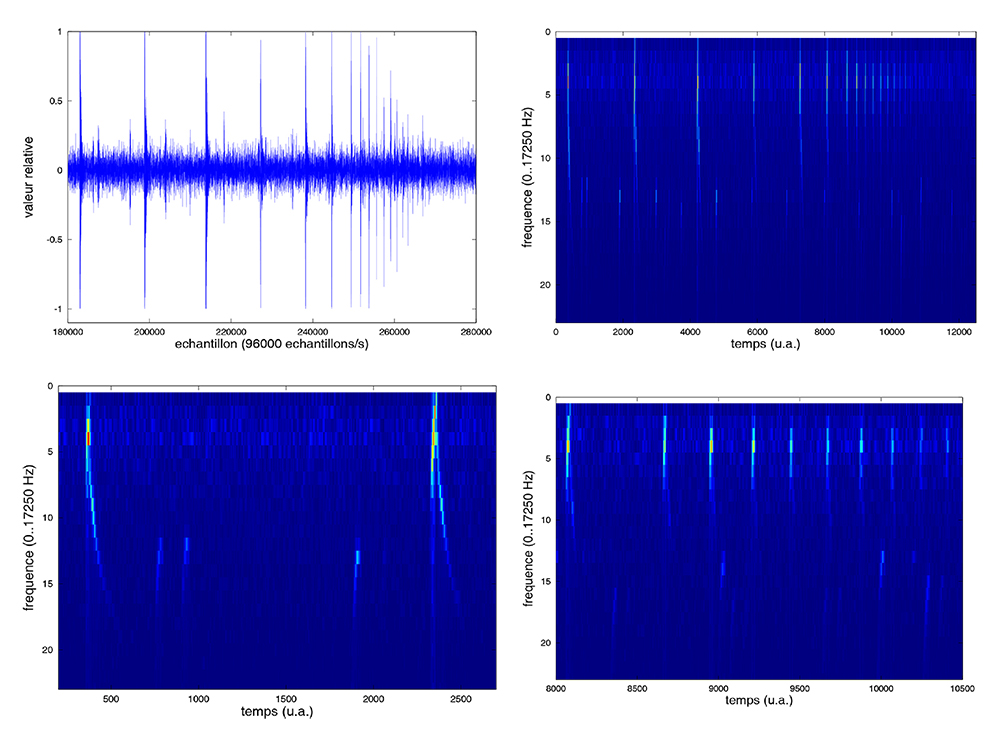
La fonction wavread() permettant de simplement lire un fichier son au format PCM (fichier .wav) pour en extraire les données et la fréquence d'échantillonnage est disponible dans le paquet octave-audio. Le résultat de ce traitement est fourni en figure 10, qui montre clairement la distribution hyperbolique d'énergie dans la représentation temps-fréquence (Fig. 11), optimale pour sa robustesse à l'effet Doppler [10, 11]. Cette méthode est l'analyse la plus grossière dans laquelle la discrétisation temps-fréquence est peu favorable [12, p. 55].

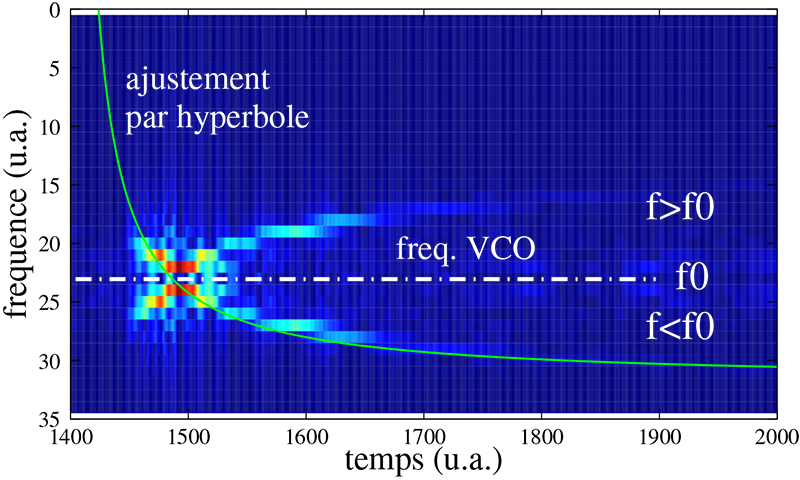
Un mélangeur tel que présenté à la figure 10 convertit une fréquence ultrasonore f par mélange avec une fréquence fixe locale f0 en deux contributions f± f0. Si f>f0, alors le filtre passe bas élimine f+f0 et seule la soustraction des fréquences est conservée. Mais si, comme c'est le cas en début d'un chirp3, nous avons f<f0, alors c'est le terme f+f0 qui entre dans la bande passante du filtre passe bas. C'est pourquoi la reconstruction du chirp complet s'obtient en concaténant une représentation temps-fréquence et son symétrique pour fournir les contribution fréquentielles en dessous et au-dessus de la fréquence locale de mélange f0. Cette opération est effectuée sur la figure 12, sur laquelle a été ajoutée un ajustement hyperbolique de la forme du chirp. Le mélangeur est donc incapable de déterminer quelle composante est physiquement pertinente : le chirp dont la fréquence s'éloigne de l'origine des ordonnées (celui sur lequel l'hyperbole a été superposée) ou celui qui s'en approche. La littérature nous enseigne que c'est la seconde composante qui est correcte [7] : l'ambiguïté est levée lorsque l'acquisition se fait directement sur le signal en sortie du microphone (nécessitant une carte d'acquisition avec une fréquence d'échantillonnage de l'ordre de 200 kHz, au-delà de ce que permet une carte son actuelle).

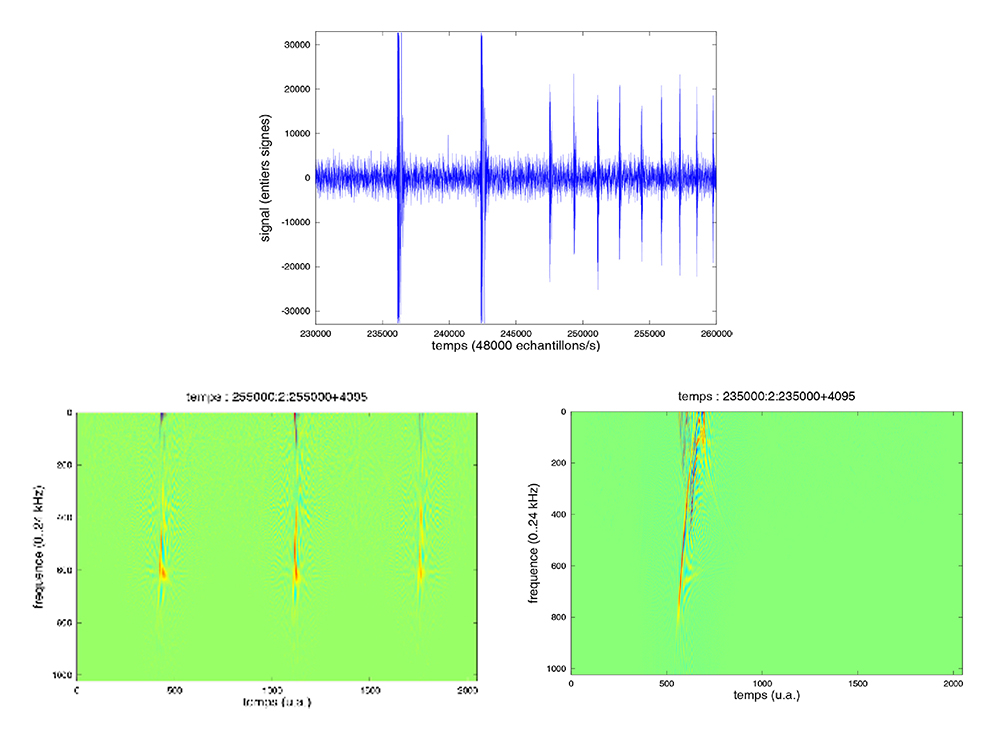
Des méthodes plus efficaces de discrétisation de l'espace temps-fréquence permettant de mieux identifier la distribution d'énergie et notamment d'affiner la résolution temporelle aux hautes fréquences. Une bilbiothèque développée pour Matlab implémentant un grand nombre de transformées pour l'analyse temps-fréquence de signaux est fournie à http://tftb.nongnu.org/. Bien qu'initialement prévue pour fonctionner sous Matlab, son utilisation se déroule sans problème sous GNU/Octave (Fig. 13). Ainsi, pour observer la distribution temps-fréquence d'énergie traitée par noyau de Wigner Ville (http://www.dsp.rice.edu/software/optkernel.shtml) dans un signal acquis par le procédé décrit auparavant sur des chauves-souris :

Cette procédure propose une autre méthode, plus manuelle, pour lire les fichiers audio non compressés au format PCM (.wav). La lecture du fichier contenant des entiers signés codés sur 16 bits résulte en un vecteur contenant des données dans la gamme ±32767 (contrairement à wavread() qui normalise pour rester dans ±1). L'affichage par imagesc() des valeurs contenues dans une matrice sous forme de couleurs dans une image bitmap est considérablement améliorée depuis que Octave utilise Gnuplot 4.2 comme interface graphique : le lecteur possédant une version antérieure de Gnuplot trouvera un intérêt à la mise à jour de ce logiciel.

Noter que ces traitements – effectués sur un Asus EEE PC avec 512 MB de RAM – portent sur plusieurs centaines de milliers de points, tandis qu'un logiciel de type Excel est limité à des séries de 32768 points au plus.

2.7 Traitement automatique de nombreux fichiers

Supposons que nous possédions un logiciel capable de caractériser de façon automatique un système physique en fonction d'un paramètre contrôlé au cours d'une expérience. Nous sauvons pour chaque caractérisation un fichier contenant dans son nom la valeur de ce paramètre. Nous désirons ensuite traiter l'ensemble de ces fichiers, de façon aussi automatique que possible afin de nous affranchir des tâches répétitives (telles qu'une multitude de File-Open dans un logiciel imposant à l'utilisateur une interface graphique) :

ou bien, si notre paramètre varie sur plusieurs décades et s'affiche avec un nombre fixe de chiffres (précédés par des 0) :

La seconde version complète le numéro du fichier par autant de 0 qu'il en faut pour avoir un nombre sur 2 chiffres, tandis que la première se contente de compléter une chaîne de caractères par un nombre de taille variable. Après cette commande, la variable x contient à chaque itération sur la variable k les nouvelles données, qui peuvent soit être simplement affichées sur un graphique, soit insérées dans un tableau indexé par k, soit traitées pour que seul le résultat soit conservé en mémoire. De telles fonctions sont utilisées régulièrement par l'auteur pour traiter des acquisitions de plusieurs centaines de fichiers, qu'il serait très fastidieux (et long) de traiter manuellement.

3. Scilab

L'auteur ne possède aucune compétence dans l'exploitation du logiciel Scilab (http://www.scilab.org/) et ne prétendra pas ici en illustrer les performances. Il semble cependant nécessaire, par souci d'exhaustivité, de mentionner ce logiciel qui fournit un complément intéressant à Octave, avec des performances supérieures dans les domaines tels que l'optimisation et la recherche de paramètres. Scilab est un projet indépendant de Matlab et GNU/Octave, issu d'activités de l'INRIA, qui semble finalement fournir des fonctionnalités assez similaires. Un certain nombre de passerelles entre ces deux logiciels semblent d'ailleurs disponibles. Là où Octave vise une compatibilité syntaxique avec Matlab, Scilab ne fait qu'utiliser une syntaxe proche mais pas directement compatible avec Matlab. Un comparatif intéressant est par exemple fourni à http://forum.hardware.fr/hfr/WindowsSoftware/Logiciels/convertir-fichiers-matlab-sujet_281803_1.htm ou de façon plus exhaustive à http://www.scilab.org/product/dic-mat-sci/M2SCI.htm. Un aspect original de Scilab est le développement d'une version pour systèmes embarqués : l'utilité d'un tel outil sur une plateforme autonome n'est pas claire, mais garantit en tous cas un délai minimal entre la phase de prototypage sur PC et l'application des algorithmes sur le système embarqué.

4. Conclusion

Nous avons présenté divers outils d'affichage et de traitement de données disponibles sous forme de fichiers ASCII. Les outils, basés sur l'interprétation de scripts pour effectuer des tâches répétitives, n'ont pas pour prétention une vitesse d'exécution, mais plutôt la souplesse nécessaire au prototypage lors de la recherche des bonnes opérations à effectuer sur des données. Nous avons en particulier présenté un outils orienté vers l'affichage et la génération de fichiers graphiques dans une multitude de format – Gnuplot – et un outil dédié au traitement du signal pour des opérations plus complexes sur les données – Octave. Une fois les fonctions de traitement des données identifiées sur quelques cas, un gain notable en performances est obtenu par l'implémentation en langage compilé (C, fortran... selon les bibliothèques disponibles), mais pour la majorité des cas qui ont concerné l'auteur, ces langages interprétés ont fourni des performances acceptables, même pour des fichiers de plusieurs millions de points traités après acquisition (cas pour lequel le temps d'exécution n'est plus un critère important). L'ensemble des programmes et fichiers sons utilisés dans ces exemples sont disponibles à http://jmfriedt.free.fr.

Remerciements

Je remercie O. Michel (http://fizeau.unice.fr/) et C. Baudet (http://www.legi.inpg.fr/) pour m'avoir introduit, il y a un moment de cela maintenant, au traitement du signal.

Auteur

Jean-Michel Friedt est ingénieur dans la société Senseor (www.senseor.com), hébergé par l'institut FEMTO-ST à Besançon, et membre de l'association Projet Aurore (projetaurore.assos.univ-fcomte.fr). Il a miraculeusement obtenu un DEA de traitement du signal en 1997.

Références

[1] http://www.gnuplot.info/

[2] FRIEDT (J.-M.), CARRY (É.), « Introduction to the quartz tuning fork », American Journal of Physics 75 (2007), pp.415-422.

[3] BUTTAY (C.) & MOREL (F.), « Des courbes harmonieuses avec Gnuplot 4.0 », GNU/Linux Magazine France 82, avril 2006.

[4] http://www.gnu.org/software/octave et en particulier la procédure d'installation pour MS-Windows : http://enacit1.epfl.ch/cours_matlab/octave.html

[5] Une page contenant les relevés annuels de température, avec des températures en fahrenheit, est disponible à http://english.wunderground.com/weatherstation/WXDailyHistory.asp?ID=IVERMOND1&day=23&year=2008&month=3&graphspan=year&format=2

[6] FRIEDT (J.-M.) & GUINOT (S.), « La réception d'images météorologiques issues de satellites : principes de base », GNU/Linux Magazine France, hors-série 24, février 2006.

[7] BARANIUK (R.G.), « Wavelets and Time-Frequency analysis », conférence 17th Dynamics Days (Lyon, 1996), et l'excellent tutorial contenu dans « Time-frequency toolbox » à : http://tftb.nongnu.org.

[8] SIMMONS (J. A.), DEAR (S. P.), FERRAGAMO (M. J.), HARESIGN (T.) & FRITZ (J.), « Representation of Perceptual Dimensions of Insect Prey During Terminal Pursuit by Echolocating Bats », Biol. Bull.191, pp.109-121 (août 1996), disponible à : http://www.biolbull.org/cgi/reprint/191/1/109.pdf

[9] Convertisseur chasseur d'ultrasons, Nouvelle électronique, janvier 1996, pp.31-35, disponible en format numérique auprès de l'auteur.

[10] http://perso.ens-lyon.fr/patrick.flandrin/Rocquencourt02.pdf (p. 32) ou brevet 5077702 disponible à http://www.google.com/patents?id=srwbAAAAEBAJ

[11] BOONMAN (A. M.), PARSONS (S.) & JONES (G.), « The influence of flight speed on the ranging performance of bats using frequency modulated echolocation pulses », J. of the Acoustical Society of America 113 (1), pp. 617-628 (2003), disponible à : http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=JASMAN000113000001000617000001

[12] FLANDRIN (P.), Temps-fréquence, Hermès, 1993.

Notes

1 http://www.xfig.org

2 La transformée de Fourier d'une gaussienne est une gaussienne, qui amènera moins d'artéfacts du point de vue spectral que le sinus cardinal, transformée de Fourier de la fenêtre rectangulaire. Pour s'en convaincre (en rouge, la gaussienne et en bleu le rectangle, en haut le signal temporel par lequel on convolue, et en bas sa transformée de Fourier) :

3 Signal dont la fréquence évolue avec le temps.