Analyse des données brutes des RADAR spatioportés Sentinel-1 : traitement des signaux radiofréquences

1. Introduction

Nous avons dans ces pages [1] présenté l’exploitation des données acquises par les RADAR spatioportés de l’ESA Sentinel-1 pour une mesure interférométrique des déplacements fins de la surface du globe sous impact anthropique (exploitation de la nappe phréatique ou des ressources minières) ou naturel (tremblement de terre). Pour ce faire, nous avons tiré parti de données complexes, au sens qu’elles sont caractérisées par une partie réelle et une partie imaginaire, fournies par l’ESA après traitement pour transformer les mesures brutes acquises dans le temps (range) et le long de l’orbite du satellite (azimut) en coordonnées spatiales géographiques de longitude et latitude. Ce faisant, nous avons exploité les données dites de niveau 1 (Level 1), convenablement traitées par l’ESA, mais nettoyées de bien des données des signaux radiofréquences bruts dont nous pourrions tirer parti si nous savions les lire. Pourquoi avoir mis des RADAR dans l’espace ? Pour paraphraser le film « The Courier » à 55 minutes, « Can they get a U-2 in the air ? This time of year there’s just too much cloud cover. ‘Til October you’re all I got. » Les observations optiques sont trop dépendantes du couvert nuageux [2], alors que les RADAR perçoivent tout mouvement (Doppler) ou infrastructure (section RADAR) variant avec une résolution millimétrique (InSAR), quel que soit le lieu observé sur la surface de la Terre (orbite polaire). Qui plus est, l’ESA met ces données à disposition de qui veut bien prendre le temps d’apprendre à les exploiter ! Alors, retroussons-nous les manches et exploitons.

L’ESA annonce [3] ne supporter que Level 1 bien que mettant les informations brutes (raw) dites de Level 0 à disposition de toute personne qui a assez de temps à perdre pour les décoder et les analyser (Fig. 1). Un bon hacker ne sait résister à ce besoin de connaître la source des données qu’il exploite, et il était évidemment impossible de résister à l’appel du décodage de Level 0, objet de la présente prose. Si un outil libre n’existe pas pour arriver à ses fins, une seule solution : se retrousser les manches et le rédiger.

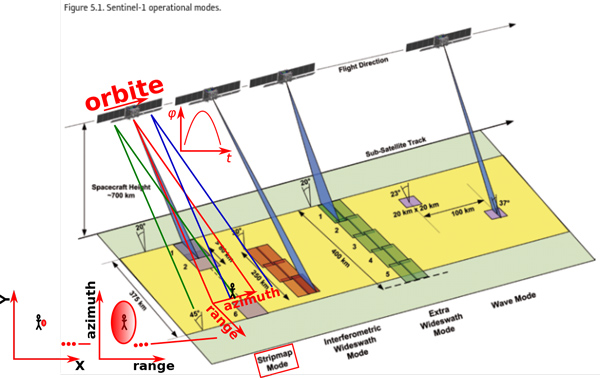
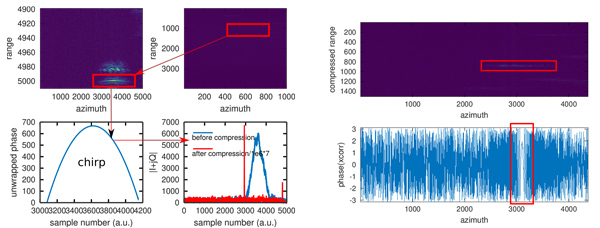
Notre objectif ne sera pas tant de reproduire l’ensemble des traitements menant des produits de niveau 0 à niveau 1 (Level 0 à Level 1), mais de démontrer la capacité à lire les données brutes et à en extraire les caractéristiques physiques, ouvrant la voie à des analyses telles que les émissions radiofréquences parasites [4], par exemple les émissions du RADAR de surveillance des batteries de missiles Patriot [5] ou les vaisseaux de la flotte russe [6] - tout RADAR militaire en bande G en général - ou le décalage Doppler induit par le mouvement des masses d’air traversées par l’onde électromagnétique [7]. Cependant, nous nous efforcerons de valider la lecture et le décodage des informations brutes transmises par le satellite en évaluant l’adéquation du traitement de compression en distance (range) et azimut pour retrouver une image en coordonnées spatiales (X,Y) correspondant classiquement à longitude et latitude (Fig. 2). En effet, ces traitements nécessitent de comprendre la forme du signal électromagnétique émis par le satellite (ϕ(t) sur la Fig. 2), les paramètres orbitaux (altitude et donc vitesse du satellite) et les caractéristiques du faisceau illuminant la cible (le bonhomme filiforme au sol) : en effet, dans le principe du RADAR à antenne à ouverture synthétique, le mouvement du satellite le long de son orbite permet d’observer la cible selon divers points de vue (faisceaux vert, rouge puis bleu) et la compression en azimut tente de faire converger la puissance réfléchie par la cible au cours du trajet du satellite en un unique point lors du passage des coordonnées (distance, azimut) à (X, Y). La compression en distance est plus simple à comprendre puisqu’elle se contente d’identifier le temps de vol entre le satellite et la cible. Nous référerons à l’axe des distances comme l’axe rapide (où le temps est représenté en microsecondes) tandis que le temps le long de l’azimut, avec un échantillonnage déterminé par le taux de répétition des impulsions, sera le temps lent où l’unité sera la milliseconde.

Pour atteindre l’objectif d’analyser les informations brutes de Sentinel-1, nous retrouverons les paquets au format CCSDS (Consultative Committee for Space Data Systems) qui uniformise le format des transactions entre vaisseaux spatiaux, que nous avions intensivement étudié auparavant [9], sans ici nous soucier de la couche physique qui a déjà été prise en charge par l’ESA lors de la restitution et du stockage des fichiers collectés depuis le satellite. Comme mentionné dans la discussion sur Meteor-M2, la raison de ce codage des informations en paquets est la multitude de satellites en orbite basse (altitude autour de 700 km) qui communiquent avec les satellites en orbite géostationnaire (altitude de 36000 km) pour router les messages vers les récepteurs sur Terre : les Sentinel communiquent avec les relais européens EDRS-A et EDRS-C par un lien optique de plus de 37000 km avec un débit de communication atteignant les 1,8 Gb/s ! Alors que les satellites en orbite basse ne sont visibles qu’une dizaine de minutes lors d’un passage au-dessus d’un point sur Terre, les satellites géostationnaires restent en position fixe relativement au récepteur sur Terre qui bénéficie donc d’une antenne de fort gain pointée dans cette direction. C’est ainsi que les données brutes de niveau 0 des Sentinel-1 sont disponibles environ 1 h après le passage du satellite, sans devoir attendre le traitement de l’ESA pour les passer en niveau 1. Nous verrons ensuite comment décompresser les données pour en extraire les coefficients complexes I et Q, pour finalement appliquer la compression d’impulsion en distance (range compression) par corrélation des signaux décodés avec l’impulsion radiofréquence émise dont les caractéristiques sont extraites de la télémesure, et poursuivrons en abordant la compression en azimut (azimuth compression) le long de l’orbite du satellite. Finalement, nous conclurons par l’analyse des phases d’écoute du RADAR spatioporté alors qu’aucune puissance des échos ne lui revient, pour écouter les signaux venus du sol dans un contexte radiométrique (écoute passive des signaux émis par le sol) ou d’illumination par les RADAR militaires ou météorologiques émettant depuis le sol ou la mer.

2. Les paquets CCSDS

Le site Copernicus de l’ESA qui distribue les données acquises par ses satellites Sentinel d’observation de la Terre propose l’option RAW, à savoir les données brutes directement reçues du satellite sans aucun traitement préalable. Nous pourrons donc tenter d’en tirer des informations qui n’étaient pas prévues au lancement. Cependant, chaque fichier fait un petit GB et il va falloir trouver de l’ordre dans cette masse d’octets. Contrairement à notre étude antérieure sur Meteor-M2, nous supposerons que l’intégrité des paquets a été prise en charge par l’ESA qui nous fournit des fichiers complets, évitant d’aborder à nouveau les codages de Viterbi et Reed-Solomon. Il faut donc comprendre la structure des fichiers.

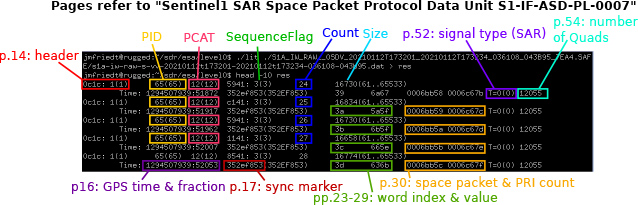
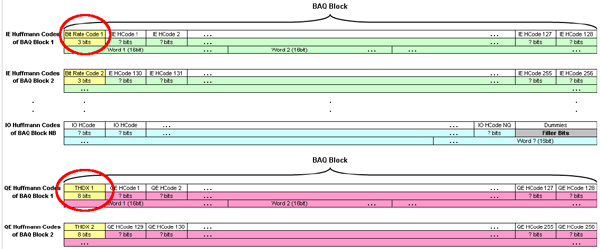
Chaque paquet CCSDS est formé d’un premier entête (primary header) qui annonce quelle plateforme spatiale a envoyé quelle information, suivi du second entête (secondary header) qui fournit les détails sur la charge utile transmise, ici les mesures du RADAR spatioporté. Ces informations incluent l’attitude et la position du satellite le long de son orbite, les paramètres d’émission et de réception des signaux radiofréquences illuminant le sol pour les mesures RADAR, et la nature des informations acquises telles que la taille du paquet de données. Nous allons déjà commencer par valider notre compréhension de cette structure avant de tenter de décoder la charge utile : si notre compréhension du format des paquets est correcte, nous devons décoder un entête, sauter la charge utile et retrouver un nouvel entête. Heureusement, chaque paquet contient un mot de synchronisation (Fig. 3) pour vérifier que nous n’avons pas sauté de bit ou d’octet dans le traitement et que nous restons synchronisés avec le flux de données (Fig. 4).

Les champs concernant l’attitude du satellite sont un peu spéciaux, car un seul registre est transmis par paquet sous la forme d’un couple indice du registre et valeur de son contenu. La lecture de la documentation technique [10] fait un peu peur au premier abord, car il est difficile de comprendre où tous les champs décrits vont tenir dans l’entête, avant de finalement réaliser que ces champs sont transmis séquentiellement paquet après paquet. Nous ne nous en servirons pas et donc ne tiendrons pas compte de ces informations, nécessaires pour positionner les points dans un contexte géographique sur la surface de la Terre.

Finalement, notons une « originalité » de la documentation qui impactera notre compréhension de la suite de l’étude : l’ESA est la première source de documentation que nous découvrons qui indexe son bit de poids fort (2⁷) par 0 et son bit de poids faible (2⁰) par 7 ! Cette organisation est documentée (Fig. 6), mais dans les pages de généralités que nous ne lisons jamais [10, p.10], et nous avions omis d’identifier cette originalité avant de chercher à comprendre l’organisation bit par bit de la charge utile telle que décrite dans la section suivante.

3. Décompression : décodage de Huffman

Une fois les deux entêtes - primaire et secondaire - convenablement décodés ainsi que la taille de la charge utile, reste à comprendre l’organisation desdites informations. Sentinel-1 transmet une telle masse de données qu’il faut optimiser la bande passante disponible en compressant. La compression est une méthode classique de traitement des données, mais elle fait intervenir une analyse bit par bit et non octet par octet ou mot par mot qui est toujours un peu pénible à mettre en œuvre. Étant donné que l’unité de traitement en C est l’octet (char), il nous faudra mémoriser l’indice (bit) au sein de quel octet nous sommes en train d’analyser.

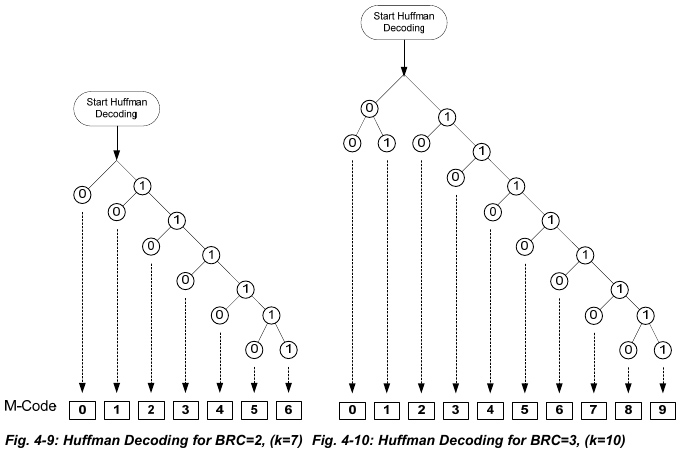
Divers articles discutent du protocole de compression FDBAQ (Flexible Dynamic Block Adaptive Quantization) et en particulier [12] qui propose l’idée fort intéressante d’afficher le taux de compression des divers paquets. En effet, l’efficacité de la compression et sa fidélité aux données originales doivent être d’autant plus efficaces que de la structure est visible dans l’image. Ainsi, la nature de la zone observée doit se retrouver dans la déclinaison du mode de compression choisi. En effet, nous apprenons de la documentation [10, pp.71-73] que cinq modes de compression sont proposés, du plus simple au plus complexe, mais aussi du plus court au plus long (Fig. 9). Au cours de nos expériences, le dernier cas (compression la plus détaillée) n’a jamais été rencontré et son implémentation jamais validée. La description du code [10, pp.71-73] peut à première vue faire peur (Fig. 7), jusqu’à ce qu’on commence l’implémentation. Nous constatons dans ces deux cas nommés BRC2 et BRC3 que nous nous contentons de compter le nombre d’occurrences de 1, puisque le premier 0 rencontré se traduit par la sortie de l’arbre avec le retour d’une valeur fournie dans la ligne du bas, et ce, avec un résultat maximal égal à k qui fait sortir du parcours de l’arbre. Le cas BRC3 impose un cas additionnel dans la machine à états qui est le premier « 0 » rencontré qui se décline encore en deux cas possibles, mais l’algorithme final de décodage reste somme toute très simple. Le résultat de ce décodage contient donc d’abord un bit de signe suivi d’une valeur, qui doit être quantifiée par un facteur valable pour une séquence consécutive de mesures nommé THIDX (Fig. 8). Nous avons longuement cherché où trouver ce coefficient avant de le trouver en début des trames paires [10, p.68]. Ainsi, les coefficients I et Q sont interlacés, avec d’abord tous les I (pairs et impairs) puis tous les Q (pairs et impairs), les I pairs (IE) étant préfixés du facteur de compression BRC valable pour les 128 valeurs qui vont suivre, et les Q pairs préfixés du facteur d’homothétie THIDX qui sera lui aussi valable pour ces mêmes 128 valeurs. Il faut donc traiter tout un tableau de 2×NQ coefficients IQ (deux, car pairs et impairs sont séparés) avant de pouvoir appliquer la quantification et donc obtenir les valeurs finales.

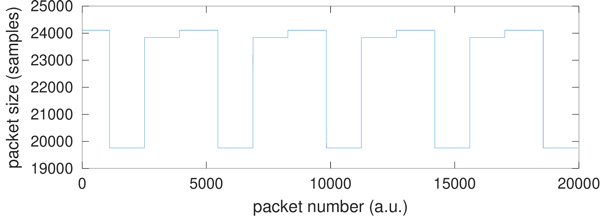
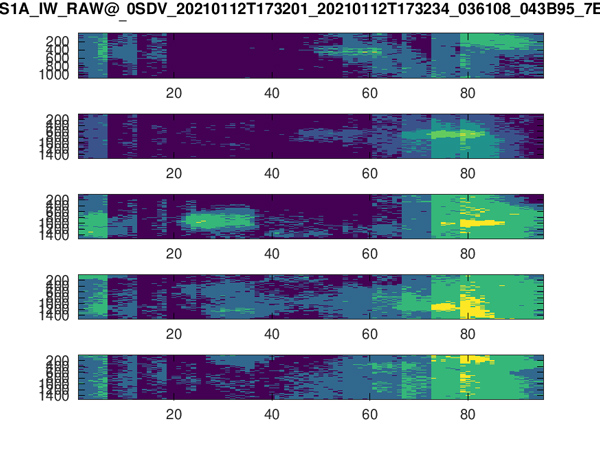
Nous constatons sur une région telle qu’au-dessus de Besançon (Fig. 9) qu’une certaine cohérence se dessine dans la distribution du facteur de compression, de 0 en bleu à 3 en jaune qui est associé à des régions plus riches en structures à analyser. Comme le facteur de compression est valable pour les 128 valeurs de coefficients (I,Q) successives, la résolution de l’image résultante est forcément médiocre dans la direction de la distance, en abscisse sur ces figures. Dans le mode IW (Interferometric Wide), le faisceau du RADAR balaie 3 zones (dites IW1 à IW3) et au sein de chaque swath, plusieurs segments (bursts) successifs sont émis. Ici, nous avons analysé uniquement IW2 et les imagettes en ordonnées correspondent aux segments successifs acquis.

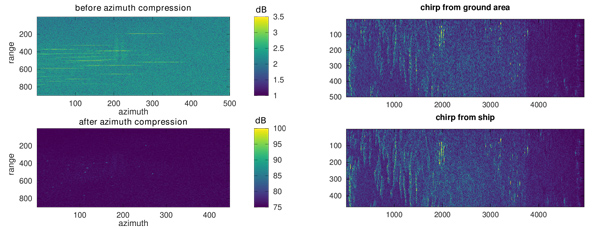
Afin de faciliter les analyses qui vont suivre et nous focaliser uniquement sur la validité du décodage et non l’assemblage d’images formées de diverses sous-structures, nous nous focaliserons dans un premier temps sur le mode StripMap le plus simple à analyser, puisque cette fois le satellite se contente de balayer une zone alors qu’il avance le long de son orbite, sans diriger le faisceau par synthèse électronique de faisceau d’antenne pour balayer les divers swaths. En prévision de la section suivante, nous traçons le module du complexe I+jQ en assemblant le nombre NQ d’échantillons indiqué dans la télémétrie, et constatons en Fig. 10 une distribution qui semble pertinente, sans structure claire visible, mais un nuage flou correspondant à des cibles potentielles avant compression en distance et azimut : il semble que nous soyons sur la bonne voie.

4. Compression d’impulsion en distance

Nous avons le sentiment d’avoir décodé une séquence de coefficients I+jQ ressemblant à une structure de signaux RADAR, mais sommes nous certains de leur intégrité ? Seule l’obtention d’une image permettra de réellement se convaincre de la cohérence des décodages et par conséquent la capacité à extraire de l’information nouvelle. La difficulté des modes Interferometric Wide (IW) et Extra Wide (EW) est que le faisceau, en plus de subir le décalage Doppler dû au mouvement du satellite, est balayé électroniquement, amenant une seconde composante de décalage de fréquence au terme constant lié au mouvement tel que décrit à https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-1-sar/products-algorithms/level-1-algorithms/topsar-processing par « For TOPSAR, the processing must handle the antenna steering rate and the DC rate due to the steering. The azimuth pre and post-processing of the data must include de-ramping of the data prior to base-band DC estimation, azimuth ambiguity estimation and GRD azimuth processing ... TOPSAR azimuth antenna sweeping causes Doppler centroid variations of approximately 5.5 kHz introducing an azimuth phase ramp (azimuth fringes) for small co-registration errors. » (où DC réfère à Doppler Centroid qui est la structure fine du chirp le long de la direction azimutale). Simplifions-nous la vie en tentant de décoder une image au format StripMap (SM) où le faisceau illumine « simplement » le sol selon un angle latéral correspondant à l’ouverture de l’antenne. Cependant, peu de zones sont imagées avec ce mode. Nous apprenons en échangeant avec les experts du domaine qu’il est classique de tester les codes de traitement de signaux RADAR spatioportés sur les ports où les bateaux apparaissent quasi ponctuels sur le fond uniforme de la mer. Heureusement, le port de Sao Paulo au Brésil est imagé de la sorte et sera donc la zone de test proposée.

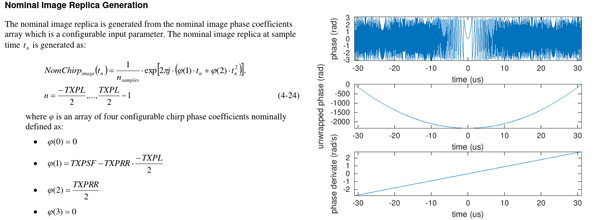
La forme de l’impulsion électromagnétique émise est utile à comprendre dans le contexte de notre étude de la structure des signaux bruts, car elle nous permettra de valider la fréquence d’échantillonnage et donc l’exploitation des étapes d’étalonnage alors qu’aucune impulsion n’a été émise. Étant donné que la résolution en distance Δ R d’un RADAR est déterminée par l’inverse de la bande passante B du signal émis, il est classique de viser à maximiser B afin d’améliorer la résolution Δ R=c/(2B) avec c la vitesse de la lumière dans le vide. Une façon intuitive d’étendre B est de réduire la durée du signal électromagnétique en émettant une impulsion brève, mais technologiquement cette solution est complexe à mettre en œuvre. Plus simple, balayer la fréquence du signal permet de commencer à émettre une sinusoïde de fréquence f₁ et de finir après un certain temps T avec une fréquence f₂ : dans ce cas B=f₂−f₁ peut être aussi grand que le permettent la synthèse de fréquence et la bande passante de l’antenne, tandis que l’intégration du signal pendant une durée T permet de moyenner le bruit et d'améliorer le rapport signal à bruit d’un facteur B× T le gain de compression d’impulsion qui cherche à être maximisé. La distribution de fréquences entre f₁ et f₂ la plus simple est linéaire de telle sorte que nous pouvons intuitivement déterminer la fréquence instantanée f(t) en fonction du temps t comme f=f₁+f₂−f₁/T× t. Comme les coefficients I+jQ lus sont caractérisés par une phase fournie par l’arctangente de Q/I, il est naturel de convertir l’évolution linéaire de la fréquence en une évolution quadratique de la phase, puisque la phase est l’intégrale de la fréquence dans l’argument de la fonction trigonométrique représentant le signal électromagnétique émis. Ainsi, il nous faut déterminer trois paramètres ϕ(0), ϕ(1) et ϕ(2) tels que ϕ(t)=ϕ(0)+ϕ(1)× t+ϕ(2)× t². Nous pouvons retrouver ces coefficients en observant une cible puissante et en la considérant ponctuelle, puisque le signal rétrodiffusé est la convolution du signal incident par la fonction de transfert qui pourra être approximée par une distribution de Dirac si la cible est ponctuelle, et observer l’évolution de la phase de I+jQ le long de l’axe de la distance des images. Alternativement, tous les paramètres pour identifier ϕ(0..2) sont fournis dans la documentation technique et la télémesure (Fig. 11), conditions nécessaires pour traiter une image ne contenant pas de cible ponctuelle. Les trois paramètres de la télémesure que nous avons décodés dans les paquets CCSDS sont TXPL (Tx Pulse Length, octet 46 [10, p.39]), TXPRR (TX Pulse Ramp Rate, octet 42 [10, p.37]) et TXPSF (Tx Pulse Start Frequency, octet 44 [10, p.38]) qui fournissent tous les paramètres comme démontré en Fig. 11, droite.

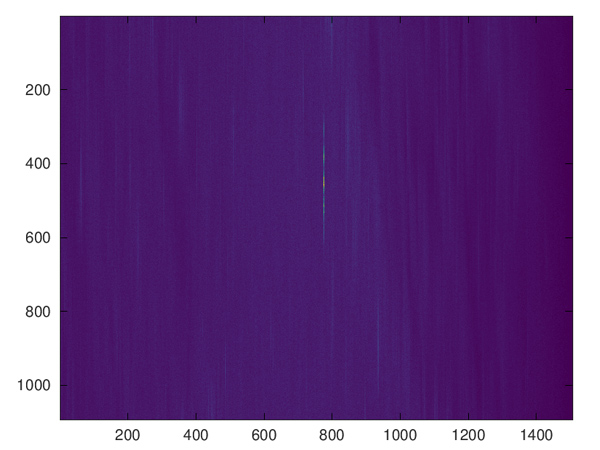
L’apothéose de la démonstration de la compréhension de la forme de l’impulsion vient de la corrélation de chaque ligne des images décodées - chaque ligne représentant l’évolution de I+jQ selon la direction de la distance - avec la forme du chirp ainsi décrite. Nous observons en Fig. 12 qu’une cible floue a été comprimée en un unique pixel dans la direction de la distance selon l’abscisse, démontrant l’adéquation de la description du chirp. L’image reste encore floue, car la compression en azimut n’a pas encore été appliquée. Alors que la compression en distance n’est déterminée que par les paramètres du chirp et donc des paramètres d’ingénierie lors de la synthèse du signal électromagnétique, la situation est un peu plus complexe pour la compression en azimut où la physique de la trajectoire du satellite intervient aussi.

On notera que ces fréquences sont sans relation avec la bande C autour de 5,405 GHz sur laquelle transmettent les Sentinel-1 : tel que l’exprime maladroitement le contributeur nuno.miranda à https://forum.step.esa.int/t/how-to-decode-sentinel-a-l0-raw-data-how-to-accomplish-range-compression-correctly/8117/12, « The txPulseLength, txPulseStartFrequency, txPulseRampRate are all what you need to construct the chirp and range compress the data » puisque toutes ces grandeurs sont exprimées en bande de base après transposition du signal par l’oscillateur local et numérisation. Ainsi, TXPSF pourra être négatif si le chirp émis est de fréquence croissante.

5. Compression d’impulsion en azimut

Le problème de l’axe des temps en azimut, donc le long du déplacement du satellite sur son orbite, est plus complexe, car dépendant du Pulse Repetition Interval (PRI). Cette information fait partie des champs en entête que nous avions omis initialement de décoder, mais qui pourrait nous être ici utile. Cependant nous allons choisir une approche plus empirique dans un premier temps, comme nous l’avions introduit auparavant sur l’analyse de l’impulsion électromagnétique émise par le satellite : en supposant qu’une réflexion puissante est induite par un réflecteur quasi ponctuel, nous supposerons que la distribution de phase en azimut autour de ce signal le plus puissant est la réponse impulsionnelle de cette cible et donc ledit chirp en azimut (Fig. 13).

Nous constatons sur Fig. 13 que nous avons sélectionné (image de gauche, quadrant haut droit) dans le plan (azimut, X) après compression d’impulsion en distance pour passer en coordonnée cartésienne X, le signal d’une cible puissante. On notera que pour faciliter la représentation, ici X est orienté selon les ordonnées et l’azimut selon l’abscisse, donc une rotation de 90° des illustrations par rapport aux autres figures de ce document. En zoomant sur cette région (quadrant haut gauche) nous observons une ligne selon l’azimut du réflecteur puissant, et en déroulant la phase des coefficients I+jQ, nous observons une structure parabolique, tout comme nous l’avions constaté dans le cas de l’impulsion modulée linéairement en fréquence et donc de réponse quadratique en phase. Cette distribution n’est pas surprenante, car le mouvement du satellite se déplaçant à vitesse v induit un décalage Doppler df=f× v/c dépendant de la vitesse relative du satellite par rapport à la cible et de la fréquence du signal émis f, que nous pouvons développer en une série de Taylor au premier ordre avec un terme constant et un terme linéaire du décalage de fréquence. Nous avons vu auparavant que s’il y a évolution linéaire de fréquence, il y a évolution quadratique de la phase, tel que nous l’observons ici. La forme du chirp est donc cohérente, mais pose question par rapport à notre affirmations antérieure [16] dans laquelle nous démontrions qu’une onde plane arrivant sur un réseau linéaire équidistant d’antennes induit un déphasage constant entre antennes successives, et donc une croissance linéaire et non quadratique de la phase le long du réseau qui permet de facilement comprimer l’impulsion en azimut par une transformée de Fourier discrète. Selon notre compréhension, la différence est la longueur de la ligne de base, en particulier lors de la mesure selon la méthode TOPS (https://earth.esa.int/web/eoportal/satellite-missions/c-missions/copernicus-sentinel-1) dans laquelle l’antenne synthétique est balayée en azimut au cours de l’acquisition ! Alors que dans notre implémentation d’un RADAR à antenne à ouverture synthétique au sol (GB-SAR pour Ground Based Synthetic Aperture RADAR), la longueur du rail portant l’antenne réceptrice est de l’ordre de 2 m, le chemin le long de l’orbite du satellite pendant lequel une cible est vue est beaucoup plus long et la variation de phase du signal réfléchi par une cible au sol plus importante : l’approximation linéaire n’est plus valable et un développement au second ordre tenant compte du terme parabolique devient nécessaire [17], terme qui pouvait être négligé sur la base courte du GB-SAR.

Si finalement nous corrélons ce chirp avec le signal observé le long de l’azimut (quadrant en bas droite), nous constatons que la cible étalée spatialement (courbe bleue) est convertie en une impulsion comprimée en un unique pixel le long de l’azimut (courbe rouge de Fig. 13 en bas à gauche) : le traitement fonctionne comme prévu. Cette dernière figure présente des courbes normalisées en amplitude et ne met pas en évidence la compression de toute l’énergie contenue dans l’intégrale de la courbe bleue pour s’accumuler dans le pic de la courbe rouge, bien plus puissant que le bruit de fond grâce à la réduction du bruit qu’amène l’intégrale de la corrélation pendant la durée T. La même séquence est illustrée sur l’image de gauche, mais avec une autre cible ponctuelle et en conservant les rotations de phase de 2π avant de la dérouler pour lui donner sa forme parabolique en fonction de la position du satellite le long de son orbite.

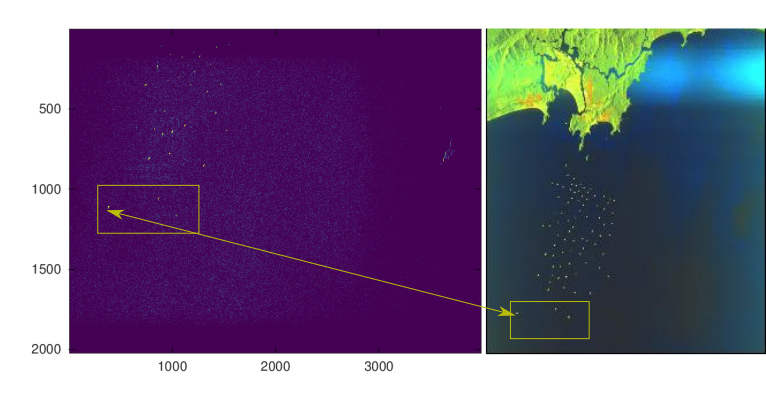
Sans en comprendre l’origine physique pour le moment, nous allons conclure en corrélant ce chirp avec l’ensemble de l’image en azimut. Le résultat est surprenamment élégant, compte tenu de la simplicité de la méthode mise en œuvre (Fig. 14).

Sur cette figure 14, nous avons considéré le cas du port de Sao Paulo avec sa flotte de bateaux en attente de transferts de produits à transporter (bas gauche) où chaque cible étendue (haut gauche) est comprimée en azimut pour donner un unique point, et à droite le traitement du signal sur la zone terrestre du jeu de données, en appliquant (haut) la distribution de phase d’une cible puissante observée sur terre et (bas) la distribution de phase d’une cible observée en mer : aucune différence notable n’est observée et toute cible puissante convient à cette analyse. L’observation est généralisée au port et comparée avec un traitement fourni par l’ESA pour illustrer les caractéristiques du jeu de données téléchargé, avec une excellente correspondance des motifs (Fig. 15).

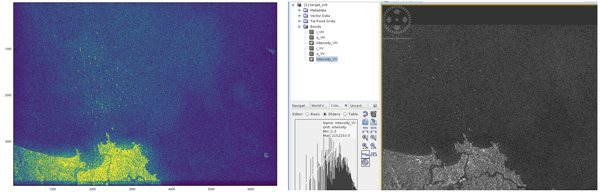
Finalement, l’application du traitement à l’interface mer-terre finit de nous convaincre de la validité du traitement (Fig. 16) en comparant le traitement proposé ci-dessus avec l’analyse par SNAP - bibliothèque Sentinel Application Platform fournie par l’ESA pour analyser les données de ses RADAR spatioportés (https://earth.esa.int/eogateway/tools/snap) - du jeu de données de niveau 1 fourni par l’ESA pour le même passage du satellite au-dessus du Brésil.

Évidemment, utiliser la réponse impulsionnelle d’une cible supposée ponctuelle pour identifier la forme du chirp et le corréler à l’ensemble de l’image n’est pas satisfaisant, puisque nombre de scènes ne présenteront pas de cible puissante ponctuelle. Essayons donc au moins d’identifier les paramètres qui déterminent la forme de ce chirp en azimut, et ce, en nous inspirant de [18, pp.51-59]. Nous apprenons dans ce document que :

1. la phase du signal réfléchi en azimut dépend de l’angle latéral d’illumination de la scène - 43,8° pour le StripMap 6 d’après https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-1-sar/products-algorithms/level-1/single-look-complex/stripmap - qui détermine la distance la plus courte R₀ de la cible au satellite lors de son survol,
2. que cette phase ϕ est développée en série de Taylor au second ordre avec un terme en dérivée Ṙ première évoluant avec s la position du satellite le long de son orbite et un terme 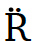de dérivée seconde qui évolue avec le carré de la position du satellite le long de son orbite :
   
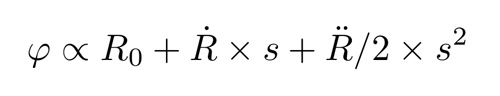
3. que R le terme qui nous intéresse dépend de la vitesse du satellite - puisque ϕ est déterminé par le décalage Doppler alors que le satellite survole la cible le long de la trajectoire sur son orbite - et donc du rapport de la circonférence de son orbite au temps qu’il met à parcourir cette orbite.

Il nous faut donc déjà identifier ces paramètres orbitaux, pour lesquels nous nous appuierons sur la troisième loi de Kepler qui indique que le carré de la période sur le cube du rayon de l’orbite d’un objet en orbite autour d’un corps céleste est une constante. Pour l’application numérique, nous avons besoin de trois données d’entrée : le rayon de la Terre est REarth=6371, l’altitude d’un satellite en orbite géostationnaire est Hgeo=35786 et l’altitude du satellite en orbite basse Sentinel-1 est Hleo=693 (https://directory.eoportal.org/web/eoportal/satellite-missions/c-missions/copernicus-sentinel-1), toutes ces grandeurs en kilomètres. Un satellite en orbite géostationnaire semble fixe au-dessus d’un point de l’équateur, donc par définition tourne autour de la Terre en 24 h. Nous en déduisons period=sqrt((Hleo+REarth)^3/(Hgeo+REarth)^3)*24*3600 en secondes qui vaut 5926.3 s, proches des paramètres orbitaux issus de Celestrak à https://celestrak.com/satcat/tle.php?CATNR=39634 qui indiquent que ce satellite tourne 14,59187... fois par jour autour de la Terre ou une période de 5921,1 s. À 5 secondes près, nos hypothèses de départ ne sont pas trop fausses.

Le satellite vole le long de son orbite en émettant périodiquement des impulsions radiofréquences dont l’analyse indique la distance (range) à chaque cible selon l’axe des abscisses de l’image, tandis que le taux de répétition indique la distance entre les points en ordonnée de l’image. Ce taux de répétition, Pulse Repetition Interval ou PRI, est indiqué dans les trames de télémesure (octet 50 dans [10]) que nous avons décodées et il vaut ici f_PRF=1663.5 Hz. Par conséquent, le temps est discrétisé le long de l’azimut par pas de 1/f_a et nous créons un vecteur de temps discret de la forme t=[0:length(mychirp)-1]/PRF; t=t-t(floor(length(t)/2)); centré sur 0, avec PRF l’inverse du PRI (passage d’un intervalle en temps à une fréquence). Nous apprenons dans [18, p.55, Eq. B13] que R₀R=v_e² avec v_e une vitesse effective déterminée comme :

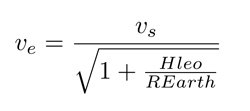
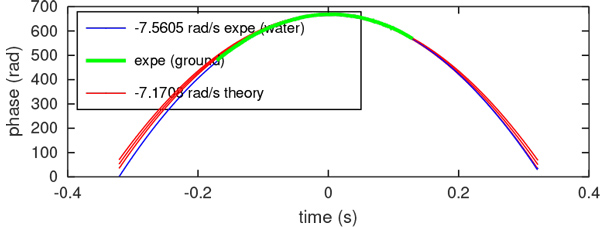
où v_s est la vitesse du satellite le long de son orbite de longueur orbit=2*pi*(Hleo+REarth)*1000 qui vaut 4,4384· 10⁷ m, donc une vitesse linéaire de v_s=orbit/period=7489 m/s et donc v_e=7112,5 m/s, en accord avec les valeurs fournies dans [18, Tab.B3]. Finalement, nous obtenons R₀ de l’altitude du satellite Hleo et de l’angle d’illumination ϑ=43,8° tel que R₀=Hleo/cos(ϑ)=9,6015· 10⁵ m (ou 960 km) qui détermine tous les paramètres pour trouver R=v_e²/R₀=52.7 m/s² qui est de l’ordre de grandeur des valeurs annoncées dans [18, Fig.B12,p.59]. Nous en déduisons le rythme auquel change la phase (dérivée de la parabole) comme étant −4π/λ× R× dt avec dt=t(2)-t(1) le pas de temps discret t et λ=300/5405 m la longueur d’onde du signal électromagnétique émis par Sentinel-1 autour de 5405 MHz. Cette pente vaut, après application numérique, −7.17 rad/s. En prenant le chirp expérimental mychirp et en dérivant la phase déroulée, un ajustement linéaire indique une pente de polyfit(t(1:end-1),diff(unwrap(angle(mychirp))),1)(1); indique une pente de −7.56 rad.s. Compte tenu de nos approximations, cet accord à 2,5 % près est plutôt satisfaisant, avec le degré de liberté d’ajuster ϑ selon que la cible soit plus proche ou plus lointaine que l’axe central de la trace (swath) : nous laissons le lecteur se convaincre qu’avec une largeur de la bande observée de 80 km, l’angle d’illumination varie entre 42,05° et 45,49° et que par conséquent le taux de variation de phase est compris entre −6.96 rad/s et −7.38 rad/s, pas encore suffisant pour atteindre la valeur empirique, mais qui laisse penser qu’un ajustement fin est nécessaire pour compresser avec précision l’impulsion en fonction de la distance à la cible, ce que la littérature semble nommer l’identification du Doppler centroid (Fig. 17).

Nous constatons dans cette analyse que l’utilisation des valeurs nominales de courbure de la phase dans la direction de déplacement du satellite (azimut) permet d’atteindre la compression d’impulsion et de relativement bien prédire la forme de l’onde (Fig. 17). Ce « relativement bien » ne suffit pas pour atteindre des performances optimales, et nombre d’articles de la littérature parlent des méthodes pour estimer finement les propriétés de la parabole pour notamment compenser les incertitudes sur l’attitude du vecteur de vol ou les conditions de propagation des ondes électromagnétiques - ces études se nomment l’estimation du « Doppler Centroid ». Nous n’avons pas persévéré dans cette voie qui mérite sûrement une implémentation détaillée, mais mentionnons que la documentation de l’ESA propose une approche par autocorrélation du signal en ne faisant que survoler le sujet sans donner les détails de l’implémentation [11, section 5]. Nous avons trouvé plus utile d’analyser [14] qui précise que l’autocorrélation n’aura de sens qu’aux indices +/- 1 et qu’elle s’annule rapidement au-delà. Nous avons en effet constaté cette propriété sur les signaux traités, mais sans en déduire une valeur exploitable de corrections des paramètres de la parabole représentant l’évolution de la phase le long de l’azimut. On notera que cette analyse du Doppler Centroid est au cœur de l’analyse des décalages Doppler induits par les vents traversés par l’onde électromagnétique et le détournement du RADAR pour des mesures fines au-delà de la cartographie des cibles au sol [7], mettant en évidence la portée d’une telle analyse.

6. Extraction et analyse des données d’étalonnage

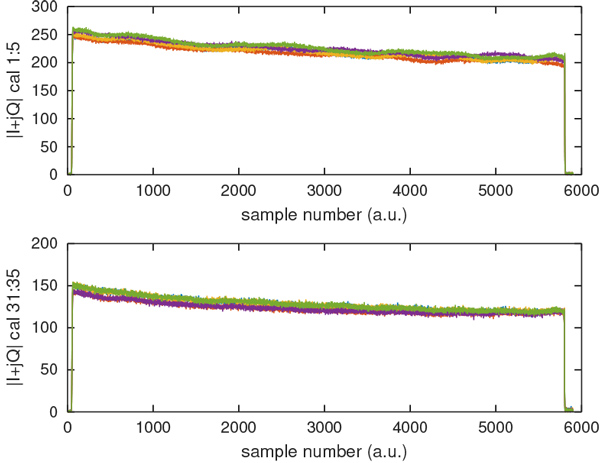
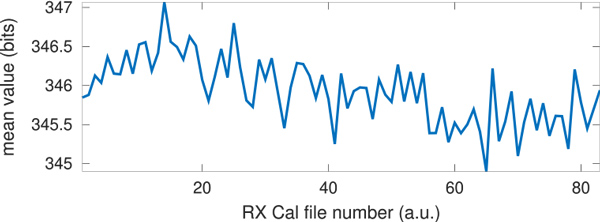
Nous nous sommes convaincus que nous comprenons les formats de données, la forme des signaux émis et reçus, et le mode de compression. Il nous reste donc à revenir au problème initial qui nous a incités à nous intéresser au problème, à savoir l’analyse des données d’étalonnage lorsque le satellite est en phase d’écoute pour voir si nous pouvons détecter des sources d’interférences radiofréquences émises depuis le sol. Nous étendons donc l’outil de traitement des fichiers bruts acquis sur le site Copernicus pour non seulement décoder les trames de codage 12 et type 0 (compression FDBAQ des échos), mais aussi les trames de type supérieur à 8 (octet 63) indiquant un étalonnage et une compression de type 0... donc inexistante ! C’était bien la peine de faire tous ces efforts avec FDBAQ pour en arriver là. Fort de l’expérience acquise, décoder les paquets de 10 bits de données est une partie de plaisir quand on prend soin d’organiser les données codées sur 16 bits de façon adéquate (https://github.com/jmfriedt/sentinel1_level0/blob/main/bypass.c) : nous traitons des paquets de 5 octets (5× 8=40 bits) qui génèrent 4 valeurs (4× 10=40) successives, et prendrons soin de bien aligner la fin du décodage d’une séquence sur un multiple de 16 bits. Ayant ajouté ce traitement, nous complétons les fichiers binaires contenant les coefficients (I,Q) des signaux rétrodiffusés par les cibles au sol par des fichiers contenant les données de calibrage dont le tracé laisse penser que l’analyse est cohérente, compte tenu de la reproductibilité de la mesure et la structure (Fig. 18).

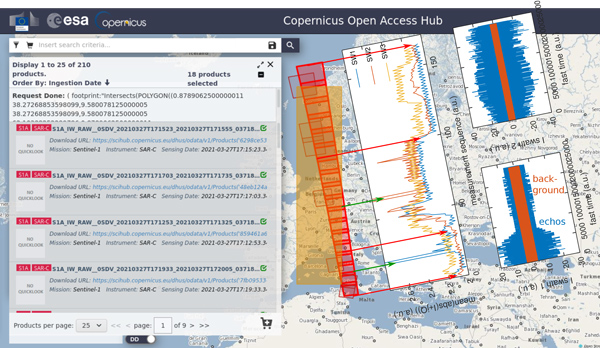
Nous avons donc maintenant deux ensembles de données pour analyser les sources d’interférences radiofréquences (RFI pour Radio Frequency Interferences) émises depuis le sol : les paquets d’étalonnage et les premières séquences échantillonnées au début des traces IW lorsque les impulsions ont été émises, mais n’ont pas encore eu le temps de revenir au récepteur. En effet, pour un RADAR situé à 700 km d’altitude et observant le sol avec un angle ϑ∈[25:45]°, la distance parcourue par l’onde est 2× 700/cos(ϑ)∈ [1550:1980] km. Une onde électromagnétique se propage à 300 m/µs donc le temps de vol de l’onde est entre 5,15 et 6,6 ms. Avec un taux de répétition PRI de l’ordre de 1600 Hz ou 625 µs, nous constatons qu’entre 5,15/0,625≃ 8 et 6,6/0,625=~ 10 acquisitions se feront avant que tout écho ne puisse revenir au satellite, et donc en ne faisant qu’écouter les RFI. Pour mettre en pratique, nous téléchargeons toutes les (18) mesures brutes d’un passage au-dessus de l’Europe (Fig. 21, moitié gauche). Évidemment, nous ne répétons pas bêtement la demande de téléchargement tel que l’imposerait l’interface graphique, mais scriptons selon les consignes décrites à https://scihub.copernicus.eu/userguide/BatchScripting pour télécharger au moyen de curl les 29 GB de séries de données pertinentes. Les archives sont décompressées en vue de traiter les séquences {I,Q} au moyen du programme décrit ci-dessus.

7. Analyse des signaux reçus par le satellite

Nous avons téléchargé les 29 GB des 18 jeux de données brutes d’un passage de Sentinel-1 depuis la Sicile jusqu’au nord de la Scandinavie pour reprendre une trajectoire proche de celle présentée en [4]. Le traitement de chaque fichier RAW dure 60 min, soit une durée totale de traitement d’environ 18 h sur un ordinateur portable Panasonic CF-19, et génère après reconstruction des signaux (donc décompression par Huffman) au total 150 GB incluant les trois swaths alternés, les étalonnages périodiques et donc toutes les informations nécessaires à la détection de sources d’interférences au sol.

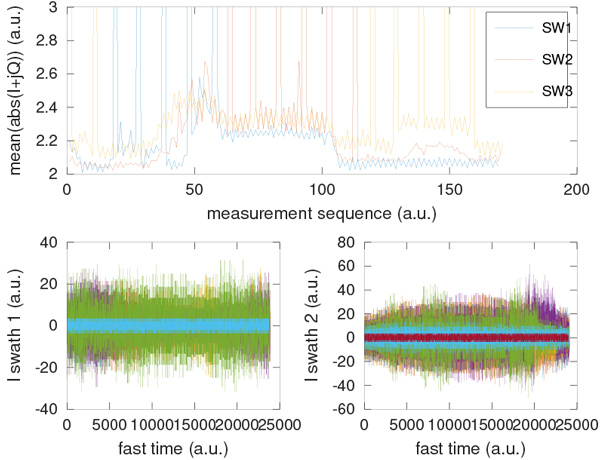
L’évolution au cours du survol de l’Europe, du sud vers le nord, des Rank Echoes et RxCal sont présentés en Fig. 19 et 20. Autant la mesure en cours d’étalonnage (Fig. 19) est décevante, autant les écoutes sans échos présentent une structure proche de celle publiée dans [4]. Ne connaissant pas les connexions électriques de l’étage de réception du RADAR lors de son étalonnage qui est peut-être connecté à une charge de référence, le résultat n’est pas complètement surprenant.

On note la présence de pics périodiques dans la puissance reçue sur les échos supposés silencieux : nous avons identifié ces sauts de puissance comme les jonctions entre les fichiers bruts découpés par paquets de 25 secondes sans tenir compte d’aucune structure sur le contenu de l’information. De ce fait, le début de ces fichiers n’est pas un rank echo et ces pics de puissance s’avèrent être le signal réellement reçu par le satellite lorsque des échos électromagnétiques sont réfléchis sur la surface de la Terre.

L’élimination de ces jeux de données, facilement identifiables par leur brièveté puisque ces segments de données sont plus courts qu’un segment complet, et la mise en contexte géographique est présentée en Fig. 21.

8. Réception au sol des signaux émis par Sentinel-1

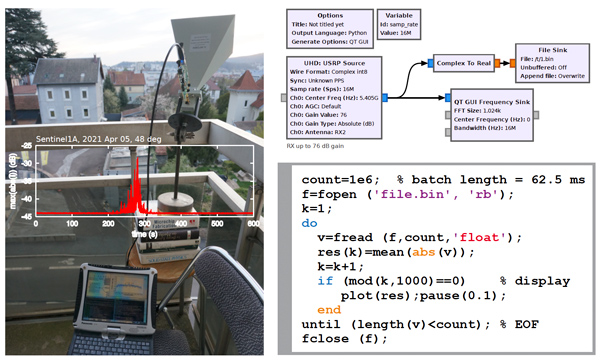
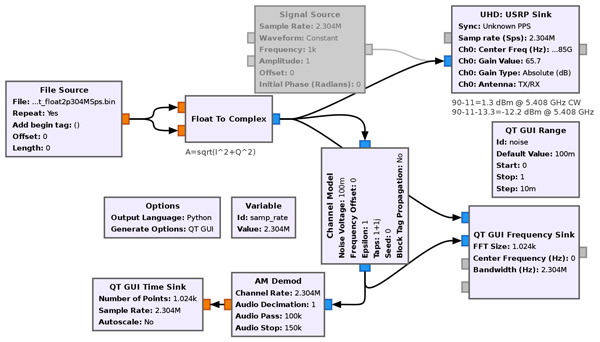
Nous sommes donc capables de convenablement traiter les signaux proposés par l’ESA sur son site web, de retrouver les images compressées en distance et azimut, et d’exploiter les phases d’écoute du RADAR spatioporté avant que tout écho ne revienne dans une application de type radiomètre. Finalement, pouvons-nous manipuler ces données depuis le sol ? Pour ce faire, nous pouvons nous interroger sur la capacité à recevoir les impulsions électromagnétiques émises par Sentinel-1. Pour ce faire, nous avons cassé notre tirelire en nous autorisant exceptionnellement l’achat d’un périphérique dédié à ce développement, une antenne de gain 20 dB fonctionnant autour de 5,4 GHz commercialisé par A-Info en Chine (représenté en France par Équipements Scientifiques) telle que décrite à http://www.ainfoinc.com.cn/en/p_ant_h_std.asp. Nous avons opté pour la référence LB-159-20 qui fournit 20 dB de gain dans la bande 4,90-7,05 GHz pour un encombrement permettant un transport aisé et la modique somme de 1000 euros incluant son support de fixation. Un émetteur-récepteur Ettus Research B210 est utilisé pour collecter le signal sans aucun traitement autre qu’envoyer dans un fichier le signal observé autour de 5405 MHz dans une bande de 16 MHz, maximum accessible sur le bus USB2 disponible sur notre ordinateur portable avec un transfert de données codées sur 8 bits (Over The Wire format - OTW - dans le bloc USRP Source de GNU Radio). Le résultat est un fichier de 4× 16· 10⁶× 600=38,4 GB quand seule la partie réelle du signal est sauvegardée. L’analyse de ce fichier en post-traitement pour extraire le maximum de la valeur absolue de segments de 1 Méchantillons (62,5 ms) fournit le résultat de la Fig. 22 qui présente à l’évidence le passage du satellite à son azimut vers lequel est pointée l’antenne. Un résultat similaire pourrait être atteint à moindres frais avec une PlutoSDR débridée pour faire croire à son AD3963 qu’il s’agit d’un AD9364 (https://wiki.analog.com/university/tools/pluto/users/customizing) et ainsi fonctionner jusqu’à 6 GHz.

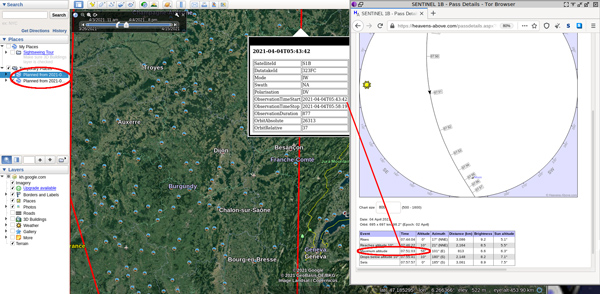
Bien entendu, le signal n’est reçu que pendant une durée relativement brève des 10 min de passage de Sentinel-1 d’horizon à horizon (en fait, 10° de l’horizon) : si en 10 minutes le satellite parcourt 160° alors les 18° d’ouverture angulaire de l’antenne dans le plan horizontal ne laissent espérer un signal exploitable que pendant 70 secondes environ, qui est bien ce que nous observons entre les dates 240 à 310 du passage représenté en Fig. 22. Les paramètres orbitaux et en particulier l’horaire de passage à l’élévation maximale ainsi que l’angle de cette élévation est obtenue en croisant les traces fournies dans les fichiers KML de l’ESA prédisant les passages des satellites au-dessus d’une région de la Terre, avec les informations fournies par Heavens Above (Fig. 23).

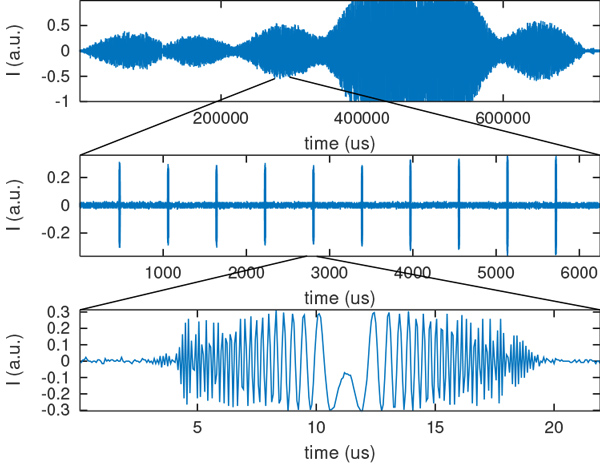
L’analyse temporelle des signaux illustre (Fig. 24) que nous avons largement saturé l’étage de réception compte tenu du gain maximum sélectionné et du gain d’antenne, que les lobes latéraux de l’antenne sont clairement visibles de part et d’autre du lobe principal, et que le taux de répétition des impulsions et les impulsions sont clairement visibles. Nous verrons dans la section suivante que la durée nominale des impulsions est TxPL=53,4 µs et nous pourrions être induits en erreur par la brièveté des impulsions observées. Rappelons qu’ici nous n’analysons qu’une bande de 16 MHz autour de 5,405 GHz alors que les impulsions sont annoncées (voir section suivante) avec une largeur de bande de 43 MHz. Ne voyant qu’un tiers de la bande couverte par les chirps, il est normal que leur durée apparaisse plus courte qu’elles ne le sont en réalité.

Tout le monde ne peut pas se permettre un achat aussi onéreux et surtout peu satisfaisant du point de vue de la compréhension de la technologie. En observant les anciennes photographies de la conquête spatiale, par exemple https://www.nasa.gov/multimedia/imagegallery/image_feature_757.html, nous constatons que l’antenne hélicoïdale fournit un certain nombre d’avantages que sont la directivité, la largeur de bande et surtout la simplicité de réalisation (Fig. 25). Tentons donc une réception de Sentinel-1 avec une telle antenne en suivant les consignes de réalisation de [19, section 10.3.1]. La spirale est de diamètre D sélectionné de façon à ce que la circonférence C=π D soit comprise entre 3/4 et 4/3 de la longueur d’onde, dans notre cas λ=5,55 cm donc D=~ 1,77 cm. Le diamètre étant choisi, l’angle de la spire doit être compris entre 12 et 14° donc si nous sélectionnons α=13°, l’espacement entre deux spires est S=Dπtan(α)=1,28 cm. Ces caractéristiques géométriques vont imposer l’impédance Z=140× C/λ=~ 140 Ω et de toute façon au mieux 100 Ω et nécessiterait une adaptation d’impédance par ligne de transmission se comportant comme transformateur pour correctement coupler avec l’entrée 50 Ω du récepteur B210. Une rapide analyse d’une telle ligne de transmission de longueur quart d’onde montre qu’elle sera loin d’être simple à réaliser et nous nous contentons d’une simple connexion directe avec le taux d’onde stationnaire dégradé résultant. Le support d’antenne a été usiné comme une gorge de 0,5 mm de profondeur dans un cylindre creux de teflon de diamètre extérieur 20 mm afin d’accueillir un fil de cuivre émaillé de 0,7 mm de diamètre. Ce fil se termine sur un connecteur SMA soudé sur une plaque de FR4 faisant office de plan de masse de dimensions importantes devant la longueur d’onde - dans notre cas une chute de 300× 300 mm. L’antenne est orientée vers le satellite au moyen d’une planchette équatoriale que nous avions réalisée pour [20] : en effet l’ouverture angulaire (moitié de la puissance rayonnée) de l’antenne est annoncée comme 52λ^3/2/C√NS degrés avec N le nombre de tours, dans notre cas N=2 limité par la longueur de l’outil qui usine la gorge. L’application numérique indique que l’ouverture angulaire est de l’ordre de 76°. Le gain d’antenne, lié à sa directivité, est proportionnel au nombre de tours N dans la limite du raisonnable - dans notre cas imposé par la longueur du cylindre de teflon disponible et l’outil utilisé pour l’usinage de la gorge.

La conclusion de la mesure est satisfaisant puisqu’avec un montage aussi simple, nous parvenons à clairement retrouver la signature de Sentinel-1 tel que nous l’avions fait auparavant avec l’antenne cornet (Fig. 25), et ce, en cohérence avec les informations fournies dans le cadre de l'utilisation de Sentinel-1 comme source non coopérative d’un RADAR bistatique passif au sol [21].

9. Encore un peu plus...

Il est strictement interdit d’émettre dans des bandes radiofréquences non autorisées (Industrielles, Scientifiques et Médicales) et ce n’est pas parce que nous possédons une plateforme de radio logicielle B210 capable d’émettre 12 dBm à 5,405 GHz (gain 89,8 dB) et une antenne cornet fonctionnant dans cette gamme de fréquences que nous nous autoriserions une telle expérience. Imaginons cependant que quelqu’un émette brièvement un signal pour imprimer une information additionnelle aux échos RADAR dans les fichiers stockés sur le site Copernicus de l’ESA.

Comment nous y prendrions-nous si nous voulions effectuer une telle émission ? Partant d’un fichier de données, nous devrions imprimer l’information sur la porteuse en manipulant une des trois grandeurs qui représente un signal périodique que sont l’amplitude, la fréquence ou la phase. Ce faisant, en traitant les signaux bruts {I,Q} fournis par l’ESA, nous serions capables de retrouver l’information ainsi transmise. Nous pourrions considérer les deux modes de modulation les plus simples que sont la modulation d’amplitude (AM) et la modulation de fréquence (FM). Ainsi, les chaînes de traitement GNU Radio pour simuler ces opérations sont proposées en Fig. 26.

Les paramètres de communication seraient sélectionnés comme un compromis entre le débit de données (d’autant plus important que la bande passante est importante), le bruit polluant le signal lors de la démodulation (d’autant plus important que la bande passante est importante) et la durée du message par rapport à la séquence d’écoute de Sentinel-1 (d’autant plus faible que la bande passante est importante) tel que nous le quantifierons ci-dessous. Imaginons un message d’une dizaine de caractères. Dans ce cas, les 5,15 à 6,6 ms d’écoute déterminées par le taux de répétition PRI des impulsions nous laissent pour émettre une dizaine de caractères de l’ordre de 600 µs ou 60 µs en encodage RS232 8N1 (10 bits/caractère transmis). L’inverse de 60 µs est 16,7 kHz qui nous approcherait des 19200 bauds nominaux de RS232. Un tel signal est simulé dans le listing ci-dessous qui serait susceptible de moduler une porteuse autour de 5,4 GHz avec la fréquence f_s ici choisie arbitrairement à 60 fois le débit de communication hypothétique.

Le signal alimentant la chaîne de modulation en amplitude est produit par le script GNU Octave

Ce programme vise à respecter la norme RS232 de la transmission à 19200 bauds sans bit de parité avec deux bits de fin et un unique bit (8N1) de départ (start) en communiquant le bit de poids le plus faible en premier. Le taux de modulation est de 80 % puisque la puissance maximale est unitaire et la puissance minimale est 0,2, mettant en évidence l’inefficacité de la modulation AM. La difficulté de cette mesure tient au bilan de liaison défavorable entre le sol et le satellite, la durée très courte de visibilité de la source par le satellite avançant le long de son orbite, mais surtout de la puissance limitée que peut émettre une B210. En effet, nous mesurons une puissance crête de 11.5 dBm à 5,4 GHz soient 14 mW alors que [4] nous apprend que la limite de détection, compte tenu du plancher de bruit thermique du récepteur de Sentinel-1, est de l’ordre de 15 mW pour une porteuse émise en continu, ou dans les meilleures conditions 8 mW donc très proches de la puissance que nous serions susceptibles d’émettre. On pourra cependant noter que l’amplificateur Skyworks SE5023L fonctionne à 5 GHz avec un gain de 32 dB et un point de compression à 26 dBm (400 mW), coûte 4,75 euros, et que sa carte d’évaluation est disponible chez Mouser pour 93 euros.

Imaginons maintenant que quelqu’un ait enfreint l’interdiction d’émettre [22] et qu’un signal ait peut-être été collecté par Sentinel-1 lors de son survol de la France. Serions-nous capables de retrouver ce signal dans les données brutes fournies par l’ESA, et surtout ce signal peut-il impacter la fonction première de mesure RADAR du satellite ? Le second point est le plus facile à appréhender : une impulsion RADAR - ou tout système de communication à étalement de spectre en général (par exemple GPS) - est caractérisée par deux grandeurs, sa durée T et son encombrement spectral B. Plus la durée est longue et meilleure est la capacité à moyenner pour rejeter le bruit, mais moins bonne est la résolution temporelle 1/T. Par ailleurs, plus la bande spectrale occupée par le signal est large, meilleure est la capacité d’identifier sa date de réception 1/B ou, en application RADAR, son temps de vol aller-retour avec une résolution en distance c/(2B). Le produit de ces deux grandeurs PCR=B× T est le Pulse Compression Ratio - rien à voir avec la Polymerase Chain Reaction qui est sur toutes les bouches en ce moment - qui indique le gain en rapport signal à bruit amené par le traitement numérique du signal impliquant la corrélation du signal émis sur le signal reçu. Dans le cas de Sentinel-1, T est donné par le Tx Pulse Length TxPL (octet 46 de la trame CCSDS) et B par le Tx Pulse Ramp Rate TxPRR (octet 42 de la trame CCSDS). Ainsi pour une impulsion émise au cours d’une mesure de type IW (Interferometric Wide), TxPRR=-1193 soit -0,805 MHz/µs et la durée de l’impulsion est TxPL=2004 ou 53,4 µs. Nous en déduisons B=TxPRR×TxPL=~ 43 MHz et PCR=B×TxPL=~ 2300. Ainsi, le gain produit par la corrélation sur le rapport signal à bruit est un facteur 2300 ou en échelle logarithmique 10log₁₀(2300)=~ 34 dB puisque la corrélation fournit déjà une puissance. Cela signifie que le RADAR sera capable de ressortir son impulsion du signal reçu bruité (ou pollué par une source d’interférence) si ce dernier est moins de 2300 fois plus puissant que l’écho reçu.

Si l’émission est incohérente avec la forme des impulsions émises par le RADAR, les risques de brouillage sont faibles dans la limite d’une puissance émise raisonnable. Bien entendu, la situation est toute autre dans le cas où le signal émis depuis le sol suivrait le même motif de phase que les impulsions émises par le RADAR, puisque dans ce cas le gain de compression s’applique tout autant au signal émis depuis le sol qu’aux impulsions émises depuis l’espace : c’est selon ce précepte que les systèmes de brouillage de GPS russes utilisés en Syrie notamment émettent un motif rappelant les messages des vrais satellites, mais sans information de position pertinente, comme décrit dans [23].

Sentinel-1 illumine Besançon avec un angle en vue oblique variant entre 35 et 45° selon les paramètres orbitaux, correspondant à une distance entre une cible au sol et le satellite entre 700cos(45)=990 km et 700cos(35)=850 km soit dans l’équation de Friis une variation de puissance de 20log₁₀(990/850)=1,3 dB. Si nous pouvions illuminer Sentinel-1 lors de son passage à l’azimut à une élévation de 90° (distance de 700 km), nous gagnerions 3 dB par rapport à son passage à 55° d’élévation, mais ce gain est négligeable face aux erreurs de pointage manuel d’antenne, et surtout dans ce dernier cas, le réseau déphasé des éléments rayonnant de l’antenne ne pointe pas dans la bonne direction.

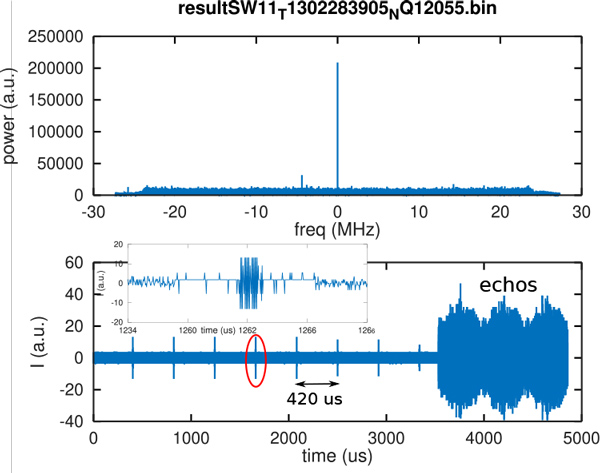
Pour conclure cette analyse, l’observation des données fournies par l’ESA, par exemple dans son enregistrement S1B_IW_RAW__0SDV_20210412T173110_20210412T173142_026437_0327F3_5F2E fournit parfois de bonnes surprises. Ainsi dans la Fig. 27, nous observons des impulsions périodiques avant les premiers échos réfléchis par le sol. L’intervalle de temps entre ces impulsions brèves est de 420 µs ou une fréquence de répétition d’impulsions (PRF) de 2380 Hz, surprenamment proche des 2232 Hz (inverse de 448 µs) annoncés dans [24] décrivant les RADAR météorologiques français interlaçant diverses formes d’impulsions pour maximiser à la fois la résolution en distance et en vitesse... et comme par hasard un tel RADAR en bande C se trouve dans le Doubs à Montancy. Ces résultats se retrouvent lors de passages précédents tel que le fichier S1B_IW_RAW__0SDV_20210331T173109_20210331T173142_026262_032260_9A62 acquis le 31 mars 2021 où ces signaux se répétant toutes les 420 µs se retrouvent vers 19 h 31 min 35 s heure locale.

Conclusion

Partant de la volonté de combler une lacune manifeste sur la chaîne de traitement des signaux bruts issus des satellites spatioportés de l’ESA Sentinel-1, nous avons exploré la séquence de décompression des fichiers et avons validé le résultat par l’analyse des données produites. Nous avons pu reproduire des images comprimées en distance et en azimut, démontrant la validité des données et la compréhension des paramètres de télémesure. Fort de ces données, nous avons dépassé le cadre classique d’exploitation des données acquises par Sentinel-1 par une analyse radiométrique de la puissance radiofréquence émise depuis le sol en l’absence d’échos émis par le RADAR. Finalement, nous avons pu détecter depuis le sol les émissions électromagnétiques du RADAR spatioporté, et évalué la capacité à retrouver sur les fichiers fournis par l’ESA des informations qui auraient pu être émises depuis le sol.

Bien entendu, la maîtrise de la technologie fournit les outils pour la détourner à ses propres fins, voir pour nuire à la collecte des données [25], des atouts que les possesseurs de cette connaissance ne manqueront pas de mettre à profit.

Saurez-vous retrouver le message extra-terrestre qui se trouve peut-être dans les fichiers bruts des données acquises par Sentinel-1 entre fin avril 2021 et début mai, par exemple le 28 autour de 5 heures, 50 minutes et 58 secondes en temps universel ? Une carte Zedboard sera offerte à la première réponse démontrant la bonne réponse, positive ou négative, à cette question. Tous les outils nécessaires à trouver la solution sont disponibles à https://github.com/jmfriedt/sentinel1_level0/.

Remerciements

Toutes les références bibliographiques qui ne sont pas librement disponibles sur le Web ont été acquises auprès de Library Genesis à gen.lib.rus.ec, une ressource indispensable à nos recherches et développements. Andrea Monti-Guarnieri (Université Polytechnique de Milan, Italie) a initié cette étude en mentionnant la disponibilité des données brutes (format RAW) des flux de données IQ sur le site Copernicus de l’ESA, garantissant la pérennité et la reproductibilité des résultats annoncés dans ce document.

Références

[1] J.-M Friedt, P. Abbé, Parler à un RADAR spatioporté : traitement et analyse des données de Sentinel-1, GNU/Linux Magazine France n° 246 (mars 2021) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-246/parler-a-un-radar-spatioporte-traitement-et-analyse-des-donnees-de-sentinel-1

[2] J.W. Caddeel Jr. Corona over Cuba: The Missile Crisis and the Early Limitations of Satellite Imagery Intelligence, Intelligence and National Security 31 (3) 416-438 (2016) à https://www.researchgate.net/publication/273520282_Corona_over_Cuba_The_Missile_Crisis_and_the_Early_Limitations_of_Satellite_Imagery_Intelligence

[3] Utilisateur « nuno.miranda » du forum step de l’ESA à https://forum.step.esa.int/t/how-to-decode-sentinel-a-l0-raw-data-how-to-accomplish-range-compression-correctly/8117/15 selon l’argument très raisonnable que « we never made available RAW decoding software ... My personal opinion is that people willing to process S-1 RAW data (or any other mission) needs to learn about the sensor specificities. If you want to process S-1 TOPS data, you have to learn about S-1. » (où S-1 réfère à Sentinel-1).

[4] N. Franceschi & al., RFI Monitoring and Classificationin C-band Using Sentinel-1 Noise Pulses à http://www.ursi.org/proceedings/2019/rfi2019/23p4.pdf et A. Monti-Guarnieri & al., Identification of C-Band Radio Frequency Interferences from Sentinel-1 Data, MDPI Remote Sensing 9 1183 (2017).

[5] D. Harel, X Marks The Spot: Identifying MIM-104 Patriot Batteries From Sentinel-1 SAR Multi-temporal Imagery (2018) à https://medium.com/@HarelDan/x-marks-the-spot-579cdb1f534b

[6] H.I Sutton, Hidden Threat To Navies: How Freely Available Satellite Imagery Can Track Radars (2020) à https://www.navalnews.com/naval-news/2020/12/hidden-threat-to-navies-how-freely-available-satellite-imagery-can-track-radars

[7] A.A. Mouche & al., On the Use of Doppler Shift for Sea Surface Wind Retrieval From SAR, IEEE Trans. on Geoscience and Remote Sensing 50 (7), 2901 (2012) ou T. Ahsbahs, Wind Farm Wakes from SAR and Doppler Radar, MDPI Remote Sensing 12 462 (2020).

[8] ESA, Sentinel-1 - ESA’s Radar Observatory Mission for GMES Operational Services, SP-1322/1, p.20, (mars 2012) à https://sentinel.esa.int/documents/247904/349449/S1_SP-1322_1.pdf

[9] J.-M. Friedt, Décodage d’images numériques issues de satellites météorologiques en orbite basse : le protocole LRPT de Meteor-M2, GNU/Linux Magazine France, en 3 parties entre mai et juillet 2019 - https://connect.ed-diamond.com/search/node?keys=Meteor-M2&date_interval=0&brands%5B%5D=1&authors%5B%5D=71197

[10] H. Flachs, Sentinel-1 SAR Instrument - SAR Space Packet Protocol Data Unit, ESA (22/05/2015) à https://sentinel.esa.int/documents/247904/2142675/Sentinel-1-SAR-Space-Packet-Protocol-Data-Unit.pdf/d47f3009-a37a-43f9-8b65-da858f6fb1ca?t=1547146144000

[11] R. Piantanida, Level 1 Detailed Algorithm Definition, ESA (07/06/2019) à https://sentinel.esa.int/documents/247904/1877131/Sentinel-1-Level-1-Detailed-Algorithm-Definition

[12] P. Guccione & al., Sentinel-1A: Analysis of FDBAQ Performance on Real Data, IEEE Trans. on Geoscience and Remote Sensing 53 (12), 6804 (2015).

[13] D. Huffman, A Method for the Construction of Minimum-Redundancy Codes, Proc. IRE 40 (9) 1098-1101 (1952).

[14] S.N. Madsen, Estimating the Doppler centroid of SAR data, IEEE Transactions on Aerospace and Electronic Systems 25 (2) 134-140 1989.

[15] J.-M. Friedt, Introduction à l’analyseur de réseau : le NanoVNA pour la caractérisation spectrale de dispositifs radiofréquences, Hackable 36 (jan.-mars 2021) - https://connect.ed-diamond.com/Hackable/hk-036/introduction-a-l-analyseur-de-reseau-le-nanovna-pour-la-caracterisation-spectrale-de-dispositifs-radiofrequences

[16] J.-M Friedt, W. Feng, Analyse et réalisation d’un RADAR à synthèse d’ouverture (SAR) par radio logicielle (2/3), GNU/Linux Magazine France n° 242 (nov. 2020) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-242/resolution-azimutale-d-un-radar-a-bruit-analyse-et-realisation-d-un-radar-a-synthese-d-ouverture-sar-par-radio-logicielle

[17] A. Moreira & al., A tutorial on Synthetic Aperture Radar, IEEE Geoscience and Remote Sensing Magazine 6-43 (March 2013).

[18] D. Sandwell & al., GMTSAR: An InSAR Processing System Based on Generic Mapping Tools (2nd Ed.), pp.51-59 (2016), à https://topex.ucsd.edu/gmtsar/tar/GMTSAR_2ND_TEX.pdf

[19] C.A. Balanis, Antenna Theory - Analysis and design, 3rd Ed., Wiley Interscience (2005).

[20] J.-M Friedt, Le télescope à particules cosmiques : principe de la mesure par coïncidence, Opensilicium 11 (juin-août 2014) - https://connect.ed-diamond.com/Open-Silicium/os-011/le-telescope-a-particules-cosmiques-principe-de-la-mesure-par-coincidence

[21] A. Anghel & al., Bistatic SAR imaging with Sentinel-1 operating in TOPSAR mode, IEEE Radar Conference (RadarConf) 2017.

[22] Émettre dans une bande interdite ne semble pas gêner la Chine : https://labo.obs-mip.fr/multitemp/le-cesbio-pique-la-chine/ et https://labo.obs-mip.fr/smos-blog/a-gigantic-rfi-source-in-china-is-still-on-and-doing-lots-of-damage/

[23] M. J. Murrian & al., GNSS Interference Monitoring fromLow Earth Orbit (2020) à https://arxiv.org/pdf/2009.04093.pdf

[24] P. Tabary, L. Perier, J. Gagneux, & J. Parent-du-Chatelet Test of a staggered PRT scheme for the French radar network, J. Atmospheric and Oceanic Technology 22(4) 352-364 (2005) à https://journals.ametsoc.org/view/journals/atot/22/4/jtech1709_1.xml

[25] A. Capaccio, U.S. Builds Ground-Based Arsenal to Jam Russia, China Satellites, Bloomberg (17 avril 2020) à https://www.bloomberg.com/news/articles/2020-04-17/u-s-space-force-is-arming-to-jam-russian-and-chinese-satellites