Nous proposons d’explorer la nature des particules cosmiques en proposant une combinaison astucieuse de mesures effectuées en points spatialement distincts par plusieurs compteurs Geiger. L’analyse des signaux acquis par ces détecteurs - et en particulier la mesure quasi-simultanée du passage de particules ionisantes par plusieurs détecteurs - permet de compléter l’information de débit de dose par une information de direction d’incidence de la particule. Nous reproduisons ainsi un certain nombre d’expériences, selon une stratégie dite de coïncidence, qui ont permis, il y a plus de 70 ans, d’élucider la nature des particules cosmiques.
1. Introduction
Un détecteur de particules ionisantes [1], par exemple un compteur Geiger [2, 3], convertit un passage de particule en une impulsion de courant observée sous forme d’une impulsion de tension. Un tel détecteur scalaire ne peut discerner la direction d’incidence de la particule qui induit un signal électrique. Par ailleurs, la mesure est polluée par diverses sources de bruits aléatoires (bruit électrique) ou de détection d’événements ne correspondant pas au sujet des investigations (bruit de fond de la radioactivité au sol couvrant le signal des particules cosmiques).
Nous avions mentionné dans un article précédent [4] que le taux d’absorption des particules cosmiques a été utilisé pour invalider la présence de cavités dans une pyramide, ou cartographier les structures sous-terraines de volcans, sans préciser comment il est possible de connaître la direction dans laquelle se fait l’analyse. De façon générale, la résolution de ce problème se nomme la tomographie, qui consiste à rechercher la structure d’absorbants permettant de justifier l’observation de taux de transmission de particules au travers de cet objet [5].
Figure 1 : Schéma de principe de la mesure par coïncidence : deux compteurs Geiger G1 et G2 sont positionnés selon une certaine orientation (ici verticalement) et ne se déclenchent simultanément que si un rayon cosmique (bleu) suffisamment énergétique traverse les deux capteurs simultanément. Ainsi, les rayonnements issus de l’environnement (en rouge) sont exclus de la mesure par coïncidence puisque observés par un seul des deux compteurs. La direction d’incidence des rayons cosmiques est déterminée par la position relative des deux compteurs : pour un angle de 45°, le second compteur est positionné en G2’. L’image de fond présente le tube Geiger de 15 mm de diamètre équipant le RM-60 de Aware Electronics.
Nous nous proposons d’exposer ici la méthode expérimentale qui, grâce à la mesure simultanée du passage d’une particule au travers de plusieurs détecteurs, permet d’une part d’éliminer la majorité des sources de bruits (électrique ou radioactivité au niveau du sol) et d’autre part de limiter la mesure uniquement aux particules respectant une direction d’incidence déterminée (Fig. 1) [6, 7]. Cette méthode expérimentale, nommée mesure par coïncidence, a été le sujet du prix Nobel de Physique décerné en 1954 [8, 9].
Le principe est aujourd’hui fort simple mais se heurtait à l’époque à des difficultés de mise en œuvre expérimentale [8] (comment limiter la mesure à des évènements simultanés à une époque précédent la logique numérique telle que nous la connaissons aujourd’hui ?) : seule une particule traversant simultanément deux détecteurs spatialement distincts induit un signal exploitable et est considérée comme provenant de la direction formée par la droite reliant les deux détecteurs. Les bruits non corrélés (fluctuation d’une alimentation électrique, particule provenant d’une source qui n’est pas dans l’alignement des deux détecteurs) sont ainsi rejetés et la mesure se limite aux évènements “intéressants”. La notion de simultanéité n’est évidemment pas exacte mais relative à la durée de l’impulsion du signal induit par le passage d’une particule dans le détecteur. Dans le cas de nos expériences, le circuit de mise en forme des impulsions d’un compteur Geiger induit des impulsions d’une durée de 50 µs. Une particule ne se déplaçant ne serait-ce qu’à 1% de la vitesse de la lumière parcourt dans cet intervalle de temps 150 m. En ne considérant que des détecteurs séparés de quelques décimètres au plus, les signaux induits par les deux compteurs Geiger peuvent donc être considérés comme simultanés lorsque produits par une même particule. Nous allons dans un premier temps analyser la statistique de la mesure par coïncidence et une méthode simple de mise en œuvre, avant de proposer quelques démonstrations expérimentales de résultats de détection de rayons cosmiques.
2. La méthode de mesure par coïncidence
Au-delà de déterminer la direction d’origine de la particule qui interagit avec le télescope, le bruit électrique et le bruit de fond de la radioactivité environnante seront rejetés par la méthode de coïncidence puisque la probabilité que deux compteurs produisent simultanément une impulsion électrique chacun, qui ne soit pas due au passage d’une particule ionisante, est faible. Nous devons cependant quantifier la probabilité de faux positifs, afin d’identifier quel nombre d’évènements est attribuable à des rayons cosmiques ou, au contraire, à des évènements produits par chance sur les deux capteurs simultanément.
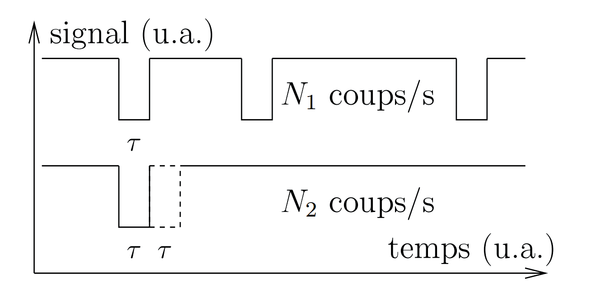
Figure 2 : Chronogramme de la mesure en coïncidence fortuite par deux compteurs Geiger détectant respectivement N1 et N2 coups/unité de temps, chaque impulsion étant d’une durée τ
La Fig. 2 illustre graphiquement les considérations que nous allons formaliser ci-dessous : supposons que deux détecteurs induisent N1 et N2 mesures respectivement par unité de temps. Chaque événement se traduit par une impulsion de durée τ. Si par hasard le second détecteur induit une transition dans un intervalle ± τ alors que le premier détecteur est excité, une transition en coïncidence sera produite traduisant un faux positif. Le premier détecteur induit N1 transitions par unité de temps, le second induit N2 transitions dans ce même intervalle de temps, et le temps de recouvrement à ±τ près des secondes impulsions sur une impulsion du premier capteur se produit statistiquement à un taux de N=2τ N1N2 par unité de temps. En pratique nous observons qu’au niveau du sol, les compteurs Geiger RM-60 (Aware Electronics, http://www.aw-el.com/) que nous utilisons induisent un décompte de l’ordre de 50 coups/minute. Par conséquent, le taux de faux positifs est de l’ordre de N=0,002 coups/minute, ou un coup toutes les 8 heures. Cette valeur est très importante car elle détermine à partir de combien de coups/minute observés dans un circuit de coïncidence nous pourrons affirmer que nous avons détecté une particule cosmique et non du bruit. Les petits compteurs Geiger que nous utilisons ne présentent qu’une surface d’interaction réduite avec les particules ionisantes et induisent donc peu de mesures par unité de temps. Deux solutions pour améliorer la statistique est soit d’augmenter la surface d’interaction (solution qui n’est pas acceptable sur un compteur Geiger que nous prétendons embarquer en avion et dont le volume doit nécessairement être réduit), soit d’augmenter la durée de la mesure pour accumuler plus de points de mesure que le niveau du bruit de fond. En effet, [10] indique que la statistique, ou en d’autres termes le rapport signal à bruit, croît comme la racine du temps de mesure, comme pour tout bruit aléatoire polluant une mesure [11].
Au-delà de la coïncidence à deux compteurs, si ce taux de faux positifs reste trop élevé devant la faible probabilité de détection d’un événement très rare, il est envisageable de multiplier le nombre de détecteurs dans la mesure de coïncidence en n’enregistrant que les évènements où tous les détecteurs sont actifs simultanément. La probabilité de faux positifs pour M détecteurs est de l’ordre de τM−1· NM si cette fois N est le nombre d’évènements détectés par chaque compteur par unité de temps. Le passage à 3 compteurs alignés fait déjà passer le taux de faux positifs à moins de 1 coup erroné tous les 22 ans !
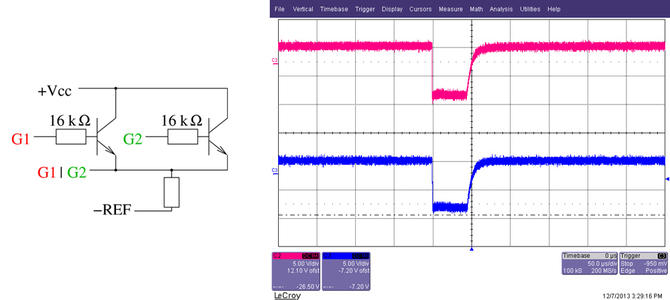
Figure 3 : Gauche : schéma de la porte OU à base de transistors permettant de mettre en œuvre la méthode de coïncidence lorsque l’état au repos de chaque compteur est haut (niveau logique 1) et la tension chute (niveau logique 0) lorsqu’une particule est détectée. Nous comptabilisons donc les mesures de chaque compteur Geiger indépendamment (G1, G2) et de la coïncidence (G1 OU G2). Droite : validation du bon fonctionnement du circuit en court-circuitant les deux entrées logiques A et B. Chaque particule détectée se traduit par les mêmes formes d’impulsion en entrée et en sortie : les transistors sont suffisamment rapides pour cette application.
Les compteurs Geiger RM-60 que nous utilisons induisent un état au repos de tension positive, pour induire une impulsion de tension négative lorsqu’une particule est détectée. Le circuit logique qui ne génère une impulsion de tension négative que si ses deux entrées sont simultanément négatives est la porte OU. Plutôt que de sortir l’artillerie lourde des portes logiques2, il nous semble plus élégant d’implémenter cette fonctionnalité au niveau du transistor (Fig. 3). Une approximation grossière de l’utilisation du transistor bipolaire NPN en régime saturé est de considérer que le courant est capable de circuler entre le collecteur et l’émetteur lorsque la base est à une tension positive (supérieure de 3 V environ) par rapport à l’émetteur et que ce courant est bloqué sinon. Ainsi, en plaçant deux transistors en parallèle tel que proposé sur le circuit de la Fig.3, nous implémentons bien une fonction OU, ici au moyen de deux transistors 2N2222 (mais toute référence NPN fera l’affaire dans cet exemple). On se convaincra du bon fonctionnement du circuit en comparant le décompte d’un compteur Geiger seul, et de la sortie de ce circuit dont l’entée est formée du même signal polarisant les deux entrées de cette implémentation de la porte OU. Si les deux résultats de mesure sont identiques, le circuit sera considéré comme fonctionnel, et en particulier validera que la vitesse de commutation du transistor est suffisante pour détecter les évènements en coïncidence sur deux compteurs Geiger identiques. On notera que ce circuit s’avère être l’implémentation moderne du circuit proposé à base de valves en 1930 dans [12] : les grilles des divers tubes sont polarisées par les sorties des compteurs Geiger, et la sortie des tubes connectés en parallèle ne change d’état que si toutes les grilles changent d’état simultanément.
Par conséquent, l’utilisation de ce circuit nécessite 3 ports série (en pratique convertisseurs USB-RS232) : deux ports comptent le nombre de coups détectés par chaque compteur Geiger individuellement (G1 et G2) et un troisième port compte le nombre de coups en coïncidence (G1 OU G2). Il semble que la simultanéité des interruptions générées par les trois interfaces ne pose pas de problème et soit géré convenablement par GNU/Linux. Par ailleurs, une option qui peut s’avérer utile, bien que générant des fichiers d’enregistrement volumineux, consiste à dater (à la seconde près, fonction time() de Linux) chaque évènement. Toutes les tensions d’alimentation sont fournies sur les ports série respectifs : la norme RS232 indiquant qu’un état 1 se traduit par une tension négative, toutes les tensions nécessaires au schéma de la Fig. 3 sont disponibles sur les signaux de contrôle du port série (DTR et RTS). Les interruptions traduisant une détection de particule sont déclenchées en connectant G1, G2 et G1 OU G2 aux trois entrées RX de chaque port série.
3. Mesures : distribution angulaire du flux de particules cosmiques
La capacité de déterminer la direction d’incidence d’une particule ionisante détectée par le télescope ouvre la perspective de cartographier la distribution angulaire des rayons cosmiques arrivant au sol. La littérature nous informe sur l’absence de distribution azimutale (nous reviendrons sur ce point plus tard, section 4) mais uniquement d’une dépendance zénithale (i.e. avec l’angle par rapport à la verticale). Étrangement, il semble que cette distribution ne soit pas uniforme, mais suive une loi en cosn(θ), avec une puissance n qui est déterminée expérimentalement autour de 2 mais ne semble pas avoir de justification théorique [13, p.25] [14, section 3], bien qu’une modélisation statistique de la propagation d’une multitude de particules semble susceptible de reproduire cette distribution en tenant compte des interactions dans l’atmosphère et la détection en coïncidence sur deux détecteurs [15, 16].
Figure 4 : Mise en œuvre expérimentale de la méthode de coïncidence au moyen de deux compteurs Geiger fixés sur un montage (planchette équatoriale) permettant de varier l’angle zénithal. En haut à droite : tension de sortie de chaque compteur Geiger, illustrant les évènements observés en coïncidence (impulsion au milieu de l’écran) et le rejet des signaux observés par un seul détecteur (impulsions sur la trace du bas, moitié droite de l’écran).
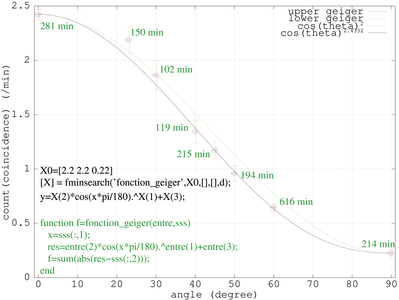
Les enregistrements se font par tranche de 1 minute et chaque mesure dure de 2 à 10 heures (Fig. 5). Nous retrouvons la loi décrite dans la littérature d’une distribution en cos2(θ) du flux de particules cosmiques, avec θ l’angle zénithal. Nous avons tracé des courbes de références pour n=2 et, afin de s’ajuster au mieux (fonction fminsearch de GNU/Octave), n=2,43. En insert dans le graphique de la Fig. 5, la fonction GNU/Octave appelée par fminsearch afin d’identifier les coefficients optimums de la loi représentant la dépendance en angle zénithal du flux de particules cosmiques. Le vecteur de paramètres p contient en premier argument la puissance du cosinus, les deux autres arguments étant simplement l’homothétie et le niveau de base de la loi. Les données expérimentales (angles pour lesquelles les mesures sont effectuées et décompte des évènements en coïncidence des deux compteurs) sur lesquelles nous cherchons à ajuster les coefficients sont fournies dans le vecteur s.
Figure 5 : Nombre d’évènements observés en coïncidence par unité de temps (ici la minute) en fonction de l’angle zénithal. Chaque compteur individuel décompte de l’ordre de 20 à 30 coups/minute au cours de ces mesures. Les valeurs au-dessus de chaque barre d’erreur indique la durée de la mesure.
Les barres d’erreur indiquées sur la Fig. 5 sont issues du calcul vu au préalable du nombre de coups dus à une coïncidence fortuite du déclenchement des deux compteurs : les valeurs de l’ordre de 0,02 coups/min sont de l’ordre de 1/100e de la mesure et cette coïncidence fortuite n’est clairement pas la source dominante d’incertitude. Pour une distribution aléatoire de N mesures pendant un intervalle de temps t, l’incertitude sur la mesure [6, 17] est √N/t : ces deux contributions respectives sont indiquées par les barres d’erreur en bleu et en rouge sur la Fig. 5.
Approcher une source radioactive générant des rayonnements faiblement ionisants - par exemple une montre aux aiguilles couvertes de radium - induit une augmentation du nombre d’évènements détectés par chaque compteur individuellement mais ne modifie par significativement la statistique des évènements observés en coïncidence. Les particules émises ne sont probablement pas assez énergétiques pour traverser les deux compteurs Geiger séquentiellement et n’interagissent qu’au travers de la vitre en mica - faiblement absorbante - sur la face avant de chaque compteur.
4. Dépendance azimutale du flux de particules cosmiques
Nous avons analysé la dépendance zénithale du flux de particules cosmiques : il semble intuitif que le nombre de particules atteignant le sol dépende de l’épaisseur d’atmosphère traversée et donc de l’angle à la verticale (dépendance zénithale). Moins intuitif, il existe une dépendance du flux de particules cosmiques en fonction de l’angle azimutal, à savoir selon que nous regardions vers l’ouest ou vers l’est [18, pp.68-73] [19, chap.3]. La cause de cette dépendance est le champ magnétique terrestre et la nature des particules cosmiques galactiques. Le champ magnétique terrestre brise la symétrie cylindrique de l’interaction de particules cosmiques supposées d’incidence isotrope avec la Terre : les particules de charge négative sont déviées dans une direction, les particules de charge positive dans la direction opposée. Or il s’avère que la majorité des particules cosmiques galactiques sont chargées positivement (protons, noyaux d’helium aussi appelés particules alpha, noyaux d’éléments plus lourds). Cette brisure de symétrie se traduit par un flux de particules plus important venant de l’ouest que de l’est (tendance qui s’inversera lors du prochain retournement du champ magnétique terrestre). Nous reproduisons expérimentalement les mesures de Rossi sur ce point en observant le nombre de particules cosmiques en coïncidence pour un angle zénithal de 45o mais orienté vers l’ouest et vers l’est.
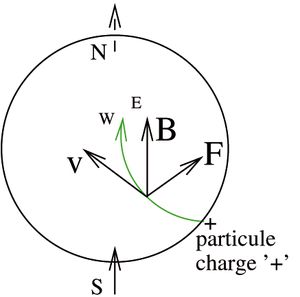
Figure 6 : Déflection d’une particule incidente à la Terre, de charge positive, par le champ magnétique terrestre. Une particule de charge positive est dirigée vers l’est par le champ magnétique terrestre et se traduira donc par un nombre supérieur de particules provenant de l’ouest que de l’est.
C’est ainsi que la charge des particules cosmiques a été historiquement déterminée en analysant la brisure de symétrie sur la trajectoire d’incidence des particules cosmiques induite par le champ magnétique terrestre (Fig. 6). Le champ magnétique orienté actuellement du sud au nord (par définition) tend à pousser les particules de charge positive vers l’est et les particules de charge négative vers l’ouest. Ainsi, le décompte du nombre de particules pour un angle zénithal donné pour une orientation azimutale vers l’ouest ou l’est peut nous renseigner sur la charge des particules cosmiques. On se rappellera en effet qu’une particule de charge q en mouvement, de vitesse v→ dans un champ magnétique B→, subit une force F→=q· v→∧B→ : le lecteur qui a oublié ses cours de physique élémentaire pourra se raffraîchir la mémoire en recherchant « force de Lorentz » sur le web. L’expérience montre que pour un angle zénithal de 45°, nous observons 1,10±0,037 (deux mesures) pour une orientation du télescope vers l’ouest et 0,96±0,03 pour une orientation vers l’est, pendant des intégrations durant un peu plus de 10 heures. La différence est donc statistiquement significative et permet de confirmer la nature majoritairement de charge positive des rayons cosmiques galactiques venant interagir avec la haute atmosphère. Ce résultat est par ailleurs cohérent avec la différence de l’ordre de 10% entre les flux venant de l’ouest et de l’est annoncé dans la littérature [18, p.69].
5. Mesures : réduction du bruit de fond lors d’une mesure en vol
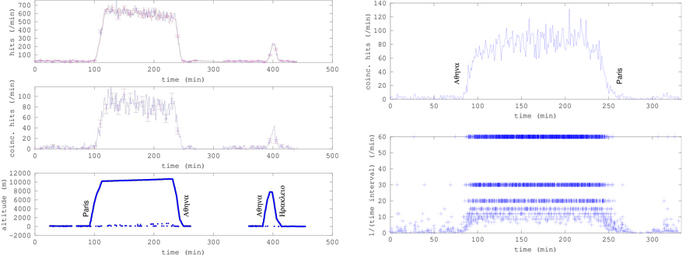
L’extension naturelle de cette séquence d’expériences est de reproduire les mesures effectuées au cours de vols en avion de ligne, mais en exploitant la coïncidence pour s’affranchir du bruit des sources radioactives au sol qui sont probablement la cause de l’absence de mesure pour une altitude inférieure à environ 3000 m lors de l’utilisation d’un seul compteur Geiger [4]. Cependant, [20] nous informe d’une difficulté dans cette expérience liée à la faible statistique du décompte par coïncidence par des capteurs ne sondant qu’un petit volume que sont les compteurs Geiger : le temps d’intégration long auquel nous avons eu recours dans la section précédente n’est simplement pas disponible lors de l’ascencion ou la descente d’un ballon sonde ou d’un avion. La solution proposée dans cette référence consiste à non seulement mesurer le nombre de coïncidences dans un intervalle de temps donné (dans notre cas des séries de 1 minute) mais en plus de dater chaque événement afin d’extrapoler la fréquence des phénomènes, même s’ils n’ont été observés que pendant une courte durée.
Figure 7 : Gauche, de haut en bas : mesure de deux compteurs Geiger positionnés avec un angle zénithal d’environ 0° ; mesure de coïncidence de ces deux compteurs Geiger ; altitude au cours du vol Paris-Athènes puis Athènes-Heraklion. Droite : mesure au cours du vol (retour) Athènes-Paris, en haut le nombre d’évènements en coïncidence et en bas l’inverse de l’intervalle de temps entre deux détections de particules en coïncidence suivant le concept proposé dans [20]. Quelques barres d’erreur ont été distributées pour indiquer la précision de la mesure sur le premier vol.
Nous constatons en effet (Fig. 7) que la mesure de coïncidence n’est pas pertinente sur une durée d’intégration aussi courte que 1 minute, mais observons néanmoins la croissance du nombre d’évènements observés avec (deux Geiger en coïncidence) et sans (chaque Geiger individuel) coïncidence en fonction de l’altitude, et une décroissance lorsque la latitude décroît. Nous avons tenté d’appliquer, sur un second jeu de données, la méthode de traitement préconisée dans [20], mais bien que nous observions la perte de résolution pour les forts débits de particules (au cours du vol), le gain sur les faibles débits (au sol) ne semble pas visible. Il n’apparaît pas clairement en quoi le changement de représentation des données datées à la seconde près améliore la résolution de la mesure aux faibles débits de dose, mais un point du traitement du signal nous a peut-être échappé.
6. Expérience de détection des particules secondaires
Afin de démontrer la génération de particules secondaires lors de l’interaction d’un rayon cosmique incident avec la matière, nous reproduisons l’expérience consistant à varier l’épaisseur de matière (ici du plomb qui présente une forte probabilité d’interaction - section efficace) au-dessus des capteurs pour, dans un premier temps, augmenter la longueur d’interaction du rayonnement incident avec la matière, avant de réduire le flux de particules secondaires par absorption dans le bloc de plomb (Fig. 8). Cette expérience est décrite et analysée dans [21].
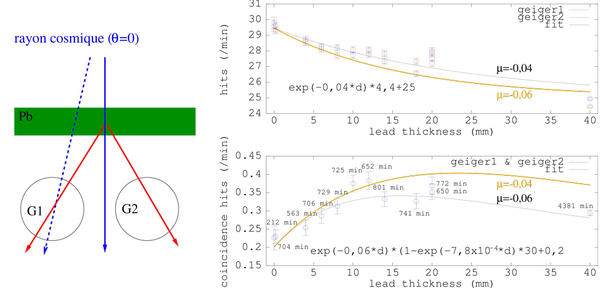
Figure 8 : Montage expérimental : les deux compteurs Geiger sont en configuration dans laquelle ils ont peu de probabilité de détecter un rayon cosmique incident et seules les gerbes de particules induites par interaction avec les feuilles de plomb peuvent induire une réponse simultanée des deux détecteurs. Les feuilles de plomb font 2 mm d’épaisseur et un nombre allant de 0 à 10 feuilles sont placées sur les compteurs. Toutes les feuilles sont découpées selon un carré de 5x5 cm2.
Nous nous plaçons dans la configuration dans laquelle un rayon cosmique incident ne présente qu’une faible probabilité d’interaction avec les deux compteurs en coïncidence (cas de l’angle zénithal de 90°). Dans l’expérience originale [18], trois compteurs Geiger étaient configurés en triangle afin de garantir l’incapacité d’une particule incidente unique de déclencher simultanément les trois détecteurs, et les compteurs Geiger étaient complètement entourés de feuilles de plomb. La durée de chaque mesure est indiquée sur la Fig. 9 en bas : compte tenu du faible nombre de coups observés dans cette configuration, des mesures de plus de 10 h sont nécessaires pour accumuler une statistique suffisante. Ici encore les barres d’erreur sont exprimées comme la racine du nombre de phénomènes observés divisée par le temps de mesure.
Figure 9 : En haut : débit de particules détectées par chaque compteur Geiger individuel en fonction de l’épaisseur de plomb placée au-dessus de chaque instrument. En bas : nombre de coups en coïncidence détectés par les deux compteurs en fonction de l’épaisseur de plomb placée au-dessus des instruments. Pour chaque courbe, la ligne noire correspond à l’identification des coefficients minimisant l’erreur au sens des moindres carrés entre les données expérimentales et la loi proposée, et en orange la loi exploitant le coefficient d’absorption de l’autre courbe (donc un coefficient de 0,04 cm−1 pour la courbe du bas et 0,06 cm−1 pour la courbe du haut). Gauche : interprétation de la mesure. La configuration “honrizontale” des deux compteurs ne présente qu’une faible probabilité de détection d’une particule incidente (bleu), et seule la création d’une gerbe de particules secondaires (rouge) atteignant “simultanément” les deux compteurs permet d’interpréter les résultats de mesures.
Une épaisseur trop faible (ou nulle) de plomb se traduit par un faible taux de particules secondaires car le rayon cosmique incident n’a pas le temps d’interagir avec la matière. Une épaisseur trop importante de plomb se traduit par une absorption des particules secondaires générées et donc une décroissance du nombre de coups observés en coïncidence par les deux compteurs. Dans cet exemple, les plaques de plomb ne sont situées que au-dessus des capteurs et non autour comme décrit dans l’expérience originale, faute de matière. Le plomb est un élément toxique et difficile à obtenir : nous avons constaté qu’une batterie au plomb n’est pas une source exploitable (plaques de plomb friables) et nous n’avons pas expérimenté avec de la soudure en alliage étain-plomb. Le lecteur plus fortuné pourra reproduire cette expérience avec de l’or qui présente un numéro atomique proche. Une analyse avec divers matériaux serait sûrement instructive [9, Fig. 5], et mériterait à être reproduite avec du fer, cuivre, laiton et autres matériaux/alliages de numéro atomique suffisamment élevé mais plus facilement accessible.
Plus formellement, les lois choisies pour comprendre ces courbes sont expliquées en détail dans [21]. La courbe du haut de la Fig. 9 indique l’absorption des rayonnements incidents par le bouclier formé des plaques de plomb. Comme toute loi d’absorption du premier ordre, il s’agit d’une loi selon une exponentielle
N=N1+N2exp(−µd)
avec N le nombre de coups observés par chaque compteur Geiger, N1 et N2 un nombre de particules incidentes issues de l’environnement sans traverser les plaques de plomb (N1) ou les traversant (N2). Le paramètre important est le taux d’absorption par unité d’épaisseur d de plomb des particules ionisantes : µ. Ce coefficient est identifié comme valant 0,04 cm−1 (trait noir de la figure du haut). La différence de configuration géométrique est probablement la cause de la différence de ce coefficient d’absorption avec la valeur proposée dans [21] (qui propose une valeur 10 fois plus élevée).
Le second graphique tient non seulement compte de la probabilité d’absorption d’une particule avec le bouclier de plomb, mais en plus de la probabilité d’interaction pour générer une gerbe de particules secondaires. Un second terme du premier ordre est donc inclus pour exprimer le nombre d’évènements en coïncidence sur les deux détecteurs :
N=N1′+N2′(1−exp(−β d))·exp(−µ d)
Le terme µ d’absorption reste a priori le même mais nous ajoutons un terme de probabilité d’interaction (1−exp(−β d)) (on vérifie que si d=0, i.e. en l’absence de plomb, la probabilité d’interaction est nulle !). La recherche des coefficients ajustant au mieux cette loi selon les points expérimentaux induit la courbe orange du bas de la Fig. 9 si nous conservons µ constant, et noire si nous permettons à µ de varier pour atteindre 0,06 cm−1. Cette variation de 50% de la valeur proposée peut sembler énorme, mais en la réinjectant dans la loi de comptage de la Fig. 9 du haut (courbe orange), nous nous rendons compte que le résultat reste visuellement très acceptable, et l’extraction de µ de la mesure en coïncidence semble plus précise car plus sensible à ce paramètre. Cette référence indique un ratio du nombre de particules n’interagissant pas avec le plomb au nombre de particules interagissant de 70% : dans notre cas, le ratio serait plutôt de l’ordre de 25/(25+4,4)=85%.
7. Utilisation d’un capteur optique CMOS pour la détection de particules ionisantes
7.1 Appareil photographique numérique pour la détection de particules ionisantes
Il est connu que les astronautes des missions Apollo ont observé des flashs de lumière attribués à l’interaction de particules cosmiques avec la rétine, phénomène qui a été étudié en plus de détails sur la station MIR [22]. Il semble par conséquent logique de considérer si un appareil photographique numérique est sensible aux mêmes phénomènes et peut faire office de capteur de particules du rayonnement cosmique [23]. Par ailleurs, l’aspect matriciel du capteur ouvre des perspectives de traitement du signal bien plus riches que les capteurs scalaires que sont les compteurs Geiger : identification de la direction d’incidence, distribution spatiale des particules interagissant avec le capteur optique par exemple. En ce sens, l’exploitation de capteurs CCD ou CMOS pour la détection de rayons cosmiques nous semble pertinente dans le contexte de la méthode de coïncidence : nous n’allons pas nous contenter d’observer le comportement d’un unique pixel, mais aussi de ses voisins lors de l’interaction avec une gerbe de particules (multitude de points allumés simultanément) ou si une particule interagit en incidence oblique (trace allongée).
Nos expériences en ce sens nécessitent des appareils capables d’enregistrer des photographies en pose longue (Bulb), uniquement accessible à notre connaissance sur les modèles réflexes haut de gamme. Nous avons donc expérimenté avec les Nikon D5100 et D3200. Quelques exemples de mesures acquises sur des temps de pose de 10 minutes, en plaçant l’appareil photographique dans un environnement aussi sombre que possible, en gain de 1600 ou 3200 ISO, sont proposés sur la Fig. 10. Nous attribuons les pixels lumineux dans les conditions d’obscurité à des interactions avec une gerbe de particules issue de rayons cosmiques [24] sans avoir étudié plus précisément la nature de ces interactions ou les causes autres telles que des effets purement électroniques du capteur.
Figure 10: Traces sur des photographies acquises en pose longue dans l’obscurité et un gain maximal, attribuées à des rayonnements cosmiques. Noter la forme allongée - incidence oblique en (b) et (c) en haut à gauche - ou la multitude de traces adjacentes ((a) à droite, (b) en bas). La photographie de (a) est prise avec un Nikon D5100, les photographies (b) et (c) avec un D3200. Les coordonnées au-dessus de chaque figure correspond aux coordonnées du centre de la vignette sur la photographie.
Le nombre de pixels illuminés sur des temps de pose de 10 minutes varie de 0 à 7 pour nos expériences. Nous ne nous sommes pas efforcés de reproduire toutes les expériences citées ci-dessus sur les appareils photographiques, si ce n’est une tentative grossière de mesure de coïncidence en suporposant les deux appareils qui ne donne pas de résultat convaincant. Nous avons évidemment vérifié que ces traces ne sont pas attribuables à des pixels défectueux (la position et la forme de la trace varie d’une photographie à une autre), et un nombre aussi conséquent d’interaction des capteurs optiques avec des particules cosmiques laisse même dubitatif quant à la capacité de nos processeurs de fonctionner sans protection contre les rayonnements ionisants. Les illustrations de la Fig. 10 sont obtenues par traitement d’image : nous acquérons un certain nombre de photographies en exposition longue (mode Bulb, 10 minutes de temps de pose), gain élevé (1600 ou 3200 ISO), et chargeons ces images dans GNU/Octave (fonction imread() pour charger les images au format JPEG, puis rgb2gray() pour passer de la couleur aux tons de gris). Une recherche automatique des points intéressants s’effectue par [u,v]=find(image>200); pour identifier les coordonnées des pixels clairs sur l’image (intensité supérieure à 200 sur une échelle de 8 bits), et les vignettes autour de ces points dignes d’intérêt sont tracées par imagesc(). La majorité des photographies contient au moins 2 traces de particules. Chaque image de la Fig. 10 est donc une vignette sur une zone de ±30 pixels extraite de la photographie initiale de 16 ou 24 Mpixels, centrée sur un évènement identifié comme intéressant par seuillage sur l’intensité lumineuse.
7.2 Utilisation des capteurs optiques équipant les téléphones portables
Les smartphones sont devenus de véritables appareils photographiques qui, malgré une qualité optique médiocre, sont équipés de capteurs CMOS présentant un nombre de pixels digne de beaucoup d’appareils photographiques dédiés. Il semble donc naturel, compte tenu de l’évolution de notre démarche, de considérer l’utilisation de ces capteurs pour la détection de rayonnements ionisants. Une rapide recherche dans la littérature [25] indique que plusieurs applications ont déjà été écrites en ce sens. Malheureusement, un objectif orienté plus vers la radioprotection que vers l’analyse scientifique des mesures rend la majorité de ces programmes d’un intérêt technique restreint, tandis que les auteurs de [25] ont décidé de ne pas publier leur logiciel au public. Radioactivity Counter3 est un logiciel propriétaire commercial qui se démarque en fournissant à l’utilisateur les données brutes (image de la caméra) utilisées pour estimer le débit de dose de rayonnement ionisant détecté par le capteur optique. Nous avons exploité cette solution, à défaut d’un outil libre qui ne semble pas disponible pour le moment4, pour poursuivre cette étude. La source de rayonnement ionisant est une montre aux aiguilles couvertes de radium (Fig. 11), et les tests sont effectués sur un Samsung Galaxy S3, même s’il s’agit du modèle le plus bruyant et donc le moins approprié pour cette expérience [25, table 14].
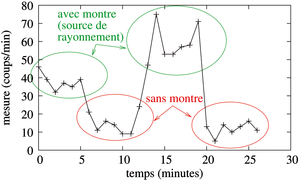
Figure 11: Montage pour la détection de rayonnements ionisants par le capteur optique d’un téléphone mobile : la lentille est couverte d’un scotch métalisé opaque à la lumière. Droite : mesure en cours en présence d’une source de rayonnement qu’est une montre aux aiguilles couvertes de radium.
La mesure ne présente pas un rapport signal à bruit exceptionnel mais démontre néanmoins la viabilité de la méthode. La présence d’un récepteur GPS, source stable de temps pour la datation des images présentant un signal intéressant, et l’acquisition d’images au rythme d’environ 16 fps (résolution temporelle de τ=62 ms), permettrait d’étendre cette application à une mesure de coïncidence pour permettre de réaliser un télescope comme nous l’avons présenté au début de cet article. Au rythme d’environ N=10 particules/minute en l’absence de source, le taux de fausses coïncidences N2·τ serait de 0,1 mesure/minute. Il s’agit là d’une valeur 10 fois plus faible que les résultats de mesures par coïncidence proposées en Fig. 5 qui tend à indiquer que l’expérience pourrait être pertinente.
Figure 12: Mesure du débit de dose de rayonnement ionisant par un smartphone Samsung Galaxy S3 en l’absence (en rouge, milieu et fin de la mesure) ou en présence (début et milieu de la mesure) d’une source de rayonnement. Nous avons pris soin au cours de cette expérience de placer le téléphone dans une pièce sombre afin de limiter la pollution potentielle des sources lumineuses.
Ce dernier paragraphe, de par l’absence d’outil libre disponible pour reproduire ces résultats, est peu satisfaisant et doit être considéré par le lecteur comme une opportunité de contribuer à un projet scientifique en fournissant un outil libre fonctionnant sur smartphone pour obtenir des détections de rayons cosmiques par traitement d’images sur capteurs CMOS de téléphones mobiles.
Conclusion
Nous avons proposé une extension simple - ne nécessitant que deux transistors et quelques composants passifs - de l’exploitation de compteurs Geiger pour exploiter une méthode de mesure permettant de s’affranchir de la majorité des sources de bruit et d’ajouter une information de direction d’incidence des particules cosmiques détectées. Le nombre de mesures ainsi obtenues n’est que de l’ordre de 1/10e du nombre d’événements observés par chaque compteur individuel (d’origine cosmique et terrestre). Ces mesures résiduelles sont attribuées à une origine cosmique exclusivement, comme en atteste la dépendance en angle zénithale du nombre d’événements par unité de temps : deux compteurs parallèles au sol comptent un nombre minimum d’événements alors qu’une orientation verticale maximise le nombre de mesures en coïncidence. Nous avons ensuite étendu les résultats obtenus par détecteurs de particules dédiés au cas de l’utilisation d’un appareil photographique numérique dont le capteur optique, placé dans l’obscurité, acquiert une image en pose longue et n’est donc illuminé que par des sources de rayonnements susceptibles de traverser les éléments mécaniques remplaçant l’objectif.
L’identification de la direction d’incidence des particules a donc été illustrée par un agencement judicieux de détecteurs, mais ces applications ne tiennent jamais compte du délai entre le passage de particules au travers des compteurs Geiger. La mesure de ce délai permettrait de remonter à la vitesse de la particule et, pour une multitude de télescopes, sur le point d’origine de la particule. Ces concepts permettent de mieux comprendre l’agencement des détecteurs de particules dans les accélérateurs, dans lesquels des couches concentriques de scintillateurs observés par des photodétecteurs permettent de remonter à la direction d’incidence et position des particules détectées, en exploitant des électroniques de mesure considérablement plus rapides que celles décrites ici.
Remerciements
Mes collègues du département temps-fréquence de FEMTO-ST à Besançon ont amené leur soutien au cours de ces activités ludiques sans relation avec les activités professionnelles de l’institut : J.-J. Boy et P. Berthelot m’ont fourni les feuilles de plomb pour l’expérience de la section 6, tandis que M. Lamothe et D. Rabus m’ont prêté leurs appareils photographiques numériques pour les expériences de la section 7.1. L’achat des compteurs Geiger de Aware Electronics a été financé par l’Associaton Projet Aurore, association pour la diffusion de la culture scientifique et technique, et le trajet en avion entre la France et la Grèce par le projet européen LoveFood.
Références
[1] S. Carlson. Counting particles from space. Scientific American, 284(2):84-86, 2001.
[2] D. Bodor. Construire un compteur Geiger-Müller soi-même, c’est possible. OpenSilicium, 3, 2011.
[3] R. G. Harrison. Meteorological radiosonde interface for atmospheric ion production rate measurements. Review of Scientific Instruments, 76:126111, 2005.
[4] J.-M Friedt. Quelques considérations sur les particules ionisantes présentes en haute altitude - aspects expérimentaux et d’analyses de données. OpenSilicium, 9:28-39, Dec 2013.
[5] N. Lesparre. Mise au point d’une méthode de tomographie utilisant les muons d’origine cosmique. applications au laboratoire souterrain du Mont Terri et au volcan de la Soufrière de Guadeloupe., 30 Septembre 2011. Disponible à www.ipgp.fr/~lesparre/Ecrits/TheseLesparre.pdf.
[6] J.D. Goldader and S. Choi. An inexpensive cosmic ray detector for the classroom. The Physics Teacher, 48:594-597, December 2010.
[7] F. Blanco, F. Fichera, P. LA Rocca, F. Librizzi, O. Parasole, and F. Riggi. Educational cosmic ray experiments with Geiger counters. Disponible à http://arxiv.org/pdf/physics/0701015.pdf.
[8] W. Bothe. Nobel lecture: the coincidence method. Disponible à nobelprize.org.
[9] L. Bonolis. Walther Bothe and Bruno Rossi: The birth and development of coincidence methods in cosmic-ray physics. Am. J. Phys., 79(11), Nov. 2011.
[10] J.W. van Holten. Statistics of coincidences. Disponible à http://www.hisparc.nl/fileadmin/HiSPARC/Lesmateriaal_fysica__jan-willem_/coinc.pdf.
[11] G.F. Knoll. Radiation detection and measurement - 3rd Ed. Wiley, 2000.
[12] B. Rossi. Method of registering multiple simultaneous impulses of several Geiger’s counters. Nature, 125:3156, 1930.
[13] P.K.F. Grieder. Cosmic Rays at Earth - Researcher’s Reference Manual and Data Book. Elsevier, 2001.
[14] J. Kempa and I.MM. Brancus. Zenith angle distributions of cosmic ray muons. Nuclear Physics B, 122, 2003.
[15] E. Harpell, W. Langeveld, D. McShurley, S. Shapiro, and J. Venutti. The CCRT: an inexpensive cosmic ray muon detector, 1995. Disponible à http://www.slac.stanford.edu/cgi-wrap/getdoc/slac-tn-95-001.pdf.
[16] M. Bektasoglu and H. Arslan. Investigation of the zenith angle dependence of cosmic-ray muons at sea level. PRAMANA - Journal of Physics, 80(5):837-846, May 2013.
[17] Disponible à http://www.phas.ubc.ca/~phys209/files/cosmicray.pdf.
[18] B. Rossi. Cosmic rays. Mc Graw Hill, 1964. Disponible à https://archive.org/details/CosmicRays_281. Cet ouvrage est de loin la meilleure référence que nous ayons consulté sur l’utilisation de la méthode de coïncidence pour comprendre la nature des rayonnements ionisants, et source d’inspiration pour les expériences reproduites dans cet article.
[19] M.W. Friedlander. A Thin Cosmic Rain: Particles from Outer Space. Harvard University Press, Novembre 2000. Un rappel historique de l’étude de la nature des particules cosmiques qui complète l’ouvrage de Rossi en abordant le problème du point de vue de l’origine extra-terrestre des particules plutôt qu’une collection d’expériences faites depuis le sol, et sera en ce sens moins utile à l’expérimentateur en recherche d’inspiration sur les combinaisons de compteurs Geiger pour des mesures en coïncidence. Une lecture agréable néanmoins.
[20] R. G. Harrison, K. A. Nicoll, and A. G. Lomas. Geiger tube coincidence counter for lower atmosphere radiosonde measurements. Review of Scientific Instruments, 84:076103, 2013.
[21] D. P. Jackson and M.T. Welker. Measuring and modeling cosmic ray showers with an MBL system: an undergraduate project. American Journal of Physics, 69(8):896-900, 2001.
[22] M. Casolino & al. Dual origins of light flashes seen in space. Nature, 422(1):680, 2003.
[23] K. Sibbernsen. Catching cosmic rays with a DSLR. Astronomy Education Review, 9(1):010111, 2010. Disponible à http://scitation.aip.org/content/aas/journal/aer/9/1/10.3847/AER2010009.
[24] A.R. Smith, R.J. McDonald, D.L. Hurley, S.E. Holland, D.E. Groom, W.E. Brown, D.K. Gilmore, R.J. Stover, and M. Wei. Radiation events in astronomical CCD images. In SPIE - Electronic Imaging 2002, volume 4669, pages 172-183, 2002.
[25] J.J. Cogliati, K.W. Derr, and J. Wharton. Using CMOS sensors in a cellphone for gamma detection and classification. arXiv 1401.0766v1, rubrique physics.ins-det, 2014. Disponible à http://arxiv.org/pdf/1401.0766v1.pdf, ou pour une version plus ludique http://www.inl.gov/research/cellphone-based-radiation-warning-system/.
1 ingénieur dans une société privée, hébergé par le département temps-fréquence de l’institut FEMTO-ST à Besançon
2 Aware Electronics commercialise un circuit de mesure de coïncidence pour la modique somme de 85 $ : http://www.aw-el.com/coinci.htm
3 https://play.google.com/store/apps/details?id=com.rdklein.radioactivity&hl=en
4 une solution aurait pu être fournie par Distributed Observatory - http://www.globalsensorweb.org/wiki/index.php/DECO - mais nous avons été incapables de faire fonctionner cette application sur un téléphone Samsung Galaxy S3 équipé de Android 4.0.4