Tous ceux qui ont utilisé Catia, Soliworks, Pro/Engineer ou autre modeleur paramétrique similaire ont sûrement été frappés par la façon de construire une esquisse, tant celle-ci diffère du dessin technique classique en 2D. A vrai dire, on s'y habitue rapidement et il devient difficile de s'en passer. Linux ne proposait rien dans ce domaine jusqu'à ce qu'apparaisse pSketcher que voici...
1. Entrée en matière
Que signifie paramétrique ?
Il n'est pas vraiment aisé de définir ce concept appliqué au dessin 2D (ou à la modélisation 3D) sans entrer dans des notions mathématiques. Pour rester simple, faisons un rapprochement entre dessin technique et figure géométrique, qui sont de même nature. Un dessin technique, qu'on appelle un plan, est un ensemble d'entités simples (segments et arcs) interdépendantes dans leurs positions relatives et leurs conditions géométriques. Cette interdépendance peut être traduite par une équation, transparente à l'utilisateur dans la plupart des cas, mais pas toujours, notamment lorsque l'utilisateur établit lui-même l'équation définissant, par exemple, la dimension d'un élément par rapport à un autre.
Dans une équation, le résultat dépend des valeurs affectées aux variables. Ainsi, dans un outil de dessin paramétrique 2D, lorsque l'on change la dimension d'un élément existant ou sa position angulaire, ou n'importe quel autre paramètre le définissant, cet élément est immédiatement « recalculé » par le logiciel qui le redessine alors en fonction des changements, tout en modifiant les autres éléments qui lui sont reliés, car ceux-ci sont contraints de respecter les conditions qui ont présidé à leur mise en place initiale.
Bref : c'est le fameux « effet papillon » d'Edward Lorenz. Quand on modifie un élément, qui n'est jamais figé sauf à être totalement contraint, les autres éléments de l'ensemble sont également modifiés en conséquence.
Le dessin technique en 2D, traditionnel ou DAO, est caractérisé par sa rigueur géométrique et dimensionnelle. Il n'est pas question dans ce domaine que l'objet représenté soit seulement ressemblant : il faut qu'il soit l'exacte représentation à l'échelle du réel. Ainsi, une ligne parallèle à une autre doit être construite en recourant à une fonction parallélisme du logiciel ; si une autre doit être tangente à un cercle, on appellera une fonction de tangence ; si encore une ligne doit faire un angle de 90° avec une autre, c'est la fonction de perpendicularité qui sera sollicitée. Et ainsi, petit à petit, en posant une entité l'une après l'autre tout en respectant les caractéristiques de dimensions et de positions relatives de chacune, le dessin se construit. C'est ainsi qu'il convient d'utiliser Qcad, par exemple.
Le dessin par contraintes, lui, obéit à une logique inverse : on dessine d'abord une forme approximativement ressemblante mais complète de l'objet, puis on assigne dimensions et caractéristiques géométriques aux éléments posés, qui alors s'étirent, se raccourcissent et se mettent en place. C'est ainsi qu'opèrent les modules d'esquisse (les sketchers) des modeleurs paramétriques d'aujourd'hui. Nous allons le découvrir par la pratique grâce à pSketcher.
2. Obtenir pSketcher
Le programme pSketcher est l'œuvre, encore en développement, de Michael Greminger, qui l'a placée sous GNU General Public Licence V2. Il s'agit donc d'un programme libre, hébergé par Google Code Hosting, disponible uniquement en code source à compiler, que l'on téléchargera à l'adresse suivante : http://code.google.com/p/psketcher/source/checkout.
L'opération de compilation est fort simple (cmake CmakeLists.txt, make, c'est tout !) mais nécessite l'installation préalable de plusieurs bibliothèques dont la liste est donnée par le fichier INSTALL, inclus dans l'ensemble des éléments rapatriés lors du téléchargement. Ajoutons simplement que pSketcher est interfacé en QT4 et qu'il ne fonctionnera donc que sur des distributions Linux récentes. Personnellement, je l'ai compilé sur Mandriva 2009.1 et 2010, toutes deux en 64 bits. L'exécutable généré se trouve dans ./psketcher-red-only/src/Interface ; il s'appelle psketcher.
Tant que nous sommes sur la page Google Code Hosting de pSketcher, prenons connaissance de ce qu'en dit son auteur : pSketcher est un outil de dessin 2D paramétrique avec contraintes, actuellement fonctionnel sous Linux, qui sera porté ultérieurement sur diverses plates-formes.
3. L'interface de pSketcher
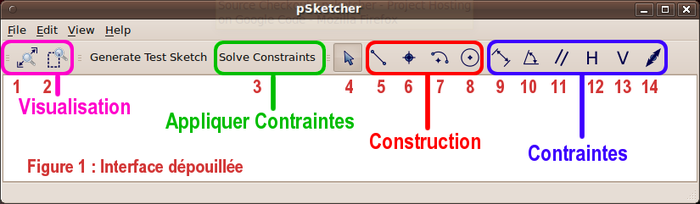
L'interface de pSketcher est très simple : dans la partie supérieure se situe la barre des menus littéraux classiques, juste au-dessus de la barre des icônes qui surmonte l'espace de dessin. La barre des icônes est structurée logiquement en quatre groupe de fonctions :
Visualisation :
- 1 : Vue optimale ;
- 2 : Vue zoom fenêtre.
Appliquer Contraintes :
- 3 : Solve Constraints, qui sert à rendre effective la contrainte appliquée à une entité.
Outil de Sélection :
- 4 : Pour désigner une entité, ou la déplacer avec le bouton milieu de la souris ;
Construction :
- 5 : Segment (non polyligne) ;
- 6 : Point de construction ;
- 7 : Arc par 3 points ;
- 8 : Cercle.
Contraintes :
- 9 : Longueur ;
- 10 : Angle ;
- 11 : Parallélisme ;
- 12 : Horizontalité ;
- 13 : Verticalité ;
- 14 : Tangence.
La facilité d'utilisation d'un tel outil de dessin se déduit de la simplicité de son interface. Quand on la compare à celle deQcad, on se rend compte à quel point la façon de dessiner diffère de l'un à l'autre, pour faire des choses analogues, bien que plus sophistiquées avec Qcad. En effet, pSketcher sert à produire des esquisses (épures serait plus juste) rigoureuses mais dépourvues des attributs de couleur, d'épaisseur de trait, de hachurage ou d'inscription de cotes tolérées sur des calques séparés comme en produisent les logiciels de DAO (CAD). Qcad et pSketcher ont des rôles différents.
Fig. 1 : Interface de pSketcher.
Les présentations étant faites, il ne reste plus qu'à utiliser les outils que l'on vient de découvrir. Le lecteur est invité à faire l'exercice décrit ici en pas à pas.
4. Démarche fondamentale
Comme il a été dit précédemment, le processus du dessin par contraintes est celui-ci :
- Poser les entités de dessin nécessaires de façon à obtenir une forme approximative de l'objet représenté ;
- Assigner des contraintes géométriques et dimensionnelles (de forme et/ou de position selon les cas) ;
- Appliquer les contraintes afin qu'elles produisent l'effet attendu.
C'est la démarche fondamentale qu'il faut garder à l'esprit.
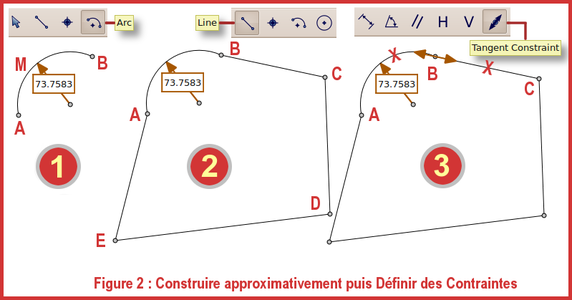
Observons la figure 2, qui illustre en trois phases la façon de procéder :
- 1 : Sélectionner dans la barre d'icônes puis cliquer en A (début de l'arc), en M (point de passage) et en B (fin de l'arc). L'arc de cercle se dessine et la cotation du rayon se met automatiquement en place. La valeur du rayon n'a pour l'instant aucune importance, bien que l'on pourrait dès cet instant lui attribuer la valeur désirée, ce qui en modifierait le dessin ;
- 2 : Sélectionner , cliquer enB, puis enC. Un segment BC est construit ; la fonction ne créant pas de polylignes automatiques, il faut de nouveau cliquer enCpuis enDpour poser le segmentCD(avec une fonction polyligne, il eût suffi de cliquer en D). De la même manière, construire DE puisEAafin d'obtenir une figure fermée. À noter que les segments s'accrochent aux points désignés sans qu'il soit nécessaire comme en DAO de spécifier le type d'accrochage des entités ;
- 3 : Supposons maintenant que l'on veuille queBCsoit tangent enBà l'arcAB, ce qui n'est pas le cas actuellement. Il va donc falloir exécuter une opération de mise en tangence pour que la figure corresponde à ce que l'on veut. Pour cela, il convient d'assigner cet impératif en sélectionnant d'abord puis en désignant l'arcABet le segmentBC(l'ordre de désignation est neutre).Le point commun entre l'arc et le segment étant le point Ble symbole de tangence se place surB. Cela signifie que quelle que soit la déformation que l'on fera subir par la suite à la figure, le segmentBCrestera tangent enBà l'arcAB : il est contraint de conserver cette caractéristique géométrique.
Pour l'instant, l'aspect de la figure n'a pas changé parce que nous n'avons pas appliqué la contrainte mise en place. La raison en est simple : c'est analogiquement comme la création des lois en France, qui sont d'abord définies et qui entrent en vigueur plus tard, lorsque leur décret d'application est publié.
Fig. 2 : Construire approximativement puis définir des contraintes
5. Appliquer des contraintes
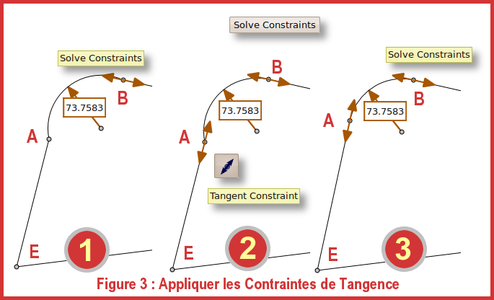
Il vient d'être dit que rien n'a été modifié après assignation d'une contrainte de tangence au point B parce que celle-ci n'a pas encore été appliquée. Pour ce faire et constater le changement qui en résulte, considérons la figure 3. On y décrit :
- 1 : Cliquer sur . Le segment BC devient tangent en B ;
- 2 : Tant que nous en sommes aux contraintes de tangence, nous allons en assigner une en A, ce qui se fait, rappelons-le, par le choix de , puis par la désignation du segment EA et de l'arc AB. Le symbole de tangence se place alors en A ;
- 3 : Cliquer sur pour appliquer la contrainte enALa figure est modifiée en conséquence.
Fig. 3 : Appliquer les contraintes de tangence.
Pour des raisons pédagogiques, une contrainte a été assignée puis appliquée (on peut aussi dire résolue) d'abord en B puis en A. En réalité, il est possible de définir tout un lot de contraintes et de les appliquer en une seule fois, avec l'inconvénient toutefois que si l'une ne produit pas le résultat souhaité, il faudra annuler la phase d'application et identifier la difficulté pour la résoudre. En procédant pas à pas, le problème qui pourrait surgir serait immédiatement mis en évidence.
5.1 Appliquer une contrainte d'horizontalité
Cette contrainte géométrique concerne une entité en propre, c'est-à-dire que son horizontalité (ou sa verticalité) ne dépend pas d'une autre entité. On pourrait donc la qualifier de « contrainte absolue », alors que parallélisme ou perpendicularité se définissent par rapport à une autre entité ; ces dernières pourraient être en conséquence qualifiées de « contraintes relatives ».
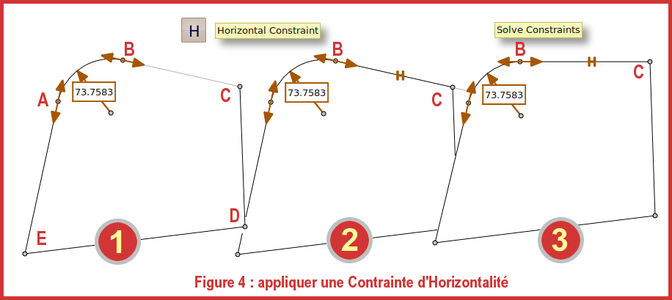
L'application de cette contrainte est illustrée par la figure 4 :
- 1 : Sélectionner dans la barre d'icônes ;
- 2 : Désigner le segment BC. Le symbole H s'inscrit sur le segment, indiquant ainsi qu'il doit être horizontal ;
- 3 : Cliquer sur Le segment BC devient horizontal.
Fig. 4 : Appliquer une contrainte d'horizontalité.
5.2 Quand ça tourne mal...
Jusqu'ici, dans l'exemple présenté, les choses se sont déroulées sans anicroche : les actions ont produit les résultats attendus. Mais il n'en est pas toujours ainsi, quel que soit d'ailleurs l'outil d'esquisse (le sketcher) utilisé ; celui de SolidWorks conduit également à des résultats non désirés, non par la faute de l'outil, mais parce que la situation géométrique de l'entité ne peut pas produire autre chose, ce qui n'apparaît pas toujours à l'opérateur. Mais il y a toujours possibilité de revenir sur ses pas et d'opérer de façon à contourner la difficulté.
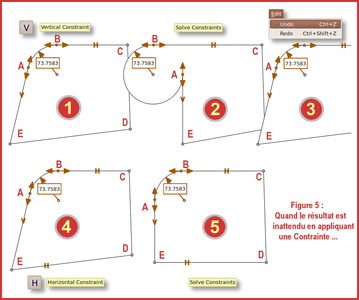
Examinons la figure 5 :
- 1 : Dans notre dessin, nous voulons que le segmentEAsoit vertical. Pour cela, il faut sélectionner et l'assigner àEA ; le symboleVs'inscrit sur le segment ;
- 2 : Comme toujours, le résultat de l'opération est effectif après application de. Et ici, dans notre exemple particulier, l'arc de cercleABinférieur à 90° devient un arc de 270°, ce qui évidemment ne nous convient pas ;
- 3 : L'annulation de l'opération s'obtient par ou le classique [Ctrl]+[Z]. Seule l'application de la contrainte est supprimée, pas son assignation. Il faudrait encore activer [Ctrl]+[Z] pour la supprimer ;
- 4 : Le segment ED devant être horizontal, nous lui assignons une contrainte d'horizontalité. Le symbole H s'inscrit sur ED, tandis que le symbole V est toujours inscrit sur EA ;
- 5 : Cliquer surpour appliquer les contraintes. La figure correspond cette fois-ci à ce que l'on attend. Il est à noter cependant que parfois cela ne suffira pas et qu'il faudra alors repositionner manuellement des entités, de sorte que la résolution des contraintes puisse correctement se faire.
Fig. 5 : Quand le résultat est inattendu en appliquant une contrainte...
5.3 Appliquer une contrainte angulaire
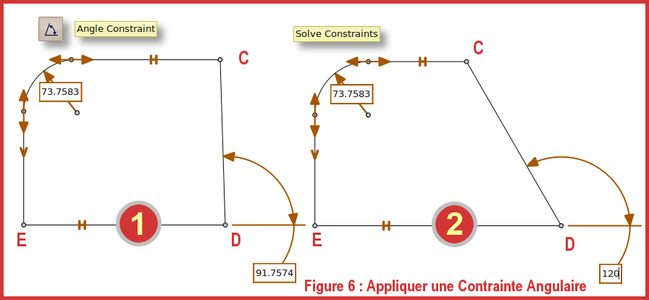
Un angle est défini par la position relative de deux segments. Cela impose la façon de procéder. À suivre sur la figure 6 :
- 1 : Sdans la barre d'icônes et désignerEDetDC, indiquant ainsi que l'on veut contraindre l'angle fait par ces deux segments ; la cote d'angle s'inscrit avec sa valeur actuelle ;
- 2 : Placer le pointeur de la souris dans la case indiquant la valeur de l'angle. Le pointeur prend la forme du curseur classique de saisie de texte. Entrer alors 120 (degrés) à la place de la valeur actuelle puis valider par [Entrée]. Rien ne se passe. En effet, il faut encore cliquer sur pour que DC(et lui seul, carEDest contraint horizontal) s'incline.
Fig. 6 : Appliquer une contrainte angulaire.
5.4 Changer la valeur du rayon
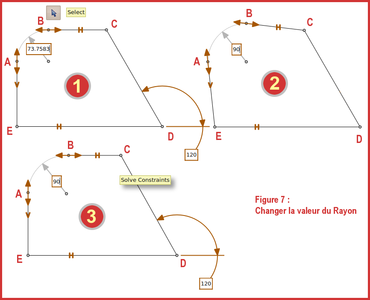
La valeur du rayon d'un arc ou d'un cercle n'est pas une contrainte : elle n'est pas contenue (pour ce logiciel) dans la palette des contraintes. Il s'agit d'une donnée dite « explicite ». Autrement dit, sur la figure 7 :
- 1 : Choisir l'outil puis désigner l'arc, qui change de couleur pour indiquer qu'il est sélectionné ;
- 2 : Placer le pointeur de la souris dans la case indiquant la valeur du rayon, changer la valeur pour 90 et valider par [Entrée]. Le rayon change et la figure est modifiée, pour ne pas dire perturbée ;
- 3 : Cliquer surpour que les contraintes précédemment appliquées retrouvent leur effet.
Fig. 7 : Changer la valeur du rayon.
5.5 Contraintes dimensionnelle et sauvegarde
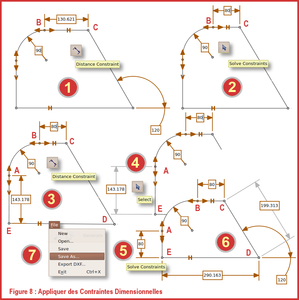
Un dessin technique, qui est le genre de dessin produit par des outils comparables à pSketcher, est précisément dimensionné et des cotes indiquent ces dimensions. Nous allons donc dimensionner l'esquisse en procédant comme indiqué par la figure 8 :
- 1 : Sélectionner et cliquer enBpuis enC. Une cote s'inscrit ;
- 2 : Choisir l'outil et désigner la cote. Elle change de couleur ; elle peut alors être déplacée n'importe où et sa valeur peut être changée. Remplacer sa valeur par 80, de la même façon que la valeur du rayon a été modifiée. Rien ne se passe avant que l'on ait appliqué la contrainte par . La dimension de BC change et la figure est modifiée ;
- 3 : Sélectionner et cliquer enEpuis enA. La cote s'inscrit à l'intérieur de la figure, ce qui est gênant et contraire aux règles du dessin technique ;
- 4 : Choisir l'outil, désigner la cote et la déplacer à l'extérieur de la figure ;
- 5 : Remplacer la valeur de la cote par80, puis appliquer la contrainte. Le dessin est modifié en conséquence ;
- 6 : Géométriquement, cette figure est entièrement définie et contrainte, sauf par sa position dans l'espace de travail.Dans un sketcher classique, il ne serait plus possible d'y appliquer d'autres contraintes sans que le système ne le signale. Pourtant, pSketcher autorise l'adjonction d'autres contraintes dimensionnelles, ce qui, en dessin technique, est une entorse aux règles, car la cotation devient alors surabondante. Ainsi, les cotes deCDet DEn'apportent rien parce qu'elles résultent des autres dimensions mises en place ;
- 7 : À ce stade, le dessin est terminé. Il peut être sauvegardé au format spécifique du logiciel ou exporté en DXF pour être récupéré comme profil d'extrusion, par exemple, dans un modeleur tel que HeeksCAD ou n'importe quel autre programme.
Fig. 8 : Appliquer des contraintes dimensionnelles.
6. Vérification de l'état contraint
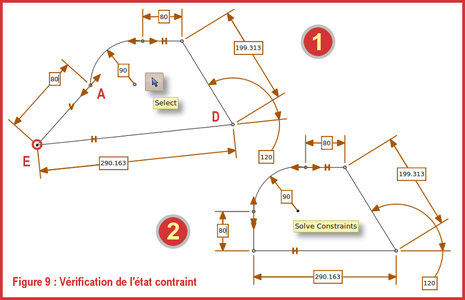
Un dessin totalement contraint ne peut normalement plus être modifié, sauf en supprimant des contraintes, ce qui, dans pSketcher, se fait en sélectionnant le symbole de la contrainte et en appuyant sur la touche [Suppr]. Toutefois, pSketcher se comporte anormalement, comme le montre la figure 9 :
- 1 : Choisir l'outil Select et déplacer le point E. La figure se déforme et les contraintes appliquées ne sont plus respectées;
- 2 : Sélectionner alors Solve Constraints pour que la figure redevienne cohérente et reprenne sa forme. Elle est donc bien contrainte.
Fig. 9 : Vérification de l'état contraint.
7. Le cas de SketchFlat
pSketcher n'est pas seul dans son genre à pouvoir être utilisé sous Linux. Il y a bien sûr les fonctions d'esquisse de HeeksCAD qui restent cependant très perfectibles ; mais il y a surtout, beaucoup plus développé, SketchFlat, placé par son auteur sous licence GPL V3. Les sources sont donc disponibles, ainsi qu'un binaire pour Windows.
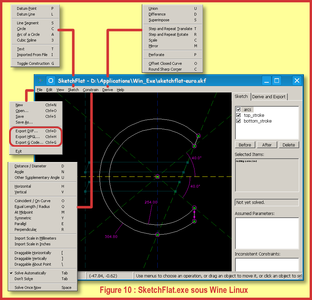
Personnellement, j'ai testé cette dernière version binaire qui, se résumant à un seul exécutable, tourne sans problème et rapidement sous Linux à travers Wine. Plus complet que pSketcher, il présente en outre l'avantage d'exporter en DXF, HPGL et Code CN, ce qui somme toute est logique pour ce dernier point, puisque ce programme a d’abord été écrit pour générer des données de FAO (CAM) destinées aux machines-outils à commandes numériques. Aujourd'hui abandonné, ce programme est remplacé par SolverSpace, un modeleur 3D paramétrique non libre. La figure 10 est un montage des différents menus de SketchFlat, exécuté sous Linux. On téléchargera source et binaire de ce programme à l'adresse suivante : http://cq.cx/sketchflat.pl.
Fig. 10 : SketchFlat.exe sous Wine Linux
En guise de conclusion
PSketcher, tout comme SketchFlat, peuvent être utilisés en l'état, soit pour produire des esquisses précises à importer dans d'autres programmes, soit dans un but pédagogique pour apprendre les techniques du dessin par contraintes. Mais l'on se prend à rêver que ce code libre intégré dans Qcad, HeeksCAD ou, pourquoi pas, OpenDraw ou Inkscape, donnerait un coup de jeune à ces logiciels et surtout un surcroît de puissance forcément bienvenu.
Site du projet : http://code.google.com/p/psketcher/



 Ajouter à une liste de lecture
Ajouter à une liste de lecture