Le traitement du signal, domaine abstrait par excellence, devient très amusant lors de sa mise en pratique. Nous nous proposons de démontrer expérimentalement un RADAR à bruit mis en œuvre par radio logicielle.
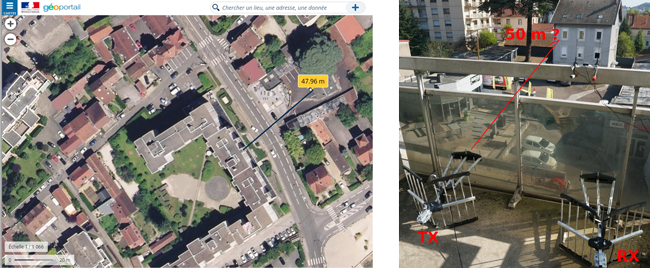
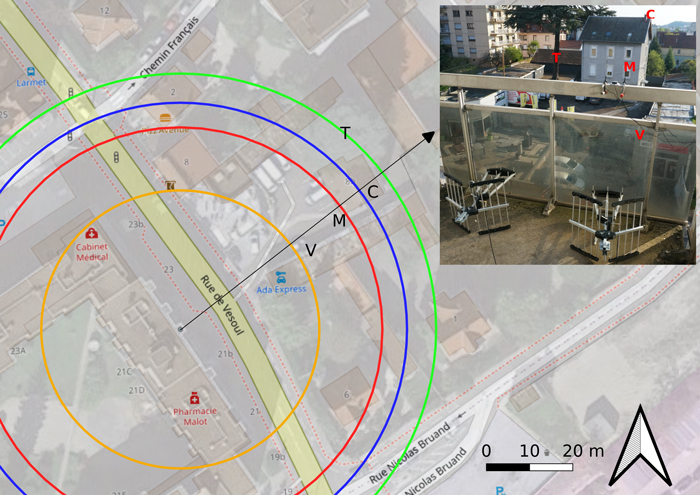
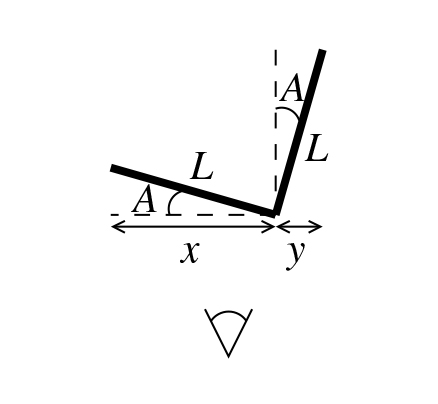
Pour paraphraser l’introduction d’une vidéo de chanteurs de rap français [1], « on a 3 minutes, un appart' rempli de bordel, une vieille émission pour les gosses dans l’ordi, on peut sûrement y aller au bluff ». Dans notre cas, nous n’avons pas 3 minutes, mais 5 semaines de confinement, on a bien un appartement rempli de bordel, et plutôt que l’émission de télévision, nous avons des antennes et des circuits de radio logicielle. Pouvons-nous mesurer la distance de la maison en face dudit appartement en réalisant un RADAR (RAdio Detection And Ranging) actif avec les moyens du bord (figure 1) ?
Cet article est le premier d'une série de trois articles sur le sujet.
1. Principe de la mesure
Un RADAR actif est associé, dans l’imaginaire populaire, à un générateur d’impulsions puissantes dont le récepteur observe le temps de vol pour identifier la distance à la cible. Bien que conceptuellement simple à appréhender en considérant le comportement dans le domaine temporel, cette approche est non seulement complexe technologiquement à mettre en œuvre, mais souffre par ailleurs d’un mauvais contrôle de l’encombrement spectral du signal émis. En effet, toute variation sur l’étage d’émission, de la chauffe/vieillissement d’un composant à la modification de l’environnement diélectrique de l’antenne faisant office de filtre passe-bande, se traduit par une variation des fronts de l’impulsion et donc des composantes spectrales occupées.
L’analyse du traitement du signal des échos nous informe que la seule propriété importante d’un signal émis par un RADAR est la bande spectrale occupée B qui détermine la résolution en distance ΔR = c/(2B) avec c la vitesse de la lumière de 300 m/μs. Une impulsion brève présente un encombrement spectral en sinus cardinal de largeur typiquement l’inverse de la durée de l’impulsion : plus l’impulsion est brève, meilleure est la résolution en distance. Mais cette approche très basique s’implémente de multiples façons. Le lecteur assez chanceux pour accéder à un analyseur de réseau peut simplement mesurer le coefficient de réflexion complexe S11 d’une antenne connectée à un port radiofréquence et observer, par transformée de Fourier inverse, la durée mise pour l’onde pour effectuer l’aller et le retour avec une résolution inverse de la bande spectrale balayée. Cette approche fonctionne bien, mais nécessite l’accès à un matériel relativement coûteux (voir encadré) et est mathématiquement inefficace, en analysant fréquence par fréquence le comportement du signal. L’avantage de cette méthode est de très bien contrôler le spectre occupé par le signal émis.
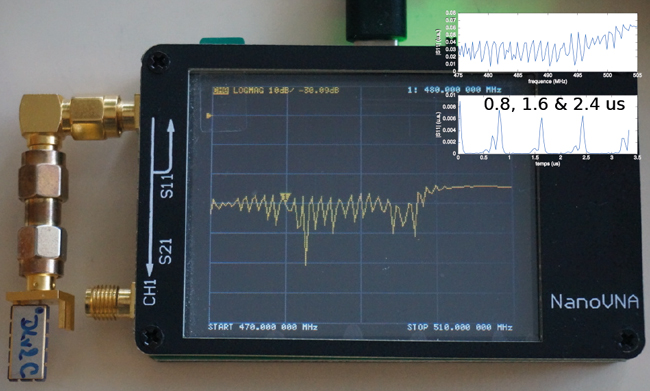
NanoVNA
Depuis un certain temps, l’avènement des composants numériques radiofréquences intégrant toutes les briques de chaînes d’émission et de réception – dont les AD936x de Analog Devices font partie – font fleurir des analyseurs de réseau portables, tous de qualité plus médiocre les unes que les autres. Cependant, nous avons été agréablement surpris par le NanoVNA (https://www.banggood.com/fr/Original-NanoVNA-Vector-Network-Analyzer-50KHz-900MHz-Digital-Display-Touch-Screen-Shortwave-MF-HF-VHF-UHF-p-1471576.html) qui pour 50 euros propose une solution tout à fait fonctionnelle, open source et open hardware (https://github.com/ttrftech/NanoVNA) qui nous a permis d’ajouter des fonctionnalités non prévues initialement (ajout de la phase du coefficient de réflexion dans le domaine temporel).
Nos tentatives de mesures de signaux réfléchis du bâtiment avec le même montage que décrit dans ces pages n’ont pas donné de résultat probant, malgré un nombre important de moyennes (128) impliquant une durée de mesure de plus de 5 minutes, soit à cause d’une puissance émise insuffisante (-9 dBm) ou d’une sensibilité du récepteur trop médiocre. L’instrument reste néanmoins très pratique pour des mesures rapides de caractéristiques de composants radiofréquences dans le domaine spectral et temporel (droite, avec la caractérisation d’une ligne à retard réflective à onde élastique servant d’étalonnage du RADAR, tel que nous le reverrons en fin de cet article).
La principale limitation, outre le plancher de bruit insuffisant pour la mesure qui nous intéresse, est le nombre de points réduit, puisque limité à 101. Cette limitation ne devrait pas être handicapante dans notre cas : pour une mesure sur une bande de 150 MHz (ou 1 m de résolution en distance), l’intervalle entre deux points est 1000/150=6,7 ns ou une durée totale de la mesure sur 6,7x101=674 ns ou une cible à 101 m, qui devrait permettre de détecter la maison à une cinquantaine de mètres.
Que pouvons-nous choisir entre l’impulsion qui couvre une très large gamme du spectre et la sinusoïde qui n’en couvre qu’une composante ? Nous pouvons choisir d’émettre un signal qui occupe une bande contrôlée. Un signal qui occupe une bande spectrale uniformément est un « bruit ». En effet, toute répétition d’un motif dans le signal modulant une porteuse (fréquence centrale de la bande occupée) se traduirait par une raie spectrale dominante dans la transformée de Fourier, si bien que l’occupation uniforme d’une large bande implique l’absence de répétition du motif modulant : l’absence de répétition définit un bruit. Un bruit n’est pas nécessairement inconnu : il existe de nombreuses méthodes pour générer de façon déterministe un signal qui ne se répète pas. Un système chaotique est une méthode [2], les générateurs récursifs pseudo-aléatoires en sont une autre [3]. L’utilisation de ces techniques d’étalement du spectre donne naissance aux RADAR à bruit [4-7](figure 3).
2. De la théorie à la pratique
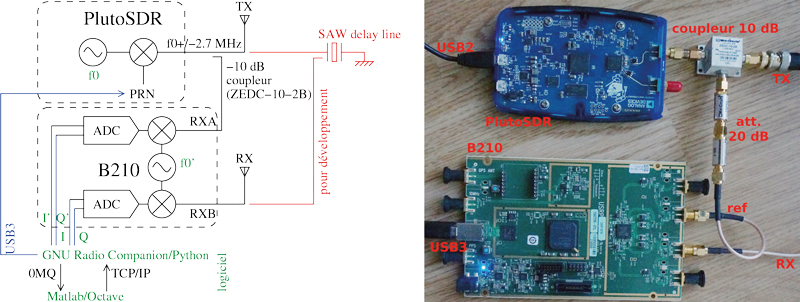
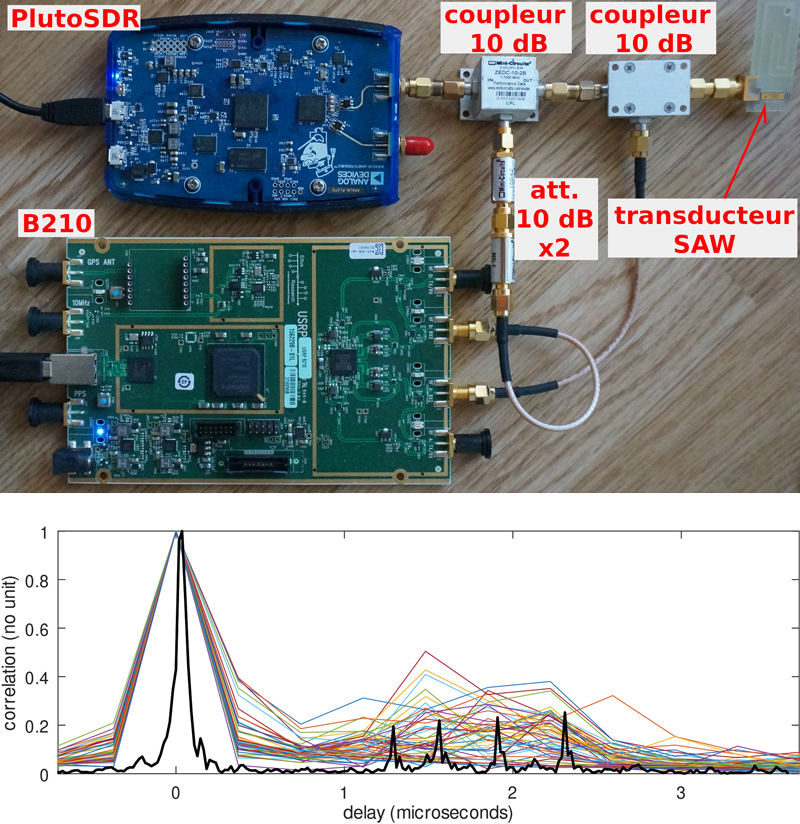
Nous avons à notre disposition deux antennes de télévision numérique terrestre directives de type Yagi-Uda à 5 éléments directeurs, une plateforme de radio logicielle de Analog Devices PlutoSDR et une Ettus Research B210. Nous pouvons utiliser la PlutoSDR comme source et la B210 comme récepteur. En effet, le principe d’une mesure RADAR consiste à rechercher les copies du signal émis dans le signal reçu. Il faut donc connaître le signal émis. Dans un RADAR à bruit, par définition le motif émis n’est pas connu : nous l’enregistrerons donc sur une des voies de la B210 tandis que la seconde voie est connectée à l’antenne de réception (figure 4). Nous avons choisi une modulation de phase en attaquant la voie « phase » du convertisseur module/phase vers complexe par un générateur aléatoire fourni par GNU Radio, tandis que l’amplitude du signal est maintenue à une valeur unitaire, garantissant une puissance transmise constante (figure 4, droite).
On pourra nous rétorquer : pourquoi ne pas utiliser une voie de la B210 comme émetteur et l’autre comme récepteur. Deux objections : d’une part, l’isolation entre les deux voies de la B210 est très médiocre – une cinquantaine de dB d’après nos mesures – limitant la portée du RADAR en éblouissant le récepteur par l’émetteur ; et le composant chargé du traitement des signaux radiofréquences de Analog Devices, l’AD936x, comporte deux oscillateurs distincts entre émission et réception, interdisant de faire l’hypothèse que la réception est cohérente avec l’émission. Il faut donc de toute façon observer l’émission pour s’affranchir de la dérive entre les oscillateurs, et la B210 ne propose que deux voies, que nous utiliserons toutes deux en entrée. On notera que les composants Lime Microsystems – concepteurs de la LimeSDR autour du LMS7002M par exemple – exploitent des oscillateurs synchronisés en émission et réception et permettent une mesure cohérente (https://wiki.myriadrf.org/LimeMicro:LMS7002M_Datasheet), mais nous ne possédons pas ce matériel et l’acquérir spécifiquement romprait avec l’objectif d’exploiter le matériel à disposition.
Bien qu’équipée d’un port USB3, la B210 ne permet d’acquérir et de transmettre un flux de données continu que jusque vers 8 Méchantillons/s. Pire, nous constatons qu’en tentant d’alimenter la PlutoSDR à plus de 2,7 Méchantillons/s, nous perdons des trames et l’émission est discontinue. En prenant soin de connecter la B210 sur un port USB3 et la PlutoSDR sur un port USB2, nous pouvons pousser le débit de données vers les deux plateformes à 3,2 MHz (mesures sur un ordinateur portable Dell Prevision M6500). Avec 3 MHz de bande passante, la résolution en distance sera de 50 m. Pas terrible pour chercher à détecter un bâtiment à moins de 50 m du balcon. Nous rencontrons ici l’obstacle majeur de la radio logicielle : la bande passante réduite des interfaces de communication. Sans port Gb Ethernet, nous devons tirer le meilleur parti du matériel existant (figure 5).
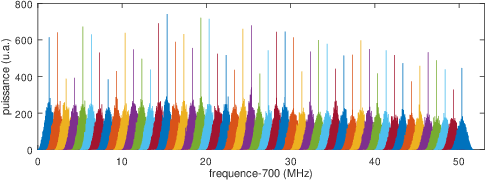
Personne n’a dit qu’il fallait mesurer la bande B d’un coup pour obtenir la résolution spatiale c/(2B) : nous pouvons balayer des sous-bandes successives et concaténer les spectres afin d’obtenir une bande de mesure globale bien plus importante que les 2,7 MHz déterminés par le débit du bus USB (figure 6). Ce constat va déterminer l’architecture logicielle que nous allons développer :
- Un flux de données « continu » (nous verrons ce que cela veut dire) est transmis de la B210 vers le PC. Nous avons tenté d’évaluer libuhd pour capturer directement les trames, mais avons finalement opté pour le bloc USRP Source de GNU Radio, l’entrelacement de deux voies étant plus compliqué que prévu et la solution GNU Radio s’avérant à terme optimale en termes de vitesse de mesure (section 6) ;
- Une séquence pseudo-aléatoire alimente la PlutoSDR : nous avons sélectionné une modulation en phase qui garantit une amplitude constante du signal tout en étalant le spectre par sauts de phase. Ici aussi, la génération des séquences aléatoires et l’alimentation de la PlutoSDR sont prises en charge par GNU Radio ;
- Une fois l’acquisition faite sur une bande de 2,7 MHz, nous désirons balayer la fréquence de porteuse. Ceci n’est pas autorisé par GNU Radio Companion. Cependant, GNU Radio Companion est un générateur de code Python que nous pouvons compléter des fonctions manquantes, par exemple un thread comportant un serveur TCP/IP pour recevoir des ordres en vue de reconfigurer les plateformes de radio logicielle PlutoSDR et B210. Nous allons donc récupérer le programme Python 3 généré par GNU Radio Companion et le modifier pour lui ajouter les fonctionnalités manquantes ;
- Finalement, un programme externe se charge de séquencer les opérations, à savoir recevoir le flux de données de la B210, programmer la fréquence suivante des oscillateurs locaux, stocker les résultats en vue de leur traitement ultérieur et effectuer un premier contrôle de qualité des mesures. Par habitude de Matlab et son implémentation libre GNU/Octave, nous contrôlerons la séquence de mesures depuis ce langage. Le lecteur plus familier avec Python retrouvera la majorité des fonctions de traitement numérique du signal dans numpy.
Le signal émis contient une séquence pseudo-aléatoire dont nous recherchons les occurrences retardées d’un délai τ dans le signal reçu. La fonction mathématique de recherche d’occurrences d’un motif m dans un signal bruité x est l’intercorrélation :
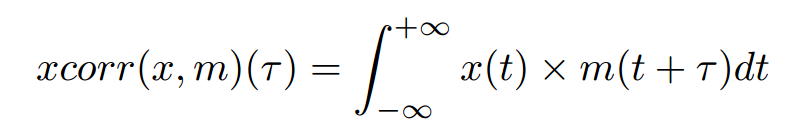
Nous avons déjà largement discuté dans ces pages [8] comment d’après le théorème de convolution, la corrélation se calcule efficacement en passant dans le domaine spectral par transformée de Fourier rapide (FFT) et que :
![]()
avec * le complexe conjugué qui retourne le temps de la corrélation par rapport à la définition de la convolution. Nous constatons qu’il est donc naturel de concaténer les spectres issus des transformées de Fourier des signaux successifs acquis par chaque voie de la B210 – une voie faisant l’acquisition du motif de référence émis m et l’autre voie le signal réfléchi par les cibles illuminées par l’émetteur x – et une fois ces spectres concaténés, d’en faire le produit après avoir pris le complexe conjugué d’un des deux, puis de finalement revenir dans le domaine temporel par transformée de Fourier inverse.
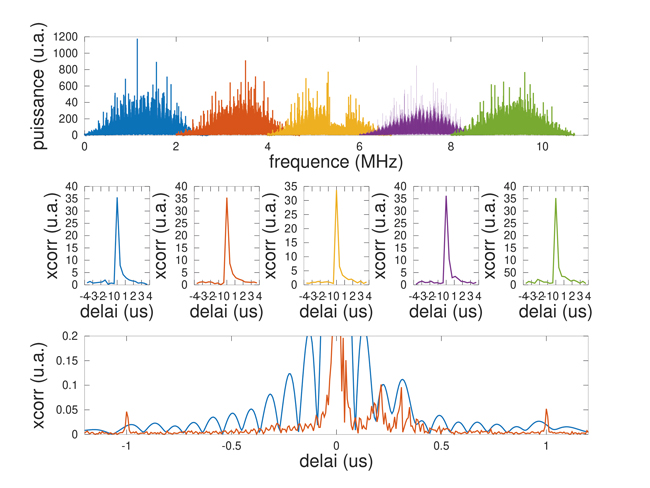
Nous appréhendons en figure 7 – sur les vrais signaux acquis en illuminant la scène se trouvant devant le balcon servant de site d’expérience – comment combiner des spectres adjacents permet d’améliorer la résolution temporelle de la mesure. Il peut sembler incroyable a priori que la combinaison de fonctions de corrélation monotones (ligne du milieu) puisse donner une fonction dans laquelle les échos individuels apparaîtront (ligne du bas). Il ne faut pas oublier que toutes les grandeurs manipulées sont complexes, et donc caractérisées par un module et une phase. Nous ne faisons que tracer le module de la corrélation ici, mais le terme de phase va permettre d’annuler en moyenne les signaux en dehors des échos et au contraire d’accumuler les contributions à la somme en présence d’échos, expliquant la capacité des échos à ressortir alors qu’ils sont invisibles sur chaque corrélation individuelle. Une fois la résolution améliorée, les deux cibles principales qui seront interprétées plus tard deviennent visibles aux retards de 200 et 300 ns environ. En pratique, la combinaison des spectres s’obtient sous GNU Octave de la façon suivante, si nous supposons avoir acquis Nfreq mesures successives de x et m par pas de fréquence finc :
La principale subtilité du code est de s’affranchir de la convention de Matlab de placer la fréquence nulle à l’abscisse 1 de la transformée de Fourier (gauche du spectre) et la fréquence d’échantillonnage fs à la droite du spectre, alors que lors de la concaténation des spectres, il est naturel de placer la fréquence nulle au centre du spectre et de faire parcourir les fréquences de -fs/2 à +fs/2. C’est le rôle de la fonction fftshift() d’intervertir les deux moitiés du spectre pour obtenir l’organisation des fréquences souhaitée. Nous partons donc de spectres vides s1 et s2, dont nous remplissons chaque composante spectrale avec les acquisitions dans les bandes successives de m et x. Les longueurs des acquisitions m et x sont les mêmes – nous avons choisi arbitrairement N=140000 points : il s’agit donc de matrices de Nfreq x N éléments. Comme la transformée de Fourier est bijective, chaque transformée de Fourier d’une colonne de N points acquis dans le temps donne N composantes spectrales que nous savons s’étaler de -fs/2 à +fs/2, ce qui détermine donc la position de chaque composante spectrale. Comme la porteuse a été incrémentée de finc entre deux acquisitions, nous en déduisons l’incrément span entre deux spectres successifs concaténés. Le fenêtrage en pondérant chaque spectre par une fonction de Hanning w a uniquement pour rôle d’atténuer l’impact des jonctions et d’éviter d’induire des artefacts lors de la transformée de Fourier inverse, mais peut être omise lors des premiers essais. Il nous reste maintenant à voir comment acquérir x et m sur les deux voies de la B210.
3. Mise en œuvre du RADAR à bruit à balayage de fréquence
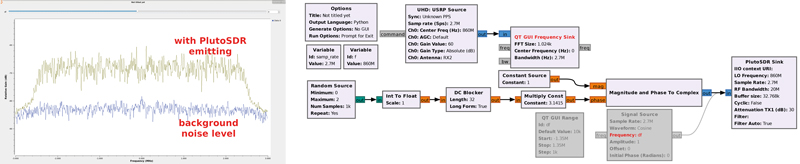
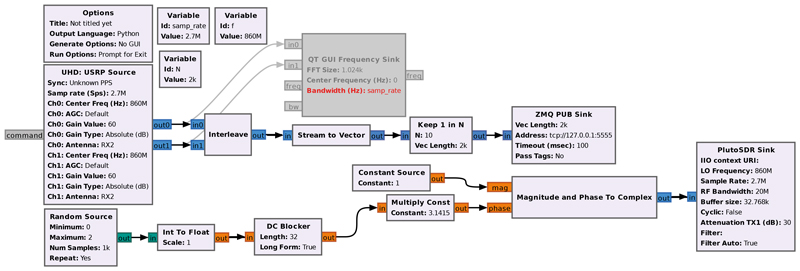
Le contexte étant défini, nous abordons la mise en pratique. Sous GNU Radio Companion, le schéma de traitement est proposé en figure 8.
Cette chaîne de traitement se lit en partant du générateur aléatoire, dont la longueur de répétition (Num Samples) est l’équivalent du Pulse Repetition Rate en RADAR qui détermine la distance au-delà de laquelle la présence de la cible devient ambiguë, car une nouvelle impulsion a été émise. Par ailleurs, ce paramètre crucial détermine aussi la durée sur laquelle nous pourrons intégrer la corrélation et ainsi abaisser le niveau de bruit. La valeur de 1000 par défaut est largement insuffisante dans notre cas et sera modifiée dans le code Python résultant. Une fois la séquence aléatoire générée, nous déterminons la phase d’un complexe de module unitaire par cette grandeur, et alimentons la PlutoSDR servant de source de signaux aléatoires centrés sur une fréquence f de l’oscillateur local et une bande samp_rate ici de 2,7 Méchantillons/s.
Une fois ce signal émis, la B210 échantillonne à la fois le signal transmis – puisque l’oscillateur local de la B210 n’est pas synchrone avec l’oscillateur local de la PlutoSDR et risque donc de dériver, et parce que la séquence aléatoire n’est pas connue – les deux voies entrelacées et transmises par une socket Zero MQ en mode Publish – équivalent de l’UDP dans lequel les paquets sont envoyés à tout client (Subscribe) susceptible de recevoir une transaction, et perdus si personne ne les collecte (en opposition à TCP où le paquet serait retransmis jusqu’à acquittement de sa réception). Afin de réduire le débit de données, nous agrégeons le flux en paquets (Stream to Vector), et ne transmettons qu’une fraction des paquets (Keep 1 in N). Nous retrouvons en commentaire (bloc grisé) l’affichage du spectre en sortie de la B210 qui ne sera pas utilisé dans l’application Python en console qui va suivre. La taille des paquets transmis N va déterminer le rapport signal à bruit – nous pouvons considérer l’intégrale de la corrélation comme une moyenne glissante rejetant le bruit d’autant plus efficacement que la longueur de la séquence est importante – et est donc un compromis entre temps d’acquisition et de communication d’une part, et signal le plus faible à détecter d’autre part. C’est cette valeur N que nous avons choisie arbitrairement à 140000 par tâtonnements successifs.
Côté GNU/Octave, la récupération des paquets s’obtient par l’utilisation de la toolbox octave-zeromq permettant de récupérer le flux de données sur un client Subscribe :
Le client va requérir Nfreq mesures successives de total_length points. Alors que nous avions initialement recherché une solution de paquets successifs, puisque la taille des informations transmises par Zero MQ recevant un Stream n’est pas connue a priori, il s’avère que transmettre un vecteur, même aussi volumineux que 140000 points, s’effectue en une unique transaction et avons constaté que recv contient toujours le nombre d’octets attendu, à savoir le nombre de points que multiplie 8 (un complexe est formé de deux flottants simple précision codés sur 4 octets chacun) que multiplie les deux voies de mesure. Comme ces deux voies, acquises chacune à 2,7 MHz, sont entrelacées, le débit résultant est de 5,4 Méchantillons complexes par seconde. La seule façon que nous ayons trouvée pour garantir la lecture de données courantes et pour ne pas risquer de lire des informations obsolètes à un tel débit est de fermer la socket et de la réouvrir à chaque itération : cette opération ne prend qu’environ 300 μs et ne handicape pas la vitesse de mesure. On notera que nous avons commenté un ordre transmis lors de chaque itération de la boucle qui a pour vocation d’incrémenter la porteuse : nous allons désormais voir comment ajouter cette fonctionnalité au code script Python généré par GNU Radio Companion.
La chaîne de traitement présentée en figure 8 génère un code Python parfaitement lisible qui contient notamment :
Les deux points qui nous intéressent sont que :
- nous pouvons changer depuis un programme extérieur la fréquence des oscillateurs locaux en faisant appel à la fonction set_f(), sous réserve de savoir comment injecter cet ordre ;
- nous n’avons pas la main sur la fonction cadençant le Top Block : il s’agit d’une boucle infinie qui gère l’ordonnanceur GNU Radio et que nous ne pouvons pas modifier.
Qu’à cela ne tienne : nous ajoutons un thread séparé contenant un serveur TCP/IP qui reçoit des commandes et fait appel à set_f() afin de commander les plateformes de radio logicielle en conséquence.
Ce serveur attend une connexion TCP/IP sur le port 5556 de l’ordinateur local. Les commandes prévues sont l’incrément de la fréquence des oscillateurs locaux (par pas de 1 MHz ici, une fraction de la bande de mesure de 2,7 MHz pour garantir un recouvrement des mesures) par la commande « + », réinitialisation de l’oscillateur local au début de la bande par la commande « 0 », et l’abandon du serveur pour nettoyer la socket. Ainsi, un programme extérieur peut commander le balayage des oscillateurs locaux et acquérir le flux Zero MQ transmis en continu en garantissant la stabilité des signaux acquis.
Côté GNU/Octave, la toolbox octave-sockets fournit la fonctionnalité de communiquer avec un serveur TCP/IP et ainsi transmettre un ordre vers le serveur que nous venons de décrire. D’un point de vue logiciel, nous implémentons ces fonctions par :
Ce code complète le précédent qui illustrait l’utilisation de Zero MQ, ici en initialisant la deuxième socket pour la liaison TCP/IP (SOCK_STREAM), d’envoyer la commande de réinitialisation des oscillateurs locaux (commande « 0 »), boucle sur les fréquences (commande « + ») pour s’achever en libérant la ressource occupée par le serveur (commande « q »). Pour chaque fréquence, la liaison ZeroMQ est ouverte (pour garantir la cohérence des mesures et ne pas récupérer des données obsolètes) et lire les données, comme nous l’avons vu auparavant. Nous avons constaté que nous devons absolument attendre une seconde (pause(1.0)) après avoir transmis l’ordre de reconfiguration des oscillateurs locaux, faute de quoi les sources radiofréquences ne sont pas stabilisées et bien entendu, la corrélation ne s’opère par correctement. Nous reviendrons sur ce point (section 6) qui handicape pour le moment considérablement la vitesse de mesure en nécessitant 1 s par acquisition ou près de 1 minute pour une bande de 50 MHz formée de 50 acquisitions par pas de 1 MHz.
Une fois les données acquises, nous devons concaténer ces mesures sur des bandes spectrales adjacentes, tel que nous l’avons vu dans la partie théorique précédente (section 2), extension du spectre qui revient à une interpolation par suréchantillonnage dans le domaine temporel.
4. Impact de la mesure
Avant de présenter les résultats, nous désirons appréhender les risques encourus en émettant dans des bandes réservées à divers services radiofréquences, notamment la télévision numérique terrestre, que nous n’avons évidemment pas le droit de brouiller volontairement.
Avons-nous empêché nos voisins de regarder la télévision pendant ces mesures qui ont duré quelques minutes chacune ? L’émetteur de télévision qui illumine Besançon depuis Montfaucon se trouve à 4850 m du site de l’expérience et émet 25 kW ou 74 dBm. Les pertes de propagation en espace libre déduites de l’équation de Friis 20 log10(d) + 20 log10(f) - 147,55 pour une fréquence f en Hz à une distance d en mètres indique environ 103 dB de pertes à 700 MHz, donc une puissance reçue de -29 dBm. Pour notre part, sans compter l’étalement spectral dans les 2 MHz qui abaisse la puissance crête de 63 dB, nous émettons -30 dBm (atténuation de 30 dB de la sortie mesurée à 0 dBm lors de l’émission d’une onde continue sans atténuation) qui à une distance de 50 m s’effondre, toujours d’après l’équation de Friis, de 63 dB ou une puissance au niveau de l’antenne des voisins de -93 dBm. Il semble donc raisonnable d’affirmer que notre contribution au signal reçu dans les bandes de télévision numérique terrestre est négligeable. De toute façon, il n’y avait rien d’intéressant ce jour-là (comme les autres, d’ailleurs) à la télévision.
5. Résultats
Rassuré de ne pas perturber la réception télévisuelle des Bisontins vers lesquels pointe l’antenne émettrice, diverses mesures sont effectuées en vue de faire varier les paramètres d’acquisition et observer leur impact. Nous vérifions dans un premier temps l’amélioration de résolution avec la bande passante d’analyse (figure 9).
Au cours de cette mesure, les deux bandes passantes analysées sont 50 et 150 MHz, c’est-à-dire en balayant par pas de 1 MHz les bandes 650 à 700 MHz et 650 à 800 MHz respectivement, ou la partie supérieure des bandes allouées à la télévision numérique terrestre, pour lesquelles nous pouvons nous attendre à ce que les antennes soient ajustées. Le gain en résolution est appréciable et permet de nettement identifier un réflecteur plus proche que celui attendu à une cinquantaine de mètres : l’écho à 200 ns environ doit se trouver à une distance de l’ordre de 150x0,2=30 m (150 étant la moitié des 300 m/μs que parcourt la lumière pour tenir compte de l’aller-retour).
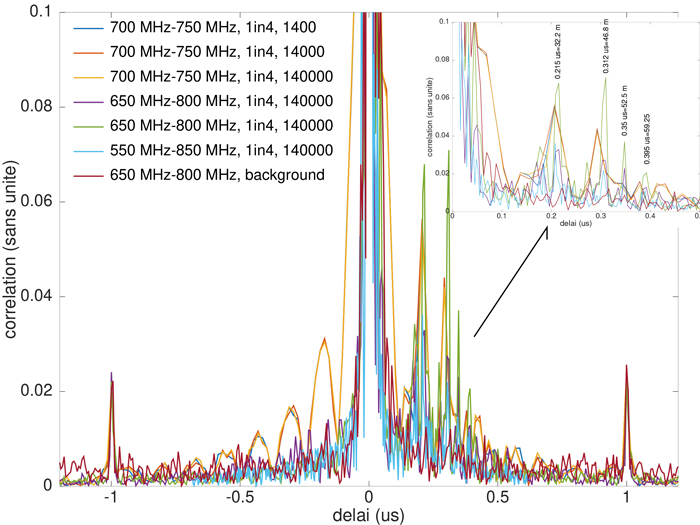
Nous systématisons cette série de mesure sur la figure 10 qui complète la vue précédente avec le niveau de base de bruit quand les antennes pointent vers le ciel, et une mesure à 250 MHz de bande passante. Nous avons étendu la visualisation de la corrélation à ±1 μs pour faire apparaître les deux artefacts à ces dates qui correspondent à l’inverse du pas d’acquisition des spectres. En effet, nous observons clairement lors de l’accumulation des spectres que le fenêtrage fait apparaître un motif de peigne de fréquence espacé de 1 MHz, dont la transformée de Fourier est un peigne en temps espacé de 1 μs. Ces pics de corrélation n’ont donc rien à voir avec des réflecteurs, tel qu’en atteste leur symétrie dans les retards négatifs. En insert, un zoom sur les temps positifs et l’identification des distances des réflecteurs associés aux échos les plus marquants.
Nous tentons une analyse dans le contexte géographique de la mesure de la source de ces réflecteurs (figure 11). Alors qu’il est à peu près indiscutable que l’écho à 46,8 m est le mur de la maison (M), les autres échos sont sujets à interprétation. Une voiture (V) garée dans le champ illuminé par l’antenne émettrice correspondrait à l’écho à 32,2 m, tandis que la cheminée métallique (C) sur le toit de la maison pourrait être attribuée au réflecteur à 52 m. Plus discutable, le réflecteur à 59,3 m est attribué à un tronc d’arbre (T) qui n’est pas indiqué sur OpenStreetMaps et dont le feuillage cache la visibilité sur Google Maps, mais pourrait tout aussi bien être dû à une des portes des garages alignés quelques mètres derrière cet arbre.
Simulation de retard par dispositif à onde élastique
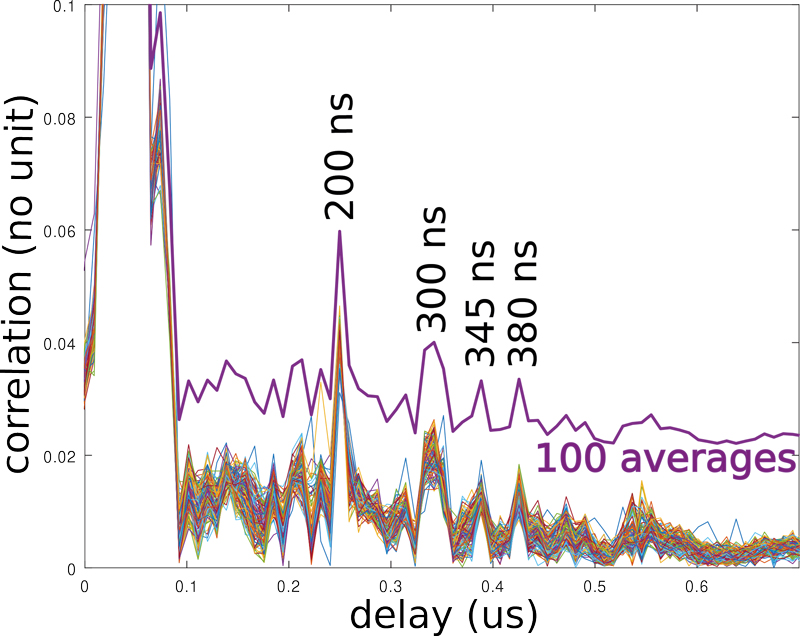
Le problème de la conception d’un RADAR est que le bilan de liaison change constamment avec les conditions environnementales. Une méthode robuste pour introduire un retard constant est appréciable en phase de déverminage. Cependant, même un câble coaxial qui abaisse de 60 % la vitesse d’une onde électromagnétique reste excessivement long quand il faut simuler 100 m de parcours aller-retour. L’alternative bien connue en traitement du signal d’onde radiofréquences est de les convertir en ondes élastiques, 105 fois plus lentes, en utilisant un substrat piézoélectrique tel que le quartz ou le niobate de lithium. Ayant la chance d’avoir accès à une telle technologie par nos liens avec la société SENSeOR qui commercialise de tels dispositifs, les premiers balbutiements de ce projet ont été validés en remplaçant la liaison radiofréquence par une ligne à retard à onde élastique de quelques millimètres de longueur introduisant un retard reproductible de 1 à 2,5 µs. Ce n’est qu’une fois le balayage de fréquence validé sur ce montage que nous avons tenté la mesure sans fil. Il est tout à fait fascinant de voir comment 50 mesures dans la bande 830–850 MHz par pas de 1 MHz, chacune avec une résolution de 1000/2, 7 = 340 ns, arrivent à se combiner pour former une mesure avec une résolution temporelle inférieure à 20 ns (figure de droite, bas en noir). La phase, mesure fine du retard et cachée dans ce graphique qui ne présente que le module de la corrélation, joue un rôle prépondérant dans cette combinaison d’informations acquises dans les diverses bandes de fréquences adjacentes.
6. Plus vite...
Nous avons mentionné de devoir attendre 1 s entre deux changements d’états des oscillateurs locaux, et ce, en accord avec la description faite sur https://files.ettus.com/manual/page_general.html qui indique « After tuning, the RF front-end will need time to settle into a usable state. [...] After tuning and before streaming, the user should wait for the lo_locked sensor to become true or sleep for a conservative amount of time (perhaps a second). » Nous avions initialement attribué cette latence à la B210 et son contrôle par libuhd, mais [9] indique des temps de stabilisation de l’étage radiofréquence de la B210 de l’ordre de la milliseconde, incompatible avec nos observations. Nous tournons donc notre attention vers la PlutoSDR qui s’avère (https://ez.analog.com/wide-band-rf-transceivers/design-support/f/q-a/107548/fast-frequency-sweep-with-the-pluto-in-gnu-radio/318711#318711) être la fautive. En effet la fonction utilisée par le Pluto Sink Block set_params reconfigure tous les paramètres de la PlutoSDR, même si nous ne voulons changer que la fréquence de l’oscillateur local. Travis Collins explique sur https://ez.analog.com/adieducation/university-program/f/q-a/91477/adalm-pluto-how-to-change-settings-with-quick-settling/199287#199287 avoir implémenté la fonction set_single_param dans la branche du même nom (https://github.com/analogdevicesinc/gr-iio/tree/single-param) de gr-iio, mais cette branche n’est pas compatible GNU Radio 3.8 et ne porte que sur le Pluto Source Block, et non le Sink. Qu’à cela ne tienne, la correction est triviale telle que décrite ci-dessous, et tient en une dizaine de lignes ajoutées au port GNU Radio 3.8 (branche upgrade-3.8 sur https://github.com/analogdevicesinc/gr-iio/tree/upgrade-3.8) de gr-iio pour permettre de remplacer self.iio_pluto_sink_0.set_params(self.f, self.samp_rate, 20000000, 30.0, '', True) proposé par GNU Radio Companion parself.iio_pluto_sink_0.set_single_param("out_altvoltage1_TX_LO_frequency",self.f) qui prend moins de 1 ms pour se stabiliser (soit un gain de plus qu’un facteur 1000 sur la vitesse de balayage).
Pour atteindre ces objectifs, la nouvelle fonction est déclarée dans include/iio/pluto_sink.h et include/iio/fmcomms2_sink.h par :
Ainsi que dans lib/pluto_sink_impl.h et dans lib/fmcomms2_sink_impl.h par :
Tandis que, dans le même fichier include/iio/fmcomms2_sink.h, sousclass IIO_API fmcomms2_sink_f32c : virtual public gr::hier_block2, nous ajoutons :
La fonction est implémentée dans lib/pluto_sink_impl.cc :
Et lib/fmcomms2_sink_impl.cc :
Désormais, c’est le temps de communication de la B210 vers le PC qui nous limite et non le temps de stabilisation de l’oscillateur local. En effet, grâce à cette modification, nous constatons qu’il faut désormais 1,3 s pour effectuer la mesure complète des 50 pas de fréquences. Cette durée est en accord avec la théorie qui prévoit qu’il faut 140000/(2,7⋅106x2)x50=1,296 s pour transmettre les 140000 points acquis sur les deux voies échantillonnées à 2,7 MHz entrelacées en répétant 50 fois la transaction. Dans ces conditions, moyenner 100 mesures ne prend qu’une paire de minutes avec le gain en rapport signal à bruit correspondant (figure 13).
Estimation de la portée de la mesure
Attention : cet encadré n’a aucune prétention d’exactitude et peut être complètement faux. Il s’agit de la meilleure analyse proposée, en l’absence d’expérience dans le domaine.
Nous désirons évaluer la portée du montage proposé et évaluer la pertinence des données acquises. Nous savons que nous émettons un signal par PlutoSDR atténué de 30 dB par rapport à sa puissance maximale de 0 dBm mesurée sur une onde continue en l’absence d’atténuation, et nous étalons dans une bande de 2,7 MHz. Nous estimons donc la puissance émise à -30-10 log10(2,7⋅106)=-94 dBm.
Nous mesurons un signal dans une bande de 2,7 MHz. Ainsi, le bruit thermique du mur illuminé par le RADAR, supposé à température ambiante de 290 K donc présentant un bruit thermique de -174 dBm/Hz, serait de -174+10 log10(2,7⋅106)=-110 dBm, auquel nous ajoutons un facteur de bruit de 2 dB au gain maximum fourni dans la documentation technique de l’AD9361, donc une limite de détection de -108 dBm.
Le bilan de liaison entre l’émetteur de puissance Pe, la cible et le récepteur recevant une puissance Pr est donné par l’équation du RADAR – extension de l’équation de Friis de pertes de propagation en espace libre lorsque le signal reçu est réfléchi par une cible de section RADAR σ :
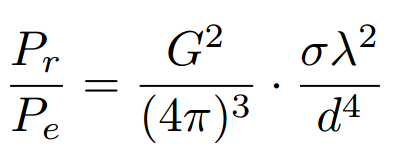
Ici d est la distance entre la cible et le RADAR monostatique, G le gain des antennes supposées identiques en émission et réception, et λ=0,4 m la longueur d’onde ici prise à 750 MHz. Le gain des antennes Yagi-Uda utilisées, Optex TNI5000, est annoncé sur la boîte du fabricant comme G=15 dB (quelle unité ? dBd, dBi...).
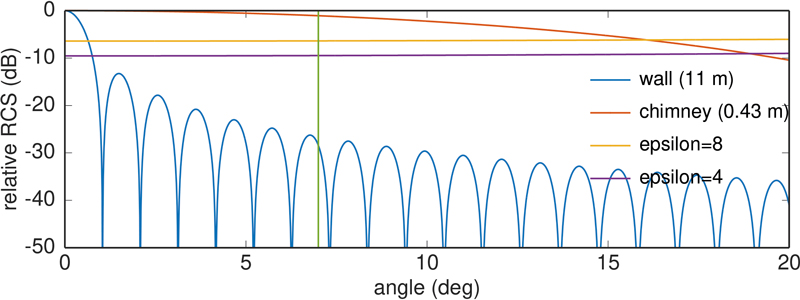
La section RADAR des cibles (RCS) est un problème complexe. En se référant à [10], un réflecteur plan de surface A présenterait une section RADAR σ=4πA2/λ2 : l’application numérique pour deux cas, un mur de 11x11 m2 et une cheminée métallique estimée à 2 m2, donnerait σ≃106 m2 et σ≃300 m2 respectivement. Cette formule est cependant valable pour un conducteur parfait en incidence normale, et surestime ici la section RADAR. D’après [11, Eq. 2.62], en incidence oblique d’un angle v, une plaque de a par b mètres présente lorsque illuminée par une onde électromagnétique de vecteur d’onde k=2π/λ une section RADAR :
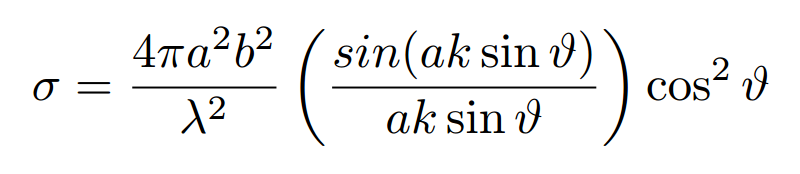
que nous avons tracé ci-dessous dans le cas du mur (bleu) et de la cheminée (orange) dont la section RADAR s’avère bien plus grande, malgré sa taille plus petite, car le mur réfléchit toute la puissance dans une direction autre que la position de l’antenne réceptrice, alors que la cheminée de largeur de l’ordre de la longueur d’onde diffracte efficacement l’onde incidente pour en réfléchir une partie vers l’antenne réceptrice.
L’angle d’incidence (trait vert vertical) a été déduit de l’analyse de la photographie de la figure 1 (droite) : GeoPortail nous indique que la maison est carrée, de longueur de mur 11 m, et une analyse géométrique triviale nous indique que la longueur apparente du mur le plus court (90 pixels) à la longueur apparente du mur le plus long (703 pixels) est la tangente de l’angle : nous estimons donc l’angle d’incidence de l’onde électromagnétique sur le mur à 7° et la largeur de la cheminée (28 pixels) à 43 cm – proche de la longueur d’onde du signal émis et expliquant donc la forte RCS de la cheminée, selon le même principe qui a incité le choix des gammes de fréquences les plus basses du RADAR utilisé en Yougoslavie pour détecter un avion furtif F117, si on en croit la légende.
Par ailleurs, le mur n’est pas un conducteur, mais un diélectrique (brique, béton) de permittivité comprise entre 4 et 8 [12]. Nous avons ajouté sur le graphique le coefficient de réflexion d’une onde électromagnétique à l’interface air-diélectrique selon l’équation de Fresnel classique en optique (on se rappellera dans ce cas que l’indice optique est la racine de la permittivité) : nous constatons que la contribution du diélectrique et de l’incidence oblique abaissent facilement la section RADAR d’une quarantaine de dB au minimum par rapport à l’estimation initiale. [13, p. 14] nous informe qu’un camion ne présente une section RADAR que de 200 m2 à 10 GHz ! Restons donc à une telle valeur de 200 m2 dans tous les cas.
D’après l’équation du RADAR, les -94 dBm émis sont réfléchis par ces cibles estimées à environ 50 m d’après les temps de vol pour revenir avec une puissance atténuée de :
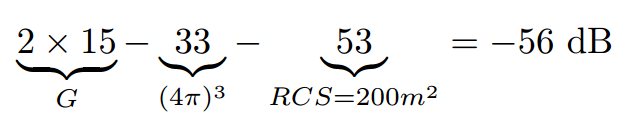
ou une puissance reçue de -94-56=-150 dBm.
Nous concluons en tenant compte du gain de compression d’impulsion par corrélation qui s’opère sur 140000 points ou 10 log10(140000)=51 dB, donc la comparaison se fait entre le plancher de bruit de -108 dBm et le signal reçu de l’ordre de -150+51=-99 dBm. Le rapport signal à bruit est donc d’une dizaine de dB, en accord avec le rapport signal à bruit de l’ordre de 10 observé expérimentalement en échelle linéaire (figure 13, courbes non moyennées).
Conclusion
Nous avons pu explorer, grâce à deux plateformes de radio logicielle, une pour l’émission et une double voie pour la réception, le principe du RADAR à bruit et tester expérimentalement la relation entre la résolution en distance et la bande passante du signal, quitte à concaténer des spectres adjacents acquis successivement. Ces principes de base ouvrent de nombreuses perspectives :
- compléter l’unique antenne réceptrice par un réseau d’antennes équidistantes pour retrouver une information angulaire d’azimut de chaque cible. Sous hypothèse que les cibles sont « loin » des antennes (condition de champ lointain avec une onde plane illuminant le réseau), la direction d’arrivée s’obtient par transformée de Fourier selon l’axe des antennes dans la matrice des échantillons temporels acquis par chaque antenne ;
- réduire la latence de communication sur bus USB en déportant la génération de la séquence pseudo-aléatoire dans le Zynq de la PlutoSDR et en effectuant la corrélation dans le FPGA de la B210. Cela nécessite de maîtriser du VHDL et RFNoc... pas facile, mais avec 56 MHz de largeur de bande entre les AD936x et les matrices de porte logiques, le gain en vitesse (au moins 20) de balayage est significatif ;
- nous nous sommes autorisé le luxe de la B210 alors que des récepteurs de télévision numérique terrestres R820T2 pourraient faire l’affaire. Dans [14], l’auteur nous enseigne à 12 minutes et 30 secondes de son discours qu’il est possible de reprogrammer la fréquence de l’oscillateur radiofréquence du R820T2 sans perdre d’échantillons sur le flux transmis du récepteur vers GNU Radio, garantissant ainsi le maintien de la cohérence entre les deux (ou plus) récepteurs : la bibliothèque implémentant ces modifications est disponible sur https://github.com/DC9ST/librtlsdr-2freq.
Finalement, mobiliser un ordinateur portable est peu satisfaisant alors que la Raspberry Pi 4 est équipée de deux ports USB2 et deux ports USB3 (figure 14). Tous les outils nécessaires ont été portés pour Buildroot – exploitant pleinement le processeur 64 bits – à l’exception de GNU/Octave qui est favorablement remplacé par Python, au moins pour la phase d’acquisition : une version complètement embarquée de l’expérience est donc assemblée grâce aux paquets fournis par G. Goavec-Merou sur https://github.com/oscimp/PlutoSDR/tree/for_next. On notera que toutes les transactions entre Octave et Python se faisant par sockets, il est trivial de commander l’acquisition depuis Python sur la Raspberry Pi par GNU/Octave exécuté sur un PC.
Les codes complets dont les extraits sont présentés dans cet article sont disponibles sur github.com/jmfriedt/active_radar afin d’encourager le lecteur à reproduire l’expérience ou les traitements sur les signaux proposés.
Remerciements
Toutes les références qui ne sont pas librement disponibles sur le Web ont été téléchargées sur Library Genesis sur gen.lib.rus.ec, une ressource indispensable à nos recherches et développements. Le calcul de section RADAR des cibles a été orienté par F. Daout (IUT Ville-d’Avray). Notre collègue F. Tolle (laboratoire ThéMA, Université de Franche-Comté) a fait découvrir [1]... mais il n’est pas certain qu’il doive être remercié pour autant.
Références
[1] Orelsan, Gringe, « Casseurs Flowters - 15h02 - Regarde comme il fait beau (dehors) », 2013 : https://www.youtube.com/watch?v=4qaTeHEo-28
[2] A.R. VOLKOVSKII, L.S. TSIMRING, N.F. RULKOV & I. LANGMORE, « Spread spectrum communication system with chaotic frequency modulation », Chaos, 15(3), 033101, 2005
[3] Y. GUIDON, « Les nombres pseudo-aléatoires pour les nuls », GNU Linux Magazine France n°81, p. 64 à 76, 2006
[4] R. BOURRET, « A proposed technique for the improvement of range determination with noise radar », Proc of IRE, 45(12), p. 1744, 1957 : https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4056465
[5] B.M HORTON, « Noise-Modulated Distance Measuring Systems », Proc. IRE, 47(5), p. 821 à 828, 1959
[6] K. A. LUKIN & R. M. NARAYANAN, « Historical overview and current research on noise radar », 3 rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), 2011 cite un numéro entier de IET Radar, Sonar & Navigation (août 2018) dédié au traitement du signal dans les RADAR à bruit, dont les titres sont accessibles sur https://ieeexplore.ieee.org/xpl/tocresult.jsp?isnumber=4607165
[7] H. SUN, « Ultrawideband and Random Signal Radar », dans J.D. Taylor Ed. « Ultrawideband RADAR – Application & Design », CRC Press, 2012
[8] J. FRIEDT, « RADAR passif par intercorrélation de signaux acquis par deux récepteurs de télévision numérique terrestre », GNU/Linux Magazine no212, février 2018 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-212/RADAR-passif-par-intercorrelation-de-signaux-acquis-par-deux-recepteurs-de-television-numerique-terrestre
[9] R. BELL, « Maximum Supported Hopping Rate Measurements using the Universal Software Radio Peripheral Software Defined Radio », Proc. GRCon 2016 sur https://pubs.gnuradio.org/index.php/grcon/article/view/2/1
[10] E.F. KNOTT, J.F. SHAEFFER & M.T. TULEY, « Radar Cross Section », 2nd Ed., SciTech Publishing, 2004
[11] B.R. MAHAFZA, « Radar Systems Analysis and Design Using MATLAB », 3rd Ed., CRC Advances in Applied Mathematics, 2013
[12] C. THAJUDEEN & al., « Measured complex permittivity of walls with different hydration levels and the effect on power estimation of TWRI target returns », Progress in Electromagnetics Research B 30, p. 177 à 199, 2011
[13] M. SKOLNIK, « Introduction to radar systems », 2nd Ed., McGraw-Hill, 1980
[14] S. SCHOLL, « DC9ST Introduction and Experiments on Transmitter Localization with TDOA », Software Defined Radio Academy, 2017 : https://www.youtube.com/watch?v=Km4TU17b05s et la description détaillée sur http://www.panoradio-sdr.de/tdoa-transmitter-localization-with-rtl-sdrs/



 Ajouter à une liste de lecture
Ajouter à une liste de lecture