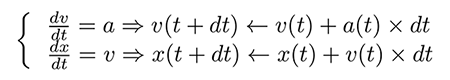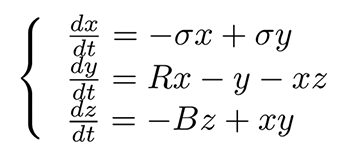Dans le contexte du traitement du signal sur systèmes embarqués et en particulier sur microcontrôleurs qui ne sont pas munis d’une unité de calcul en virgule flottante (FPU), nous reprenons une célèbre observation de 1963 sur l’évolution de systèmes dynamiques excessivement sensibles aux conditions initiales, et donc qualifiés de chaotiques lors de simulations en représentation des nombres à virgules fixes.
René Descartes considérait au 17e siècle que si les lois de la physique sont connues et les conditions initiales (position, vitesse des particules) de la modélisation d’un environnement sont identifiées, alors l’évolution du système est parfaitement prévisible. Cette vision dominante en Occident pendant les deux siècles qui suivirent au cours du siècle des Lumières et jusque dans les années 1950 [1] fut mise à mal par les physiciens de la seconde moitié du 20e siècle qui gâchèrent cet élégant déterminisme en introduisant les phénomènes non linéaires, notamment nécessaires pour modéliser les fluides. Le plus grand fluide qui entoure cette planète est l’atmosphère, et la discussion de comptoir la plus intéressante reste encore la prévision du temps, déterminée par les mouvements de masses d’air induisant températures, précipitations et vents.
Edward Norton Lorenz (1917–2008) est le météorologue qui sera remémoré [2] pour avoir enterré le déterminisme de René Descartes en mettant en évidence la croissance exponentielle (et non polynomiale comme dans les lois considérées par Descartes) de l’erreur de la solution à un problème physique non linéaire en fonction du temps avec l’erreur sur les conditions initiales. Couplée avec les relations d’incertitude temps-fréquence (ou position-vitesse, ou temps-énergie) de Heisenberg, toute capacité de prévision de la météorologie à long terme est vaine, mais probablement la plus grande découverte de Lorenz est de concevoir que même si le temps (soleil, pluie, vent) ne peut être prévu à une date ultérieure lointaine, la solution reste bornée dans une gamme de valeurs plausibles. C’est la différence entre météorologie (quel temps fera-t-il ?) et climatologie (quelle sera la température moyenne au siècle prochain ?).
Telle que nous l’observons lors de nos séjours en arctique au Spitzberg, la prévision météorologique est toujours juste avec les modèles les plus fins actuels, mais la date à laquelle les événements météorologiques surviennent est incertaine, et ce d’autant plus que la prévision est lointaine dans le futur : la pluie viendra bien après le beau temps, mais la date de transition est d’autant plus incertaine qu’elle est lointaine dans le futur. L’Arctique fut un enjeu majeur pendant la Seconde Guerre mondiale, puisque les conditions météorologiques en Europe occidentale se déduisent des conditions météorologiques arctiques [3].
James Gleick [1] relate l’histoire de la découverte d’un système chaotique par E. Lorenz [4] par « One day in the winter of 1961, wanting to examine one sequence at greater length, Lorenz took a shortcut. Instead of starting the whole run over, he started midway through. To give the machine its initial conditions, he typed the numbers straight from the earlier printout. Then he walked down the hall to get away from the noise and drink a cup of coffee. When he returned an hour later, he saw something unexpected, something that planted a seed for a new science.
This new run should have exactly duplicated the old. Lorenz had copied the numbers into the machine himself. The program had not changed. Yet as he stared at the new printout, Lorenz saw his weather diverging so rapidly from the pattern of the last run that, within just a few months, all resemblance had disappeared. He looked at one set of numbers, then back at the other. He might as well have chosen two random weathers out of a hat. His first thought was that another vacuum tube had gone bad.
Suddenly he realized the truth. There had been no malfunction. The problem lay in the numbers he had typed. In the computer’s memory, six decimal places were stored: .506127. On the printout, to save space, just three appeared: .506. Lorenz had entered the shorter, rounded-off numbers, assuming that the difference – one part in a thousand – was inconsequential.
[...]
... in Lorenz’s particular system of equations, small errors proved catastrophic. »
Ainsi donc, Edward Lorenz avait mis en évidence un système d’équations dont le comportement change drastiquement selon que l’on omet ou non les décimales de l’état représentant le système. Nos ordinateurs ne peuvent représenter le nombre qu’avec une précision finie : quelle conséquence a le chaos sur notre capacité de modélisation, et en particulier sur systèmes embarqués avec les contraintes de représentations des nombres à virgules ? À une époque où l’« intelligence artificielle » et toutes les méthodes de traitement non linéaires du signal sont à nouveau à la mode [5], il est peut-être bon de se remémorer les limites imposées par la physique, aussi « intelligent » que nous voulions rendre l’ordinateur (à défaut de son programmeur).
1. Une balle qui tombe
Commençons cette démonstration par un système trivial qu’aurait prôné R. Descartes pour sa démonstration – une balle qui tombe dans le vide, parfaitement déterministe et dont la solution ne dépend que faiblement de l’identification des conditions initiales. La simulation des équations différentielles régissant ce système est peu sensible aux conditions de simulation et nous obtiendrons toujours le même résultat. Extrapolant les mêmes méthodes de simulation en virgule flottante ou virgule fixe avec un pas de temps de simulation variable, nous verrons que la modélisation de l’atmosphère sera considérablement modifiée (« météo »), tout en restant bornée (« climat »).
Arithmétique en virgule fixe
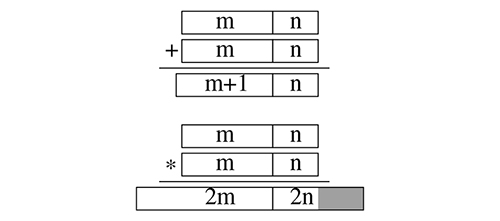
La représentation en virgule flottante représente chaque nombre sous forme scientifique de la forme mantisse (inférieure à 1 en valeur absolue) multipliée par un exposant, rendant les opérations arithmétiques complexes pour une unité arithmétique et logique (ALU) qui ne sait manipuler que des entiers, notamment pour aligner la position de la virgule lors de la somme. La représentation en virgule fixe bénéficie, par rapport à la représentation en virgule flottante, d’une arithmétique de la somme et la différence qui s’apparente à celle des entiers que l’ALU sait manipuler (figure de gauche, haut). Cependant, maintenir la position de la virgule lors des multiplications et divisions nécessite d’effectuer l’homothétie des arguments. Par exemple, en décimal 10-2× 10-2=10-4 mais si seules 2 décimales sont significatives, les deux décimales ajoutées par le produit (10-3 et 10-4) doivent être éliminées pour maintenir la représentation sur deux décimales significatives. Cette opération est représentée par la zone grisée du produit en bas de la figure de gauche. Contrairement à l’arithmétique des entiers (long, short et char en C) qui est exacte, car conservant tous les bits de poids faible, ici n bits de poids faible sont perdus lors de chaque multiplication.
Galileo Galilei définit la masse comme l’incapacité d’un corps à être mis en mouvement sous l’effet d’une force extérieure. L’accélération a que subit un corps détermine sa variation de vitesse v telle que la variation infinitésimale de vitesse dv pendant un temps infinitésimal dt est dv/dt=a ou en d’autres termes dv=a·dt et entre deux instants séparés de dt la vitesse évolue de v=v+dv. De la même façon, la vitesse est la dérivée avec le temps de la position, donc la balle qui tombe sous l’effet de la gravité voit sa position x évoluer par dx/dt=v -> dx=v·dt et x <- x+dx=x+v·dt. Avec v qui évolue tel que nous l’avons vu auparavant, il est évident d’effectuer la double intégration pour retrouver x=1/2a·t2 l’évolution de la position avec le temps. La résolution numérique du système
de la balle qui tombe en subissant l’accélération constante de la gravité de a=10 m.s-2 sur la Terre, qui impacte l’évolution de la vitesse v <- v+a·dt qui impacte l’évolution de la position x <- x+v·dt entre chaque instant dt, se modélise trivialement selon la méthode d’Euler [6] que nous venons de décrire en représentation des variables à virgule flottante par :
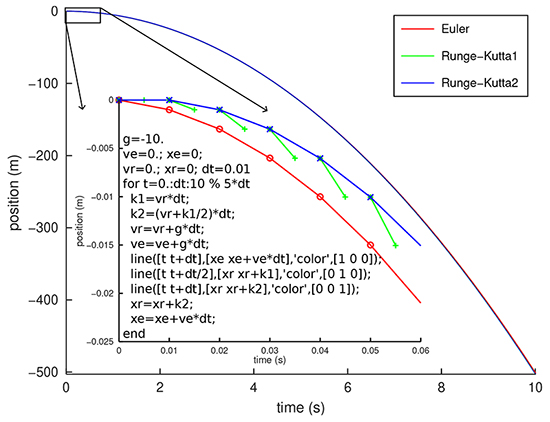
L’infinitésimal étant très petit, nous pourrons arbitrairement choisir dt=0,1 s, dt=0,01 s ou dt=0,001 s pour obtenir respectivement -505 m, -500,5 m, -500,05 m, mais remonter à -499,21 m avec un pas de dt=0,1 ms, et René Descartes ne verra que peu d’implication de l’intervalle de temps entre deux mesures, le système étant déterministe et l’approximation de la parabole par une série de segments de droites pas trop fausse en comparant avec la solution analytique 1/2at2 qui s’achève par 0,5×10×100=500 m parcourus par la balle en 10 s. Cette formulation est la plus simple pour résoudre une équation différentielle, mais la moins précise et le lecteur curieux d’améliorer le résultat pourra consulter [6, p.602] pour une description des méthodes de Runge-Kutta pour améliorer la précision de la solution.
Méthode de Runge-Kutta
La méthode d’Euler consistant à linéariser localement l’équation différentielle en considérant que le point suivant x+dx se déduit uniquement de la droite liant le point courant par sa dérivée vers le point suivant dx=v×dt est un peu grossière et peut s’affiner en considérant des points intermédiaires aux temps dt/2, dt/4... Ces méthodes évoluées dites de Runge-Kutta, nommées d’après leurs concepteurs [7], améliorent l’exactitude et les chances de convergence de la solution telles qu’illustrées sur la figure de droite, avec en insert le code GNU/Octave permettant de tracer ce graphique.
Nous avons déjà longuement expliqué [8] que la représentation en nombre à virgule flottante est inadéquate pour un système embarqué qui ne sait manipuler que des entiers, et qu’il est efficace d’utiliser la représentation en nombre à virgule fixe qui consiste à non plus conserver tous les bits de poids faible comme le fait l’arithmétique sur les entiers (avec potentiellement une croissance démesurée des bits de poids fort), mais de considérer que des bits de poids faible ne sont que du bruit et qu’ils peuvent être éliminés lors de l’arithmétique sur les nombres à virgule fixe. Ainsi, en considérant que m bits représentent la partie entière d’un nombre et n bits représentent la partie fractionnaire (d’où la nomenclature introduite par Texas Instruments d’une représentation Qm.n), alors la somme de nombres en virgule fixe respecte l’arithmétique des entiers (la retenue se propagera de la partie fractionnaire vers la partie entière), mais la multiplication produit 2 m bits de partie entière et 2n bits de partie fractionnaire dont la moitié est éliminée par décalage du résultat sur les entiers vers la droite de n bits. Ainsi, le programme que nous venons de voir en virgule flottante devient en virgule fixe en remplaçant les opérations arithmétiques « + » mais surtout « * » par addfix() et mulfix(), et en prenant soin d’effectuer l’homothétie sur les constantes que sont l’accélération et la date de fin de simulation :
en exploitant les fonctions suivantes de calcul en virgule fixe qui conservent SCALE décimales (une version binaire avec un décalage au lieu de division par puissance de 10 est plus efficace mais moins pédagogique) :
qui utilise le fichier d’en-tête fixed.h définissant notamment la constante SCALE ou le nombre de décimales à conserver :
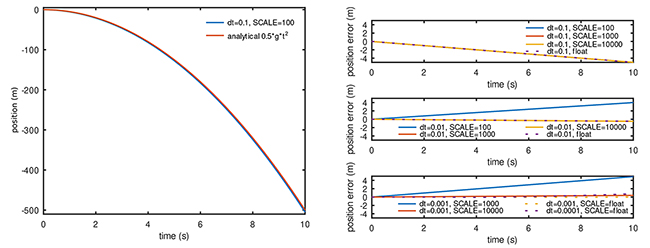
Quel que soit l’intervalle de temps entre deux points de simulation, nous retrouvons un résultat proche de la solution analytique (Fig. 2) et l’hypothèse de Descartes est validée. Reproduisons maintenant la même expérience sur le système d’équations de Lorenz.
2. Un typhon ou un temps calme
Aux balbutiements de la résolution numérique de systèmes d’équations différentielles, notamment pour la modélisation des fluides et donc de l’atmosphère, alors que les ordinateurs possédaient moins de puissance de calcul que n’importe quel microcontrôleur actuel, E.N. Lorenz poursuit un calcul en reprenant le résultat de la veille, mais en omettant d’insérer quelques décimales qu’il n’avait pas sauvegardées lors de l’impression de l’état de variables représentant l’atmosphère selon trois grandeurs que nous nommerons arbitrairement (x,y,z) et que nous pourrons nous représenter par exemple comme x la température, y la pression et z la vitesse du vent. Une modélisation simplifiée de l’atmosphère se résume par un ensemble d’équations différentielles (Fig. 3) qui se résume [4] par
avec les constantes σ=10, B=8/3 et R=28 (Fig. 3). L’équation de Lorenz est dite non linéaire, car fait intervenir des produits entre variables de la forme xz et xy, qui se traduisent par un comportement chaotique défini comme une croissance exponentielle des erreurs sur les conditions initiales de la simulation ou le pas de temps de simulation. Ce comportement se distingue des systèmes linéaires que nous avons vus auparavant avec la balle qui tombe, dont les erreurs sur les conditions initiales croissent selon des lois polynomiales, donc beaucoup plus lentes (et donc déterministes). Cependant bien que chaotique, la solution de ce système reste bornée dans des gammes de solutions « raisonnables », par exemple avec des températures supportables et des vitesses de vent qui ne raseront pas des villes dans la majorité des conditions de simulation. La prévision du temps est considérée comme chaotique, car il est très difficile (impossible) de connaître précisément les conditions de l’atmosphère à une date lointaine dans le futur, contrairement à la prévision du climat qui maintient les solutions bornées dans des solutions globalement reproductibles, mais sans prétention d’annoncer quelle condition sera observée à quelle date.
En généralisant la méthode de résolution vue auparavant que l’évolution infinitésimale dx de chaque variable x évolue au cours de l’intervalle de temps infinitésimal dt pour une mise à jour x <- x+dx, l’opération est itérée sur les trois grandeurs (x,y,z). Dans un premier temps en représentation à virgule flottante et avec la condition initiale (x,y,z)=(0,1, 0., 0.), le programme de résolution s’écrit :
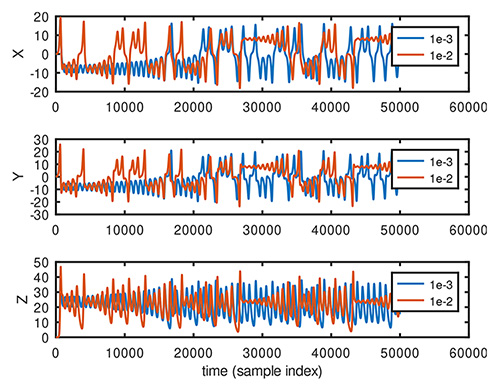
et la première surprise survient lorsque nous traçons en fonction du temps x ou z pour des pas de simulation dt=10-2 ou dt=10-3. La forme des courbes est reproductible, mais la transition d’un état à l’autre (haut ou bas de la courbe) intervient à des dates très différentes (Fig. 4). Toutefois, les solutions restent bornées dans des intervalles similaires.
Par ailleurs, avec un pas de temps trop grossier, par exemple dt=10-1, la solution diverge pour ne plus être représentable par un nombre à virgule flottante et l’obtention de NaN ou Not a Number.
La transposition de la résolution par une représentation en virgule fixe s’exprime sous forme de :
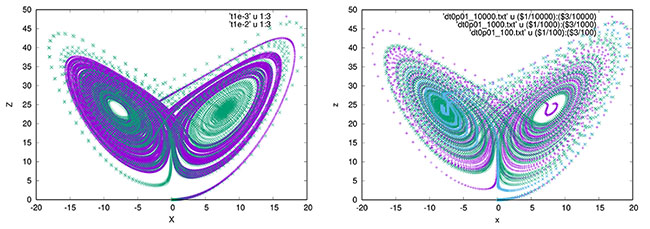
et en traçant cette fois l’évolution d’une variable, par exemple z, en fonction d’une autre variable, par exemple x, nous observons l’« attracteur étrange » qui exhibe la solution dans l’espace des phases (x,z), toujours avec un ensemble de solutions bornées, mais se comportant très différemment selon que le pas de temps est dt=10-2 ou 10-3, interdisant toute prévision de savoir si la solution se trouve sur l’aile droite ou gauche du papillon après un certain temps de simulation (Fig. 5).
L’exécution sur STM32F1 du code proposé à https://github.com/jmfriedt/stm32/ dans le sous-répertoire lorenz indique une durée d’exécution de 1,25±0,05 seconde par itération d’une simulation de 50 secondes par pas de 10-3 en virgule fixe contre 1,38±0,05 s pour une version en virgule flottante en l’absence d’optimisation (option -O0 par défaut de GCC) pour passer à 0,89±0,05 seconde par itération en virgule fixe lors d’une optimisation par -O3 ou le classique -Os, qui n’amènent aucun bénéfice en virgule flottante. Ainsi, le bénéfice de la virgule fixe existe et devient significatif en laissant le compilateur optimiser l’exploitation des entiers par l’unité arithmétique et logique, pour gagner un facteur 1,5 sur le temps d’exécution, sachant que le facteur d’homothétie est une puissance de 10 et non une puissance de deux qui permettrait de remplacer les divisions entières par des décalages.
Conclusion
La résolution numérique de systèmes d’équations différentielles a été abordée dans le contexte de systèmes embarqués favorisant la représentation en nombre à virgule fixe sur les processeurs qui ne sont pas munis d’une unité matérielle de calcul en virgule flottante tel que le STM32F1. Alors que les systèmes physiques les plus courants respectant la linéarité de leur comportement sont peu sensibles aux conditions initiales et conditions de simulation, les systèmes non linéaires sont connus depuis les années 1960 et l’avènement de la théorie du chaos pour être excessivement sensibles à ces conditions de simulation. Néanmoins, même s’il est difficile (impossible) de prédire à long terme la météo qu’il fera, les tendances climatiques qui sont modélisées par de tels systèmes restent bornées dans un ensemble cohérent de solutions, sans permettre d’identifier précisément à quelle date il fera beau. Et toute intelligence artificielle ne pourra pas déroger aux conditions imposées par la physique...
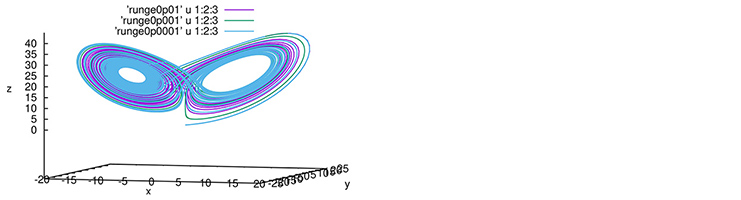
Pour conclure, nous avons mentionné que la méthode d’Euler qui ne propage que la dérivée première pour prédire l’évolution du système est peu stable et que la méthode de Runge-Kutta présente de meilleures conditions de convergence en considérant la dérivée vers un point intermédiaire. Toutefois, notre code de résolution des équations de Lorenz par cette méthode présente bien entendu les mêmes sensibilités aux conditions de simulation dans le cas du système chaotique (Fig. 6) en ayant doublé le nombre d’opérations arithmétiques nécessaires à l’incrément du pas de temps :
Références
[1] J. Gleick, Chaos: Making a New Science, Random House UK (1997).
[2] E.N. Lorenz, Deterministic nonperiodic flow, J. of Atmospheric Sciences 20(2) 130–141 (1963) at
https://journals.ametsoc.org/view/journals/atsc/20/2/1520-0469_1963_020_0130_dnf_2_0_co_2.xml
[3] W. Dege, War North of 80 – the last German Arctic weather station of World War II, University of Calgary Press (2004).
[4] H.O. Peitgen, H Jürgens, D. Saupe, & M.J. Feigenbaum, Chaos and fractals: new frontiers of science, Springer New York (1992).
[5] A. Sidder, The AI Forecaster: Machine Learning Takes On Weather Prediction (2022) à
https://eos.org/research-spotlights/the-ai-forecaster-machine-learning-takes-on-weather-prediction
[6] Chap. 15, Integration of Ordinary Differential Equations dans W.H. Press & al., Numerical Recipes in Pascal – the Art of Scientific Computing, Cambridge University Press (1989) ou chap. 16 de Numerical Recipes in C, 2nd Ed, Cambridge University Press (1992).
[7] J.C. Butcher, A history of Runge-Kutta methods. Applied numerical mathematics 20(3) 247–60 (1996) à
https://people.cs.vt.edu/~asandu/Public/Qual2011/DiffEqn/Butcher_1996_RK-history.pdf
[8] J.-M Friedt, Arithmétique sur divers systèmes embarqués aux ressources contraintes : les nombres à virgule fixe, GNU/Linux Magazine France Hors-Série 113 (mars 2021) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmfhs-113/arithmetique-sur-divers-systemes-embarques-aux-ressources-contraintes-les-nombres-a-virgule-fixe



 Ajouter à une liste de lecture
Ajouter à une liste de lecture