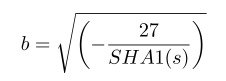Standardisation des courbes elliptiques : à qui faire confiance ?

Introduction

La cryptographie à base de courbes elliptiques a été introduite il y a maintenant plus de trente ans et l'intérêt de son usage ne fait aujourd'hui plus de doute. D'une part, les algorithmes de décomposition en produits de facteurs premiers ont été largement améliorés ces dernières années, rendant ainsi certaines tailles de clefs RSA obsolètes et obligeant par là même à augmenter sensiblement la taille des clefs. D'autre part, le meilleur algorithme connu pour calculer le logarithme discret dans un groupe multiplicatif (une structure mathématique classique très utilisée en cryptographie) ne s'applique pas pour la plupart des courbes elliptiques. Du fait de sa solidité, les tailles de clefs nécessaires sont plus petites et rendent également les coûts de calculs plus faibles que d'autres systèmes tels que RSA. D'abord largement breveté et standardisé par des organismes états-uniens, le domaine des courbes elliptiques a connu dernièrement des développements importants, notamment avec l'introduction de nouvelles courbes (Edwards), le développement d'attaques contre les implémentations et l'usage désormais régulier de celles-ci avec par exemple ECDHE ou ECDSA dans TLS. Seulement, il apparaît aujourd'hui primordial de développer des standards reconnus pour leur transparence, ce qui n'est entre autres pas ou plus le cas des standards du NIST. En effet, au-delà même du fait que des mathématiciens de la NSA soient à l'origine des courbes du NIST, la compromission du standard Dual_EC_DRBG (du NIST également) montre bien qu'il est impératif d'être en pleine maîtrise des choix relatifs à la structure d'un algorithme en cryptographie (et de ses constantes bien sûr).

C'est ainsi que ces derniers mois ont vu naître beaucoup de recherches et de discussions autour des courbes à normaliser. L'enjeu étant de taille, cela va certainement définir quelles courbes vont se retrouver massivement utilisées et remplacer peu à peu les vieilles courbes du NIST (même si ces dernières sont encore considérées comme sûres). La sécurité des courbes repose sur plusieurs critères mathématiques qui sont à l'heure actuelle majoritairement partagés par la communauté de la cryptographie. La tension principale autour de la sélection des courbes à normaliser ne se joue pas sur ce dernier terrain, mais bien sûr celui de l'évaluation des avantages et inconvénients de chaque courbe (performance, résistance aux attaques par canaux auxiliaires, simplicité d'implémentation) et, fait assez nouveau, la transparence (reproductibilité ou vérifiabilité) du processus qui a mené à développer et choisir certains paramètres de courbes plutôt que d'autres. Ce dernier point, que l'on retrouve parfois sous le terme de « rigidité », sera l'objet principal traité dans cet article. Après un bref rappel sur les courbes elliptiques et leur histoire, seront discutées les différentes méthodes existantes pour la procédure de génération des courbes, pour terminer sur différents travaux de normalisation en cours. Cet article cherche volontairement à simplifier les descriptions des structures liées aux courbes elliptiques afin de rendre l'ensemble des explications plus accessible aux non-initiés. Ainsi, que les esprits rigoureux pardonnent par avance les abus de langage et les raccourcis un peu simplistes.

1. Rappel sur l'utilisation des courbes elliptiques

1.1 Notions et logarithme discret

Introduisons tout d'abord quelques rudiments de mathématiques. Ce sujet faisant déjà l'objet d'un article dans le présent hors-série, seront utilisées quelques notions définies par ce dernier en essayant malgré tout d'épurer un maximum les équations. Dans tout cet article, les notations suivantes seront utilisées :

• y2 = x3 + ax + b comme équation d'une courbe elliptique classique (forme simplifiée de Weierstrass) ;
• a et b comme les constantes de cette équation ;
• p un nombre premier définissant le corps premier (toutes les opérations se font modulo p) ;
• G un point générateur (point de base) ;
• X,Y des points quelconques de la courbe, dont les coefficients sont définis sur Fp ;
• k un scalaire.

Comme évoqué en introduction, l'intérêt principal des courbes elliptiques est la difficulté de calcul du logarithme discret dans une courbe : il est facile de calculer Y = k * X pour k et X connus, mais il est par contre très difficile de trouver k pour X et Y connus : c'est le calcul du logarithme discret. L'opération notée ici * correspond à la multiplication d'un point de la courbe par un scalaire et produit un autre point sur la courbe. La méthode la plus efficace pour faire ce dernier calcul dans un cadre général (il existe des optimisations dans des cas particuliers) se nomme « pollard-rho » et a été introduite il y a maintenant plus de vingt ans.

1.2 Exemple : échange d'un secret partagé : Diffie-Hellman

L'un des usages les plus courants des courbes elliptiques est la génération d'un secret partagé en utilisant le mécanisme de Diffie-Hellman dans le groupe d'une courbe elliptique. De la même manière que dans le groupe multiplicatif d'un corps fini (le cas « classique »), le protocole se définit comme suit :

• Alice génère un entier aléatoire a puis envoie G * a ;
• Bob génère un entier aléatoire b puis envoie G * b ;
• Alice et Bob utilisent le nouveau secret ainsi généré (G * a) * b  (égal à (G * b) * a).

L'ensemble des opérations se faisant dans le groupe de la courbe utilisée, c'est-à-dire en fonction des paramètres de celles-ci : un point de base, un grand nombre premier et des constantes liées à la structure de la courbe. Par exemple, si l'on décide d'utiliser la courbe Curve25519 [1] alors les paramètres sont les suivants :

• équation de la courbe : y2 = x3 + Ax2 + x (forme de Montgomery) ;
• nombre premier : 2255 - 19 ;
• point de base : x = 9 ;
• constantes A = 486662.

On retrouve ce mécanisme sous le nom X25519 (pour l'utilisation de la courbe Curve25519 et du mécanisme Diffie-Hellman). Cette primitive est notamment utilisée dans des applications telles qu'OpenSSH, Tor ou Signal. La question centrale qui va être traitée ici est l'origine et la confiance que l'on va pouvoir accorder aux constantes utilisées. Comme on peut le voir dans ce premier exemple, un ensemble de paramètres a été sélectionné par les développeurs de la courbe Curve25519, répondant à des critères de sécurité, mais aussi de performance. Les questions qui peuvent être soulevées sont alors : quels sont ces critères ? Sont-ils publiés ? Y a-t-il une procédure transparente pour la génération des constantes ? Qui sont les développeurs derrière cette courbe ? Puis-je leur faire confiance ?

2. Brève histoire des courbes elliptiques

La cryptographie à base de courbes elliptiques a été introduite en 1985 par Koblitz et, de manière indépendante, par Miller. Au début des années 1990, ECDSA voit le jour (la variante de DSA utilisant les courbes elliptiques). Quand bien même de vives critiques existent au sujet des courbes elliptiques (des personnalités de la cryptographie à cette époque qualifient ce domaine d'ésotérique), l'ANSI (American National Standards Institute), avec l'appui de la NSA, approuve les premiers standards à la fin de l'année 1995. Le NIST publiera par la suite, en 1999, un ensemble de courbes destinées à la cryptographie. De l'ensemble de ces courbes, mises au point essentiellement par Jerry Solinas et quelques autres mathématiciens de la NSA, on retient surtout aujourd'hui celles encore considérées comme sûres d'un point de vue mathématique, c'est-à-dire celles définies sur un corps premier tel que P-224, P-256, P-384 (où le nombre situé après le P correspond à la taille du nombre premier en bits). Dans ce même temps, quelques résultats mathématiques sont obtenus, identifiant notamment des familles de courbes plus faibles en termes de sécurité. La NSA annonce en 2005 la « suite B », après notamment un accord commercial avec Certicom qui possédait alors quantité de brevets sur le domaine. Cette « suite B » est un ensemble de recommandations cryptographiques visant notamment la protection des communications classées « Top Secret » par le gouvernement états-unien, reposant à ce moment-là uniquement sur des primitives utilisant les courbes elliptiques. Cette même année verra également arriver une implémentation de quelques primitives à base d'ECC (Elliptic Curve Cryptography) dans la célèbre librairie OpenSSL ainsi que l'introduction de courbes issues d'un développement en milieu universitaire, notamment la Curve25519 de Daniel Bernstein. Milieu universitaire qui va également mettre au point les années suivantes de nouvelles familles de courbes aux propriétés intéressantes en termes de performance et de résistance aux attaques par canaux auxiliaires, telles que la famille des courbes d'Edwards, qui seront introduites en cryptographie par Daniel Bernstein et Tanja Lange.

3. Les critères de sélection concernant la sécurité

Les deux sous-parties suivantes visent à introduire quelques éléments nécessaires à la sécurité d'une courbe elliptique. Bien entendu, l'objet de ce travail vise essentiellement à définir des critères mathématiques pour la structure d'une courbe : c'est-à-dire rendre difficile le calcul du logarithme discret dans le groupe de la courbe. Cependant, il existe d'autres critères de sécurité ayant été mis en exergue par des attaques réelles, tels que la sécurité de la courbe tordue (« twisted curve ») ou encore la nécessité d'une loi d'addition unifiée, pour ne citer que ces deux exemples.

Mais ce n'est pas tout. Il y a également des critères comme la simplicité d'implémentation d'une courbe (et donc des opérations associées) qui sont d'une importance suffisante pour considérer cet aspect comme un élément de sécurité. Sur ce dernier point, afin d'appuyer l'argument de simplicité, on pourra prendre en exemple des implémentations largement répandues qui ont été cassées à cause d'une mauvaise implémentation, notamment à cause d'une difficulté supplémentaire rajoutée par certaines courbes. Par exemple, l'implémentation de ECDH pour TLS dans le cas de Bouncy Castle a été cassée à cause d'une étape de vérification manquante (si un point utilisé était effectivement sur la courbe ou non) ayant permis d'effectuer une attaque en utilisant une courbe invalide. Cette étape de vérification de la présence d'un point sur une courbe peut paraître triviale, mais ajoute en réalité un niveau de complexité qui pourrait être réduit si quelques contre-mesures simples étaient prises en amont dans la structure de la courbe elle-même.

Cette partie n'a pas pour objectif de lister de manière exhaustive les critères de sécurité nécessaires, mais simplement d'introduire quelques notions. Pour plus de détails, vous pouvez consulter différentes publications récentes qui tentent, elles, de définir de manière relativement complète les besoins en matière de structure mathématique afin qu'une courbe soit considérée comme sûre [3][6][7].

3.1 Difficulté de résolution du logarithme discret

Bien que le calcul du logarithme discret soit considéré comme difficile pour une grande partie des courbes, il est nécessaire d'établir quelques critères afin de ne pas tomber dans des classes de courbes vulnérables à des attaques permettant l'utilisation d'un algorithme avec une complexité moindre. Le critère de base étant que la meilleure méthode disponible pour calculer le logarithme discret n'ait pas une complexité inférieure à une certaine borne fixée, correspondant à la complexité du calcul dans un cas « classique » (c'est-à-dire une courbe n'ayant pas de faiblesse). Pour ce faire, plusieurs critères sont établis sur différents éléments de la structure de la courbe elliptique (nombre de points de la courbe, ordre du sous-groupe, degré de plongement) afin de garder une telle complexité. Pour plus de détails, le site SafesCurve donne de bonnes explications dans sa catégorie « ECDLP security » [8].

Un élément supplémentaire visant à se protéger de futures attaques non connues contre le logarithme discret est l'utilisation d'une courbe générique, c'est-à-dire ne reposant par exemple pas sur un corps de base trop structuré. Pour la courbe NIST-P256, le nombre premier utilisé est de la forme 2256 – 2224 + 2192 + 296 - 1, ce qui permet, dans le cas d'un groupe multiplicatif, une nette optimisation du calcul du logarithme discret. Certains cryptologues proposent donc de ne pas utiliser une telle forme de nombre premier pour les courbes elliptiques dans la crainte de la découverte d'une attaque identique contre ces dernières. On notera qu'il s'agit ici d'un compromis à faire entre la performance (les nombres premiers construits de cette dernière manière permettant d'optimiser les calculs) et la généricité de la courbe.

3.2 Sécurité des implémentations

Même si les critères précédents sont respectés, il est toujours possible d'attaquer l'implémentation même avec une possibilité de succès. Par exemple, il existe de nombreuses attaques par canaux auxiliaires (analyse des temps de calcul, injection de fautes) contre la méthode de multiplication d'un point par un scalaire (qui fait partie du cœur des opérations sur une courbe elliptique). Pour ne citer que le cas d'OpenSSL, son implémentation de l'échelle de Montgomery (algorithme de multiplication par un scalaire) a été l'objet d'une attaque par un canal auxiliaire « FLUSH+RELOAD » permettant l'extraction des « nonces » utilisés par ECDSA [11]. Bien d'autres problèmes potentiels existent concernant la structure de la courbe : sécurité de la courbe tordue, petit sous-groupe, points spéciaux, nécessité d'avoir une loi d'addition unifiée ; il existe dans tous les cas des contre-mesures efficaces. Pour plus de détails pratiques une fois de plus, consultez le site SafesCurve dans sa catégorie « ECC security » [8].

4. Les critères de sélection en termes de confiance

Comme vu précédemment, les critères de sélection concernant la sécurité des courbes elliptiques, allant de la difficulté de calcul du logarithme discret à la résistance aux attaques par canaux auxiliaires, font l'objet d'un accord relativement général de la part de la communauté. Cependant, un nouveau critère est apparu ces dernières années concernant la procédure de génération d'une courbe. En effet, même si l'ensemble des critères de sécurité est respecté, une certaine souplesse existe pour un attaquant qui aurait par exemple connaissance d'une vulnérabilité pour une certaine classe de courbes. C'est essentiellement ce dernier point qu'essayent de résoudre les différentes initiatives qui ont vocation à rendre transparente et non manipulable la procédure de génération de la courbe.

4.1 Processus de génération des constantes

4.1.1 Des paramètres… tombés du ciel

La première façon de fournir des paramètres relatifs à une courbe est de les donner simplement sans explication. Difficile alors d'établir une confiance dans ces derniers, à moins justement d'avoir une confiance aveugle dans l'organisme ou la personne qui les a générés. Les paramètres de la courbe de l'ANSSI sont ainsi fournis par le biais de leur site ainsi que du Journal Officiel [2] :

Il apparaît trivial, avec cette manière de procéder, qu'une très grande marge de manœuvre soit offerte à celui qui fournit la courbe elliptique, quand bien même l'état de l'art en termes de sécurité serait respecté. Dans une publication visant à mettre en exergue la manipulabilité des procédures destinées à générer les paramètres de courbes elliptiques [3], une méthode est proposée afin de générer une courbe possédant des propriétés particulières. Afin d'illustrer leurs propos, les auteurs proposent de générer une constante b (cf. équation classique d'une courbe) très structurée (cf. l'exemple ci-après) pour démontrer une attaque fictive. Ainsi, en respectant les meilleurs critères de sécurité connus, ils arrivent à obtenir après 78 minutes sur un cœur de CPU AMD une constante avec le motif « 5AFEBADA55ECC » (je vous laisse décoder le « leet speak ») :

L'idée ici est de démontrer que, si un attaquant connaît une classe de vulnérabilité non connue sur les courbes elliptiques, il est alors simple de générer une courbe présente dans cette classe (l'idée derrière la structure du paramètre b étant ici de mimer une courbe appartenant à cette classe) tout en respectant les critères de sécurité connus. Le problème ici étant bien l'absence même de procédure permettant de vérifier la génération des paramètres.

4.1.2 Paramètres dérivés d'un « hash »

Une autre manière de fournir les paramètres d'une courbe est de les proposer sous la forme de « seed » et d'une fonction de hachage (plus quelques étapes afin de générer la constante finale). Le résultat de la fonction sera ainsi une partie de la sortie de la fonction de hachage. L'idée est donc de faire reposer la confiance sur la solidité de la fonction de hachage : il est très difficile de choisir un paramètre selon une certaine structure, car il est très difficile d'inverser la fonction de hachage. C'est notamment ce que proposent les courbes du NIST pour les paramètres de la courbe, à l'exception du nombre premier utilisé. Pour le paramètre b de la courbe P-256, la formule suivante est utilisée afin de le générer :

Avec :

L'origine de cette dernière valeur ? Nul ne le sait. Ou plutôt, seuls les développeurs de ce paramètre (des mathématiciens de la NSA). On a donc remplacé, par rapport à la situation précédente sans procédure, un paramètre inexpliqué par une valeur de « seed » inexpliquée produisant ce paramètre. Cela complexifie donc légèrement la génération d'un paramètre répondant à une structure bien précise qui permettrait d'exploiter une vulnérabilité non connue, mais ne la rend en rien impossible. Pire, en termes de confiance, le processus n'étant en définitive pas transparent (on ne sait tout simplement pas d'où vient le « seed »), la procédure de génération n'est en rien améliorée. Cependant, concernant la difficulté de génération d'une constante avec une structure pouvant exploiter une vulnérabilité inconnue, le coût en est effectivement augmenté. De la même manière que précédemment, les auteurs de BADA55 [3] ont effectué une attaque cherchant, par la force brute, la présence d'un motif de 8 symboles hexadécimaux dans la constante b (BADA55EC) afin de simuler une vulnérabilité potentielle avec une probabilité de 2-32 . Dit autrement, l'idée est de maîtriser 32 bits de la constante b. Cela représente, contrairement à l'attaque fictive précédente, une quantité de calcul bien plus élevée à effectuer avant d'obtenir un résultat dans les contraintes proposées. Il ne faut pas oublier que cette attaque n'est effectuée qu'une seule fois avant de publier ou normaliser la courbe et pourrait ne représenter aucune difficulté pour un organisme disposant de gros moyens de calcul. En témoigne d'ailleurs la réaction de Michael Scott en 1999 au moment de la publication des courbes du NIST :

Le problème était donc déjà bien présent dans les esprits il y a maintenant dix-sept ans.

4.1.3 Paramètres dérivés de valeurs connues

Utiliser des valeurs de « seed » inconnues (quand bien même générées potentiellement de manière aléatoire) ne permet donc en rien d'améliorer la confiance dans la procédure. Plusieurs initiatives ont vu le jour afin d'utiliser des nombres provenant de constantes connues, par exemple : cos(1), pi ou sqrt(2). On parle alors de NUMSN, « Nothing Up My Sleeve Numbers ». Ces dernières valeurs étant considérées comme n'ayant pas, par construction, de propriétés cachées pouvant être exploitées. C'est notamment le cas de la procédure Brainpool [4] qui vise à générer les paramètres d'une courbe en utilisant une « seed » initiale basée sur la constante exp(1). Bien entendu, cette valeur de « seed » initiale ne remplissant pas les critères de sécurité nécessaires une fois passée dans le processus de génération (entre autres une fonction de hachage), cette valeur est incrémentée jusqu'à ce que les critères fixés soient effectivement atteints. La valeur du nombre premier utilisé est également générée selon cette procédure. Cette fois-ci on ne peut donc pas manipuler la « seed » utilisée. Malgré tout, rien ne garantit que la procédure entière n'ait pas été élaborée délibérément pour obtenir certaines constantes : le choix de la fonction de hachage, la taille des données d'entrées de celle-ci, la manière d'extraire une partie de la constante naturelle, la constante naturelle elle-même et bien d'autres petites étapes de la procédure. Il y a, une fois de plus, beaucoup de degrés de liberté pour celui qui élabore la procédure pour arriver à obtenir une certaine structure dans les constantes générées. Dans le numéro 8 de « Poc||GTFO », J.-P. Aumasson propose, dans un article élégamment nommé « Backdoors up my sleeve », une preuve de concept permettant de générer 1'990'656 constantes dérivées de « seed » ayant pour valeur uniquement des nombres NUMSN et en manipulant les méthodes d'encodage et décodage ainsi que le choix de la fonction de hachage. Bref, rien qui pourrait sembler étrange lors d'une analyse de la procédure. Cela démontre combien il est aisé, même en utilisant un nombre en apparence objectif, de manipuler quelques bits du paramètre résultants d'une telle procédure.

4.1.4 Paramètres dérivés d'une source d'aléa publique

Plus récemment, une initiative visant à utiliser une source d'aléa publique a vu le jour : « Million Dollar Curve ». L'objet intéressant de la procédure ici est d'utiliser les résultats de plusieurs loteries dans le monde afin d'en extraire des « seeds » pour générer ensuite les constantes d'une courbe. Cela réduit encore plus les degrés de liberté pour celui qui souhaiterait mettre au point une procédure biaisée en se basant sur une source d'aléa publique sans avoir à modifier directement les critères de sécurité. Cette différence complique hautement la tâche de l'attaquant et rendrait la procédure nettement plus alambiquée s'il essayait de la biaiser. Bien entendu, cette procédure repose largement sur l'hypothèse qu'un attaquant disposant de grosses capacités ne puisse influencer les résultats des différentes loteries utilisés par « Million Dollar Curve », ce qui est notamment critiqué par certains cryptologues.

4.1.5 Paramètres générés de manière déterministe

Une tout autre manière de générer les constantes est de proposer une procédure entièrement déterministe qui ne repose que sur des contraintes de sécurité, mais également de performance. L'idée est de minimiser le choix dans les constantes disponibles. C'est par exemple le cas des courbes proposées par Microsoft. Ces courbes, nommées « NUMS Curves » (cela n'est pas sans rappeler les NUMSN), utilisent par exemple cette procédure afin de générer un nombre premier :

• on définit un niveau de sécurité s (par exemple 128, 192 ou 256) ;
• on prend un nombre premier p de la forme 22s - c (cette structure de nombre premier permettant d'effectuer des calculs plus rapidement) ;
• on cherche c le plus petit entier tel que p 3 mod 4 (choix assez courant permettant d'optimiser certains calculs, tels que celui de la racine carrée, utile dans la compression de point).

Dans ce simple cas également, plusieurs critères sont manipulables afin de structurer le nombre premier qui sera choisi. La procédure n'apporte en définitive que les raisons pour lesquelles Microsoft a choisi précisément ces courbes. La confiance ici est donc déplacée sur les bons choix en termes de sécurité et de performance que pourrait avoir faits Microsoft (dans le cas présent, ils n'ont choisi que des éléments basés sur des critères reconnus). Exprimée de façon plus claire encore, la confiance repose sur le fait que les ingénieurs de chez Microsoft n'ont pas délibérément sélectionné l'ensemble de ces critères afin de choisir une certaine classe vulnérable de courbe.

Quand bien même les courbes Curve25519 et Curve41417 ne prétendent pas définir de procédure permettant de générer leurs paramètres, elles apportent de manière transparente, à l'instar de celles de Microsoft, un ensemble d'explications détaillant les raisons des choix de leurs constantes (notamment concernant les besoins de sécurité et performance).

4.2 Confiance, sécurité et performance : des usages aux compromis

L'ensemble des procédures détaillé précédemment met en évidence un élément important dans la sélection d'une courbe : on ne peut pas obtenir des performances intéressantes (nécessitant une courbe plus structurée, par exemple dans la forme du nombre premier utilisée) et une courbe générée selon une procédure qui dérive ses paramètres depuis des données aléatoires (ou des NUMSN). Pareillement, on ne peut pas obtenir une courbe avec une procédure totalement transparente (telle que la courbe à un million de dollars) et une courbe avec des paramètres dédiés à optimiser certains calculs. Des compromis sont effectivement nécessaires et dépendent clairement des besoins de l'utilisateur. Besoins qui d'ailleurs nécessitent la définition de différents standards en identifiant clairement des usages, proposant par là même plus de diversité. Il existe malgré tout une certaine concurrence pour obtenir certaines propriétés de performance et de sécurité, telles que les courbes NUMS de Microsoft et les courbes Curve25519 et Curve41417, prétendant toutes à détailler de manière transparente l'ensemble des choix effectués sur leurs constantes.

5. Les processus de standardisation

5.1 Modèles de décision

Pour faire très court et très simple, il existe principalement deux grandes catégories de modèles de décision au sein des organismes de recommandation et de standardisation. Ceux qui visent à établir un consensus de la communauté (l'IETF parle de « rough consensus ») en fournissant un processus ouvert impliquant des personnes extérieures : liste de diffusion publiquement accessible, prise de décision par les personnes responsables du standard ou de la recommandation en fonction des discussions apportées par la communauté. C'est par exemple le cas de l'IETF ou du W3C. D'un autre côté, il y a les organismes fermés (pouvant malgré tout faire intervenir des personnes extérieures) prenant des décisions en interne auxquelles on ne peut pas participer. On pourra citer par exemple le NIST ou l'ANSSI, dont l'objet dépasse dans les deux cas l'élaboration de standards ou de recommandations.

5.2 Quoi de neuf au NIST ?

Dans une récente publication [9], Daniel Bernstein et Tanja Lange font une analyse des échecs des premières courbes du NIST. Ils mettent en exergue entre autres :

• une complexité d'implémentation ;
• l'absence d'explication dans les choix des paramètres ;
• de mauvais choix d'optimisation.

Malgré tout, le NIST est en passe de développer un nouveau standard afin de proposer de nouvelles courbes (même si ce n'est pas encore sûr pour le moment). C'est ainsi qu'il a organisé un workshop durant le mois de juin 2015 [10]. On remarquera que l'ANSSI était présente avec deux de ses chercheurs, qui ont apporté d'ailleurs une pièce intéressante [7] aux débats : « Diversity and Transparency for ECC ». En effet, malgré que l'ANSSI n'ait pas apporté de justification aux paramètres de sa courbe par le passé, il semble, avec cette contribution, que la transparence et la vérifiabilité du processus de génération des constantes soient désormais d'un intérêt important.

5.3 IRTF/IETF : RFC 7748, « Elliptic Curves for Security »

Bien que pour la cryptographie l'IETF (et surtout le Crypto Forum Research Group) dépende largement des choix faits par le NIST (une bonne partie des primitives conseillées proviennent du NIST), le groupe de travail sur TLS a demandé au CFRG de lui recommander de nouvelles courbes à utiliser. Une des motivations principales pour cette demande était la nécessité d'avoir un processus de génération de courbe auquel on puisse effectivement faire confiance. Il y a eu également beaucoup de discussions sur l'intérêt des courbes dites « aléatoires » (c'est-à-dire dont les paramètres sont générés selon une procédure faisant intervenir à la base une valeur aléatoire) vis-à-vis des courbes avec des paramètres « optimisés ». La conclusion de ce débat met en avant les courbes « optimisées » avec plusieurs tailles pour les longueurs de clefs (notamment pour la crainte d'attaques futures, il est simplement proposé d'utiliser une taille de clef plus grande). C'est ainsi que les courbes candidates les plus discutées étaient celles de Microsoft (les fameuses « NUMS ») et de Daniel Bernstein (Curve25519) pour, en définitive, recommander Curve25519 (pour un niveau de sécurité de 128 bits) et la courbe Ed448-Goldilocks (une courbe d'Edwards avec des choix conservateurs où l'ensemble des paramètres est justifié) développée par Mike Hamburg (pour un niveau de sécurité de 224 bits). Pour le moment, cela ne concerne que les primitives ECDHE et ECDH (des travaux sur les signatures sont en cours), et le RFC concernant leurs usages dans TLS est en préparation.

5.4 W3C : Web Cryptography API

On pourra également remarquer que du côté du W3C, la toute récente API « web cryptography » encore en normalisation ne propose pour le moment que les vieilles courbes du NIST malgré de longues discussions sur la possible inclusion des courbes NUMS de Microsoft et la courbe Curve25519. En effet, les différents problèmes d'intégration dans la norme ainsi que l'absence de recommandation du CFRG vis-à-vis des courbes à sélectionner (au moment du débat au W3C, car depuis le RFC a été publié) n'ont pas permis de créer le consensus nécessaire pour intégrer d'autres courbes que celles du NIST [12].

Conclusion

Ainsi, même si les courbes elliptiques représentent une avancée intéressante en termes de sécurité, de performance et comme une alternative à RSA, il apparaît aujourd'hui primordial d'avoir des processus de sélection totalement transparents et, idéalement, ouverts. Même si, comme souvent, il n'y a pas de solution parfaite, plusieurs courbes peuvent être aujourd'hui considérées comme ayant des paramètres élaborés de façon transparente (que cela soit de manière aléatoire ou déterministe) même si les procédures sous-jacentes pour les générer (Brainpool, NUMS) restent faillibles. Aussi, les compromis à faire sont encore discutés quant aux courbes à utiliser (y a-t-il un vrai intérêt à utiliser les courbes « aléatoires » ? Même en second choix ? Pourquoi ne pas plutôt choisir une solution secondaire telle qu'une primitive « post-quantique » si l'on néglige les performances ?) et devrait certainement s'atténuer quand le NIST aura pris une décision par rapport à de potentielles prochaines recommandations. Pour l'heure, l'IETF a déjà fait ses choix pour la future version de TLS et la transparence est au rendez-vous.

Remerciements

Bien évidemment, cet article est essentiellement basé sur les différents travaux de recherche référencés dans les notes et j'en remercie sincèrement leurs auteurs. Merci également à Éloi Vanderbeken et Alexander pour leurs relectures et conseils avisés. Merci aussi à Aurélien pour ses nombreuses relectures.

Références

[1] https://cr.yp.to/ecdh.html

[2] http://www.legifrance.gouv.fr/affichTexte.do;jsessionid=?cidTexte=JORFTEXT000024668816&dateTexte=&oldAction=rechJO&categorieLien=id

[3] https://bada55.cr.yp.to/

[4] https://tools.ietf.org/html/rfc5639

[5] https://cryptoexperts.github.io/million-dollar-curve/

[6] https://eprint.iacr.org/2014/130.pdf

[7] https://eprint.iacr.org/2015/659.pdf

[8] http://safecuves.cr.yp.to/

[9] https://cr.yp.to/newelliptic/nistecc-20160106.pdf

[10] http://www.nist.gov/itl/csd/ct/ecc-workshop.cfm

[11] https://eprint.iacr.org/2014/140.pdf

[12] https://lists.w3.org/Archives/Public/public-webcrypto/2014Aug/0186.html