OTR existe depuis plus de dix ans, et permet à tout le monde de protéger ses échanges instantanés, non seulement d’attaquants externes, mais aussi d’un interlocuteur mal intentionné.
À la fin de son documentaire Citizenfour [1], Laura Poitras remercie plusieurs personnes, mais également plusieurs logiciels : TrueCrypt, Tor, GnuPG, OTR… En effet, ce sont eux qui ont été utilisés pour établir et maintenir une communication entre elle et le lanceur d'alerte Edward Snowden, pendant la transmission de documents top secret, à l'insu de la NSA. Ce n'est pas un hasard, car justement, un de ces documents mentionne le fait que ces outils causent des « problèmes majeurs » aux agences de surveillance.
Pourtant, si aujourd'hui tout le monde connaît les trois premiers (Truecrypt pour le chiffrement de disques, Tor pour l'anonymat, GnuPG pour chiffrer les courriels), OTR reste relativement méconnu, ce qui est bien dommage, car il offre des possibilités uniques et très intéressantes pour s'assurer que des conversations secrètes le soient, et le restent, y compris dans des situations ubuesques.
1. OTR, mais encore ?
OTR signifie Off the record, un terme journalistique d'origine anglo-saxonne se référant à la règle dite de Chatham House, énonçant que les participants sont libres d'utiliser les informations, mais qu'ils ne doivent révéler ni l'identité, ni l'affiliation des personnes à l'origine de ces informations, de même qu'ils ne doivent pas révéler l'identité des autres participants. C'est précisément l'une des fonctionnalités d'OTR : garantir que dans un échange, il ne sera pas possible de lier la conversation à son interlocuteur, tout en étant certain que c'est bien à lui que l'on s'adresse durant celle-ci.
OTR a été présenté en 2004 par Nikita Boris, Ian Goldberg et Éric Brewer dans leur papier Off-the-Record Communication, or, Why Not To Use PGP [2]. Le but était d'offrir une réponse à deux soucis posés par GPG :
- Le manque de sécurité persistante lié au fait que les clefs privées de GPG sont des clefs de long terme. La confidentialité persistante, appelée Forward secrecy en anglais, empêche un attaquant de déchiffrer les échanges précédents en cas de compromission de la clef privée.
- Son authentification forte ne permet pas la répudiabilité, les messages étant signés avec les clefs de long terme. La répudiabilité permet de désavouer le contenu d'une conversation précédente. Comme dans la vie réelle, lorsque deux personnes discutent, c'est la parole de l'une contre celle de l'autre pour savoir ce que chacun a dit ou non.
Le papier était accompagné (chose assez rare pour être mentionnée) d'une implémentation complète dans un logiciel de chat populaire : Gaim, aujourd'hui connu sous le nom de Pidgin. En effet, OTR cible davantage la messagerie instantanée que les échanges asynchrones (de type courriels par exemple), déjà couverts (tant bien que mal) par GPG.
Autre trait inhabituel du papier, son modèle de menace (threat model en anglais). En effet, d'habitude, les papiers de cryptographie racontent l'histoire de Bob et d'Alice tentant de communiquer, pendant qu'Eve les espionne de diverses manières. Ici, il s'agit non seulement de ça, mais également du fait qu'Alice ou Bob pourrait décider de trahir son interlocuteur à tout moment.
OTR vise en fait à fournir les mêmes caractéristiques qu'une conversation en tête à tête dans une pièce entre Alice et Bob :
1. Personne ne sait ce qui y est dit, à part Alice et Bob.
2. Personne ne sait ce qui y a été dit, sauf si Alice et Bob le racontent.
3. Personne ne peut modifier la conversation sans qu'Alice et Bob ne le remarquent.
4. Personne ne peut prouver ce qui y a été dit, pas même Alice et Bob !
En plus de 10 ans d'existence, OTR a reçu plusieurs peer-review, certaines débouchant sur des attaques concrètes, a évolué pour les corriger, pour se simplifier, ajouter des fonctionnalités… Bref, c'est un protocole sérieux, qui a été consciencieusement scruté par des experts en mathématiques, cryptographie, programmation et sécurité informatique. C'est sûrement pour ça qu'il est implémenté dans bon nombre de logiciels de messagerie instantanée : Pidgin, Irssi, WeeChat, Gajim, Adium, TorBirdy, Cryptocat…
2. Fonctionnement
2.1 Transport
Le protocole OTR est agnostique quant à sa couche de transport : chaque message est envoyé encodé en base64, un encodage utilisant uniquement 64 caractères affichables : 26 lettres en minuscule, 26 en majuscule, 10 nombres, ainsi que les signes +, / et =. Cela rend possible l'utilisation d'OTR sur n'importe quel protocole permettant de transmettre du texte. Par exemple, Pidgin va jusqu'à proposer de s'en servir sur le chat Facebook.
Pour initier une conversation OTR, il y a deux méthodes possibles. On peut envoyer soit un tag OTR de la forme ?OTR suivit d'un indicatif de version, soit un ensemble d'espaces et de tabulations. Les deux ont une différence sémantique : le premier indique qu'Alice aimerait que Bob ait une conversation OTR avec elle, tandis que la deuxième indique que son client est capable de converser en OTR.
2.2 Authentification (SMP)
Qui a déjà tenté d'utiliser GPG sait à quel point la vérification d'empreintes de clefs publiques est une étape fastidieuse, qui a très vite tendance à devenir kafkaïenne quand il s'agit d'établir un canal sécurisé, pour échanger les empreintes, pour les valider, pour s'en servir pour pouvoir communiquer à travers un… canal sécurisé. Bref, ça n'est pas pratique du tout, encore moins quand on essaye de s'en servir avec quelqu'un qui n'est pas habitué à ce genre de manœuvres.
C'est pour ne pas reproduire cette erreur qu'OTR propose une alternative plus facile à utiliser : le SMP, pour Social Millionaire Protocol.
L'idée vient du Problème des millionnaires posé par Andrew Yao en 1982 [3], dans lequel deux millionnaires veulent savoir lequel d'entre eux possède la plus grosse fortune, sans pour autant en divulguer le montant. La solution repose sur des mathématiques de niveau lycée, qui ne seront pas détaillées dans cet article. Ici, le montant de la fortune sert en fait de secret partagé, connu à la fois d'Alice et de Bob, qui peuvent s'assurer mutuellement qu'ils le connaissent bien, tout en ne le divulguant jamais.
Cette méthode fait partie des méthodes d'authentification dites de type ZKIP, pour Zero Knowledge Identity Proof, en français : preuve à divulgation nulle de connaissance. En effet, dans les systèmes plus classiques, comme une authentification sur un site web, le serveur demande le mot de passe, et le client lui transmet. Les problèmes arrivent quand l'utilisateur se connecte à un attaquant se faisant passer pour le vrai site, auquel il donnera son mot de passe. Dans une authentification de type ZKIP, l'utilisateur ne divulgue rien que le site (ou l'attaquant) ne connaisse déjà.
Un attaquant passif (qui se contente d'écouter le trafic) n'aurait aucune information quant au mot de passe ; un attaquant actif (qui modifie le trafic) pourrait savoir uniquement s'il a deviné ou non ledit secret, et faire échouer le protocole, mais rien de plus. Il serait incapable de se faire passer pour l'un des deux protagonistes.
Dans le cadre d'OTR, il est également possible d'utiliser une question (transmise en clair), sa réponse étant la valeur secrète. Par exemple « Quand on s'est rencontré pour la dernière fois, qu'est-ce que je t'ai fait à manger comme dessert ? », avec comme réponse « Un chausson aux pommes ». Ce qui est bien plus convivial et facile à utiliser qu'une vérification réciproque d'empreintes de clefs publiques comme on a l'habitude d'en faire.
2.3 Confidentialité persistante
Traditionnellement (avec GPG), pour envoyer un message à Bob il suffit à Alice de récupérer la clef publique de Bob, de chiffrer le message puis de lui envoyer, afin qu'il soit reçu, déchiffré avec la clef privée, puis finalement lu par Bob.
Le souci se pose quand Eve enregistre les échanges, et parvient à voler la clef privée (saisie, vol, virus…). Elle est alors en mesure de déchiffrer l'intégralité des messages échangés.
Pour répondre à ce problème, les protocoles modernes de cryptographie comme OTR utilisent un système de clefs éphémères : au lieu d'utiliser les clefs de long terme pour chiffrer/déchiffrer le message, elles servent uniquement à authentifier la négociation de clef éphémère, qui a lieu pour OTR au début d'un échange.
Il existe plusieurs méthodes de négociation de clef éphémère, OTR utilisant la plus connue : Diffie-Hellman. Elles permettent la création d'un secret partagé (ici, des clefs de chiffrement temporaires) sans jamais le faire transiter. Le fait que ce soit ces clefs éphémères qui soient utilisées pour le chiffrement permet d’empêcher que des échanges passés soient déchiffrables si les clefs de long terme venaient à être compromises, car elles interviennent uniquement pour l'authentification, et pas pour le chiffrement.
2.4 Répudiabilité
Bob et Alice ont une conversation au sujet de leur liaison secrète, mais Bob menace de tout révéler au grand jour ! Heureusement, la propriété de répudiabilité d'OTR signifie que Bob ne peut pas prouver qu'Alice était réellement l'auteure des messages, même s'il en était sûr pendant la conversation.
Ce type de propriété est appelé répudiabilité faible ; il existe également de la répudiabilité forte, et OTR fournit les deux. La première indique que si l'un des protagonistes rend public un message reçu, il est possible qu'il l'ait entièrement fabriqué.
La seconde garantit que si un message vient à être rendu public, il peut avoir été fabriqué par n'importe qui, et non pas uniquement par Alice ou Bob : chacun d'entre eux pourrait donc légitimement nier que la conversation ait eu lieu.
Le fait qu'OTR soit un protocole authentifié n'est pas incompatible avec ces propriétés de répudiabilité, même si cela peut sembler contre-intuitif au premier abord. L'astuce est de ne pas utiliser de signatures issues de clefs de long terme, comme le fait GPG, mais plutôt des MAC (Message Authentication Codes), garantissant l'intégrité d'un message, à l'aide d'une clef éphémère connue à la fois de l'expéditeur et du destinataire.
Pour chaque message à envoyer :
1. l'expéditeur chiffre le message ;
2. calcule son MAC ;
3. envoie le message chiffré ainsi que son MAC associé au destinataire ;
4. le destinataire recalcule le MAC pour vérifier que le message n'a pas été altéré, et qu'il provient bien du bon expéditeur ;
5. finalement, le destinataire déchiffre et lit le message.
La beauté de la chose est que pour vérifier qu'un message est authentique, il faut posséder la clef du MAC, ce qui permet donc de contrefaire ce message ! En effet, pour contrefaire un message, il suffit de connaître deux choses : sa clef de MAC (qui est rendue publique une fois ledit message reçu), et sa clef de chiffrement. Grâce à la MAC, il est possible de contrefaire de nouveaux échanges à loisir. Par contre, il est impossible de faire de même pour un message futur. Impossible de trahir son interlocuteur en révélant des échanges, car dès qu'on est en mesure de déchiffrer un message, on ne peut pas prouver son authenticité à qui que ce soit : c'est là-dessus que repose la répudiabilité forte d'OTR.
L'implémentation originale sous forme de plugin pour Gaim était accompagnée d'un outil pour contrefaire des messages, afin que n'importe qui puisse le faire.
3. OTR en pratique
Cette partie explique plus en détail certaines parties jugées intéressantes de la dernière version d'OTR, la 3.4. Pas d'inquiétude, les primitives cryptographiques utilisées sont expliquées en détail, à la fois dans le cas général (la cryptographie ne se limite pas à OTR), et dans le cas d'OTR.
3.1 Primitives
3.1.1 Hashage et HMAC
Une fonction de hashage est une fonction qui prend en entrée une donnée de taille arbitraire, et retourne une donnée de taille fixe, appelée hash, ou condensat, voire empreinte en français.
Par exemple, l'opérateur modulo est une fonction de hashage :
1 % 42 = 1
43 % 42 = 1
1337 % 42 = 35
Celle-ci projette l'ensemble des entiers dans l'ensemble [0, 41].
Une fonction de hashage dite cryptographique doit satisfaire quatre propriétés :
1. Il est facile de calculer le hash de n'importe quelle donnée ;
2. Il est impossible de retrouver un message à partir de son hash ;
3. Il est impossible de modifier un message sans modifier son hash ;
4. Il est impossible de trouver deux messages avec le même hash.
Notre fonction modulo ne satisfait ni la troisième, ni la dernière propriété.
Grâce aux fonctions de hashage cryptographique, il est possible de construire ce qu'on appelle un HMAC, pour (key-)Hash Message Authentication Code (code d'authentification d'une empreinte cryptographique de message avec clé en français). Il s'agit d'une primitive permettant de vérifier l'intégrité de données, mais aussi l'authenticité.
3.1.2 Échange de clefs Diffie-Hellman
Un échange de clefs Diffie-Hellman est une méthode par laquelle deux entités se mettent d'accord sur un secret sans qu'un attaquant passif puisse le trouver.
Son fonctionnement repose sur le problème du logarithme discret, qui dit grosso modo que dans un ensemble modulo p, pour α et β donnés dans cet ensemble, il est très difficile de trouver k pour αk = β.
Une propriété intéressante de la multiplication (une élévation à une puissance étant une suite de multiplications) est que (ax % p)y = a(x·y) % p.
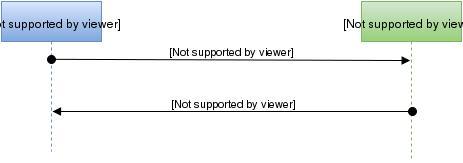
Concrètement, Alice et Bob se mettent d'accord sur deux nombres, g et p, génèrent chacun un nombre aléatoire secret, et procèdent comme suit :
1. Alice envoie A = ga % p à Bob, qui l'élève à la puissance b, donnant K = g(a·b).
2. Bob répond par B = gb % p à Alice, qui l'élève à la puissance a, donnant K = g(a·b).
Alice et Bob ont donc créé un secret partagé, K.
Fig 1 : Échange Diffie-Hellman entre Alice et Bob.
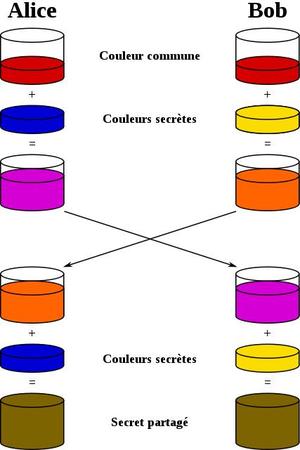
Mais pour ceux qui n'aiment pas les maths, un échange Diffie-Hellman peut être facilement expliqué avec des pots de peinture. Si on admet que le fait de retrouver deux couleurs à partir de leur seul mélange est impossible, alors :
Fig 2 : Échange Diffie-Hellman avec de la peinture.
Ce type d'échange est en général utilisé comme primitive pour construire des protocoles de création de clefs éphémères.
3.1.3 Chiffrement/signature
La cryptographie traditionnelle (aussi appelée cryptographie symétrique) utilise la même clef pour chiffrer et déchiffrer, ce qui pose une multitude de problèmes, comme celui de la distribution de clefs. Heureusement, aux alentours des années 80, Hellman et Diffie (encore eux !) commencèrent à dessiner une cryptographie asymétrique, avec deux clefs : une clef publique, distribuée à tous, et une clef privée, gardée secrète.
La clef publique permet à tous de chiffrer un message, qui ne peut être déchiffré que par la clef privée.
La clef privée permet de signer un message, signature qui peut être vérifiée par tous, grâce à la clef publique.
3.2 Échange de clefs et envoi de message
Maintenant que les primitives ont été définies, entrons dans le vif du sujet. Alice et Bob possèdent chacun une paire de clefs : une clef publique, et une clef privée. Cette paire est appelée master key.
3.2.1 Échange de clefs
3.2.1.1 Échange de clefs dans le cadre d'OTR 1.0
Pour s'échanger des messages, ils effectuent un AKE, pour Authenticated Key Exchange, un échange de clefs authentifié de type Diffie-Hellman : Alice et Bob signent chacun de leurs échanges Diffie-Hellman avec leur propre master key.
Le secret partagé est ensuite hashé pour donner une clef de court terme (aussi appelée clef éphémère), qui est elle-même hashée pour donner la clef de MAC.
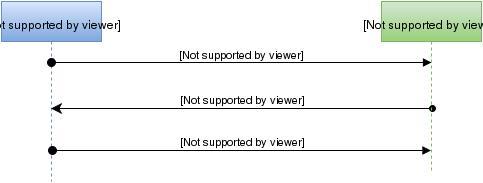
Cette étape leur a permis de :
Fig 3. Diffie-Hellman authentifié.
1. Créer une clef éphémère, amenant la propriété de confidentialité persistante : si leurs master keys viennent à être compromises, il ne sera pas possible de déchiffrer les messages précédents.
2. S'assurer de l'absence d'attaquant actif. En effet, les échanges Diffie-Hellman étant signés avec les master keys, il est impossible pour un attaquant de se placer entre Alice et Bob sans qu'ils ne le remarquent.
3.2.1.2 Attaque sur l'échange de clefs d'OTR 1.0
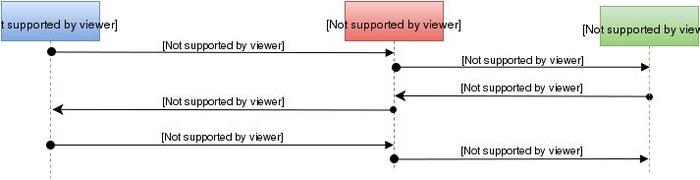
Cette méthode, utilisée dans la première itération du protocole est malheureusement insuffisante. En effet, elle permet à Eve de se placer entre Alice et Bob de manière active :
- Alice envoie gx a Eve, ainsi que sa signature ;
- Eve envoie gx à Bob, qu'elle signe avec sa clef ;
- Bob répond donc à Eve gy, signé avec sa clef à lui ;
- Eve envoie à Alice la réponse de Bob, qui est donc signée avec la clef de Bob.
Fig 4. Attaque de type misbinding.
Bien qu'incapable de déchiffrer le trafic, Eve a réussi à faire croire à Bob que sa clef de long terme est celle d'Alice. Une fois que Bob et Alice auront effectué une authentification mutuelle avec l'aide du protocole SMP, Bob pensera qu'Eve est Alice. Ce qui permettra à Eve de se faire passer pour Alice durant les prochaines conversations !
La solution évidente (utilisée par ISO-9796) serait d'inclure la clef publique du correspondant dans les échanges Diffie-Hellman, mais une telle manœuvre offrirait une preuve qu'Alice et Bob ont bien conversé (la clef publique de Bob serait dans un message signé par Alice, et inversement), compromettant la propriété de répudiabilité forte d'OTR.
Fig 5. Échange de clefs de type ISO-9796.
Un autre type d'attaque est également possible : une attaque de type replay. Dans un protocole d'échange de clefs, la seule manière de se faire passer pour quelqu'un dans l'échange actuel est de compromettre la master key d'un protagoniste. En d'autres termes, la compromission d'échanges précédents ne devrait pas affecter des échanges futurs. Or, si un attaquant arrive à trouver une valeur x' utilisée par Alice durant une session précédente, il lui suffira d'envoyer gx' et la signature associée, pour établir une session avec Bob, en se faisant passer pour Alice !
Fig 6. Attaque de type replay avec un x fixé.
Ces failles furent publiées par Mario Di Raimondo, Rosario Gennaro et Hugo Krawczyk, en 2005, dans leur papier intitulé Secure Off-the-Record Messaging [4].
3.2.1.3 Échange de clefs dans le cadre d'OTR 2.0
Pour corriger les vulnérabilités évoquées plus haut, la version 2.0 d'OTR change d'AKE : elle utilise le protocole SIGMA (pour SIGn-and-MAc), développé en 1995, par les développeurs d'IPSEC pour remplacer leur ancien protocole d'échange de clefs[5]. L'idée de SIGMA est de lier le secret partagé aux master keys des interlocuteurs, avec une signature et un MAC, d'où son nom. Pour ce faire, il établit un canal chiffré, dans lequel se déroule un échange Diffie-Hellman classique (donc non authentifié), grâce auquel l'authentification mutuelle se fera : bref, un gros sandwich de cryptographie en trois couches, la dernière servant à vérifier la première.
Une telle stratégie permet d'empêcher Eve de se faire passer pour Alice et d'effectuer des attaques par replay. Un effet de bord intéressant de la transposition de l'authentification à l'intérieur d'un canal confidentiel est la dissimulation des clefs publiques d'Alice et de Bob à un attaquant passif, augmentant un peu plus l'anonymat de la conversation.
Le protocole SIGMA étant fastidieux (mais simple), il ne sera pas détaillé ici, mais la lecture du papier original est vivement recommandée aux curieux : http://webee.technion.ac.il/~hugo/sigma.html.
3.3 Envoi de message, et régénération de clefs
Ensuite, le message à proprement parler est envoyé d'Alice à Bob. Il est chiffré à l'aide d'AES-CTR (un chiffrement symétrique) grâce à la clef éphémère précédemment générée, afin de garantir sa confidentialité, et son MAC est envoyé en clair avec lui, calculé avec HMAC-SHA1 et sa clef de MAC.
Pour chaque message envoyé, Alice et Bob refont un échange Diffie-Hellman, afin de générer une nouvelle clef éphémère et une clef de MAC. Chaque échange est authentifié grâce à la clef de MAC précédente. Une fois l'échange terminé, l'ancienne clef de MAC est publiée.
En revanche, les clefs de chiffrement ne le sont pas !
Le fait d'utiliser la clef de MAC actuelle pour garantir l'intégrité de la suivante permet de se prémunir contre les réordonnancements/la suppression de messages : par exemple, en envoyant un mot par message, il y a une différence notable entre « Je suis content » et « Je [ne] suis [pas] content ».
3.3.1 Limites
Dans cette partie, le terme adversaire désigne l'entité (agence de renseignement, compagnon, force de police, parent…) tentant de briser la confidentialité de la conversation, avec l'aide, volontaire ou contrainte de Bob, pour confondre Alice.
Si Bob était malveillant dès le début de la conversation, il lui suffirait de donner sa master key à l'adversaire, qui aurait la preuve que la conversation n'est pas contrefaite, car elle aurait lieu directement entre lui et Alice.
La répudiabilité forte ne protège pas non plus d'un adversaire capable d'enregistrer l'intégralité de la conversation, car il serait impossible de prétendre qu'un message a été contrefait. Ce problème peut être résolu en utilisant des réseaux anonymisants, comme Tor par exemple. Il serait bien sûr possible pour Bob d'enregistrer le trafic, mais s'il n'était pas malveillant dès le départ, il est raisonnable de penser que l'adversaire ne lui fera pas confiance pour lui donner une capture réseau de l'intégralité de la conversation sur sa seule bonne foi.
3.4 Utiliser OTR
Comme évoqué au début de l'article, grâce à son encodage en base64, OTR est implémenté dans une multitude de clients, pour à peu près n'importe quel protocole. Par exemple, sur Debian, pour utiliser OTR avec Pidgin, il suffit de taper apt install pidgin-otr, pour Irssi apt install irssi-plugin-otr. D'autres applications le proposent nativement, comme Jitsi (un client de VOIP en Java), TorBirdy (le client de messagerie instantanée du projet Tor), Cryptocat (une application web), TextSecure (un client mobile par le Guardian Project)…
Par exemple, avec Pidgin :
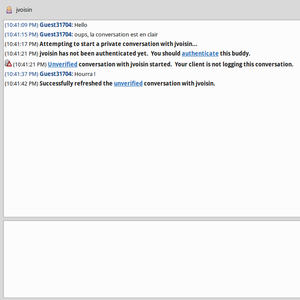
Fig 7. Conversation entre Guest31704 et jvoisin, en clair, puis chiffrée.
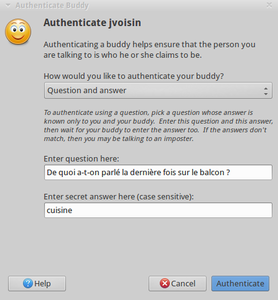
Fig 8. Dialogue d'authentification de type question/réponse.
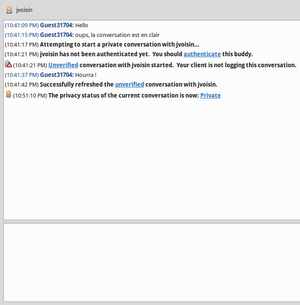
Fig 9. Une fois que Guest31704 a correctement répondu à la question secrète, les échanges sont chiffrés et authentifiés.
Bref, OTR est dans plein de clients, et est facile à utiliser.
4. Héritages, écueils, et développements futurs
En tant que pionnier dans le domaine du chiffrement de messagerie instantanée et de la répudiation, OTR a engendré un héritage important.
Aujourd'hui, l'implémentation de référence d'OTR, libotr, n'est plus activement développée. Elle est en phase de maintenance : si des bugs apparaissent, ils sont corrigés, mais aucune nouvelle fonctionnalité n'a été ajoutée depuis des années.
D'autres implémentations, comme python-otr, ocaml-otr, otr4j… continuent de fleurir, mais le protocole n'a plus bougé depuis sa version 3, qui commence à se faire vieille.
Par exemple, la publication des MAC ne permet qu'à ceux ayant enregistré la conversation de contrefaire de nouveaux messages : la répudiation serait encore plus forte si n'importe qui pouvait le faire.
L'avènement des communications mobiles amène de nouvelles problématiques, principalement en raison de leur nature asynchrone : les utilisateurs ne sont plus forcément connectés en même temps. Mais qui dit communications mobiles dit aussi soucis de connectivité : les AKE en trois échanges (comme ceux utilisés par OTR) tendent à être remplacés par des AKE en deux échanges seulement, pour gagner du temps et de la bande passante.
Un autre reproche souvent émis à l'encontre d'OTR est le fait qu'il ne permette qu'à deux personnes à la fois de converser en toute intimité. Un papier nommé Improved Group Off-the-Record Messaging [6] publié en 2013 liste les principaux obstacles à surmonter avant de pouvoir créer un protocole avec les mêmes garanties qu'OTR. Mais des initiatives existent, comme le projet np1sec [7], crée pour le logiciel Cryptocat, qui est au stade de l'implémentation (le projet cherche à embaucher un développeur C++ d'ailleurs), ou encore mpOTR [8], qui lui n’en est qu’à l'ébauche.
Bien que des initiatives existent (mpOTR, Axolotl, np1sec…), aucune ne s'est encore dégagée de la masse.
Néanmoins, c'est par ses primitives cryptographiques qu'OTR accuse le plus son âge. En 2004, quand OTR a été créé, l'algorithme DSA était un bon algorithme de signature cryptographique. Malheureusement, il n'est pas évident à implémenter correctement (Sony en a fait les frais : le piratage de sa console PS3 a pu avoir lieu grâce à une mauvaise implémentation de DSA.) Son algorithme de hashage, SHA-1 commence également à montrer des signes de faiblesse, et n'est plus utilisé dans le cadre des certificats TLS, car considéré comme trop faible. Enfin, la taille du modulo Diffie-Hellman (1536 bits) est inférieure aux recommandations actuelles, qui conseillent d'utiliser un modulo d'au moins 2048 bits.
Heureusement, la relève est là : Signal. Une application mobile écrite par Open Whisper Systems, la société de Moxie Marlinspike. Anciennement connue sous le nom de TextSecure, elle utilise une version plus compacte et moderne d'OTR [9], qui corrige les soucis énumérés plus haut. L'application est (évidemment) open source, disponible sur Android et iPhone, et bientôt sous forme d'un client lourd.
Conclusion
Bien que vieillissant et possédant des défauts, OTR est toujours le protocole de référence pour assurer confidentialité et répudiation lors d'échanges instantanés. L'avancement en matière de cryptographie et de puissance de calcul le mettent peu à peu hors course, mais il a encore quelques années devant lui avant d'être remplacé, ou qui sait, peut-être mis à jour dans une quatrième version.
Références
[1] Laura Poitras, Citizenfour, https://citizenfourfilm.com/
[2] https://otr.cypherpunks.ca/otr-wpes.pdf
[3] Andrew C. Yao, « Protocols for secure computations », FOCS, 1982, 2013 IEEE 54th Annual Symposium on Foundations of Computer Science, 2013 IEEE 54th Annual Symposium on Foundations of Computer Science 1982, pp. 160-164, doi:10.1109/SFCS.1982.88
[4] Mario Di Raimondo, Rosario Gennaro et Hugo Krawczyk, Secure Off-the-Record Messaging, 2004,https://www.dmi.unict.it/diraimondo/web/wp-content/uploads/papers/otr.pdf
[5], Hugo Krawczyk, 2003, SIGMA: The « SIGn-and-MAc » Approach to Authenticated Diffie-Hellman and Its Use in the IKE-Protocols, http://www.iacr.org/cryptodb/archive/2003/CRYPTO/1495/1495.pdf
[6] Liu, Hong; Vasserman, Eugene Y.; Hopper, Nicholas, Improved Group Off-the-Record Messaging, 2013, http://krex.k-state.edu/dspace/handle/2097/20141
[7] https://learn.equalit.ie/wiki/Np1sec
[8] https://cypherpunks.ca/~iang/pubs/mpotr.pdf
[9] https://github.com/trevp/axolotl/wiki



 Ajouter à une liste de lecture
Ajouter à une liste de lecture