Dans un contexte de convergence de technologies alliant centrale inertielle précise, batterie légère, moteurs électriques compacts, capteur optique de haute résolution et puissance de calcul infinie, les microdrones sont devenus réalité. Nous proposons d'exploiter les photographies aériennes pour une analyse quantitative de modèle numérique d'élévation.
Nous avions présenté dans Open Silicium [1] le logiciel Micmac [2] développé principalement par le laboratoire MATIS associé à l’Institut Géographique National (IGN). Dans cet article, nous nous proposons d’exploiter Micmac dans un contexte pratique de cartographie de la moraine d’un glacier en région arctique (Spitsberg, Norvège). Le contexte peut sembler trivial mais a son importance : il s’agit d’une région sans végétation (donc peu de variation du terrain entre deux prises de vues tel que pourraient l’induire des mouvements de végétation soumis au vent), dynamique avec une érosion par la circulation d’eau, et libre de la majorité des dangers de vol connu en milieu urbain (mais nécessitant néanmoins une autorisation de vol). Nous nous sommes intéressés à l’observation de cette région par microdrone commercialement disponible pour un coût inférieur à 2500 euros. En effet, alors que la surface d’un glacier se cartographie par quelques points de mesure judicieusement distribués et entre lesquels l’interpolation est raisonnable, une moraine présente une topographie variable sur laquelle l’interpolation entre des points de mesure distants n’est pas valable.
D’un autre côté, le travail en région quelque peu isolée impose de nouvelles contraintes [3] : autonomie des batteries aux basses températures et transport du matériel à pied, qui nous ont induit à évaluer la pertinence de ce mode de mesure par rapport à des approches de référence basées sur le LiDAR (Light Detection and Ranging [4] – version optique du RADAR) aéroporté ou terrestre, avec un coût dépassant ce qui est accessible par l’amateur. Ce compte rendu n’a pas vocation à considérer et interpréter les aspects d’évolution de la morphologie du terrain observé, mais de proposer un flux de traitement des données acquises et évaluer la résolution et l’exactitude des modèles numériques d’élévation (MNE) établis pour diverses dates séparées d’un intervalle de temps allant jusqu’à une semaine.
1. Conditions de prises de vues et résolution attendue
Une étude préliminaire des conditions de prises de vues est de rigueur. Elle considère la résolution attendue des structures au sol, le taux de recouvrement nécessaire à une analyse photogrammétrique, et la vitesse horizontale du vecteur de vol au cours de la prise de vue pour couvrir la zone envisagée. Nous avons acquis et exploité un microdrone commercial DJI Phantom3 Professional : ce modèle, récent à la date d’acquisition des données en fin-septembre 2015, ne possédait pas l’option de planification de la trajectoire à l’avance, et tout le pilotage s’est fait à la radiocommande avec vol à vue et suivi sur la télé-mesure de la position GPS retransmise en temps réel ainsi que des images observées par le drone (voir figure 1). Cette option, a priori un gadget sans intérêt, s’est révélée primordiale pour garantir le recouvrement latéral des trajectoires successives. La consigne de Micmac sur les prises de vues des photographies successives est d’obtenir un recouvrement de 80%. Avec une ouverture angulaire de 94° selon la largeur de la photographie, une élévation de vol de 100 m induit un pixel de 4 cm de large, sous le décimètre visé mais surtout avec une élévation de vol sous les 120 m autorisés (voir figure 2, droite). Les 2250 pixels de hauteur d’image couvrent donc une longueur au sol de 56 m. Avec une vitesse horizontale maximale de 10 m/s (que nous utiliserons pour couvrir une distance maximale lors de chaque vol), une prise de vue chaque seconde vérifie la consigne de recouvrement. Le logiciel de commande de DJI ne permet pas une prise de vue aussi rapprochée : nous déclenchons à la main la prise de vue avec un intervalle aussi régulier que possible et proche du hertz, avec un recouvrement vérifié lors du vol sur le retour vidéo.
Un point, qui pourra paraître trivial au lecteur mais qui nous a interpellés au cours du premier vol : un drone asservit son vol sur une élévation constante par rapport au point de décollage. En région présentant une forte variation de topographie – telle que la langue d’un glacier – les 100 m séparant le drone du sol au décollage se réduisent rapidement lorsque la distance de vol dépasse les 500 m. Un défilement rapide des images du terrain alors que la vitesse horizontale est maintenue constante sera considéré comme un indicateur de proximité du sol nécessitant de reconsidérer la trajectoire avant de rentrer en collision avec le versant de montagne ou de glacier survolé. Nous sommes ainsi arrivés à une élévation de moins de 20 m au-dessus de la glace (d’après le traitement issu de Micmac) avant de nous interroger sur la cause de ce défilement excessivement rapide !
Fig. 1: À gauche : conditions expérimentales - le DJI Phantom3 répond aux exigences de facilité de transport, de déploiement rapide, d’autonomie et de couverture du champ de vision de la caméra. Il s’est avéré idéal pour cette campagne de mesures.
À droite : canyon dans la moraine du glacier étudié, qui sera au cœur de l’étude car proposant des structures identifiables susceptibles de varier à court terme. La langue du glacier est visible en bas à gauche de cette photographie.
Fig. 2: À gauche : planche contact d’une série de photographies prises par drone en vue azimutale, en vue de leur traitement pour générer un MNE haute résolution et une image orthorectifiée de la zone analysée.
À droite : estimation de la résolution au sol compte tenu de l’ouverture angulaire, du nombre de pixels dans la largeur de l’image, et l’élévation de vol.
2. Géoréférencement des sites de prises de vues
Ayant acquis les images, nous désirons les traiter pour en extraire une image unique orthorectifiée (compensant les déformations induites par la topographie du sol) et le produit associé qu’est le MNE. Chaque image acquise par le DJI Phantom3 est munie de sa position GPS avec une latitude et longitude en degrés, minute et seconde d’angle, ainsi qu’une élévation relative au point de décollage. Ces informations seront exploitées deux fois au cours du traitement : lors de l’appariement des photographies adjacentes, et lors du géoréférencement dans un référentiel absolu du modèle d’élévation. L’extraction dans un format exploitable de ces informations est donc un pré-requis à tout traitement ultérieur :
1. extraire les 3 informations de position de chaque photographie ;
2. convertir les degrés-minute-seconde en degrés décimaux ;
3. convertir le géoréférencement en coordonnées sphériques (WGS84 du GPS) en coordonnées dans un référentiel plan approximant localement l’orientation de la sphère formant la surface de la Terre (UTM33N pour le Spitsberg) ;
4. tronquer ces coordonnées pour s’affranchir, lors des calculs ultérieurs, des erreurs d’arrondis lors du calcul sur les flottants.
Ces opérations utilisent trois outils en plus du shell bash : exiftool extrait les informations des en-têtes des photographies, GNU/Octave [5] effectue les calculs sur les coordonnées, et QGis [6] effectue le changement de projection.
$ for i in *.JPG; do echo $i ; done > noms
$ for i in *.JPG; do echo -n $i ; exiftool $i | grep atitu | grep -v R; done > latitude
$ for i in *.JPG; do echo -n $i ; exiftool $i | grep ngitu | grep -v R; done > longitude
$ for i in *.JPG; do echo -n $i ; exiftool $i | grep Altit | grep -v R; done > altitude
$ cat latitude | cut -c 56-100 | cut -d\ -f1,3,4 | sed "s/’//g" | sed ’s/"//g’ > latitude.txt
$ cat longitude | cut -c 56-100 | cut -d\ -f1,3,4 | sed "s/’//g" | sed ’s/"//g’ > longitude.txt
$ cat altitude | cut -c 56- | cut -d\ -f1 > altitude.txt
Les trois fichiers latitude, longitude et altitude contiennent les informations de position de chaque photographie nom. L’argument 56 est susceptible de devoir être ajusté selon l’arborescence de l’utilisateur et les noms de fichiers manipulés.
Ces trois fichiers alimentent les commandes GNU/Octave suivantes pour générer des coordonnées en degrés décimaux :
load latitude.txt
l=latitude(:,1)+latitude(:,2)/60+latitude(:,3)/3600;
save -text latitude.dec l
load longitude.txt
l=longitude(:,1)+longitude(:,2)/60+longitude(:,3)/3600;
save -text longitude.dec l
Les deux fichiers d’extension .dec sont édités avec notre éditeur de texte favori (vi) pour en éliminer l’en-tête, et finalement toutes ces informations sont combinées dans un unique fichier par :
$paste latitude.dec longitude.dec altitude.txt noms > for_qgis.txt
La conversion de ce jeu de coordonnées en degrés décimaux dans un référentiel en coordonnées cartésiennes s’effectue sous QGis. En effet, la conversion n’est pas triviale, le passage de la sphère de WGS84 aux plans tangents locaux UTM (Universal Transverse Mercator) tenant compte des déformations de la Terre par rapport à la sphère. Sous QGis, un fichier comportant 4 colonnes (longitude, latitude, altitude, nom du fichier) est chargé au moyen de l’icône en forme de virgule sur la gauche de l’interface graphique. Nous pouvons faciliter l’identification de la signification de chaque colonne en ajoutant, dans le fichier texte à charger, trois labels “Y X Z N” signifiant latitude, longitude, altitude et nom (les identifiants X et Y sont reconnus par QGis, les autres seront simplement reproduits dans le fichier de sortie). Une fois le fichier chargé, cliquer par le bouton de droite dans l’entrée sur la liste des structures de données chargées, Save As et choisir le mode de projection cartésien approprié (dans notre cas au nord de la Norvège, CRS WGS84-UTM33N (EPSG :32633) – valeur qui doit être ajustée pour chaque région géographique, par exemple UTM31N pour la majorité de la France). Finalement, nous sauvons dans un fichier dont les colonnes sont séparées par des virgules (CSV, nommé p.csv) et ne conservons que les colonnes utiles par :
$cat p.csv | cut -d, -f1-2,5,6 | sed ’s/,/ /g’ | sed ’s/^43//g’ | sed ’s/ 875/ /g’ > p.fin
Dans cette ligne de commande, les champs 1, 2, 5, 6 sont la longitude et la latitude projetées, l’altitude et le nom de fichier. Cette information sera transmise à Micmac en ajoutant en en-tête de ce fichier, toujours avec son éditeur de texte favori, la séquence #F=X Y Z N qui signifie que le caractère de commentaire est un # et indique l’ordre des données (N est compris comme nom de fichier).
À l’issue de ces manipulations préliminaires, nous avons un fichier associant coordonnées en référentiel cartésien avec chaque photographie. Il s’agit d’une information cruciale à toute la séquence de traitement qui va suivre.
3. Assemblage des images individuelles
Un vol de 20 minutes génère environ photos. Une approche naïve d’appariement en testant tous les couples possibles nécessite essais, un nombre qui devient rapidement prohibitif, avec par exemple 499500 couples si . Micmac offre la possibilité d’exploiter la position de prise de vue de chaque photographie pour évaluer les couples susceptibles de présenter des points homologues sur les prises de vue. En pratique, cette option a permis de limiter, pour 614 images traitées, à 10413 couples au lieu de 188191.
Validation des couples d'images sélectionnés par Micmac
Nous n’avons pas de raison a priori de faire confiance à l’algorithme d’appariement des images par Micmac. Pour nous convaincre de sa validité, nous désirons tracer une droite entre chaque couple d’images sélectionnées. Nous avons d’une part un fichier contenant la position de chaque photographie, et d’autre part un fichier contenant les couples. Comment générer un fichier expliquant à QGis de relier ces ensembles de points ? Une solution porte sur le langage WKT [7] compris par QGis, qui permet de définir des opérations entre éléments géoréférencés. Dans notre cas, la commande sera le tracé de droite par LINESTRING(X1 Y1,X2 Y2). Ainsi, partant du fichier de couples FileImagesNeighbour.xml, nous allons remplacer le nom de chaque photographie par ses coordonnées :
$ cat FileImagesNeighbour.xml | sed ’s/<Cple>//g’ | sed ’s/\/Cple>//g’ | grep -v S | grep -v x | sed ’s/ //g’ > imgpairs
Ceci génère le fichier qui sera passé comme argument d’un script awk (nommé s.awk) sensé rétablir le biais de position que nous avons inséré :
{ print "sed ’s/"$4"/43"$1" "875$2"/g’ | \\" } par cat p.fin | awk -f s.awk > p.sh
Dans le script p.sh, nous remplaçons la première ligne par cat imgpairs | \ et nous retirons le dernier caractère \ pour obtenir un script qui génère le fichier wkt :
$ sh ./p.sh | sed ’s/^/LINESTRING(/g’ | sed ’s/$/)/g’ | sed ’s/ /,/2’ > couples.wkt
Ce fichier est chargé dans QGis au moyen de l’icône en forme de virgule (résultat ci-dessous).
Les couples sélectionnés par Micmac semblent donc corrects, nous voilà rassurés.
Cette étape de traitement réduit considérablement le nombre de comparaisons et permet d’aboutir rapidement à une liste de points homologues entre paires d’images :
$ mm3d OriConvert OriTxtInFile p.fin jmfgps MTD1=1 NameCple=FileImagesNeighbour.xml CalcV=1 \
ImC=DJI_0115.JPG NbImC=25
La ligne précédente informe Micmac de la création du répertoire d’orientation Ori-jmfgps (qui nous servira à la fin du traitement pour convertir, par homothétie et translation, le nuage de points généré par Micmac dans un référentiel arbitraire vers le référentiel absolu géographique) et d’un fichier de couples FileImagesNeighbour.xml en s’inspirant (OriTxtInFile) du fichier de configuration p.fin.
Par ailleurs, une image de référence est sélectionnée – ici DJI_0115.JPG – qui servira avec ses voisines à estimer les propriétés optiques de l’appareil de prise de vue. Le choix de cette image devrait se faire en respectant autant que faire se peut la condition d’un coin pour caractériser les propriétés optiques des lentilles – pour autant qu’un coin puisse se trouver sur le terrain observé. Une vallée entre deux collines semble convenir. La variable PATC qui est générée à l’issue de cette étape contient la liste des photographies pour cet étalonnage. Nous complétons la définition de PATC par une variable P qui pointe vers toutes les photographies stockées dans le répertoire courant, en supposant que nous ayons déjà fait le ménage dans les prises de vues et n’avons conservé que celles utiles, en vue azimutale exclusivement : P=".*JPG".
La recherche de points homologues se conclut par :
$mm3d Tapioca File "FileImagesNeighbour.xml" -1
Cette commande doit être suivie de l’étalonnage des propriétés de la lentille de l’appareil de prise de vue (modifier le modèle de lentille vers un fish eye par exemple si une GoPro ou un ancien appareil DJI est utilisé) :
$mm3d Tapas RadialStd "$PATC" Out=Cal
Ce point est critique car fortement dépendant de la photographie de référence sélectionnée : il faut parfois plusieurs étapes pour que le modèle converge (résidu < 1 pixel) et ne diverge pas (résidu NaN).
Finalement cet étalonnage est appliqué à toutes les photographies pour établir la position de la caméra lors de chaque prise de vue.
$mm3d Tapas AutoCal "$P" InCal=Cal Out=Init
Nous utilisons ici le répertoire d’orientation pour convertir le référentiel arbitraire dans lequel Micmac effectue ses calculs vers le référentiel géographique : CenterBascule "$P" Init jmfgps tmp avant de générer le nuage de points grossier qui permet de valider le positionnement des prises de vue et la cohérence du nuage de points (voir figure 3) mm3d AperiCloud "$P" tmp.
Il est envisageable, après le passage au référentiel géographique par CenterBascule, de créer une nouvelle orientation pondérant les informations issues du GPS (avec leur imprécision inhérente) et de la photogrammétrie au moyen de Campari :
$Campari "$P" tmp tmp-Campari EmGPS=[jmfgps,2] FocFree=1 PPFree=1
Dans ce cas, le nuage de point grossier et la suite des opérations s’effectuent sur le répertoire d’orientation tmp-Campari au lieu de tmp.
Fig. 3: Nuage de points grossiers, incluant la position identifiée par traitement photogrammétrique, de la position de la caméra au moment de chaque prise de vue. Les points rouges sont la position de la caméra, le nuage grossier gris est la surface reconstruite à partir des images.
4. Produits issus du traitement des images
4.1 Image orthorectifiée
Ayant validé la cohérence du nuage de points (meshlab ou cloudcompare), nous calculons le nuage de points dense par :
$mm3d Malt Ortho "$P" tmp "DirMEC=Resultats" UseTA=1 ZoomF=2 ZoomI=32 Purge=true AffineLast=false
Avant d’en déduire les photographies orthorectifiées (compensées des effets de la topographie et assemblant les photographies adjacentes) :
$mm3d Tawny Ortho-Resultats/ RadiomEgal=0
Et finalement le nuage de points dense est drapé de l’image orthorectifiée :
$Nuage2Ply Resultats/NuageImProf_STD-MALT_Etape_7.xml Attr="Ortho-Resultats/Ortho-Eg-Test-Redr.tif"
Les images ainsi produites sont immenses – tellement grandes qu’elles dépassent la taille d’une image TIF et occupent plusieurs giga-octets pour le flux de traitement qui nous intéresse. Bien entendu, avec un pixel de 4 cm, une couverture d’une zone de 800 m de long nécessite 20000 pixels ! Il est donc courant d’obtenir des images de 20000 x 30000 pixels d’1,2 GB en l’absence de compression. Nous convertissons donc ces images au format TIF vers du PNG – plus efficace au détriment d’un algorithme de compression à perte – et assemblons le résultat. Toutes ces opérations se font évidemment par ImageMagick, qui peut cependant rencontrer des problèmes si /tmp est trop petit (par exemple si c’est un ramfs de taille modeste). Nous exportons le répertoire temporaire vers notre maison export MAGICK_TMPDIR=$HOME avant de lancer conversions et assemblages convert Ortho-Eg-Test-Redr_Tile_0_0.tif Ortho-Eg-Test-Redr_Tile_0_0.png dans Ortho-Resultats avant d’assembler par :
$ montage -tile 1x2 -geometry +0+0 Ortho-Eg-Test-Redr_Tile_0_0.png \
Ortho-Eg-Test-Redr_Tile_0_1.png out.png
Les images restent immenses en nombre de pixels, mais au moins exploitables en terme de taille de stockage : geeqie arrive parfois à les afficher sans se figer.
Les images obtenues sont associées à un fichier de positionnement qui informe de la position du coin en haut à gauche (aussi connu comme le nord-ouest – deux dernières lignes du fichier) et de la taille du pixel : le fichier d’extension tfw est renommé pngw pour l’image que nous venons d’assembler. La position doit cependant être incrémentée du biais de position que nous avions éliminé lors de la génération du fichier de position initial : nous avions retiré le préfixe 43 aux longitudes et 875 aux latitudes, que nous prenons soin de réinsérer ici. Dans notre cas, un fichier typique de position ressemble à
0.045
0
0
-0.045
438839.62
8760127.52
Noter en lignes 1 et 4 la taille du pixel (4,5 cm, en accord avec nos attentes), et que la latitude étant de l’ordre de 105 m, l’ajout de 8750000 se traduit par les premiers chiffres devenant 876.
À première vue, les images orthorectifiées ainsi acquises semblent convenablement se superposer à une image satellite de référence (voir figure 4). Cependant, les sources libres d’images satellites (par exemple Landsat) présentent une taille de pixel considérablement plus importante que ce que nous visons – typiquement 30 m/côté – et cette cohérence ne fait que valider grossièrement notre flux de traitement, sans préjuger de l’exactitude du résultat avec la résolution décimétrique visée.
Fig. 4: Image orthorectifiée sur un fond d’image satellitaire. Noter que le fond opaque de l’image orthorectifiée a été éliminé en sélectionnant Transparency > Add et le triplet 0 0 0 comme couleur à considérer comme transparente dans les attributs de cette entrée dans QGis. Noter le gain en résolution par rapport à l’image satellite de fond considérée comme référence.
Nous allons donc nous efforcer ci-dessous d’estimer quantitativement la reproductibilité de la mesure, en particulier en comparant des jeux de données acquis à plusieurs jours d’intervalle.
4.2 Modèles numériques d’élévation (MNE)
Le problème du positionnement du MNE, accessible dans Resultats/Z_Num7_DeZoom2_STD-MALT*, est le même, avec un fichier geoTiff à modifier pour y insérer le biais de position que nous avions introduit. Par ailleurs, un fichier XML associé nous informe du biais en élévation et le facteur d’homothétie entre le fichier TIF et les dimensions réelles :
<OrigineAlti>9.675</OrigineAlti>
<ResolutionAlti>0.09</ResolutionAlti>
Lors du chargement de l’image dans QGis (icône de chargement des images matricielles – raster), le MNE est convenablement positionné, mais les altitudes sont fausses.
Nous effectuons l’homothétie et la translation en altitude au moyen de Raster > Raster Calculator et en créant une nouvelle couche (Output layer) au format GeoTIFF qui contient la transformée affine du jeu de données d’entrée (voir figure 5).
Sur la figure 5 , nous proposons à gauche une vue satellitaire d’une région de la moraine présentant une topographie identifiable depuis l’espace, et à droite le modèle numérique de terrain, reproduisant fidèlement le réseau hydrographique. Ce résultat est le produit de nos traitements, dont il nous reste à établir la résolution et l’exactitude.
Fig. 5: À gauche : image satellitaire de la moraine.
À Droite : MNE positionné uniquement par la position GPS du coin supérieur gauche, sans recalage manuel. La cohérence des structures visibles est particulièrement convaincante aux limites entre image et MNE de la figure de droite.
5. Comparaisons de mesures effectuées à plusieurs jours d’intervalle
Bien que la résolution de la constellation GPS soit de l’ordre du mètre dans une configuration donnée de satellites, l’exactitude n’est que de la dizaine de mètres et induit un décalage inacceptable entre jeux de données acquis à plusieurs heures ou jours d’intervalle. Un recalage des orthophotos et des MNEs est donc nécessaire pour une comparaison entre jeux de données acquis à plusieurs jours ou mois d’intervalle (lorsque la configuration des satellites et des conditions ionosphériques ont significativement évolué). Dans notre cas, nous avons omis de placer des points de contrôle au sol géoréférencés au cours des prises de vues, compte tenu des contraintes de délai de déploiement du drone sur site, mais nous allons recaler a posteriori les jeux de données sur des structures remarquables au sol. Ainsi, même si nos jeux de données ne sont pas positionnés dans un référentiel géographique absolu, ils seront au moins cohérents entre eux pour permettre une inter-comparaison (voir figure 6).
Fig. 6: Recalage de deux images orthorectifiées prises à 1 semaine d’intervalle. Les points rouges sont des points de référence (shapefile contenant des points) permettant de repérer les points remarquables supposés fixes entre les deux photographies.
Deux approches sont disponibles pour ce recalage. La première consiste à exploiter le greffon rasmover de QGis : bien que graphique et trivial d’emploi (il suffit de faire glisser la flèche indiquant le vecteur de déplacement de l’image), cette approche souffre de l’absence d’information quant à la valeur numérique de la translation (de combien de mètres l’image a été ainsi déplacée). Nous préférons donc directement manipuler l’en-tête world des images pour y ajouter les quantités nécessaires au recalage. Ainsi, nous contrôlons la cohérence de ce vecteur de translation et évitons tout risque de manipulation aberrante que permettrait une interface graphique.
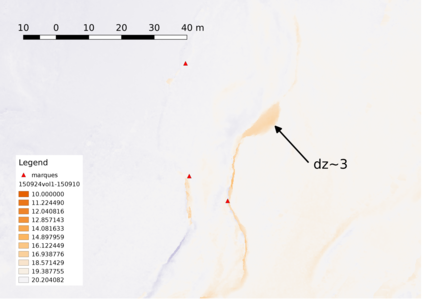
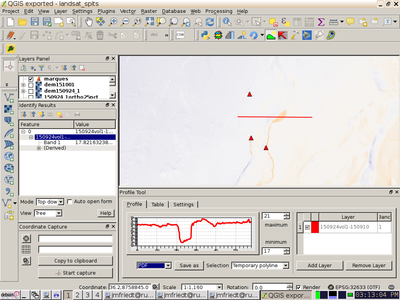
Après une manipulation fine de la position des orthophotos, et donc des MNEs associés, une comparaison de deux jeux de données pris à 1 semaine d’intervalle est proposée sur la figure 7. Nous y constatons que le canyon sur lequel nous focalisons notre attention ne présente que peu de variation puisque les différences d’élévation sont proches d’une valeur constante (non nulle car nous n’avons pas retranché la différence d’élévation de décollage du drone aux deux dates) : les tons clairs sont distribués dans les 70 cm du bas de la palette. Un léger écart résiduel entre les positions des deux MNEs est visible par les versants du canyon qui ne se superposent pas exactement, avec son versant ouest en bleu et le versant est en rouge. Cependant, une zone rouge sombre est nettement visible (indiquée par ), attribuée à un glissement de terrain sur une épaisseur de 3 m (quatrième tranche de couleur de la palette à partir du bas), une épaisseur cohérente avec la profondeur du canyon. Cette analyse est confirmée par l’analyse le long d’un transect par le greffon Terrain Profile (voir figure 7, droite).
Fig. 7: Analyse de l’écart de deux MNE pris à 1 semaine d’intervalle. À gauche : noter le glissement de terrain de 3 m de profondeur, cohérent avec la profondeur du canyon adjacent, sur la carte de la différence des MNEs.
À droite : capture d’écran de QGis avec l’outil Terrain Profile actif, la ligne rouge indiquant la section considérée.
Conclusion
Nous avons proposé une séquence d’acquisitions et de traitements de données pour générer un modèle numérique d’élévation de résolution décimétrique. Nous avons comparé l’exactitude des données acquises et ayant conclu à la nécessité d’un recalage manuel en l’absence de points de contrôle au sol géoréférencés, avons observé un glissement de terrain sur un intervalle de temps d’une semaine.
Cette approche, développée initialement sur un intervalle de temps d’environ trois mois après l’acquisition du jeu de données, nécessite désormais une journée de traitements sur un ordinateur quad-cœur Xeon cadencé à 2,13 GHz (8 nœuds de calcul, 32 GB RAM) par vol (en supposant 700 photographies exploitables acquises sur la durée de vol de 20 minutes). Nul doute que les présentations proposées lors du « Colloque Photogrammétrie Numérique et Perception 3D : les Nouvelles Conquêtes » par la Société Française de Photogrammétrie et de Télédétection (http://www.spft.fr [8]) entre les 15 et 17 mars apporteront des pistes d’améliorations à cette séquence de traitements.
En attendant, les données sont disponibles sur http://jmfriedt.free.fr/dji_micmac et, pour un second exemple plus proche de nous portant sur le parc de l’Observatoire de Besançon (mettant en évidence les difficultés liées à la végétation), sur http://jmfriedt.free.fr/dji.
Remerciements
Cette activité prospective d’exploitation de microdrone pour la cartographie et la génération de MNE est soutenue financièrement par la Région Franche-Comté. Les mesures en Arctique sont soutenues financièrement par l’Agence Nationale pour la Recherche (projet PRISM) et par l’Institut Paul-Émile Victor (projet GRAAL). J.-P. Culas (CM-Drones, Besançon) fournit le soutien technique à la maintenance du drone. Les contributeurs au forum Micmac () ont patiemment répondu aux questions et fourni les solutions ayant permis de faire fonctionner cette séquence de traitements : leur contribution est aussi importante que celle des auteurs du logiciel Micmac lui-même.
Notes et Références
[1] FRIEDT J.-M., « Reconstruction de structures tridimensionnelles par photographies : le logiciel MicMac », OpenSilicium n°12, Sept-Oct-Nov 2014.
[2] PIERROT-DESEILLIGNY M., « MicMac, a free open source solution for photogrammetry », RMLL 2015 (vidéo disponible surhttps://2015.rmll.info/micmac-une-solution-libre-de-photogrammetrie?lang=en).
[3] NOLAN M., LARSEN C. et STURM M., « Mapping snow depth from manned aircraft on landscape scales at centimeter resolution using structure-from-motion photogrammetry », The Cryosphere, 9, 1445–1463, 2015, disponible sur http://www.the-cryosphere.net/9/1445/2015.
[4] LIN Y., HYYPPÄ J. et JAAKKOLA A., « Mini-UAV-borne LIDAR for fine-scale mapping », IEEE Geoscience and Remote Sensing Letters, 8 (3), 426–430, 2011.
[5] GNU/Octave est une version open source de Matlab proposant une compatibilité syntaxique excellente pour les applications qui nous intéresseront ici
[6] Quantum GIS est un outil open source de Gestion d’Informations Spatialisées. Outre sa capacité de conversion entre les modes de projection, il offre un certain nombre de fonctions de traitements sur données vectorielles et matricielles (bitmap), ainsi que l’analyse statistique de données géoréférencées. Nous nous en servirons pour projeter les points GPS sur un plan tangent à la région d’intérêt, puis insérer nos images dans un fond de carte servant de référence et estimer l’exactitude de nos calculs.
[7] http://gis.stackexchange.com/questions/11519/draw-lines-between-two-points-in-qgis



 Ajouter à une liste de lecture
Ajouter à une liste de lecture