La compression est cet art fascinant de représenter les informations avec le moins de bits possible. Une des premières façons de compresser des données est d'éviter de gaspiller de la place à cause de représentations redondantes ou inutiles. Les codes binaires classiques sous-utilisent souvent l'espace de codage occupé, alors que les techniques de codage efficaces augmentent considérablement la complexité du code. Nous allons étudier un compromis, appelé Code Binaire Tronqué, et plus particulièrement une version peu connue : les codes phase-out.
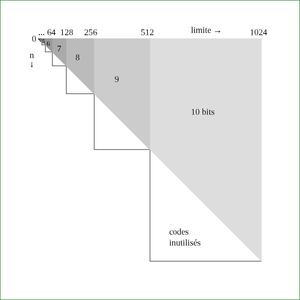
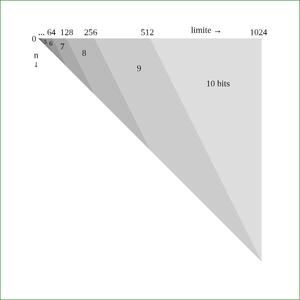
Les codes phase-out sont dérivés des codes phase-in, qui m'ont été suggérés en 2003 par Steven Pigeon [1], l'auteur d'une thèse (en français) sur le codage binaire [2] (voir en particulier la partie 5.3.4.2 « Codes phase-in »). Ils résolvent un petit souci rencontré lors de l'utilisation de codes binaires classiques : lorsqu'on connaît la limite que peut prendre un nombre, jusqu'à la moitié des codes peuvent être inutilisés. La figure 1 montre qu'en moyenne, un quart de l'espace de codage est perdu, ce qui représente jusqu'à un demi-bit par nombre.
Fig. 1 : L’espace de codage inutilisé en codage binaire classique est représenté par les triangles blancs.
1. Quelques repères
Pour situer le contexte, précisons d'abord que nous voulons créer un flux de données, qui représentent dans notre cas des signaux échantillonnés, tels que des sons ou des images. Chaque échantillon est transformé en une suite de bits, qui sera ensuite concaténée au flux binaire, afin d'être écrit dans un fichier ou transmis.
Le sport consiste ici à réduire la taille totale que ce flux de bits occupe, sans perdre d'information : chaque nombre encodé doit redonner le même en sortie après décodage. Il existe de nombreuses techniques avec des traitements plus ou moins compliqués, mais nous allons ici considérer que chaque nombre à coder (appelé n) est indépendant des voisins. On traite ainsi chaque échantillon sans se soucier du précédent ou du suivant, ce qui fait de n un nombre un peu abstrait, mais pour les besoins de l'expérience, c'est toujours un entier supérieur ou égal à zéro.
Là où l'expérience commence à devenir intéressante est que le décodage des bits de notre nombre n nécessite de connaître au préalable, d'une manière ou d'une autre, une information auxiliaire : la limite (appelée L) qui indique quelle valeur maximale notre nombre n peut prendre. On peut donc écrire l'inéquation suivante : 0 ≤ n ≤ L
L'art de l'entropiste (ou de l'entropologue ?) consiste donc à transmettre cette limite sans prendre plus de place que l'original, mais cet article se concentre sur comment ces deux valeurs n et L peuvent se combiner, pour que n utilise juste le nombre idéal de bits.
Un code binaire classique utilise k bits pour représenter un nombre entre 0 et 2k-1. Par exemple, avec k=4, on peut représenter 24=16 symboles, qui sont le plus souvent associés aux nombres 0 à 15. Si notre limite est 15 alors notre nombre n utilisera 4 bits, ni plus ni moins. En règle générale, si la limite L est égale à 2k-1, alors on utilise k bits. Inversement, quand on connaît L, alors on peut calculer le nombre de bits k=log2(L).
Mais une limite exactement égale à une puissance de deux est un cas assez rare. La plupart du temps, notre limite L se situera entre deux puissances de deux : 2k-1 < L < 2k. Nous devons alors toujours allouer k bits, mais il restera 2k-L codes inutilisés, des codes qui prendront une place virtuelle, une fraction de bit qui finit par peser sur l'ensemble des données. Cet espace de codage perdu est représenté par les triangles blancs de la figure 1, car un bit n'est pas divisible.
Il existe des techniques proches de l'idéal, telles que les codes arithmétiques [3] et le codage par intervalle [4] avec lesquels un symbole se retrouve mélangé aux précédents, ce qui affranchit les nombres de la limite arbitraire des bits individuels. L'inconvénient est que ce type de code est relativement complexe et délicat à mettre en œuvre. En particulier, les codes arithmétiques effectuent des calculs sur les entiers avec des multiplications, ce qui occupe des ressources matérielles conséquentes dans le cas d'une réalisation matérielle. Et comme je développe un CODEC destiné à utiliser le moins de portes logiques possible, ce type d'approche est écarté.
Les codes de Huffman (voir Wikipédia) sont une autre classe de codes binaires répandus, qui ne nécessitent pas de multiplication. Ils sont capables eux aussi de gérer des probabilités complexes, au moyen d'une table qu'il faut stocker et construire. Donc pour utiliser un code de Huffman classique, il faut d'abord collecter, encoder et reconstituer des statistiques et histogrammes, avant même de pouvoir commencer à transmettre des données utiles... Sinon il y a aussi les codes de Huffman adaptatifs ou dynamiques.
Nous allons explorer ici les codes phase-in, parfois aussi appelés codes binaires tronqués : c'est un cas spécial des codes de Huffman, à mi-chemin entre les codes arithmétiques et les codes binaires classiques. Comme les codes de Huffman, les codes phase-in ne se mélangent pas entre mots consécutifs, donc chaque mot binaire reste toujours bien distinct. Pour réduire la taille, les nombres sont représentés par une chaîne de bits de longueur variable alors que la longueur est fixe dans un codage binaire classique.
La simplicité est à la fois un avantage et un inconvénient. Le codage n'est pas optimal, car il ne modélise pas les probabilités, on suppose ainsi que tous les nombres sont équiprobables. En retour, l'algorithme ne nécessite pas de gérer des tables en mémoire, qui sont une source de complexité, de latence et de bugs. Le codage phase-in utilise juste quelques additions ou soustractions, ce qui promet des réalisations simples et très rapides, en logiciel comme en matériel.
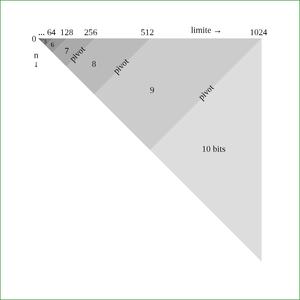
La figure 2 montre la différence de comportement avec le code binaire classique. Il n'y a plus de changement brutal de la taille du code en fonction de la limite, au contraire la longueur du mot varie linéairement, suivant une diagonale, ce qui évite tout gâchis de code.
Fig. 2 : Utilisation des bits et taille progressive des mots avec un code phase-in.
Comme on le voit sur la figure 2, les codes correspondant à un nombre sont divisés en deux zones, selon la limite :
- une moitié des codes utilise k bits ;
- l'autre moitié utilise k-1 bits.
Ces deux moitiés (qui ne sont pas forcément de taille égale) sont séparées par une valeur appelée ici pivot, qui permet de décider si le code binaire de n peut être raccourci d'un bit. Sur la figure 2, les pivots sont les lignes diagonales parallèles qui séparent deux zones grises contiguës.
Ainsi, dans le pire des cas, les codes phase-in n'augmentent pas le nombre de bits utilisés. Dans le meilleur des cas, un bit est économisé. Le gain n'est pas énorme en pratique, mais puisqu'il n'y a pas de risque de perte de place, et comme l'algorithme correspondant est très simple, il peut être ajouté sans risque à un système de compression. Sur un bloc entier de données, les fractions de bits ainsi économisées s'accumulent et peuvent grappiller approximativement (selon les données) quelques pourcents de la taille totale d'un fichier, avec peu d'efforts, donc c'est toujours bienvenu.
Comme tous les codes, ils ne peuvent être utilisés seuls, ils ont besoin d'un contexte, c'est-à-dire d'informations auxiliaires permettant leur décodage. Ils s'inscrivent idéalement dans un algorithme tel que 3R (présenté dans [5][6][7]) et tout système utilisant des nombres entiers positifs dont on connaît implicitement ou explicitement les bornes.
L'idée des codes phase-in semble avoir été cristallisée vers 1995, année de la publication des articles dénichés par Steven Pigeon ([2] p.104) :
[Les auteurs] Acharya et Já Já [8][9] référèrent aux codes phase-in sous le nom de economy codes. C’est l’une des améliorations qu’ils proposent au codage des index dans l’algorithme de compression LZW.
[...]
La documentation sur les codes phase-in et récursivement phase-in, outre les articles d’Acharya et Já Já, est essentiellement anecdotique.
Cela fait donc trois noms pour une même technique : la méthode de codage phase-in est aussi appelée « Code binaire tronqué » par Wikipédia [10], mais nous utiliserons les termes phase-in et phase-out, car ils permettent de distinguer la sous-méthode spécifique.
2. Exemple numérique
Pour encoder et décoder les nombres, l'algorithme doit calculer d'abord le pivot, puis la valeur ajustée du code. Cela nécessite juste un peu d'arithmétique linéaire. Rien de bien compliqué, comme nous allons le voir avec un exemple simple où nous codons les nombres de 0 à 10.
Le nombre 10 est représenté en binaire par 1010, donc il faut quatre bits. Cependant 4 bits permettent de coder des nombres de 0 à 15 et les nombres de 11 à 15 ne sont pas utilisés, ce qui est une perte de 5 codes, soit près d'un tiers de l'espace de codage. D'un autre côté, 3 bits permettent de représenter seulement 8 codes (de 0 à 7), ce qui est insuffisant. Voici la table de codage en binaire classique :
Code valeur
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 10
1011 *
1100 *
1101 *
1110 *
1111 *
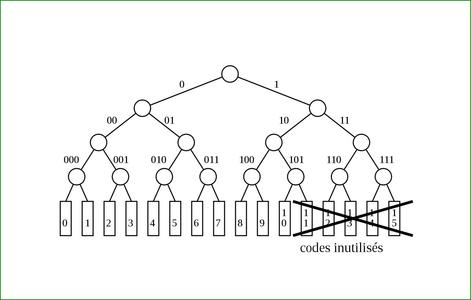
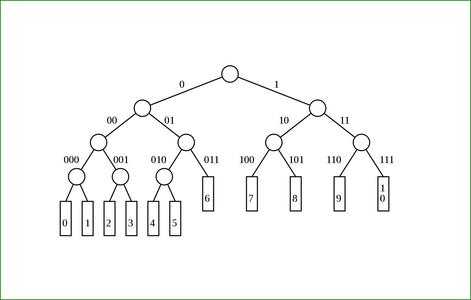
Tout l'enjeu est alors de faire un mélange équilibré entre les deux tailles de mots binaires. La figure 3 représente la table ci-dessus sous forme d'un arbre binaire : les codes 11 à 15 prennent de la place que nous allons maintenant tenter de récupérer.
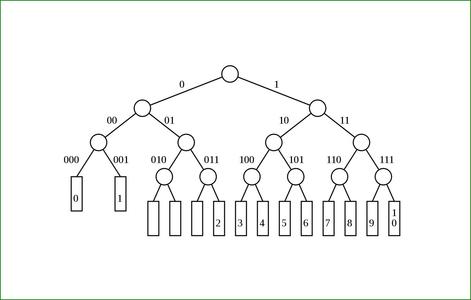
Fig. 3 : Les codes de 0 à 10 sont projetés sur un arbre binaire équilibré de profondeur 4, laissant 5 codes inutilisés.
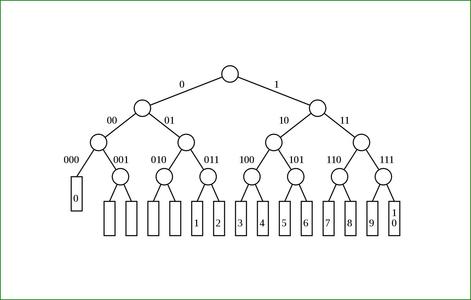
La figure 4 montre la première étape, où les codes sont d'abord décalés vers la fin. Ensuite, on déplace le premier élément vers un niveau supérieur de l'arborescence : le nombre 0 est donc représenté avec le code 000 au lieu de 0000. En remontant ainsi, le code « perd » un bit, mais aussi occupe la place de deux codes plus longs, donc il ne reste que 4 codes perdus.
Fig. 4 : Décalage des codes et élévation du code 0.
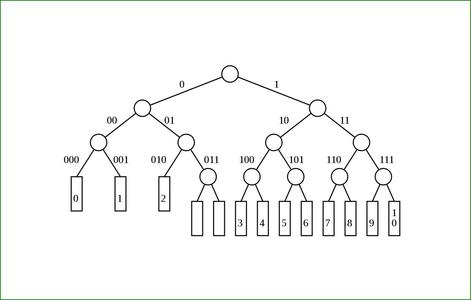
Fig. 5 : Élévation du code 1.
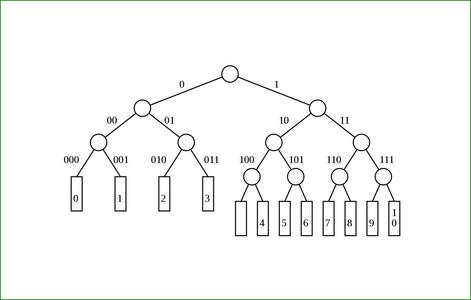
Fig. 6 : Élévation du code 2.
Fig. 7: Élévation du code 3.
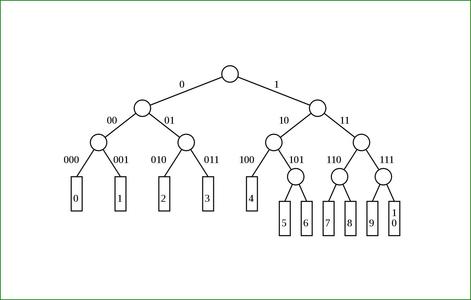
Fig. 8 : Élévation du code 4.
Les figures 5, 6, 7 et 8 répètent cette opération de substitution, déplaçant un code vers un nœud plus élevé et éliminant ainsi un code mort. L'arbre final de la figure 8 représente la table de codage suivante :
Code valeur
000 0
001 1
010 2
011 3
100 4
------------- pivot
1010 5
1011 6
1100 7
1101 8
1110 9
1111 10
5 opérations d'élévation sont donc nécessaires pour compenser les codes morts (si on ne compte pas le décalage). Ainsi il y a autant de codes « promus » que de codes morts, c'est-à-dire 2k-L. Cette valeur est donc notre fameux nombre pivot :
- en dessous de 2k-L, on écrit le nombre directement avec k-1 bits ;
- sinon, on utilise k bits. Mais il faut encore ajuster le nombre et tenir compte du décalage, qui était de 2k-L positions (le pivot, encore une fois).
L'algorithme d'encodage s'écrit donc facilement. Le dernier détail consiste à déterminer k, le nombre de bits nécessaires pour encoder la limite L, mais on va considérer pour l’instant que ce calcul est pris en charge par le reste du programme. Le pivot dépend de L donc son calcul peut aussi être factorisé si les conditions le permettent.
pivot = (1 << k ) - L;
bits = k;
if n < pivot then
bits = bit – 1;
else
n = n + pivot;
endif;
envoyer n avec k bits.
Le décodage est plus subtil, car on ne connaît pas à l'avance le nombre de bits à lire. L'approche sûre consiste à lire k-1 bits et, s'il s'avère que le nombre fait k bits, lire un bit supplémentaire. Mais c'est lent. Surtout s'il faut réaliser l'opération avec des circuits électroniques : il faut au moins deux cycles pour décoder un mot.
L'autre approche est un peu plus expéditive : on lit directement k bits. On décode le nombre obtenu, on l'ajuste s'il le faut, et éventuellement on « remet le bit en trop » dans le flux binaire. En pratique, cela revient à incrémenter un compteur, ou même sélectionner entre k et k-1.
Qui dit grande vitesse, dit risque de foncer dans les murs et il faut correctement traiter le cas particulier de la fin du flux : le décodeur est susceptible de lire un bit de trop, à la fin du flux de données. Il faut donc s'attendre à un dépassement, même s'il ne devrait avoir aucun effet. Mais à part cela, l'ajustement est toujours assez simple : on doit détecter si le nombre n (long de k bits) est inférieur au pivot.
L'autre subtilité est que le pivot doit être multiplié par deux puisqu'il s'applique maintenant à un nombre de k-1 bits. En effet, puisqu'on lit k bits, les codes courts ont été doublés :
Code valeur
0000 \ 0
0001 /
0010 \ 1
0011 /
0100 \ 2
0101 /
0110 \ 3
0111 /
1000 \ 4
1001 /
------------- pivot
1010 5
1011 6
1100 7
1101 8
1110 9
1111 10
Le pivot n'est plus au code 1012=510, mais au code 10102=1010. Le décodage s'effectue donc presque aussi simplement que l'encodage :
pivot = (1 << k ) - L;
n = lire k bits;
if n < (pivot << 1) then
renvoie le dernier bit dans le flux;
n = n >> 1;
else
n = n - pivot;
endif;
Cet algorithme est tellement simple, pourquoi donc s'en passer ? Une fois toutes ces petites subtilités traitées, le plus compliqué consiste à déterminer le nombre k.
3. Inverser les codes
En jouant avec les codes phase-in en 2008, j'ai testé une variation, que j'ai nommée phase-out, puisqu'elle reprend le principe du phase-in, mais l'applique à l'envers. On retrouve cette idée à la fin du chapitre sur les codes récursivement phase-in de la thèse ([2] p. 105). La différence est simple : contrairement aux codes habituels qui allouent moins de bits pour les petits nombres, on va allouer moins de bits aux grands nombres. Bien que ce ne soit pas parfaitement juste, on peut le justifier ainsi :
- Les petits nombres prennent déjà peu de bits, donc on ne gagne pas grand-chose à enlever un bit.
- Par contre, si on suppose une probabilité uniforme, les grands nombres, par définition, sont beaucoup plus nombreux, donc plus probables, et enlever un bit a plus d'impact.
Steven Pigeon aborde ainsi la problématique dans sa thèse :
En fait, dans l'article d'Acharya et Já Já, les codes sont inversés dans la mesure où ce sont les grands nombres qui reçoivent les codes les plus courts. Cela est parfaitement raisonnable puisque dans l’algorithme LZW qu’ils se proposent d’améliorer, les index qui sont les plus susceptibles d’être utilisés correspondent aux dernières concordances trouvées, lesquelles viennent d’être ajoutées au dictionnaire et ont reçu par conséquent un index près de la fin du dictionnaire. On peut transformer trivialement les codes récursifs présentés ici en codes qui assignent des codes courts aux grands entiers :
C′ρ(N)(i) = Cρ(N)(N−1−i)
Les tests préliminaires [7] ont montré que ce simple changement de perspective ou d'heuristique peut apporter un autre gain supplémentaire, marginal, mais pas insignifiant, et sans ajouter trop de complexité par rapport aux codes phase-in.
Figure 9 : Pour déterminer les codes promus à utiliser moins de bits, on reprend la figure 8 puis on applique un miroir vertical.
La figure 9 doit être comparée à la figure 8 : la forme est identique, mais l'ordre des valeurs a été inversé. D'ailleurs la manière de réaliser le code phase-out est d'inverser le nombre avec la formule N = N−1−i donnée dans la citation précédente.
Figure 10 : Les codes phase-out sont un corollaire des codes phase-in, mais ils favorisent les nombres élevés.
Cette inversion a un effet important sur la répartition des tailles, que l'on observe sur la figure 10 : la forme est différente de celle de la figure 2. Et comme les codes phase-in sont des codes à préfixes donc parfaitement réversibles, les codes phase-out le sont aussi.
Vous pouvez jouer avec le code grâce à la page interactive sur Hackaday [11] ou GitHub. Le projet 3RGB [12] fournit aussi un autre fichier JS/HTML [13] qui montre en détail l'intégration du phase-out dans un flux de bits.
4. Comparaison des performances
Le comportement des codes phase-in et phase-out dépend essentiellement des propriétés statistiques des données à encoder. Il est donc impossible a priori de prédire quelle version fonctionnera le mieux sans un minimum d'informations sur les données. Nous disposons déjà d'une heuristique :
- Si on traite surtout des nombres de faible amplitude (par rapport à la limite), alors on utilise le phase-in.
- Si on traite surtout des nombres de grande amplitude, alors on utilise le phase-out.
Évidemment, tout est relatif et les termes « faible amplitude » et « grande amplitude » changent selon le contexte et d'un bloc de données à l'autre... Donc le choix entre phase-in et phase-out dépend des propriétés et de la distribution des nombres.
Par exemple, on pense naturellement au codage phase-in pour compacter les résidus de prédictions (c'est-à-dire les erreurs par rapport aux valeurs calculées à partir des précédentes). Si les prédictions sont bonnes, donc si les données correspondent au modèle et aux heuristiques, alors les erreurs à encoder auront de faibles valeurs. Cela permet de gagner encore un peu de place dans le flux binaire. Mais en pratique, on ne peut pas savoir à l'avance, on peut juste faire des suppositions !
Une stratégie plus avancée consiste à tester les deux versions, valeur par valeur, puis indiquer par un bit quelle version est retenue. C'est la stratégie in-out qui a été testée en même temps que les deux versions sur [7], mais le résultat est décevant. Pour indiquer quel encodage prend le moins de place, il faut ajouter un bit par valeur dans le flux. Puisque ce bit supplémentaire prend autant de place que le bit économisé, la stratégie in-out est mécaniquement toujours la plus mauvaise.
On peut appliquer la stratégie in-out sur des blocs de différentes longueurs, mais là encore, le compromis est difficile à trouver et n'est pas bénéfique puisqu'un avantage en chasse un autre. Transmettre la taille du bloc prend encore de la place que nous essayons justement d'économiser.
On se retrouve donc avec des blocs de taille fixe, qui sont à la merci des variations des données à traiter. Un bloc trop petit va ajouter un surcoût avec ce bit supplémentaire, alors qu'un bloc trop gros diluera les statistiques fines et réduira l'avantage d'une stratégie sur une autre. Il n'y a donc pas de taille de bloc idéale sans une bonne connaissance des données et des heuristiques fiables.
Les mesures effectuées dans le cadre de l'algorithme 3R mettent en lumière les transformations que les nombres subissent et le changement de contexte qui s'opère. En effet, l'algorithme 3R a comme raison d'être l'affinage des limites, ce qui augmente les chances d'obtenir des limites proches des nombres à encoder. Ainsi, 3R biaise les statistiques d'une manière qui favorise le phase-out, puisqu'il tente de rapprocher L de n.
Encore une fois, c'est la simplicité qui gagne : si on évite de se focaliser sur quelques cas particuliers, on traite les cas généraux moins mal. Tant qu'on ne doit pas encoder une information supplémentaire, on empêche ainsi les données de grossir dans le pire des cas (qui ne manque jamais d'arriver).
5. Optimisation
La partie précédente concernait la performance de codage, ou plutôt le gain de place apporté par telle ou telle version. Maintenant nous allons nous occuper de la vitesse d'exécution, qui dépend de différents facteurs et surtout du contexte. Dans ce cas particulier, le développement du code répond aux objectifs et contraintes spécifiques suivants :
- Le décodeur est plus important que l'encodeur (pour l'instant), donc nous allons nous focaliser dessus.
- Le décodeur doit être réalisable en circuits logiques dans un FPGA, ce qui limite les opérations utilisables aux plus basiques : opérations booléennes et décalages. Les additions et soustractions doivent être limitées autant que possible à cause de la longueur des chaînes de retenue, qui sont la cause principale de lenteur d'un circuit.
- Le circuit logique doit contenir le moins de portes logiques possible, même si cela augmente légèrement le nombre de lignes de code pour la réalisation logicielle.
- Le CODEC utilise la version phase-out, car il est plus efficace que phase-in dans l'algorithme 3R.
- Les nombres à encoder en phase-out sont limités à 16 bits.
La version électronique est préparée et prototypée en logiciel, ce qui pourrait avoir des effets bénéfiques (comme ce fut le cas en optimisant l'algorithme 3R [14]).
Le fait d'utiliser phase-out avec 3R implique que la limite change à chaque nombre à coder et décoder, donc le pivot doit être recalculé à chaque fois, ce qui augmente la quantité de calculs et rend l'optimisation plus importante. Ici nous utiliserons essentiellement deux techniques : la parallélisation (réaliser plus d’une opération en même temps, en superscalaire ou avec des circuits parallèles) et la réduction du nombre d'opérations.
5.1 Le logarithme
La première étape consiste à déterminer combien de bits doivent être lus dans le flux. En termes mathématiques, on calcule le logarithme en base 2 de la limite : k=log2(L). En termes informatiques, on compte simplement les bits :
k=0;
n=L;
while n != 0
k = k+1;
n = n>>1;
end while
Cette approche itérative est sympathique, mais fonctionne avec une complexité en O(n) et la vitesse d'exécution dépend de la taille du nombre, ce qui n'est pas très efficace. Quand on réalise l'algorithme 3R, on peut partir de la taille précédente et la diminuer puisqu'on sait qu'elle est inférieure ou égale : c'est un peu plus rapide, mais toujours aléatoire.
Le logarithme peut être calculé en O(log n) étapes et comme nous savons que le nombre de bits est limité à 16, il faudra au maximum log2(16)=4 itérations, que nous pouvons dérouler. En logiciel, un test supplémentaire court-circuite le tout si L=0 :
k=0;
if L>0
n=L;
k=1;
if (n & ~255) k+=8; n=n>>8; end if;
if (n & ~ 15) k+=4; n=n>>4; end if;
if (n & ~ 3) k+=2; n=n>>2; end if;
if (n & ~ 1) k+=1; n=n>>1; end if;
end if;
Le lecteur attentif remarquera qu'on additionne des puissances de 2 à k, donc les 3 premières étapes peuvent être réalisées avec un OU logique au lieu d'une addition : en matériel, cela revient tout simplement à mettre des fils côte à côte pour former un bus. Le dernier +1 est une simple incrémentation. Côté logiciel, on peut même remplacer la première addition par une assignation :
k=0;
if L>0
n=L;
k=1;
if (n & ~255) k =9; n=L>>8; end if;
if (n & ~ 15) k|=4; n=n>>4; end if;
if (n & ~ 3) k|=2; n=n>>2; end if;
if (n & ~ 1) k+=1; n=n>>1; end if;
end if;
Un circuit électronique sera plus efficace et rapide grâce à d'autres techniques, mais nous avons déjà une bonne idée de sa complexité. Les quelques petites modifications du code ci-dessus devraient rendre la vie un peu plus facile aux processeurs à exécution dans le désordre, tels les processeurs Intel actuels ou les derniers ARM.
5.2 Le masque
La partie suivante est une étape importante qui n'a pas encore été abordée, mais qui prend une nouvelle dimension quand on examine plus profondément la réalisation de l'algorithme. Il s'agit de créer un « masque » (appelé m), qui est un champ de bits contigus qui sont tous à 1, dont la taille est égale à la limite : m≥L>(m>>1). Comme tous les bits sont à 1, on obtient aussi la relation booléenne L&m=L.
Ce masque a un premier usage : il permet de filtrer les bits que nous recevons du flux binaire, ce qui isole ceux qui nous intéressent.
n = lecture de k bits;
n &= m; // garde juste k bits de poids faible
Le masque a un autre usage grâce à une relation très intéressante : m+1=2k, donc le masque sert à calculer le pivot !
En logiciel, il existe deux manières de calculer ce masque. La version en O(log n) est recommandée, car elle montre comment cela peut être réalisé en matériel. Cela consiste à effectuer un OU bit à bit avec tous les bits de poids fort, comme dans le code suivant :
m = L | (L >> 1);
m = m | (m >> 2);
m = m | (m >> 4);
m = m | (m >> 8);
Ainsi, le bit de poids faible sera un OU logique de tous les autres bits. Cependant, nous avons déjà calculé k avec un algorithme en O(log n) et la relation m+1=2k nous permet de calculer le masque d'un seul coup, pour réduire la quantité de code de la version logicielle :
m=(1<<k)-1;
Pour ce qui est de la version matérielle, le calcul du masque est déjà effectué par le circuit qui calcule le logarithme. Il a été étudié et présenté dans l'article qui détaille la conception de l'algorithme 3R [14], nous faisons ainsi d'une pierre deux coups !
Dans [15], la partie 2 décrit un encodeur de priorité qui utilise quasiment les mêmes idées, à la différence que nous cherchons la position du bit de poids fort au lieu du bit de poids faible. Le sens des bits est changé, mais on retrouve les mêmes opérations :
- D'abord, une cascade binaire de OU logiques, pour mettre à 1 tous les bits suivant le bit de poids fort. C'est une traduction directe du code à 4 étapes ci-dessus.
le mot 0000111101011010
devient 0000111111111111
- Ensuite, un XOR ou un ANDN entre les bits consécutifs afin de déterminer où se trouve le bit de poids fort : un seul bit est à 1. En logiciel, cela s'écrit en incrémentant le masque : l'instruction m2 = m+1 propage la retenue et met tous les LSB à zéro, et ne garde plus qu'un bit à 1. En matériel, le code équivalent est juste booléen : m2 = m & ˜(m>>1) ce qui est facile à câbler, mais cela nécessite trois instructions de processeur au lieu d'une seule.
le mot 0000111111111111
devient 0000100000000000
- Enfin, la position est encodée en binaire naturel au moyen de portes logiques OU. Pour un calcul sur n bits, chaque bit du résultat est à 1 une fois sur deux, donc chaque porte OU a n/2 entrées. Pour des mots de 16 bits, il faut donc Log2(16)=4 portes avec 16/2=8 entrées.
le mot 0000100000000000
devient 1011
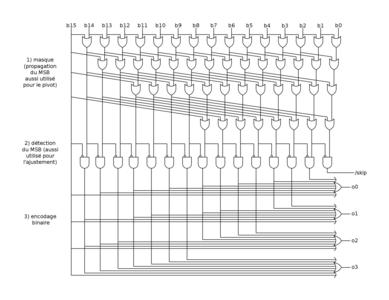
Figure 11 : Schéma d'un circuit de calcul du logarithme d'un nombre binaire. Les étapes intermédiaires génèrent aussi des résultats utiles pour les autres parties de l'algorithme.
Le fait de disposer du masque très vite après la lecture de la limite permet de calculer rapidement le pivot. Encore mieux : si le masque est nul, le circuit peut sauter un cycle de lecture du flux de bits. C'est la fonction du signal /skip sur la figure 11.
5.3 Bernard
Si la limite n'est pas nulle, il faut encore calculer le pivot. C'est là qu'une relation binaire très heureuse apparaît, pour l'encodage comme pour le décodage. Je vous épargne les détails du pourquoi du comment, et je vous livre le résultat :
if (n > (((L<<1) & m) |1 )) then
(ajustement)
endif;
En gros, l'utilisation du phase-out au lieu du phase-in a économisé (miraculeusement ?) une soustraction, puisque le calcul d'origine du pivot est (1<<k)-L. Où est passée la soustraction ?
Le tour de passe-passe se révèle quand on remarque que 1<<k est égal à m+1, donc on peut réécrire le pivot ainsi : (1<<k)-L=m+1-L.
L'autre astuce utilise la représentation binaire en complément à deux, où -N=(~N)+1. Autrement dit, le calcul du complément revient à inverser tous les bits puis incrémenter. Mais même l’incrémentation est économisée puisque le pivot du phase-out est inversé par rapport au pivot du phase-in, donc le circuit équivalent ne comporte qu'une seule chaîne de retenue, celle de la comparaison entre n et la limite modifiée.
Le calcul du pivot peut encore être amélioré. D'abord on peut étudier l'expression (((L<<1)&m)|1) qui revient à effectuer une rotation de L sur k bits. Le bit de poids fort de L est par définition toujours à 1, et il se retrouve effacé par le décalage à gauche puis le masquage par m. Mais ce bit est de nouveau réécrit dans le bit de poids faible... Malheureusement, il n'est pas évident d'effectuer une telle rotation plus efficacement donc il faut trouver une autre méthode.
L'autre chose à remarquer est que le bit à 1 réinjecté dans le bit de poids faible est une constante, ce qui n'affecte pas la comparaison. L est décalé à gauche, mais on pourrait tout aussi bien décaler n à droite, ce qui économiserait ainsi une opération OR avec la constante. D'autre part, l'ajustement (voir plus loin) utilise le masque décalé à droite (m>>1), ce qui est une valeur qu'on peut réutiliser pour le calcul du pivot. La condition de pivot s'écrit donc ainsi :
if (n>>1) > (L&(m>>1)) then
(ajustement)
endif;
La comparaison s'effectue habituellement au moyen d'une soustraction (c’est-à-dire une addition modifiée), donc au niveau électronique, c'est la seule opération qui va consommer des portes logiques et du temps. Le masquage ne consomme presque rien et les décalages logiciels se traduisent en ignorant le bit de poids faible, donc on ne compare que 15 bits (au lieu de 16).
5.4 L'ajustement
On y est presque ! Le dernier morceau de code s'occupe de modifier n lorsqu'il dépasse le pivot.
Dans le cas de l'envoi comme de la réception, la taille du mot doit être décrémentée. Par contre, l'envoi diffère de la réception par deux détails :
- L'ajustement de n se fait par une addition à l'envoi, et une soustraction à la réception (puisque l'un est la réciproque de l'autre). La formule magique à l'encodage est n=(n+(m>>1))-L donc le décodage s'effectue avec n=(n+L)-(m>>1).
- À la réception, avant l'ajustement, il ne faut pas oublier d'enlever le bit qui a été spéculativement lu (sinon le résultat n'aura pas de sens). Le décodage devient ainsi n=((n>>1)+L)-(m>>1).
Encore une fois, il existe une astuce qui permet de simplifier le circuit logique correspondant puisque m est directement lié à L. Pour l'encodage, en appliquant de nouveau la relation -N=(~N)+1, l'expression (m>>1)-L peut être réécrite ainsi : (m>>1)+(1+ ~L). Cette deuxième expression est composée de (m>>1)+1, que nous savons déjà équivalente à 1<<k (à un décalage fixe près, ce qui ne consomme pas de porte logique). Donc même si la représentation logicielle contient une addition et une soustraction, le circuit logique ne réalise qu'une addition (n + ~L). Le masque n'est pas utilisé directement, on réutilise le deuxième étage du circuit de logarithme (où un seul bit est à 1 pour indiquer le MSB de la limite) pour ensuite faire un XOR de ~L. En fait tout cela revient à enlever le MSB de L, et l'inversion de ses bits finit de calculer l'expression du pivot 2k-L.
On peut aussi en profiter pour effectuer quelques simplifications supplémentaires. Par exemple, dans le cas de l'encodage, seule l'expression (m>>1) est utilisée (m n'est pas utilisé seul) alors qu'on calcule m au moyen de l'expression 1<<k (moins un). On peut économiser les décalages de m en calculant le logarithme afin de retourner k-1 au lieu de k. En propageant cette modification, le code source de l'encodeur se retrouve alors apparemment plus clair, même si c'est trompeur. Afin d'éviter les confusions, la valeur (m>>1) est appelée m1.
6. Le code complet
Tous ces éléments algorithmiques sont assemblés pour former une fonction d'encodage et une fonction de décodage réciproque.
L'encodage a l'air assez simple, reprenant tous les morceaux discutés précédemment :
// encodage :
int send_phaseout(unsigned int val, unsigned int lim) {
uint32_t k=0, l=lim, m1; // m1 = m >> 1
if (lim) {
// génère m avec lim, démarre avec k=0
if (l & ~255) { k =8; l=lim>>8; }
if (l & ~ 15) { k+=4; l>>=4; }
if (l & ~ 3) { k+=2; l>>=2; }
if (l & ~ 1) { k+=1; l>>=1; }
m1=(1<<k)-1;
if ( (val>>1) > (lim & m1) ) // lim sans MSB
val+=m1-lim;
else
k++;
send_bits(val, k); // à voir plus tard
}
return k; // cette valeur peut être utile
}
Le seul point nouveau est la fonction send_bits() que nous devrons étudier dans un prochain article. Le décodage est similaire, mais diffère par la méthode de calcul du masque, qui commence avec k=1.
// décodage :
unsigned int receive_phaseout(unsigned int lim) {
uint32_t
val=0, // valeur par défaut si retour immédiat
val1, // val >> 1
k, // nombre de bits
l=lim, // limite temporaire
m,
m1; // m >> 1
if (lim) {
// génère le masque, mais départ avec k=1
k=1;
if (l & ~255) { k =9; l=lim>>8; }
if (l & ~ 15) { k+=4; l>>=4; }
if (l & ~ 3) { k+=2; l>>=2; }
if (l & ~ 1) { k+=1; l>>=1; }
m = (1<<k)-1;
m1 = m>>1;
val = receive_bits(k) & m; // à voir plus tard
val1 = val>>1;
if (val1 > (lim & m1)) {
val = (val1+lim)-m1;
adjust_bits_queue(); // à voir plus tard
}
}
return val;
}
On retrouve les mêmes éléments qu'à l'encodage, mais l'algorithme nécessite val et mask ainsi que leurs valeurs décalées d'une position à droite, ce qui donne l'impression que le code est plus lourd. Les fonctions receive_bits() et adjust_bits_queue() seront étudiées en même temps que send_bits() dans un prochain article.
Conclusion
Les codes binaires tronqués sont un outil supplémentaire dans la grande boîte à outils des entropistes. Ils ne permettent pas de gagner beaucoup de place, mais complémentent avec peu d'efforts des algorithmes existants. En supposant des limites et des nombres aléatoires, on peut gagner environ un quart de bit par nombre, ce qui fait un octet économisé pour 32 nombres. Un bloc de 64 pixels monochromes perd ainsi environ deux octets, mais il ne faut pas oublier que la gestion de la limite requiert aussi des informations auxiliaires...
Ce n'est pas la panacée, mais ce petit gain est d'autant plus notable qu'il ne nécessite aucun calcul compliqué et ignore toute considération de statistique, de distribution ou de contexte par exemple. Ce codage est idéal, entre autres, pour améliorer l'algorithme de compaction 3R, dans lequel il s'intègre facilement.
Dans un prochain article, je présenterai d'ailleurs comment le codage phase-out s'inscrit dans des fonctions d'insertion et d'extraction de flux binaire. L'article suivant rebondira sur le sujet, car tout cela permet de construire les codes sigma-alpha, qui vont encore améliorer l'algorithme 3R et d'autres choses assez surprenantes...
Références
[1] PIGEON S., page personnelle : http://stevenpigeon.org/
[2] PIGEON S., « Contributions à la compression de données », thèse de l’Université de Montréal, décembre 2001 : http://www.stevenpigeon.org/Publications/publications/phd.pdf
[3] Wikipédia, « Codage Arithmetique », https://fr.wikipedia.org/wiki/Codage_arithmétique
[4] Wikipédia, « Codage Par Intervalle », https://fr.wikipedia.org/wiki/Codage_par_intervalle
Voir aussi la version anglaise :
Wikipedia, « Range Coding », https://en.wikipedia.org/wiki/Range_encoding
[5] GUIDON Y., « Compactez une suite de nombres avec peu d'efforts grâce à l'algorithme 3R », Open Silicium n°16, octobre 2015, https://connect.ed-diamond.com/Open-Silicium/OS-016/Compactez-une-suite-de-nombres-avec-peu-d-efforts-grace-a-l-algorithme-3R
[6] GUIDON Y., « Data compression: the 3R algorithm », octobre 2003,
http://ygdes.com/ddj-3r/ddj-3r_compact.html
[7] GUIDON Y., « Lossless data compression with the Recursive Range Reduction algorithm », 2006, http://ygdes.com/3r/
[8] ACHARYA (Tinku) et Já (Joseph Já), « Enhancing LZW Coding Using a Variable-Length Binary Encoding. » Rapport technique n° TR-95-70, Institute for Systems Research, 1995
[9] Acharya (Tinku) et Já (Joseph Já), « An Online Variable Length Binary Encoding of Text. », Informatics & Computer Science, vol. 94, 1996, pp. 1–22
[10] Wikipedia, « Codage binaire tronqué », https://fr.wikipedia.org/wiki/Codage_binaire_tronqué
[11] GUIDON Y., Démonstration interactive et graphique du codage phase-out https://cdn.hackaday.io/files/248341062497856/test-phase-out.html (voir aussi sur le compte GitHub du magazine)
[12] GUIDON Y., « Le projet 3RGB »,
https://hackaday.io/project/24834-3rgb-image-lossless-compression-format
[13] GUIDON Y., Banc de test pour l’insertion et l’extraction de codes phase-out dans un flux de bits https://cdn.hackaday.io/files/248341062497856/exercise-phase-out.html (voir aussi sur le compte GitHub du magazine)
[14] GUIDON Y., « Optimisation de l'algorithme de décompression de flux 3R », Open Silicium n°17, janvier 2016, https://connect.ed-diamond.com/Open-Silicium/OS-017/Optimisation-de-l-algorithme-de-decompression-de-flux-3R
[15] GUIDON Y., « Décompressez un flux de données 3R avec un circuit écrit en VHDL », Open Silicium n°18, avril 2016, https://connect.ed-diamond.com/Open-Silicium/OS-018/Decompressez-un-flux-de-donnees-3R-avec-un-circuit-ecrit-en-VHDL



 Ajouter à une liste de lecture
Ajouter à une liste de lecture