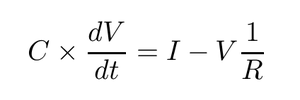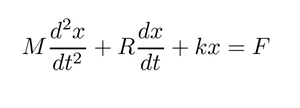Toute conception de circuit électronique analogique qui ne soit pas complètement triviale passe par une phase de simulation, ne serait-ce que pour identifier l’influence des divers blocs de référence entre eux, ou l’effet de l’incertitude de la valeur des composants sur la fonction de transfert du montage.
Nous nous proposons d’illustrer quelques exemples concrets de mise en œuvre d’un outil de simulation open source – SPICE – pour la simulation du comportement de circuits électroniques, avec une extension vers les simulations multiphysiques.
SPICE (Simulation Program with Integrated Circuit Emphasis) est un ensemble d’outils de simulation de circuits électroniques initialement développés à l’Université de Berkeley. Comme tout logiciel développé sur des fonds publics américains1, il est librement disponible et est ainsi devenu la référence des outils pour simuler des circuits à basse fréquence. SPICE ne tient pas compte de l’agencement des composants ni du substrat diélectrique qui servira à la réalisation du circuit imprimé, mais ne considère qu’un ensemble de composants reliés entre eux : il est donc performant pour des fréquences allant du continu (DC) aux radio-fréquences. Les modèles de composants sont cependant complexes et tiennent compte d’effets aussi subtils que les variations de propriétés avec la température.
La stratégie d’utilisation de SPICE ne dépaysera pas l’utilisateur de GNU/Linux : après avoir tapé avec son éditeur favori la liste des composants et leur agencement en un circuit électronique (netlist), l’utilisateur appelle depuis une fenêtre de commandes interactive divers types de modélisations sur ce circuit. Les résultats de ces calculs sont disponibles soit immédiatement sous forme graphique, soit sous forme de tableaux de points redirigeables dans un fichier pour un traitement ultérieur – notamment avec des outils plus performants pour le traitement et l’affichage de données que les fonctions rudimentaires proposées par SPICE [1]. Alternativement, la netlist est traitée en mode batch depuis la ligne de commandes, permettant une interaction efficace avec le shell pour automatiser les simulations : dans ce mode, SPICE est capable de sauver l’intégralité des résultats de la simulation dans un fichier binaire (format .raw), dont les informations sont accessibles depuis GNU/Octave au moyen des scripts fournis à ngspice.sourceforge.net/osctavespice.html.
Ce document n’a en aucun cas vocation à se substituer à la documentation officielle [2] ou à la fonction help accessible depuis la ligne de commandes pour détailler la syntaxe et la fonctionnalité de chaque commande, mais plutôt d’introduire quelques concepts ludiques accessibles au moyen de cet outil de simulation.
1. Installation
La licence de SPICE n’est pas GNU puisque SPICE (années 1970) est antérieur à GNU (1989) et ce logiciel n’est donc disponible sous forme de paquet Debian que dans l’archive non free. De toute façon, il est toujours meilleur, par souci de cohérence avec son système, de recompiler depuis les sources : pour ce faire, nous récupérons la dernière archive disponible sur sourceforge à http://ngspice.sourceforge.net/. La compilation par le traditionnel trio ./configure && make && make install nécessite de disposer des bibliothèques de développement libxt-dev et libxaw-dev (faute de quoi, SPICE compile sans la possibilité d’affichage graphique sous X11, et perd un peu de son interactivité sans pour autant perdre de fonctionnalité) [4].
2. Premiers pas
Prenons l’exemple trivialement simple – mais d’un intérêt pratique indéniable – de la capacité de découplage que tout électronicien se doit de placer sur chaque alimentation des composants de son circuit. Une alimentation réelle (de résistance interne non nulle) débite dans un composant qui effectue des appels de courant à une fréquence d’autant plus élevée que les signaux traités par ce circuit son de fréquence élevée (le pire cas étant celui des composants numériques rapides qui doivent effectuer des transitions de plusieurs volts en quelques nanosecondes). Afin de réduire les fluctuations de tension d’alimentation le long des pistes d’alimentation, nous plaçons des condensateurs (dits de découplage) qui se comportent comme des réservoirs d’électrons qui absorbent les appels de courant. Comment choisir la valeur des condensateurs de découplage ?
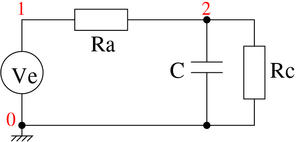
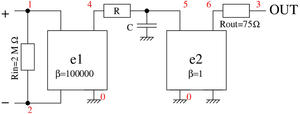
Ces concepts se modélisent par le circuit de la figure 1, dans lequel la consommation du circuit est modélisée par la résistance de charge Rc et le condensateur de découplage est C.
Figure 1 : Circuit servant d’exemple pour la première simulation sous SPICE
Ce circuit se décrit dans un fichier ASCII décrit dans le listing 1.
* exemple alim.cir
* toute ligne commencant par une etoile est un commentaire
* tout fichier doit commencer par au moins 1 commentaire
Ra 1 2 10
Rc 2 0 500
C 2 0 500n
Ve 1 0 ac 1 dc 5
.control
ac dec 10 100 1meg
plot v(2)
alter C=500u
ac dec 10 100 1meg
plot v(2)
.endc
Tableau 1 : Premier exemple d’un circuit de découplage RC fonctionnel sous ngspice
Nous constatons que le circuit est défini par des composants, dont la première lettre définit la nature (R pour les résistances, C pour les condensateurs, L pour les inductances... Les extrémités de ces composants sont définies par des nœuds : par convention, le nœud 0 définit la masse. Le premier nœud fournit la borne positive, le second la borne négative (cet ordre n’a évidemment de sens que pour les alimentations et les composants polarisés tels que les diodes D). Enfin, à chaque composant est affectée une valeur, avec les suffixes habituels (n pour 10−9, u pour 10−6, m pour 10−3, k pour 103 et, plus inhabituel, meg pour 106). La source de tension est notée V : cette source sera l’origine de la simulation, donc nous allons définir le comportement selon les modalités proposées ci-dessous.
SPICE permet d’analyser le comportement de ce circuit de diverses façons, dont les plus courantes sont :
- l’analyse du potentiel de sortie en fonction du potentiel constant (DC) d’une source de tension en entrée dc.
- l’analyse temporelle, et notamment du comportement lors de la mise en marche ou de la transition d’un signal, i.e. la réponse transitoire tran.
- l’analyse spectrale, ou la dépendance de la puissance radiofréquence en sortie connaissant la fréquence du signal en entrée ac.
Le fichier de configuration cité auparavant (Tab. 1), tapé dans un fichier d’extension par convention .cir au moyen de son éditeur de texte favori (donc vi), est chargé dans ngspice par la commande source fichier.cir. Une fois la configuration chargée, nous définissons la nature de l’analyse en fournissant les propriétés de la source de tension ve : il peut s’agir d’une analyse dc ve début fin incrément pour rechercher le point de fonctionnement en tension continue alors que l’alimentation balaie la gamme de début à fin par pas d’incrément, d’une analyse en signaux alternatifs ac dec nombre_points début fin (dec signifiant que nous balayons les fréquences de début à fin Hz par décade, en vue d’une analyse dans un graphique log-log avec la tension en décibels), ou d’une analyse temporelle par pas de pas pour une durée de durée au moyen de tran pas durée. Ainsi, dans l’exemple précédent, l’exécution de la simulation s’obtient au moyen de :
jmfriedt@eee:~/$ ngspice
******
** ngspice-20 : Circuit level simulation program
** The U. C. Berkeley CAD Group
** Copyright 1985-1994, Regents of the University of California.
** Please submit bug-reports to: ngspice-bugs@lists.sourceforge.net
** Creation Date: Fri Nov 20 10:19:22 GMT 2009
******
ngspice 1 -> source alim.cir
Circuit: * exemple alim.cir
ngspice 2 -> ac dec 100 50 1meg
Doing analysis at TEMP = 27.000000 and TNOM = 27.000000
ngspice 3 -> plot v(2)
ngspice 4 -> plot vdb(1) vdb(2)
Les lignes en fin de l’exemple 1 commençant par .control et finissant par .endc contiennent la liste de commandes à exécuter par défaut au chargement de la netlist. Ainsi, dans cet exemple, la configuration du circuit elle-même commence avec la première ligne et s’achève avec la définition de la source Ve, tandis que les lignes qui suivent lancent la simulation pour une première configuration (C=500 nF) du comportement en petits signaux compris entre 10 Hz et 1 MHz, affichent le résultat (plot v(2)) ainsi que la source d’excitation d’amplitude constante (plot v(1)), puis nous reprenons cette simulation après avoir modifié (commande alter) la valeur de C pour qu’il prenne la valeur de 500 µF. L’alternative au traitement de commandes fournies dans le fichier entre .control et .endc est de taper ces ordres dans la fenêtre interactive afin de rechercher les informations pertinentes caractérisant le circuit sans devoir recharger la netlist pour chaque nouvel essai.
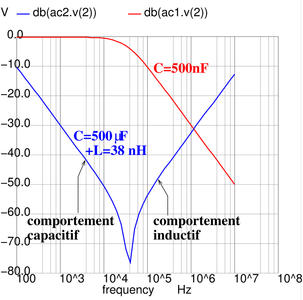
Cet exemple permet de comprendre pourquoi un condensateur de quelques dizaines ou centaines de µF est nécessaire pour filtrer les composantes basses fréquences d’une alimentation connectée au secteur, tandis que les condensateurs de petites valeurs (quelques dizaines ou centaines de nF) éliminent les fluctuations à haute fréquence (Fig. 2). Ce graphique s’analyse de la façon suivante : il fournit l’amplitude du signal au nœud 2 (la borne de la charge Rc, qui en pratique serait le composant à alimenter) pour un signal au nœud 1 (la source de tension) oscillant à une fréquence variable, fournie en abscisse du graphique. L’objectif du découplage est de réduire au maximum ces fluctuations, donc de réduire au maximum les fluctuations au nœud 2 afin d’alimenter Rc par une tension continue présentant peu de fluctuations. Ainsi, notre objectif est d’identifier les conditions sur C pour minimiser la courbe de la figure 2. Pour ce faire, nos degrés de liberté sont la valeur de la capacité, en tenant compte de la technologie associée et des effets parasites qui sont associés : au-delà du microfarad, les condensateurs tantale (l’oxyde de tantale présente une permittivité très élevée et est utilisée en industrie des semi-conducteurs pour former des capacités élevées sur des surfaces réduites) et électrochimiques, en deçà du microfarad, le condensateur céramique.
En pratique, une capacité électrolytique présente une inductance en série [6] qui n’est pas négligeable aux fréquences élevées (au-delà de quelques kHz) : cette valeur est documentée par les fabricants [7] : dans l’exemple proposé sur la figure 2, nous avons placé en série avec la capacité de 500 µF une inductance de 38 nH. Dans ces conditions, l’inductance la plus élevée est bien la plus efficace à empêcher un signal basse fréquence d’atteindre le nœud 2 (filtrage efficace de la composante basse fréquence), mais est incapable d’efficacement couper un signal de fréquence supérieure au MHz. Au contraire, le condensateur céramique (technologie différente, ne présentant pas de composante inductive significative dans cette gamme de fréquences), coupe efficacement au-delà de 1 MHz. Cette démonstration justifie la mise en parallèle de ces deux types de composants pour un découplage efficace des composants numériques en vue de rendre leur alimentation immunisée aux fluctuations basses fréquences (condensateur de valeur élevée, électrolytique) et hautes fréquences (condensateur céramique de valeur de l’ordre du nF).
Figure 2 : Résultat de la simulation en petits signaux – AC – du modèle de condensateur de découplage dont le schéma est proposé en figure 1. En rouge, un condensateur de petite valeur, ici 500 nF, typiquement en technologie céramique, donc avec un comportement proche de l’idéal dans cette gamme de fréquences. Le modèle du condensateur électrolytique (500 µF, en bleu) est complété d’une inductance en série de 38 nH, en accord avec la valeur proposée dans une datasheet de fabricant.
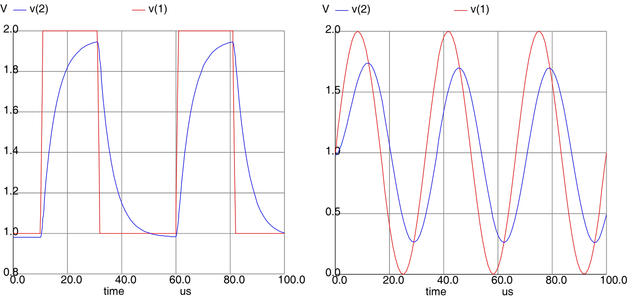
La source peut être plus complexe qu’un simple générateur DC ou AC : nous sommes capables de définir des sinusoïdes ou des impulsions pour exciter le circuit, et ainsi obtenir la réponse temporelle par tran à ces sollicitations. Si dans cet exemple, nous remplaçons la définition de la source Ve par Ve 1 0 dc 1 pulse(1 2 10u 0 0 20u 50u), alors nous générons une série d’impulsions commençant 10 µs après le début de la simulation, de 20 µs de long et se répétant toutes les 50 µs, avec des temps de montée et de descente de 0 s. De la même façon, Ve 1 0 dc 1 sin(1 1 30k) définit une source de tension moyenne de 1 V, d’amplitude 1 V et de fréquence 30 kHz. Le résultat de ces simulations en transitoire (i.e. comportement temporel) pendant 100 µs est illustré sur la figure 3.
Figure 3 : Gauche : alimentation du circuit de découplage RC série par un créneau (en rouge la tension d’excitation et en bleu la sortie du filtre). Droite : alimentation du circuit de découplage RC série par une sinusoïde (en rouge la tension d’excitation et en bleu la sortie du filtre).
Lors d’une série de simulations, SPICE recalcule l’ensemble des paramètres du circuit mais mémorise les anciens résultats. Le choix de la simulation à exploiter lors de l’affichage s’obtient par setplot. La liste des variables au sein d’une simulation s’obtient par display all. Au lieu de passer d’une simulation à l’autre par setplot, il est possible de fournir en préfixe à la variable affichée la simulation qui contient cette variable : dans l’exemple précédent, plot ac1.v(2) ac2.v(2) superpose sur un même graphique les simulations obtenues pour les deux valeurs de condensateurs 500 µF et 500 nF.
L’ensemble des paramètres d’un composant s’obtient par show, qui prend en argument le nom du composant, tandis qu’une simulation est détruite au moyen de destroy. Ces deux commandes acceptent comme argument all.
Afin d’inclure le résultat de simulations dans un rapport de bonne qualité graphique, il est naturel de vouloir exporter les schémas représentatifs des simulations au format Postscript. SPICE doit être configuré pour exporter ses graphiques dans ce format : set hcopydevtype=postscript passe le périphérique de sortie en mode Postscript, set hcopypscolor=true permet d’afficher chaque courbe en couleur au lieu de tons de gris, set color0=rgb:f/f/f et set color1=rgb:0/0/0 définissent la couleur de fond à blanc et les caractères en noir respectivement. Une fois ces configurations mémorisées, l’affichage s’obtient comme dans le cas de plot, mais en remplaçant cette commande par hardcopy fichier.ps tensions (Figs. 3 et 4).
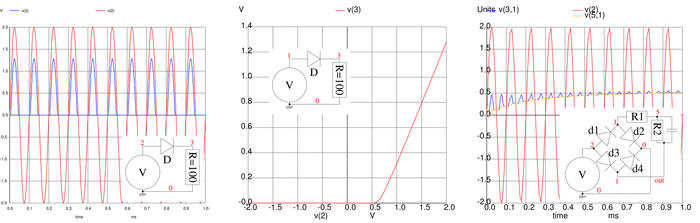
Nous ne sommes évidemment pas restreints à l’exploitation de composants linéaires : l’exemple de la figure 4 illustre dans un premier temps la caractérisation d’une diode avec ses paramètres par défaut – avec notamment la tension de seuil classique à 0,6 V pour les diodes silicium – puis l’association des diodes dans un circuit redresseur tel qu’utilisé classiquement dans les convertisseurs AC-DC ou DC-DC. On notera dans ce dernier cas la visualisation du transitoire, avec la tension de sortie du régulateur (en orange) qui prend environ 7 périodes (soit 0,7 ms) pour atteindre un régime stationnaire, tandis que la sortie du pont redresseur (en bleu) illustre bien l’exploitation des deux alternances pour charger le condensateur en sortie.
Figure 4 : Gauche : caractérisation de la diode par sa réponse temporelle lorsque excitée par une sinusoïde, et au milieu, la caractérisation par une tension en entrée variant de -2 à +2 V, illustrant la tension de seuil de 0,6 V qui se traduit par cette chute de tension lors du redressement de la sinusoïde. Droite : exploitation de cette diode dans un pont redresseur chargé par un circuit RC de lissage représentatif d’une charge. La tension de seuil est notamment source d’inefficacité dans les applications RFID ou convertisseurs DC-DC qui nécessitent une tension d’entrée au-dessus de ce seuil pour fonctionner.
L’option .model permet de modifier les paramètres par défaut exploités par les modèles de SPICE. À titre d’exemple pratique, la tension de jonction de diode telle que nous venons de le voir est de 0,6 V, en accord avec le comportement d’une diode silicium. Il se peut cependant que nous voulions varier cette tension de jonction, que ce soit pour avoir une diode sans seuil (telle que nous l’obtiendrions en plaçant une vraie diode dans la boucle de rétroaction négative d’un amplificateur opérationnel), ou pour élever ce seuil à 1,2 voire 1,5 V, tel qu’observé expérimentalement pour une LED. Le modèle complexe de la diode, décrit dans la documentation de ngspice [2, chap.8, p.70], ne permet pas de simplement définir la tension de jonction, mais nécessite de passer par le coefficient d’émission N avec lequel elle est proportionnelle. Ainsi, nous utiliserons :
.model nom D(N=0.01)
pour modifier les paramètres par défaut de la diode D, en remplaçant le paramètre N de 1 à 0,01, et ainsi générer le modèle nom qui sera appelé par D1 noeud1 noeud2 nom pour une diode de seuil négligeable (une valeur de 0 ne permet pas la convergence d’une solution). De la même façon, un paramètre de N>2 donnera un modèle pertinent pour une LED. Nous encourageons le lecteur à retracer les schémas de la figure 4 avec ce paramètre.
3. Exemples concrets : électronique
Les exemples qui vont suivre ne sont pas pris au hasard, mais on été piochés dans une collection de circuits développés par l’auteur lors de diverses activités plus ludiques que professionnelles.
3.1 Caractérisation de circuits passifs
Un circuit nécessite une source et une charge : en connectant un circuit passif entre une source de tension (d’impédance nulle) et une charge élevée, nous pouvons caractériser le comportement d’un réseau de composants passifs et la dépendance de son impédance avec les valeurs d’un de ses éléments. Le résultat d’une simulation peut être redirigé vers un fichier comme nous le ferions classiquement dans un shell unix : print vdb(3) > nom_fichier, permettant de facilement explorer l’espace des paramètres dont dépend la fonction de transfert2.
Afin d’illustrer l’analyse paramétrique d’un filtre passe-bas radiofréquence (filtre passe-bas de Chebychev à 4 pôles visant à éliminer les harmoniques d’une oscillateur numérique conçu pour fonctionner à 10 MHz) [3, p.17.98], nous proposons l’exemple qui suit qui, en plus d’illustrer une nouvelle netlist, fournit un exemple de script de commandes SPICE afin de balayer une plage de valeurs d’un composant :
* low-pass filter: cutoff @ 20 MHz (p.17.98 ARRL Handbook)
.control
destroy all
set units = degrees
foreach parameter 0.2 0.5 1 2
set c=$parameter
echo $c $parameter*1n
alter @c2[capacitance]=$parameter*1n
ac dec 50 1meg 200meg
end
* unset parameter
plot db(ac1.v(4)) db(ac2.v(4)) db(ac3.v(4)) db(ac4.v(4)) xlabel f[Hz] ylabel magnitude[dB] title 'AC analyses'
* * plot p(ac1.(4)) p(ac2.(4)) p(ac3.(4)) p(ac4.(4)) xlabel f[Hz] ylabel phase[degrees] title 'AC analyses'
unset units
* destroy all
.endc
v1 1 0 dc 0 ac 1 pulse 0 -1 1ms
* R0=impedance d'entree, R1=sortie
R0 1 9 50
C0 9 2 0.1u
L1 2 3 134n
C1 3 0 680p
L2 3 4 433n
C2 4 0 220p
Rl 4 0 50
.end
L’exemple ci-dessus – sous forme de netlist et de schéma associé – est l’opportunité de mentionner que SPICE implémente un langage scripté pour contrôler l’exécution de la simulation dans le bloc commençant par .control et finissant par .endc. Ce langage supporte les notions de variable, de listes et de contrôle du flux d’exécution.
Ainsi, la séquence
foreach parameter 0.2 0.5 1 2
set c=$parameter
echo $c $parameter*1n
end
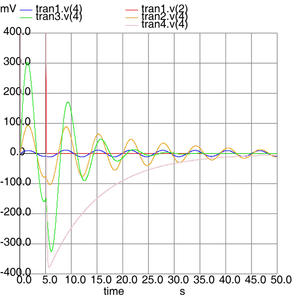
affecte à la variable c le contenu courant de parameter pioché dans la liste définie par foreach, et affiche cette valeur ainsi que la conversion de parameter en un format compatible avec une valeur de composant. Nous avons déjà vu auparavant que l’instruction alter permet de modifier la valeur d’un composant défini dans le fichier source .cir. Finalement, l’ajout de l’ordre de simulation tran ou, ici, ac, au sein de cette boucle, implique une séquence de 4 simulations pour 4 valeurs du paramètre c2. Une fois ces simulations achevées, nous affichons sur un unique graphique le diagramme de Bode obtenu pour chaque valeur du paramètre (Fig. 5). Nous avions déjà vu auparavant un cas particulier d’affectation de variable du système lors de la définition de hcopydevtype pour obtenir un affichage en Postscript : l’affectation s’obtient par set, et l’appel au contenu de la variable nécessite d’en précéder le nom par le symbole $. Toute combinaison de variable avec les constantes prédéfinies du système (affichables par print const.all) ou les unités (dans cet exemple, 1n) est possible lors d’une affectation.
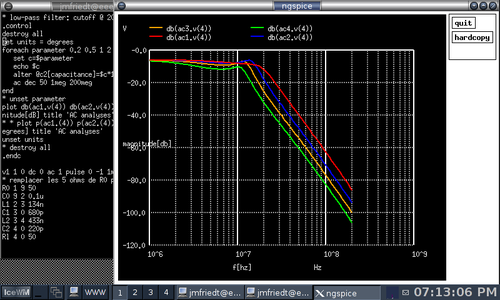
Figure 5 : Capture d’écran de la simulation d’un filtre de Chebychev, avec évolution de la fonction de transfert en fonction de la valeur d’un des condensateurs.
Le script commence par effacer toute simulation en mémoire (destroy all) afin de savoir quelle valeur de C2 a été affectée pour quelle simulation (la séquence des simulations ac1, ac2, ac3, etc., s’incrémentant automatiquement par rapport aux résultats déjà en mémoire au moment de l’exécution du script). Puis nous cyclons les diverses valeurs de paramètres, de 0,2 à 2 nF, que nous affectons à C2 dans la boucle, avant d’afficher le résultat par l’instruction plot sur un unique graphique de toutes ces simulations. Notez l’exploitation de la syntaxe db(ac1.v(4)) pour afficher le potentiel au point 4 de la simulation ac1 en décibels : la notation ac1.vdb(4) n’est en effet pas reconnue. La même opération visant à afficher le déphasage induit par le filtre au lieu du gain s’obtient en remplaçant db par p.
3.2 Filtrage idéal
Dans le cas d’un filtrage, le signal électrique ne traverse qu’une fois la chaîne de traitement, entre son entrée et sa sortie, et le comportement du circuit est par conséquent faiblement dépendant des propriétés des composants utilisés (contrairement au cas de l’oscillateur que nous verrons plus loin (section 3.4), qui boucle la sortie de l’amplificateur sur son entrée et réinjecte donc toute erreur du modèle qui se voit amplifiée pendant la durée de la simulation). Ainsi, un modèle idéal d’amplificateur opérationnel suffira en général à décrire convenablement le comportement d’un filtre allant à des fréquences jusqu’au mégahertz. Le rôle de l’amplificateur opérationnel est de rendre le comportement des composants insérés dans un filtre aussi proche de l’idéal que possible. Ainsi, un redresseur sans seuil – éliminant la tension de jonction d’une diode – s’obtient en remplaçant une simple diode par une diode en rétroaction négative sur un amplificateur opérationnel (l’amplificateur opérationnel s’efforce d’ajuster la sortie à l’entrée, et de cette façon somme naturellement la tension de jonction de la diode à la sortie pour fournir un redresseur sans seuil). De façon générale, l’amplificateur opérationnel a pour rôle de compenser les pertes dans les composants contenus dans le filtre.
Nous savons qu’un amplificateur se comporte comme une source de tension contrôlée en tension de gain classiquement noté β : SPICE nous fournit un tel composant sous la nomenclature e qui prend comme arguments les bornes positives et négatives de la source, les bornes de la commande et le gain. Pour ajouter un minimum de réalisme au modèle, nous ajoutons la contrainte d’une impédance grande mais finie aux bornes inverseuse et non inverseuse de l’amplificateur (Rin), ainsi que la dépendance du gain de l’amplificateur opérationnel en boucle ouverte avec la fréquence de fonctionnement (produit gain-bande passante constant au travers du filtre RC) qui permet de garantir la stabilité du circuit, et l’empêche d’osciller à haute fréquence (Fig. 6). Ce modèle servira de base pour les analyses de circuits plus complexes exploitant l’amplificateur opérationnel en fonctionnement linéaire comme bloc de base.
.subckt opamp 1 2 3
* +in (=1) -in (=2) out (=3)
rin 1 2 2meg
e 4 0 1 2 100k
rbw 4 5 0.5meg
cbw 5 0 31.85nf
eout 6 0 5 0 1
rout 6 3 75
.ends opamp741
SPICE propose – au même type que les procédures dans les langages de programmation – de découper un circuit complexe en blocs de base individuels nommés des sous-circuits (subcircuits). La syntaxe de cette fonction est :
.subckt nom noeuds
avec noeuds, l’équivalent des arguments de la procédure, ici la liste des nœuds permettant de connecter le sous-circuit au circuit principal. Un bloc de sous-circuit se termine par .ends. Le sous-circuit de nom nom s’appellera dans la netlist principale par un identifiant commençant par x. Ainsi, dans cet exemple, si le circuit de la figure 6 fournit le schéma de principe d’un amplificateur idéal que nous nommerons opamp741 dans une procédure prenant pour argument les entrées non inverseuse, inverseuse et la sortie
.subckt opamp741 1 2 3
alors tout circuit nécessitant un amplificateur opérationnel fera appel à ce composant par
x1 10 11 12 opamp741.
Nous pouvons nous convaincre du peu d’influence du modèle d’amplificateur opérationnel dans la conception de filtres fonctionnant aux fréquences audio (< 1 MHz) par le modèle de filtre passe-bande proposé dans le listing 2, qui exploite le modèle simple proposé ci-dessus et un modèle complexe proposé dans [8]) (Fig. 7).
*band pass filter
* set options
.opt nopage
.width in=72
.width out=80
.subckt opamp741 1 2 3
* +in (=1) -in (=2) out (=3)
rin 1 2 2meg
rout 6 3 75
e 4 0 1 2 100k
rbw 4 5 0.5meg
cbw 5 0 31.85nf
eout 6 0 5 0 1
.ends opamp741
.subckt AD712 13 15 12 16 14
VOS 15 8 DC 0
EC 9 0 14 0 1
C1 6 7 .5p
RP 16 12 12k
GB 11 0 3 0 1.67k
RD1 6 16 16k
RD2 7 16 16k
ISS 12 1 DC 100u
CCI 3 11 150p
GCM 0 3 0 1 1.76n
GA 3 0 7 6 2.3M
RE 1 0 2.5MEG
RGM 3 0 1.69k
VC 12 2 DC 2.8
VE 10 16 DC 2.8
R01 11 14 25
CE 1 0 2p
R02 0 11 30
RS1 1 4 5.77k
RS2 1 5 5.77k
J1 6 13 4 FET
J2 7 8 5 FET
DC 14 2 DIODE
DE 10 14 DIODE
DP 16 12 DIODE
D1 9 11 DIODE
D2 11 9 DIODE
IOS 15 13 5e-12
.MODEL DIODE D
.MODEL FET PJF(VTO=-1 BETA=1M IS=25e-12)
.ENDS
* band pass filter
.subckt BPF 1 6
R1 1 3 22.0k
C1 3 2 560p
R2 3 4 22k
C2 4 0 0.1n
C3 2 5 220n
R3 5 6 820
xao1 4 2 2 opamp741
* xao1 4 2 100 101 2 AD712
.ends BPF
* current and voltage sources
vin 1 0 dc 0 ac 1 sin 0 100u 2.247kHz
vcc 100 0 dc 12
vss 101 0 dc -12
* circuit elements
xc2 1 2 BPF
Rout 2 0 10k
* analysis control 50 Hz-50kHz with 5 points/decade, tran step total
* either dec num start stop ; or lin points start stop
.control
ac dec 100 1 100k
* .tran 1u 10m
* .plot vdb(2)
* .plot vp(2)
plot vdb(2) vp(2)
.endc
Tableau 2 : Programme de simulation SPICE pour simuler le comportement d’un filtre passe-bande, soit avec un modèle simple d’amplificateur opérationnel (opamp741) tel que proposé sur la figure 6, soit avec un modèle plus complexe (AD712) tel que proposé dans [8].
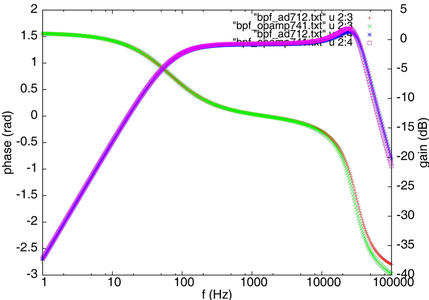
Figure 7 : Résultat de l’exécution du script 2, pour deux modèles d’amplificateurs opérationnels : le circuit se comporte bien comme un filtre passe-bande, et la seule différence significative entre les modèles apparaît aux fréquences les plus élevées.
3.3 Oscillateur : injection d’énergie en phase et synthèse de facteur de qualité
L’exemple qui suit a pour vocation d’illustrer l’assemblage de circuits simples – validés individuellement lors de simulations n’incluant que l’unique bloc dont on vérifie le comportement – afin de fournir une fonctionnalité complexe. La figure 3 illustre ce découpage en exploitant explicitement 4 amplificateurs opérationnels, qui forment chacun le cœur d’une fonction de base : convertisseur courant-tension, déphaseur, amplificateur et sommateur. Cette netlist reprend donc le concept de sous-circuit, avec notamment l’amplificateur opérationnel que nous venons de proposer, pour en déduire des blocs aux fonctionnalités plus complexes. Chaque bloc prend en argument autant de nœuds qu’il a d’entrées et de sorties : une entrée et une sortie pour un déphaseur, deux entrées et une sortie pour un additionneur-inverseur.
Nous proposons une approche des oscillateurs qui passe par l’injection en phase d’un signal afin de compenser les pertes induites par un élément dont la fonction de transfert présente un faible encombrement spectral (résonateur, sous-circuit quartz dans la netlist 3) [5]. Un amplificateur est un dispositif large bande, capable d’amplifier un signal quelle que soit sa fréquence d’entrée, avec un gain d’autant plus faible que la fréquence est élevée. Un oscillateur est en général conçu pour fonctionner à une fréquence bien précise, définie par un élément passif d’encombrement spectral réduit dont le rôle est de tuer toute ambition de l’amplificateur d’entretenir une oscillation à une fréquence autre qu’à celle du résonateur (pertes excessives qui ne peuvent être compensées par l’amplificateur pour les fréquences en dehors de la bande passante du résonateur). L’exemple ci-dessous permet d’illustrer la conception d’un circuit électronique sous forme d’assemblage de blocs de base dont chacun est convenablement caractérisé avant d’être inclus dans la chaîne de traitement, et ce en vue de présenter l’oscillateur comme condition asymptotique de l’injection d’énergie en phase dans un résonateur pour en augmenter le facteur de qualité apparent.
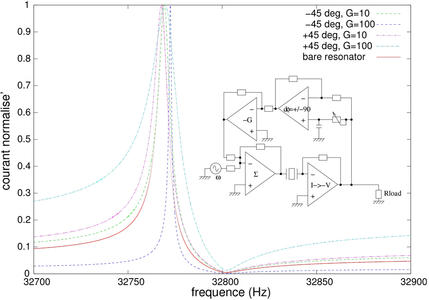
Dans son principe (Table 3), la sortie d’un amplificateur (x1) est injectée dans un résonateur (x2). La sortie de ce résonateur, un dipôle qui ne laisse passer du courant que si la tension en entrée respecte une condition de synchronisme avec le dispositif mécanique qui sélectionne la fréquence (comme le ferait un pendule), est convertie en tension au moyen d’un convertisseur courant-tension idéal (du fait de la présence d’un amplificateur opérationnel qui isole la résistance de charge de l’impédance du circuit suivant : x2b). Ce signal est déphasé (x3), amplifié (x4) et sommé (boucle fermée sur x1) au signal initial. Si le déphasage (constant) a amené le signal additionné en phase avec le signal original, il y a amplification. Si le signal déphasé est en opposition de phase avec le signal d’origine, il y a annulation ou tout au moins réduction de la puissance réinjectée dans le résonateur. Un choix judicieux de la phase – ajustée en faisant varier les valeurs des composants du déphaseur au moyen de SPICE – permet soit d’étaler l’encombrement spectral équivalent du résonateur3 (réduction du facteur de qualité apparent), soit de le réduire (augmentation du facteur de qualité apparent) (Fig. 8).
* quartz tuning for Q tuning
.options nopage
.width in=72
.width out=80
* current and voltage sources
vin input 0 0V ac 1 sin 0 1m 2.247kHz
x1 input 1 2 adder
x2 2 3 quartz
x2b 3 9 iv
x3 9 4 dphi90min
x4 4 1 amplini
ro 9 0 1000000
* circuit elements:
* Q=2*pi*fs*L1/R1, fs=1/(2*pi*sqrt(L1*C1))
* ie L1=1/(4*pi^2*fs^2*C1)
.subckt quartz 1 2
c0 2 1 1.7p
r1 3 1 180k
l1 4 3 6740
c1 4 2 3.5f
.ends quartz
* Op amp: non-inverting; inverting; output
.subckt oa3 2 3 1
Rin 2 3 2e6
E1 4 0 2 3 2e5
RQ 4 5 1000
CQ 5 0 2.12e-5
E2 6 0 5 0 1
Rout 6 1 75
.ends oa3
* I->V converter (V=-RI)
.subckt iv 1 2
R 1 2 100k
xao1 0 1 2 oa3
.ends iv
* adder-inverter
.subckt adder 1 2 3
R1 1 4 10k
R2 2 4 10k
R3 4 3 10k
xao1 0 4 3 oa3
.ends adder
* non inverting amplifier: G=1+R2/R1
.subckt amplini 1 2
xao1 1 3 2 oa3
R2 3 2 1.6k
R1 3 0 1k
.ends amplini
* dphi filter: out=in*(1-j2pi*f*RC)/(1+j2pi*f*RC),
* phi=-2atan(2pifRC) Rf=R1 -- changer C
.subckt dphi90plus 1 2
R1 1 3 10k
R 0 4 1.0k
Rf 3 2 10k
C 1 4 10n
xao1 4 3 2 oa3
.ends dphi90plus
* dphi filter: out=in*(1-j2pi*f*RC)/(1+j2pi*f*RC),
* phi=-2atan(2pifRC) Rf=R1 -- changer C
.subckt dphi90min 1 2
R1 1 3 10k
R 1 4 20.0k
Rf 3 2 10k
C 0 4 0.100n
xao1 4 3 2 oa3
.ends dphi90min
.ac lin 5000 32.7k 32.9k
.print ac v(9)
.op
.end
Tableau 3 : Programme de simulation SPICE pour générer les résultats de la figure 8, dont les variables sont le signal du déphasage (+90 ou -90o par dphi90min ou dphi90plus) du signal injecté dans la seconde branche de l’additionneur, et le gain de la boucle de rétroaction (amplificateur non inverseur amplini).
Un tel circuit est exploité en pratique lorsque l’encombrement spectral d’un résonateur utilisé comme capteur (gyroscope, accéléromètre) doit être réduit pour permettre une identification fine de la fréquence de résonance (cas de l’augmentation du facteur de qualité), ou lorsque le temps de réponse du résonateur – inversement proportionnel au facteur de qualité – à une sollicitation extérieure doit être amélioré (cas des résonateurs exploités en microscopie à sonde locale : réduction du facteur de qualité). Sa plage fréquentielle de fonctionnement est limitée par la bande passante des amplificateurs opérationnels : en pratique, nous utilisons ce circuit dans la bande 1-100 kHz, qui inclut notamment les diapasons à quartz horlogers.
Figure 8 : Résultat de la modélisation par le programme proposé en figure 3, et schéma bloc associé. On constate bien que pour un déphasage de -45o, le facteur de qualité est réduit, et +45o augmente le facteur de qualité. Cet effet est d’autant plus marqué que le gain sur la rétroaction est important. Le cas asymptotique de pertes compensées par le gain, dans le cas d’un déphasage de +45o, qui induit une oscillation à la fréquence propre du résonateur indépendamment de tout signal injecté, n’est pas illustré ici.
Le cas des oscillateurs est plus complexe que celui des filtres, car par conception, le signal en sortie de l’amplificateur est réinjecté en entrée, et l’oscillation est entretenue si les pertes dans l’élément filtrant la fréquence de fonctionnement (résonateur) sont compensées par le gain de l’amplificateur (une des conditions dites de Barkhausen). En l’absence de point de compression, i.e. une amplitude du signal en entrée à partir de laquelle le gain de l’amplificateur chute, la rétroaction positive fait diverger la tension dans la boucle vers l’infini. Ce cas n’est pas réaliste, et un modèle plus précis du comportement de l’amplificateur est nécessaire, limitant son gain à partir d’une certaine puissance de sortie. La façon la plus grossière d’atteindre ce résultat est de définir une tension de saturation à partir de laquelle quelque soit la tension d’entrée, la sortie reste constante (en pratique égale à la tension d’alimentation).
Une source de modèles de composants – et notamment d’amplificateurs opérationnels réalistes – est le site web de National Semiconductor à www.national.com/analog/amplifiers/spice_models. Les fichiers de modèles .mod se chargent au moyen de .include fichier.mod. De la même façon, Maxim/Dallas donne accès aux modèles de ses composants à www.maxim-ic.com/tools/spice et Fairchild fournit les modèles de quelques composants (nécessite de s’enregistrer gratuitement). Prenons l’exemple du fameux dual-amplificateur opérationnel LM358 de Maxim : nous récupérons son modèle lmx358.fam dans les Operational Amplifier Macromodel à www.maxim-ic.com. Nous l’assemblons, pour en valider le comportement, autour d’un amplificateur non inverseur tel que décrit en figure 9.
* demo du modele Maxim LM358
.include lmx358.fam
* OPAMP : VCC VEE IN+ IN- OUT
vcc 99 0 dc 5
vss 98 0 dc -5
ve 97 0 dc 1
x1 99 98 97 5 1 OPAMP
r1 5 1 10k
r2 5 0 10k
Ra 1 2 10
Rc 2 0 500
C 2 0 500n
.control
dc ve -8 8 0.1
plot v(2)
.endc
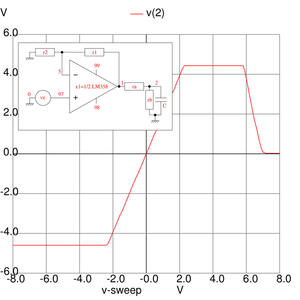
Figure 9 : Exploitation du modèle SPICE de l’amplificateur opérationnel double LM358 proposé par Maxim/Dallas. Ce circuit est monté en amplificateur-inverseur de gain -2, avec une alimentation de ±5 V. La tension d’entrée ve balaie la gamme ±8 V : nous constatons dans un premier temps la saturation négative lorsque la tension de sortie est en-dessous de la tension d’alimentation (tension d’entrée entre -8 et -2,5 V). La région linéaire pour une tension d’entrée entre -2,5 et +2,5 correspond au fonctionnement correct de la boucle de rétroaction négative. La saturation positive est atteinte au-dessus de 2,5 V de tension d’entrée. Le régime au-delà d’une tension d’entrée de 7 V, générant une tension de sortie nulle, se traduirait probablement par une destruction du composant. Notez que nous avons exploité ici un sous-ensemble du modèle proposé par Maxim, en ne prenant qu’un amplificateur opérationnel OPAMP au lieu du composant complet LMX358.
3.4 Le circuit de Chua
Il est habituel de considérer le comportement des circuits électroniques soit comme trivialement linéaire, et ne proposant que peu d’intérêt autre que d’identifier des points de fonctionnement correspondant aux attentes du concepteur, soit en mode saturé tel que nous le retrouvons dans les circuits numériques.
Un cas pathologique et élégant, accessible au moyen de SPICE, est le circuit dit de Chua [8], du nom de son concepteur à l’Université de Berkeley, représentatif du comportement d’une classe de circuits dont l’intérêt pratique – au-delà de l’aspect esthétique et d’illustration de concepts physiques associés aux éléments non linéaires – tient en la communication sécurisée [9].
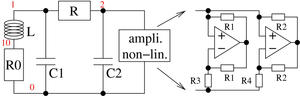
Figure 10 : Schéma de principe du circuit de Chua : un choix approprié des couples (R1,R3) et (R2,R4) permet de définir les pentes et tensions seuils de changements de gain de l’amplificateur non linéaire par saturation d’un des deux étages d’amplification, tel que décrit dans [8]. Le reste du circuit est composé d’un filtre RLC classique, avec R0 représentatif de la résistance finie de la bobine (en pratique, R0 est faible, ici égale à 10 Ω).
Le circuit de Chua est un circuit chaotique4 excessivement simple à réaliser et dont le comportement est impossible à prédire. Concrètement, SPICE va nous aider à identifier des ensembles de valeurs de composants amenant au comportement chaotique du circuit, et éventuellement fournir des séries de points issues de modélisations du comportement du circuit (Fig. 10).
L’originalité du circuit de Chua est de comporter un amplificateur explicitement non linéaire dont le gain change en fonction de la tension à son entrée. La stratégie exploitée dans cet exemple consiste à utiliser deux amplificateurs en parallèle, dont un passe en saturation et donc ne participe plus au gain global à partir d’une certaine tension d’entrée. Une alternative est l’exploitation de diodes pour injecter la non-linéarité : le gain de l’amplificateur change selon que la tension d’entrée soit au-dessus ou en-dessous de la tension de jonction de la diode. Ce circuit illustre donc le comportement grossièrement exagéré d’effets qui pourraient se manifester subtilement lorsqu’un amplificateur réel pas tout à fait linéaire est utilisé.
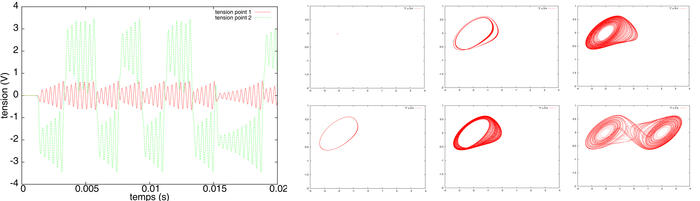
Figure 11 : Gauche : évolution temporelle des tensions V(1) et V(2) (voir figure 10 pour la nomenclature des nœuds), illustrant l’alternance entre deux bassins d’attraction de V(2) alors que V(1) apparaît comme un signal pseudo-périodique (ici, L=18 mH). Droite : évolution de l’attracteur dans l’espace des phases (V(2), V(1)). De gauche à droite et de haut en bas : solution stable où V(1) et V(2) restent constantes (position (-2,0)) avec le temps (L=14,3 mH), solution périodique (L=15,3 mH), bifurcation pour obtenir une solution bi-périodique (16,8 mH), développement d’un attracteur (17,2 et 17,6 mH) avant d’atteindre une nouvelle bifurcation produisant un attracteur à deux bassins (18 mH).
La modélisation de ce circuit par un simple modèle d’amplificateur opérationnel de source de tension commandée en tension avec un gain variable avec la fréquence n’est pas possible, ne serait-ce que parce qu’un modèle aussi simple n’inclut pas la notion de saturation de la sortie lorsque la valeur absolue de l’entrée dépasse un certain seuil. Nous constatons dans cet exemple qu’un modèle complexe, publié par le fabricant de l’amplificateur (Analog Devices AD712), est nécessaire pour illustrer le comportement chaotique du circuit. Le lecteur pourra constater que les modèles plus simples d’amplificateurs ne permettent pas d’atteindre ce résultat.
Afin de compléter l’analyse proposée sur la figure 11, nous avons fait le choix de passer par un fichier décrivant la netlist dans lequel la valeur de l’inductance porte un nom quelconque, et de passer par sed pour remplacer ce nom par des valeurs issues d’une boucle itérée en shell. L’instruction print de SPICE, exécutée en batch mode (ngspice -b fichier.cir), renvoie au shell le résultat de la simulation, qui est alors traité et exploité par gnuplot pour tracer l’évolution des tensions dans l’espace (V(1),V(2)).
4. Au-delà de l’électronique
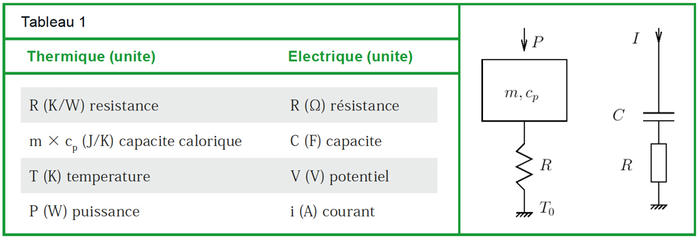
Il est classique [10, pp.786 & 806] [11, p.381] d’introduire les équations différentielles régissant les systèmes physiques dynamiques pour illustrer la généralité de la représentation mathématique quel que soit le système considéré – électrique, thermique ou mécanique. Deux analogies sont généralement fournies pour présenter la portée des résultats : les analogies entre oscillateurs électroniques et mécaniques, et la diffusion thermique. Dans le premier cas, une équation différentielle du second ordre régissant un oscillateur s’applique aussi bien au pendule (mécanique) qu’à l’oscillateur électronique. L’identification des termes de pulsation et de pertes permet de retrouver les analogies entre position/charge électrique, vitesse/courant, et entre propriétés de composants mécaniques et électroniques. Les valeurs des composants équivalents dépendent de la géométrie des éléments mécaniques ou thermiques (dimensions, masse, ...) et suivent évidemment les mêmes lois de compositions que les composants électriques.
4.1 Thermique
La loi d’évolution temporelle de température T(t) dans un problème unidimensionnel d’un bloc de matière de masse m composé d’un matériau de capacité calorifique cp et de résistance thermique R dont on chauffe une face avec la puissance P est :
avec T0, la température ambiante du bloc de matière (en l’absence de source externe d’énergie). Cette équation différentielle du premier ordre suit la même structure que le formalisme de résolution du premier exemple que nous avons résolu au moyen de SPICE :
L’analogie thermique-électrique consiste donc en l’identification des termes, à savoir un condensateur C se comportant comme la capacité calorifique de la masse chauffée (son inertie aux sollicitations externes), le potentiel V par rapport à la masse est analogue à la différence de température T−T0, R la résistance à la propagation du signal et P le flux de l’énergie (en J/s, soit des W), l’apport de puissance, équivalent au courant injecté dans un circuit électronique.
La puissance de cette analogie tient non seulement en l’exploitation de SPICE pour résoudre un problème de thermique, mais surtout pour modéliser le comportement couplé d’un asservissement thermique par un circuit électronique. Au moyen de composants électroniques équivalents représentatifs du comportement thermique d’un thermostat, les constantes de temps ou dépassement de consigne d’asservissements analogiques au moyen de boucles de rétroactions négatives peuvent être modélisées sous SPICE [12, 13].
4.2 Mécanique
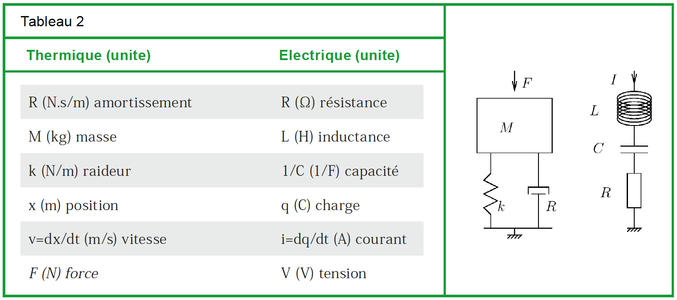
Le même raisonnement s’applique à la mécanique5, par exemple, avec l’analogie entre l’équation du second ordre régissant le comportement d’un circuit RLC série et un oscillateur mécanique amorti (ressort-masse-piston). Là encore, une masse M liée par un ressort de raideur k avec dissipation d’énergie dans un amortisseur R suit une loi de sa position x(t) en fonction du temps t et de la force F qui lui est appliquée :
dont on déduit les analogies
La conséquence de cette analogie est que d’une part, SPICE est un outil approprié pour résoudre le comportement d’un système dynamique mécanique (Fig. 12), mais surtout, qu’il permet de combiner des comportements mécaniques, thermiques et électroniques de systèmes.
Figure 12 : Simulation d’un montage masse-ressort-amortisseur, pour diverses valeurs d’amortissement. L’analogie mécanique-électrique démontre ici que la période est bien égale à 2π lorsque nous choisissons une raideur et une masse de 1, et que l’amortissement n’influe par sur la période mais uniquement sur la vitesse de décroissance du signal. Dans cet exemple, la masse est excitée par une force (tension) pendant les 5 premières secondes, avant d’être relâchée. En rouge, le signal d’excitation (la force appliquée sur la masse, qui atteint 1 V et sort donc de l’axe des ordonnées), puis respectivement en bleu, orange, vert, et rose, des valeurs croissantes de l’amortissement. Notez que la courbe bleue, qui présente le plus faible amortissement, présente aussi la plus faible amplitude : en effet, un système fortement résonnant (faibles pertes) nécessite de nombreuses périodes d’excitation pour atteindre un régime stationnaire, et les deux impulsions (front montant puis descendant du créneau d’excitation) sont insuffisantes pour fournir suffisamment d’énergie dans ce cas. D’un point de vue syntaxique, toute ligne commençant par « + » est considérée comme la suite de la ligne précédente.
Un cas particulier qui rend l’interaction mécanique-électrique explicite est l’exploitation de composants piézoélectriques, dont les constantes de couplage électromécaniques traduisent explicitement la dépendance du courant avec la vitesse de déplacement (effet piézoélectrique direct), et du déplacement mécanique avec le potentiel appliqué (effet piézoélectrique inverse), pour donner le modèle classique de Butterworth-Van Dyke.
Conclusion
SPICE est un outil libre, portable sur toute plate-forme compatible avec la norme POSIX, de modélisation permettant de caractériser le comportement temporel ou spectral de circuits électroniques. Après un bref rappel des concepts généraux de la simulation – comportant un code source décrivant la topologie du circuit et quelques commandes simples pour paramétrer la simulation – nous avons proposé un certain nombre d’exemples pratiques incluant la simulation du comportement de filtres passifs, actifs et oscillateurs. Nous nous sommes finalement efforcés d’étendre la plage d’utilisation de cet outil à des problèmes autres qu’électroniques – et notamment mécaniques et thermiques, en exploitant les analogies classiques avec l’électronique – en vue de simulations multiphysiques. L’ensemble des références bibliographiques sont disponibles en versions numériques auprès de l’auteur, tandis que les codes sources des exemples proposés dans ce document sont disponibles à http://jmfriedt.free.fr.
Il peut être utile de mentionner que divers projets – notamment gspiceui et xcircuit6 – s’efforcent de fournir une interface graphique pour la réalisation des netlists. L’outil propriétaire mais gratuit Eagle de CADSoft propose des scripts (ULP) de conversion de schémas en netlist SPICE. Un point commun de tous ces outils est leur inefficacité à gérer des circuits complexes, et surtout, à maîtriser les paramètres de simulation et les modèles associés aux composants : le lecteur désireux de quitter la ligne de commandes pour ces interfaces graphiques le fera à ses propres risques quant à la validité de ses simulations.
Remerciements
L’inspiration concernant l’analyse de problèmes multiphysiques sous SPICE est issue de discussions avec R. Boudot et S. Galliou (département temps-fréquence, FEMTO-ST, Besançon). R. Brendel a proposé une présentation de SPICE dans le cadre de son cours à l’École Nationale Supérieure de Mécanique et Microtechniques (ENSMM), qui a fourni la trame de ce document.
Références
[1] J.-M Friedt, « Affichage et traitement de données au moyen de logiciels libres », GNU/Linux Magazine France 111 (Décembre 2008)
[2] P. Nenzi & H. Vogt, Ngspice Users Manual, ver. 22, Sept. 2010, disponible à http://ngspice.sourceforge.net/docs/ngspice-manual.pdf
[3] The ARRL Handbook for Radio Amateurs, Ed. ARRL (1998)
[4] http://ubuntuforums.org/showthread.php?p=4953252#post4953252
[5] F.H. Lei, J.- F. Angiboust, W. Qiao, G.D. Sockalingum, S. Dukic, L. Chrit, M. Troyon & M. Manfait, Shear force near-field optical microscope based on Q-controlled bimorph sensor for biological imaging in liquid, J. of Microscopy, 216 (3), 2004, pp. 229-233, ou pour une version commerciale d’un produit fournissant les mêmes fonctionnalités : http://www.nanoanalytics.com/en/hardwareproducts/q-control
[6] S.G. Parler Jr., Improved Spice Models of Aluminum Electrolytic Capacitors for Inverter Applications, IEEE Trans. on Industry Applications 34 (4) (2003) 929-935
[7] http://www.vishay.com/docs/28327/030031.pdf pour les condensateurs électrolytiques commercialisés par Vishay, http://www.murata.com/emc/knowhow/pdfs/te04ea-1/12to16e.pdf pour une note d’application de Murata
[8] M.P. Kennedy, Three Steps to Chaos – Part II: A Chua’s Circuit Primer, IEEE Trans. on Circuits and Systems 40 (10), Octobre 1993, disponible à http://www.eecs.berkeley.edu/~chua/papers/Kennedy93b.pdf
[9] J. Neff & T.L. Caroll, The Amateur Scientist: Circuits That Get Chaos in Sync, Scientific American pp.101-103, Aout 1993
[10] C. More & D. Augier, Physique 2nde année, MP, MP*, PT, PT*, Editions TEC & Doc, Lavoisier, 2004
[11] S. Olivier, Physique 2nde année PC, PC*, Editions TEC & Doc, Lavoisier, 2004
[12] S. Galliou, Thermal behaviour simulation of quartz resonators on an oven environment, IEEE Trans. Ultrason. Ferroelectrics and Frequency Control 42 (5), (1995) 832-839
[13] R. Boudot, C. Rocher, N. Bazin, S. Galliou, & V. Giordano, High-precision temperature stabilization for sapphire resonators in microwave oscillators, Rev. Sci. Instrum. 76, 095110 (2005)
Notes
1 au même titre que les manuels d’enseignement de l’armée tels que ceux disponibles à http://www.tech-systems-labs.com/navy.htm pour une formation en électronique et électricité, ou http://metalworking.com/tutorial/ARMY-TC-9-524/9-524-index.html pour l’usinage de pièces mécaniques.
2 attention, dans une version antérieure de ngspice – version 17 notamment – la redirection depuis l’interpréteur ngspice se traduisait par une erreur de segment, erreur qui a été corrigée au moins dans la version 20 de ngspice disponible au moment de la rédaction de ce document.
3 le facteur de qualité est par définition une qualité intrinsèque au résonateur, égal au ratio de l’énergie emmagasinée par l’énergie dissipée à chaque période. Nous parlons ici de facteur de qualité équivalent car il s’agit de pertes en partie compensées ou augmentées par le circuit de réinjection d’énergie – en phase ou en opposition de phase.
4 excessivement sensible à ses conditions initiales, i.e. dont la trajectoire ne peut pas être prédite à long terme du fait de la croissance exponentielle de toute erreur sur les conditions initiales, bien que le comportement général soit borné autour d’un ensemble de trajectoires nommé « attracteur ».
5 http://www.swarthmore.edu/NatSci/echeeve1/Ref/LPSA/Analogs/ElectricalMechanicalAnalogs.html
6 http://opencircuitdesign.com/xcircuit



 Ajouter à une liste de lecture
Ajouter à une liste de lecture