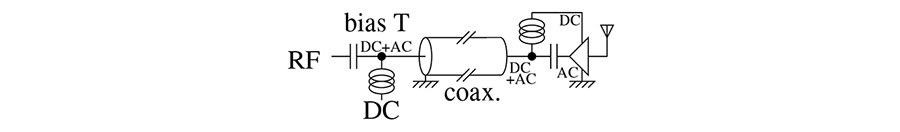Le temps et son transfert par satellite géostationnaire : réception avec une parabole de télévision et une radio logicielle

Le temps atomique international est défini par la comparaison de nombreuses horloges distribuées sur divers continents. Avec sa vitesse d’escargot de 300 m par microseconde, la lumière (ou toute autre onde électromagnétique) a bien du mal à servir de vecteur d’échange d’informations temporelles avec une exactitude subnanoseconde telles que l’exigent nombre d’applications technologiques actuelles sur des distances aussi grandes que quelques kilomètres à milliers de kilomètres. Tous les jours, les instituts nationaux de métrologie du temps et des fréquences échangent des informations permettant de compenser le temps de vol de l’onde électromagnétique du sol à un satellite géostationnaire et de nouveau vers le sol et d’observer la dérive de leurs horloges respectives. Pourrions-nous profiter de ces liaisons pour synchroniser nos propres horloges, et ce, à investissement financier raisonnable ? Nous allons démontrer comment détourner une parabole de réception de télévision par satellite, munie d’une radio logicielle, pour recevoir et décoder ce signal.

1. Introduction

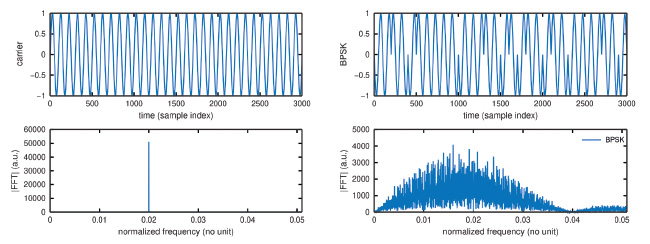
Temps et fréquence sont deux grandeurs étroitement liées : la fréquence (exprimée en hertz) est l’inverse du temps (exprimée en seconde). Cette définition formelle, digne d’un dictionnaire de la langue française ainsi que le propose le Robert avec pour le temps « (Grandeur mesurable) La division du temps en années, mois, semaines, jours, heures, minutes, secondes. » et pour la fréquence « (Sciences) Nombre de périodes ou de cycles complets de variations qui se succèdent en une seconde. », n’apporte aucune précision sur la complexité technologique d’échanger le temps face à la trivialité du concept de fréquence. Un point clé qui différencie ces deux grandeurs est l’encombrement spectral nécessaire à échanger une information spectrale (fréquence) ou temporelle (temps) : alors que la fréquence est caractérisée par une sinusoïde continue aussi reproductible que possible d’une période à l’autre – donc de transformée de Fourier représentée par un Dirac dans le domaine spectral – le temps implique de distinguer l’évolution du signal, et nous verrons que cette opération est intrinsèquement une opération large bande gourmande en ressources spectrales. Technologiquement, les deux opérations sont orthogonales et les préceptes pour transmettre ces deux informations sont très différents (Fig. 1).

Formellement, une fréquence f est la dérive linéaire de la phase Φ dans l’expression d’un signal périodique v en fonction du temps t de la forme v(t) = sin(Φ) où Φ = 2π f t+ϕ(t), ϕ(t) fluctuation aléatoire de la phase. Le signal v est en bande étroite, présentant un spectre dont la composante spectrale se situe en f, mais étalée à cause de ϕ autour de la porteuse. Les métrologues de la fréquence cherchent d’une part à connaître la position de f le plus exactement possible et sans fluctuations d’une mesure à l’autre, tandis que les utilisateurs de signaux radiofréquences (p. ex. communications numériques ou mesures RADAR) cherchent à conserver f aussi stable que possible pendant que l’onde se propage entre les deux interlocuteurs ou l’émetteur, la cible et le récepteur afin que toute variation de fréquence du signal reçu puisse être attribuée de façon univoque à l’information portée – modulation de phase ou vitesse de la cible induisant un décalage Doppler – et non aux fluctuations de l’oscillateur local. La fréquence est donc une grandeur peu intéressante puisqu’elle n’évolue pas et nous cherchons simplement à reproduire aussi fidèlement que possible le processus d’une période à l’autre, par exemple au moyen de résonateurs de facteur de qualité aussi important que possible pour emmagasiner un maximum d’énergie et le rendre insensible aux perturbations externes (Fig. 1, gauche).

Le temps est beaucoup plus intéressant, car est intrinsèquement une grandeur large bande, de grande occupation spectrale, ou en d’autres termes la résolution temporelle dt est l’inverse de la bande passante B : en RADAR, la résolution spatiale est c/(2B) puisque la résolution de mesure du double temps de vol (aller-retour, d’où le facteur 1/2) est inverse de la bande passante, le temps étant converti en distance par la vitesse de la lumière c=300 m/µs. Toutes les périodes d’un signal périodique se ressemblent et ne portent aucune information temporelle : il va falloir trouver une astuce pour coder le temps sur la porteuse afin de différencier les périodes les unes des autres. Cette problématique est au cœur du GPS, mais de toute liaison radiofréquence partageant le temps en général (Fig. 1, droite) tel que nous le décrirons en section 2.

Les horloges atomiques actuelles utilisées pour définir le temps atomique international (TAI) présentent des stabilités de quelques picosecondes par seconde (10⁻¹² de stabilité relative [1]) qu’une approche naïve pourrait nécessiter plusieurs GHz de bande passante – inverse de la résolution temporelle recherchée – pour comparer. Pire, le temps de vol entre le sol, un satellite géostationnaire – choisi pour pointer une parabole fixe comme pour recevoir la télévision, et surtout s’affranchir du décalage Doppler du mouvement du satellite – à 36000 km d’altitude, et le sol, prend 240 ms au minimum. Comment donc occuper une bande passante « raisonnable » (moins qu’une chaîne de télévision qui occupe 30 à 50 MHz d’après ETSI EN 300 421) pour échanger une information horaire entre laboratoires de métrologie respectant ces contraintes ? Si nous comprenons ce mécanisme, peut-être pourrons-nous en tirer profit, en en comprenant les limitations et les enjeux. Mais plus intéressant, en comprenant la solution à ce problème, nous pourrons exploiter les signaux transmis tous les jours et diffusés sur le continent européen à nos propres fins, par exemple de comparaison et de calage de fréquence d’oscillateurs, voire éventuellement de correction du temps de l’horloge locale de notre récepteur radiofréquence.

Alors que ce travail est étroitement lié aux activités professionnelles de l’auteur, il en diverge par son objectif de diffusion au public incapable d’émettre, mais devant se contenter d’écouter, mais surtout nous avons pris soin de nous assurer que toutes les informations divulguées sont disponibles dans la littérature publiquement accessible telle qu’en atteste la référence bibliographique associée à chaque affirmation. Évidemment en connaissant la réponse, il est beaucoup plus facile de demander à un moteur de recherche de trouver l’information sur Internet !

2. Principe du transfert de temps

Pour transformer un signal périodique – une onde électromagnétique, par exemple – en vecteur de transfert de temps, il faut étaler son spectre. Un signal périodique est caractérisé par trois (en réalité deux) grandeurs : son amplitude, sa fréquence et sa phase (sa fréquence n’étant que la composante de dérive linéaire avec le temps de la phase). Pour distinguer les périodes successives et imprimer une signature temporelle, nous pouvons jouer sur chaque grandeur, amplitude ou phase. Les opticiens sont obligés de se contenter de l’amplitude, mais en radiofréquence nous pouvons manipuler la phase, bien plus efficace. Dans le cas du GPS, la phase saute entre 0 et π pour imprimer une information binaire (et non « digitale » comme le disent les journalistes, les doigts restent sur le clavier) qui permet de coder le temps. Le rythme auquel ce code se répète – longueur du code en bits dans une approche numérique – détermine l’incertitude sur le temps de vol (Pulse Repetition Interval en RADAR) : un code court induit une forte incertitude sur le temps de vol, un code long une incertitude moindre, mais nécessite une puissance de calcul plus importante pour être identifié. La vitesse à laquelle le code est émis détermine la résolution avec laquelle le temps de vol sera mesuré. Le signal émis peut être une sinusoïde, mais peut très bien n’être qu’un bruit électromagnétique tant que l’émetteur a pris soin d’enregistrer le motif émis en vue d’identifier le retour de ce motif et de mesurer son temps de vol, tel que nous l’avions discuté dans l’implémentation du RADAR à bruit [2].

En effet, comment trouver le temps de vol entre émission et réception ? Le problème est de trouver un motif m(t) – aléatoire, mais connu [3] – émis à un instant, dans le signal s(t) bruité reçu : le filtre adapté optimal est la corrélation de s par m exprimé comme :

avec * le complexe conjugué si nous manipulons des grandeurs complexes tel qu’il est habituel de le faire en radio logicielle en sortie de détecteur IQ, ou en d’autres termes effectuer le produit du motif par le signal décalé dans le temps de τ et rechercher pour chaque τ la puissance moyenne résultante par intégration. Si s et m sont de valeur moyenne nulle, alors leur intégrale vaut 0, sauf si pour un certain retard τ, m se retrouve dans s : dans ce cas, les alternances positives se superposent aux alternances positives pour donner un produit positif, mais aussi les alternances négatives se superposent aux alternances négatives pour donner un produit positif à nouveau, et l’intégrale accumule l’énergie dans un pic étroit de corrélation, d’autant plus étroit que le motif émis est de bande passante importante. Ce principe d’étalement de spectre par modulation en phase de la porteuse est utilisé par tous les instruments de transfert de temps, et en particulier les constellations de navigation par satellite, et le transfert de temps et fréquence par satellite géostationnaire n’échappe pas à la règle.

Voici le chemin de l’étude tout tracé :

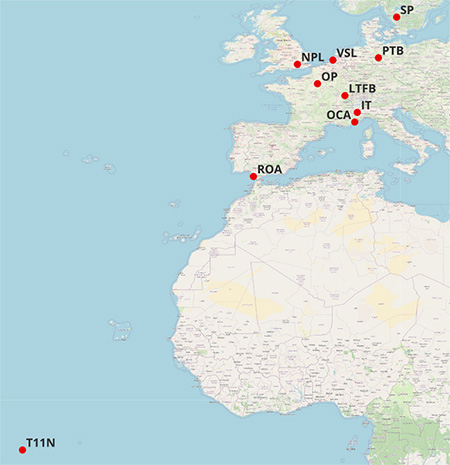
1. Apprendre à recevoir le signal micro-onde transmis depuis le sol par les instituts de métrologie et rediffusés sur toute l’Europe (Fig. 2) par le satellite géostationnaire servant à la communication.
2. Identifier le codage et la nature des motifs m(t) imprimés sur la porteuse pour transmettre le temps.
3. Décoder ces signaux et les comparer à l’horloge locale – celle que nous voulons étalonner – qui cadence la radio logicielle [4, 5, 6] servant à la réception des signaux.
4. Identifier les limitations de l’approche unidirectionnelle, en particulier parce qu’un satellite géostationnaire que nous croyons fixe dans le ciel danse en réalité autour de son point d’équilibre au ballet des astres qui entourent la Terre, et en particulier le Soleil et la Lune.

Nous ne montrerons pas ici comment synchroniser une horloge, mais comment une parabole de réception de télévision par satellite permet d’observer le mouvement du satellite à une distance de plus de 36000 km du récepteur, et comment ces résultats sont en excellente adéquation avec les mesures diffusées par le Bureau International des Poids et Mesures (BIPM) qui centralise les informations collectées chaque jour.

3. Transfert de temps en pratique

Le premier site qui nous fournira nombre d’informations est le dépôt de fichiers du BIPM à https://webtai.bipm.org/ftp/pub/tai/data/2022/time_transfer/twstft/ qui regroupe les informations échangées par les laboratoires primaires de métrologie de temps et fréquence. Les fichiers contenus dans ces répertoires, classés par origine, incluent en entête la fréquence de communication et les coordonnées de la parabole communiquant avec le satellite géostationnaire.

Par exemple, https://webtai.bipm.org/ftp/pub/tai/data/2022/time_transfer/twstft/roa/twroa59.729 commençant par :

nous informe que l’Observatoire de la Marine espagnole (https://en.wikipedia.org/wiki/ROA_Time) se trouve à Cádiz à 36° de latitude nord et 6° de longitude ouest et communique en liaison montante autour de 14 GHz pour recevoir à 10,95395 GHz [8] avec une bande passante de l’ordre de 4,1 MHz. Nous sommes donc informés de quel satellite viser avec la parabole (Telstar 11N [9]) et à quelle fréquence écouter, sur une bande passante largement accessible avec une radio logicielle.

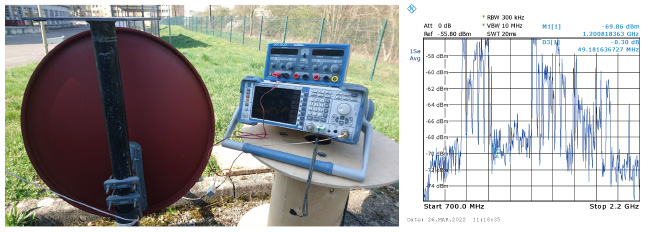
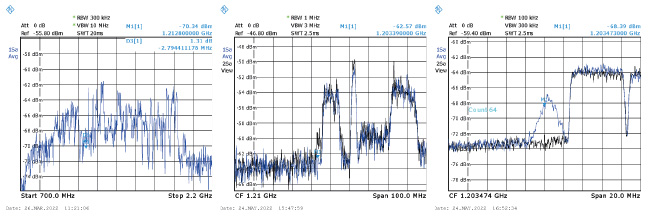
Le pointage de la parabole vers le satellite se fait selon les consignes de https://www.dishpointer.com/ depuis Besançon, Telstar 11N situé à 37,5° ouest au-dessus de l’Atlantique sera pointé à une élévation de 21,4° et azimut de 229,7° par rapport au nord magnétique. Avec une parabole de 60 cm de diamètre, la décimale n’a que peu d’importance, l’ouverture de l’antenne étant suffisamment large pour trouver facilement le satellite. On prendra cependant soin de noter que l’orbite géostationnaire est tellement encombrée qu’il est facile de se tromper de satellite en visant le voisin (Fig. 3) ! Nous avons en effet passé plusieurs semaines à essayer de détecter un signal du satellite voisin, le pointage manuel étant grossier malgré la disponibilité d’un analyseur de spectres large bande permettant de facilement visualiser les émissions les plus puissantes de chaque satellite le long de l’équateur. La Fig. 3 illustre cet encombrement avec un satellite tous les 0,3° de longitude environ, imposant un pointage précis de la parabole pour trouver le signal recherché (Fig. 4).

4. Liaisons satellitaires

Les paraboles pour la réception de télévision par satellite ont à une époque fleuri pour maintenant tomber en désuétude avec la diffusion de la télévision numérique terrestre (Fig. 5) ou la fibre optique. Nombre de paraboles abandonnées sont donc disponibles pour de l’expérimentation, pour peu qu’on prenne le temps de comprendre le fonctionnement du bloc de réception qui se trouve au foyer, le LNB (Low Noise Block). Malgré son prix ridiculement modique, cet ensemble de circuits électroniques s’acquitte de deux étages d’amplification (micro-ondes et radiofréquence), d’un oscillateur local et d’une transposition de fréquence de la bande micro-ondes (10-15 GHz) vers la bande radiofréquence (1-3 GHz). L’oscillateur local est de fréquence nominale 9,75 GHz (Fig. 6), et s’alimente au travers d’un T de polarisation (une inductance sur l’alimentation et un condensateur bloquant la composante DC vers le récepteur radiofréquence) entre 13 et 18 V, la polarisation de l’élément récepteur tournant de 90° entre ces deux tensions. Finalement, injecter dans le T de polarisation un signal audiofréquence à 22 kHz permet de commander l’oscillateur local pour le faire passer à 10,6 GHz, fonctionnalité dont nous ne nous servirons pas ici, mais qui peut étendre les fonctionnalités du LNB si besoin, par exemple pour écouter la télémétrie des satellites de la constellation Starlink [10]. Nous constatons donc que le signal de Telstar 11N annoncé par le BIPM comme étant émis en liaison descendante à 10953,95 MHz va se retrouver après transposition de fréquence par le LNB à 1204 MHz : c’est cette fréquence de porteuse qu’il nous faudra enregistrer par radio logicielle en sortie de LNB.

Le récepteur de radio logicielle sera programmé sur la fréquence nominale de 1,204 GHz pour recevoir les signaux qui nous intéressent, mais dans la pratique l’oscillateur local du LNB fluctue de quelques centaines de kHz à quelques MHz et la bande passante de la majorité des radios logicielles est insuffisante pour compenser numériquement cet écart à la valeur nominale : il faudra donc peut-être rechercher quelques centaines de kHz de part et d’autre de la fréquence nominale de porteuse transposée par le LNB.

Avec une parabole de 60 cm, le signal de Telstar 11N est puissant, même si un « vrai » analyseur de spectre avec 2 GHz de bande facilite la recherche par rapport à la simple radio logicielle. On notera qu’un voisin juste au-dessus du signal qui nous intéresse émet continûment et beaucoup plus fort (Fig. 7), facilitant la recherche. Par ailleurs, nous avons appris que la bande passante du signal est 4,1 MHz et nous verrons plus bas que nous nous simplifierons la vie en échantillonnant à 5 MS/s : alors que les récepteurs RTL-SDR ne proposent pas une bande passante suffisante (2,4 MS/s seulement), nous utiliserons au cours des mesures présentées ici un récepteur Ettus Research B210. Nous avons cependant vérifié qu’un clone de SDRPlay, RSP1, convient pour le décodage des signaux acquis sur une bande passante de 8 MHz après avoir câblé l’entrée en bande L entre 1 et 2 GHz (voir [11] dans Hackable 43), et nombre d’autres récepteurs de radio logicielle un peu plus onéreux conviendront (HackRF, PlutoSDR...).

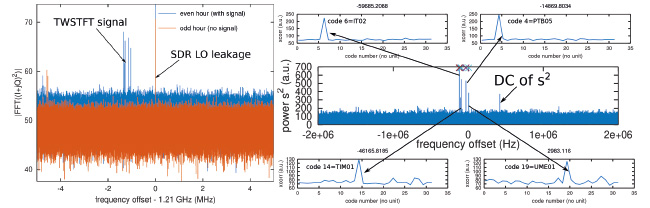
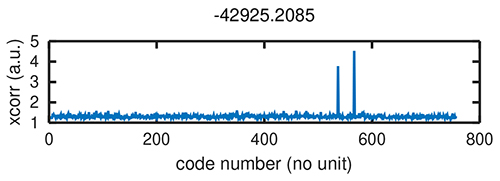
Ayant obtenu un spectre d’un signal occupant une bande passante relativement large – 4,1 MHz – il nous faut nous convaincre qu’il s’agit du bon signal : nous pouvons commencer par vérifier qu’il s’agit d’un signal modulé en modulation de phase binaire BPSK en observant le spectre du signal mis au carré. En effet, un signal modulé en phase ϕ(t), mais avec un écart δω entre la porteuse émise et l’oscillateur local du récepteur présente une expression de la forme s(t) = exp(j(δω t+ϕ)) tel que s²(t) = exp(j(2δω t+2ϕ)) et puisqu’en BPSK ϕ(t) = {0,π} alors 2ϕ = {0,2π} = 0[2π] donc l’étalement du spectre par la modulation a été annulé et toute l’énergie du signal se trouve dans une porteuse pure à 2δω sur le spectre (Fig. 8, gauche). La vraie preuve que nous avons bien identifié les signaux et sommes capables de les décoder vient de la capacité à identifier périodiquement les pics de corrélation du motif transmis dans le signal reçu (Fig. 8, droite) : ce point est développé en section 5.

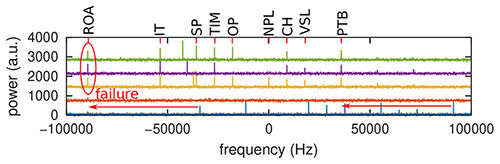
Décoder les signaux communiqués par les radio-modems au sol nécessite d’exactement compenser l’écart entre l’oscillateur local émetteur et l’oscillateur local récepteur : Fig. 9 illustre notre approche en considérant que chaque observatoire s’est vu attribuer un décalage de fréquence porteuse [13] et qu’en faisant l’hypothèse que la composante spectrale pure à la plus basse fréquence du signal mis au carré correspond aux Espagnols du ROA, nous déplaçons tous le spectre (multiplication du signal par exp(j2πδ ft) avec δ f la moitié de l’écart en fréquence observé sur le signal mis au carré par rapport à sa valeur nominale) : nous constatons qu’en cas de succès tel que le montrent les trois premières courbes, tous les observatoires s’alignent sur leur porteuse respective, mais que parfois un bruit excessif fait échouer la procédure par l’identification erronée d’un bruit sur le spectre comme signal recherché (bas). La vraie preuve que le signal que nous analysons est le bon viendra dans la section suivante avec le décodage des codes transmis.

Finalement, nous pouvons nous interroger sur l’impact de remplacer une parabole de 2,4 m par une parabole de 60 cm en réception dans le bilan de liaison. L’émission, l’arrivée au satellite et la ré-émission ne sont pas contrôlées dans le contexte de cette présentation, mais il est intéressant de mentionner que la documentation technique de Telstar 11N à https://dokumen.tips/documents/telstar-11n-technical-manual-telesat-telstar-11n-technical-manual-esd-002.html contient toutes les informations nécessaires à retrouver le bilan de liaison décrit dans la littérature par la description des paraboles embarquées sur le satellite, et que finalement un bilan de liaison convaincant peut être établi sous hypothèse que le satellite se comporte comme un amplificateur de 100 dB en plus de transposer la fréquence d’uplink vers downlink, hypothèse vérifiée en variant la puissance émise et en constatant que la puissance reçue varie à l’identique (remerciements à É. Meyer, observatoire de Besançon, pour cette mesure).

En fin de compte, remplacer 2,4 m par 0,6 m de réflecteur parabolique à la fin de la chaîne de réception ne fait perdre « que » 12 dB sur le gain en réception d’antenne qui se compenseront facilement avec la souplesse de programmation de la radio logicielle.

5. Décodage des signaux horaires

L’identification d’un code pseudoaléatoire dans la communication de signaux CDMA a largement été abordée, par exemple lors du lancement du premier satellite européen Galileo dont le code aurait dû rester secret, mais qui a rapidement été identifié [15]. Le problème est beaucoup plus simple ici.

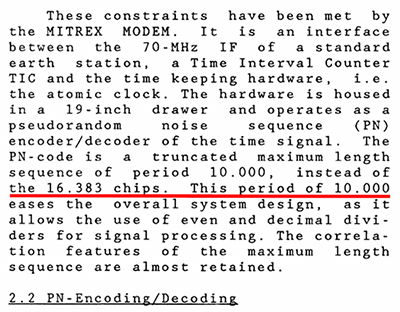
Le fichier obtenu auprès du BIPM auparavant nous informe dans le champ MODEM que les signaux de transfert de temps sont générés par l’instrument SATRE (Satellite Time and Ranging Equipment) commercialisé par la société allemande TimeTech. Comme tout bon produit commercial, aucune documentation sur le fonctionnement interne ou le protocole de communication fermé n’est disponible. Un peu d’histoire nous informe cependant que TimeTech a obtenu la technologie développée sous le nom de MITREX dans les années 1980 à Stuttgart (Fig. 10), et quelques articles allemands, hollandais et japonais décrivent superficiellement le fonctionnement interne de ce modem dont nous pouvons faire l’hypothèse que la société privée a gardé tous les fondements scientifiques pour n’ajouter qu’une couche cosmétique ainsi qu’une couche applicative de transmission lente de données numériques que nous n’aborderons pas dans ce document.

Ainsi, nous apprenons dans [16, 17, 18] que les auteurs du MITREX ont utilisé un code pseudoaléatoire sur 14 bits tronqué à 10000 éléments pour être facilement divisible par 10, et que ce code est transmis toutes les heures paires en temps universel UTC [14]. Nous aurions pu retrouver cette information en observant le spectre reçu, car nous savons que le premier nul de part et d’autre d’un spectre de signal modulé en BPSK se trouve à son débit de transfert – ici 2,5 MHz donc 2,5 Mb/s – et même sans connaître le code émis par chaque observatoire, l’autocorrélation du signal présente des pics toutes les 4 ms, longueur du code après lequel il se répète (2,5·10⁶× 4·10⁻³ = 10000), mais aussi incertitude sur le temps absolu de vol qui, rappelons-le, est de plus de 240 ms entre le sol, le satellite géostationnaire et le sol.

Bien qu’il existe des façons relativement complexes de générer de telles séquences qui ne se répètent pas tel que les Gold Codes de GPS L1, l’approche la plus intuitive [19] est le registre à décalage à rétroaction linéaire (Linear Feedback Shift Register – LFSR) dans laquelle un registre à décalage est alimenté à chaque coup d’horloge par une combinaison de OU exclusifs (XOR) de certaines valeurs de ce registre dont la localisation est nommée taps. Une recherche exhaustive de cette méthode n’est pas très gourmande en ressources de calcul actuel puisque https://users.ece.cmu.edu/~koopman/lfsr/ nous informe qu’il n’existe « que » 756 possibilités de générer des codes de longueur 2¹⁴−1 qui ne se répètent pas, et même en ne connaissant pas la valeur de départ de la troncature à 10000 de la séquence, la longueur de 16383 éléments laisse un recouvrement de 61 % pour un pic de corrélation bien défini si la bonne séquence est testée (Fig. 11). Puisque la valeur initiale de 0 est interdite (XOR(0,0)=0 donc le code reste indéfiniment à 0), on peut pressentir qu’un démarrage à 0x3FF avec tous les bits à 1 est naturel, mais reste à identifier le formalisme de calcul de la séquence entre Fibonacci et Galois qui convergent vers la même séquence, mais avec un délai. Cette analyse ne mérite pas d’être développée plus avant ici, mais est décrite en détail à https://github.com/oscimp/gr-satre pour le lecteur désireux de la reproduire.

Dans la pratique, une recherche par Google de « satre modem manual » donne comme deuxième lien (dépendant de tous les traceurs que le browser web a accumulés) un site ftp://ftp.npl.co.uk/npl/twstft/ qui s’avère laisser fuiter toutes les informations nécessaires, dont le générateur de codes pseudoaléatoires. Nous avons sauvegardé dans https://github.com/oscimp/gr-satre/blob/main/taps.txt les séquences de 10000 valeurs binaires correspondant au code pseudoaléatoire de chaque station émettrice au sol.

La démarche de décodage consiste donc à :

1. Calculer le carré du signal reçu pour établir l’écart de fréquence de porteuse entre chaque émetteur et le récepteur. Bien que les émetteurs des laboratoires de métrologie soient cadencés sur des horloges dont l’exactitude est (par définition) parfaite et que le décalage soit principalement lié au LNB, nous observons d’une part que le satellite est source de décalage en fréquence lors de la conversion du lien montant (14 GHz) vers le lien descendant (11 GHz), et par ailleurs que chaque observatoire se voit attribuer un écart de fréquence de quelques kHz pour augmenter l’orthogonalité de la corrélation [13].
2. Pour chaque écart de porteuse identifiée δ f, compenser numériquement pour centrer le signal sur 0 Hz en multipliant par exp(j2πδ f t) et corréler avec tous les codes possibles. La valeur de δ f est issue d’une transformée de Fourier rapide sur N points sur un signal échantillonné à la fréquence f_s donc de résolution spectrale f_s/N. Sachant que le code de 10000 éléments (chips) de long est transmis à f_r=2,5 Méchantillons/s tel qu’en attestent les deux premiers nuls à +/-2,5 MHz sur le spectre du signal reçu, le spectre d’une modulation BPSK étant un sinus cardinal qui s’annule à +/- f_r, la durée de chaque séquence de 10000 chips est 4 ms, donc il faut trouver δ f à mieux que 1000/4=250 Hz pour garantir l’accumulation de l’énergie lors de la corrélation, sans être perturbé par la sinusoïde résiduelle d’un écart de fréquence trop important dont la valeur moyenne serait nulle. Pour une fréquence d’échantillonnage de f_s=5 MS/s qui couvre largement la bande et reste compatible avec le débit de la B210, nous déduisons N ≫ 5·10⁶/250 = 20000. Dans la pratique, nous choisirons N de l’ordre de quelques centaines de milliers de points.
3. Les corrélations se calculent sur des paquets de 20000 séquences de valeurs IQ successives acquises au rythme de 5 Méchantillons/s (20000 = 5·10⁶× 4·10⁻³), garantissant l’unicité du pic de corrélation sur cette durée si l’émetteur correspondant à la séquence recherchée est actif.
4. Finalement, le pic de corrélation identifié avec un pas de 200 ns (inverse de la fréquence d’échantillonnage de 5 MHz) est ajusté avec une parabole de la forme at²+bt+c passant par le sommet et ses deux voisins de part et d’autre, dont la position exacte se trouve en t₀−b/(2a) avec t₀ l’abscisse (indice entier) du pic de corrélation : la correction −b/(2a) fractionnaire sera d’autant plus précise que le rapport signal à bruit de la mesure qui détermine a et b sera bonne.
5. La recherche du pic de corrélation est répétée sur toute la séquence de mesure et une valeur moyenne est déduite après correction parabolique de la dérive du satellite le long de son orbite.

Ce dernier point est fondamental pour passer de la période d’échantillonnage de 200 ns aux quelques nanosecondes recherchées : nous pouvons démontrer que sous hypothèse de l’unicité du pic de corrélation, le gain en résolution de la position en temps du pic de corrélation est égal au rapport signal à bruit de la mesure [20]. Cette approche est aussi largement utilisée lors de la mesure de déplacements subpixels par traitement d’images.

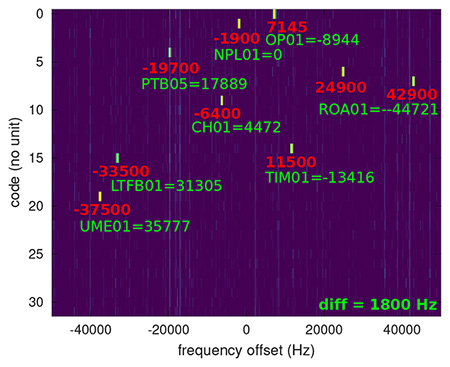
La Fig. 12 généralise ces considérations en testant tous les codes pseudoaléatoires possibles pour tous les décalages possibles de fréquence – calcul que nous aurions pu simplifier en nous limitant aux demi-fréquences détectées par mise au carré du signal (Fig. 9). L’écart de 1800 Hz aux valeurs nominales de porteuses est introduit par le transpondeur du satellite géostationnaire.

6. Messages numériques transmis entre modems SATRE

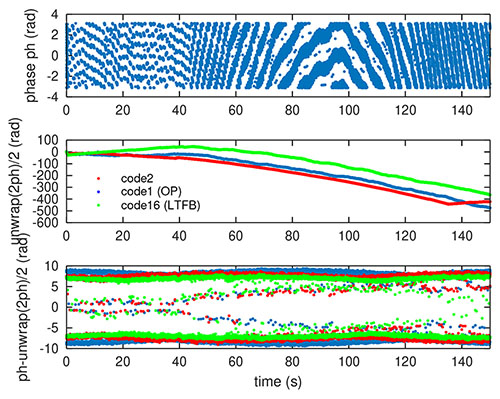
Maintenant que nous avons trouvé les pics de corrélation séparés de 4 ms ou 10000 chips au rythme de 2,5 Méchantillons/s, avons-nous extrait toute l’information possible des signaux transmis ? Si nous nous inspirons de GPS [21], nous savons que le message de navigation est superposé à 50 bits/seconde au-dessus du code qui identifie chaque satellite au rythme d’une corrélation toutes les millisecondes. Ainsi, 20 corrélations successives représentent la valeur du bit de navigation, avec une corrélation qui vaut soit +1 soit -1 selon que le bit du message soit 1 ou 0. TimeTech ne documente pas de telle fonctionnalité de SATRE qui n’est par ailleurs jamais mentionnée dans les publications sur MITREX, mais le manuel (Fig. 13) laisse penser qu’une communication numérique existe au-dessus du code de transfert de temps. Comme nous avons trouvé la phase de la corrélation par compensation de l’écart de fréquence entre oscillateurs locaux des émetteurs et récepteurs, nous pouvons en étudier le signe pour déduire la nature du bit transmis. Ainsi, en retranchant à la phase du signal reçu la demi-phase du signal mis au carré (Fig. 14), nous retrouvons uniquement le terme modulé pour transmettre un contenu numérique en plus du code : Φ = ϕ−unwrap(2ϕ)/2 vaut exp(j0)/exp(jπ) c.-à-d. ± 1∈ℝ qui encode les deux états possibles du bit transmis. Ainsi, pour SATRE (Fig. 13), l’histoire s’avère être la même que pour GPS, sans redondance et avec un débit plus rapide autorisé par le meilleur bilan de liaison. Alternativement, si au lieu de regarder le module du pic de corrélation, nous observons sa partie réelle, nous nous attendons à voir un code numérique apparaître par linéarité de la corrélation, et il serait assez intuitif que ce code soit transmis à un rythme de l’ordre de 250 bits/seconde, inverse des 4 ms de période des pics de corrélation. Nous vérifions en effet par autocorrélation de la trame numérique que des pics apparaissent aux valeurs multiples de 250, signature de certains motifs qui se répètent à ce rythme.

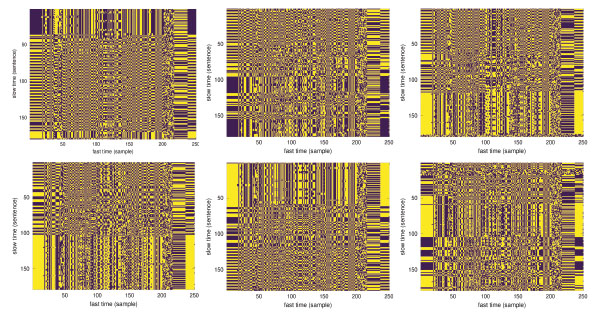
En effet, en réorganisant les séries temporelles des pics de corrélation en matrices de 250 colonnes (axe du temps rapide) et autant de lignes que de signaux traités (axe des temps lents selon lesquels les messages se répètent), nous voyons apparaître des motifs (Fig. 15) qui laissent penser à un codage numérique.

Si comme nous pourrions l’imaginer, un des champs code le temps en seconde, nous nous attendrions à voir le bit de poids faible alterner entre 0 et 1 selon que la seconde soit paire ou impaire, et le bit suivant alterner toutes les deux lignes, mais rien d’aussi trivial n’apparaît dans l’analyse de ces motifs. Il se pourrait qu’un code convolutif soit utilisé pour corriger les erreurs de communication, mais rien de tel n’est détecté par une attaque telle que décrite dans [22] implémentée dans https://github.com/BatchDrake/cccrack. Nous n’avons pas persévéré dans cette voie, même si l’absence de compréhension du mode de communication numérique est peu satisfaisante. Faute de temps, nous passons à l’étape suivante de traitement des signaux horaires qui sont au cœur de nos considérations.

7. Transfert de temps : observation des signaux horaires des mesures bidirectionnelles

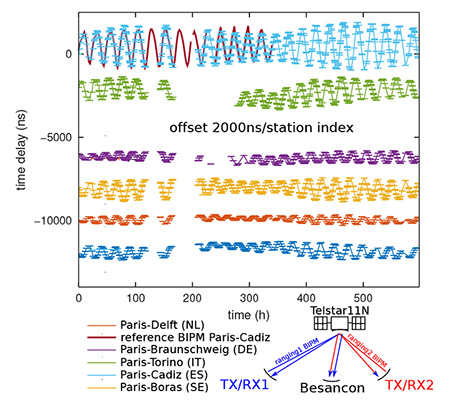
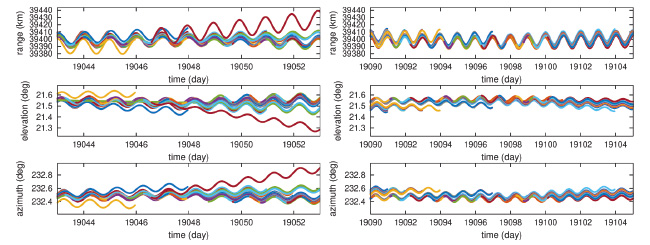
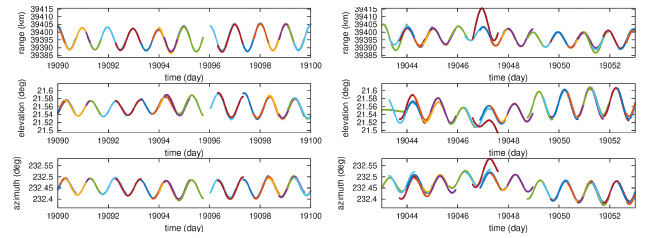
La Fig. 16 illustre l’évolution de l’écart de temps entre les pics de corrélation attribués à chaque observatoire, avec un décalage introduit artificiellement pour mieux distinguer les diverses courbes. Comme les divers observatoires distribués en Europe ne voient pas le satellite du même point de vue, la projection du vecteur vitesse du satellite qui bouge autour de son point d’équilibre du fait des forces gravitationnelles (Lune, Soleil, forme non sphérique de la Terre) diffère pour chaque observatoire et un mouvement résiduel est observé. Chaque observatoire communiquant avec ses voisins échange la distance entre lui-même et le satellite, ainsi que le temps de vol entre lui-même et son interlocuteur. De ces deux informations, le temps absolu sur chaque site peut être déduit. Ces informations sont celles collectées par le BIPM sur le site mentionné auparavant, et nous constatons un excellent accord entre nos observations et les données publiées par le BIPM, par exemple en comparant les écarts de temps entre l’Observatoire de Paris et le PTB allemand en Fig. 16 en haut, le bleu étant nos observations et le violet les mesures du BIPM.

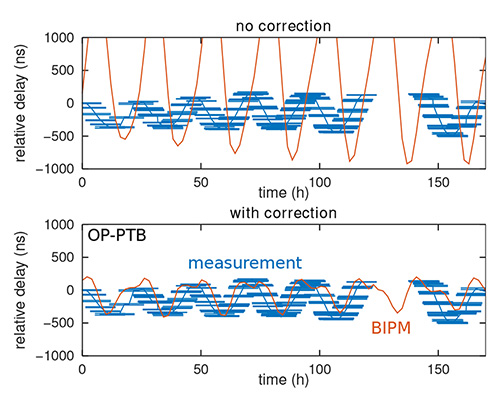
Une subtilité subsiste pour atteindre cet excellent accord. Alors que les radios logicielles que nous utilisons peuvent traiter les signaux de tous les observatoires simultanément – nous avons enregistré l’intégralité des informations sous forme de coefficients IQ dans la bande de fréquence de 5 MHz autour de la porteuse pendant toute la durée des liaisons – l’antique SATRE ne peut traiter que deux stations à la fois, et les échanges imposent un séquençage des interlocuteurs qui ne parlent que deux à deux à chaque instant. Cela implique un décalage temporel dans les mesures collectées par le BIPM qu’il faut compenser : nous constatons en effet sur ce graphique que le satellite se déplace au rythme de quelques nanosecondes par seconde (pour rappel, la lumière se déplace à 30 cm/ns, donc quelques nanosecondes par seconde correspondent à une vitesse de quelques mètres par seconde) et que par conséquent, un écart de 10 minutes entre deux observations se traduit rapidement par quelques microsecondes d’écart entre les mesures. Ce n’est qu’en interpolant les mesures publiées par le BIPM pour les replacer au même instant – dans notre cas une interpolation linéaire suffit compte tenu de la vitesse lente du satellite – que nous obtenons cet excellent accord tel qu’illustré en Fig. 17. En l’absence d’interpolation, les écarts dépassent plusieurs microsecondes entre données du BIPM et nos observations, un désaccord qui eut été inacceptable compte tenu des objectifs de résolution de quelques nanosecondes.

Nous sommes maintenant convaincus d’être capables de décoder les signaux horaires transmis par les observatoires européens et d’identifier l’écart de temps entre leurs émissions, compte tenu du mouvement du satellite. Pouvons-nous tirer parti de cette connaissance pour asservir une horloge locale par une observation purement passive, en l’absence de liaison bidirectionnelle, uniquement en observant les signaux échangés quotidiennement ? Le problème vient de ce qu’en présence du mouvement du satellite, les informations collectées par le BIPM permettraient de corriger a posteriori la distance variable observatoire-satellite lors de la mesure différentielle, mais le terme commun satellite-observateur passif est incontrôlé (Fig. 16, bas). C’est ce terme qu’il faut chercher à identifier et à corriger.

8. Transfert de temps : observation des signaux horaires pour une correction unidirectionnelle

Figure 18 : Code GNU Octave de simulation du temps de vol lorsque le satellite se déplace.

La première approche qui vient à l’idée pour compenser le mouvement du satellite est de l’observer avec plusieurs paraboles proches du site de réception et par mesure de phase de détecter, puis compenser ce mouvement. Cette approche, qui s’apparente classiquement à la direction d’arrivée (DoA) de signaux radiofréquences ou au RADAR à synthèse d’ouverture (SAR), se heurte à la physique : le satellite situé à 36000 km se déplace autour de son point d’équilibre d’une trentaine de km. Deux antennes au sol séparées de 3 m pour choisir une base de taille raisonnable verront les signaux se décaler de seulement quelques picosecondes, impossibles à mesurer compte tenu de la bande passante disponible, et il faut espacer les antennes de plus de 300 m pour atteindre quelques centaines de ps de variation de temps de vol, raisonnablement mesurable sur les pics de corrélation reçus, mais beaucoup moins pratique pour la mise en place de l’expérience (Fig. 18). La conclusion que plus l’extension de la base d’antennes est grande, plus le retard induit par le mouvement du satellite ou de l’astre observé sera aisé à observer, est à l’origine de la distribution des radiotélescopes sur des bases aussi larges que possible, s’étendant parfois entre plusieurs continents.

Dans notre cas, nous pouvons prendre le problème à l’envers en considérant qu’il y a une multitude d’observatoires qui émettent des signaux supposés synchrones, et que l’unique observateur que nous sommes peut bénéficier de cette diversité spatiale des sources pour retrouver la position du satellite et donc la compenser, connaissant les coordonnées géographiques de tous les observatoires européens. Cette approche a été abordée dans [23] sans que nous y trouvions la mise en œuvre technique autre que des résultats prometteurs.

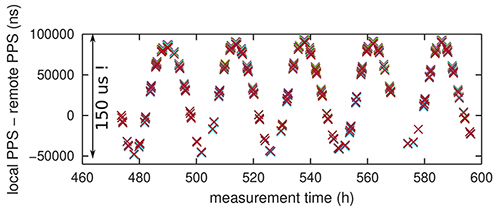
Nous pouvons déjà nous convaincre de la nécessité de mesurer et de compenser le retard induit par le mouvement du satellite en datant les pics de corrélation par rapport à une référence de temps locale, par exemple fournie par l’impulsion 1-PPS d’un récepteur GPS U-Blox. En effet, comme dans le problème qui nous intéresse ici, chaque satellite de la constellation GPS émet un signal horaire supposé parfaitement synchrone et la trilatération au sol permet de compenser le temps de vol de l’onde électromagnétique et de retrouver la position du récepteur. Cette impulsion par seconde 1-PPS est supposée stable dans le temps puisqu’asservie sur les horloges atomiques embarquées dans les satellites et observées quotidiennement par l’USNO américain qui en garantit l’exactitude. La Fig. 19 illustre l’évolution de la date des pics de corrélation observés depuis Besançon pour les émissions d’un observatoire européen : pour obtenir ce résultat, le récepteur de radio logicielle B210 a été configuré pour amorcer son acquisition sur le front montant du 1-PPS du récepteur GPS. Ce résultat s’obtient en éditant le fichier d’acquisition produit par GNU Radio Companion et en ajoutant les commandes après la connexion des divers blocs de traitement (deux premières lignes produites par GNU Radio Companion, notre ajout en dessous) :

qui indique à la bibliothèque UHD qui contrôle pour GNU Radio la B210 d’attendre le passage du prochain PPS avant de lancer l’acquisition. Nous constatons sur la Fig. 19 que la date des pics de corrélation fluctue de jour en jour de plus de 150 µs, soit une excursion du mouvement du satellite de l’ordre de 0,3 km/µs× 150 µs = 45 km, tout à fait raisonnable compte tenu des paramètres orbitaux connus. Cependant, la synchronisation d’horloges à 150 µs serait une performance pire que celle fournie par la synchronisation sur le signal très basse fréquence émis depuis Mainflingen à 77,5 kHz (DCF77 des horloges « radiocommandées ») [24] et insuffisant pour respecter la norme européenne MiFID2 qui impose de dater les transactions boursières à mieux que 100 µs.

Nous avons donc maintenant deux options : prévoir ou observer le mouvement du satellite, dans les deux cas en vue de corriger l’évolution de sa position et compenser les variations de temps de vol de l’onde électromagnétique émetteur-satellite-récepteur, les deux extrémités du lien étant supposées fixes. Les deux solutions ne sont pas triviales et prévenons dès ici que nous n’aboutirons pas à une solution acceptable, même si le simple fait de déjà pouvoir observer le mouvement d’un satellite à 36000 km du récepteur semble incroyable.

8.1 Analyse de la prévision de position du satellite

Sachant que les orbites des satellites sont documentées par les TLE (Two Line Elements) publiés par le NORAD et que des outils de prévision de la position du satellite tel que (défunt) SatTrack, Gpredict, PreviSat ou la bibliothèque skyfield pour Python [25] sont disponibles, il semblerait envisageable de prédire la position du satellite dans l’espace et donc de compenser le temps de vol de l’onde. Alors que le calcul de la trajectoire de satellites en orbite basse permet de prévoir à la seconde près l’horaire de passage des satellites météorologiques ou de la station spatiale internationale ISS, nous avons découvert que la situation est beaucoup plus complexe dans le cas des objets en orbite moyenne [26] ou géostationnaire qui implique d’autres méthodes d’identification des solutions, voire pour lesquelles les TLE qui indiquent l’excentricité et le nombre d’orbites par jour ne sont simplement pas appropriées. Avec un TLE de la forme

il est clair que le nombre d’orbites par jour (1.00270830) ou la partie fractionnaire de l’excentricité (0001723) vont souffrir d’un nombre insuffisant de décimales pour alimenter l’algorithme SGP4 implémenté pour rechercher la solution tels que confirmé par https://rhodesmill.org/skyfield/earth-satellites.html qui cite [27] :

« The maximum accuracy for a TLE is limited by the number of decimal places in each field. In general, TLE data is accurate to about a kilometer or so at epoch and it quickly degrades. »

Et complète avec :

« Satellite elements go rapidly out of date. You will want to pay attention to the “epoch” - the date on which an element set is most accurate - of every TLE element set you use. Elements are only useful for a week or two on either side of the epoch date. For later dates, you will want to download a fresh set of elements. For earlier dates, you will want to pull an old TLE from the archives.

Expect a satellite’s orbit to constantly change as the SGP4 propagation routine models effects like atmospheric drag and the Moon’s gravity. In particular, the true anomaly parameter can swing wildly for satellites with nearly circular orbits, because the reference point from which true anomaly is measured - the satellite’s perigee - can be moved by even slight perturbations to the orbit. »

Ainsi, [27] prévient qu’il serait illusoire de rechercher ainsi la position d’un objet céleste à mieux que quelques kilomètres, soit dans notre cas une incertitude de plusieurs dizaines de microsecondes. Cette observation ne remet pas en cause la capacité des TLE à prédire avec précision la date d’apparition et de disparition d’un satellite en orbite basse : la station spatiale internationale (satellite météorologique NOAA) à 400 km (850 km) d’altitude parcourt son orbite de 43000 km (46000 km) de long en 93 minutes (101 minutes) donc une erreur de 10 km sur sa position ne décalera que de 1,3 seconde la date de lever ou de coucher sur l’horizon, à peine perceptible pour un survol d’horizon à horizon qui dure de l’ordre de 6 minutes (11 minutes).

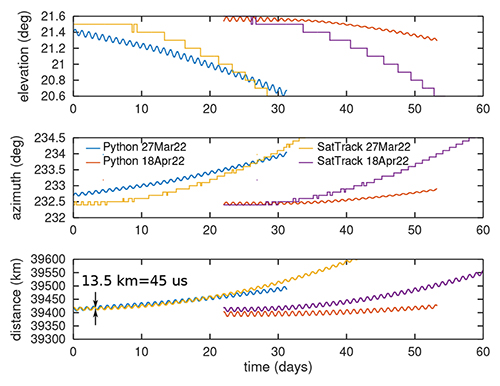
Afin de néanmoins évaluer la faisabilité de cette approche, T.S. Kelso de CelesTrak nous a transmis les TLE du 1er janvier 2022 au 18 avril 2022, et nous avons tenté de voir sur quel horizon il est possible de prévoir la position du satellite et quand cette solution se met à diverger. Commençons tout de suite par éliminer SatTrack (Fig. 20) qui, bien que capable de fournir une solution, diverge rapidement et ne fournit pas assez de décimales pour même voir les fluctuations journalières de position. Nous nous sommes donc focalisés sur skyfield qui semble approprié pour notre objectif :

Ce script définit le site d’observation (lab situé à Besançon par 6°E et 47°N) puis pour chaque entrée des paramètres orbitaux du satellite dans le fichier sat34111.txt, nous calculons {azimut, élévation, distance} du satellite par topocentric.altaz() que nous sauvons dans un fichier pour analyse. Bien que la tendance générale des fluctuations journalières de position du satellite soit bien visible (Fig. 21 et 22), tenter de prédire la position du satellite à 8 jours est déjà difficile (Fig. 21) quand la solution ne diverge pas carrément, même sur un délai aussi court que 1 jour (Fig. 22).

Cette approche semble donc sans issue, ou en tous cas pas avec des outils aussi simples que ceux facilement accessibles et décrits ici. C. Rieck [23] mentionne décrire l’orbite « by a GPS ICD [7] compatible Kepler model, which is estimated using iterative nonlinear least squares » que nous ne savons pas utiliser, tandis que ces auteurs précisent que la position du satellite géostationnaire est régulièrement corrigée pour le maintenir dans le volume d’espace qui lui est alloué au-dessus de l’équateur, corrections qui ne peuvent être prédites, mais uniquement subies et observées.

8.2 Analyse de l’observation de position du satellite

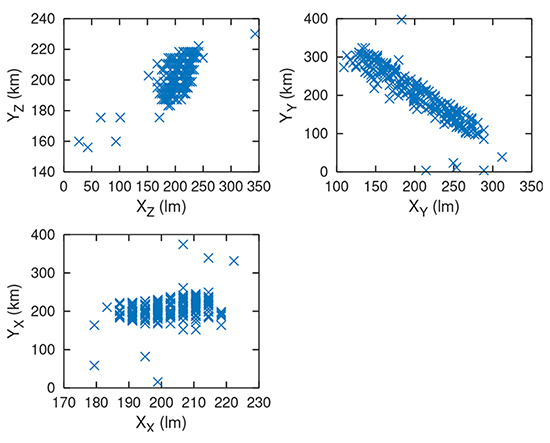
Nous avons vu que la diversité spatiale des émetteurs doit permettre, grâce à la base suffisamment large, de distinguer les projections du vecteur de déplacement du satellite sur les divers vecteurs reliant le satellite au sol, et ainsi d’identifier chaque composante. Avec 8 observatoires distribués sur le continent européen (Fig. 2), la solution est surcontrainte et nous devrions rechercher une optimisation au moindre carré, mais en pratique les observatoires sont très groupés et nous favoriserons les bases les plus larges fournies par les Suédois de SP, les Espagnols de ROA, les Anglais du NPL et les Italiens d’INRIM (Fig. 22). La carte de la Fig. 2 illustre bien comme le problème est mal conditionné, avec un satellite très excentré puisqu’il sert aussi à communiquer avec l’Amérique du Nord, et donc vu d’à peu près la même direction de tous les points en Europe.

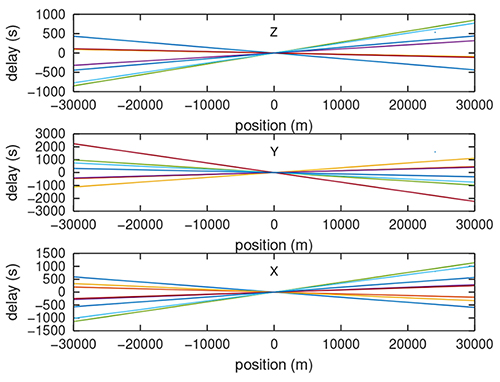
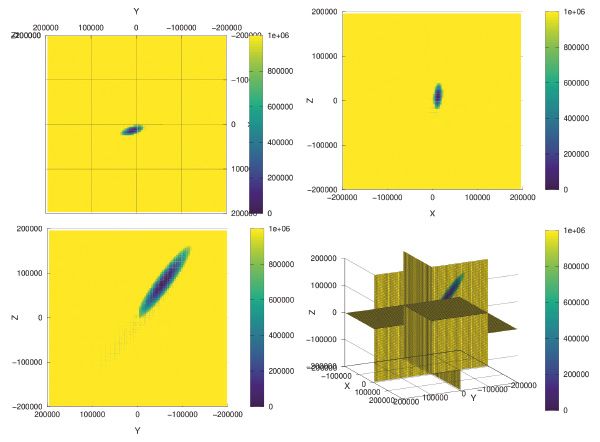
Après avoir estimé le problème direct, à savoir le retard de plusieurs centaines de nanosecondes induit sur le temps de communication à chaque observatoire par le mouvement du satellite le long des 3 axes en coordonnées cartésiennes (Fig. 23), l’approche la plus naïve, mais la plus facile est une recherche par descente de gradient : nous exprimons le problème en évaluant le temps de vol introduit par une liaison entre le satellite de position libre et chaque observatoire de position connue, et demandons à GNU/Octave de minimiser par le choix judicieux de la position de satellite l’erreur résiduelle entre l’estimation et l’observation des retards. En pratique, cette approche est très sensible au bruit et fournit un résultat peu crédible. Le résultat est décevant et échoue à converger, avec en particulier une forte dépendance sur le choix du nombre d’observatoires inclus dans l’analyse, signature d’une sensibilité excessive au bruit de mesure (Fig. 24) : de l’avis général, cette méthode doit être implémentée par filtre de Kalman, méthode que nous ne maîtrisons pas (encore !).

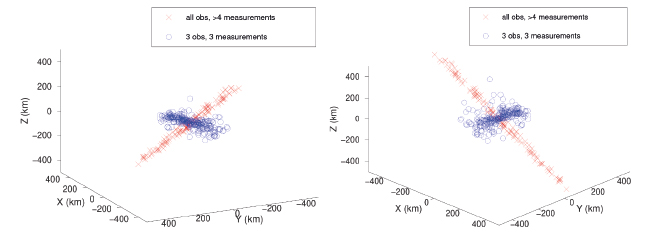
L’alternative à une descente de gradient est une recherche exhaustive de la solution optimale en balayant l’espace des possibilités. Nous calculons dans un cube de 200 km de côté centré sur la position nominale du satellite et discrétisé par pas de 3,9 km (13 µs qui est déjà énorme, mais choisi pour maintenir la durée du calcul raisonnable) le retard introduit par la liaison entre chaque observatoire et le satellite, et pour chaque position effectuons la somme des carrés des différences des estimations à la mesure : ainsi, la solution la plus probable apparaît comme un minimum dans cette cartographie du signal d’erreur. Compte tenu des temps de calcul mis en jeu, cette carte n’a été estimée que sur les plans horizontaux (Z=0) et verticaux (X=0 et Y=0) et non dans tout l’espace du cube (Fig. 25). La Fig. 26 illustre quelques résultats de cette analyse sur un peu moins d’un mois, moins délirants que la descente de gradient, mais toujours excessivement bruités qui ne permettent pas d’espérer de remonter à la position du satellite pour compenser sa contribution à la variation du temps de vol.

Conclusion

Nous avons commencé l’exploration des liaisons radiofréquences par satellite géostationnaire en nous proposant de décoder les signaux échangés par les observatoires européens pour comparer leurs horloges de référence. Ce faisant, nous avons découvert le fonctionnement du bloc de réception LNB au foyer des paraboles chargé d’amplifier et de transposer en fréquence le signal descendant du satellite pour alimenter une radio logicielle. Forts d’une bande passante suffisante, nous avons exploré la modulation en phase à deux états BPSK pour identifier les codes pseudoaléatoires orthogonaux transmis par chaque observatoire, et ainsi retrouver le temps de vol de chaque émetteur distribué en Europe vers l’unique récepteur : cette mesure permet d’observer les oscillations du satellite géostationnaire autour de son point d’équilibre, mais surtout de déduire de l’intervalle entre les pics de corrélation l’instabilité de la fréquence de l’oscillateur local, en vue de la corriger. Après avoir tenté de prédire ce déplacement du satellite qui handicape notre capacité à recevoir avec précision une information de temps, nous nous sommes efforcés d’observer ce déplacement. La mesure trop bruitée ne permet pas de retrouver suffisamment finement la position du satellite dans l’espace pour compenser les variations de temps de vol, qui restent par ailleurs polluées du délai ionosphérique et troposphérique entre le satellite et le récepteur que nous ne saurons pas observer. Nombre de difficultés techniques mettant en œuvre un large spectre de compétences restent à résoudre pour fournir une solution complète d’horloge asservie sur les signaux métrologiques transmis par les observatoires européens.

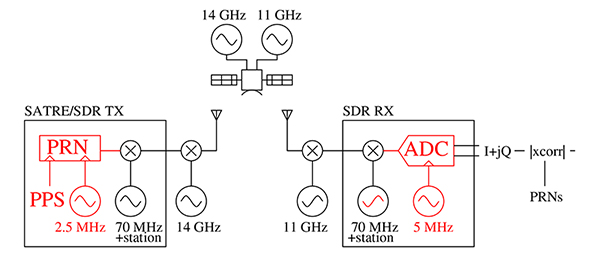
Il est habituellement proscrit d’amener une information nouvelle dans la conclusion, mais comment se fait-il que nous n’ayons parlé dans tout ce document que de transfert de fréquence et de temps au travers des pics de corrélation et pas des signaux de correction des oscillateurs locaux, comme cela se ferait habituellement sur une liaison au sol ? Le problème vient du satellite qui est une boîte noire dont le fonctionnement n’est pas maîtrisé : la liaison montante peut être aussi bien maîtrisée que nous puissions l’implémenter, le satellite transpose de 14 GHz vers 11 GHz le signal incident pour le placer dans la bande descendante, pour être reçu au sol par un oscillateur micro-ondes qui est ou n’est pas asservi sur la référence métrologique. Ainsi, seul le code de temps fourni par les pics de corrélations périodiques est exploitable, les transpositions de fréquences étant incontrôlées (Fig. 27).

Cette aventure a surtout été l’opportunité d’aborder un nouveau domaine de signaux radiofréquences à recevoir et à décoder, ceux relayés par les satellites géostationnaires, pour un coût modique compte tenu de la disponibilité de paraboles de réception de télévision inutilisées et de la capacité à alimenter une radio logicielle à une vingtaine d’euros avec ces signaux.

Le dépôt recensant ces développements se trouve à https://github.com/oscimp/gr-satre et ne demande qu’à être complété par les contributions des lecteurs.

Remerciements

Cette étude est un effet de bord d’un projet financé par le Laboratoire d’Excellence (Labex) FIRST-TF entre le SYRTE de l’Observatoire de Paris, l’OSU Theta de l’observatoire de Besançon et le département temps-fréquence de l’institut FEMTO-ST. Les informations diffusées dans ce document sont toutes publiquement disponibles pour qui sait chercher assez longtemps, mais je (JMF) n’aurais jamais pu accumuler en une année toutes ces données sans avoir communiqué avec les partenaires du projet que sont J. Achkar, M. Lours et M. Dupont au SYRTE ainsi que F. Meyer et É. Meyer à l’observatoire de Besançon. Les participants à la liste de diffusion time-nuts@lists.febo.com ont fourni des informations précieuses, en particulier A. Bauch du PTB allemand et F. Meynadier du BIPM qui sont chaleureusement remerciés. Les signaux transmis quotidiennement par les observatoires nationaux sont accessibles à tout contribuable qui finance ces études et à défaut de trouver une utilisation concrète à leur dissémination, il semble au minimum raisonnable d’informer de la nature et de la disponibilité de ces signaux telle que la FSFE en fait la promotion à https://fsfe.org/activities/publiccode/publiccode.fr.html.

Références

[1] C. Audoin & B. Guinot, The measurement of time – time, frequency and the atomic clock, Cambridge University Press (2001), Fig. 5.6 p. 105

[2] J.-M Friedt, W. Feng, « Analyse et réalisation d’un RADAR à bruit par radio logicielle » (1/3), « Analyse et réalisation d’un RADAR à synthèse d’ouverture (SAR) par radio logicielle » (2/3) et « Mesure fine de déplacement par RADAR interférométrique à synthèse d’ouverture (InSAR) par radio logicielle » (3/3), GNU/Linux Magazine France 240,242 et 244 (2021) - https://connect.ed-diamond.com/gnu-linux-magazine

[3] Recommendation ITU-R TF.1153-4 – The operational use of two-way satellite time and frequency transfer employing pseudorandom noise codes (08/2015)

[4] I. Lucresi & al., SDR-based System for Satellite Ranging Measurements, IEEE A&E Systems Magazine 8–13 (2016) exploite une radio logicielle X310 et compare avec le SATRE.

[5] Z. Jiang & al., Implementation of SDR TWSTFT in UTC Computation, Proc. 49th Annual Precise Time and Time Interval Systems and Applications Meeting, pp. 184-208 (2018)

[6] Z. Jiang & al., Use of software-defined radio receivers in two-way satellite time and frequency transfers for UTC computation, Metrologia 55 685-698 (2018)

[7] A.C. Clarke, Extra-terrestrial relays – Can Rocket Stations Give World-wide Radio Coverage? Wireless World (1945), 305

[8] CCTF/17-20, RISE Research Institutes of Sweden, Report on Activities to the 21th meeting of the Consultative Committee for Time and Frequency, June 2017 section 7.2. Passive Utilization of TWSTFT

[9] C. Rieck, P. Jarlemark & K. Jaldehag, Utilizing TWSTFT in a Passive Configuration, Proc. 48th Annual Precise Time and Time Interval Systems and Applications Meeting (2017)

[10] Derek OK9SGC, Receiving Starlink satellite beacons on a budget (25 November 2021) à https://sgcderek.github.io/blog/starlink-beacons.html annonce des signaux à 11325, 11575, 11950 et 12450 MHz.

[11] J.-M Friedt, « Le récepteur de radio logicielle RSP1 : 8 MHz de bande passante pour moins de 20 euros » Hackable 44 (2022) - https://connect.ed-diamond.com/hackable/hk-044/le-recepteur-de-radio-logicielle-rsp1-8-mhz-de-bande-passante-pour-moins-de-20-euros

[12] Eutelsat, Antenna and VSAT – Type Approval/Characterization – ESOG 120 – Issue 8 - Rev. 1, May 2021 à https://www.eutelsat.com/files/contributed/satellites/pdf/esog120.pdf

[13] A. Kanj, Étude et développement de la méthode TWSTFT phase pour des comparaisons hautes performances d’étalons primaires de fréquence, thèse Univ. Pierre & Marie Curie (2012) avec les sous-porteuses décrites p.53

[14] V. Zhang & al., A Study on Using SDR Receivers for the Europe-Europe and Transatlantic TWSTFT Links, Proc. 2017 Precise Time and Time Interval Meeting (2017)

[15] M.L. Psiaki & al. Searching for Galileo: Reception and Analysis of Signals from GIOVE-A, GPS World 17 (6) 66-72 (2006) semble introuvable, mais est décrit à https://news.cornell.edu/stories/2006/07/cornell-sleuths-crack-secret-codes-europes-galileo-satellite et ses liens.

[16] P. Hartl, Present state of long distance time transfer via satellites with application of the Mitrex modem IEEE Military Communications Conference MILCOM 2 (1986)

[17] K. Imamura & F. Takahashi, Frequency and Time Comparison – Two-way time transfer via a geostationary satellite, J. of the Communication Research Laboratory 39(1), 91–100 (1992)

[18] G. De Jong. Two-way satellite time transfer: Overview and recent developments Proc 25th Annual Precise Time and Time Interval (PTTI) (1993) à https://apps.dtic.mil/sti/pdfs/ADA280955.pdf#page=112

[19] Y. Guidon, « Comprendre les générateurs de nombres pseudoaléatoires », GNU/Linux Magazine France 81 64–76 (2006) et « Sciences/Théorie de l’information : propriétés et dérivés des CRC et LFSR », GNU/Linux Magazine France 85 84–93 (2006)

[20] J.-M Friedt, C. Droit, G. Martin, and S. Ballandras, A wireless interrogation system exploiting narrowband acoustic resonator for remote physical quantity measurement, Rev. Sci. Instrum. 81 014701 (2010)

[21] J.-M Friedt, G. Cabodevila, « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », OpenSilicium 15 (2015) - https://connect.ed-diamond.com/open-silicium/os-015/decodage-des-signaux-de-satellites-gps-recus-par-recepteur-de-television-numerique-terrestre-dvb-t

[22] M. Marazin, R. Gautier, G. Burel, Dual Code Method for Blind Identification of Convolutional Encoder for Cognitive Radio Receiver Design, Proc IEEE GLOBECOM Workshops (2009)

[23] C. Rieck, P. Jarlemark & K. Jaldehag, Passive Utilization of the TWSTFT Technique, Proc EFTF (2018)

[24] J.-M Friedt, C. Eustache, É. Carry, E. Rubiola, Software defined radio decoding of DCF77: time and frequency dissemination with a sound card, Radio Science 53 (1) 48–61 (2018)

[25] https://rhodesmill.org/skyfield/installation.html

[26] T.S. Kelso, Validation of SGP4 and IS-GPS-200D Against GPS Precision Ephemerides, Proc. 17 th AAS/AIAA Space Flight Mechanics Conference (2017), AAS 07-127 à https://celestrak.com/publications/AAS/07-127/AAS-07-127.pdf dont la figure 2 montre la divergence des prévisions avec les observations en fonction du temps pour les satellites en orbite moyenne du GPS.

[27] D.A. Vallado, P. Crawford, R. Hujsak, T.S. Kelso, Revisiting Spacetrack Report #3: Rev 3, Proc. AIAA/AAS Astrodynamics Specialist Conference (2006) à https://celestrak.org/publications/AIAA/2006-6753/AIAA-2006-6753-Rev3.pdf