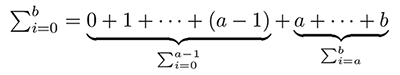Entre algorithmique et programmation

J’ai pour habitude d’expliquer la différence entre algorithmique et programmation en faisant une analogie avec le bâtiment, entre l’architecture et la construction. Ainsi, l’architecte est l’algorithmicien et les artisans (maçons, électriciens, plombiers…) sont les programmeurs. Cette analogie s’accompagne de mes expériences d’étudiant où pour financer mes études, j’ai eu l’opportunité de faire l’arpète (la petite main) auprès d’ouvriers issus du compagnonnage qui parfois (euphémisme) critiquaient les plans qu’on leur demandait de mettre en œuvre par des « personnes qui n’avaient jamais mis les mains dans le cambouis » (c’est la traduction la plus politiquement correcte que j’ai pu formuler pour retranscrire le message). Parfois au contraire, les « chefs » avaient droit au respect, car on voyait bien qu’ils avaient une réelle expérience de terrain. À l’inverse, j’imagine très bien les architectes décrier le travail des ouvriers en constatant qu’ils n’ont pas suivi à la lettre leurs plans techniques.

En se basant sur cette analogie, on serait donc tenté de répondre qu’il faut être un bon programmeur pour être un bon algorithmicien et vice-versa. Ceci ne serait pourtant pas très sérieux comme argumentaire et risquerait de m’attirer les foudres des gens de lettres qui, à juste titre, commenceraient par me reprocher de n’avoir pas défini les termes des deux questions, pour ensuite constater que j’ai glissé de l’algorithmique à l’algorithmicien et de la programmation au programmeur. À cela, je leur réponds : « OK, vous avez raison. C’est pourquoi vous trouverez les définitions et la terminologie dans la section suivante, votre dictionnaire préféré ou sur Wikipédia ».

Plus sérieusement, je vous propose une démonstration par l’exemple (donc encore une fois, ce n’est pas sérieux, scientifique, tangible… mais ce n’est pas grave, ce qui m’importe c’est de vous faire partager une expérience que je trouve jolie).

1. Un programme simple pour un problème simple

Tout au long de cet article, nous nous focaliserons sur un problème simple : l’écriture d’un programme permettant de calculer la somme des n premiers entiers consécutifs. Nous étudierons également sa version plus générale, l’écriture d’un programme permettant de calculer la somme des entiers consécutifs compris entre a et b inclus.

Pour répondre à cela, j’ai choisi d’implémenter les codes en langage C qui, je le rappelle, est un langage de haut niveau, puisqu’il permet de faire abstraction des caractéristiques techniques du matériel utilisé pour exécuter le programme (c’est probablement l’un des plus bas parmi les langages de haut niveau, d’accord et il intègre également des instructions permettant de faire du bas niveau, d’accord).

J’ai donc choisi d’utiliser le type unsigned int pour représenter le paramètre n, par conséquent le type de retour sera également unsigned int. Pour rappel, le type unsigned int désigne un entier non signé codé sur au minimum 2 octets, ce qui permet de représenter les entiers naturels compris dans l’intervalle [0 ; 2¹⁶[, soit entre 0 et 65535. En réalité, la plupart des compilateurs utilisent 4 octets pour ce type de données et donc cela permet de représenter les entiers naturels compris dans l’intervalle [0 ; 2³²[, soit entre 0 et 4 294 967 295.

Ainsi la signature de la fonction devrait ressembler à unsigned int SommeEntiersConsecutifs(unsigned int n).

Pour écrire une implémentation, il faut donc commencer par définir une méthode de résolution du problème, donc un algorithme (idéalement, écrivez votre solution sur papier avant de lire plus avant).

1.1 Un premier programme

Basiquement, le calcul des n premiers entiers consécutifs consiste, en partant de 0, à ajouter 1, puis, 2 puis 3… jusqu’à n et à renvoyer le résultat. Il convient donc d’utiliser une variable d’accumulation du même type que le paramètre d’entrée qui sera initialisée à 0 et de procéder par itérations successives. Un tel algorithme n’ayant rien de difficile à mettre en œuvre et n’exploitant aucune subtilité est communément qualifié de naïf.

C’est super, mais il faut tout de même pouvoir l’encapsuler dans un programme pour pouvoir le tester. J’ai choisi de créer un simple fichier test_sommes.c (dans le répertoire programmes/V0/ sur le GitLab), qui commence par une fonction permettant d’afficher un message d’aide en cas de mauvaise utilisation du programme (je passe l’explication du code qui ne présente pas d’intérêt dans le cadre de cet article), suivie de la fonction de calcul de la somme, suivie enfin du point d’entrée de notre programme, la fonction main.

Pour compiler et tester ce programme, c’est assez simple, il suffit d’écrire :

Bien évidemment, les bonnes pratiques de programmation suggèrent d’ajouter quelques arguments à la ligne de compilation afin de garantir que le code n’est pas trop moisi.

Les premières options sont ici pour s’assurer que le code respecte la norme de programmation ISO C99. La quatrième permet d’alourdir le code avec des symboles de debuggage si d’aventure nous devions l’examiner avec un outil spécialisé (p. ex., GDB ou Valgrind) et la cinquième option permet de désactiver toutes les optimisations de compilation que GCC aurait pu produire. Ainsi, le résultat de la compilation est au plus proche du code que l’on a écrit (cf. encadré).

1.2 Des solutions alternatives

Peut-être que parmi vous, certains ont proposé d’autres solutions, par exemple une version utilisant une boucle « tant que » (while) à la place du « pour » (for). Ceci ne change globalement pas grand-chose et reste tout aussi valable. Peut-être aviez-vous envisagé une version récursive basée sur l’idée que la somme vaut 0 quand n vaut 0 et qu’autrement, la somme des entiers consécutifs jusqu’à n est égale à la somme jusqu’à l’entier n-1 auquel il suffit d’ajouter n. Peut-être aviez-vous également pensé à utiliser les mathématiques en renfort, en vous rappelant que cette somme vaut :

La question sous-jacente (que me posent souvent les étudiants) est alors de savoir quelle est la bonne solution. Ce qui me permet de leur répondre : « Vous savez, moi je ne crois pas qu’il y ait de bonne ou de mauvaise [solution]. Moi, si je devais résumer ma vie aujourd’hui avec vous, je dirais que c’est d’abord des rencontres. Des gens qui m’ont tendu la main, peut-être à un moment où je ne pouvais pas, où j’étais seul chez moi… » [1]. Sans retranscrire la tirade complète, l’idée, c’est que pour décider si telle ou telle proposition est meilleure qu’une autre, il faut définir des critères de comparaison. Le critère qui revient le plus souvent auprès de mes étudiants est le temps de calcul. Plus la fonction ira vite, meilleure elle sera. Dans la même idée, la question de la mémoire requise pour faire le calcul figure également parmi les propositions les plus courantes. Normal, me direz-vous, car ce sont les deux piliers de la complexité ; mais parfois, il m’a été proposé de noter la beauté du programme (là, ça devient assez vite subjectif, c’est comme si les enseignants se mettaient à donner des notes à leurs élèves en fonction de la qualité de leur travail). Néanmoins (ce qui probablement légitime l’acte d’évaluation des enseignants), il apparaît que si les notes de « beauté du programme » peuvent radicalement différer d’un étudiant à l’autre, la relation d’ordre qu’elle induit est souvent la même (donc, le classement final est inchangé). Peut-être est-ce cela que certains enseignants ont oublié... mais là, je m’égare.

Étonnamment, mes étudiants ne me proposent pour ainsi dire jamais la justesse du programme dans les critères d’évaluation, comme si le simple fait d’appeler la fonction SommeEntiersConsecutifs était suffisant. Pourtant, il me semble qu’un programme qui renvoie un résultat erroné devrait être sorti de la comparaison et que par principe, il conviendra de tester tout de même ce critère (même si sur cet exemple simple, cela semble évident).

Comme en C il n’est pas possible d’avoir deux fonctions portant le même nom dans un même programme, je propose de suffixer les fonctions par le principe algorithmique sous-jacent afin de permettre leur coexistence (et cela simplifiera considérablement le discours). Ainsi, la version que j’ai proposée précédemment deviendra SommeEntiersConsecutifsIterative, la version récursive sera nommée SommeEntiersConsecutifsRecursive et la version utilisant la formule close sera nommée SommeEntiersConsecutifsMath.

Plutôt que de tout écrire dans un seul fichier monolithique, il est déjà temps de structurer et d’organiser notre code afin de s’y retrouver plus facilement. J’ai donc choisi de déclarer les fonctions à comparer dans un fichier intitulé fonctions.h (dans le sous-répertoire programmes/V1 du dépôt GitLab), et de fournir leurs implémentations dans le fichier fonctions.c. reproduit ci-après :

Assez facilement, il est possible de voir que le temps de calcul requis par la version itérative dépend directement de la valeur de n, puisqu’il y a un tour de boucle pour chaque valeur entre 0 et n. Donc, le temps de calcul dépendra du temps requis pour effectuer une addition (ligne 6). Il se trouve que les calculs arithmétiques de base (addition, soustraction, multiplication, division) sur les entiers ainsi que l’affectation d’entiers dans une variable requièrent un temps constant (en ordre de grandeur), quelles que soient les valeurs calculées / affectées. Donc, cette solution requiert un temps d’exécution linéairement proportionnel à la valeur de n. Sans entrer dans les détails de la notation (de Landau), on écrit que le temps de calcul est dans O(n). A contrario, le calcul de la version mathématique requiert un nombre temps de calcul constant, quelle que soit la valeur de n. On écrit alors que ce temps est dans O(1). Concernant le temps de calcul de la version récursive, si n vaut 0, alors le temps de calcul est constant. Si n est strictement positif, le temps de calcul est donc égal à une constante (non nulle) à laquelle il faut ajouter le coût du calcul de la somme des entiers jusqu’au rang (n-1). Donc, cette fonction nécessitera autant d’étapes de calcul (appels récursifs) que la version itérative nécessite de tours de boucles. Le temps de calcul sera donc également dans O(n). La version mathématique est donc la grande gagnante selon ce critère et les deux autres versions sont deuxièmes ex æquo.

Concernant la mémoire requise pour effectuer le calcul, les versions itératives et mathématiques vont nécessiter un nombre constant de variables, quelle que soit la valeur de n. Ce n’est pas le cas de la version récursive qui pour calculer la somme au rang 5 devra calculer préalablement la somme au rang 4, qui devra également calculer la somme au rang 3… jusqu’à atteindre le cas d’arrêt, à savoir le calcul de la somme au rang 0. Il faut donc que la machine garde en mémoire (empile) les appels récursifs de la fonction, puis les dépile une fois arrivée au cas d’arrêt. Il en résulte donc que cette version requiert un espace mémoire dans O(n). Ainsi, la version mathématique et la version itérative sont premières ex æquo selon ce critère et la version récursive arrive dernière.

Le classement final sur la base de ces deux critères est donc en première position, la version mathématique, en seconde position, la version itérative et en troisième position, la version récursive.

2. La différence entre la théorie et la pratique…

… c’est qu’en théorie, il n’y en a pas !

Pour s’en assurer, il convient de mettre en place un petit protocole de test. Avant toute chose, pour effectuer des mesures de temps d’un programme, il convient de l’exécuter plusieurs fois, puis de calculer une valeur moyenne. Le souci, c’est que nos ordinateurs étant vraiment très rapides, la moyenne sera ici peu exploitable, donc on se contentera de sommer les temps de toutes les exécutions, tout en veillant alors à exécuter le même nombre de fois chaque fonction.

Créons donc un fichier test_fonctions.h dans lequel nous commençons par définir un type de données correspondant aux fonctions unaires, dont le paramètre en entrée est un entier non signé et qui renvoie un entier non signé :

Ce type permet de déclarer des variables auxquelles il est possible d’assigner l’adresse d’une fonction (qui respecte la signature déclarée).

Définissons ensuite une structure de données permettant de créer un lien sémantique entre une fonction testée sur un nombre d’exécutions donné, le résultat renvoyé par la fonction pour un paramètre donné, le temps de calcul utilisé en millisecondes et la mémoire utilisée en kilo-octets.

Enfin, définissons une fonction dont le rôle sera d’exécuter un nombre donné de fois une fonction donnée sur un paramètre donné. Cette fonction renverra une structure infos_t (que l’on vient de définir) :

Pour être « propre », définissons une fonction permettant d’afficher les informations sur la sortie standard.

Ainsi qu’une fonction permettant de renvoyer une chaîne de caractères, car ce sera plus agréable que de récupérer l’adresse d’une fonction :

Côté implémentation, pour mesurer les ressources utilisées, nous allons exploiter la fonction getrusage() (voir encadré).

Tester une fonction consiste donc essentiellement à effectuer deux mesures de l’état des ressources, la première juste avant de lancer les tests, la seconde après la fin des tests, et de mesurer les différences. Il faut donc bien évidemment créer des variables locales pour stocker ces mesures, mais également la structure qui sera renvoyée par la fonction de test. Une fois les tests achevés, il reste à calculer la différence de temps CPU (que l’on convertit à la volée en millisecondes), puis à mesurer l’écart de mémoire entre le début et la fin des tests.

Pour pouvoir exploiter et analyser facilement les résultats des différents tests, j’ai une fâcheuse habitude à générer des fichiers textes tabulés (TSV – pour Tabulation-Separated Values – mieux connus comme étant des CSV – pour Comma-separated values – utilisant la tabulation comme séparateur de valeurs, ce qui est en soi une mauvaise dénomination). Pourquoi générer des sorties dans ce format ? Eh bien, parce qu’il est possible de les ouvrir avec Excel. Non, je rigole !!! Parce que c’est un format facile à triturer avec awk, cut, paste, gnuplot, etc. D’ailleurs, je ne me prive pas d’utiliser le symbole # (ceci est donc un dièse, pas un hashtag, ce qui ne voudrait rien dire dans le contexte) pour marquer le début d’un commentaire, ce que gnuplot gère parfaitement, par opposition aux tableurs graphiques remplis de super fonctionnalités et parfois onéreux.

Enfin, la fonction permettant de renvoyer une chaîne de caractère représentative d’une fonction est assez rudimentaire :

Maintenant que nous disposons d’une mini API pour tester nos fonctions, il reste à modifier le programme principal (et à adapter le message d’usage) du fichier test_sommes.c de sorte qu’il accepte dorénavant trois paramètres : le nom de l’algorithme à tester, la valeur du paramètre n, ainsi que le nombre de tests à réaliser (les lignes mises en évidence dans le code correspondent aux modifications apportées à la première version).

Pour créer (proprement) un exécutable à partir de ces fichiers, il conviendrait de décrire en partie le Makefile disponible dans le sous-répertoire programmes/V1 du dépôt GitLab, mais ceci alourdirait considérablement cet article, aussi résumons la ligne de commande de compilation à sa version la plus simple :

Une fois compilé, il est possible de le tester rapidement :

Comme on peut l’observer ici, les versions itératives et récursives semblent consommer plus de temps que la version utilisant la formule close.

Il est possible de générer un fichier par algorithme contenant les tests pour un algorithme donné en faisant varier la valeur de n en effectuant deux boucles imbriquées en Bash :

À partir de ces fichiers, il va être possible de faire assez facilement quelques analyses.

2.1 Observations des ressources consommées

Pour produire mes graphiques, j’aime bien utiliser gnuplot [3]. Cet outil mériterait un hors-série à lui tout seul, mais globalement pour ce que nous allons faire, il ne devrait pas y avoir trop de difficultés à le prendre en main.

Si vous ne l’avez pas encore installé sur votre système, je suis certain qu’il est disponible avec votre gestionnaire de package. Sous Debian/Ubuntu, c’est :

Tout d’abord, gnuplot est un interpréteur, donc lorsqu’on l’exécute en ligne de commande, on arrive sur une invite précédée d’un message d’accueil vous fournissant deux indications essentielles (en plus de toutes les informations non moins essentielles que je passerai sous silence) : le numéro de version de l’outil et le fait que par défaut, le terminal utilisé est x11 (donc, notre environnement fenêtré).

Pour le tester très rapidement, la commande qui permet de générer un graphique est plot et si l’on veut afficher une fonction de x, il suffit de l’écrire assez intuitivement :

Vous devriez voir une parabole apparaître dans une fenêtre ressemblant à l’image suivante :

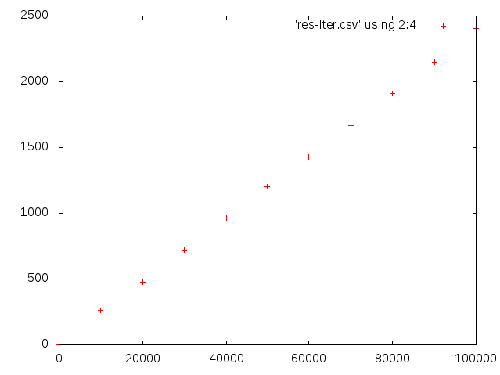
Bon, ça, c’est pour tracer une fonction. Mais gnuplot permet aussi de lire un fichier tabulé et de tracer un point par ligne (hors commentaires commençant par un dièse) en spécifiant les colonnes à utiliser pour l’abscisse et l’ordonnée. Typiquement, dans les fichiers que l’on a générés, la colonne 2 correspond aux valeurs de n et la colonne 4 aux temps de calcul. Ainsi, nous pouvons écrire l’instruction :

Celle-ci génère un graphique où chaque point correspond au temps de calcul passé pour calculer la somme des n premiers entiers consécutifs en utilisant l’algorithme itératif :

Il est également possible de superposer plusieurs graphiques en les énumérant (en les séparant par une virgule), mais aussi de tracer une ligne entre les points consécutifs, de mettre la légende en dehors, de spécifier un titre de graphique…

Enfin, comme gnuplot est un interpréteur (à l’instar de Bash, Perl, Python, etc.), il est possible de créer un fichier texte reprenant l’ensemble des instructions à interpréter et de le passer en argument. Mieux que cela, comme gnuplot considère tout ce qui suit le symbole dièse jusqu’à la fin de la ligne comme du commentaire, il est possible de rendre ce fichier exécutable et de le faire commencer par le shebang indiquant le chemin de l’interpréteur à utiliser (donc, typiquement #!/usr/bin/gnuplot). Ainsi, avec un programme de quelques lignes, il est possible de créer un graphique assez complexe.

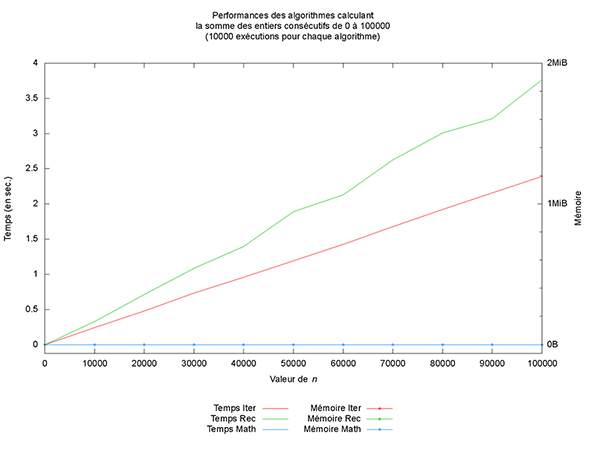
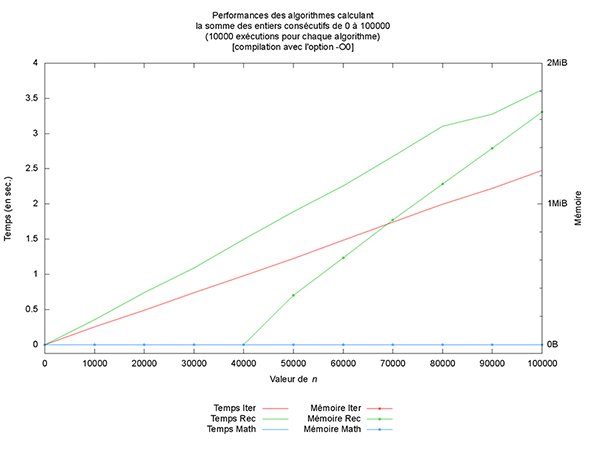
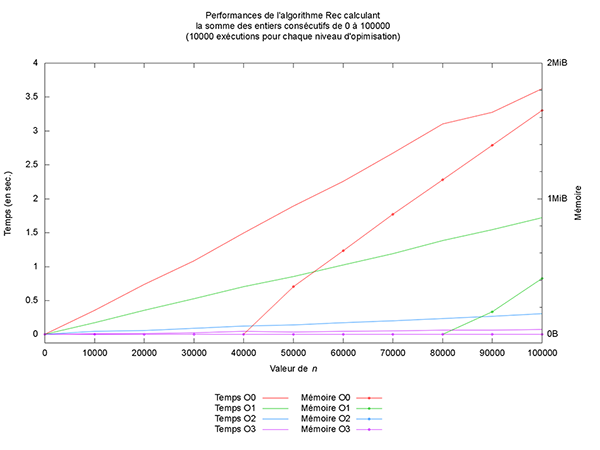
Ceci permet typiquement d’afficher une image qui devrait peu ou prou ressembler à la figure suivante :

Sur cette image, on retrouve bien les résultats théoriques attendus (un temps linéaire pour les versions itératives et récursives et une mémoire constante, sauf pour la version récursive).

Lors de la discussion sur les critères de classement des bonnes et moins bonnes solutions, j’avais mentionné la validité en termes de résultat. Il est possible assez facilement de tracer la courbe correspondant aux colonnes 2 et 3 des fichiers, soit les points (n, f(n)) où f est alors la valeur résultat calculée par chacun des [programmes implémentant les] algorithmes. Il suffit de reprendre le script précédent en adaptant le titre (ligne 21) et en remplaçant le précédent code à partir de la ligne 32 par :

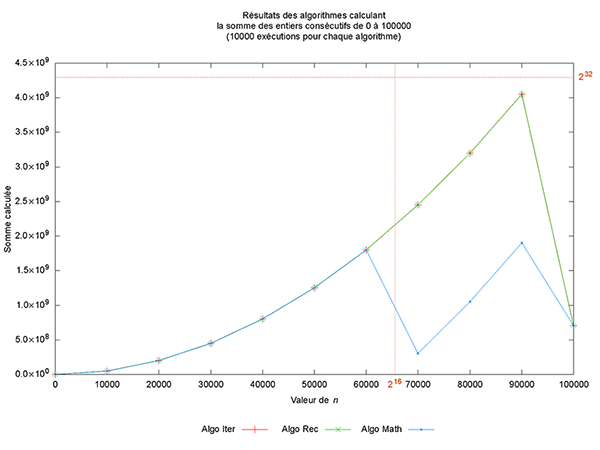
Ceci permet de générer la figure :

Damn it ! Ma qué sé passé-t-il ? L’algorithme le plus efficace semble ne pas être capable de calculer la bonne valeur pour n compris entre 60000 et 70000 et les deux autres algorithmes semblent s’effondrer également à partir d’une valeur de n comprise entre 90000 et 100000 (les repères permettant de visualiser les valeurs 2¹⁶ en abscisse et 2³² en ordonnée ont été générés par le code des lignes 39 à 46 et de la ligne 50).

Bon, il faut revenir sur un détail, le codage des entiers naturels en C se fait sur au moins 2 octets, mais généralement sur 4 octets sur les machines actuelles, donc effectivement il n’est pas possible de représenter une valeur plus grande que 2³² – 1. Ainsi, pour toute valeur de n > 92681, la somme dépasse la valeur maximale représentable et donc, quel que soit l’algorithme utilisé, le résultat sera mathématiquement erroné. Une solution consisterait à utiliser le type long long unsigned int, qui utilise 8 octets, mais cela ne fait que repousser le problème rencontré (certes, assez loin). J’écarte de facto la solution consistant à utiliser un float ou un double, puisque par essence, ce sont des approximations de valeurs réelles et non des valeurs exactes. J’entends au loin des personnes me disant que c’est parce que C n’est pas aussi haut niveau que d’autres langages comme le P... Ricanez, ricanez, mais c’est faux, car si vous voulez avoir une précision infinie, il suffit d’utiliser une librairie qui le permet à l’instar de gmp et tant d’autres [4]. Le souci, c’est que lorsque l’on utilise ces librairies, les opérations de calcul (les additions, dans le cas présent), les affectations ne se font plus à coût constant, ni en temps, ni en espace et cela m’éloigne de la grande question qui se pose ici : pourquoi la formule close échoue-t-elle avant les deux autres solutions ? Eh bien, la réponse est finalement assez simple, cela tient au fait que lorsque l’on calcule n * (n+1) / 2, les opérations sont exécutées en fonction de leur priorité, et en cas d’égalité, de la gauche vers la droite. Donc, dans le cas présent, le premier calcul effectué est n+1 (priorité des parenthèses sur les autres opérations), puis la multiplication, pour terminer sur la division. Lorsque le résultat de la multiplication dépasse 2³², et bien le reste du calcul est erroné. Or, quand n ≥ 2¹⁶, alors n² ≥ 2³² et donc n (n+1) > 2³².

Voilà qui vient disqualifier celui qui était présumé le meilleur des trois algorithmes.

2.2 Un peu d’algo à la rescousse

Il n’est pas envisageable de terminer l’article sur ce cuisant échec de conception. Mais en regardant de plus près, une solution assez simple consiste à effectuer la division par deux avant la multiplication. Il faut juste faire attention, car si n est impair (donc, n peut s’écrire n = 2m + 1), alors le résultat de la division entière de n par 2 donnera m, et le reste de la division sera perdu (et donc, le résultat final sera faux). Ceci étant dit, si n est impair, cela signifie que n+1 est pair.

L’algorithme consiste donc à tester la parité de n, et selon le résultat, il suffit alors de calculer n/2*(n+1) ou bien (n+1)/2*n.

Ceci donne une nouvelle version (disponible dans le sous-répertoire programmes/V2 du dépôt GitLab) à ajouter dans le fichier fonctions.c (ainsi que sa signature dans le fichier fonctions.h) :

Pourquoi l’avoir appelé SommeEntiersConsecutifsOptimiseeV1, vous demandez-vous sûrement. Eh bien tout simplement parce qu’il est possible de faire une version identique qui utilise des instructions binaires plutôt que des calculs arithmétiques, pour tester la parité d’une valeur ou faire une division par 2. C’est pourquoi voici la version SommeEntiersConsecutifsOptimiseeV2 à ajouter (les différences par rapport à SommeEntiersConsecutifsOptimiseeV1 sont mises en évidence) également pour le plaisir de tendre vers le bas niveau :

Bien évidemment, il faut également modifier la fonction get_fct_name() dans le fichier test_fonctions.c :

Et pour finir, il faut modifier le programme principal (fichier test_sommes.c) :

Comme précédemment, il suffit de recompiler tout et de générer les fichiers de données pour ces deux nouvelles implémentations :

Ensuite, dans les deux scripts gnuplot précédents, il suffit de modifier leur ligne 8 ainsi :

Les graphiques (non montrés ici) confirmeront que ces deux nouvelles versions sont exactes, tant que le résultat est représentable et la différence de temps de calcul entre les deux n’est pas perceptible.

2.3 Que peut-on faire de mieux ?

Et oui, l’optimisation de code en utilisant du binaire n’a visiblement rien changé, ce qui est rapide reste rapide. La question de savoir ce qui peut-être fait de mieux semble donc sans réponse. Et pourtant, il est intéressant de regarder ce que les options d’optimisation du compilateur apportent… ou pas.

Pour cela, reprenons les codes précédents, en les compilant avec les options d’optimisation allant de 0 à 3, puis pour chaque exécutable produit, testons-le.

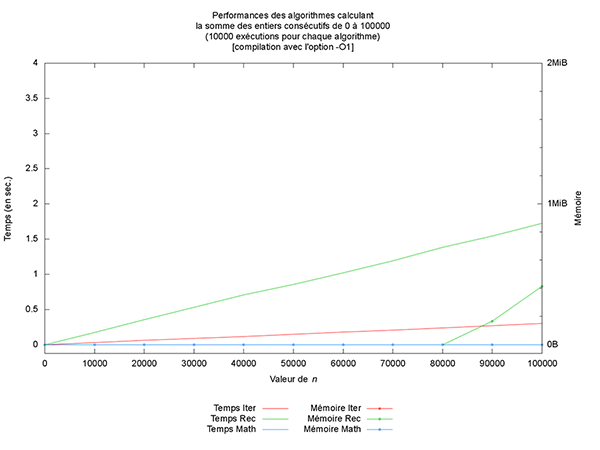
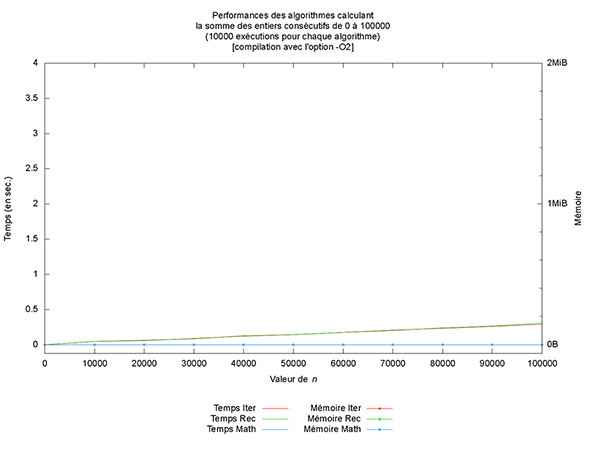
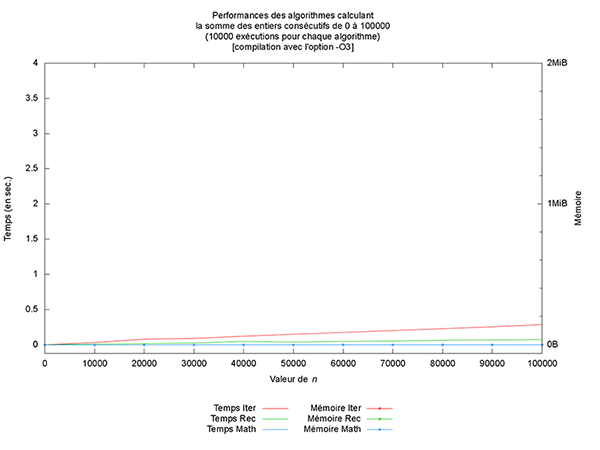
Première chose (non montrée ici), les optimisations du compilateur n’altèrent pas les résultats produits. Par contre, les performances observées sont clairement différentes (cf. figures ci-après). L’optimiseur de code porte vraiment bien son nom.

Mais outre une amélioration des temps de calcul, ce qui est le plus intéressant à mon sens est l’optimisation qui est faite en mémoire pour la version récursive. En effet, à partir du niveau 2, la version récursive n’utilise plus de mémoire additionnelle, comme montré sur la figure des performances de l’algorithme Rec. Cela provient du fait que le compilateur est capable de réécrire le code en exploitant la récursivité terminale et l’associativité de l’addition (mais cela est une autre histoire).

3. Généralisation et réutilisation

Maintenant que nous disposons d’un moyen de calculer la somme des n premiers entiers consécutifs, nous pouvons aborder le cas plus général consistant à sommer les entiers consécutifs allant de a à b, avec a ≤ b. Sa signature sera tout naturellement unsigned int SommeEntiersConsecutifsGenerale(unsigned int a, unsigned int b).

3.1 Sois fainéant (bis), tu vivras content

Bien évidemment, en bon feignant d’informaticien, nous avons tout intérêt à exploiter les codes précédents.

Une première version simple consiste donc à considérer que :

Et donc que :

Ceci donnerait hâtivement lieu à l’implémentation suivante (a est supposé inférieur ou égal à b ; je ne le teste pas pour plus de lisibilité des codes) :

Ceci pose bien évidemment un gros problème lorsque a vaut 0. En effet, ce paramètre étant de type entier non signé, a - 1 renvoie le plus grand entier non signé représentable, soit 2³²-1. Ceci étant dit, le résultat renvoyé sera 0 malgré tout, mais si la version utilisée pour calculer est linéaire en temps, alors cela prendra un temps vraiment considérable (y compris sur une bonne machine).

En réalité, il faut donc écrire :

Malgré d’éventuels dépassements de capacité lors des calculs intermédiaires (par exemple si b ≥ 2³¹), si le résultat est représentable, alors il sera correct (question de congruence).

3.2 Sois fainéant (bis), tu vivras longtemps

Le programmeur que je suis aurait allégrement pu crier « Hourra », si je n’avais aussi ma casquette d’algorithmicien. En effet, il y a un hic ! J’ai utilisé un cas particulier pour calculer un cas général. C’est à contresens d’une démarche logique.

Qu’à cela ne tienne, il suffit d’exploiter la formule générale suivante :

Ce qui se traduit (en repartant de ce qu’on avait écrit précédemment) par :

Et c’est là que le bât blesse ! Il y a quelques cas limites où cela ne fonctionne plus (par exemple, lorsque la somme de a et b vaut 2³², eh bien la fonction renverra 0, même si le résultat est représentable ; c’est le cas quand a = b = 2³¹).

Ici, les versions V0, V1 et V2 correspondent aux trois versions présentées.

Pour garantir de ne pas avoir de dépassement de capacité, plutôt que de calculer la somme de a et b, il suffit de vérifier s’ils sont tous les deux pairs ou bien tous les deux impairs (impliquant alors que leur somme est paire). Le cas échéant, en additionnant le quotient de a divisé par 2 et de b divisé par 2, nous obtenons la somme (a+b)/2 si a et b sont pairs et (a+b)/2 - 1 si a et b sont impairs. Il faut donc rajouter 1 si a (et donc b) est impair. Dans le second cas de figure, où a et b ne sont pas de même parité (donc leur somme est impaire), le calcul de la différence entre le quotient de b divisé par 2 et de a divisé par 2 nous donnera (b-a+1)/2 si b est pair et (b-a+1)/2-1 sinon. Le reste demeure inchangé.

Enfin, le cas particulier de la somme des n premiers entiers consécutifs s’écrit trivialement :

Conclusion

À travers cet exemple apparemment simple, nous pouvons tirer de nombreuses conclusions. Les premières que je propose sont des lapalissades, mais demeurent fondamentales : il ne faut pas se contenter de la première solution qui nous vient à l’esprit. Ensuite, ce n’est pas parce que le problème est simple qu’il ne mérite pas de s’y attarder. Ensuite (et ce n’est pas faute de le lire dans GLMF), il faut tester ses programmes, même les plus simples, cela évite des désagréments ultérieurs. J’ajouterai par ailleurs qu’un algorithme naïf ne signifie pas un algorithme bête. Il ne faut pas le déconsidérer. Enfin, concernant les morales de l’histoire, sous Linux, il existe de nombreux outils plus ou moins faciles d’utilisation en ligne de commande (p. ex. gdb, valgrind, gnuplot) qui peuvent vous aider à tester vos programmes et à visualiser vos résultats.

Nous pouvons également profiter de cette expérience pour remarquer que celle-ci est complètement reproductible, quel que soit votre système d’exploitation, confirmant par la même occasion que C est bien un langage de haut niveau, puisque nous avons fait abstraction du matériel.

Enfin, j’aime beaucoup cet exemple, car il illustre parfaitement mon point de vue sur la question posée en introduction de cet article. Je suis intimement persuadé qu’il faut être un bon programmeur pour être un bon algorithmicien et vice-versa (à moins que ce ne soit le contraire).

Références

[1] Monologue d’Otis (interprété par Édouard Baer) en réponse à Panoramix dans le film « Astérix & Obélix, mission Cléopâtre » (Alain Chabat, 2002).

[2] T. COLOMBO, « Des Giga-octets aux Gibi-octets », GNU/Linux Magazine n°191, mars 2016 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-191/Des-Giga-octets-aux-Gibi-octets

[3] Page d’accueil de l’outil gnuplot : http://www.gnuplot.info/

[4] Référencement de programmes et librairies permettant de faire du calcul en précision arbitraire :
https://en.wikipedia.org/wiki/List_of_arbitrary-precision_arithmetic_software 
et http://www.gnulinuxmagazine.com

Pour aller plus loin

Petite question qui ne sera pas posée non plus pour le bac 2021 : existe-t-il une différence entre programmeur et développeur ?