YaDiff est un outil permettant la propagation d’informations d’une base IDA vers une autre pour assister l’analyse de codes binaires. Il utilise un réseau de neurones entraîné à identifier les routines similaires.
Le projet YaDiff a vu le jour suite au problème récurrent du suivi de version lors de la rétro-ingénierie de binaires sous IDA. En effet, quel rétro-concepteur n'a jamais été confronté, après de longues heures d'analyse d'un binaire, à la difficulté de devoir transposer le fruit de son travail sur la toute dernière version dudit binaire ? Pour pouvoir porter les symboles de documentation d’une base IDA vers une autre, YaDiff doit être capable d’identifier les parties de code semblables de deux binaires différents.
La documentation qui accompagne les binaires désassemblés peut être issue de l’analyste ou du code source. Elle peut être présente sous forme de « symboles », c’est-à-dire de noms de fonctions, de données globales, de labels, commentaires, prototypes de fonctions ou données, renommage (variables, registres...), typage de structures, etc. Ces symboles, le nom des objets sont des informations essentielles pour l’analyse de binaires complexes.
Fréquemment, les références aux chaînes de caractères (« toto »), valeurs immédiates (0x42), instructions folkloriques (fabs), appels système (call WriteFile) permettent d’identifier des parties de code semblables. En effet, il s’agit de caractéristiques facilement identifiables qui agissent comme des marqueurs naturels, des points d’accroches pour une comparaison. Il existe plusieurs scripts qui identifient ces marqueurs et permettent parfois de reconnaître quelques fonctions. En fait, presque chaque analyste a le sien. Les plus téméraires propagent même les symboles entièrement à la main !
Cependant, afin de pouvoir exploiter intelligemment l’ensemble vertigineux de ces marqueurs, une des solutions les moins complexes aujourd’hui est d’utiliser un réseau de neurones. Ce réseau est le cœur d’un système qui prend en entrée deux fonctions (routines) et donne, en sortie, un score de similarité.
À la fin de ce bref article, non seulement vous comprendrez comment reconnaître les fonctions semblables au sein de binaires compilés, mais aussi, puisque la méthode employée est générique, vous serez capables d’utiliser un réseau de neurones afin d’identifier les éléments semblables de n’importe quelle collection à condition que :
- suffisamment de caractéristiques puissent être extraites de ces éléments ;
- suffisamment d’éléments connus (i.e. : étiquetés) existent pour constituer le corpus d’apprentissage.
La méthode décrite ci-après pourrait être adaptée pour cataloguer des logiciels, bâtiments, pages web, molécules, galaxies...
1. Des vecteurs de caractéristiques
Les informations de documentation d’un binaire accompagnent le code. Elles sont donc, à son image, encapsulées dans des fonctions. Le nom d’une fonction et son prototype sont des éléments cruciaux pour un analyste. D’autant qu’IDA propage les symboles de prototypages. Une fois une fonction reconnue, il n’est pas trop difficile d’identifier ses blocs basiques : la commande diff sur du code désassemblé puis standardisé donnera de bons résultats.
Les fonctions en langage assembleur peuvent être des objets complexes. Leur comparaison n’est alors pas une tâche évidente : si elle repose sur des marqueurs trop stricts tels que les hashs, l’association ne sera pas robuste aux changements, mais si elle repose sur des marqueurs trop simples, elle pourrait produire de fausses associations (i.e. : faux-positifs).
Puisque les marqueurs complexes (tels que des strings, n-grams, plus longue sous-chaîne commune) sont difficiles à exploiter, il est prudent de n’utiliser que des nombres entiers ou réels pour représenter les fonctions. Une fois mis côte à côte, ces scalaires forment des vecteurs représentant les fonctions, lesdits vecteurs de caractéristiques. Aux dépens de la perte de certaines informations, parfois marquantes, il est plus facile de travailler avec des vecteurs de taille fixe qu’avec une collection (i.e : tuple) de taille variable d’objets différents : (ex : séquences, arbres).
1.1 Une comparaison tolérante
Une même fonction peut différer de multiples façons :
|
Événement perturbateur |
Conséquence pour une fonction |
|
Nouvelle Compilation |
Changement d’offset Réagencement d’instructions |
|
Changement d’option de compilation |
Inclusion d’instruction ou données dans le code Aplatissement du graphe de flot de contrôle Inlining d’une fonction |
|
Changement de compilateur |
Changement de convention d’appel, changement des options d’optimisation Traitement différent des variables : des registres et de la mémoire (pile) |
|
Changement d’OS cible |
Changement d’API, d’appels systèmes Changement d’implémentation des bibliothèques statiques Différentes implémentations pour une même fonctionnalité, nom et prototype (exemple dans Vim [6] : mch_dirname implémenté dans os_unix.c ou os_win32.c) |
|
Mise à jour du code |
Ajout ou suppression d’instructions Changement de données référencées (tableaux, chaînes de caractères) Modification du graphe d’appels |
Au vu des changements que peut subir une fonction, pour la reconnaître au sein de binaires inconnus, il faut utiliser des signatures tolérantes aux changements. Mais de plus, ce n’est pas parce que deux fonctions partagent une signature rare qu’elles sont semblables. Par exemple, deux fonctions différentes pourraient référencer la même chaîne de caractères. Ce qui empêche l’usage exclusif de signatures complexes.
1.2 Recherche de scalaires
Une fois l’objectif fixé de représenter les fonctions par des vecteurs, il faut établir les coordonnées de ces vecteurs en cherchant les caractéristiques scalaires qui donnent un sens à une fonction. Une fonction est un ensemble d’instructions (1) formant son graphe de flot de contrôle (2). Une fonction peut en appeler d’autres ou être appelée par d’autres. Le graphe des appels est appelé à juste titre graphe d’appels (3). Il est possible de cueillir des valeurs scalaires de ces trois champs. La liste complète et à jour est présente dans le code de YaDiff [3].
1.2.1 Les instructions en langage assembleur
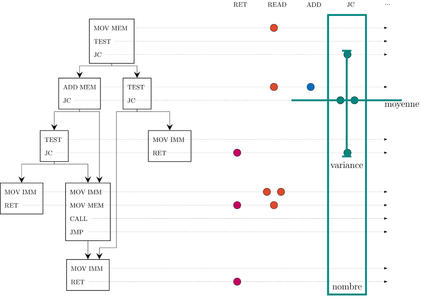
Une instruction est l’atome de tout code assembleur et donc des fonctions qui le constituent. Le logiciel de désassemblage en source libre Capstone [9] permet de les décoder. Les instructions reçoivent une ou plusieurs étiquettes selon leur type (arithmétique, lecture mémoire, saut conditionnel...). Chaque type d’instruction est compté. Par exemple, dans la fonction de la figure 1 il y a un appel (call). Mais de plus, la distribution de chaque type d’instructions au sein de la fonction est prise en compte. Puisqu’il est difficile de représenter une dispersion au sein des nœuds d’un arbre, ce dernier est aplati et puisque ces arbres aplatis sont de taille variable, la position d’une instruction est normalisée de zéro à un. Les positions moyennes, variances, kurtosis, etc. de chaque type d’instruction sont sauvegardés. Ce qui permet, toujours dans l’exemple de la figure 1, de conserver l’information que 4 sauts conditionnels (jc) sont plutôt vers le haut et séparés en moyenne d’une instruction.
Fig. 1 : Étiquetage des instructions, aplatissement du graphe de flot de contrôle puis extraction des moments centrés de leur distribution : moyenne, variance, kurtosis ...
1.2.2 La forme du graphe de flot de contrôle
Le graphe de flot de contrôle représente l’imbrication et les relations causales des instructions. Formellement, c’est un arbre binaire ordonné, orienté et enraciné. Il existe diverses manières de comparer les arbres : parcours de sous-arbres [1], distance d’édition, expressions régulières [2]… C’est toute une science de comparer des arbres : la dendrologie. Mais n’oublions pas le principe de tolérance aux changements : des nœuds peuvent être interchangés sans que cela change le flot d’exécution. Par exemple, des conditions d’optimisation pour sortir d’une boucle plus tôt peuvent apparaître. Quelques informations pourtant donnent rapidement un aperçu de l’arbre : sa hauteur, largeur, son nombre de feuilles, de nœuds, de branches, d'intersections en diamant (if ... then ... else), etc. Par exemple, le graphe de flot de contrôle de la fonction figure 1 possède 8 nœuds, 9 branches et 3 feuilles. Ces informations sont précieusement sauvegardées dans le vecteur de caractéristiques de chaque fonction.
1.2.3 Le graphe d’appels
À l’image du graphe de flot de contrôle, le graphe d’appels ne peut être exploité directement sous forme de graphe. Réduisons-le ! Pour chaque fonction, ce graphe apporte l’information de qui l’appelle (les appelants) et qui est appelé par elle (les appelés). Par exemple, vim_snprintf appelle vim_vsnprintf ainsi que deux petites fonctions et est appelée par une grande diversité de fonctions (198). Des objets référençant des objets semblables sont potentiellement semblables. Ici encore la probabilité de similarité dépendra d’autres facteurs venant des instructions ou du graphe de flot de contrôle.
Les fonctions sont représentées par un vecteur, nous en bénéficions pour la première fois. Chaque fonction s’est déjà vu attribuer un vecteur interne représentant ses instructions et son graphe de flot de contrôle. La moyenne et la médiane des vecteurs internes de ses appelants et de ses appelés seront sauvegardées dans le vecteur de caractéristiques de chaque fonction.
1.3 Concaténation : 1000 scalaires pour 1 vecteur
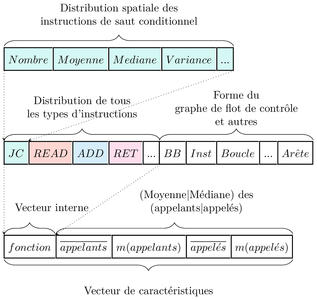
Fig. 2 : Concaténation des caractéristiques émanant du graphe de flot de contrôle, des différents types d’instructions d’une fonction et de ses appelants.
Le vecteur de caractéristiques est issu, comme prévu, d’une longue concaténation :
- Les scalaires indépendants (nombre d’appelés, nombre de références aux données …) : 10 nombres.
- La forme du graphe de flot de contrôle : on extrait 20 nombres.
- Les paramètres de distributions (au nombre de 5) de chaque type d’instruction (au nombre de 20) : 20 x 10 = 200 nombres.
- La moyenne et la médiane (2) des appelants et des appelés (2) du vecteur précédent : 2 x 2 x (10 + 20 + 200) = 920 nombres.
Il résulte donc de mise en commun de toutes ces caractéristiques, un vecteur de dimension 10 + 20 + 200 + 920 = 1150. Les deux fonctions C++ suivantes implémentent le processus de concaténation : après avoir accumulé pour chaque fonction ses caractéristiques dans une grande structure FunctionData_t, la fonction CreateConcatenatedVector crée les vecteurs de caractéristiques de toutes les fonctions.
#include<vector>
std::vector<double> FunctionData2Vector(const FunctionData_t& function_data);
/* Crée le vecteur de caractéristique pour toutes les fonctions
* - function_signature_map : Table de hashage qui associe à chaque fonction ses données
* Retourne : Le vecteur de caractéristique dans la function_signature_map
*/
void CreateConcatenatedVector(FunctionSignatureMap_t& function_signature_map)
{
// Crée le vecteur interne de chaque fonction
for (auto& it : function_signature_map)
{
FunctionSignature_t& function_signature = it.second;
function_signature.vector = FunctionData2Vector(function_signature.function_data);
}
// Pour chaque fonction
for (auto& it: function_signature_map)
{
FunctionSignature_t& function_signature = it.second;
// 1/ Interne : Initie le vecteur de caractéristique comme copie du vecteur interne
function_signature.concatenated_vector = function_signature.vector;
// 2/ Appelants
// Réunis les vecteurs internes des appelants dans une matrice
typedef std::vector<std::vector<double>> Matrix;
Matrix matrix = Matrix();
for (auto& parent_id : function_signature.parents)
{
std::vector<double> parent_vector = function_signature_map[parent_id].vector;
matrix.push_back(parent_vector);
}
// Concatène la moyenne et médiane des lignes (appelants) dans le vecteur de
// caractéristiques de la fonction courante
ConcatenateFamilly(function_signature.concatenated_vector, matrix);
// 3/ Appelés (même travail que les appelants)
....
}
}
/* Aplatie dans un vecteur les caractéristiques internes d'une routine
* - function_data: structure contenant l'ensemble des caractéristiques
* internes d'une fonction (nombre de blocs basiques, d'instructions de saut ...)
* Retourne: Vecteur interne de la fonction
*/
std::vector<double> FunctionData2Vector(
const FunctionData_t& function_data
{
std::vector<double> res ;
// Concatène les caractéristiques du graphe de flot de contrôle
res.push_back(static_cast<double>(function_data.cfg.bb_nb));
.............
res.push_back(static_cast<double>(function_data.cfg.flat_len));
// Concatène les moments centrés de la distribution de chaque type d'instruction
for (int i = 0; i < INST_TYPE_COUNT; i++)
{
InstructionData_t instruction_data = function_data.insts[(InstructionType_e)i];
res.push_back(static_cast<double>(instruction_data.total));
.............
res.push_back(static_cast<double>(instruction_data.offset_kurt_per_inst));
}
return res;
}
1.4 Diversité des caractéristiques
La démarche jusqu’ici consistait à rassembler un maximum de features (dans ce travail ce sont des nombres entiers ou réels) pour chaque objet. Puisqu’ils viennent de champs différents, ces caractéristiques ne sont pas faciles à exploiter ensemble. Elles sont nombreuses, parfois liées, suivent une dispersion variée, certaines sont plus importantes que d’autres. Pourtant, ce qui complique le plus la comparaison de ces vecteurs est la définition du semblable. Il serait possible de définir des limites du type : « si une fonction diffère d’une autre de plus de 3 instructions alors elles sont différentes », mais une instruction mov dans une boucle est potentiellement équivalente à 4 instructions mov à la suite (inlining). C’est ici que la solution des réseaux de neurones paraît la plus prometteuse : premièrement, les transformations ne sont pas limitées aux transformations linéaires des entrées, et deuxièmement, l’algorithme peut apprendre la logique derrière les données et être capable de plus de généricité.
En choisissant de représenter les fonctions sous forme d’un vecteur de taille fixe (mais tout de même avec beaucoup de valeurs), nous avons choisi de simplifier la problématique. Car analyser les chaînes (non orientées) des graphes devient vite très compliqué, surtout en apprentissage machine. Il reste maintenant à exploiter cela intelligemment afin que cela fonctionne.
2. Un réseau de neurones comme opérateur de projection
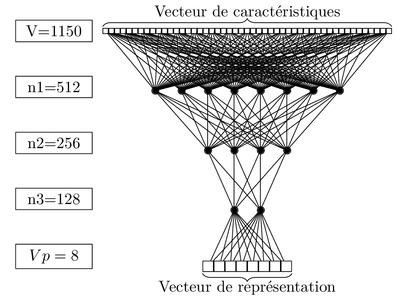
Fig. 3 : Une fois entraîné, ce réseau de neurones projette les vecteurs de caractéristiques dans un espace de dimension 8 (i.e. un vecteur réel de dimension 8) tel que les routines qui étaient considérées semblables lors de l’entraînement soient proches.
L’intérêt d’un réseau de neurones est qu’il peut être considéré comme un « approximateur universel » de fonctions très complexes qui prennent des entrées (routines) et donnent une sortie (décision). Cela marche bien aussi avec les fonctions simples, mais pour ces dernières, il y existe des méthodes plus directes. C’est en gros apprendre à faire « y = f(x) » connaissant les « x » et « y », mais pas « f ». Plus il y a de couples (x, y) à donner en exemple, meilleur sera le système. Dans notre cas, les « x » sont les vecteurs de caractéristiques des routines (avec ~1000 valeurs par fonction). Reste à déterminer « y », ce qui revient à se demander : que cherche-t-on exactement à trouver ? En reprenant l’exemple « y = f(x) », cela transforme une routine en langue assembleur en quelque chose de différent. Mais puisque le but est de comparer des routines entre elles, nous sommes plutôt dans le cas où nous essayons de trouver « y = f(x1, x2) » avec « x1 » et « x2 » deux routines et « y » la similarité (ou dissimilarité).
2.1 Les corpus
2.1.1 Le corpus d’apprentissage : les dépôts Debian
Comme dit précédemment, plus le système aura d’exemples pour apprendre plus il sera pertinent, un peu à la manière du cerveau humain. Par exemple, quelqu’un qui aurait vu l’ensemble des épisodes des 35 premières saisons des Feux de l’Amour (soit 8799 épisodes au total [7]), aurait alors une bien meilleure estimation des chances de succès du mariage entre Ashley et Tucker tout juste sorti de son coma [8], contrairement à une autre personne avec « seulement » 5 saisons à son actif.
Dans notre cas (qui est au moins aussi intéressant), il faut des binaires, plein de binaires. Et c’est encore mieux de savoir ce qu’il y a dedans (étiquetage). Les binaires des dépôts Debian (généralement compilés avec des options semblables) sont d’excellents candidats pour cela. Leurs étiquettes sont conservées (noms de binaires, noms de fonctions, architecture, etc.). Les vecteurs de caractéristiques de chaque fonction sont calculés comme vu précédemment. Cela constitue le corpus d’apprentissage (i.e. le dataset).
Dernière étape, l’ensemble du corpus (les valeurs flottantes) est normalisé pour avoir des valeurs aux mêmes échelles : cela améliore l’apprentissage. Pour les valeurs très importantes, une normalisation logarithmique est effectuée. Puis une simple normalisation linéaire borne les valeurs entre -1 et 1. À cette étape, il ne reste plus qu’à fournir ces données au réseau de neurones pour qu’il apprenne à notre place ce qui définit deux fonctions semblables (outre leur nom).
2.1.2 Le corpus de validation : nfsd.ko, cc1plus, libxhtml
La validation est cruciale pour … valider le modèle appris (d’où son nom). En effet, si on repose toujours les mêmes questions à un enfant et qu’on le corrige quand il se trompe, il saura donner la bonne réponse à la 3ème ou 4ème question, même s’il ne comprend pas la question.
Pour valider le système, une partie des binaires est donc mise de côté et tout vecteur de fonction qui serait similaire dans l’entraînement est écarté afin d’être sûr de demander au système d’évaluer des fonctions qu’il n’aura jamais vues. Le plus simple est d’isoler 3 ensembles de binaires avec des usages éloignés, pour limiter le biais d’une validation reposant uniquement sur un sous-ensemble spécifique de fonctions écrites pour un même objectif.
2.2 L’apprentissage
2.2.1 Un réseau triplet
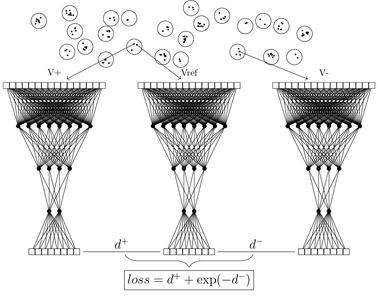
Fig. 4 : Un réseau triplet qui simultanément s’entraîne à obtenir un espace de sortie tel qu’une fonction semblable (V+) soit proche de la référence (Vref) et une fonction différente (V-) en soit loin.
L’algorithme utilisé est relativement simple. Basé sur un réseau de neurones, il emploie le principe des réseaux siamois, voir [10] par exemple, car il a pour but de comparer deux fonctions. Mais en fait, il en compare trois à chaque fois. Pourquoi trois ?
Trois vecteurs de caractéristiques sont fournis en entrée. Le premier vecteur est un vecteur dit de référence, le deuxième dit positif est un vecteur appartenant au même groupe de fonctions, et pour terminer un troisième vecteur dit négatif appartenant à un autre groupe de fonctions. Cela permet de fournir aux réseaux en même temps des fonctions similaires et dissimilaires. A posteriori, un espace de sortie à 8 dimensions suffit pour que le réseau de neurones représente correctement les fonctions en regroupant celles qui sont similaires. Passer de 1000 caractéristiques à 8 c’est plutôt sympa !
Le réseau qui est un réseau de type perceptron multicouche fait une projection non linéaire du vecteur d’entrée dans un espace de plus petite dimension. Le résultat de cette projection est appelé vecteur de représentation (embedding). L’opérateur de projection est défini dans la fonction Python projectron et la fonction de coût du réseau triplet dans la fonction triplet.
import tensorflow as tf
def projectron(vecteur_entrée, assertion_réutilise):
""" Crée un réseau de projection : 1150 -> 8
- vecteur_entrée: vecteur d'entrée, s'obtient avec
`tf.placeholder(tf.float32, [None, ts.vecsize], name='ref')`
- assertion_reutilise: booléen ce réseau est-il le clone d'un autre ?
Retourne: le réseau de neurones
"""
# La première couche du réseau est le vecteur de caractéristiques d'entrée
reseau = vecteur_entrée
with tf.variable_scope("réseau_de_décision"):
# Ajoute les couches densément connectées
for index, taille in enumerate([512, 256, 128]):
# Connecte la couche courante avec le réseau amont
reseau = tf.layers.dense(
inputs = réseau,
units = taille,
reuse = assertion_réutilise,
activation = tf.nn.leaky_relu,
name = 'dense_%d' % index,
)
# Ajoute la dernière couche qui décide avec une tangente hyperbolique
reseau = tf.layers.dense(
inputs = réseau,
units = 8,
reuse = assertion_réutilise,
activation = tf.nn.tanh,
name = 'output',
)
return reseau
def triplet(self):
""" Crée un réseau triplet pour l'apprentissage
- self: vecteurs de référence, positif et négatif dans leurs
placeholders
Retourne (dans self): les trois réseaux qui pourront prendre en entrée
les vecteurs de référence.
Le coût à minimiser pour ce réseau
"""
# Définition des caractères de remplissage (placeholders)
self.vecteur_reférence = tf.placeholder(tf.float32, [None, 1150], name='ref')
self.vecteur_positif = tf.placeholder(tf.float32, [None, 1150], name='pos')
self.vecteur_negatif = tf.placeholder(tf.float32, [None, 1150], name='neg')
# Création du réseau triplet
self.réseau_reférence = projectron(self.vecteur_reférence, False)
self.réseau_positif = projectron(self.vecteur_positif, True)
self.réseau_negatif = projectron(self.vecteur_negatif, True)
# Calcul de la métrique (ploss = positive loss)
ploss = tf.reduce_mean(tf.square(net_ref - net_pos), 1)
nloss = tf.exp(-tf.reduce_mean(tf.square(net_ref - net_neg), 1))
self.loss = ploss + nloss
return self
2.2.2 La Descente de gradient
L’entraînement consiste à donner au réseau de neurones des vecteurs en entrée et à évaluer ce qu’il en sort. Et s’il ne donne pas la bonne réponse (par exemple des vecteurs de représentation de fonctions différentes sont trop proches), il reçoit comme une décharge électrique au sens mathématique, qui va remonter tout le long du réseau de neurones pour qu’il se corrige. Et plus un neurone participe à la décision erronée, plus la puissance de la décharge et donc sa correction seront importantes.
En apprentissage machine, les termes suivants sont fréquemment employés :
- Taux d’apprentissage (learning rate) : c’est tout simplement l’amplitude de la châtaigne en cas d’erreur.
- La fonction de coût (loss function) : la « bonne » réponse attendue.
- Le surapprentissage (overfitting) : quand le système a appris par cœur les bonnes réponses, sans comprendre le pourquoi du comment. Et ça se voit en lui demandant de résoudre des exercices nouveaux, car il se loupe bien. Il existe des techniques pour éviter ou tout du moins limiter ces effets, voir [11] et [12].
2.3 Exploitation du réseau
L’extraction de caractéristiques puis le réseau de neurones entraîné projettent les fonctions dans un espace de dimension 8 où les distances euclidiennes ont le sens qu’on a voulu leur donner. Enfin, nous retrouvons notre sacré théorème de Pythagore ! Maintenant, il suffit de faire appel à des algorithmes anciens, simples, rapides, génériques, déjà implémentés de recherche de plus proches voisins afin de retrouver les fonctions semblables au sein de deux binaires différents. Dans un espace vectoriel euclidien, un analyste peut également mettre en base ces objets. Cette démarche permet principalement de donner un nom aux objets étudiés, ici des fonctions en langage assembleur.
Un article plus détaillé accompagné d’une vidéo, pour chacun des outils YaDiff et YaCo est disponible sur le site de la conférence SSTIC [4,5].
Conclusion
Le lecteur attentif est maintenant capable d’expliquer comment :
- Différencier des fonctions en langage assembleur.
- Différencier tout type d’objets représentables sous forme de vecteurs (et il en existe un paquet) !
- Collaborer avec une intelligence artificielle. Dans les deux sens, l’humain donne à la machine les données jugées pertinentes. En échange, en plus de cataloguer ces objets, la machine retourne à l’humain l’information des données qui étaient effectivement pertinentes lui suggérant par là même de décrire plus précisément ces données, d’approfondir ce secteur d’études.
- Déterminer lorsqu’un réseau de neurones est une méthode adaptée (i.e. : possible) ou non pour résoudre un problème.
Remerciements
Benoît Amiaux, Jérémy Bouetard, Léonard Caquot, Valérian Comiti, Frédéric Grelot et Maxime Pinard pour avoir participé au développement de YaDiff pour la Direction Générale de l’Armement sur le site de Maîtrise de l’Information (Rennes).
Références
[1] Gorille : G Bonfante, M Kaczmarek, Jean-Yves Marion : Architecture of a Morphological Malware Detector, Journal in Computer Virology. 5(3):263–270, 2009
[2] Tregexp : https://nlp.stanford.edu/software/tregex.shtml
[3] YaDiff: https://github.com/DGA-MI-SSI/YaCo
[4] YaCo: https://www.sstic.org/2017/presentation/YaCo
[5] YaDiff: https://www.sstic.org/2018/presentation/yadiff
[6] Vim 8.1.0000 : https://github.com/vim/vim/commit/b1c9198afb7ff902588b45fbe44f0760a9f48375
[7] Les Feux de l’Amour – Wikipédia : https://fr.wikipedia.org/wiki/Les_Feux_de_l%27amour
[8] Description épisode 9682 : https://www.programme-tv.net/news/series-tv/59986-les-feux-de-l-amour-ashley-a-epouse-tucker-mais-qui-sont-ses-anciens-epoux/
[9] https://www.capstone-engine.org/
[10] http://www.cs.utoronto.ca/~gkoch/files/msc-thesis.pdf
[11] A. Géron : Machine Learning avec Scikit-Learn, Mise en Œuvre et cas concrets, Dunod, 2017
[12] A. Géron : Deep Learning avec TensoFlow , Mise en Œuvre et cas concrets, Dunod, 2017



 Ajouter à une liste de lecture
Ajouter à une liste de lecture