Le ciel offre une variété étonnante d'objets célestes. Ces variétés ont fait l'objet depuis l'antiquité de classifications plus ou moins précises au fur et à mesure que les observations élargissaient le champ de nos connaissances. L'oeil et le cerveau humain ont su regrouper, expliquer et inventorier les éléments de l'Univers. Essayons alors d'utiliser la puissance du Machine Learning pour caractériser automatiquement ces galaxies lointaines et mystérieuses.
La data science c'est-à-dire l'utilisation des méthodes automatiques d'analyse de données de masse, n'a pas seulement pour but de chercher la photo de chat la plus « cute » pour la poster sur Facebook. Le Machine Learning est de plus en plus employé dans les différents domaines scientifiques et l'astrophysique n'échappe pas à la règle. En effet, l'augmentation de la puissance de traitement de données, mais aussi de la quantité de données fournie par les différents télescopes à travers le monde et les télescopes spatiaux a engendré une modification des méthodes d'analyse. Il est devenu indispensable de traiter statistiquement les observations et de pouvoir appliquer des algorithmes automatiques de traitement, de classification, afin de relier, trier, ordonner. Vous me direz que l'Univers a plus d'un tour dans son sac et que l'on ne pourra pas tout mettre dans des boîtes, et vous aurez raison. Toutefois, la science obéit à des règles auxquelles est soumise une grande majorité des objets célestes. Mettre en évidence ces règles permet de mieux expliquer les évolutions des galaxies et des étoiles et permet aussi de trouver des « outlyers », ces objets étranges qui peuvent défier la science et engendrer de nouvelles découvertes.
À noter avant d'aller plus loin, que cet article n'a pas la prétention d'être un cours de machine learning (ML), ni de proposer une méthode scientifique, et encore moins d'être exhaustif sur les différentes façons d'aborder ce problème. Nous vous proposons de vous montrer quelques exemples classiques de ML autour d'images de galaxies parce que cela vous laissera encore plus le loisir de découvrir la diversité du ciel nocturne. Avant de lire cet article, assurez-vous d'avoir lu les articles précédents de ce magazine sur les introductions sur le machine learning. N'hésitez pas à vous nourrir aussi d'Internet sur les sites listés en bibliographie.
1. Classification des galaxies
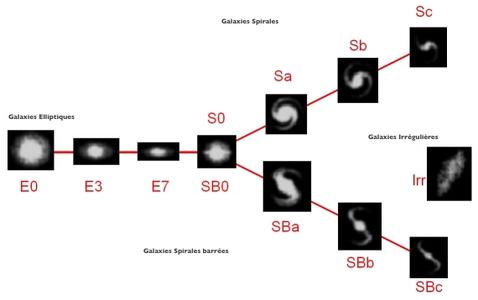
Depuis l'antiquité, les astronomes ont fourni une classification des objets du ciel, en partant des plus brillants, observés à l'œil nu, il y a plus de 5000 ans, vers les plus difficiles à observer, même avec un télescope de 8m de nos jours. Si le ciel est dominé par les étoiles de notre propre galaxie, la « Voie lactée», et les planètes de notre système solaire, il a fallu attendre les premiers télescopes pour accéder au monde un peu plus obscur, de faible luminosité, et observer les galaxies. Messier, en 1774, édite un catalogue de 110 objets diffus, qui en fait le premier référencement de nébuleuses et de galaxies. Vous pouvez voir ces objets sur le site de Wikipédia [1]. En 1936, E. Hubble (celui qui donna son nom au télescope spatial américain) a proposé une classification des galaxies en proposant un diagramme d'évolution [2] (figure 1). Ce diagramme a évolué durant les années (de Vaucouleurs, 1959 et 1964), Kormendy et Bender (1996), et d'autres par la suite, mais il reste encore la base des systèmes de classification d'aujourd'hui.
Fig. 1 : Séquence de Hubble (http://astronomy.swin.edu.au/cosmos/H/Hubble+Classification).
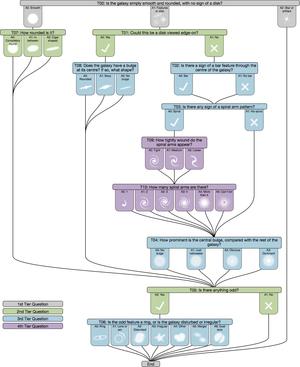
La classification des galaxies est une étape complexe qui vise à rassembler les objets par des caractéristiques communes dans des catégories fondamentales. Elle fait appel à des processus de décision qui implique une analyse de la morphologie, de la nature des objets, mais parfois aussi une analyse multidimensionnelle (temporelle et en longueur d'onde). Parfois même la classification dépend de la personne classant les données. Un bon exemple de ces processus de classification faite par les internautes, après un apprentissage initial, se trouve sur le site Galaxy zoo [3]. Vous pouvez vous amuser à visualiser et classer tout type de galaxies. Ce qui pourra non seulement vous faire rêver à d'autres mondes, mais aussi vous faire participer à la science astrophysique internationale.
Fig. 2 : Exemple de système de classification pour le site Galaxy zoo.
En restant synthétique, l'ensemble des galaxies peut être classé selon trois grandes catégories (voir figure 1), elliptiques (E), Spirales (S) (normales ou barrées) et Irrégulières (Irr). C'est cette approche (simpliste) que nous allons utiliser pour cette initiation dans le cadre de cet article. Nous allons dans la suite essayer de traiter automatiquement les nouvelles images afin de définir de classer les galaxies dans ces 3 classes.
2. Classification des galaxies avec du ML
2.1 Introduction
Le ML est une façon de modéliser un phénomène dans le but de prendre une décision ou de prédire une valeur. Le principe est de construire une représentation des données de façon automatique en entraînant notre machine sur un jeu de données de référence, c'est la phase d'apprentissage. Cette machine est ensuite utilisée pour prédire des valeurs ou identifier des propriétés. Les points importants de cette méthode sont :
- En premier lieu, les données, c'est la base ! Plus elles seront propres et comprises, plus la suite sera facile. Dans le cadre de cet article, les données ont déjà été traitées et nettoyées, les traitements supplémentaires que nous allons faire auront seulement pour but d'adapter au mieux nos données aux algorithmes ;
- La tâche à accomplir : comme pour les données, plus elle sera claire et précise, plus la suite sera facile. Dans le cadre de cet article, la tâche est d'effectuer une classification supervisée des objets identifiant le type de galaxie ;
- L'algorithme d'apprentissage, à choisir en fonction des données, de leur dimension, de leur quantité, mais aussi en fonction de la tâche à accomplir, régression ou classification, supervisé ou non-supervisé. Dans le cadre de cet article, plusieurs algorithmes seront testés pour avoir une vision globale des possibilités du machine learning ;
- L'évaluation des performances du modèle : cette évaluation est nécessaire pour valider le modèle et pour comparer plusieurs algorithmes. Dans le cadre de cet article, plusieurs tests seront définis pour comparer les algorithmes utilisés.
2.2 Les données astrophysiques
Nous allons travailler avec les données astrophysiques du projet COSMOS (Cosmic Evolution Survey) [6]. Ce sondage a été défini par une collaboration de 200 scientifiques conduits par Peter Capak pour résoudre les problématiques de formation et d'évolution des galaxies. Il couvre une région d'environ 2 degrés carrés qui a été couverte par un ensemble de télescopes donnant une couverture unique en longueur d'onde et en précision d'un échantillon de près de deux millions de galaxies.
Fig. 3 : Champ d'observation du projet COSMOS : http://cosmos.astro.caltech.edu/page/public.
Nous allons nous limiter à une partie de quelques milliers de galaxies qui ont été classées visuellement. Ces données sont disponibles sur le site https://gitlab.com/jz_42/AstrophysicML/.
$ git clone git://gitlab.com/jz_42/AstrophysicML.git <mydatadirectory>
$ cd <mydatadirectory>/data/
En n'oubliant pas de modifier le <mydatadirectory> par un répertoire local de votre choix.
Dans le dossier <mydatadirectory>, vous devriez avoir un répertoire data contenant :
- un fichier texte de 13000 objets ayant été classés ;
- un répertoire image contenant 3998 images de galaxies déjà classifiées ;
- un répertoire new_image contenant 1000 images de galaxies non classifiées.
Attention, ces données représentent environ 474 Mio de données, prévoyez un peu de temps pour les télécharger.
3. Avant d'aller plus loin
Avant d'aller plus loin, et en attendant que le téléchargement des données se termine, je vous invite à installer, si ce n'est pas déjà fait, les bibliothèques Python que nous allons utiliser par la suite. Nous allons utiliser pip, l'outild'installation de packages Python (https://pypi.python.org/pypi/pip). Vous pouvez bien évidemment, utiliser votre gestionnaire de paquets préféré à la place. Voici les paquets à installer :
- numpy/scipy : comme le conseille la documentation, vous pouvez installer également toute leur suite, afin de pouvoir manipuler les données, faire des plots. Ces outils vous seront très utiles ;
$ pip install --user numpy scipy matplotlib ipython jupyter pandas sympy nose
- scikit-learn, une bibliothèque simple et efficace d'outils pour le data mining et l'analyse de données (oui j'ai juste traduit ce qu'on peut lire sur leur page d'accueil, mais c'est la vérité) ;
$ pip install --user scikit-learn
- Keras, une API de réseaux de neurones de haut niveau que nous utiliserons dans la dernière section pour nous essayer au deep learning ;
$ pip install --user keras tensorflow np_utils
- fitsio : cette bibliothèque va vous permettre de lire les fichiers FITS (https://fits.gsfc.nasa.gov/fits_documentation.html), format souvent utilisé en astrophysique.
$ pip install --user fitsio
Attention, ces bibliothèques de calcul scientifique évoluent rapidement et il est possible que quelques ajustements soient nécessaires pour reproduire les exemples si vous n'avez pas exactement les mêmes versions. Je vous invite à consulter les documentations de chaque package. Si vous voulez être sûr de pouvoir copier-coller chacune des commandes, voici comment installer les mêmes versions de bibliothèques que celles utilisées dans cet article :
$ pip install --user numpy==1.13.3 fitsio==0.9.11 matplotlib==2.1.0 sklearn==0.19.1 keras==2.0.9
Votre environnement est prêt, nous pouvons enfin charger nos données.
- Python 2.7 n'est plus maintenu depuis le 1er janvier 2020, passez à Python 3.
- Le code de l'article est en principe compatible avec python 2.7 grâce aux "from future". Si l'encodage des fichiers est différent de l’encodage par défaut de python 2.7 (ASCII), il faut le préciser dans l'entête des fichiers. Par exemple pour de l'utf-8, il faut ajouter la ligne suivante:
Pour plus de détails, voir la pep 263 : https://www.python.org/dev/
# ce programme est aussi compatible avec python 2
from __future__ import print_function
import os,glob
import numpy
import fitsio
# Initialisation d'une liste pour contenir les images
# et d'une liste pour contenir les types morphologiques
raw_data =[]
type_morph =[]
# Définir les chemins vers les images et le catalogue,
# à remplacer par vos chemins bien sûr!
mydataDir ='</mydatadirectory/>'
mycatalog_path =os.path.join(mydataDir,'data-COSMOS-10000-id.txt')
# Chargement des données qui nous intéressent dans le catalogue
ids, mod = numpy.loadtxt(mycatalog_path, unpack=True, usecols=(0,3))
# Chargement des images
for one inglob.glob(mypath_template):
# Extraction de l'id à partir du nom de fichier
idi =int(one.split('/')[-1].split('_')[0])
modi = mod[ids==idi][0]
# On va ignorer les out layer ie les mod == 0
if modi>0:
# Ajout de l'image
raw_data.append(fitsio.read(one))
# Ajout du type morphologique
type_morph.append(modi)
# Reformatage en numpy pour plus de facilité
raw_data = numpy.asarray(raw_data)
type_morph = numpy.asarray(type_morph)
Nous pouvons utiliser l'utilitaire de plot de matplotlib pour vérifier et visualiser les données (figure 4) :
# Dans un ipython notebook
# utiliser la commande %matplotlib inline
from matplotlib import pyplot as plt
# Un petit graphique pour illustrer
fig = plt.figure(figsize=(7,7))
for i inrange(9):
plt.subplot(330+i+1)
plt.imshow(raw_data[i])
plt.title('type %d'%(type_morph[i]))
plt.axis('off')
# Visualiser le plot
plt.show()
Fig. 4 : Visualisation des 9 premières images de galaxies de l'échantillon ainsi que du type morphologique associé (1 = « Elliptiques », 2= « Spirales », 3 = « Irrégulières »).
3.1 Transformation des données
Bien que les données aient déjà été traitées et nettoyées, deux transformations sont toutefois requises.
D'une part, l'implémentation des algorithmes de scikit-learn s'attend à recevoir en entrée des données standardisées, c'est-à-dire transformées de façon à avoir une moyenne nulle et une variance égale à un. Sans rentrer dans le détail, le but de cette transformation est de permettre une variation de poids uniforme quand on les applique aux données.
D'autre part, la plupart des algorithmes de scikit-learn n'acceptent que des données sous forme de vecteurs en entrée alors que nos images sont des matrices. On peut simplement convertir nos matrices M x N (nos images donc) en vecteur de taille MN. Par exemple, 100 matrices de 100 x 100 pixels chacune, peuvent être converties en 100 vecteurs contenant chacun 10000 éléments.
Voici le code qui va nous permettre de transformer nos données :
# Normalisation des images
data_scaled = numpy.asarray([(img-img.mean())/img.std()for img in raw_data])
# Transformation en 1d array
data_1d = data_scaled.reshape((data_scaled.shape[0],-1))
# Vérifions avec la dimension des données sous forme de vecteurs
print(data_1d.shape)
# Et une valeur moyenne d'environ 0
print(data_1d.mean())
3.2 Modélisation
Il existe de très nombreux modèles d'apprentissage, nous allons en tester quelques-uns, mais avant cela vous vous demandez probablement : « Quelle est la différence entre un bon et un mauvais modèle d'apprentissage ? ». Bon, comme diraient les célèbres inconnus, « y a le mauvais modèle d'apprentissage : y voit un truc qui bouge : ben y tire... ».
Plus sérieusement, cela dépend du problème. Mais dans le choix du modèle, un point devrait toujours revenir : sa capacité à être généralisé. C'est le fait de pouvoir être utilisé sur un autre échantillon de données en conservant les mêmes performances. Par exemple, un modèle très complexe peut donner l'impression de reproduire parfaitement les données utilisées pour l'entraîner, mais lorsqu’on l'utilise sur un autre échantillon équivalent, ce même modèle donne des résultats aberrants. C'est ce qu'on appelle le sur-apprentissage. Au contraire, un modèle trop simple ne permettra pas de représenter la complexité des données et génèrera toujours trop d'erreurs. En d'autres termes (en termes statistiques), il faut trouver le bon compromis entre biais et variance. Le bon modèle est suffisamment complexe pour bien représenter les propriétés des données, mais suffisamment simple pour ne pas interpréter les erreurs comme une propriété de ces données.
Bien souvent, il s'agit surtout de poser le problème correctement, c'est-à-dire de choisir le meilleur modèle, mais il ne faut pas non plus omettre les contraintes de temps de calcul. Par exemple pour cet article, il serait inutile d'utiliser un exemple qui demanderait des mois d'entraînement sur un superordinateur. Le choix s'est porté sur un apprentissage qui peut tourner sur un laptop en quelques minutes.
Avant de commencer à mettre en place notre « classifier », et pour mieux comprendre les résultats, il est indispensable de parler en quelques mots de l'évaluation des performances.
3.3 Évaluation des performances
L'évaluation des performances sert à comparer deux modèles afin de déterminer quel est le meilleur. Cela peut être pour choisir entre deux algorithmes d'apprentissage ou d'optimiser, pour un même algorithme, les différentes valeurs d'hyper-paramètres ou enfin de sélectionner différentes façons de pré-processer les données...
Une méthode facile à mettre en place, en général, est la validation croisée qui consiste, dans sa version la plus simple, à séparer son échantillon en un jeu d'entraînement et un jeu de test. Le jeu d'entraînement sera utilisé pour entraîner le modèle et le jeu de test pour évaluer les performances. Ce test peut être, toutefois, dépendant de la méthode de séparation de l'échantillon. Il faut s'assurer que la distribution des propriétés des ensembles est bien la même dans l'échantillon initial et dans les jeux d'entraînement et de test. Mais, même dans ce cas, le résultat peut dépendre de la proportion des deux jeux.
Des versions d'évaluation des performances plus évoluées sont souvent utilisées pour pallier à ces différents biais. Par exemple, la validation croisée « k-fold » consiste à séparer l'échantillon initial en k jeux de données, choisir un jeu de test et entraîner sur les (k - 1) autres jeux et répéter l'opération k fois en changeant le jeu de test. Bien que plus fiable, on voit bien que cette méthode nécessite beaucoup plus de temps de calcul. Dans la suite, nous allons nous contenter de la validation croisée avec un jeu d'entraînement et un jeu de test.
4. Méthodes de classifications
4.1 Support Vector Machine
Nous allons commencer notre étude par l'utilisation d'une machine à vecteur de support (en anglais support vector machine, ou SVM) parce qu’a priori c'est un algorithme simple de prédiction linéaire, c'est-à-dire qu'il calcule une combinaison linéaire (somme pondérée) des variables d'entrée pour prédire la valeur de sortie. Dans le cas de la classification, vous pouvez voir ça comme un algorithme qui essaie de séparer vos points par des droites. Ce n'est pas complètement aussi simple. Il existe des hyper-paramètres, c'est-à-dire des paramètres fixés a priori dans le modèle. Par exemple la « marge » permet de donner, en quelque sorte, une largeur aux droites de séparations. Il est aussi possible, par changement de référentiel, de faire des séparations avec des fonctions plus complexes qu'une droite dans le référentiel d'origine.
Tout ce blabla peut être résumé en deux lignes de code avec scikit-learn :
from sklearn import svm
# Création d'un classifieur
# (Support Vector Classifier)
svm_clf = svm.SVC()
Nous pouvons lancer l'apprentissage de notre SVM (cette étape prend quelques minutes). Dans cet exemple, l'apprentissage se fait sur une partie de l'échantillon et les données sont entraînées sur les données data_train et type_train qui ont été sélectionnées par la fonction split().
from sklearn.model_selection import train_test_split
# Utilisation de la fonction train_test_split de sklearn
# pour séparer les jeux d'entraînement et de test
data_train, data_test, type_train, type_test = train_test_split(data_1d, type_morph, test_size=0.33)
# La méthode fit() permet de réaliser l'apprentissage sur le jeu d'entraînement
svm_clf.fit(data_train, type_train)
La façon de la plus simple de calculer la performance de l'algorithme dans le cas d'une classification est d'utiliser l'échantillon de test pour prédire la classe avec le modèle entraîné et de comparer les prédictions avec les classes de références.
En ne s'intéressant qu'à un cas binaire, quatre cas sont possibles pour une valeur testée :
- le cas vrai positif (VP), la valeur testée est identifiée comme appartenant à la classe et cette valeur appartient bien à la classe ;
- le cas vrai négatif (VN), la valeur test est identifiée comme n'appartenant pas à la classe et n'appartient effectivement pas à la classe ;
- le cas faux positif (FP), la valeur test est identifiée comme appartenant à la classe, mais elle n'appartient pas à la classe ;
- le cas faux négatif (FN), la valeur test est identifiée comme n'appartenant pas à la classe alors qu'elle appartient à la classe.
Toujours dans le cas d’une seule classe, il est possible d'estimer le nombre de vrai/faux positifs/négatifs pour toutes les valeurs de l'échantillon de test et d'obtenir ainsi la matrice de confusion. En appliquant le même principe au cas avec N classes, il y aura (N - 1) cas faux différents (en fonction de la classe choisie par erreur) et la matrice de confusion sera de taille N x N.
À partir de ces chiffres, nous pouvons dériver plusieurs estimateurs de performance comme :
- la précision = #VP / (#VP + #FP), c'est-à-dire le taux de bonnes réponses sur l'ensemble des réponses mesurées comme vraies ;
- la sensibilité (recall en anglais) = #VP / (#VP + #FN), c'est-à-dire le taux de bonnes réponses positives par rapport à l'ensemble des réponses qui sont effectivement vraies ;
- la spécificité = #VN / (#VN + #FP), c'est-à-dire le taux de bonne réponse négative par rapport à l'ensemble des réponses qui sont effectivement vraies ;
- le f-score = 2 x ( précision x sensibilité ) / ( précision + sensibilité ).
Les estimateurs de performance étant multiples, choisir le meilleur modèle n'est pas évident et dépend de l'utilisation qui sera faite du modèle. L'exemple classique, afin de bien comprendre, est celui de la classification des champignons. On veut bien sûr identifier avec la meilleure précision possible les champignons comestibles, mais on préfèrerait éviter de classifier comestible par erreur un champignon hallucinogène et on ne veut surtout pas se tromper sur un champignon mortel !
Il existe bien sûr d'autres façons d'estimer les performances que nous n'utiliserons pas. Pour aller plus loin, vous pouvez utiliser la courbe de ROC, comme dans l'exemple de scikit-learn (http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html), et les comparaisons aux cas naïfs, aussi illustrés dans la documentation de scikit-learn (http://scikit-learn.org/stable/auto_examples/calibration/plot_compare_calibration.html).
Enfin voici un peu de code pour illustrer tout ça ! Dans un premier temps, il faut calculer les valeurs prédites par le modèle :
from sklearn import metrics
# Maintenant on calcule les prédictions du modèle
type_mod = svm_clf.predict(data_test)
On peut ensuite s'intéresser à la matrice de confusion :
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod))
Le résultat obtenu est :
Matrice de confusion
[[211 79 0]
[ 31 788 0]
[ 0 208 1]]
Dans le cas idéal, cette matrice serait diagonale, et la valeur de l'élément (i,i) de la diagonale, donnerait le nombre de galaxies dans la classe i. Ici, les éléments non diagonaux ne sont pas nuls et la valeur de l'élément (i,j) est le nombre de galaxies de classe i, mais prédites comme appartenant à la classe j. Le nombre total de galaxies de la classe i (appartenant réellement à la classe i) est la somme des éléments de la ligne i et le nombre total de galaxies prédites avec la classe i est la somme des éléments de la colonne i.
Enfin, nous pouvons afficher la précision, la sensibilité et le f-score :
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod))
Résultat :
Précision, sensibilité, f-score
precision recall f1-score support
1.0 0.87 0.73 0.79 290
2.0 0.73 0.96 0.83 819
3.0 1.00 0.00 0.01 209
avg / total 0.81 0.76 0.69 1318
Les différentes valeurs de précision et de sensibilité, permettent de se faire une idée des résultats croisés par rapport aux différentes valeurs attendues. Les valeurs 1, 2, 3 représentent les classes (Elliptiques, Spirales, Irrégulières). Idéalement, les niveaux de précisions, sensibilités et f-scores de chaque classe devraient être égales à 1. Le support est simplement le nombre d'objets considérés dans les différents calculs.
Pour revenir rapidement sur les hyper-paramètres, il existe une classe dans scikit-learn pour optimiser ces hyper-paramètres : GridSearchCV. Attention, toutefois, avant de lancer le code qui suit, cela prend typiquement 20 minutes avec 8 jobs tournant en parallèle (1 par processeur) sur un laptop. À ne lancer que si vous avez du temps ou une machine assez puissante.
from sklearn.model_selection import GridSearchCV
# Les hyper-paramètres à explorer :
# * les quatre noyaux implémentés dans SVC
# * 4 valeurs de marge
parameters ={'kernel':('linear','poly','rbf','sigmoid'),'C':[1,5,10,20]}
# Attention adapter njob à votre machine !
grid_clf = GridSearchCV(svm_clf, parameters, n_jobs=8)
grid_clf.fit(data_train, type_train)
type_mod = grid_clf.best_estimator_.predict(data_test)
print("Meilleur classifieur\n", grid_clf.best_estimator_)
Nous obtenons :
Meilleur classifieur
SVC(C=10, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Nous pouvons ajouter :
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod))
Avec pour résultat :
Matrice de confusion
[[227 62 1]
[ 42 735 42]
[ 0 161 48]]
Ou encore :
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod))
Et nous obtenons :
Précision, sensibilité, f-score
precision recall f1-score support
1.0 0.84 0.78 0.81 290
2.0 0.77 0.90 0.83 819
3.0 0.53 0.23 0.32 209
avg / total 0.75 0.77 0.74 1318
Par défaut, GridSearchCV optimise le score par défaut du classifier, le f-score dans le cas du SVC. Avec les nouveaux hyper-paramètres, le f-score est effectivement meilleur, on remarque qu'en revanche la précision a été dégradée.
4.2 Les méthodes ensemblistes
Le principe des méthodes ensemblistes est de combiner statistiquement plusieurs modèles pour prédire un résultat plus robuste. Ces méthodes se décomposent en deux catégories : les méthodes dites parallèles, qui entraînent les modèles indépendamment et les méthodes séquentielles, aussi appelées « boost », qui génèrent les modèles de façon itérative en pondérant les données qui sont sources d'erreurs.
4.2.1 Random Forest
Parmi ces modèles, le Random Forest est un modèle très intéressant dans les méthodes ensemblistes parallèles. Cet algorithme est réputé pour avoir d'excellentes performances sur la plupart des problèmes et il est intrinsèquement parallélisable. C'est une bonne façon d'aborder un problème pour avoir une estimation des performances sans trop se poser de questions !
Faisons un essai :
from sklearn.ensemble import RandomForestClassifier
# Une bonne valeur pour n_estimator est en général sqrt(m)
# m étant la taille des données
# ici n_estimators=100 pour nos images de 100 x 100
rf_clf = RandomForestClassifier(n_estimators=100)
rf_clf.fit(data_train, type_train)
type_mod = rf_clf.predict(data_test)
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod))
Le résultat est :
Matrice de confusion
[[192 98 0]
[ 5 814 0]
[ 0 207 2]]
En ajoutant des informations :
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod))
Nous obtenons :
Précision, sensibilité, f-score
precision recall f1-score support
1.0 0.97 0.66 0.79 290
2.0 0.73 0.99 0.84 819
3.0 1.00 0.01 0.02 209
avg / total 0.83 0.76 0.70 1318
Les performances sont tout à fait comparables à notre SVM pour un temps de calcul bien meilleur.
4.2.2 Boost-tree
Les boost-tree sont également très intéressants, bien que plus coûteux en temps de calcul. Nous pouvons tester AdaBoostClassifier puis GradientBoostingClassifier :
from sklearn.ensemble import AdaBoostClassifier
ab_clf = AdaBoostClassifier(n_estimators=100)
ab_clf.fit(data_train, type_train)
type_mod = ab_clf.predict(data_test)
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod))
Avec le résultat pour AdaBoostClassifier :
Matrice de confusion
[[229 55 6]
[ 63 618 138]
[ 0 123 86]]
Et comme toujours, ajout d'informations :
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod))
Ce qui donne :
Précision, sensibilité, f-score
precision recall f1-score support
1.0 0.78 0.79 0.79 290
2.0 0.78 0.75 0.77 819
3.0 0.37 0.41 0.39 209
avg / total 0.71 0.71 0.71 1318
Puis pour GradientBoostingClassifier :
from sklearn.ensemble import GradientBoostingClassifier
gb_clf = GradientBoostingClassifier(n_estimators=100)
gb_clf.fit(data_train, type_train)
type_mod = gb_clf.predict(data_test)
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod))
Résultat :
Matrice de confusion
[[209 80 1]
[ 27 766 26]
[ 0 186 23]]
Ajout des informations :
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod))
Et nous obtenons :
Précision, sensibilité, f-score
precision recall f1-score support
1.0 0.89 0.72 0.79 290
2.0 0.74 0.94 0.83 819
3.0 0.46 0.11 0.18 209
avg / total 0.73 0.76 0.72 1318
Pour notre problème, les deux algorithmes testés donnent des résultats plus homogènes et plus stables et permettent un degré de confiance plus important dans les résultats.
4.3 Les réseaux de neurones
Un neurone artificiel est une fonction mathématique qui reçoit une ou plusieurs entrées et les additionne pour produire une sortie. Habituellement, chaque entrée est pondérée séparément et la somme est filtrée par une fonction non linéaire appelée fonction d'activation. Un réseau de neurones (artificiels) est donc un ensemble de neurones connectés. Chaque connexion entre les neurones peut transmettre un signal à un autre neurone. Le neurone de réception peut traiter les signaux qui lui sont envoyés et transmet sa sortie aux neurones qui lui sont connectés en aval dans le réseau.
Le réseau de neurones le plus simple est le perceptron composé d'une couche d'entrée avec un neurone par entrée tous reliés à un neurone de sortie. Ce réseau permet de représenter des modèles basés sur une combinaison linéaire des variables. Pour des modèles plus complexes, on peut ajouter des couches intermédiaires, appelées couches cachées. Chaque neurone d'une couche est connecté à tous les neurones de la couche au-dessus de lui. C'est ce qu'on appelle le perceptron multi-couches (ou multilayer perceptron en anglais, « MLP »). Empiler des perceptrons en un réseau de neurones multi-couches permet de modéliser des fonctions arbitrairement complexes. C'est ce qui donne aux réseaux de neurones profonds la puissance prédictive qui fait actuellement leur succès. Mais plus il y a de paramètres, plus la quantité de données d'apprentissage nécessaire afin de définir les valeurs de ces paramètres sans risquer le sur-apprentissage, est important. Il existe de nombreuses autres architectures de réseaux de neurones, on utilisera notamment dans la section sur le deep learning les « CNN ».
Entraînons donc un MLP sur nos images de galaxies. Commençons sagement avec une couche cachée de 100 neurones :
from sklearn.neural_network import MLPClassifier
# Créer un classifier avec 100 neurones cachés
mlp_clf = MLPClassifier(hidden_layer_sizes=100)
mlp_clf.fit(data_train, type_train)
type_mod = mlp_clf.predict(data_test)
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod))
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod))
Résultat :
Matrice de confusion
[[238 46 6]
[219 538 33]
[ 25 182 31]]
Précision, sensibilité, f-score
precision recall f1-score support
1.0 0.49 0.82 0.62 290
2.0 0.70 0.68 0.69 790
3.0 0.44 0.13 0.20 238
avg / total 0.61 0.61 0.59 1318
Les résultats ne sont pas fameux ! En effet, les valeurs de la précision et de la sensibilité (recall) sont bien inférieures à celles obtenues avec les méthodes de SVM. Et le score f1 reste en deçà des valeurs obtenues précédemment. Notre modèle génère probablement trop d'erreurs parce que trop simple, c'est-à-dire que le réseau de neurones ne dispose pas de suffisamment de neurones pour bien reproduire les propriétés de nos galaxies. Bien choisir le nombre de neurones et de couches est un problème assez difficile. Il existe des méthodes très intelligentes pour aborder ce problème, mais pourquoi être subtil quand on peut ne pas l'être. Essayons donc la manière brute :
# Boucle sur quelques valeurs de nombre de neurones par couche
for n_neu in[50,100,200]:
# Boucle sur le nombre de couche
for n_lay in[1,2,3]:
# Pour définir plusieurs couches, il suffit de passer au MLPClassifier
# un hidden_layer_sizes sous forme de tuple
layer = tuple([n_neu for n inrange(n_lay)])
print("Layers: %s"%str(layer), end=' ')
mlp = MLPClassifier(hidden_layer_sizes=layer)
mlp.fit(data_train, type_train)
print("Test set score: %f"% mlp.score(data_test, type_test))
Nous obtenons :
Layers: (50,) Test set score: 0.526555
Layers: (50, 50) Test set score: 0.600152
Layers: (50, 50, 50) Test set score: 0.583460
Layers: (100,) Test set score: 0.597876
Layers: (100, 100) Test set score: 0.597876
Layers: (100, 100, 100) Test set score: 0.603187
Layers: (200,) Test set score: 0.596358
Layers: (200, 200) Test set score: 0.629742
Layers: (200, 200, 200) Test set score: 0.628225
Pour être gentil avec les personnes impatientes qui ont fait du copier/coller rapidement, les valeurs explorées pour le nombre de neurones par couche et le nombre de couches ont été choisis de façon raisonnable. Les résultats restent toujours peu satisfaisants, mais il est notable qu'augmenter le nombre de neurones augmente significativement la valeur du score. En comparant deux modèles avec le même nombre de neurones comme (100, 100) et (200) les scores, respectivement 0.597876 et 0.596358, ne sont en revanche pas très différents. Cela suggère qu'une première optimisation de notre modèle serait d'utiliser une seule couche cachée et d'augmenter le nombre de neurones de cette couche jusqu'à ce que l'ajout de neurones n'améliore plus le score. Vous pouvez bien sûr vous amuser à faire cela et, éventuellement, essayer ensuite de trouver le nombre de couches idéales. Mais le temps d'entraînement risque de rapidement devenir très long. Je vous invite donc avant d'essayer, à jeter un œil à la suite pour découvrir le deep learning.
4.4 Le Deep Learning
Le Deep Learning est une façon de construire des modèles de machine learning qui peuvent apprendre une « représentation hiérarchique » des données. Ce qu'on appelle « représentation hiérarchique » peut être illustré par la façon dont nous (humains) traitons les données, c'est-à-dire que toute l'information dans l'image n'a pas la même importance. Par exemple, si je regarde les photos de vacances d'un ami, je vais être capable de reconnaître mon ami dans beaucoup de situations différentes, dont certaines ne me sont pas familières du tout. Un réseau de neurones en revanche, lui aurait besoin de réapprendre à reconnaître mon ami dans chaque situation. Donc le but du deep learning est de doter nos modèles de cette capacité à reconnaître certaines propriétés dans des contextes très différents.
À noter que le concept de deep learning n'est pas lié aux réseaux de neurones, mais qu'il est très bien illustré par les réseaux de neurones profonds, en particulier celui utilisé par la suite : le « CNN » (Convolutional Neural Networks). Les CNN sont très semblables aux réseaux neuronaux présentés dans la section précédente. Mais d'une part, les architectures de CNN peuvent explicitement supporter des entrées sous forme d'images, ce qui nous permet d'encoder certaines propriétés dans l'architecture, dans le cas d'une image, une information 2D. D'autre part, la convolution est une fonction mathématique très efficace pour mettre en valeur certaines structures et cela permet, dans une certaine mesure, de hiérarchiser l'information, de se concentrer sur certaines propriétés. Ces outils améliorent l'efficacité de l'apprentissage et réduisent considérablement le nombre de paramètres dans le réseau et par construction le temps d'apprentissage.
Nous nous éloignons un peu des modèles de base, donc pour plus de simplicité et de clarté, voici un exemple pour utiliser la bibliothèque keras (qui utilise TensorFlow) en se basant sur un CNN inspiré d'un exemple que vous pourrez trouver ici : https://github.com/fchollet/keras/blob/master/examples/mnist_cnn.py. Cet exemple a été adapté pour pouvoir faire le test sur notre échantillon de galaxies et pour que les phases d'entraînement soient plus rapides.
Comme dit précédemment, le CNN peut gérer des images. Repartons donc des données précédemment renormalisées (data_scaled), mais avant de les reformater en tableau (data_1d), voir la partie 2.3 sur les transformations des données. Dans le code suivant, les nouveaux jeux d'entraînement et de test sont créés à partir de data_scaled :
ntest =int(0.33*data_scaled.shape[0])
ntrain = data_scaled.shape[0]-ntest
data_train = data_scaled[:ntrain]
type_train = type_morph[:ntrain]
data_test = data_scaled[ntrain:]
type_test = type_morph[ntrain:]
Keras est une bibliothèque d'API python qui permet de lancer et d'interagir avec TensorFlow, CNTS ou Théano. Keras est pensé pour pouvoir gérer plusieurs canaux comme le RGB par exemple. Nos données ne sont codées qu'avec un seul canal, il nous faut, donc, redimensionner nos données pour correspondre à ce format. Attention, Keras permet de gérer deux façons de formater ces données avec plusieurs canaux, soit « channels_first » (nombre d'éléments, nombre de canaux, nombre de pixels x, nombre de pixels y), soit « channels_last » (nombre d'éléments, nombre de pixels x, nombre de pixels y, nombre de canaux). Le mode utilisé est défini dans le backend de Keras. Voici comment tester le mode configuré et reformater les données correctement :
import keras
from keras import backend as K
if K.image_data_format() =='channels_first':
x_train = data_train.reshape(data_train.shape[0],1, data_train.shape[1], data_train.shape[2])
x_test = data_test.reshape(data_test.shape[0],1, data_test.shape[1], data_test.shape[2])
input_shape =(1, data_scaled.shape[1], data_scaled.shape[2])
else:
x_train = data_train.reshape(data_train.shape[0], data_train.shape[1], data_train.shape[2],1)
x_test = data_test.reshape(data_test.shape[0], data_test.shape[1], data_test.shape[2],1)
input_shape =(data_scaled.shape[1], data_scaled.shape[2],1)
Et il faut également convertir les vecteurs contenant les classes en une représentation matricielle binaire :
num_classes =3
# Soustraire 1 pour avoir des valeurs de 0 à 2 au lieu de 1 à 3
y_train = keras.utils.to_categorical(type_train-1, num_classes)
y_test = keras.utils.to_categorical(type_test-1, num_classes)
Création du modèle, inspiré de l'exemple cité précédemment :
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
model = Sequential()
model.add(Conv2D(32, kernel_size=(3,3), activation='relu', input_shape=input_shape))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
Passons à la phase de l'entraînement.
L'algorithme de Keras utilise deux paramètres qu'il est intéressant de comprendre :
- La taille du lot batch_size : qui définit le nombre d'échantillons qui vont être propagés à travers le réseau par itération. Par exemple, pour 1000 échantillons d'entraînement et un batch_size de 100, l'algorithme va entraîner 10 fois 100 échantillons jusqu'à couvrir tous les échantillons. La couverture de tous les échantillons définit une époque epochs. Plus le batch_size sera petit, plus l'utilisation mémoire sera petite et plus l'entraînement du réseau sera rapide, mais moins le gradient calculé sera précis ;
- le nombre d'époques epochs qui est simplement le nombre de fois que l'on répète la procédure décrite précédemment. Plus le nombre d'époques est grand, plus on va s'approcher de la meilleure performance possible, mais plus le temps d'entraînement sera long.
Avec les paramètres suivants, le temps de calcul sur un laptop (toujours 8 processeurs) est de 15 minutes :
batch_size =20
epochs =50
# Configuration du processus d'apprentissage
model.compile(loss=keras.losses.categorical_crossentropy,optimizer=keras.optimizers.Adadelta(),metrics=['accuracy'])
# Apprentissage
model.fit(x_train, y_train,batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, y_test))
Résultat :
Train on 2675 samples, validate on 1317 samples
Epoch 1/50
2675/2675 [==============================] - 17s 6ms/step - loss: 0.7526 - acc: 0.7417 - val_loss: 0.6334 - val_acc: 0.7267
Epoch 2/50
2675/2675 [==============================] - 16s 6ms/step - loss: 0.5758 - acc: 0.7529 - val_loss: 0.6129 - val_acc: 0.7593
Epoc 3/50
2675/2675 [==============================] - 16s 6ms/step - loss: 0.5302 - acc: 0.7787 - val_loss: 0.6391 - val_acc: 0.7540
...
Epoch 47/50
2675/2675 [==============================] - 20s 7ms/step - loss: 3.7794e-04 - acc: 1.0000 - val_loss: 1.9076 - val_acc: 0.7509
Epoch 48/50
2675/2675 [==============================] - 16s 6ms/step - loss: 2.0340e-04 - acc: 1.0000 - val_loss: 1.9327 - val_acc: 0.7540
Epoch 49/50
2675/2675 [==============================] - 18s 7ms/step - loss: 1.1411e-04 - acc: 1.0000 - val_loss: 1.8046 - val_acc: 0.7456
Epoch 50/50
2675/2675 [==============================] - 17s 7ms/step - loss: 4.6328e-04 - acc: 1.0000 - val_loss: 1.8094 - val_acc: 0.7540
Enfin, il est important de mesurer la performance de la même façon que précédemment :
# Utilisation du modèle pour prédire les classes
type_mod = model.predict_classes(x_test)
# Ne pas oublier que l'on a introduit un offset pour l'échantillon égal à 1
print("Matrice de confusion\n", metrics.confusion_matrix(type_test, type_mod+1))
print("Précision, sensibilité, f-score\n", metrics.classification_report(type_test, type_mod+1))
Nous obtenons :
Matrice de confusion
[[214 82 1]
[ 26 722 60]
[ 0 155 57]]
Précision, sensibilité, f-score :
precision recall f1-score support
1.0 0.89 0.72 0.80 297
2.0 0.75 0.89 0.82 808
3.0 0.48 0.27 0.35 212
avg / total 0.74 0.75 0.74 1317
Les résultats sont satisfaisants par rapport aux exemples précédents, mais toujours peu convaincants en comparaison du SVM initial ou du Random Forest. Cela reste un test quasiment à l'aveugle, en tout cas sans réfléchir et il existe beaucoup plus de marge d'optimisation avec le CNN qu'avec le SVM, sans compter que le CNN a l’air également plus stable quand on multiplie les tests. Avec les CNN, en plus de pouvoir augmenter la complexité du modèle, il est possible de jouer sur les paramètres de la convolution ou d'augmenter artificiellement la taille de notre échantillon d'entraînement à l'aide de transformations simples (des rotations par exemple). Vous trouverez un tutoriel intéressant sur le blog de keras qui donne les clés pour commencer ces optimisations : https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html.
Au final, après ces différents tests, la pré-conclusion avant la conclusion finale est la suivante : le temps n'est pas encore venu où les machines feront tout le boulot pour vous pendant que vous vous prélassez sur votre transat à l'autre bout du monde. L'analyse des différents résultats est encore une majeure partie de la résolution des problématiques soumises.
Conclusion
Nous avons introduit, dans cet article, quelques applications en utilisant les différentes méthodes des bibliothèques scikit-learn et TensorFlow à travers Keras. Vous avez pu voir que les approches nécessitent quelques tests et demandent une optimisation. Le choix de telle ou telle méthode dans l'analyse de vos données, dépend à la fois de la nature des données, du but attendu et de la puissance de calcul mis à votre disposition. Cela paraît évident, mais il est indispensable de prendre en compte ces différentes contraintes pour avoir des résultats satisfaisants.
Dans le cadre de nos données, les différentes méthodes montrent qu'une approche SVM ou Random Forest bien que simple est suffisante pour la caractérisation en 3 classes d'objets. Toutefois, l'approche Deep Learning apporte une possibilité d'évolution qui est sans pareille et pourrait être préférée, malgré la difficulté de tuning et le temps de calcul plus important. De plus, le Deep Learning nécessite une quantité de données beaucoup plus importante pour un apprentissage plus réaliste. Nous avons, dans cet article choisi aussi un cas d'étude simple permettant de valider les différentes approches. Gardez en mémoire que plus vous désirez définir des contraintes et des classes supplémentaires, plus le modèle devient complexe et nécessite une réflexion et des validations afin d'éviter les classifications en un seul groupe ou un sur-apprentissage.
À l'aide de ces modèles, vous êtes donc en mesure de prédire le type d'une galaxie à partir de son image. Et ça tombe bien, on vient de recevoir un nouvel échantillon ! Vous pouvez le retrouver dans votre sous-répertoire <myDirectory>/data/new_image/.
Les données sont au même format que précédemment, voici comment les charger dans un numpy array :
new_data =[]
# À remplacer par vos chemins bien sûr!
mynewimgDir ='</myDirectory/>/data/new_image/'
mypath_template =os.path.join(mynewimgDir,'*_acs_I_mosaic_30mas_sci.fits')
# Chargement des images
for one inglob.glob(mypath_template):
# Chargement de l'image
img = fitsio.read(one)
# On ajoute l'image à la liste
# et on en profite pour la normaliser
new_data.append((img-img.mean())/img.std())
# Reformatage en numpy pour plus de facilité
new_data = numpy.asarray(new_data)
Pour utiliser un des modèles de scikit-learn, il faut comme précédemment reformater les images en tableau 1D. On peut ensuite utiliser la méthode predict() comme nous l'avons fait avec l'échantillon de test :
new_1d = new_data.reshape((new_data.shape[0],-1))
type_rf = rf_clf.predict(new_1d)
Ici, nous utilisons la méthode Random Forest , mais vous pouvez faire la même chose avec n'importe lequel des modèles scikit-learn que l'on a déjà entraîné.
Si vous voulez utiliser Keras, l'appel est un peu différent : on utilise les images et non les tableaux 1D et il ne faut pas oublier de les reformater pour ajouter une dimension canal, en bref, on traite ces nouvelles données de la même façon que l'échantillon utilisé pour l'entraînement :
# Comme précédemment on reformate correctement en fonction du backend
if K.image_data_format() =='channels_first':
x_new = new_data.reshape(new_data.shape[0],1, new_data.shape[1], new_data.shape[2])
input_shape =(1, new_data.shape[1], new_data.shape[2])
else:
x_new = new_data.reshape(new_data.shape[0], new_data.shape[1], new_data.shape[2],1)
input_shape =(new_data.shape[1], new_data.shape[2],1)
L'appel du modèle se fait à l'aide le la méthode predict_classes(), mais il ne faut pas oublier d'ajouter 1 (parce qu'on avait soustrait 1 au type de l'échantillon d'entraînement pour avoir des valeurs entre 0 et 2, voir la section précédente).
type_dl = model.predict_classes(x_new)+1
Afin de mieux illustrer cette classification, optons pour une visualisation identique à la figure 1 :
# Un petit graphique pour illustrer
fig = plt.figure(figsize=(7,7))
i in range(9):
type_rf[i] == type_dl[i]:
plt.title('type_rf %d ; type_dl %d ' % (type_rf[i], type_dl[i]))
else:
plt.title('type_rf %d ; type_dl %d ' % (type_rf[i], type_dl[i]), color='C1')
plt.axis('off')
plt.show()
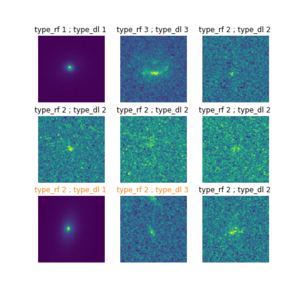
Fig. 5 : Visualisation des 9 premières images de galaxies du nouvel échantillon, ainsi que leurs types morphologiques prédits par le Random Forest (type_rf) et par le Deep Learning (type_dl), le texte des prédictions en désaccord est affiché en orange.
La figure 5 montre les 9 premières images des nouvelles données ainsi que le type prédit par les modèles Random Forest et Deep Learning. Pour deux des galaxies dans la figure, les modèles sont en désaccord. En se référant aux performances des deux modèles, en particulier à la matrice de confusion, on peut en déduire les performances et les probabilités de se tromper de chaque modèle en fonction de chaque cas :
- Dans le cas où le Random Forest a prédit un type 2 (Spiral) et le Deep Learning un type 1 (Elliptique), la matrice de confusion du Random Forest nous montre que sur l'échantillon de test, le modèle a prédit un type 2 au lieu de 1 pour 98 galaxies, soit un peu plus de 30% des types 1. En revanche, la matrice de confusion du Deep Learning nous montre que le modèle a prédit un type 1 au lieu d'un type 2 pour 26 galaxies soit un peu plus de 3% des types 2. Il est donc dans ce cas plus probable que le Deep Learning ait raison.
- Dans le cas où le Random Forest a prédit un type 2 (Spiral) et le Deep Learning un type 3 (Irrégulière), de la même façon on peut estimer à partir de la matrice de confusion qu'il est très peu probable que le Random Forest se trompe alors qu'il est très probable que le Deep Learning se trompe. De plus en regardant l'image, on voit sur le bord une tâche qui a l'air d'être une autre source et qui pourrait bien faire ressembler une galaxie Spirale à une galaxie Irrégulière. Le Random Forest semble l'emporter.
Et dans les 2 cas, le traitement des données est… immédiat. Et c'est bien là l'intérêt de l'application des méthodes de machine learning. Vous voilà maintenant nouvel astrophysicien ou presque, have fun !
Références
[1] Objets du calatolgue de Messier : https://fr.wikipedia.org/wiki/Liste_des_objets_de_Messier
[2] SANDAGE A., SANDAGE M., et KRISTIAN J. (éditeurs), « Galaxies and the Universe », 1975.
[3] Site officiel de Galaxy Zoo : http://www.galaxyzoo.com
[4] BUTA R. J., « Galaxy morphology», Planets, Stars, and Stellar Systems, Vol. 6, 2011.
[5] https://www.galaxyzoo.org/#/classify
[6] http://cosmos.astro.clatech.edu
[7] HUERTAS-COMANY et al., « A Catalog of Visual-like Morphologies in the 5 CANDELS Fields Using Deep Learning », ApJS, 2015.
[8] LOCHNER M. et al., « Photometric Supernova Classification With Machine Learning », ApJS, 225(2), p.31, 2016.
[9] SCHAWINSKI K. et al., « Generative Adversarial Networks recover features in astrophysical images of galaxies beyond the deconvolution limit », arXiv:1702.00403.
[10] JAMAL S. et al., « Automated reliability assessment for spectroscopic redshift measurements », arXiv:1706.01103.
Pour aller plus loin
Les méthodes d'apprentissage en Astrophysique sont devenues des méthodes très puissantes de plus en plus utilisées dans la classification de galaxies [7], dans la reconnaissance et la classification de Super novae [8], dans l'amélioration de visualisation de structures dans les images [9], dans la qualité des données [10], ou dans la reconnaissance de champs... Nous n'avons pas abordé les modèles non supervisés qui dans le cas de nos galaxies pourraient nous permettre d'optimiser nos classes, voire d'en découvrir de nouvelles ! Je vous invite à consulter la documentation du module clustering de scikit-learn : http://scikit-learn.org/stable/modules/clustering.html.
Dans tous les cas, l'arrivée des grandes masses de données donne un avantage certain sur les applications du Deep Learning. Dans ce cadre, vous pourrez aussi vous intéresser à l'utilisation de la nouvelle clé USB Movidius et utiliser davantage le framework Tensorflow qui demeure une référence dans le cadre d'une utilisation commerciale. L'arrivée de TensorFlow Lite pour les appareils mobiles est encore une option pour l'utilisation de programmes à exécuter sur les appareils limités en ressources, et de pouvoir emporter avec vous des outils puissants pour la détection et la classification d'objets célestes lors de vos soirées à admirer le ciel nocturne.