Les paraboles fleurissent sur nos balcons et nos toits, mais rares sont les utilisateurs conscients des règles de conception et d’utilisation de ce réflecteur d’antenne. Nous nous proposons de modéliser diverses formes de réflecteurs afin de comprendre les diverses configurations classiquement envisagées, puis démontrerons leur utilisation pour étendre la portée d’un réseau wifi, pour conclure sur quelques concepts de sécurité des réseaux sans fil et le danger d’éliminer la protection de la couche physique dans ce mode de transport d’informations.
Toute antenne se résume à un élément rayonnant – fil (monopôle, dipôle), fente, surface (patch) [balanis], chargé de capter ou émettre un signal électromagnétique. Ces éléments sont faiblement directifs, avec en général une direction dans laquelle la propagation est inexistante (null), et un rayonnement qui se diffuse dans toutes les autres directions de l’espace. Lorsque la puissance électromagnétique doit être concentrée dans une direction particulière, par exemple vers un satellite ou un émetteur de télévision, des éléments chargés de canaliser (cas des antennes Yagi-Uda) ou concentrer la puissance vers l’élément rayonnant sont ajoutés. Dans cette dernière classe, les paraboles agissent comme réflecteur chargé de concentrer l’onde plane incidente vers un élément rayonnant qui se résumera, dans notre cas, à un fil (monopôle).
Balanis ([balanis], p.18) introduit le concept de dipôle en ouvrant une ligne de transmission. Son argumentaire se développe comme suit :
- Une ligne de transmission est formée de deux conducteurs parallèles : le champ électrique induit par le déplacement des charges dans un conducteur est compensé par le champ électrique induit par le déplacement des charges dans l’autre conducteur. Par conservation de la charge, la somme de ces deux champs s’annule.
- Pour un signal périodique, les conditions de la ligne de transmission (potentiel, courant, champ électrique) se répètent tous les λ/2 en amplitude, avec λ=c/f la longueur d’onde du signal périodique, de fréquence f se propageant à la célérité c dans la ligne de transmission.
- Supposons que maintenant nous coupions en un point la ligne de transmission et que nous en séparions les deux conducteurs. Dans ce cas, les champs électriques induits par les déplacements de charges dans les brins séparés ne se compensent plus, mais se somment : un champ électrique est rayonné.
- Les conditions limites vérifiant un ventre de courant au milieu des deux brins séparés et un nœud de courant (courant nul) aux extrémités sont vérifiées pour le dipôle formé de deux brins de longueur λ/4.
- En présence d’un plan conducteur, le principe dit des charges miroirs, qui garantit l’annulation du champ électrique à la surface du conducteur, permet de s’affranchir d’un des brins du dipôle. En plaçant un seul des brins du dipôle selon une orientation perpendiculaire au plan conducteur, le second brin est virtuellement créé par la surface conductrice : il s’agit d’un monopôle.
Toutes les dimensions de structures agissant sur un signal périodique de fréquence f se normalisent par rapport à la longueur d’onde λ=c/f avec c la célérité de l’onde. Ce concept est en particulier valable pour les paraboles : bien que conçues pour fonctionner autour de 10 GHz – fréquence des liaisons satellite-sol pour les transmissions de télévision – nous pouvons parfaitement reprendre une telle parabole et la faire fonctionner dans la bande wifi – 2,40 à 2,48 GHz – certes avec un gain [1]plus faible, mais une performance qui restera utile à notre démonstration.
Comme tout système ondulatoire, deux aspects complémentaires permettent de rendre compte de la propagation des signaux électromagnétiques autour d’une antenne : un aspect ondulatoire qui sera pris en compte plus tard, et un aspect corpusculaire dans lequel des billes se propagent dans l’espace et rebondissent sur les réflecteurs rencontrés. Les lois classiques de l’optique des miroirs sont vérifiées, avec une direction de rebond symétrique par rapport à la normale à la surface rencontrée. Cette approche, dite par tracés de rayons [2](raytracing), est la plus simple à appréhender et sera donc développée en premier.
1. Méthode du tracé de rayons
Nous faisons l’hypothèse que la source des signaux que nous recevrons se situe à l’infini, et que par conséquent le signal incident est une onde plane. Ainsi, le point de départ de la simulation consiste en un faisceau de rayons parallèles à la direction d’incidence. Connaissant l’équation de l’élément réflecteur, nous calculerons l’intersection entre le faisceau incident et le réflecteur, appliquerons la loi de conservation des angles par rapport à la normale de la surface pour connaître la direction du signal réfléchi, puis tracerons un segment de ce faisceau réfléchi. Par souci de simplicité, nous tiendrons compte des symétries de révolution du problème qui ne sera donc traité que dans un plan (2D) et non dans l’espace (3D).
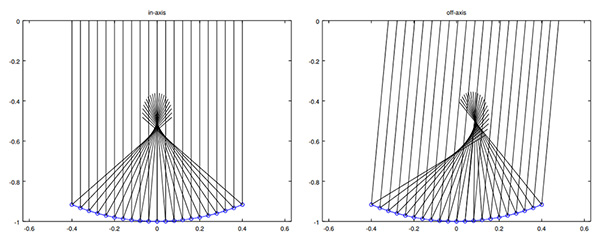
Engageons la démarche dans le cas le plus simple : une calotte sphérique, et une onde incidente parallèle à l’axe de révolution de la calotte sphérique. Un cercle de rayon R est défini en coordonnées cartésiennes (x,y) comme x2+y2=R2⇔ y=±√R2−x2 dont nous ne garderons qu’un des signes de la racine pour avoir un réflecteur en demi-cercle. Sous GNU/Octave, la modélisation du tracé de rayons s’écrit donc :
R=1; % rayon sphere
x=[-0.4:0.04:0.4];
y=-sqrt(R^2-x.^2);plot(x,y,'o-') % cercle
for k=1:length(x) % faisceaux incidents
line([x(k) x(k)],[1 y(k)]);hold on
end
Nous constatons que le faisceau incident, parallèle à l’axe y, présente une abscisse constante x(k), et s’étend de l’ordonnée 1 à l’intersection avec le cercle y(k). Le faisceau incident tracé, nous devons calculer la tangente au point d’intersection et donc l’angle de réflexion :
r=0.64; % longueur rayon reflechi
theta=acos(x/R);
for k=1:length(x)
line([x(k) x(k)-r*sin(2*theta(k))],[y(k) y(k)-r*cos(2*theta(k))]);hold on
end
axis([-0.63 0.63 -1 0]);
L’angle θ que fait le faisceau incident avec la surface se calcule d’une multitude de façons avec les relations trigonométriques qui caractérisent un cercle : ici nous utilisons le cosinus de cet angle comme le rapport de l’abscisse au rayon.
Nous constatons (Fig. 1) que tous les faisceaux réfléchis ne convergent pas vers un unique point, une condition peu favorable puisque nous ne savons alors pas où placer l’élément rayonnant. Nous laissons l’exercice au lecteur de pencher la direction d’incidence d’un angle dθ – cas d’une onde plane incidente qui n’est pas parallèle à l’axe de révolution de la sphère – pour constater que le problème s’empire avec un défaut de pointage de l’antenne.
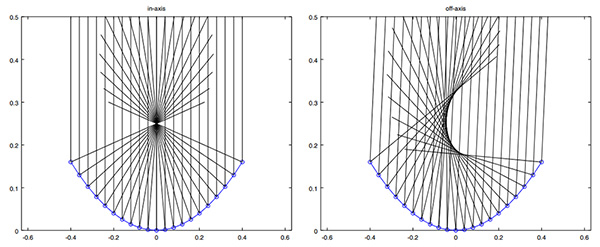
Ces considérations nous amènent à comprendre le choix du réflecteur parabolique, qui possède la propriété bien connue de cette conique de faire converger tous les faisceaux parallèles à son axe de révolution vers un unique point nommé le foyer. Ce calcul reprend exactement le code ci-dessus, mais en reprenant l’équation du réflecteur y=a· x2 et par conséquent la tangente, dont la pente est donnée par la dérivée, dy/dx=2· a.
x=[-0.4:0.04:0.4];
y=a*x.^2; % ze parabole
...
dy=2*a*x; % derivee au point x => theta=atan(dy/dx)
theta=(atan2(dy,1));
for k=1:length(x)
line([x(k) x(k)-r*sin(2*theta(k))],[y(k) y(k)+r*cos(2*theta(k))]);hold on
end
Nous constatons (Fig. 2) qu’en incidence normale les faisceaux réfléchis convergent en un unique point qu’est le foyer, tandis que l’erreur de pointage qui rend les faisceaux incidents penchés par rapport à l’axe de révolution se traduit par une distribution de la puissance réfléchie dans une région étendue. Ce dernier point n’est pas anodin, car un satellite géostationnaire oscille sur son orbite en fonction de l’attraction des corps célestes (lune et soleil) et même une antenne pointée au moment de l’installation verra le bilan de liaison dégradé alors que le satellite oscille sur son orbite.
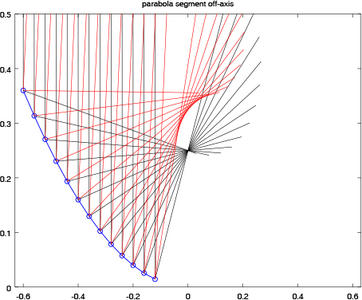
Le dernier point que nous abordons concerne les antennes que nous voyons désormais le plus couramment connectées aux récepteurs de télévision, à savoir le récepteur placé de façon excentrée afin que la tête de réception ne vienne pas cacher une partie du faisceau incident. La difficulté de pointage de ce type de parabole tient au fait que la tête ne se trouve pas dans l’axe de révolution de la parabole, et l’angle que fait l’onde plane incidente avec le plan moyen de la parabole n’est pas intuitif pour pointer une cible donnée. Ayant constaté que décaler la direction d’incidence de l’axe de révolution se traduit par des rayons réfléchis qui ne convergent pas vers un unique point qu’est le foyer, comment sont conçues les paraboles excentrées ? Il s’agit d’un segment du bord de la parabole, tel que nous le présentons en Fig. 3.
L’analyse par tracés de rayons est pratique, car elle permet de facilement s’accommoder d’une multitude de géométries et de lois physiques de propagation : c’est la méthode classique de modélisation de montages optiques (dans ce cas, ce sont les lois de réfraction et non de réflexion qui sont appliquées aux passages dans les lentilles) ou pour la représentation réaliste de scènes (e.g. logiciel POVRay). Cependant, malgré sa souplesse, il ne s’agit pas d’une méthode physique tenant compte des conditions de propagation des ondes, et l’extraction de grandeurs quantitatives telles que le gain d’une antenne n’est pas simple. Nous allons donc considérer une méthode classique de modélisation d’antenne : la méthode des moments, telle qu’implémentée dans le Numerical Electromagnetics Code, NEC.
2. Méthode des moments : NEC2
Figure 3 : Segment de parabole pour une configuration excentrée qui permet de décaler la tête de réception pour ne pas obstruer la surface réceptrice du réflecteur. Il s’agit de la configuration la plus couramment observée pour la réception de télévision transmise par satellite.
Nous avions déjà introduit NEC2 [3] dans ces pages pour modéliser le dipôle croisé conçu pour recevoir les images de satellites météorologiques en orbite basse : il s’agit d’un logiciel libre permettant de modéliser les assemblages d’éléments filaires rayonnants ou perturbant le champ électromagnétique. Très souple et scriptable donc simple d’emploi, ce logiciel ne sait cependant pas appréhender le cas des sources étendues telles que les plaques (antennes patch). Nous allons modéliser une antenne avec son réflecteur parabolique au moyen de cet outil. La première approche qui vient à l’esprit consiste à mailler le réflecteur parabolique par un réseau dense de fils. Cette approche s’avère excessivement coûteuse lorsque nous prenons soin d’implémenter toutes les règles de conception de modèles respectant les hypothèses de bon fonctionnement de la méthode des moments [4], à savoir :
- une longueur de chaque segment inférieure au dixième de la longueur d’onde ;
- un rayon inférieur au centième de la longueur d’onde et au huitième de la longueur du segment ;
- lors de la modélisation de surfaces, un rayon de segment sélectionné tel que la somme des surfaces des segments encadrant une région plane à modéliser soit égal à la surface de cette région [rub].
Sachant qu’un réflecteur parabolique, pour proposer un gain significatif, doit présenter des dimensions de plusieurs longueurs d’ondes notamment pour son rayon, le nombre de segments croît rapidement pour dépasser la quantité de mémoire allouée en statique avec la version originale de NEC2 (en Fortran), et même avec la version traduite en C que nous utiliserons par la suite, nec2c [5]. Ce dilemme se résout simplement en exploitant une autre fonctionnalité de NEC2 que sont les segments plans de réflecteurs. Les segments plans (patch) ne peuvent pas être sources de rayonnement dans NEC2, mais ils se comportent comme réflecteurs de l’onde incidente. Dans ce cas, il n’existe pas de règle sur les dimensions des éléments réflecteurs pour faire converger la simulation, et seule l’erreur d’approximer un segment de parabole par une succession de segments de droites va diriger notre choix de réduire les dimensions de ces segments. Le compromis avec le temps de calcul – d’autant plus long que le nombre de segments est important – est aussi un critère de choix lors de la phase de prototypage, ou lors de l’exploitation de NEC2 dans un processus d’optimisation tel que nous le verrons plus bas, condition dans laquelle le modèle sera exécuté plusieurs dizaines de fois avant d’obtenir une solution optimale.
Le problème se résume donc à écrire un générateur de code qui définisse la surface de la parabole en vue d’alimenter une simulation NEC2. Pour rappel, un fichier de configuration de NEC2 est un fichier ASCII, commençant par un commentaire (carte CM) et finissant par la ligne CE (Comment End). Suivent les éléments géométriques de la structure simulée, généralement des segments de droite (GW) et, dans le cas qui va nous intéresser ici, des patchs sur lesquels nous nous étendrons un peu plus puisqu’ils n’avaient pas été introduits auparavant [noaa]. Finalement, les paramètres de la simulation sont introduits : fréquence(s) de simulation par FR, condition de plan de masse GN, et finalement couverture angulaire du diagramme de rayonnement (radiation pattern RP) calculé : compte tenu de la symétrie de révolution du problème, nous nous contenterons d’évaluer le diagramme pour un angle azimutal compris entre 0 et 90° pour raccourcir le temps de simulation. Un patch est soit de forme rectangulaire, soit de forme triangulaire : compte tenu du nombre excessif de paramètres (12 coordonnées dans le cas du patch carré puisque trois coordonnées de l’espace sont fournies pour chaque sommet), il faut deux cartes pour définir un patch : SP et SC (rappelons que le Fortran date de l’époque où des cartes perforées étaient utilisées pour paramétrer un ordinateur, avec un nombre fini d’arguments par ligne de carte). Dans le cas d’un segment carré, SP prend la valeur 3 comme second argument pour définir la géométrie, puis les six coordonnées des deux premiers sommets. La carte suivante SC reprend l’argument 3 pour finir la séquence des coordonnées des sommets. Le cas du patch triangulaire est identique avec l’argument 2 comme forme du motif, et plus qu’un sommet défini comme argument de SC. Par habitude nous générons le fichier de configuration NEC2 sous GNU/Octave, mais tout langage capable d’effectuer les opérations trigonométriques, et en particulier Python, conviendra :
clear;close
freq=1500; % frequence en MHz
% freq=10000; % frequence en MHz
lambda=300/freq; % freq en MHz => c en m/us
p=0.3; % foyer est a 1/(4*p)
dtheta=10; % pas en angle azimutal
dr=0.1; % pas en direction radiale
n=13;
% points/segment 11->2m20 (24.5 dBi) ; 7->0m52 (20 dBi) ; 13->3m28 (24.8 dBi)
rad=lambda/100;
% rayon des segments, << lambda
r=[dr:dr:1-dr]; theta=[0:dtheta:360-dtheta]*pi/180;
% plage des angles et des rayons
x1=r'*cos(theta); y1=r'*sin(theta); r1=abs(x1+i*y1);z1=p*r1.^2;
% 1er coin du patch
theta=[dtheta:dtheta:360]*pi/180;
% incremente theta de dtheta : on tourne de dtheta
x2=r'*cos(theta); y2=r'*sin(theta); r2=abs(x2+i*y2);z2=p*r2.^2;
% 2eme coin du patch
r=[dr+dr:dr:1]; theta=[0:dtheta:360-dtheta]*pi/180;
% meme angle que x1, inc. rayon dr
x3=r'*cos(theta); y3=r'*sin(theta); r3=abs(x3+i*y3);z3=p*r3.^2;
% 3eme coin du patch
theta=[dtheta:dtheta:360]*pi/180;
% r increment'e de dr et theta tourne' de dtheta
x4=r'*cos(theta); y4=r'*sin(theta); r4=abs(x4+i*y4);z4=p*r4.^2;
% 4eme coin du patch
[u,v]=size(x1);
printf("CM parabole\n");
% debut fichier NEC avec le titre CM et fin de commentaire CE
printf("CE\n");
inc=1;
for k=1:u-1
% def de chaque patch carr'e (x1,y1,z1) ... (x4,y4,z4) en 2 cartes SP SC
for l=1:v
printf("SP 0 3 %f %f %f %f %f %f\n",x1(k,l),y1(k,l),z1(k,l),x2(k,l),y2(k,l),z2(k,l));
printf("SC 0 3 %f %f %f %f %f %f\n",x4(k,l),y4(k,l),z4(k,l),x3(k,l),y3(k,l),z3(k,l));
end
end
k=1;
for l=1:v
% sommet parbole forme' de patchs triangulaires : SP SC avec 1 coord a SC
printf("SP 0 2 %f %f %f %f %f %f\n",0,0,0,x1(k,l),y1(k,l),z1(k,l));
printf("SC 0 2 %f %f %f 0 0 0\n",x2(k,l),y2(k,l),z2(k,l));
inc=inc+1;
end
% conclusion en placant un dipole au foyer de la parabole
printf("GW %d 11 %f %f %f %f %f %f %f\n",inc,-lambda/4,0,1/(4*p),lambda/4,0,1/4/p,rad);
printf("GE 0\n");
% fin de la geometrie de l'antenne (Geometry End)
printf("EX 0 %d 6 0 1.00000E+00 0.00000E+00\n",inc);
% source de courant dans dipole
printf("FR 0 1 0 0 %f 3.00000E-00\n",freq);
% plage des frequences analysees
printf("RP 0 18 9 0 0.00000E+00 0.00000E+00 1E+01 1E+01\n");
% angles diag. rayonnement
printf("EN");
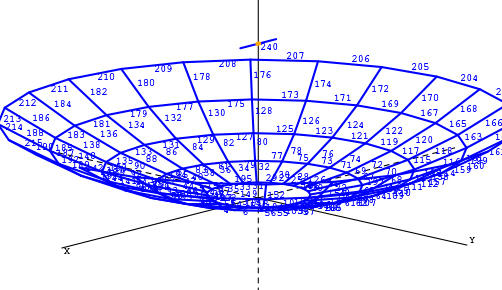
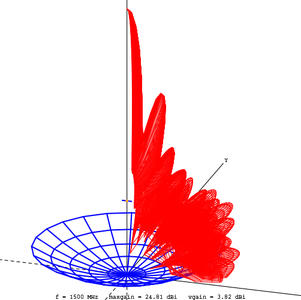
qui donne par exemple, après exécution et redirection de la sortie dans un fichier entree.nec pour générer la géométrie de la Fig. 4, dont l’utilisation en simulation par nec2c -i entree.nec -o sortie.out génère le diagramme de rayonnement de la Fig. 5 (sortie de xnecview, logiciel permettant de visualiser le maillage si le fichier d’entrée à NEC2 est fourni en argument, ou le diagramme de rayonnement si l’argument est le fichier de sortie de la simulation).
Figure 4 : Maillage d’antenne parabolique généré depuis GNU/Octave pour alimenter une modélisation de diagramme de rayonnement par NEC2.
Notez la présence de l’élément rayonnant (numéro 240) au foyer de la parabole dans la Fig. 4. Le diagramme de rayonnement est conforme à nos attentes, avec un lobe principal dans l’axe de révolution de la parabole, et des lobes latéraux particulièrement visibles dans cette représentation logarithmique (option ARRL de xnecview) de la puissance rayonnée dans une direction azimutale/élévation donnée (Fig. 5). On prendra par ailleurs soin de proposer un pas de simulation angulaire suffisamment fin pour ne pas créer d’artéfact compte tenu de la finesse de structures observées.
Figure 5 : Diagramme de rayonnement de la parabole.
3. Optimisation de la solution
Travailler avec une géométrie d’antenne décrite par un fichier ASCII est très puissant, car nous pouvons dynamiquement changer les propriétés du réflecteur dans une application externe – dans notre cas GNU/Octave, et son module d’optimisation. Ainsi, nous pouvons rechercher la géométrie d’antenne qui optimise un critère – adaptation d’impédance, gain, rejet d’un signal venant d’une direction donnée pour éviter une interférence par exemple. Ayant auparavant décrit le réflecteur parabolique sous forme d’un script GNU/Octave paramétrable, il devient trivial de dynamiquement modifier un des paramètres géométriques de l’antenne afin d’en optimiser une propriété. Illustrons ce concept avec la position du dipôle, en supposant que nous ne connaissions pas la propriété des coniques de rendre les faisceaux issus de l’antenne parallèles à l’axe de révolution de la parabole si, et seulement si, le dipôle se trouve au foyer. Nous cherchons donc à trouver la position du dipôle qui maximise le gain de l’antenne. Le problème est à symétrie cylindrique et nous nous contentons, pour accélérer le calcul, d’analyser une unique direction en azimut, et de balayer finement l’angle d’élévation. Le paramètre libre est l’altitude du dipôle, sachant que par symétrie du problème il est probable que son abscisse et son ordonnée soient nulles (i.e. un dipôle situé sur l’axe de révolution de la parabole). Nous recherchons l’altitude du dipôle maximisant le gain, en exploitant la fonction de descente de gradient fminsearch() de GNU/Octave. Maximiser un gain revient à minimiser une fonction de coût que nous choisirons comme l’inverse du maximum du gain d’antenne.
Nous reprenons donc la fonction vue auparavant pour générer les cartes NEC2 décrivant la géométrie d’antenne, mais en transformant la procédure en une fonction prenant comme argument la position de l’élément rayonnant, et renvoyant le coût qui sera minimisé. Pour produire cette fonction de coût, nous faisons appel à nec2c appliqué sur le fichier que nous venons de remplir. Après avoir extrait les lignes contenant le résultat de la simulation – toujours placées aux mêmes indices pour un jeu de paramètres donnés de RP – nous recherchons le maximum du diagramme de rayonnement maxgain, avant d’en renvoyer l’inverse.
function maxgain=parabole_optim(ydipole)
freq=1500; % frequence en MHz
lambda=300/freq;
...
f=fopen('entree.nec','w');
[u,v]=size(x1);
fprintf(f,"CM parabole\n");
fprintf(f,"CE\n");
...
fprintf(f,"EN");
fclose(f);
system('/usr/bin/nec2c -i entree.nec -o sortie.out && cat sortie.out | tail -186 | head -180 | cut -c 1-46 > sortie.octave');
load sortie.octave
maxgain=max(sortie(:,3))
maxgain=1/maxgain;
end
Cette fonction est appelée autant de fois que nécessaire pour faire converger la solution maximisant le gain : nous proposons un jeu de paramètres initiaux X0 (ordonnée du dipôle sur l’axe de révolution), et laissons fminsearch rechercher le minimum de la fonction de coût.
p=0.3; % foyer est a 1/(4*p)
X0=1.4; % ydipole initial
Xopt=fminsearch('parabole_optim', X0); % Use fmins to find the best fit p
printf("optimisation=%f theorie=%f\n",Xopt,1/(4*p))
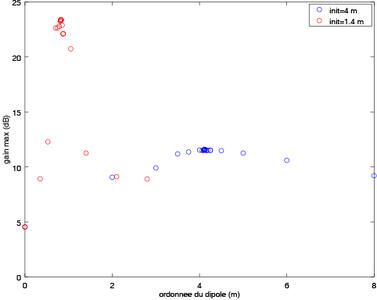
Comme tout problème d’optimisation, les minima locaux fournissent une solution peu satisfaisante. La méthode mise en œuvre par fminseach() est peu robuste à ce genre de problème, et un choix judicieux du point de départ de la recherche d’optimisation, aussi proche que possible de la solution attendue, est désirable. La figure 6 illustre le problème lorsque nous choisissons volontairement un point de départ du paramètre complètement faux : en plaçant initialement le dipôle très loin du foyer sur l’axe de révolution, fminsearch trouve bien une solution maximisant localement le gain, mais il ne s’agit pas de la solution globalement optimale qui, nous le savons bien maintenant, consiste à placer le dipôle au foyer.
Figure 6 : Évolution du gain d’antenne au cours de l’optimisation : le résultat bleu, initialisé avec une condition de départ plaçant le dipôle loin du foyer, propose une solution locale, mais seul un choix d’initialisation de la position proche de la solution (courbe rouge) fournit la solution globalement satisfaisante d’une position au foyer d’ordonnée 0,83 m.
De nombreux paramètres peuvent être modifiés dans une conception d’antenne, et les fonctions de descente de gradient qui visent à minimiser un coût sont peu performantes s’il faut minimiser une fonction dans un espace de trop grande dimension. Il est judicieux, si possible, de séparer les problèmes en variables indépendantes et les optimiser indépendamment, voire séquentiellement, afin de maximiser les chances de convergence de la descente de gradient.
4. Résultats expérimentaux
Mettons toutes ces considérations en pratique, en recherchant une solution à l’absence d’abonnement à une connexion internet de l’auteur. Les liaisons FreeWifi souffrent d’une faible robustesse lorsque le propriétaire utilise sa liaison pour regarder la télévision, un fléau en période d’actualités sportives, et le palliatif consiste à rechercher les solutions plus lointaines telles que, par exemple, les hôtels. Situé proche de la gare de Besançon, le logement de l’auteur est en vue directe d’un certain nombre d’hôtels qui sont cependant bien trop loin (300 m d’après Google Earth) pour permettre une liaison wifi. Placer un élément rayonnant (ici un monopôle dans une cantenna – voir encart ci-dessous) proche du foyer de la parabole [6]étend suffisamment la portée – certes de façon très directive – pour étendre la couverture de 12 à 22 points d’accès FreeWifi, mais plus important, fournit une liaison suffisamment puissante vers un hôtel que nous nommerons Volatile Pacher (Fig. 7). Pour ce faire, une carte wifi-USB SMC EZ Connect 802.11g [7]est connectée par un connecteur SMA au monopôle placé dans la cantenna. Cette carte wifi est appropriée pour un tel montage, car l’antenne intégrée est reliée au circuit récepteur par un condensateur : dessouder ce condensateur d’une part déconnecte l’antenne interne imprimée sur le circuit, et d’autre part donne un point de connexion pour souder le connecteur SMA (Fig. 7, gauche en bas). Ainsi, une nouvelle antenne externe répondant à de nouvelles contraintes de performances (directivité au lieu d’un diagramme de rayonnement isotrope) est installée. Nous plaçons le récepteur wifi au plus près du monopôle afin d’éviter de transporter un signal à 2,45 GHz sur un câble induisant nécessairement des pertes, au profit d’une transmission sur rallonge USB du signal numérisé.
La cantenna consiste en un monopôle – un bout de fil conducteur de longueur égale au quart de la longueur d’onde – placé dans un guide d’onde pour diriger le diagramme de rayonnement dans une direction privilégiée et ainsi améliorer le gain d’antenne. Afin de créer une interférence constructive entre le fond du guide d’onde (ici le fond d’un récipient métallique prévu pour contenir du café) et l’onde incidente, la position de l’élément par rapport au fond de la canette est importante. En se rappelant que pour que le champ électrique soit nul dans le conducteur, une onde électromagnétique réfléchie par une surface conductrice subit une rotation de phase de 180°, placer le monopôle à une distance d’un quart de longueur d’onde du fond de la canette induit (aller-retour) une demi-longueur d’onde de retard ou 180°, qui combinés aux 180° de rotation de phase de la réflexion, font bien 360° ou une interférence constructive. Finalement, le diamètre de la canette doit être suffisant pour ne pas atténuer l’onde propagée dans le guide : de diamètre trop faible, le guide d’onde atténue l’onde évanescente qui tente d’arriver au monopôle, d’où le choix d’un récipient à café au lieu de la classique boite de Pringles, trop petite pour opérer efficacement à 2,40 GHz (borne inférieure de la bande Wifi).
Ayant atteint un bilan de liaison acceptable grâce au gain fourni par le réflecteur parabolique au foyer duquel nous avons placé notre élément rayonnant, il nous reste à résoudre un point de détail, à savoir obtenir un accès internet sans être client de l’hôtel. Comme dans de nombreux hôtels, l’authentification ne se fait pas par clé cryptographique pour obtenir une autorisation de connexion au réseau, mais par la fourniture d’un identifiant et mot de passe dans une page web proposant un portail captif.
Un portail captif est une solution peu sécurisée qui donne libre cours aux attaques [portail]. En effet, atteindre la page web d’authentification impose d’autoriser l’utilisateur à s’associer au réseau (iwconfig wlan1 essid MON_RESEAU ap MON_POINT_DACCES). De fait, les restrictions d’accès à la couche physique sont éliminées, une grave entrave aux règles de sécurité.
Les couches OSI [stevens] décrivent la hiérarchie des protocoles mis en œuvre pour router des paquets sur un réseau, de la couche physique qui décrit la nature des signaux circulant sur le medium de communication (cuivre, fibre optique, éther) pour la couche 1, à la couche de liaison qui définit les conditions d’accès au médium (couche MAC pour Medium Access Control dans la couche 2 qui va nous intéresser dans le texte). Suivent les couches de plus haut niveau d’abstraction que sont l’organisation des paquets dans la couche 3 (par exemple IPv4), puis la couche de transport – connectée (TCP) ou non (UDP) – dans la couche 4, et les couches applicatives qui suivent de 5 à 7. Chaque couche de niveau supérieur fait l’hypothèse que les services fournis par les couches inférieures sont disponibles : obtenir l’accès aux couches basses donne automatiquement accès aux couches supérieures.
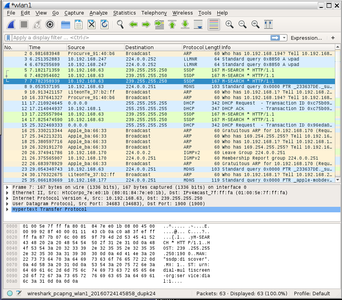
Les présentations austères des couches OSI en cours de réseau informatique prennent ici tout leur sens : en attaquant les couches du protocole réseau par le bas, il suffit de remonter jusqu’au premier point faible pour que toutes les couches supérieures se libèrent. Contrairement à un réseau filaire qui peut être physiquement sécurisé (nécessité d’une intrusion physique sur le site), une liaison radiofréquence retire la couche de protection physique en diffusant le signal électromagnétique sur l’éther. Restent donc les deux couches supérieures, MAC et IP, si on ne veut pas s’attaquer au problème de l’authentification par la couche applicative. En effet, si nous reprenons les identifiants d’un ordinateur authentifié sur le réseau, il devient impossible de nous distinguer de l’utilisateur authentique, et le routeur autorise l’accès. Tout utilisateur de wireshark ou tcpdump sait que l’écoute passive d’un réseau est triviale une fois que l’accès physique est acquis, et quelques secondes d’enregistrement sur le réseau du portail captif suffisent à trouver une transaction depuis un ordinateur authentifié, avec des paquets contenant son adresse MAC (OSI couche 2) et son adresse IP (OSI couche 3). Il nous reste à fournir ces caractéristiques à notre carte Wifi dont l’adresse MAC est, comme pour tout matériel récent, définie en mémoire volatile (ifconfig hw ether AA:BB:CC:DD:EE:FF) et refaire une requête d’allocation d’adresse IP (dhclient wlan1). Le serveur DHCP nous fournit évidemment la même adresse que l’ordinateur authentifié, puisque lui même authentifié par son adresse MAC que nous venons de dupliquer, et tout paquet que nous émettons est considéré comme valide sur le réseau du portail captif. Quelques corruptions de paquets peuvent survenir dans la pile TCP lorsque l’utilisateur authentifié tente des transactions en même temps que nous, donc il sera poli de laisser l’utilisateur authentique achever ses activités sur le réseau avant d’utiliser les caractéristiques de son matériel. La portée du montage du récepteur wifi au foyer de la parabole, avec une portée de plus de 300 m, amène une opportunité d’appliquer le principe à peu près tous les hôtels bisontins à proximité de la gare dans l’exemple que nous démontrons ici (Fig. 8).
Figure 8 : écoute des transactions sur le réseau sans fil de Volatile Pacher par wireshark. L’adresse MAC des interlocuteurs est visible dans le champ Ethernet, tandis que l’utilisation d’une trame TCP portant un message HTTP est la garantie d’un utilisateur se promenant sur le Web avec une connexion fonctionnelle.
Une fois la liaison authentifiée, un traceroute valide non seulement l’accès au DNS et la table de routage, mais surtout illustre le mode d’authentification des paquets :
jmfriedt@rugged:~/$ traceroute whitehouse.gov
traceroute to whitehouse.gov (104.124.184.110), 30 hops max, 60 byte packets
1 192.168.1.1 (192.168.1.1) 0.202 ms 0.443 ms 0.434 ms
2 controleur.wifipass.org (10.192.168.1) 6.840 ms 7.696 ms 9.301 ms
3 192.168.1.1 (192.168.1.1) 13.302 ms 13.921 ms 18.031 ms
4 * * *
5 225.233.70.86.rev.sfr.net (86.70.233.225) 77.822 ms 81.038 ms 83.656 ms
6 193.239.103.84.rev.sfr.net (84.103.239.193) 82.650 ms 64.128 ms 43.985 ms
7 53.202.96.84.rev.sfr.net (84.96.202.53) 52.730 ms 55.858 ms 69.112 ms
8 205.104.66.86.rev.sfr.net (86.66.104.205) 72.298 ms * 84.604 ms
9 37.202.96.84.rev.sfr.net (84.96.202.37) 85.293 ms 89.637 ms 91.245 ms
10 222.230.154.77.rev.sfr.net (77.154.230.222) 96.163 ms 102.108 ms 124.951 ms
11 a104-124-184-110.deploy.static.akamaitechnologies.com (104.124.184.110) 129.953 ms 130.695 ms 131.549 ms
tandis qu’en l’absence d’authentification, nous sommes redirigés vers https://passman02.wifipass.org/w2p/login-url-real.php?id=etap_besancon_gare&domain=controleur.wifipass.org&mac=00-13-F7-78-A5-32&page=http%3A%2F%2Fwhitehouse.gov%2F. Nous retrouvons donc dans cette url le nom de l’hôtel qui requiert l’authentification ainsi que l’adresse MAC du demandeur, service fourni par wifipass.org.
Nous constatons qu’une qualité de liaison de 15/100 garantit entre 1 et 5,5 Mb/s (d’après iwconfig), soit 90 kB/s (d’après firefox).
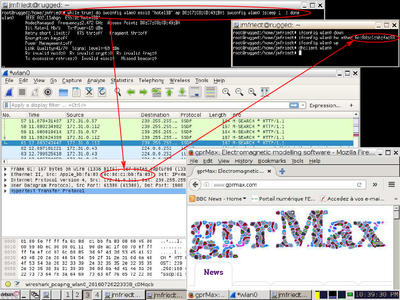
Figure 9 : Procédure identique d’accès au réseau des hôtels Lit et Petit-Déjeuner, auquel l’auteur avait légalement accès au moment de ces tests : ici encore l’adresse MAC spoofing permet de passer le portail captif sans fournir le code de sa chambre. En bas à droite, le site web accessible sans authentification explicite par le portail captif.
L’expérience est reproduite avec succès sur le réseau des hôtels B&B (Fig. 9), qui nécessiterait quant à lui un numéro de chambre et le code d’accès correspondant, un couple de données qu’il serait compliqué d’acquérir si nous tentions d’obtenir un accès en attaquant la couche applicative (la page web du portail). Dans cet exemple, où l’auteur avait l’autorisation (étant client de l’hôtel) d’accéder à ce réseau, l’utilisation de l’adresse MAC d’un ordinateur Apple garantit que le propriétaire de l’ordinateur a peu de chances d’avoir les compétences techniques pour identifier ou palier à la déficience possible de sa connexion réseau. Nous sommes obligés de forcer la reconnexion périodique au point d’accès en faisant appel à la fonction iwconfig dans une boucle afin de répéter la requête de connexion périodiquement : while true; do iwconfig wlanX essid XXX ap XX:XX:XX:XX:XX:XX; sleep 1;done en bash.
Conclusion
Nous avons introduit les concepts de conception de réflecteurs pour diriger un faisceau électromagnétique dans une direction donnée et ainsi augmenter le gain d’antenne. Nous avons conclu que la géométrie parabolique est optimale pour focaliser une onde plane incidente vers un point unique qu’est le foyer, et avons exploité expérimentalement un tel réflecteur pour considérablement augmenter la portée d’une liaison wifi, et ainsi obtenir une connexion internet.
La triste conclusion de ces expérimentations (Fig. 10) est que le réflecteur parabolique n’est pas indispensable, mais le simple guide d’onde formé par la cantenna autour du monopôle suffit à améliorer le bilan de liaison : le faible gain introduit par la parabole est probablement lié à son pointage médiocre vers la cible. La cantenna se modélise exactement comme la parabole, exercice laissé au lecteur curieux de sélectionner la boîte de conserve qui conviendra le mieux à cette tâche (on notera que les boîtes de fruits au sirop marchent mieux que les emballages de chips).
L’utilisation d’un réflecteur n’est qu’une façon parmi d’autres pour augmenter le gain d’antenne – une stratégie permettant des gains énormes (tous les radiotélescopes, à l’exception des grands réseaux d’antennes à balayage électronique, sont basés sur ce principe), mais avec un réflecteur de grandes dimensions et surtout présentant une forte prise au vent. Une alternative consiste à diriger le champ électromagnétique dans une direction en plaçant des éléments conducteurs pour annuler la propagation dans la direction opposée (interférences destructives) et concentrer le faisceau dans la direction voulue : c’est le principe de l’antenne proposée par Yagi et Uda [refYagi], dont l’optimisation n’est pas triviale. Le lecteur est encouragé à reprendre la modélisation sous NEC2 et l’optimisation sous Octave pour concevoir une telle antenne, et démontrer son bon fonctionnement sur une liaison wifi : malgré la disponibilité commerciale de nombreuses antennes de ce modèle, l’exercice est formateur, malgré la difficulté à gérer le grand nombre de degrés de liberté.
Références
[balanis] C.A. Balanis, Antenna theory : analysis and design, John Wiley & Sons (1997)
[rub] A. Rubinstein, F. Rachidi & al., On Wire-Grid Representation of Solid Metallic Surfaces, IEEE Trans. on Electromagnetic Compatibility 47 (1), pp.192-195 (2005)
[noaa] J.-M Friedt, S. Guinot, La réception d’images météorologiques issues de satellites : principes de base, GNU/Linux Magazine Hors-Série n°24 (février 2006)
[portail] C. Blancher, Wi-Fi et Portails captifs – Principes et limitations (2007), disponible à http://sid.rstack.org/pres/0705_Rectorat_Hotspots.pdf, et la vidéo http://www.authsecu.com/multimedia/hotspot-wifi-dns-ssid-spoofing.php
[stevens] K.R. Fall & W. R. Stevens, TCP-IP Illustrated, Vol. 1 : The Protocols (2nd Ed.) Addison-Wesley (2012), p.9
[refYagi] L’article original de Yagi et Uda de 1926 est disponible comme référence 3 de http://en.wikipedia.org/wiki/Yagi-Uda_antenna. Le papier original de Uda ne semble pas trivialement accessible sur le web.
Notes
[1] Le gain est défini comme la fraction de la puissance rayonnée dans la direction la plus favorable, à la puissance qui serait rayonnée par une antenne isotrope dans cette même direction. On parle donc, en unité logarithmique, de dBi, ou décibels normalisés à l’antenne isotrope.
[2] http://www.faculty.virginia.edu/rwoclass/astr511/lec16-teloptics-f03.html
[3] www.nec2.org
[4] http://www.qsl.net/4nec2/Tutorial.pdf
[5] Paquet du même nom dans Debian/GNU Linux ou http://www.qsl.net/5/5b4az//pkg/nec2/nec2c/
[6] Parabole Fuba de 85 cm de diamètre, d’un type s’apparentant à http://www.conrad.fr/ce/fr/product/941586/antenne-SAT----85-cm----fuba----DAA-850-A----Materiau-du-reflecteur-Aluminium
[7] http://www.smc.com/en-global/products/product/86/0 pour un coût de moins de 10 euros



 Ajouter à une liste de lecture
Ajouter à une liste de lecture