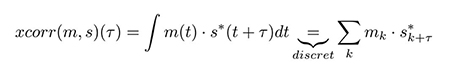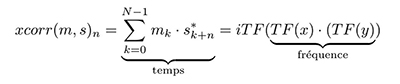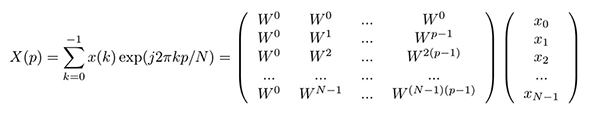Nous proposons d’aborder la transformée de Fourier rapide dans le contexte de l’environnement exécutif multitâches FreeRTOS à destination de microcontrôleurs ARM émulés dans QEMU. Ce faisant, nous découvrirons les plaisirs du partage de ressources et des queues pour échanger les données entre tâches, ainsi que quelques appels de fonctions cachées dans les bibliothèques dont l’utilisation s’avérera quelque peu périlleuse.
La corrélation est probablement une des opérations mathématiques les plus courantes autour de nous à notre insu. Chaque trame de télévision numérique (DVB) ou de radio numérique (DAB, Fig. 1) doit être synchronisée en temps et en fréquence pour permettre sa démodulation, tout comme la réception des signaux de navigation GPS [1] : la recherche d’un motif m(t) dans un signal bruité s(t) dépendant du temps t – ou dans sa version discrétisée de l’indice n – s’obtient par corrélation xcorr entre m et s dépendante d’un écart de temps τ et exprimée comme :
avec * le complexe conjugué si s∈ℂ, par exemple un flux IQ en sortie d’un récepteur de radio logicielle comme nous en avons déjà longuement discuté dans les applications de détection de cibles par RADAR [2].
Chaque intégrale dans la somme nécessite N multiplications avec N la longueur des vecteurs s et m, et ce, pour τ∈[−N/2:N/2], donc au total le calcul de la fonction de corrélation nécessite N2 multiplications.
Selon la relation classique du théorème de convolution conv(m,s)(τ)=∑k mk· sτ−k qui indique que TF(conv(m,s))=TF(m)·TF(s) avec TF la transformée de Fourier et considérant que le passage d’un temps positif k+τ à un temps négatif k−τ s’obtient par conjugué du complexe, nous déduisons que TF(xcorr(m,s))=TF(m)·TF*(s) ou en d’autres termes :
avec iTF la transformée de Fourier inverse. Ce résultat n’aurait que peu d’intérêt, la transformée de Fourier étant elle-même un algorithme de complexité de l’ordre N2, si Gauss [3] ne nous avait enseigné la transformée de Fourier rapide FFT de complexité N·log2(N) et le gain phénoménal en temps de calcul associé.
Nombre de démonstrations de la FFT existent dans la littérature et recopier ici une de ces démonstrations n’amènerait aucune originalité à ce document. Ainsi, [4] exploite récursivement les conditions de symétrie entre les termes pairs et impairs de l’exponentielle complexe pour construire un arbre binaire de profondeur seulement log2(N) pour effectuer la transformée de Fourier sur N éléments, mettant en évidence que seuls des puissances de 2 de N seront considérées, quitte à compléter la séquence trop courte de zéros pour atteindre cette condition (zero-padding). Attirons toutefois l’attention sur la démonstration de [5] qui explicite l’expression matricielle de la transformée de Fourier, pour la décomposer et trouver des termes redondants. Cette expression matricielle est élégante, car elle permet d’appréhender la transformée de Fourier X d’un signal temporel x selon un axe des fréquences qui ne soit pas régulier, comme le supposerait l’expression :
en considérant W=exp(j2π/N). En effet :
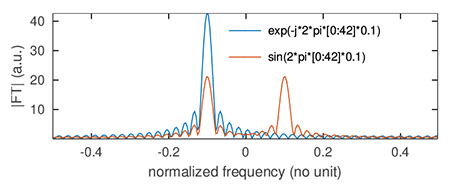
assemble la matrice F des exposants du complexe W=exp(j2π/N) afin d’effectuer par produit matriciel la transformée de Fourier des signaux signal, complexe ou réel pour bien montrer la cohérence avec le signal attendu puisque sin(x)∝ exp(jx)−exp(−jx).
Notre objectif est d’évaluer la capacité à séquencer sur microcontrôleur ARM Cortex-M exécutant FreeRTOS la séquence de calculs de chaque transformée de Fourier rapide FFT(s) et FFT(m), d’effectuer le produit du premier terme avec le complexe conjugué du second, puis FFT inverse. Pour ce faire, nous essaierons de nous appuyer sur diverses bibliothèques pour en découvrir les écueils. Le lecteur qui ne s’intéresse pas à la corrélation pourra toujours bénéficier de l’analyse spectrale, du filtrage par convolution, voire de la résolution d’équations aux dérivées partielles représentant un problème physique dans le formalisme des opérateurs de Green, qui sont fournis par l’exécution de la FFT sur microcontrôleur.
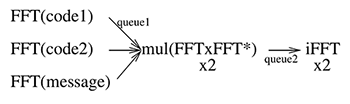
Nous allons explorer deux implémentations de la FFT, implémentée par CMSIS (Common Microcontroller Software Interface Standard) dédié aux processeurs ARM Cortex-M, et par KISSFFT, une implémentation qui se veut le plus simple possible et que nous verrons finalement moins adaptée que nous aurions pu le croire aux microcontrôleurs. Nous séquencerons les tâches au moyen de FreeRTOS sur Cortex-M3 ou M4 (https://www.freertos.org/RTOS-Cortex-M3-M4.html), et en particulier en passant les paramètres par des queues bloquantes entre les diverses tâches, garantissant qu’une tâche ayant besoin de résultats antérieurs attend la fin des calculs dont dépendent ses résultats (Fig. 2).
Dans la Fig. 2, message réfère au signal bruité à analyser, tandis que code1 et code2 réfèrent aux deux séquences pseudoaléatoires connues qui identifient par exemple deux interlocuteurs en multiplexage par code CDMA (Code Division Multiple Access) tel qu’utilisé par GPS. Le résultat sera deux vecteurs, l’un présentant un pic de corrélation significatif lorsque le code est identifié, et l’autre ne présentant pas de pic de corrélation en l’absence du motif dans le signal reçu. Les trois instances de la même tâche FFT sont reliées à la tâche de multiplication des vecteurs mul par trois queues de communication, et l’unique transformée de Fourier inverse est reliée à la tâche mul par une unique queue de communication qui transportera les deux vecteurs issus des multiplications terme à terme de la transformée de Fourier du message avec la transformée de Fourier de chaque code.
Queues de communication sous GNU/Linux
La communication entre processus – équivalent sur un système d’exploitation multitâche tel que GNU/Linux à la communication entre tâches sous FreeRTOS – peut prendre beaucoup de formes, que ce soient des pipes, un fichier partagé, une socket réseau, mais ici nous choisissons le formalisme le plus proche de la queue de communication de FreeRTOS qu’est la queue d’IPC (Inter-Process Communication). Dans l’exemple ci-dessous, N threads sont créés par un processus et chaque thread reçoit le calcul de son prédécesseur et renvoie le résultat de son calcul (ici, un incrément d’une unité) au successeur. Afin de démontrer l’absence de dépendance du résultat avec l’ordre d’ordonnancement, nous avons choisi d’initier la chaîne de transactions par le dernier thread (d’indice N-1) et conclure par le premier thread (d’indice 0). Les fonctions clés utilisées sont msgget() pour créer la queue de communication entre deux threads, msgrcv() pour recevoir et msgctl() pour envoyer un message contenu dans la structure de donnée qui doit contenir un entier positif identifiant la nature du message (ici, arbitrairement égal à 1) et le message lui-même sous forme de tableau d’octets (ici, 4 octets pour un entier).
Nous vérifions que, quel que soit l’ordre de création des threads, le résultat est toujours le même et vaut 45 pour le thread recevant le résultat de la chaîne de calcul (N-1 envoie 42 à N-2 qui incrémente de 1 pour envoyer 43 à N-3 qui incrémente... et envoie 45 à 0 quand N=5). On prendra soin en testant ce programme de s’assurer qu’aucune queue de communication IPC n’existe avant lancement par ipcs et de même en fin d’exécution qu’aucune queue n’a oublié d’être éliminée, qui résulterait sinon d’un comportement aléatoire d’une exécution à l’autre. Dans le cas contraire, on éliminera toutes les queues de communication en attente par ipcrm --all=msg.
1. CMSIS
La bibliothèque CMSIS (https://github.com/ARM-software/CMSIS_5) propose un ensemble d’outils de traitement numérique du signal, incluant la transformée de Fourier rapide. Elle est explicitement orientée vers les cœurs ARM, notamment Cortex-M, et donc appropriée pour les cibles que nous visons au travers de libopencm3 (https://github.com/libopencm3/libopencm3), notamment Texas Instruments Stellaris et ST Microelectronics STM32. Étant donné que nous désirons tester les codes sur émulateur QEMU, notre choix du Stellaris est dirigé par la disponibilité du support des LM3S dans sa version officielle pour ARM (paquet qemu-system-arm sous Debian) tandis que l’émulation du STM32 se fera sur la version proposée par André Beckus à https://github.com/beckus/qemu_stm32. Toutes les compilations se font au moyen de GCC ciblant des processeurs ARM sans système d’exploitation installé au moyen du paquet gcc-arm-none-eabi de Debian (version 10.3.1 pour Debian/Sid). FreeRTOS est la version de décembre 2021 disponible à https://www.freertos.org/a00104.html que nous désarchivons au même niveau d’arborescence que le dépôt contenant les codes mis en œuvre dans ce document, à savoir https://github.com/jmfriedt/tp_freertos/ et pour ce qui nous concernera ici, le sous-répertoire 8_xcorr_fft. On prendra soin de cloner les dépendances externes du dépôt par git clone --recursive https://github.com/jmfriedt/tp_freertos.
L’arborescence de CMSIS est relativement limpide avec tous les fichiers liés à la FFT dans CMSIS/DSP/Source/TransformFunctions qui font appel à arm_const_structs.c et arm_common_tables.c de CMSIS/DSP/Source/CommonTables. Le choix de l’implémentation de la FFT – sur une représentation des nombres en virgule flottante en simple précision sur 32 bits, en virgule fixe sur 16 bits ou sur 32 bits – s’effectue par un choix judicieux des fichiers sources compilés selon le bon suffixe (f32, q15 ou q31 respectivement).
Représentation des nombres en virgule fixe
Nous avions largement discuté des représentations des nombres dans [6]. Pour rappel, une représentation en virgule flottante, avec sa représentation scientifique sous forme de mantisse et d’exposant, est peu favorable aux microcontrôleurs aux ressources réduites, faute de périphérique matériel de gestion des opérations arithmétiques sur ce type de représentation. L’arithmétique sur des entiers est efficace, mais en conservant tous les bits de poids faibles, elle risque d’aboutir à des dépassements de capacité et d’exploiter des décimales qui sont dans le bruit de mesure. La représentation en virgule fixe est intermédiaire, manipulant des entiers, mais en supposant que la virgule entre la partie entière et décimale se trouve en position fixe selon la nomenclature Qm.n avec m bits assignés à la partie entière et n à la partie fractionnaire. En notant Q15 ou Q31, la représentation en virgule fixe est implicitement Q1.15 ou Q1.31 respectivement, avec un bit de signe et 15 ou 31 bits de partie fractionnaire. Les nombres compris entre -1 et 1 sont décalés de 15 ou 31 bits respectivement vers la gauche pour une représentation en virgule fixe, et on prendra soin de décaler d’autant vers la droite le résultat de la multiplication afin de maintenir la virgule en position fixe. L’addition quant à elle se fait comme sur des entiers.
CMSIS suppose que les données complexes sont représentées sous forme entrelaçant la partie réelle et la partie imaginaire, donc un vecteur contenant l’alternance R0I0R1I1R2I2... avec R et I la partie réelle et imaginaire respectivement de l’élément indexé.
Comme FreeRTOS ne fournit aucune abstraction, on se contentera donc d’ajouter ces fichiers à la liste des sources compilées en même temps que le cœur de FreeRTOS formé des cinq fichiers contenus dans FreeRTOS/Source. Nous devons par ailleurs ajouter le support du Cortex-M3 proposé par FreeRTOS dans /FreeRTOS/Source/portable/GCC/ARM_CM3/port.c et le gestionnaire de mémoire selon les fonctionnalités attendues tel que décrit à https://www.freertos.org/a00111.html. Le consensus semble être que heap_2.c est le minimum pour permettre une allocation dynamique de mémoire telle que nous allons l’utiliser, mais que heap_4.c est désormais le choix le plus courant. Le Makefile résultant se retrouve à https://github.com/jmfriedt/tp_freertos/blob/master/8_xcorr_fft/Makefile.stellaris qui fait en plus appel à quelques fonctions d’initialisation des périphériques et de communication qui reste à la charge du programmeur, toujours en l’absence d’abstraction du matériel par FreeRTOS.
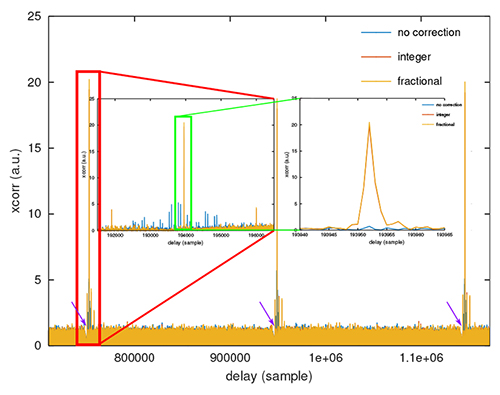
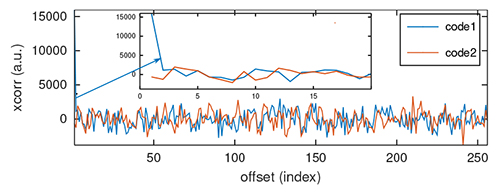
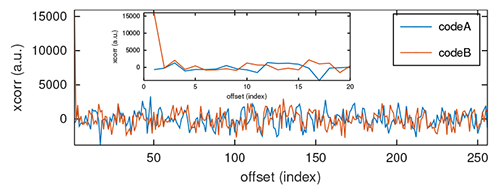
Le cas pratique que nous nous proposons d’étudier, représentatif de toute communication CDMA, est de rechercher lequel parmi deux interlocuteurs communique sur un signal bruité acquis : ces données sont proposées dans https://github.com/jmfriedt/tp_freertos/blob/master/8_xcorr_fft/src/data.h avec pattern les deux motifs orthogonaux tel qu’on pourra par exemple s’en convaincre avec l’intercorrélation dans GNU/Octave (plot(xcorr(pattern1-mean(pattern1),pattern2-mean(pattern2)))), et measurement le signal bruité sur lequel un des codes est superposé (Fig. 3).
Notre objectif est donc d’effectuer trois FFT, produit de la FFT de chaque code avec le complexe conjugué de la FFT du message, et FFT inverse de ces deux résultats pour rechercher par corrélation la présence ou l’absence de chaque message dans le signal transmis. Nous proposons de séparer le travail en trois tâches, une chargée d’implémenter la FFT, qui sera appelée trois fois par l’ordonnanceur en passant en argument les trois tableaux possibles (code 1, code 2 et message), une tâche chargée des multiplications de vecteurs, et finalement une dernière tâche chargée des deux transformées de Fourier inverse. Le séquencement se fait au travers des queues de communication, avec la multiplication en attente de trois résultats de transformée de Fourier, et la transformée de Fourier inverse en attente des multiplications. Nous devons donc échanger les informations entre les diverses tâches, et il serait bien entendu très inefficace de fournir les données elles-mêmes, quand un simple pointeur suffit à informer la tâche suivante de l’emplacement en mémoire des informations sans avoir à les dupliquer.
1.1 Argument des queues de communication : un pointeur de pointeur
Le point qui nous a surpris – et est aussi bien entendu valable pour un échange de pointeur sur des structures complexes contenant une multitude de champs – est que pour passer l’adresse de l’emplacement des tableaux par la queue, il faut échanger des pointeurs de pointeurs, donc l’emplacement en mémoire où se trouve l’adresse à laquelle se trouvent les données. Ceci est clairement défini sur la page de manuel de xQueueSend() à https://www.freertos.org/a00117.html qui démontre avec :
que l’argument de xQueueSend est le pointeur (&pxMessage) vers l’emplacement en mémoire où se trouve le pointeur (pxMessage = &xMessage) vers la structure de données. Ce formalisme quelque peu tordu – ou en tout cas que nous n’avions jamais rencontré jusqu’ici – met en évidence une différence de comportement entre déclaration statique et dynamique de tableaux par allocation de pointeur, dont nous avions toujours répété à qui voulait l’entendre qu’elles étaient strictement identiques (le principe de base de l’enseignement : affirmer avec conviction des demi-vérités si ce ne sont des erreurs, pour ne pas prêter à discussion ou mise en cause de l’affirmation). Le petit test suivant sur architecture ARM, car exploitant des adresses physiques plus faciles à interpréter que des adresses virtuelles générées par le gestionnaire de mémoire MMU des PC, illustre la différence de comportement entre l’allocation dynamique de mémoire et le traitement des adresses résultantes, par rapport à une allocation statique :
que nous compilons par : arm-none-eabi-gcc -I$(OPENCM3)/include -I../common -fno-common -ffunction-sections -fdata-sections -msoft-float -mfix-cortex-m3-ldrd -Os -mcpu=cortex-m3 -mthumb -g3 -DSTM32F1 -DSTM32F10X_MD analyse_pointeur_arm.c ../common/usart_opencm3.c -o analyse -L$OPENCM3/lib -nostartfiles -lopencm3_stm32f1 --static -Wl,--start-group -lc -lgcc -lnosys -Wl,--end-group -T../ld/stm32f103.ld -Wl,--gc-sections dont le -Wl,--gc-sections peut paraître anodin, mais évite de charger les tables de constantes de CMSIS, ou ci-dessous, KISSFFT inutilisée, pour ensuite convertir l’exécutable ELF en binaire. arm-none-eabi-objcopy -Obinary analyse analyse.bin qui permet l’exécution dans QEMU pour STM32F103 d’André Beckus au moyen de qemu-system-arm -M stm32-p103 -serial stdio -serial stdio -serial stdio -kernel analyse.bin qui finalement indique le résultat (avec les annotations manuelles de l’auteur en commentaires) :
Nous constatons donc que :
- toutes les zones mémoire se trouvent dans la RAM dont l’adresse commence en 0x20000000 et dont la longueur a été définie à 132 KB (0x21000) – un des intérêts de l’émulateur par rapport au matériel est de pouvoir définir une taille de RAM arbitraire pour se libérer, au moins en phase de déverminage, des contraintes de place du dispositif physique pour stocker les tableaux ;
- toutes les structures de données manipulées par FreeRTOS sont localisées dans le tas de mémoire qu’il s’alloue lors de :
- dans FreeRTOSConfig.h avec la seule condition que cette taille mémoire tienne dans la mémoire physique, sans nécessairement l’englober totalement ;
- alors que p et q définissent tous deux des pointeurs vers des entiers codés sur 16 bits par allocation dynamique dans le premier cas et statique dans le second, le pointeur vers cette zone de stockage (pointeur de pointeur) diffère du pointeur initial dans le premier cas (&p!=p), mais est égal dans le second (&q==q) et donc l’arithmétique sur les pointeurs de pointeurs diffère elle aussi (&p+1!=&q+1). Dans tous les cas, le premier élément p[1] (ou q[A]) se trouve bien à un offset d’une unité du pointeur original.
Alors que nous avions initialement identifié l’allocation statique comme incompatible avec le passage de paramètre par pointeur de pointeur comme argument des queues de communication, il n’en était rien. Comme souvent en C, notre erreur tenait dans la gestion des tailles de tableaux, puisque nous utiliserons un N+1ème élément pour mémoriser la nature du contenu de chaque tableau lors de l’ordonnancement des opérations arithmétiques. FreeRTOS fournit nombre de fonctions très pratiques pour détecter la taille restante de mémoire sur la pile ou la corruption de celle-ci : l’affichage de la liste des tâches par la fonction vTaskList() permet de vérifier l’intégrité de la pile en donnant toutes les fonctions connues de l’ordonnanceur et l’espace restant sur chaque pile de la forme :
avec ici un peu moins de 1 KB restant pour chaque tâche sur les 4 KB initialement alloués. La fonction vTaskList est activée dans FreeRTOS en définissant :
dans src/FreeRTOSConfig.h et en prenant soin de make clean pour recompiler les sources de FreeRTOS en activant ces options lors de make.
Par ailleurs, on pourra surveiller le dépassement de pile allouée à une tâche par ailleurs en activant cette fonction par
dans FreeRTOSConfig.h et en ajoutant dans le code source la fonction :
qui affichera le nom de la fonction fautive.
CMSIS fournit donc bien les fonctionnalités attendues grâce à arm_cfft_q31(&arm_cfft_sR_q31_len32,(q31_t*)in,1,1); dont l’avant-dernier argument est la direction de la transformée de Fourier (0 pour directe, 1 pour inverse) et &arm_cfft_sR_q31_len32 est une structure de données imposée, dont la fin du nom indique la longueur du vecteur sur lequel s’effectue l’opération, nécessairement puissance de deux entre 16 et 4096 tel que l’indique arm_const_structs.c. Classiquement, un vecteur dont la longueur n’est pas une puissance de 2 sera complété de zéros (zero-padding) pour respecter cette contrainte. On notera que ce faisant, nous n’introduisons aucune information et l’apparent lissage de la FFT en augmentant artificiellement le nombre de points subit un filtrage passe-bas qui ne saurait être interprété comme une super-résolution qu’introduirait une hypothèse additionnelle sur les données acquises.
Cependant, la présence de code assembleur ARM CMSIS/DSP/Source/TransformFunctions/arm_bitreversal2.S interdit toute perspective de portabilité vers des plateformes non ARM, que ce soit pour une simulation sur PC basé sur un processeur Intel ou toute autre plateforme embarquée, et nous désirons donc nous affranchir de cette contrainte en explorant une bibliothèque alternative en C générique.
2. KISSFFT
KISSFFT (Keep It Simple and Stupid) se veut une implémentation minimaliste de la FFT pour rester aussi compacte et lisible que possible. En pratique, la bibliothèque se réduit pour notre application à un unique fichier C et deux fichiers d’en-tête, une facilité de mise en œuvre appréciable. Cependant, KISSFFT n’a pas été explicitement conçue pour une compilation sur système embarqué à faibles ressources et notamment n’exécutant pas de système d’exploitation : lors de la compilation de la bibliothèque, nous devrons prendre soin de désactiver l’appel à des bibliothèques complexes de test qui ne sont pas disponibles pour Cortex-M par la définition de CC="arm-none-eabi-gcc -mhard-float -mfloat-abi=hard -mfpu=fpv4-sp-d16" et surtout KISSFFT_TOOLS=0 pour désactiver ces tests. Finalement, la bibliothèque statique dont nous aurons besoin (en contraste à la bibliothèque dynamique que nous ne saurons charger en l’absence de système d’exploitation) sera générée grâce à l’option KISSFFT_STATIC=1. Pour conclure, nous compilons KISSFFT au moyen de KISSFFT_TOOLS=0 KISSFFT_STATIC=1 CC="arm-none-eabi-gcc -mthumb -mhard-float -mfloat-abi=hard -mfpu=fpv4-sp-d16 -mcpu=cortex-m4 -DLM4F" make pour un processeur compatible LM4F (Cortex-M4 avec unité matérielle de calcul sur nombres en représentation à virgule flottante) par exemple. Le choix de la représentation des données s’obtient en incluant -DFIXED_POINT=32 -DKISSFFT_DATATYPE=int32_t pour préciser que les calculs se font sur des données au format Q31 dans la bibliothèque. Bien entendu, nous devrons prendre soin de respecter nous-mêmes ce mode de représentation lors des opérations arithmétiques : alors que les additions se font comme sur des entiers, les produits doivent éliminer les décimales inutiles en replaçant la virgule au bon emplacement après un produit sur des entiers qui nécessite de caster sur une structure intermédiaire de grande dimension tel que nous l’expliciterons ci-dessous :
Contrairement au format entrelacé de CMSIS, KISSFFT propose une structure de données complexes kiss_fft_cpx contenant deux éléments que sont .r et .i pour représenter la partie réelle et imaginaire respectivement dans le mode de codage sélectionné au cours de la compilation parmi flottant, virgule fixe sur 16 bits ou sur 32 bits.
Initialement attirés par cette philosophie plus que louable de simplicité, nous nous sommes heurtés à deux écueils lors de son utilisation :
- Alors que l’utilisation d’une représentation en virgule fixe (Q15 ou Q31) laisse présager des calculs sur des entiers exclusivement, le code cache deux appels à des nombres représentés en virgule flottante, à https://github.com/mborgerding/kissfft/blob/master/kiss_fft.c#L310 et https://github.com/mborgerding/kissfft/blob/master/kiss_fft.c#L359.
- Une allocation dynamique de mémoire non protégée à https://github.com/mborgerding/kissfft/blob/master/kiss_fft.c#L346.
Le second point a été la cause de nombre de soucis, l’allocation de mémoire n’étant pas une opération atomique (lecture de l’état de la mémoire, allocation d’un segment et mémorisation du segment alloué) qui peut donc être préemptée lors de son exécution et rendre le gestionnaire de mémoire incohérent. On s’en rend rapidement compte si on omet de protéger la fonction kiss_fft_alloc par un mutex qui garantit qu’une seule tâche peut allouer de la mémoire à un instant donné, et comme d’habitude en l’absence de mutex avec un comportement aléatoire selon le bon vouloir de l’ordonnanceur.
Le problème du calcul flottant caché dans le code ne devrait a priori pas poser problème si une émulation logicielle est fournie par la bibliothèque mathématique libm.a, puisque seules les initialisations requièrent ces fonctionnalités. Pour notre malheur, nous avions par erreur cru que le LM3S était un Cortex-M4 muni d’une unité matérielle de gestion des nombres à virgule flottante (FPU) et compilions le code en -mhard-float -mfloat-abi=hard. L’appel à la FPU lors de l’émulation par QEMU d’un processeur Cortex-M3 sans FPU se traduisait par une Hard Fault et l’opportunité de mettre en pratique gdb sur ARM émulé par QEMU. En effet, plusieurs gestionnaires d’erreurs fatales sont gérées par libopencm3 par l’appel à la boucle infinie : blocking_handler(void) est appelée par hard_fault_handler, mem_manage_handler, ou bus_fault_handler. Nous n’avons finalement pas eu besoin d’aller aussi loin que proposé dans
https://www.freertos.org/Debugging-Hard-Faults-On-Cortex-M-Microcontrollers.html puisque le problème a disparu lors du passage à la compilation en Cortex-M3 sans support matériel des nombres à virgule flottante, mais une émulation logicielle par libm.
QEMU pour analyser du code issu de compilation croisée
Nous avons mis un temps certain à identifier l’instruction fautive de l’arrêt pur et simple de QEMU sans information quant à la cause du dysfonctionnement. Bien entendu dans ce cas, le GNU Debugger GDB devient indispensable. GDB permet maintenant de debugger un code « cross compilé » sur l’architecture hôte grâce à gdb-multiarch. Lors de l’émulation du code « cross compilé » à destination du Cortex-M4 avec support matériel d’une unité de calcul sur nombre à virgule flottante FPU, nous exécutons :
dont le -s -S en fin de commande indique que nous lançons un serveur gdb qui attend qu’un client s’y connecte pour exécuter le code par continue. Le client (paquet gdb-multiarch de Debian) se lance par gdb-multiarch output/main.elf que nous configurons par :
Les commandes classiques de GDB telles que l’affichage du code source autour du point courant d’exécution par list ou l’ajout d’un point d’arrêt par break do_fft sont bien sûr disponibles. Cependant, dans tous les cas, l’exécution du code s’achève par la boucle infinie de libopencm3 qui gère l’erreur ingérable (dans lib/cm3/vector.c) par :
et ce n’est que l’analyse du code source de KISSFFT qui nous a permis de trouver l’appel à l’opération sur nombre à virgule flottante fautive.
Une fois tous ces déboires résolus, KISSFFT se résume à kiss_fft_cfg cfg=kiss_fft_alloc(N,1,NULL,NULL ); suivi de kiss_fft(cfg,in,out); qui n’affranchit pas de lire kissfft/kiss_fft.c pour trouver :
signifiant qu’au lieu de fournir NULL en derniers arguments, nous aurions pu allouer nos propres structures de données et le fournir en argument préalloué, KISSFFT s’assurant que leur taille est suffisante pour ses opérations.
3. Multiplication des vecteurs
Une fois les valeurs des transformées de Fourier des coefficients et des mesures obtenues, il reste à multiplier les vecteurs afin de calculer FFT(m)· FFT*(s) pour obtenir un nouveau vecteur de même longueur. Peu de subtilité ici, si ce n’est de ne pas se tromper dans le calcul du produit complexe (mr+jmi)·(sr−jsi)=(mrsr+misi)+j(misr−mrsi) et effectuer le calcul intermédiaire sur les nombres représentés en virgule fixe sur B bits sur une variable de 2B bits avant de décaler pour éliminer les bits superflus.
3.1 Approche naïve
Ainsi en représentation Q31, nous aurons une boucle sur chaque élément de sortie de la forme :
en prenant bien soin du cast sur chaque terme pour ne pas laisser au hasard du compilateur la taille du codage de chaque élément du calcul.
Cependant, en l’absence de contrainte sur l’ordonnancement par FreeRTOS des FFT initiales, nous ne saurions prévoir quelle queue de données a reçu quel vecteur parmi les mesures bruitées, le premier code ou le second code. Afin d’identifier la fonction de chaque vecteur, nous ajoutons un N+1ème élément (donc d’indice N en C) contenant un indice qui permet de retrouver quelle est la nature du vecteur transmis. Lors de la réception de la queue de données fournie par la FFT, cet indice nous informera s’il s’agit d’un des vecteurs de référence ou de la mesure. L’assignation du pointeur fourni par la queue vers la structure adéquate n’est que manipulation de pointeurs et ne prend donc que peu de place :
qui se répète pour les trois queues recevant les pointeurs du résultat de calcul des trois tâches chargées de calculer les FFT.
3.2 Parallélisons (ou pas)
Le produit de deux vecteurs est l’archétype de la fonction qui se parallélise parfaitement, chaque coordonnée de chaque vecteur étant indépendante de ses voisins et pourtant sujette aux mêmes opérations arithmétiques qui bénéficient donc des instructions Single Instruction, Multiple Data SIMD. Yann Guidon a largement abordé dans [7] les bénéfices de ces instructions dans le cas du Jeu de la Vie de Conway, mais en se limitant au bestiaire des processeurs issus de Intel. La situation n’est pas beaucoup plus simple chez ARM, entre l’extension NEON qui équipe leurs plus gros cœurs et dont l’utilisation bénéficie largement aux performances de GNU Radio par l’utilisation de la bibliothèque VOLK [8], mais qu’en est-il sur petit microcontrôleur ? La situation est simple sur le Cortex-M3 qui nous a intéressés jusqu’ici (p. ex. STM32F103) : le jeu d’instruction ARMv7-M n’a aucune instruction arithmétique parallélisable [9], donc pas d’accélération possible. Le Cortex-M4 et son jeu d’instructions ARMv7E-M sont un peu plus intéressants, tel que nous le constatons en lisant les sources de CMSIS_5/CMSIS/DSP/Source/BasicMathFunctions/arm_mult_q15.c qui montre comment en l’absence de la définition de la constante ARM_MATH_MVEI, la bibliothèque CMSIS se contente de concaténer deux opérations sur 16 bits (entiers signés en virgule fixe au format Q15) pour effectuer une multiplication sur 32 bits. Le réel bénéfice de l’instruction SIMD apparaît en présence du M-Vector Extension Instructions (MVEI, aussi connu sous le nom d’« Helium ») où les registres adéquats sont remplis pour effectuer 8 multiplications en une instruction vst1q(pDst, vqdmulhq(vecA, vecB));, mais ceci uniquement sur cœur M33 ou M35. Ces optimisations restent encore loin de ce qu’amène NEON, tel qu’en atteste la même fonction fournie dans VOLK à https://github.com/gnuradio/volk/blob/main/kernels/volk/volk_16ic_x2_multiply_16ic.h.
Finalement, une fois le produit achevé, la transformée de Fourier inverse est obtenu par l’appel de la fonction adéquate dans chaque bibliothèque, le calcul étant strictement identique à un signe près, puisque exp(−jωt) devient exp(jωt) selon que la transformée de Fourier soit directe ou inverse.
4. Résultats
La dernière subtilité lors du déverminage de ces codes, et notamment de l’affichage des grands tableaux contenant les données initiales, leurs FFT, les produits des FFT et les FFT inverses, est que la tâche en cours d’affichage se fait préempter compte tenu de la lenteur de la communication, et tous les tableaux sont mélangés. Nous prendrons donc soin de protéger l’affichage de chaque tableau par un unique mutex représentant l’unique ressource commune de communication qu’est par exemple un port de communication asynchrone compatible RS232 :
Le lecteur désireux de comparer les temps de calcul par l’approche spectrale par rapport à l’algorithme de complexité N2 dans le domaine temporel pourra s’inspirer de la fonction suivante pour calculer la corrélation entre x et y, tableaux de n valeurs, en déroulant les deux boucles imbriquées, celle sur ko pour balayer les indices du retard de la corrélation et ki la boucle intérieure pour accumuler les valeurs de l’intégrale :
mais surtout se convaincra ainsi de l’exactitude de la dérivation du calcul dans le domaine spectral.
Conclusion
Nous avons mis en œuvre une bibliothèque complexe, la transformée de Fourier rapide, dans un environnement multitâches qu’est FreeRTOS. Ce faisant, nous nous sommes heurtés aux problèmes classiques d’accès concurrent aux ressources (allocation dynamique de mémoire), d’ordonnancement des tâches et de synchronisation par échanges de données au travers des queues. La plus grande difficulté rencontrée a été la cohérence des options de compilation lors de l’exécution dans QEMU : nous avions par erreur cru que les plateformes lm3s* de qemu-system-arm étaient des Cortex-M4 avec support matériel de l’unité de calcul flottante (option -mhard-float -mfloat-abi=hard) qui se traduisait par une instruction erronée lors de l’exécution d’un appel caché dans la bibliothèque KISSFFT aux calculs à virgule flottante.
Cette introduction à CMSIS dans FreeRTOS ouvre de nombreuses perspectives de développement supportant une multitude d’architectures, et en particulier l’utilisation de FreeRTOS dans un environnement POSIX (https://github.com/ARM-software/CMSIS-FreeRTOS/tree/develop/Demo/Posix_GCC) afin d’avoir accès aux outils de profilage fournis sur PC.
Références
[1] J.-M Friedt, G. Cabodevila, « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », OpenSilicium n°15 (2015) - https://connect.ed-diamond.com/Open-Silicium/os-015/decodage-des-signaux-de-satellites-gps-recus-par-recepteur-de-television-numerique-terrestre-dvb-t
[2] J.-M Friedt, W. Feng, « Analyse et réalisation d’un RADAR à bruit par radio logicielle » (1/3), GNU/Linux Magazine France n°240 (2020) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-240/analyse-et-realisation-d-un-radar-a-bruit-par-radio-logicielle
[3] M. Heideman, D. Johnson, C. Burrus, « Gauss and the history of the fast Fourier transform », IEEE ASSP Magazine 1(4), 14–31 (1984) à https://www.cis.rit.edu/class/simg716/Gauss_History_FFT.pdf
[4] W. H. Press & al., « Numerical Recipes in Pascal – the Art of Scientific Computing », Cambridge University Press (1989).
[5] E.O. Brigham, « The Fast Fourier Transform: An Introduction to Its Theory and Application », Prentice Hall (1973) a un titre à peine mensonger, car la FFT n’est abordée qu’en page 148/230, mais la version en Algol du programme vaut le détour.
[6] J.-M Friedt, « Arithmétique sur divers systèmes embarqués aux ressources contraintes : les nombres à virgule fixe », GNU/Linux Magazine France Hors-Série n°113 (mars 2021) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmfhs-113/arithmetique-sur-divers-systemes-embarques-aux-ressources-contraintes-les-nombres-a-virgule-fixe
[7] Y. Guidon, « La logique du Jeu de la Vie : exercices amusants de pensée latérale », GNU/Linux Magazine France n°213 (mars 2018) - https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-213/la-logique-du-jeu-de-la-vie-exercices-amusants-de-pensee-laterale
[8] G. Goavec-Merou & J.-M Friedt, « On ne compile jamais sur la cible embarquée » : Buildroot propose GNU Radio sur Raspberry Pi (et autres), Hackable n°37 (avril 2021) - https://connect.ed-diamond.com/hackable/hk-037/on-ne-compile-jamais-sur-la-cible-embarquee-buildroot-propose-gnu-radio-sur-raspberry-pi-et-autres
[9] ARM nous informe dans https://community.arm.com/cfs-file/__key/telligent-evolution-components-attachments/01-2057-00-00-00-01-28-35/Cortex_2D00_M-for-Beginners-_2D00_-2017_5F00_EN_5F00_v2.pdf que « M4 provides all the features on the Cortex-M3, with additional instructions target at Digital Signal Processing (DSP) tasks, such as Single Instruction Multiple Data (SIMD) and faster single cycle MAC operations. »
Remerciements
Alors que la corrélation est probablement notre activité quotidienne requérant le plus de puissance de calcul dans le cadre du décodage de signaux CDMA (notamment pour la navigation par satellites), de mesure de temps de vol de signaux RADAR ou de transfert de temps par satellite, cette étude sur la FFT sur microcontrôleur à faibles ressources a été menée au cours de la rédaction de l’examen de Master1 d’Électronique Embarquée pour les étudiants de l’Université de Franche-Comté à Besançon.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture