Pas besoin d'être mentaliste et d'avoir compris Nostradamus pour deviner les pensées de ses voisins : une connexion internet, un peu de programmation, quelques notions de probabilité et du temps CPU feront l'affaire !
1. Introduction
Guesswork [1] est le terme utilisé par les anglo-saxons pour désigner la science qui permet de retrouver-deviner des valeurs. C'est une discipline très importante pour l'expert en sécurité, car de nombreux mécanismes de sécurité reposent sur l'ignorance par l'attaquant de certaines valeurs comme une clef de chiffrement ou un mot de passe. Les applications du guesswork augmentent, car les services en ligne ou les applications dans les smartphones utilisent de plus en plus souvent des identifiants anonymes très intrigants. Ces identifiants anonymes sont construits à partir d'un identifiant unique ou d'une combinaison d'identifiants uniques comme l'adresse MAC de l'appareil, une adresse mail ou le numéro IMEI de son téléphone. Ces identifiants uniques ne sont pas utilisables tels quels, car ils donnent trop d'informations sur la personne physique : elles ont un caractère personnel selon la CNIL. La question à laquelle nous allons répondre est de savoir s'il est difficile de retrouver ces identifiants uniques à partir des identifiants anonymes.
2. Comment deviner ?
Quels sont les outils à la disposition de l'attaquant ? Le premier outil est la recherche exhaustive. On énumère toutes les valeurs possibles jusqu'à trouver la bonne. Le coût temporel de cette méthode dépend de la taille de l'espace à énumérer. Si la valeur que l'on cherche est de longueur m bits, il faut en moyenne essais pour retrouver une valeur. Pour mener à bien ce genre d'attaque, on dispose d'outils tel que JTR ou Hashcat qui disposent d'implémentations optimisées des principales fonctions de hachage cryptographiques pour CPU et GPU.
Le deuxième outil pour réduire le coût temporel de l'attaque par recherche exhaustive est l'attaque par dictionnaire. On construit un dictionnaire contenant l'association entre tous les condensés et tous les textes clairs. La recherche dans le dictionnaire est quasi immédiate, mais il faut une mémoire et un pré-calcul (construction du dictionnaire). Le compromis entre ces deux attaques est possible avec les rainbow tables qui sont décrites en détail dans le numéro 58 de MISC.
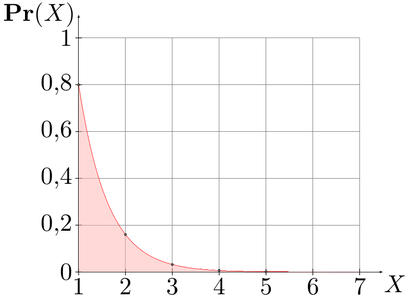
Les attaques précédentes sont les meilleures quand les valeurs que l'ont doit deviner sont uniformément réparties dans l'espace à énumérer. On peut faire beaucoup mieux si on connaît la distribution de probabilité associée aux valeurs à deviner. Soit un ensemble de valeurs à deviner. On note les probabilités des éléments triés dans l'ordre décroissant. L'attaque qui vient tout de suite à l'esprit consiste à énumérer toutes les solutions possibles par ordre décroissant de probabilité. Si on effectue la recherche de cette façon, le nombre moyen d'essais qu'il faudra effectuer est donné par : . Cette quantité est appelée dans la littérature guessability [1] d'une valeur. Elle est très utilisée pour les mots de passe (voir [2]). Quel est le gain de cette méthode ? Tout dépend de la distribution. Imaginons que l'on cherche à retrouver une valeur qui suit une distribution géométrique. Cette distribution de paramètre p est définie par . Le paramètre p nous donne l'élément ayant la plus forte probabilité. Prenons, et comme sur la Figure 1. Au lieu de devoir tester valeurs en moyenne avec la recherche exhaustive, on a . On teste en moyenne 2 valeurs.
Cet exemple est relativement convaincant, mais il ne correspond à aucun cas concret. Nous allons considérer le cas des adresses MAC.
Figure 1 : Distribution géométrique pour p=0.8.
3. Exemple
Euclid (http://www.euclidanalytics.com) est une société qui fait des systèmes de physical tracking qui exploite les communications WIFI de vos smartphones pour traquer leurs utilisateurs. Euclid construit des bases de données identifiant chaque utilisateur par son adresse MAC. Conscient que stocker l'adresse MAC en clair représente un risque, Euclid a pris des mesures pour protéger cette information :
« Data is transferred securely (using SSL) and is "hashed" (scrambled into a meaningless string of numbers and letters) before it is stored on Amazon Web Services. Hashed data can not be reverse engineered by a third party to reveal a devices MAC addresses This means that anyone who gains access to the database directly from Amazon – authorized or unauthorized - will only see long strings of numbers and letters. They would not be able o get any information that could be linked to a back to a particular mobile device owner. »
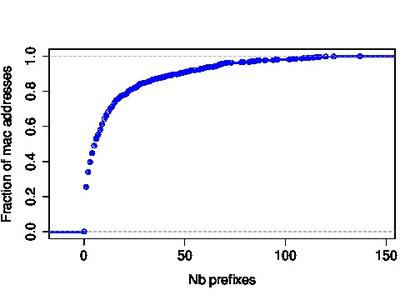
En gros, on hache les adresses MAC en utilisant une fonction de hachage cryptographique comme SHA-1 ou (mieux) SHA-3. Une adresse MAC est longue de 48 bits. L'attaque exhaustive coûte . Avec Hashcat, il faut environ 25 h de calcul si l'on dispose d'un certain nombre de cartes graphiques (voir le site de Hashcat). Si comme moi vous ne disposez pas de ce matériel, on peut heureusement faire beaucoup mieux sans matériel dédié. Pour cela, on va exploiter la structure d'une adresse MAC. Les adresses MAC sont constituées de 2 champs de 24 bits. Les bits de poids fort désignent le Organizationally Unique Identifier (OUI). Les OUI sont attribués par IEEE et on peut tous les retrouver sur http://standards.ieee.org/develop/regauth/oui/oui.txt. Le nombre de OUIs alloués à ce jour est de 18189 sur les possibles. On est très loin de devoir tester, mais plutôt . On a 1000 fois moins de valeurs à tester en moyenne ! Mais on peut encore faire mieux. En France, il n'existe pas des centaines de constructeurs qui vendent des cartes réseaux. Nous avons collecté avec Mathieu Cunche un dataset de quelque dizaines de milliers d'adresses MAC en capturant des probe requests. La Figure 2 nous montre la distribution cumulative des adresses OUI observées. En pratique, avec 111 adresses OUI, on couvre 99.9 % du dataset. Si on calcule la quantité exploitant toutes ces informations, on trouve :. On a ainsi gagné un facteur 262144 sur la recherche exhaustive. Sur votre ordinateur portable, il ne vous faudra que quelques secondes pour retrouver l'adresse MAC correspondant à un haché SHA-1. La méthode d'anonymisation d'Euclid n'est donc pas respectueuse de la vie privée. Les développeurs d'Euclid ont oublié un principe très important en cryptographie :
L'entropie de la sortie d'une fonction de hachage ne dépasse pas l'entropie de son entrée.
Dans un français plus littéraire, une fonction de hachage ne transforme pas l'eau en vin. Pour anonymiser une adresse MAC, une solution peut consister à utiliser un MAC : Message Authentication Code. Ces fonctions prennent en entrée une clef. Si ce paramètre est inconnu de l'attaquant et suffisamment grand, alors retrouver l'adresse MAC n'est plus possible à partir du haché.
On peut s'amuser à répondre à des questions cruciales ! Combien faut-il d'essais en moyenne pour trouver l'âge du capitaine ? Si on suppose qu'il est français et toujours en vie, d'après la pyramide des âges de l'INSEE (http://www.insee.fr/fr/themes/tableau.asp?ref_id=ccc), il faut alors en moyenne 40 essais.
Figure 2 : Distribution des adresses OUI observées.
Conclusion
Il y a deux conclusions importantes à donner à cet article.
La première s'adresse aux programmeurs d'applications qui veulent identifier leurs utilisateurs : le hachage de valeur unique comme les adresses MAC, le numéro IMEI, nom et prénom ou encore une adresse mail ne garantit pas la protection de la vie privée des utilisateurs ! Il existe malheureusement encore beaucoup d'applications comme Gravatar (https://gravatar.com/), qui hachent votre adresse mail [3], l'application mobile de la RATP qui hache le numéro IMEI de votre smartphone [4]. Ces applications construisent des identifiants à partir d’identifiants uniques et espèrent que le hachage transforme l'eau en vin. Si on veut créer des identifiants, il veut mieux utiliser les Universally Unique Identifiers (UUID) qui sont définis dans la RFC 4122 (http://www.ietf.org/rfc/rfc4122.txt). On peut noter que pour Linux, les versions implémentées de l'UUID (uuid_generate) reposent soit sur le temps, soit sur l'utilisation de nombres aléatoires (si tant est qu'il soit possible d'accéder à de tels nombres sur une machine Linux, mais c'est un autre débat).
La deuxième conclusion de ce papier est pour les attaquants : exploitez au mieux les informations qui sont à votre disposition. Il est très tentant de faire une recherche exhaustive sur un espace de en investissant dans du matériel haut de gamme. Il est plus élégant et meilleur marché d'utiliser son cerveau.
Références
[1] James L. Massey « Guessing and entropy », ISIT 1994.
[2] Joseph Bonneau « The science of guessing: analyzing an anonymized corpus of 70 million passwords », S&P 2012.
[3] « De-anonymizing Members of French Political Forums », PASSWORD CON 2013.
[4] Jagdish Prasad Achara, James-Douglass Lefruit, Vincent Roca, and Claude Castelluccia « Detecting Privacy Leaks in the RATP App : how we proceeded and what we found », Grehack 2013.