Détection d'anomalies par ACP

Un analyste SOC, posté devant son SIEM préféré, manque parfois d’outils simples lui permettant de mettre à profit son expertise dans la recherche proactive d’anomalies. Cette absence d’outils est parfois la raison principale d’absence d’une telle activité, qui cantonne l’analyste à traiter uniquement les alertes remontées par les signatures configurées dans le SIEM. La détection d'anomalies statistiques apporte un outil complémentaire dans la trousse à outils des analystes.

1. L'ACP, en résumé

1.1 Utilisation courante de l’ACP

L’ACP ne sera pas totalement détaillée dans cet article. Le lecteur trouvera de nombreuses ressources sur Internet pour approfondir ses connaissances (dont [1]). Il s’agit simplement ici de donner les informations strictement nécessaires à la bonne compréhension de l’article aux lecteurs découvrant cette méthode. Nous définissons un jeu de données multivariées (multidimensionnels) comme un tableau représentant des « individus » (en lignes) qui sont caractérisés par « p » variables quantitatives (ou caractéristiques, en colonnes) avec p > 1. Le nombre « p » est appelé la dimension du jeu de données.

L’ACP est une méthode statistique puissante, emblématique de l’analyse des données, qui est utilisée principalement :

• pour explorer et comprendre un jeu de données multivariées. L’ACP permet de simplifier, résumer, un jeu de données de hautes dimensions (dizaine, centaines de variables...). En synthétisant les données d’origine, elle rend possible ou simplifie l’interprétation de ces données ;
• pour réduire les dimensions d’un jeu de données multivariées. Cette réduction est utilisée notamment pour permettre la visualisation de données (quand la réduction s’opère en ne gardant pas plus de 3 dimensions), pour optimiser des algorithmes (espace mémoire et temps de calcul) ou réduire les effets indésirables quand ils opèrent sur des données de grandes dimensions ([2]) ;
• pour détecter des anomalies. L’analyse des valeurs extrêmes sur les composantes principales (high scores) ainsi que l’erreur de reconstruction des individus permettent de détecter des individus en anomalies. L’erreur de reconstruction caractérise la distance entre l’individu d’origine et son approximation (liée à la réduction de la dimension des données que sait opérer l’ACP). C’est une métrique utile pour permettre de réaliser une détection d’anomalies. Ces méthodes seront présentées dans cet article.

1.2 Comment ça marche ?

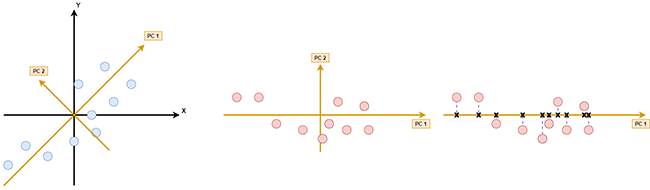
La figure 1 montre des individus (points bleus) caractérisés par 2 variables (x et y). Le résultat d’une ACP sur ce jeu de données de dimension 2 est un nouvel espace déterminé par les deux composantes principales du jeu de données (PC1 et PC2). Chaque composante principale est orthogonale (comprendre perpendiculaire) à toute autre composante principale. La variance (comprendre la dispersion) des données selon l'axe PC1 est maximale : c’est la première composante principale du jeu de données. PC2 définit le deuxième axe de variation principale des données, orthogonal à PC1. Les individus projetés sur ce nouvel espace sont désormais représentés par deux nouvelles variables (PC1 et PC2). À ce stade, aucune perte d’information, nous n’avons fait que changer de repère (deuxième image) sur deux nouveaux axes maximisant la variance des données. La réduction de données s’opère en projetant (orthogonalement) sur PC1 (troisième image). En conservant cet axe comme unique dimension, on réduit la dimension de nos données (de deux à une dimension) : on perd donc de l’information (en ne conservant que les croix noires), mais en limitant au maximum cette perte : la variance principale des données est conservée.

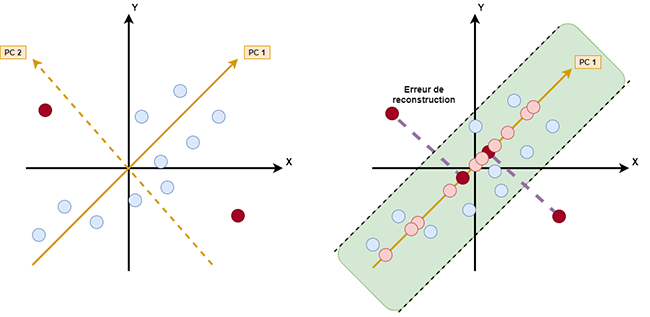
La figure 2 présente le principe de détection d’anomalies par erreur de reconstruction. Toute projection entraîne une perte d’information (on abandonne des dimensions). La distance euclidienne entre l'individu d’origine et son approximation (sa projection) est appelée « erreur de reconstruction » de l'individu. Cette erreur n’existe que s’il y a projection de l’individu sur un sous-ensemble des composantes principales. Si cette erreur est supérieure à un seuil arbitraire à définir, alors l’individu sera considéré comme une anomalie. L’approximation en dimension 1 (k=1) est réalisée en projetant chaque individu sur PC1. L’erreur de reconstruction des points rouges sera plus forte que pour les autres points. Nous voyons aussi que les points rouges ont des valeurs beaucoup plus fortes sur PC2 que les autres points.

En généralisant à des dimensions supérieures (p>2), calculer une erreur de reconstruction nécessitera d’abord de choisir sur quel sous-espace projeter l’individu pour obtenir son approximation, avant de calculer la distance avec l’individu d'origine. Cela consiste à conserver les « k » premières composantes principales (ou, autrement dit, d’abandonner les « p-k » dernières composantes) pour avoir l’approximation en dimensions k de notre individu (avec 0 < k < p).

1.3 Théorie

Le résultat d'une ACP normée (on centre et réduit les données d’origine au préalable) sur un jeu de données de dimensions « p » est une nouvelle base orthonormée définissant un nouvel espace de dimension « p » tel que la variance des données selon ces nouveaux axes soit maximisée. Les vecteurs composant cette nouvelle base orthonormée sont appelés les composantes principales du jeu de données. Chaque composante est classée par ordre décroissant de variance expliquée. Ainsi, la première composante principale détermine le premier axe principal du nouvel espace : c’est cet axe qui explique d’abord la plus grande variance des données, puis c’est autour de la seconde composante d’expliquer le maximum de la variance résiduelle (inertie) et ainsi de suite. Mathématiquement, les composantes principales d’une ACP normée sont les vecteurs propres de la matrice de corrélation (matrice carrée de dimension p) du jeu de données, classées par ordre décroissant de valeur propre correspondante. Il existe donc bien p composantes principales. Chaque composante principale est une combinaison linéaire des variables initiales du jeu de données. Lorsqu’on cherche à réduire les dimensions d’un jeu de données, il suffit de choisir 0 < k < p et de projeter les données d’origine dans le nouvel espace défini par les k premières composantes principales. Identifier les individus ayant les erreurs de reconstruction les plus fortes avec les « k » premières composantes retenues pour l’approximation (projection) permet d’identifier les individus ayant des valeurs plus fortes que les autres individus sur au moins l’une des (p-k) composantes non retenues.

2. Analyse de l'activité réseau

Nous allons dans la suite de cet article considérer comme exemple la détection d’anomalies de flux réseaux. Le choix de présenter un tel exemple de détection d’anomalies par ACP est notamment motivé par l’existence de datasets publics de flux réseaux comportant du trafic jugé « normal » avec quelques « anomalies » (de types attaques réseaux) qui peuvent servir de support pour cet article en rendant les résultats et analyses reproductibles. Dans tous les cas, l’objectif est bien de mettre en lumière l’ACP dans sa capacité de détection d’anomalies, quelles que soient les données analysées.

Nous définissons l'anomalie comme une activité réseau atypique vis-à-vis des autres activités réseaux observées dans le jeu de données considéré. On note donc que l'anomalie n'est pas définie ici comme un écart vis-à-vis d'une activité référence (aucun apprentissage nécessaire) et nous n’excluons aucune cause possible pour cette anomalie : elle pourrait tout à fait provenir d’une attaque informatique comme d’un événement de production courant (mauvaise configuration, panne.). Autrement dit, nous ne chercherons pas à réaliser une détection d’attaques réseaux, mais bien une recherche d’anomalies (statistiques) sur l’activité réseau. Nous faisons l’hypothèse que ces anomalies sont en minorité dans le jeu de données à analyser (activité « normale » majoritaire) et suffisamment « différentes » de l’activité normale. Ceci répond au cas d’usage exposé dans l’introduction : on souhaite trouver des périodes de temps atypiques à soumettre à un analyste lorsqu’il regarde, a posteriori, une période de temps donnée (par exemple, la dernière quinzaine ou dernier mois d’activité d’un firewall). On ne prédira en rien la cause des anomalies détectées, ce travail est laissé à l’expertise de l’analyste.

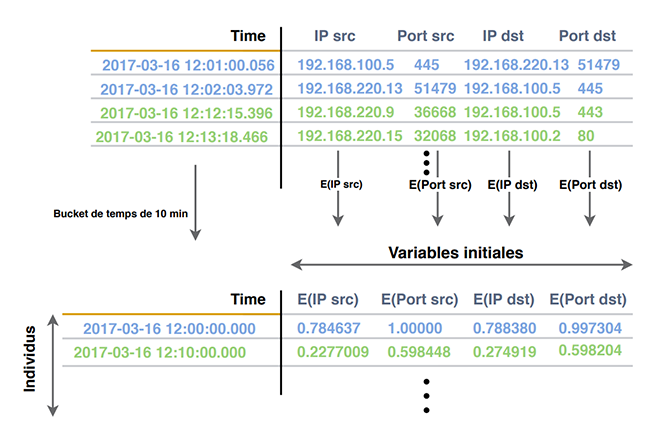
Maintenant, il nous reste à définir ce qu'on entend par activité réseau et tenter de la caractériser. La première approche pourrait consister à considérer que chaque ligne de log fournie par notre équipement réseau (firewall, routeur) représente une activité réseau. Cette approche n’est pas pertinente pour notre objectif. Un log, unitairement, représente un flux, une communication. L’activité réseau est alors décrite par l’ensemble des flux présents au cours d’une certaine période de temps. Nous choisissons donc de représenter « l'activité réseau » en découpant les logs par tranches de 10 minutes (choix arbitraire) et en extrayant des caractéristiques issues de l'agrégation des flux réseaux pour chaque tranche. Le choix se porte sur les caractéristiques suivantes, calculées pour chaque tranche de 10 minutes : E(IP sources), E(IP destinations), E(Ports sources), E(Ports destinations) où E est la fonction d’entropie de Shannon ([3]). Cette entropie, issue du concept de la thermodynamique et adapté à la théorie de l’information est sûrement familière à tous ceux qui ont cherché à détecter des noms de domaines générés automatiquement, et plus généralement aux analystes malware. Dans la détection d'anomalie réseau, cette mesure de la dispersion est également pertinente [4]. De nombreuses anomalies réseaux vont en effet perturber (entre autres) la distribution des adresses IP et ports. L’entropie de Shannon est alors une mesure efficace de cette perturbation. L'intuition qui peut en être donnée est la suivante : si une machine commence à prédominer dans une tranche (imaginons un scan massif provenant d'une seule adresse IP), alors l'entropie de Shannon des adresses IP sources aura tendance à diminuer, car l'espace des IP sources se « concentrera » sur l'adresse IP malveillante. De même si un DDOS a lieu sur un serveur donné, alors l'entropie de Shannon des adresses IP sources aura au contraire tendance à augmenter pendant l’attaque.

Bien évidemment, bien d’autres caractéristiques pourraient être exploitées dans la détection d’anomalies : la taille des paquets, les flags, etc., suivant ce qu’on cherche à détecter comme types d’anomalies et les informations disponibles dans les logs considérés (routeur, firewall), mais nous nous limiterons à ces quatre caractéristiques dans la suite de l’article.

En réalisant une détection d’anomalies par ACP sur les individus « tranches de temps » caractérisés par quatre variables, nous souhaitons découvrir et pointer des périodes de temps « anormales ».

2.1 Présentation du dataset

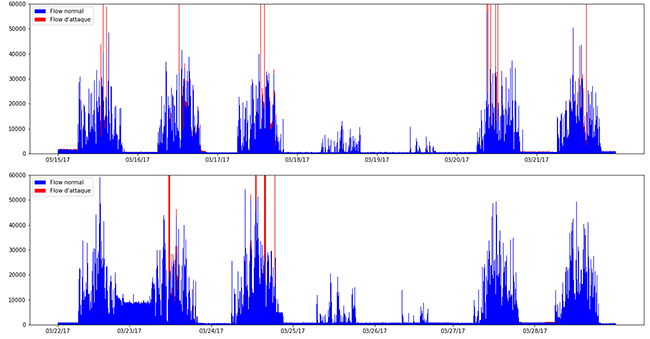
Nous utilisons pour l’exemple, le dataset CIDDS-01 (Coburg Intrusion Detection Dataset) publié par une université allemande de sciences appliquées [5] [6]. Il présente l’avantage d’être bien documenté, réalisé sur une période correspondant à notre cas d’école (28j), de posséder une majorité de flux normaux (90%) et quelques attaques de type scans, DoS, ou bruteforce (10%) (ce qui correspond à nos hypothèses sur la répartition entre trafic normal et potentielles anomalies) et surtout d’être labellisé. Les logs générés par les attaques sont clairement mentionnés, ce qui facilite l’analyse des résultats obtenus. À noter qu’il s’agit de logs au format Netflow unidirectionnel (une communication TCP est représentée par deux logs, un représentant le sens aller (« client » vers « serveur ») et l’autre, le sens retour. La figure 4 présente la répartition des logs liés à l’activité normale et aux attaques sous forme d’histogrammes empilés.

2.2 Implémentation de l'ACP

Pour implémenter l’ACP, nous avons d’abord créé un notebook Python, dans JupyterLab, s'appuyant notamment sur les librairies pandas, scikit-learn, ainsi que matplotlib et seaborn. La librairie pandas a été utilisée essentiellement pour les étapes de prétraitement de nos données : chargement à partir des CSV, filtrage, création des tranches de temps et calcul de l'entropie de chacune des variables initiales retenues (par application de la fonction scipy.stats.entropy). Nous avons effectué le centrage et la réduction des données, ainsi que l'ACP, avec les classes standards de scikit-learn : sklearn.preprocessing.StandardScaler et sklearn.decomposition.PCA. Les librairies matplotlib et seaborn ont, quant à elles, servi à créer les visualisations telles que le cercle de corrélations ou les nuages de points. Le notebook python est disponible ici [7].

2.3 Analyse des résultats

2.3.1 Éboulis des valeurs propres (« scree plot »)

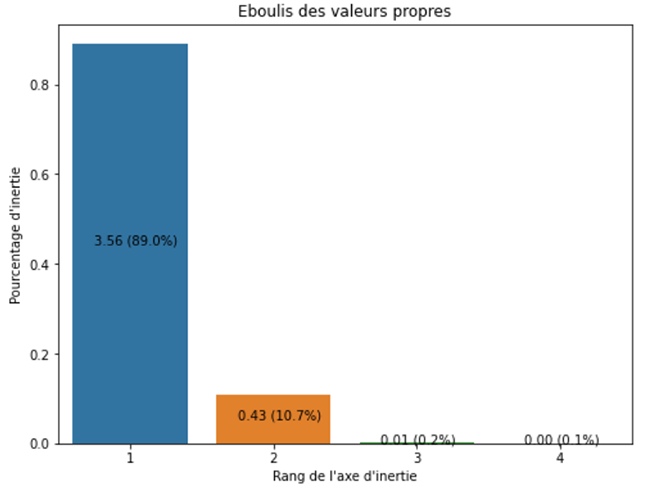
Le diagramme présenté en figure 5 représente le pourcentage de variance conservée par chaque composante principale (la valeur propre de chaque composante est reportée ici). Le jeu de données ayant 4 variables et l’ACP réalisée étant normée, la variance totale du jeu de données vaut 4 (chaque variable ayant une variance de 1). Ce diagramme nous permet de constater que les deux premières composantes principales conservent 99% de la variance de notre jeu de données initial et que la première composante, à elle seule, en cerne près de 90%. On peut également interpréter ces valeurs en termes de quantité d’information : en projetant nos données sur les deux premières composantes principales, plus de 99% de l’information de notre jeu de données de départ serait conservé.

Ce diagramme nous montre aussi que si les quatre variables initiales (entropies) peuvent être résumées à près de 90% par une seule nouvelle variable (PC1), c’est que l’information contenue par chacune des 4 entropies est redondante. Les 4 entropies de notre jeu de données semblent donc fortement (linéairement) corrélées. La matrice de corrélation permet de le confirmer. La corrélation, dans notre jeu de donnée, entre les 4 entropies s’explique principalement par le format des logs unidirectionnels Netflow : les adresses IP (ports) sources du sens aller sont les IP (ports) destinations du sens retour. Cette symétrie corrèle fortement les entropies correspondantes. Une analyse de trafic avec des flux Netflow bidirectionnels limiterait cette corrélation.

En termes d’anomalies, maintenant, on en déduit que PC3 et PC4 sont clairement des composantes principales qui cernent « le bruit » de nos données (la quantité d’information portée par ces composantes est minime) et donc, des composantes d’intérêt pour capter des anomalies.

2.3.2 Analyse des composantes principales

Comme évoqué dans la première partie, chaque composante principale est une combinaison linéaire des variables initiales (entropies de Shannon). Le résultat de l’ACP normée sur notre jeu de données définit les composantes principales comme suit :

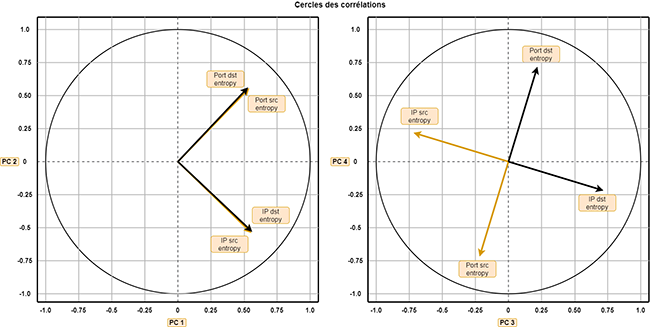
Pour interpréter ces composantes principales (comprendre le lien avec les quatre entropies), nous utilisons les cercles des corrélations [8]. Ces cercles permettent de cerner les corrélations entre les variables initiales et les composantes principales, visuellement.

L’interprétation d’un cercle de corrélation nécessite quelques précautions pour ne pas mal interpréter les résultats. Il est recommandé de ne s’intéresser uniquement qu’à la longueur relative entre chaque flèche et à leur projection sur les axes (valeur et signe).

Le premier cercle nous montre d’abord que l’information portée par nos quatre variables initiales est équitablement cernée par le plan formé par PC1 et PC2 (longueur des flèches identiques). Autrement dit, il n’y a pas de variable initiale dont l’information serait beaucoup mieux ou moins bien captée par le premier plan. Ce cercle nous permet aussi de réaliser que les quatre variables initiales sont positivement corrélées avec PC1 (toutes les projections sur PC1 sont positives). Les individus (tranches de temps) ayant des valeurs fortes sur PC1 ont donc de fortes entropies sur les quatre variables, et donc inversement les points ayant des valeurs faibles sur PC1 ont de faibles entropies : PC1 cerne donc l’entropie « globale » de la tranche de temps analysée. À droite les grands, à gauche les petits, c’est ce qu’on appelle l’effet « taille ». Le premier cercle nous montre également que les entropies des ports (source et destination) sont positivement corrélées avec PC2 et anti corrélées (ou négativement corrélées) avec les IP (source ou destination) : les points ayant de fortes valeurs positives sur PC2 ont donc une forte entropie de ports et une faible entropie d’adresses IP. En caricaturant, il pourrait s’agir d’une activité de 10 minutes pendant laquelle on ne verrait qu’une unique communication entre un client et un serveur sur de nombreux ports distincts… Il semble intéressant de regarder les individus ayant de fortes valeurs sur PC2 pour pouvoir détecter un pattern de scan de ports vertical !

Le deuxième cercle nous montre que PC3 comme PC4 cernent une corrélation négative entre source et destination : cela est très étonnant puisque le format Netflow unidirectionnel a tendance justement à faire corréler positivement source et destination (symétrie du sens « aller » et sens « retour »). L’éboulis des valeurs propres nous indiquait déjà en termes de quantité d’information captée par ces composantes qu’elles ne représentaient pas l’information principale de notre jeu de données. Mais grâce au cercle de corrélation, on sait que c’est cette symétrie entre source et destination qui est parfois rompue et captée par les valeurs fortes sur PC3 ou PC4.

En interprétant les différentes composantes principales rapidement grâce au cercle des corrélations et en ayant imaginé ce qu’une valeur extrême peut signifier, on est alors capable de cerner le type d’anomalies que l’on pourrait détecter en visualisant les valeurs extrêmes de certaines composantes.

3. Détection d'anomalies réseaux

3.1 Analyse des « high scores » par représentation graphique

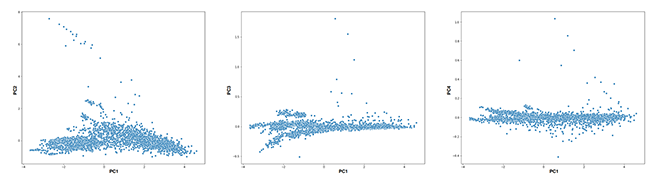
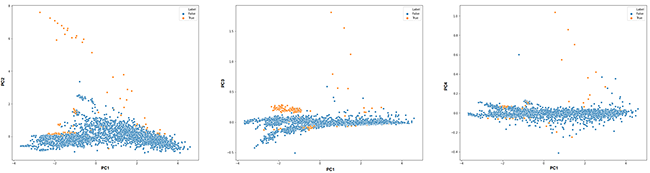
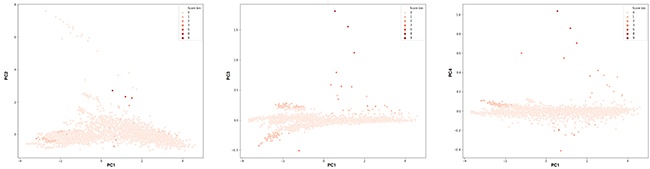
La figure 7 représente différentes projections de nos tranches de temps sur les composantes principales (nuages des individus). Des anomalies peuvent être visualisées en s’intéressant aux individus ayant les plus fortes valeurs sur les composantes principales. Nous voyons certains points se dégager de la masse dans les valeurs positives extrêmes (« high scores ») des composantes PC2, PC3 et PC4. Nous savons, grâce au cercle des corrélations ce que signifient ces valeurs fortes en termes de distribution des entropies. Est-ce que ces points capteraient des périodes où des attaques du dataset auraient lieu ? Vérifions-le. Nous profitons que chaque ligne de log du dataset soit labellisée pour, à notre tour, labelliser nos tranches de temps. Nous considérons qu’une tranche est alors soit « normale » (si elle ne contient aucun log d’attaque), soit taguée « attaque » si au moins 10% des logs sont tagués comme attaque dans cette tranche.

Le résultat est présenté ici :

Dans les anomalies statistiques remontées par les valeurs fortes de certains individus sur les composantes principales, nous voyons que des attaques sont présentes (points jaunes). Ces attaques ont donc effectivement perturbé la distribution « majoritaire » des entropies observées dans le dataset. Lorsque la représentation graphique est une option possible, elle constitue donc une première piste d’outil potentiellement simple et relativement efficace pour pointer les périodes les plus atypiques.

3.2 Erreur de reconstruction

Une métrique permettant de détecter les individus prenant des valeurs fortes sur les composantes principales est l’erreur de reconstruction. Pour classer les individus en termes d’anomalies, nous pouvons calculer l’erreur de reconstruction pour chaque individu et les trier par ordre d’erreur de reconstruction décroissant. Comme précédemment évoqué, pour calculer l’erreur de reconstruction, il faut choisir le nombre de composantes principales sur lesquelles projeter nos individus. Le sous-espace formé par les composantes retenues est alors considéré comme l’espace « normal », les composantes non prises en compte pour la projection constituent alors notre « sous-espace d’anomalies ». Les individus présentant les valeurs extrêmes sur les composantes non retenues (« sous-espace d’anomalies ») ressortiront via une erreur de reconstruction plus forte que pour les autres individus (ayant des valeurs faibles sur le sous-espace d’anomalie). Pour capter les anomalies portées par PC3 et PC4 par exemple, nous projetons les individus sur le sous-espace porté par PC1 et PC2. Nous faisons ainsi le choix de ne retenir que les deux premières composantes pour définir l’approximation de nos individus (k=2). Nous calculons l’erreur de reconstruction pour chacun des individus, les trions par ordre décroissant et présentons le « Top 10 » à l’analyste. Les résultats sont présentés ici.

La figure 9 montre qu’en fixant k=2, nous retrouvons des individus ayant des valeurs fortes sur les composantes non retenues pour la projection de nos individus (PC3 et PC4), mais pas forcément ceux de l’axe PC2 (plus la couleur est foncée, plus l’erreur de reconstruction est grande). En effet, l’erreur de reconstruction est une distance euclidienne. Lorsqu’on fixe k, et que l’on décide de ne pas retenir les « p-k » dernières composantes, l’erreur de reconstruction de l'individu vaut alors la somme des carrés des coefficients de cet individu sur ces « p-k » composantes (à la racine carrée près). Chercher les plus grandes erreurs permet de retrouver les individus ayant des valeurs plus fortes que les autres individus sur ces composantes non retenues. De plus, vu que les composantes principales sont classées par ordre de variance décroissant, nous savons que les valeurs les plus fortes sur la composante « k+1 » sont en valeur absolue supérieures à celles de la composante « k+2 », etc. On peut donc estimer qu’en fixant k, les individus ayant de fortes valeurs sur la « k+1 » ième composante devraient ressortir dans les premiers du « Top N » correspondant. Cela nous montre que fixer « k » va fixer des types d’anomalies cernées par ce « Top N ». Il suffirait de faire varier « k » pour être sûr de capter les différents types d’anomalies statistiques du jeu de données. Le « TOP N » constitue un outil simple à mettre en place, qui permet à l’analyste de concentrer son analyse sur les points les plus atypiques.

3.3 Industrialisation dans Splunk

Afin de tester et de mettre potentiellement ces méthodes en production, l'implémentation de l'ACP dans un SIEM prend tout son sens. Le passage du notebook python au SIEM Splunk nécessite un minimum de développement, sur la base de l’utilisation de l'application « Splunk Machine Learning Toolkit ». Tout d’abord, la fonction de calcul d’entropie a été développée sous forme de « custom search command » Splunk, de type transforming (anciennement reporting) [9]. Le code est également mis à disposition [7]. Ensuite, malgré l’encapsulation des classes standard scikit-learn par l’application « Splunk Machine Learning Toolkit », certaines informations très utiles n’apparaissent pas dans la méthode summary de l’algorithme PCA (ACP). Pour connaître les valeurs des composantes principales (utile pour permettre leur interprétation), nous avons par simplicité directement modifié la méthode summary de l'implémentation PCA pour renvoyer ces éléments qui sont facilement accessibles (attribut components_ du modèle scikit-learn), mais non inclus par défaut.

L’implémentation d’un « TOP 10 » donne alors une requête de type :

Conclusion

L’ACP est une méthode statistique relativement simple à comprendre et néanmoins puissante pour l’analyse de données multidimensionnelles. Son apport dans la détection d’anomalies a été abordé dans cet article. Nous avons choisi de présenter l’approche sans apprentissage où l’anomalie est un écart vis-à-vis des autres individus d’un jeu de donnée considéré, mais cette méthode est totalement compatible avec une phase d’apprentissage classique (machine learning) : une référence « saine » peut être utilisée pour en retenir un modèle (les composantes principales) et ensuite observer par l'erreur de reconstruction les individus les plus en écart de cette référence. Dans tous les cas, elle constitue un outil simple à considérer pour compléter la supervision à base de signatures.

Références

[1] https://openclassrooms.com/fr/courses/4379436-explorez-vos-donnees-avec-des-algorithmes-non-supervises/4379481-calculez-les-composantes-principales-de-vos-donnees

[2] https://en.wikipedia.org/wiki/Curse_of_dimensionality

[3] https://fr.wikipedia.org/wiki/Entropie_de_Shannon

[4] http://www.haakonringberg.com/work/papers/pca_tuning.pdf

[5] https://www.hs-coburg.de/fileadmin/hscoburg/Forschung/WISENT_cidds_Technical_Report.pdf

[6] https://www.hs-coburg.de/forschung-kooperation/forschungsprojekte-oeffentlich/informationstechnologie/cidds-coburg-intrusion-detection-data-sets.html

[7] https://github.com/jakjohnson/pca4outliers

[8] https://openclassrooms.com/fr/courses/4525281-realisez-une-analyse-exploratoire-de-donnees/5278723-interpretez-le-cercle-des-correlations

[9] https://dev.splunk.com/enterprise/docs/developapps/customsearchcommands/