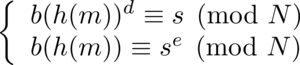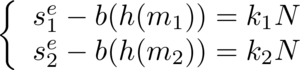Extraction de clef publique : le cas des vouchers de m0n0wall

1. Extraction de clef publique

Il se peut, pour des raisons allant de la volonté de cacher une faiblesse (clef trop petite) à un simple usage privé ou interne, qu'un système utilisant un mécanisme de cryptographie asymétrique ne publie pas sa clef publique. Or, comme on a pu le voir lors de conférences données par Renaud Lifchitz l'an passé [0] avec des applications pratiques sur PGP et VIGIK, il est possible d'exploiter une faiblesse de certains schémas de signature afin d'extraire le module de la clef publique. C'est une faiblesse connue avec des solutions d'ores et déjà existantes (par exemple RSA-PSS), dont la portée est toute relative, on parle bien de la clef publique ! Cependant, la sécurité de RSA repose à l'heure actuelle sur la difficulté à pouvoir factoriser le module de la clef publique, ce qui, avec le temps devient de plus en plus réalisable et efficace en engageant de gros moyens. Ainsi, des systèmes ne mettant pas à jour leur clef ou étant simplement limités par la capacité de stockage de cette dernière (typiquement les systèmes embarqués) se verront exposés à une attaque d'extraction puis de factorisation de la clef. Pour ne citer qu'un exemple, tiré de la conférence citée précédemment, le système de contrôle d'accès VIGIK largement déployé en France pour permettre aux usagers (ainsi qu'à La Poste, France Telecom et EDF) d'accéder aux immeubles résidentiels, ne permet pas de stocker une clef plus grande que 1024 bits. On peut noter également qu'en accédant à la clef publique, il est possible d'authentifier toute communication utilisant cette dernière : par exemple, pour une série d'e-mails signée par une même source, il sera possible de vérifier que les signatures ont été effectuées par la même clef et cela sans la nécessité d'accéder à un serveur de clef.

1.1 Schéma de signature

Pour rappel, voici les éléments essentiels de RSA (on ne décrira pas les relations élémentaires) :

• le module RSA N, produit de deux grands nombres premiers p et q ;
• l'exposant public e ;
• l'exposant privé d , inverse de e modulo φ(N)) (φ étant l'indicatrice d'Euler) ;
• la clef privée est le couple (N, d) ;
• la clef publique est le couple (N,e) .

Une valeur très courante de l'exposant public e est le nombre de Fermat F4 (2²ⁿ  + 1 avec n=4), soit 65537, qui permet quelques optimisations dans les calculs. C'est notamment cette valeur qui est utilisée par défaut par GnuPG et OpenSSL lors de la génération des clefs. Détail d'importance, car cela signifie que si l'on cherche à extraire la clef publique, alors seul le module sera considéré comme inconnu. Dans un schéma classique de signature utilisant RSA, on a les relations suivantes, étant la signature :

La seconde relation est obtenue en utilisant le théorème d'Euler. Avec h une fonction de hachage et b une fonction de bourrage (padding), servant notamment à se prémunir d'attaques exploitant la propriété de multiplicativité de RSA, et m le message. Pour de plus de détails sur les notions de base relatives aux attaques sur un tel schéma de signature, voir « How (Not) to Design RSA Signature Schemes » [1].

1.2 Extraction du module RSA

Connaissant deux messages en clair m₁ et m₂ ainsi que leurs signatures respectives s₁ et  s₂ , générées selon le schéma présenté précédemment, on a par définition :

Avec k₁ et k₂ deux entiers positifs ou nuls. On peut alors écrire :

Le gcd correspond ici au calcul du plus grand commun diviseur. Ce résultat donne un multiple du module RSA  qui, dans la plupart des cas, ne nécessite que quelques divisions afin de tomber sur une taille de module connue (1024, 512, etc.). Aussi, il est bien entendu possible d'effectuer le même calcul en rajoutant des messages et leurs signatures correspondantes, ce qui permettrait de réduire la taille du résultat du gcd.

2. Qu'est-ce qu'un voucher ?

2.1 Définitions 

On retrouve le mécanisme de voucher au sein du portail captif de m0n0wall (mais également pfsense) afin de fournir à un utilisateur invité un moyen de s'authentifier pour une durée finie. L'idée est de fournir une chaîne de caractères de faible longueur qui pourra être aisément recopiée et que l'utilisateur saisira sur la page du portail captif. Une fois la période expirée, ce voucher sera alors inutilisable. L'usage classique qui en est fait dans la réalité est la génération et l'impression de quelques centaines de vouchers qui seront distribués à l'unité par un hôtel ou un bar pour chaque nuit ou café réglés par exemple.

2.2 Format et implémentation

Il y a plusieurs possibilités pour implémenter un tel concept de voucher. Celle qui va être décrite ici correspond à l'implémentation présente sur les systèmes m0n0wall et pfsense, tous deux étant des distributions basées sur FreeBSD et centrées sur un service de pare-feu, la seconde étant un fork du premier. Afin d'effectuer les tests, l'outil en ligne de commandes qui est appelé par le portail captif sera directement utilisé. Vous pourrez retrouver le code utilisé sur le svn de m0n0wall [2]. Les raisons avancées relatives aux choix effectués, du fait de leurs caractères parfois atypiques, ont été discutées avec le développeur principal de m0n0wall. Tout d'abord, voici le format d'un voucher, tel que défini selon la configuration par défaut (présent dans le fichier voucher.cfg) :

Notons tout d'abord un élément déterminant quant à la solidité du voucher, sa taille. Elle sera fixe et de 64 bits, du fait de la taille de la clef utilisée pour chiffrer celui-ci (oui, même une calculette pourrait la factoriser).  Les trois premiers nombres concernent respectivement la taille des champs roll ID, ticket ID et checksum. Le roll ID sert à définir une durée d'accès (configurée sur m0n0wall directement, on ne voit ici qu'un ID) et le ticket ID offre, en quelque sorte, un numéro de ticket valable. Le checksum permet de vérifier l'intégrité du voucher (sa présence semble injustifiée). Le nombre suivant (ici 174491274) est un magic number qui sert à effectuer un bourrage constant (dans le sens où sera toujours utilisé le même magic number). Le dernier élément correspond au charset qui est utilisé par le voucher (on pourrait limiter à abcd par exemple pour faciliter la mémorisation de celui-ci). Ce voucher en clair est ensuite chiffré en utilisant la clef privée d'une paire de clefs RSA afin de fournir notre voucher final. En reprenant les équations d'un schéma classique de signature RSA, en considérant que b est l'ajout du bourrage et m le voucher sans la partie magic number, on a :

Ce résultat sera alors converti dans le charset donné. Avant de rentrer dans l'analyse, voici un exemple pour rendre tout cela un peu plus intelligible. Tout d'abord, la génération de la paire de clefs RSA de 64 bits :

Ensuite, l'utilisation du programme en ligne de commandes (source[2]) afin de générer nos fameux vouchers :

Les deux derniers arguments de la ligne de commandes permettent de spécifier le roll ID à utiliser ainsi que le nombre de tickets à générer pour celui-ci, le résultat sont les deux vouchers P4qkV2H5snc et asQ1CctSuKa. Enfin, la vérification de la validité de ces deux vouchers (vérification qui ne fait pas partie du processus de génération des vouchers, seulement lorsqu'ils seront saisis sur le portail captif) :

Plusieurs remarques : rien n'est stocké hormis le format du voucher et la paire de clefs (c'est au portail captif de faire la différence entre les vouchers en cours de validité et ceux ayant expiré). Lors de la validation, notons que c'est bien la partie checksum et la partie magic number qui sont vérifiées. Concernant la sécurité de ce système, il y a beaucoup d'aspects à remettre en cause : tout d'abord, la complexité générale du fait notamment des contraintes initiales (m0n0wall est un système en quasi lecture seule sans capacité de stockage réelle, pas de comptes temporaires générés préalablement et stockés sur le système donc), mais aussi à cause de la configurabilité de celui-ci (permettant par exemple de changer le format même des vouchers offrant par exemple un nombre disponible de tickets très grand par l'agrandissement du champ ticket ID) ; l'usage d'un bourrage constant (l'auteur indique même en commentaire dans le code que le message est trop petit pour appliquer PKCS1) ; et, de manière générale l'usage de RSA avec des clefs de 64 bits qui est justifié par le développeur de cette implémentation par le fait que la vérification et la génération des vouchers pourraient avoir lieu sur des machines distinctes : d'un côté le service délivrant des vouchers en utilisant la clef privée et de l'autre, le portail captif avec la clef publique permettant la validation de ceux-ci.

3. Extraction de clef publique sur les vouchers

3.1 L'attaque

Le schéma présenté ici utilisant RSA ressemble de près à un schéma de signature : l'ensemble d'un voucher est chiffré, non pas pour protéger son contenu (principalement le roll ID et le ticket ID qui seront de toute façon vérifiés par le portail captif lui-même après avoir été validés par le système de voucher), mais afin de fournir une authentification lors de sa validation, c'est-à-dire qu'il a bien été émis par l'administrateur du portail captif. L'attaque proposée est l'extraction de la clef publique et sa factorisation afin de générer des vouchers valides dans le but d'avoir un accès invité valide. Les hypothèses sont :

• le magic number est connu ;
• au moins deux vouchers sont connus ainsi que leurs valeurs en clair ;
• l'exposant public RSA est connu ;
• le format du message est connu ;
• le charset du message est connu.

Il est à noter que l'attaque proposée ici a une portée nulle si elle n'est pas combinée avec une autre attaque qui permettrait de deviner ou extraire efficacement le magic number. Aussi, le contournement d'un portail captif est dans de nombreux cas très simple au niveau réseau (avec tunnel DNS par exemple) : cette attaque a donc un but avant tout didactique. Les trois dernières hypothèses relèvent souvent d'un travail consistant à deviner ces éléments qui, dans une majorité de cas sont triviaux. Ainsi, l'attaque présentée en section 1.2 va permettre l'extraction du module RSA.

3.2 Implémentation

Les sources de la preuve de concept développées ici sont en golang version 1.3 et sont disponibles en ligne [3]. Cette section s'attachera à décrire succinctement comment a été implémentée l'attaque.

En premier lieu, il est nécessaire de générer les vouchers en clair (on utilisera les deux vouchers P4qkV2H5snc et asQ1CctSuKa illustrant l'exemple précédant) via une fonction gen_voucher_plain qui prend en argument le contenu et le format détaillé d'un voucher (voucher_magic étant une constante ayant comme valeur le magic number) :

Comme les vouchers chiffrés sont présentés sous une forme convertie dans un charset donné, il faut leur redonner leur format initial via conv_voucher :

L'extraction du module RSA peut alors commencer, comme présentée en section 1.2 :

Est alors obtenu un multiple du module RSA. Afin d'extraire celui-ci, une division sera répétée jusqu'à l'obtention d'un nombre d'une taille de 64 bits, fonction k_extraction :

3.3 Factorisation

Une fois le module RSA extrait, un algorithme de factorisation peut être utilisé afin de retrouver p et q (les deux nombres premiers à l'origine de celui-ci) permettant ainsi de recalculer la clef privée. Un bon nombre d'algorithmes existent, avec leurs avantages et inconvénients. Les travaux de Daniel J. Bernstein, Nadia Heninger et Tanja Lange présentés lors du 29C3 [4] sous le titre élégant de « FactHacks : RSA factorization in the real world », résument ce dont nous, utilisateurs pressés, avons besoin. L'algorithme utilisé ici sera la crible quadratique dont une implémentation est disponible en golang sur GitHub [5]. Une légère modification a été appliquée à cette dernière afin de pouvoir utiliser directement dans le code le résultat de la factorisation [3]. Une fois le module RSA factorisé, il suffira de calculer l'exposant privé d qui est l'inverse de e (l'exposant public) modulo   (connaissant p et q,   ).

3.4 Démonstration

Voici une séquence d'exécution de la preuve de concept, avec verbosité (mettre DEBUG à true) :

Comme on peut le constater, après avoir extrait le module RSA , le programme s'attaque à la factorisation de celui-ci, pour enfin calculer l'exposant privé en utilisant les deux nombres premiers ainsi trouvés. Il est à noter que l'attaque prend une dizaine de minutes sur un processeur calibré à 2.4Ghz, la partie longue à calculer n'étant pas la factorisation (quelques secondes suffisent avec une crible quadratique pour un module de 64 bits), mais bien le calcul du plus grand commun diviseur (on a effectué une exponentiation non modulaire, les nombres sont donc très grands !). De manière générale, le calcul du   dépend essentiellement de l'exposant public et très peu de la taille de la clef : l'extraction du module RSA sera donc le plus souvent triviale face au temps nécessaire pour la factorisation de celui-ci pour des tailles plus conventionnelles (1024, 2048 bits). Enfin, pour vérifier que l'on a la bonne clef et que tout s'est bien passé, voici les détails de la clef privée utilisée au moment de la génération des vouchers :

Tous les paramètres sont bons ! Le résultat de la preuve de concept sans les messages de DEBUG donne directement la clef privée dans un format manipulable :

3.5 Contre-mesures

L'attaque a été l'objet d'un patch chez pfsense [6], qui rend l'extraction du module encore plus difficile en choisissant de manière aléatoire l'exposant public. On notera d'ailleurs que ce dernier est incomplet, car si l'utilisateur décide de regénérer la clef pendant la configuration de pfsense c'est alors l'application openssl qui est lancée pour générer la clef (utilisant par défaut la valeur F4). 

Remerciements

Un grand merci à Renaud Lifchitz pour son retour et ses précieux conseils ainsi qu'à Aurélien pour ses multiples relectures.

Références

[0] http://2014.hackitoergosum.org/slides/day3_A_common_weakness_in_RSA_signatures:extracting_public_keys_from_communications_and_embedded_devices_Renaud_Lifchitz_hes2014.pdf

[1] http://crypto.rd.francetelecom.com/publications/p29

[2] http://svn.m0n0.ch/wall/branches/freebsd8/build/tools/voucher.c

[3] http://dud-t.org/code/poc-voucher.tar.gz

[4] http://facthacks.cr.yp.to/

[5] https://github.com/hydroo/quadratic-sieve

[6] https://redmine.pfsense.org/projects/pfsense/repository/revisions/32837bb4ee1c687e40e0da5abcbce100149f84e1/diff/usr/local/www/services_captiveportal_vouchers.php