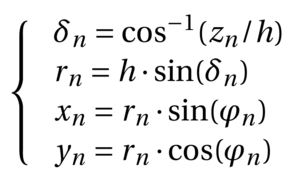Les antennes de petites dimensions sont un sujet qui a toujours été à la mode auprès des ingénieurs, désireux de faire rayonner un signal électromagnétique par un conducteur de dimensions aussi réduites que possible (penser « faire tenir une antenne dans un téléphone portable »). Le problème a été abordé très tôt, alors que les émissions sub-MHz, donc avec des longueurs d’onde de plusieurs kilomètres, étaient courantes [1]. Alors qu’il a été rapidement montré qu’il existe des limitations physiques aux performances de telles antennes, qui ne sont déterminées que par le rayon de la sphère englobant l’antenne [2] – et en particulier, sur le facteur de qualité de l’antenne, qui est d’autant plus élevé que l’antenne est petite, réduisant ainsi sa bande passante – le sujet reste d’actualité, dans un contexte de prolifération des objets communiquant par onde radiofréquence, de plus en plus petits [3].
La conception de telles antennes n’a que peu d’intérêt si l’on en croît [4], qui réduit toute petite antenne à une sphère « A small coil wound on a perfect spherical magnetic core is conceived as an ideal small antenna ». Le problème est à peine plus subtil, si l’on désire adapter en impédance à une charge qui doit transmettre efficacement sa puissance à ce petit élément rayonnant. Comme toute antenne efficace se résume à un dipôle [5], la question est de savoir comment tordre suffisamment un dipôle pour le faire rentrer dans la sphère. Comme les interactions en champ proche (i.e. une distance bien plus petite que la longueur d’onde) seront prédominantes dans une telle conception, les solutions analytiques seront peu exploitables et nous devrons nous appuyer sur des simulations numériques, pour estimer la fréquence de fonctionnement et l’impédance de la géométrie d’antenne considérée. De toute façon, il nous faudra un modèle numérique pour réaliser l’antenne, donc autant tout faire d’un coup : conception, modélisation, réalisation. Évidemment, les logiciels chargés de ces étapes ne parlent pas le même langage, donc des équations de base définissant la géométrie d’antenne sélectionnée, notre travail consistera à générer les fichiers aux différents formats, pour alimenter ces logiciels. Nous choisissons en particulier NEC2 (New Electromagnetic Code, nec2.org, disponible comme paquet nec2c dans la distribution Debian, en complément de son outil d’affichage des géométries d’antenne et des diagrammes de rayonnement xnecview) pour la modélisation électromagnétique, avec un format parfaitement documenté et facile à générer [6] ; nous vérifierons les simulations avec le logiciel propriétaire HFSS (High Frequency Structure Simulator de Ansoft, maintenant Ansys – version 13, qui a le bon goût d’être suffisamment ancien pour fonctionner sous Wine), capable notamment d’appréhender des environnements diélectriques hétérogènes, qui a besoin d’un modèle de CAO (Conception Assistée par Ordinateur), par exemple au format STEP ; et finalement, nous voulons imprimer notre antenne, nécessitant la définition de la surface au format STL. Alors qu’il existe sûrement des bibliothèques fort complexes pour effectuer ce travail (i.e. numpy-stl, disponible à pypi.org/project/numpy-stl/), nous nous contenterons de générer les fichiers ASCII depuis GNU Octave. Nous conclurons en caractérisant les antennes que nous réaliserons, pour vérifier qu’elles rayonnent à une longueur d’onde petite devant leur rayon.
1. Conception d’antenne
L’objectif est donc de tordre un dipôle pour le faire rentrer dans une petite sphère. Pour des raisons qui dépassent le cadre de cette présentation [7], nous désirons insérer une antenne dans un puits de diamètre bien inférieur à la longueur d’onde, et voir cette antenne rayonner vers la surface. En pratique, nous nous imposons de faire tenir l’antenne dans une sphère de 10 cm de diamètre, ou a=5 cm pour une fréquence de fonctionnement de f=200 MHz, donc une longueur d’onde de λ=300/fMHz=1,5 m. Ces contraintes technologiques viennent d’une part de notre capacité à forer un puits de petit diamètre, sans faire appel à de l’équipement lourd et d’autre part, de celle qu’a une onde électromagnétique de se propager d’autant plus loin dans le sol que sa fréquence est basse : ce compromis est donc classique en instrumentation géophysique de structures souterraines. Cet objectif répond bien à la contrainte de petite antenne, puisque 2π·a/λ=0,21<< 1 (critère sans dimension, issu du produit du vecteur d’onde 2π/λ par le rayon de la sphère).
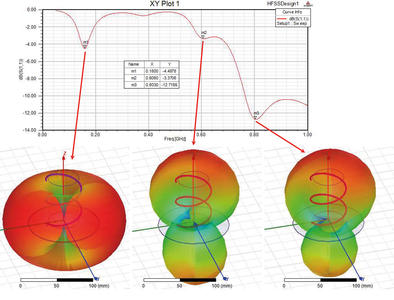
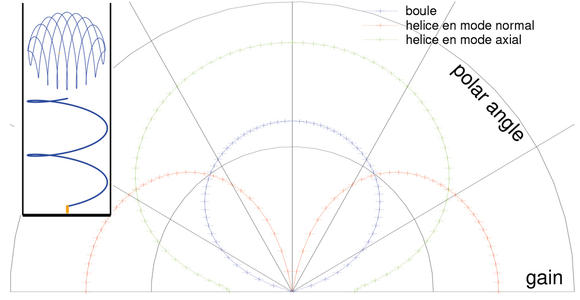
Nous avions initialement porté notre intérêt sur l’antenne hélicoïdale, en espérant la faire rayonner dans l’axe de révolution de l’hélice. La physique nous interdit malheureusement un tel fonctionnement, une hélice de circonférence petite devant la longueur d’onde se comportant comme un dipôle et rayonnant donc dans la direction normale à l’axe de révolution. Pour rayonner dans la direction axiale, il faut que la circonférence de chaque boucle soit de l’ordre de la longueur d’onde, ou à 200 MHz une hélice de diamètre de l’ordre de 50 cm, ne répondant pas au cahier des charges de faire tenir l’antenne dans une sphère de 5 cm de rayon, loin de là.
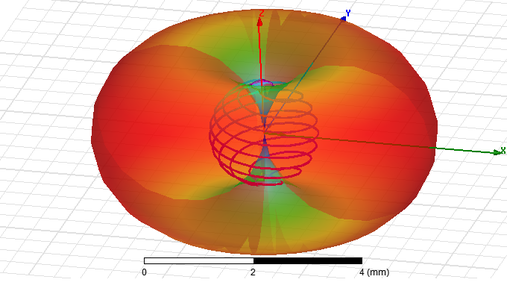
La figure ci-contre illustre l’évolution des diagrammes de rayonnement, alors que la fréquence d’excitation d’une même antenne hélicoïdale augmente, pour passer de la forme de beignet caractéristique du dipôle (mode normal) à basse fréquence, vers un diagramme de rayonnement axial aux hautes fréquences.
Au-delà du projet qui nous intéresse, l’objectif de faire tenir une antenne dans un volume aussi réduit que possible répond à la mode actuelle de vouloir rendre communiquant par onde radiofréquence tout et surtout n’importe quoi, avec une contrainte sur les dimensions d’antenne, qui sont en général bien supérieures aux tailles du système embarqué communiquant (« smart dust » [8]). Il n’y a pas beaucoup de façons de tordre un dipôle dans une sphère : une rapide étude de la littérature nous porte vers le Small Folded Spherical Helix [9], qui est finalement une antenne hélicoïdale imprimée sur une sphère.
Le problème d’imprimer une antenne sur une sphère est qu’une sphère n’est pas plate et donc, un peu compliquée à manipuler. L’article de référence qui nous fournit la description pour aborder le problème est [9], qui a le bon goût d’inclure le jeu d’équations paramétriques décrivant l’antenne qui nous intéresse :
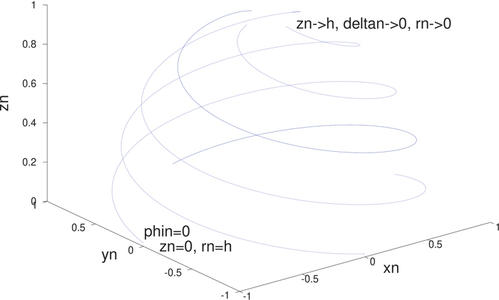
Avec ϕn un indice angulaire définissant le nombre de tours en fonction de la hauteur zn=h·n/N, N∈N étant le nombre de segments par hélice et n∈[1..N] (ou N−1, si on ne veut pas fermer au sommet les spires où le rayon deviendra nul, posant problème à l’impression 3D).
Nos degrés de liberté sont donc le nombre de bras de l’hélice et le nombre de tours de chaque hélice. Le passage des coordonnées cylindriques en coordonnées cartésiennes permettent de trivialement tracer la forme d’une telle antenne sous GNU/Octave :
1 N=64; % segments par spire
2 h=1;
3 Ntours=2;
4 n=[1:N-1]/N; % N pour fermer sommet
5 for phst=0:pi/2:2*pi % même vvv borne que n
6 phin=linspace(0,Ntours*pi,N-1)+phst; % +k*pi/2 ...
7 zn=h*n; % ... pour les autres hélices
8 deltan=acos(zn/(h));
9 rn=h*sin(deltan);
10 xn=rn.*sin(phin);
11 yn=rn.*cos(phin);
12 plot3(xn,yn,zn,'b-');hold on
13 end
Ayant appréhendé la conception de l’antenne, plusieurs tâches vont devoir maintenant être réalisées : modéliser l’antenne, en vue de simuler sa fonction de transfert et son diagramme de rayonnement ; générer les fichiers de CAO 2D et 3D pour fabriquer cette antenne ou la simuler par éléments finis (logiciel libre NEC2 ou propriétaire HFSS et impression additive) ; et finalement, mesurer la fonction de transfert de l’antenne, pour estimer son adéquation à la modélisation et à l’utilisation qui doit en être faite.
2. Modélisation d’antenne : NEC2
Nous avions déjà largement discuté dans les pages d'une regrettée publication cousine [6] le format de description d’antennes de NEC2 et la façon de simuler une antenne. Pour un rapide rappel, les cartes de configuration de NEC2 sont une succession de fils respectant quelques contraintes quant à leur longueur et leur diamètre, par rapport à la longueur d’onde (carte GW suivie des coordonnées des extrémités, en mètres), finissant par la configuration de la simulation incluant la bande de fréquence (en MHz), couverture angulaire et point d’excitation. Seule subtilité qui va nous intéresser ici : alors qu’en nous contentant de tracer le diagramme de rayonnement, il suffit de choisir des plages angulaires des coordonnées polaires couvrant plus de 360° dans les deux axes, le post-traitement que nous considérerons ici sera simplifié si nous couvrons dans l’axe des élévations de 0 à 360° et en azimut de 0 à 180° afin d’éviter les recouvrements, lors de la génération de la surface correspondante.
Le script Octave est donc modifié pour générer le fichier de géométrie d’antenne, sous forme de succession de fils (carte GW) définis par les coordonnées des deux extrémités de chaque segment et du rayon du conducteur, se concluant par la configuration de la simulation :
1 N=64; % nombre de segments par hélice
2 nseg=5; % nombre d’éléments par segment
3 radius=1e-2; % devient 1 mm après mise à l'échelle de 0.1
4 h=1;
5 phst=0
6 Ntours=2;
7 n=[0:N]/N; % sommet de la sphère fermée
8 phin=linspace(phst,Ntours*pi,N+1);
9 z1n1=h*n;
10 deltan=acos(z1n1/(h));
11 rn=h*sin(deltan);
12 xn=rn.*sin(phin);
13 yn=rn.*cos(phin);
14 f=fopen('sphere.nec','w');
15 fprintf(f,'CM sphere antenna\nCE\n');
16 seg=1;
17 for k=1:length(x1n1)-1
18 P1=[xn(k), yn(k), zn(k)];
19 P2=[xn(k+1),yn(k+1),zn(k+1)];
20 fprintf(f,'GW %d %d %f %f %f %f %f %f %f\n',seg,nseg,P1(1),P1(2),P1(3),P2(1),P2(2),P2(3),radius);
21 seg=seg+1;
22 fprintf(f,'GW %d %d %f %f %f %f %f %f %f\n',seg,nseg,-P1(1),P1(2),-P1(3),-P2(1),P2(2),-P2(3),radius);
23 seg=seg+1;
24 end
25 [... on continue pour les autres spirales ...]
26 seg=seg-1;
27 fprintf(f,'GS 0 0 0.1\n'); %
28 fprintf(f,'GE 0\n'); % espace libre
29 fprintf(f,'EX 0 %d 1 0 1.00000E+00 0.00000E+00\n',segex);
30 fprintf(f,'FR 0 30 0 0 115E+00 1.0E+0\n'); % 1 -> 100
31 fprintf(f,'RP 0 73 144 0 0.00000E+00 0.00000E+00 2.50000E+00 2.50000E+00\n');
32 fprintf(f,'EN\n');
33 fclose(f);
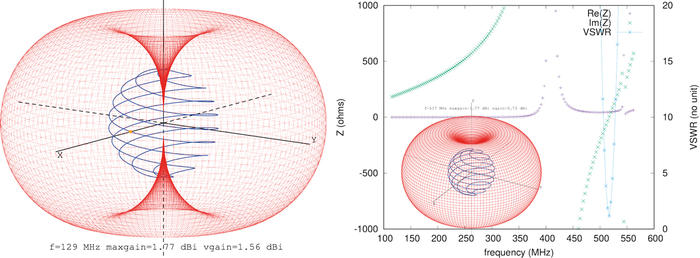
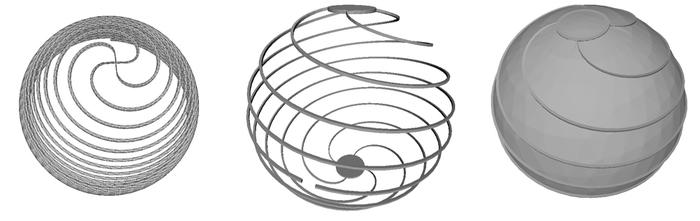
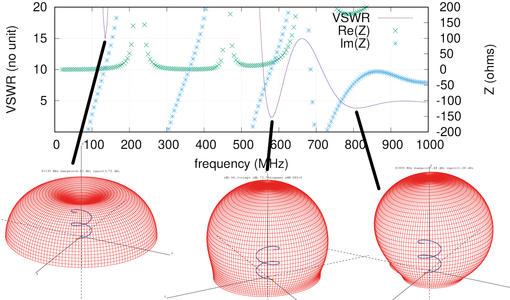
Le script génère tout de suite 4 hélices imbriquées afin d’abaisser l’impédance de l’antenne et de nous approcher des 50 Ω nominaux des systèmes radiofréquences. Le résultat de l’exécution de ce script Octave est un fichier de géométrie compréhensible par NEC2 et affiché par xnecview en Fig. 1.
Figure 1 : Gauche : diagramme de rayonnement dans le contexte de l’antenne ; droite : taux d’ondes stationnaires (VSWR) et impédance de l’antenne, démontrant sa bonne adaptation à 517 MHz (VSWR=~ 1) pour un rayon de 25 mm (droite) ou 129 MHz pour un rayon de 100 mm (gauche), correspondant à la fréquence pour laquelle la partie imaginaire de l’impédance s’annule et la partie réelle s’approche de 50 Ω.
La simulation s’opère par nec2c au moyen de la commande nec2c -i sphere.nec -o sphere.out et le résultat de la simulation est affiché par xnecview sphere.out, qui accepte aussi comme entrée le fichier de géométrie sphere.nec pour se convaincre de sa validité (Fig. 1). Cette simulation indique que l’antenne rayonne (minimum du taux d’ondes stationnaires VSWR au passage à 0 de la partie imaginaire de l’impédance) autour de 517 MHz pour une sphère de 5 cm de diamètre. À cette fréquence, la longueur d’onde dans l’air est de 58 cm, ce qui nécessiterait donc un dipôle de 29 cm de longueur : notre antenne est donc bien considérée comme petite, puisque k· a≃ 0,27. Si un plan de masse est disponible, l’antenne peut être coupée en deux au point d’alimentation, pour profiter des charges virtuelles miroir [10] et réduire d’un facteur de 2 l’encombrement de la sphère, en formant un monopôle.
Un calcul sur un ordinateur Panasonic CF-19 muni d’un processeur i5-3320M cadencé à 2,60 GHz prend environ 20 minutes pour résoudre le diagramme de rayonnement à 30 fréquences différentes, ou 40 secondes par fréquence simulée pour une structure comportant quatre branches de 128 segments chacune. Le temps de calcul est donc loin d’être prohibitif pour une simulation unique, mais rend une optimisation automatique, par exemple par descente de gradient, hors de question en l’état. nec2c n’est pas parallélisé et ne profite donc pas des multiples cœurs de calcul disponibles sur les processeurs modernes.
Maintenant que nous avons conçu l’antenne et simulé son comportement, nous désirons la réaliser. Pour cela, nous ferons appel à l’impression additive pour imprimer le motif de l’hélice sur une sphère de support.
3. Réalisation d’antenne en impression additive : format STL
Le format STL, qui décrit une surface sous forme de ses sommets et de sa normale, reconnu par les imprimantes 3D, est largement décrit sur diverses pages web et nous ne reprendrons pas ici sa description, si ce n’est pour mentionner que le plus simple est de passer par le format ASCII, dans lequel chaque facette est encapsulée entre les balises « facet ... endfacet », entre lesquelles nous définissons la normale de la surface « normal nx ny nz » et les 3 sommets (vertices) formant le triangle de la surface « outer loop vertex x1 y1 z1 vertex x2 y2 z2 vertex x3 y3 z3 endloop ». Le plus simple pour identifier le vecteur de la normale au plan est d’effectuer le produit vectoriel entre les arrêtes P1→(x1,y1,z1)−P2→(x2,y2,z2) et P1→(x1,y1,z1)−P3→(x3,y3,z3), fonction disponible sous GNU/Octave, sous la nomenclature cross(). Le résultat de ces travaux se valide aisément dans meshlab. On notera que pour créer le volume, nous devons dessiner 4 spirales adjacentes séparées d’une épaisseur, selon le rayon dr et selon l’ordonnée dz (Fig. 2).
Figure 2 : Prises de vue par Meshlab des fichiers STL représentant la moitié de l’antenne (configuration monopôle – gauche), assemblage de deux monopôles pour former un dipôle (milieu) – notez le point d’alimentation au premier plan à gauche – et finalement, renforcement de la structure en la plaçant sur une sphère (droite).
L’ajout de la sphère s’effectue dans FreeCAD, qui sait lire un fichier STL et lui ajouter les diverses formes géométriques habituellement manipulées dans un logiciel de CAO.
4. Validation de la simulation : STEP
Un fichier STL n’est qu’une surface. Un logiciel de CAO ou de modélisation d’antenne propriétaire tel que HFSS a besoin d’un volume. Le passage de l’un à l’autre doit garantir qu’aucune surface ouverte ne subsiste, laissant une incertitude sur la distinction entre intérieur et extérieur. Nous avons pris soin dans notre fichier STL de fermer les extrémités telles que les valide FreeCAD, dont nous nous servons pour convertir STL en STEP. Pour ce faire, lancer dans FreeCAD le menu Mesh Design, charger (Open) le ficher STL et analyser son intégrité (Meshes→Analyze→Evaluate and repair mesh...). Une fois les normales corrigées et les surfaces éventuellement dupliquées éliminées, nous sauvons (Export) au format STEP. Cette étape est aussi l’occasion de manipuler le modèle, en lui ajoutant des structures telles qu’un sommet ou des jonctions entre les deux monopôles, pour former un dipôle (Fig. 3). Ce modèle en volume permet d’alimenter HFSS et après ajout du port de mesure (lumped port) entre les brins du dipôle, de simuler ses caractéristiques (Fig. 3). Sans faire l’apologie d’un logiciel propriétaire dans ces pages, l’intérêt de HFSS est de permettre la simulation d’antennes en milieux diélectriques hétérogènes que NEC2 ne sait pas appréhender, ainsi que faire rayonner des surfaces (alors que NEC2 ne simule que des fils, bien qu’il soit possible de simuler une surface comme un maillage de fils). Le cas des milieux de permittivité homogène est plus simple, car la célérité dans ce milieu est divisée par la racine de la permittivité et l’axe des fréquences est donc multiplié d’autant. Une alternative libre à HFSS pour les milieux hétérogènes est GPRMax3D (http://www.gprmax.com/), un code de FDTD (Finite Difference Time Domain) qui nécessite cependant un maillage manuel des structures et rend l’affichage du diagramme de rayonnement un peu plus complexe. Alors que les diagrammes de rayonnement entre NEC2 et HFSS sont en accord avec nos attentes de comportement d’un dipôle, la fréquence de fonctionnement est imprévisible dans le second cas, n’ayant pas été capables de convaincre HFSS d’effectuer une simulation sur l’homothétie de la spirale pour l’amener aux dimensions voulues : pour une sphère de 1 mm de rayon, HFSS prédit une fréquence de fonctionnement de 12,25 GHz (minimum du coefficient de réflexion S11), soit après une homothétie d’un facteur 25 une fréquence prédite de 490 MHz, proche de ce qu’annonçait NEC (517 MHz), malgré une section de conducteurs complètement différente (rectangulaire ou cylindrique) et une méthode de simulation par éléments finis, au lieu de la méthode des moments.
Figure 3 : Le modèle volumique de l’antenne exporté au format STEP a permis de l’importer dans HFSS et d’effectuer le calcul du diagramme de rayonnement et des propriétés électriques.
L’insertion du modèle de l’hélice dans FreeCAD est l’opportunité de la supporter sur une sphère. Initialement, nous avions naïvement supposé qu’une imprimante pourrait fabriquer une hélice, en flottant par un processus physique inconnu pour le moment, pour compenser la gravité. Il n’en est évidemment rien et une sphère de support est nécessaire. Après plusieurs itérations de conception qui passaient notamment par l’idée de placer le motif de l’hélice en relief sur la sphère pour la peindre de peinture conductrice (nous reviendrons sur la qualité ce cette peinture plus bas), la conception a convergé vers une hélice en relief inverse dans la sphère, permettant non seulement de remplir la gorge de peinture conductrice, mais aussi de conformer des fils de cuivre émaillés dans cette gorge, afin de former l’antenne. Nous verrons que c’est cette dernière approche qui a fourni les meilleurs résultats.
5. Réalisation et mesures des antennes
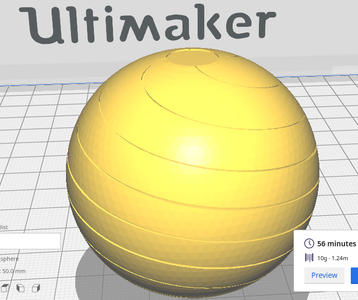
Le modèle STL est fourni à CURA (ultimaker.com/software/ultimaker-cura, Fig. 4), l’outil de conversion de la surface vers les commandes contrôlant une imprimante additive UltiMaker 2+. Le fil en acide polylactique (PLA) est standard : une tentative de tracer la spirale en PLA conducteur, au moyen d’une imprimante UltiMaker 3 avec sa double extrusion indispensable à ce mode d’impression, se solde par un échec avec une résistance excessive : un ohmmètre indique 10 kΩ pour une section d’un millimètre de côté et d'une dizaine de centimètres de longueur, en cohérence avec les valeurs annoncées à www.proto-pasta.com/pages/conductive-pla.
Figure 4 : Modèle de la sphère dans CURA avec ses dimensions, son temps d’impression de l’ordre de l’heure pour un diamètre de 5 cm, et la masse de plastique résultante.
Par ailleurs, diverses tentatives de peindre l’hélice par une peinture conductrice (Bare Conductive, référence 835-2693 chez RS) se solde ici encore par une résistance excessive, bien que moindre qu’avec le PLA conducteur. Des résistances de quelques centaines d’ohms sont observées en courant continu, toujours bien plus que l’impédance attendue de l’antenne. Il nous reste donc la solution d’insérer un fil de cuivre émaillé dans la fente formée par la spirale dans la sphère, lors de la soustraction du premier motif du second dans FreeCAD. La question du diamètre du fil se résout simplement : la profondeur de peau d’une onde électromagnétique dans un conducteur δ=√2ρ/µω où le champ de surface a été atténué d’un facteur e (pour rappel, le champ électrique dans un conducteur doit être nul, sinon les électrons se mettent en mouvement pour le compenser), avec ρ=1,68·10−8 Ω.m la résistivité du conducteur (ici, le cuivre), ω=2π f la pulsation angulaire liée à la fréquence f du signal électromagnétique rayonnant de l’antenne, et µ la perméabilité (4π· 10−7 pour l’air). À 100 MHz, l’épaisseur de peau du cuivre est 6,5 µm, donc n’importe quel fil de plus d’une centaine de micromètres de diamètre conviendra pour réaliser l’antenne (Fig. 5).
Figure 5 : Étapes d’impression (gauche) et de fabrication de l’antenne (droite) sur imprimante UltiMaker 2+. La structure est vide pour pouvoir la remplir de diélectrique (silicone) et ainsi tenter d’abaisser sa fréquence de fonctionnement.
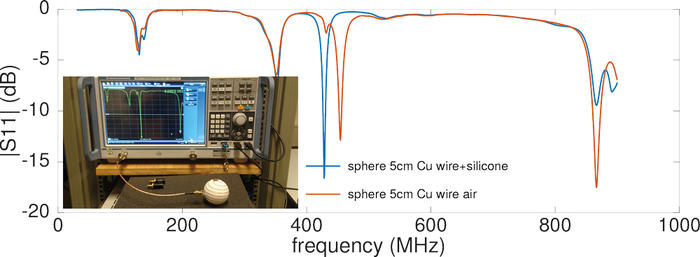
Le résultat de l’impression et la mesure du coefficient de réflexion S11 résultant sont illustrés en Fig. 6. La fréquence de fonctionnement est quelque peu inférieure à celle modélisée, mais l’absence de chambre anéchoïque pour effectuer les mesures fausse quelque peu l’adéquation entre expérience et simulation, comme en attestent les nombreux modes parasites que nous attribuons aux ondes stationnaires formées avec l’environnement métallique, autour de l’antenne.
Figure 6 : Caractérisation de la sphère de 5 cm de diamètre, soutenant l’antenne hélice sphérique réalisée en fil de cuivre émaillé : mesure avec la sphère vide, puis « remplie » de silicone afin d’abaisser sa fréquence de fonctionnement. Seul le mode un peu au-dessus de 400 MHz est attribué à l’antenne.
Nous concluons donc cette étude de la conception d’une antenne susceptible de s’insérer dans un tuyau vertical, mais rayonnant vers la surface par le tracé des diagrammes de rayonnement simulés des antennes considérées, à savoir l’hélice de petites dimensions s’insérant verticalement dans le puits étroit devant la longueur d’onde, l’hélice de circonférence grande devant la longueur d’onde qui ne correspond pas à notre cas pratique (nécessité de forer un puits de diamètre excessif) et l’antenne sphère qui permet, en tournant de 90 degrés la sphère dans le tuyau, de rayonner vers la surface (Fig. 7).
Figure 7: Diagrammes de rayonnement simulés pour l’hélice en mode axial (vert) qui rayonne bien vers la surface, mais ne peut être réalisée en pratique, compte tenu du diamètre du forage qui nous intéresse, l’hélice en mode normal (rouge) qui ne rayonne pas vers la surface, et la sphère (boule) tournée de 90° dans le tube pour rayonner vers la surface. À gauche, la géométrie considérée pour placer les antennes au fond d’un tuyau.
6. Impression et affichage des diagrammes de rayonnement
6.1 Du virtuel au réel
Pour conclure, ayant appris à générer des fichiers STL pour imprimer une antenne, il nous reste l’aspect ludique et pédagogique d’imprimer... les diagrammes de rayonnement modélisés par NEC2 en impression additive [11]. Pour ce faire, nous observons que les fichiers en sortie de NEC2 sont des fichiers ASCII contenant, les uns après les autres, les résultats des calculs de la puissance rayonnée dans une direction en coordonnées polaires pour chaque fréquence, avec les deux premières colonnes représentant les angles des coordonnées polaires (ϑ, ϕ) et en cinquième colonne, le gain de l’antenne dans cette direction. Tracer la surface est donc simplement une question d’extraire ces champs et de convertir les coordonnées polaires en coordonnées cartésiennes :
- avec son éditeur de texte favori (donc Vi), rechercher le mot clé « FREQUENCY : » (il y a bien un espace entre le mot clé et les deux points !), suivi de la fréquence en notation scientifique ; ayant identifié ce point, rechercher le mot clé RADIATION PATTERN qui suit ; éliminer (d1G) tout ce qui est au-dessus de ces mots clés et tout ce qui suit (dG) la prochaine occurrence de FREQUENCY, afin de n’obtenir un fichier qui ne contient que le diagramme de rayonnement ;
- sauver ce fichier et en extraire les 5 premières colonnes, soit cut -c 1-51 fichier, puisque les cartes FORTRAN proposent des champs de taille fixe ;
- le fichier résultant, de la forme :
%---- ANGLES ----- ----- POWER GAINS -----
% THETA PHI MAJOR MINOR TOTAL
%DEGREES DEGREES DB DB DB
0.00 0.00 -16.33 -999.99 -16.33
2.50 0.00 -16.25 -31.30 -16.11
5.00 0.00 -15.84 -25.56 -15.40
7.50 0.00 -14.89 -23.22 -14.29
10.00 0.00 -13.54 -22.65 -13.04
12.50 0.00 -12.21 -23.00 -11.86
...
est lu par GNU/Octave pour fabriquer le fichier STL, tel que vu auparavant :
1 load sphere.tostl
2 th=sphere(:,1); ph=sphere(:,2);
3 G=sphere(:,5)-min(sphere(:,5))+1;
4 plot3(G.*cosd(ph).*sind(th),G.*sind(ph).*sind(th),G.*cosd(th),'.');hold on
5 dth=diff(th);m=find(dth>0);m=m(1);dth=dth(m)
6 dph=diff(ph);m=find(dph>0);m=m(1);dph=dph(m)
7 p=m % m=144 increment from one ph to another adjacent
8
9 f=fopen('radiation.stl','w');
10 fprintf(f,'solid radiation\n');
11 for k=1:length(G)/2
12 P1=[G(k).*cosd(ph(k)).*sind(th(k)),G(k).*sind(ph(k)).*sind(th(k)),G(k).*cosd(th(k))];
13 P2=[G(k+p).*cosd(ph(k+p)).*sind(th(k+p)),G(k+p).*sind(ph(k+p)).*sind(th(k+p)),G(k+p).*cosd(th(k+p))];
14 P3=[G(k+1).*cosd(ph(k+1)).*sind(th(k+1)),G(k+1).*sind(ph(k+1)).*sind(th(k+1)),G(k+1).*cosd(th(k+1))];
15 n1=cross(P2-P1,P2-P3);
16 fprintf(f,' facet normal %f %f %f\n',n1(1),n1(2),n1(3));
17 fprintf(f,' outer loop\n');
18 fprintf(f,' vertex %f %f %f\n',P1(1),P1(2),P1(3));
19 fprintf(f,' vertex %f %f %f\n',P2(1),P2(2),P2(3));
20 fprintf(f,' vertex %f %f %f\n',P3(1),P3(2),P3(3));
21 fprintf(f,' endloop\n');
22 fprintf(f,' endfacet\n');
23 [... on recommence en échangeant le premier coin avec le coin oppose en k+p+1]
24 end
25 fprintf(f,'endsolid radiation\n');
26 fclose(f);
Le résultat est visible en Fig. 8, où nous constatons l’importance d’avoir balayé les angles en élévation de 0 à 360° et en azimut de 0 à 180° pour obtenir un volume fermé.
Les diagrammes de rayonnement sont souvent des motifs à symétrie de révolution autour de l’axe de l’antenne : afin de faciliter l’appui de la forme sur le plateau d’impression, nous avons choisi de couper en deux chaque diagramme de rayonnement au moment de l’impression (calculer l’ordonnée maximale dans CURA et soustraire sa moitié, afin de n’imprimer que la moitié du motif) pour les coller, aussi maladroitement que possible, après impression. Simulation et fabrication ont donc fini par converger (Fig. 8, droite).
Figure 8 : Gauche : diagrammes de rayonnement du petit dipôle sphérique, qui ressemble à s’y méprendre au diagramme de rayonnement du dipôle en espace libre, et d’une antenne directive Yagi-Uda (« râteau de télévision »), vue du côté de l’élément réflecteur. Milieu : réalisation en impression additive de ces diagrammes de rayonnement. Droite : modèle de l’antenne Yagi-Uda, avec son diagramme de rayonnement calculé par NEC2.
6.2 Du réel au virtuel
Maintenant que nous avons des modèles de diagrammes de rayonnement imprimés et manipulables, nous proposons le complément qui est d’inclure le diagramme de rayonnement au-dessus du modèle physique de l’antenne : une telle fonction est possible grâce à la réalité augmentée [14], qui prend une importance croissante dans divers domaines stratégiques [15, 16, 17]. Ici encore, le problème est la conversion de format des diagrammes de rayonnement vers un format compréhensible par l’infrastructure que nous avons sélectionnée, à savoir ar.js telle que disponible à github.com/jeromeetienne/AR.js. Cette infrastructure permet de s’interfacer à A-Frame (aframe.io), capable de charger un modèle en 3D de CAO et de le placer dans un contexte de la caméra d’un périphérique mobile, tel qu’un téléphone portable. L’objet que nous désirons inclure dans la vidéo capturée par la caméra du téléphone portable est localisé au moyen d’une image de référence, nommée AR-Code (Augmented Reality Code). Le motif classique de cet AR-Code est le mot Hiro, d’après le nom d’un des auteurs de ARToolKit Hirokazu Kato (Nara Inst. of Science and Technology) [18]. L’image de référence, à afficher sur écran ou à imprimer, est disponible à https://jeromeetienne.github.io/AR.js/data/images/HIRO.jpg. A-Frame conseille de charger des modèles au format glTF, encore un format de plus pour représenter des structures tridimensionnelles. Qu’à cela ne tienne, Meshlab charge le diagramme de rayonnement au format SRL pour sauver un format DAE de COLLADA (COLLAborative Design Activity) compréhensible par https://cesiumjs.org/convertModel/ pour former un fichier exploitable. Ce fichier se charge alors « trivialement », une fois les tutoriels obsolètes éliminés lors de la recherche des informations, par le script Javascript de la forme :
1
2 <script src="https://aframe.io/releases/0.9.2/aframe.min.js"></script>
3 <script src="https://jeromeetienne.github.io/AR.js/aframe/build/aframe-ar.js"></script>
4
5 <!-- convert COLLADA DAE exported from Meshlab to GLTF using https://cesiumjs.org/convertModel/ -->
6 <body style='margin : 0px; overflow: hidden;'>
7 <a-scene embedded arjs='trackingMethod: best;'>
8
9 <a-assets> <!-- first model -->
10 <a-asset-item id="dipole" src="https://jmfriedt.org/dipole.gltf">
11 </a-assets>
12
13 <a-assets> <!-- second model -->
14 <a-asset-item id="tree" src="https://jmfriedt.org/coffee.gltf">
15 </a-assets>
16
17 <a-marker type="pattern" preset="custom" url="https://jmfriedt.org/pattern-cantenna.patt">
18 <a-gltf-model src="#tree" position="-0.1 0 0" scale=".018 .018 .018"></a-gltf-model>
19 <a-box color="#2EAFAC" material='opacity: 0.5;'></a-box>
20 </a-marker>
21
22 <a-marker preset="hiro">
23 <a-gltf-model src="#dipole" position="-0.1 0 0" rotation="180 0 0 " scale=".018 .018 .018"></a-gltf-model>
24 <a-box color="#AEAF2C" material='opacity: 0.5;'></a-box>
25 </a-marker>
26 <a-entity camera></a-entity>
27 </a-scene>
28 </body>
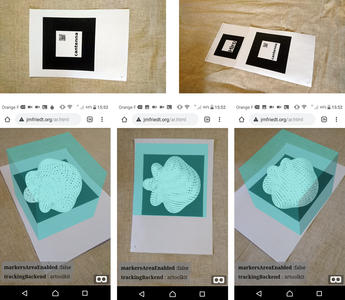
Nous avons superposé le diagramme de rayonnement à un cube pour faciliter la visualisation de l’orientation du modèle (Fig. 9). La seule subtilité dans le déploiement de cette application est que le serveur web doit absolument être un service chiffré (https://) pour que la visualisation de la caméra soit accessible. Comme le nom de l’URL n’est pas toujours simple à mémoriser, nous nous sommes proposés de superposer un nom d’antenne un peu plus pertinent que le nom de l’auteur d’AR-Code, avec un QRcode contenant l’URL de la page web contenant le modèle du diagramme de rayonnement (qrencode "https://jmfriedt.org/ar.html" -t PNG -s 5 -o ar.png). Noter que l’outil de conversion de cette image PNG vers le motif supportant le modèle virtuel, https://jeromeetienne.github.io/AR.js/three.js/examples/marker-training/examples/generator.html, impose d’avoir une couleur de fond grise (0xF0F0F0) et non blanche (0xFFFFFF).
Figure 9: Gauche : le motif définissant la position de l’objet en réalité augmentée – ici un diagramme de rayonnement de cantenna. Droite : la vue de l’interface web d’un téléphone portable superposant l’objet virtuel à l’AR-Code au chargement de https://jmfriedt.org/ar.html. À gauche et au milieu un unique AR-code, et à droite deux AR-codes supportant chacun leur modèle de diagramme de rayonnement.
Ces méthodes de représentation des champs de grandeurs physiques, par impression additive ou par réalité augmentée, s’inscrivent dans la longue tradition de les visualiser par des maquettes multidimensionnelles, tel que décrit par exemple à dataphys.org/list/solid-3d-curves-for-engineering/. Le lecteur pourra se convaincre du rendu, en imprimant ou en affichant sur son écran l’image de jmfriedt.free.fr/both.png et en chargeant sur son téléphone portable https://jmfriedt.org/ar.html.
Conclusion
Nous proposons une chaîne complète de conception d’antenne, de l’identification de la géométrie respectant les contraintes d’encombrement, à la modélisation du diagramme de rayonnement et coefficient de réflexion en fonction de la fréquence, à la génération des fichiers de Conception Assistée par Ordinateur. Ces fichiers permettent d’une part d’alimenter des modèles complexes d’antennes, tenant compte de divers milieux de permittivité variable (solution par éléments finis par HFSS) et d’autre part, de réaliser les antennes par impression additive. Les mesures de coefficient de réflexion des antennes fabriquées, après enroulement de fils de cuivre émaillé dans les gorges définissant le motif d’antenne sur la sphère de support, sont cohérentes à quelques pour cent près avec la fréquence d’accord de l’antenne dans la simulation.
Nous avons commencé cette présentation en fournissant des diagrammes de rayonnement issus d’un logiciel propriétaire (HFSS). Nous ne pouvons évidemment pas rester sur cette approche et fournissons ici la solution avec NEC, exploitant la carte GH pour définir une hélice selon les prescriptions de www.gunthard-kraus.de/Vortrag_Weinheim/4nec2_article.pdf :
CM Helix antenna using GH card
CE
GH 1 120 0.14 0.28 0.1 0.1 0.1 0.1 0.001
GM 0 0 0 0 0 0 0 0.015 0
GW 150 1 .1 0 0 .1 0 0.015 0.001
GS 0 0 0.5
GE 1
GN 1
EX 0 150 1 0 1. 0
FR 0 196 0 0 2.0E+01 5.0E+00
RP 0 73 144 0 0.0+00 0.0+00 2.5+00 2.5+00
EN
L’hélice GH est translatée (GM) pour laisser la place à l’alimentation (GW) au-dessus du plan de masse (GE 1 et GN 1).
La conception d’antenne est un domaine fascinant, facilement accessible à l’amateur par la disponibilité de NEC2 pour la simulation. Alors que le coût unitaire d’une antenne dépasse facilement la centaine d’euros, la capacité à les réaliser en impression additive offre des perspectives de démocratisation, voire d’applications innovantes avec par exemple, le gain en masse d’une antenne cornet imprimée en plastique couvert de peinture conductrice [12] par rapport à sa version usinée en cuivre, si l’application vise à être embarquée sur drone – sous réserve de prendre un peu soin à la rugosité de surface. Des formes tordues – et les concepteurs d’antenne sont très imaginatifs en ce sens, par exemple avec les antennes fractales [13] – deviennent ainsi accessibles au prototypage rapide.
Les antennes sont un élément primordial dans une chaîne de réception radiofréquence, fut-elle orientée vers un traitement logiciel des échantillons. Elles feront partie intégrante des considérations de la prochaine European GNU Radio Days, qui se tiendra à Poitiers les 22 et 23 juin 2020 (jmfriedt.org/gnuradiodays2020). Tous les fichiers pour reproduire les illustrations de cet article se trouvent sur http://github.com/jmfriedt/und.
Remerciements
Cette étude a été initiée par le projet UNDERGROUND, financé par l’Agence Nationale de la Recherche. Les diagrammes de rayonnement ont été réalisés avec les moyens d'impression 3D des CMI PICS et SCUBE financés par l'EUR EIPHI (contrat ANR-17-EURE-0002). Toutes les références bibliographiques qui ne sont pas librement disponibles sur le Web ont été obtenues auprès de Library Genesis sur gen.lib.rus.ec, une ressource indispensable à nos activités de recherche.
Références
[1] H.A. Wheeler, Fundamental Limitations of Small Antennas, Proc. IRE. 35 (12) pp.1479–1484(1947)
[2] L.J. Chu, Physical Limitations on Omni-Directional Antennas, J. Appl. Phys. 9, pp.1163–1175 (1948)
[3] C. Pfeiffer, Fundamental Efficiency Limits for Small Metallic Antennas, IEEE Trans. on Antennas and Propagation 12 (2016)
[4] H.A. Wheeler, The Radiansphere around a Small Antenna, Proc. IRE 47, pp.1325–1331 (1959)
[5] C.A. Balanis CA, Antenna theory: analysis and design, John Wiley & Sons (1996)
[6] J.-M Friedt, Modélisation et utilisation d’une parabole : application au WiFi, Open Silicium 20 pp.44–55 (2016)
[7] Description du projet UNDERGROUND : https://anr.fr/Project-ANR-17-CE24-0037
[8] N. Stephenson, The Diamond Age – or, Young Lady’s Illustrated Primer, Spectra (1995)
[9] S.R. Best, The Radiation Properties of Electrically Small Folded Spherical Helix Antennas, IEEE Trans. on Antennas and Propagation 52 (4), 953– (2004) et : http://www.antennamagus.com/database/antennas/antenna_page.php?id=306 pour une description de la Folded Spherical Helix Dipole
[10] R.P. Feynman & al., The Feynman lectures on physics, vol.2 (1964), Chap 6–7 « The method of images ».
[11]M. Uttmark, 3D Printed Radiation Patterns : hackaday.com/2017/06/11/3d-printed-radiation-patterns/ et la vidéo originale : www.youtube.com/watch?v=rthNZFHG-Zo
[12] 3D Printing Your Own Antennas : https://antennatestlab.com/3dprinting
[13] S.Yun Jun & al., Manufacturing Considerations in the 3-D Printing of Fractal Antennas, IEEE Trans on Components, Packaging and Manufacturing Technology 7 (11), pp.1891– (2017) : https://ieeexplore.ieee.org/iel7/5503870/5673025/08012467.pdf
[14] T. Colombo, Partez à la découverte de la réalité augmentée, GNU/Linux Magazine 197 (oct. 2016) : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-197/Partez-a-la-decouverte-de-la-realite-augmentee
[15]S. Castellanos, Lockheed Martin Deploys Augmented Reality for Spacecraft Manufacturing, Wall Street Journal (1er août 2018) : blogs.wsj.com/cio/2018/08/01/lockheed-martin-deploys-augmented-reality-for-spacecraft-manufacturing/ consulté après la visite du Marshall Space Center et les infrastructures de conception du SLS et Orion
[16] D.H. Nguyen & al., BeamViewer: Visualization of dynamic antenna radiation patterns using Augmented Reality, 2016 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS)
[17] Beam Visualization and Using Augmented Reality for Control and Interaction, brevet US20180350149 (2018)
[18] K. Shabalina & al., ARTag, AprilTag and CALTag Fiducial Systems Comparison in a Presence of Partial Rotation: Manual and Automated Approaches, pp. 536–558, dans O. Gusikhin & K. Madani Ed., 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO), 2017