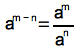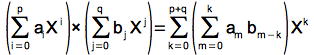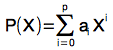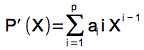Pour corriger un code QR avec erreur ou rature, nous avons besoin de construire le corps fini F256 et son anneau de polynômes.
La correction d’erreur de Reed-Solomon travaille dans l’anneau des polynômes à coefficients dans F256. Cet article présente une construction de ces deux structures emboîtées en Python orienté objet.
Dans l’article précédent [1], nous avons présenté le minimum mathématique pour une bonne compréhension de ce qui suit.
1. Construction du corps F256
Le corps fini utilisé n’est pas un corps du type ℤ/pℤ avec p premier, il s’agit, d’un point de vue ensembliste, de
qui a 256 éléments. Son corps premier est bien ℤ/2ℤ={0,1}, on travaille avec un ordinateur après tout et ses éléments sont modélisables comme des octets. Attention cependant, les opérations effectuées ne sont PAS celles de ℤ/256ℤ qui n’est PAS un corps, on ne peut donc pas utiliser sans précaution les nombres entiers de 0 à 255, il faut malgré tout mettre un peu les mains dans le cambouis.
Mathématiquement, on a besoin de quatre structures emboîtées :
- Le corps premier ℤ/2ℤ=F2 dont on a vu une construction possible [1] (mais [False,True] peut très bien convenir) ;
- L’anneau F2[X] des polynômes à coefficients dans F2 ;
- Le corps F256 qui est mathématiquement le quotient de F2[X] par un polynôme irréductible dans le corps F2 (par l'idéal engendré par ce polynôme si on veut être précis), notre polynôme annulateur est X8+X4+X3+X2+1 (si on l’évalue en X=2, on obtient 285, voir plus loin) ;
- Les polynômes à coefficients dans F256 utilisés dans la correction d’erreurs notées F256[X].
Nous avons donc techniquement besoin de polynômes de polynômes. Vous suivez ? Pas trop, alors on va simplifier la construction et ne pas emboîter trop de structures les unes dans les autres, les deux dernières suffiront.
J’ai donc codé dans qrcorps.py (disponible dans le GitHub du magazine) un moyen terme entre la structure mathématique abstraite et générale (plus propre mathématiquement mais pénible à utiliser) et celle de Wikiversity [2] (qualités et défauts inverses) : je code directement le corps F256 sans passer par F2 (comme Wikiversity) tout en conservant la création de classes d’éléments du corps et de polynômes (comme Kun [3]). Cela me facilitera la correction des éventuelles erreurs tout en conservant la souplesse de la surcharge des opérations. J’espère que ce ne sera ni moche ni pénible.
01: #!/usr/bin/python3
02:
03: from qrcodeoutils import *
Le code a besoin de quelques fonctions purement mathématiques comme les algorithmes d’Euclide.
2. La classe F256
2.1 Préliminaires
La classe est mémorisée (voir section précédente), on commence par le constructeur :
05: annulateur=285
06:
07: @memorise
08: class F256():
09: def __init__(self,s):
10: if isinstance(s,str) or hasattr(s,'__iter__') or hasattr(s,'iter'):
11: self.val=bin2dec(s)
12: elif type(s) is F256:
13: self.val=s.val
14: else:
15: self.val=s
16: while True:
17: ch=bin(self.val)[2:]
18: if len(ch)<=8:
19: break
20: self.val^=annulateur*2**(9-len(ch))
21: self.corps=F256
Une instance de la classe F256 contient deux attributs :
- val est un entier entre 0 et 255 par commodité mais on utilise en fait sa décomposition en base 2, autrement dit sa représentation binaire ;
- corps est le nom de notre corps, ce qui permet de ne pas ajouter deux éléments de corps différents (on n’est pas concerné ici mais cela peut empêcher une mauvaise surprise, voir [1] pour l’explication de @memorise).
Selon le type de l’élément qu’on veut convertir en élément de F256, si c’est :
- une chaîne de caractères ou un tuple qui ne contient que des 0 et des 1, on convertit l’écriture binaire en un entier ;
- un membre de F256, on recopie la valeur dans l’attribut val,
- un entier, de même.
Ensuite, si val est supérieur ou égal à 256 on effectue sa division par 285 (c’est-à-dire 1000111012 ou 11d16) tant qu’elle est trop grande. Par division, j’entends soustraction ou addition bit à bit, c’est-à-dire un XOR (le shérif de l’espace). Par exemple, bin(28) retourne "0b11100" voilà pourquoi on ne conserve pas les deux premiers caractères. De même, hex(28) retourne "0x1c".
22: def __str__(self):
23: nb=hex(self.val)[2:]
24: return nb
25: def __repr__(self):
26: return str(self)
Quand on veut utiliser print ou str, on utilise la méthode __str__. Quand on affiche une liste qui contient des instances de F256, on utilise la méthode __repr__. On retourne sa valeur hexadécimale.
2.2. Les opérations
27: def __add__(self,n):
28: return F256(self.val^n.val)
29: def __sub__(self,n):
30: return self+n
31: def __neg__(self):
32: return self
L’addition est en fait un XOR car le corps F256 est un espace vectoriel de dimension 8 sur le corps F2, où l’addition a cette table :
|
+ |
0 |
1 |
|---|---|---|
|
0 |
0 |
1 |
|
1 |
1 |
0 |
En effet, 1+1=2=0 modulo 2. Comme on ajoute des vecteurs à 8 coordonnées à valeurs dans F2, on utilise un simple XOR entre les deux valeurs.
Par exemple, si on veut ajouter les vecteurs de coordonnées respectives (1,0,1,1,0,1,0,1) et (0,1,1,1,1,0,1,1) autrement dit 181 et 123 en représentation décimale, on ajoute coordonnée à coordonnée, ce qui donne (1,1,0,0,1,1,1,0) soit 206. On a déjà utilisé cette technique quand on a démasqué.
Pour la même raison (la caractéristique de F256 vaut 2), ∀a,b∈F256, a−b=a+b et −a=a.
33: def __mul__(self,n):
34: if self.val==0 or n.val==0:
35: return F256(0)
36: return F256(F256.exp((self.log()+n.log())))
La multiplication utilise une table pré-calculée de puissances d’un élément primitif de F256. Un tel élément existe et engendre complètement F256 à partir de ses puissances (à part bien sûr 0). On utilise la propriété bien connue d’additivité des exposants : ∀a∈F, ∀n,m∈ℤ, am+n=am×an. Ici, a est notre élément primitif et on additionne les deux exposants des puissances de a égales à nos deux éléments. Les exposants sont déterminés à partir d’un logarithme discret, pré-calculé un peu plus bas.
Bien entendu, si un des multiplicandes est nul, le produit est nul. Je n’ai pas codé les opérations externes (avec un entier, par exemple 3a=a+a+a) parce que je n’en ai pas besoin.
38: def __truediv__(self,n):
39: if n.val==0:
40: raise ZeroDivisionError
41: if self.val==0:
42: return F256(0)
43: return F256(F256.exp((self.log()-n.log())))
La division utilise la même propriété : ∀a∈F
, ∀n,m∈ℤ,
. On teste d’abord si le diviseur est nul (division par zéro), si le dividende est nul (quotient nul), sinon on utilise la propriété.
44: def __pow__(self,e):
45: if self.val==0:
46: if e<0:
47: raise ZeroDivisionError
48: elif e==0:
49: return F256(1)
50: else:
51: return F256(0)
52: return F256(F256.exp((e*self.log())))
Pour calculer une puissance, on teste d’abord si le nombre est nul. Dans ce cas, on vérifie si l’exposant est négatif, nul ou positif. Sinon, on utilise la propriété suivante : ∀a∈F256, ∀n,m∈ℤ, anm=(an)m.
53: def log(self):
54: if self.val==0:
55: raise ZeroDivisionError
56: return F256.log[self.val]
Le logarithme discret est pré-calculé, cela évite de le recalculer à chaque fois. En effet, sa détermination par un algorithme meilleur que la recherche exhaustive n’est pas résolue pour le moment. La méthode est en fait un attribut de classe, lequel est un dictionnaire.
58: F256.log=dict()
59: exp=[]
60: nb=1
61: for i in range(255):
62: F256.log[nb]=i
63: exp.append(nb)
64: nb*=2
65: if nb>=256:
66: nb^=annulateur
67: F256.exp=lambda i:exp[i%255]
68: F256.__name__="F_2⁸"
L’élément primitif générateur de notre corps fini est 2 (c’est-à-dire le polynôme X puisque 210=102), on calcule ses puissances successives. On stocke l’exposant dans F256.log et la puissance dans F256.exp. On aurait pu écrire :
67: def F256.exp(i):return exp[i%255]
Et on définit le nom de la classe.
213: if __name__=="__main__":
214: a=F256(140)
215: print(a)
216: b=F256("101")
217: print(b)
218: print(a.log())
219: print(b+a)
220: print(a*a*a*a*a*a)
221: print(a**6)
222: print(F256.log[128])
Exécutons ce code :
8c
5
49
Donc, selon notre écriture, 249=140 (soit 10001100 en binaire) car X49 modulo X8+X4+X3+X2+1 vaut X7+X3+X2 (ces polynômes sont à coefficients dans F2).
89
35
35
7
Et on vérifie que l’addition et la puissance sont correctement codées.
3. La classe Polynome
Pour corriger les éventuelles erreurs d’un code QR, on a besoin de polynômes à coefficients dans F256, or les polynômes forment un anneau : les règles de calcul sont celles d’un corps à ceci près que les éléments non nuls ne sont pas tenus d’être tous inversibles pour la multiplication. Par quel polynôme multiplier X pour obtenir 1 ?
3.1 Construction et affichage
68: @memorise
69: class Polynome(ElementAnneau):
La classe Polynome est une sous-classe de la classe ElementAnneau, présente dans qrcodeoutils.py :
class ElementAnneau(object):
def __radd__(self,autre):
return self+autre
def __rsub__(self,autre):
return -self+autre
def __rmul__(self,autre):
return self*autre
Ici, on s’assure de la commutativité de l’addition et de la multiplication, le code est dans qrcodeoutils.py.
Le constructeur :
71: def __init__(self,c):
72: if type(c) is Polynome:
73: self.coefficients=tuple(c.coefficients)
74: elif type(c) is Polynome.corps:
75: self.coefficients=(c,)
76: elif not hasattr(c,'__iter__') and not hasattr(c,'iter'):
77: self.coefficients=(Polynome.corps(c),)
78: else:
79: self.coefficients=tuple(c)
80: try:
81: while self.coefficients[0]==Polynome.corps(0):
82: self.coefficients=self.coefficients[1:]
83: except IndexError:
84: pass
Si on envoie au constructeur :
- un polynôme, il retourne le même polynôme ;
- un élément du corps fini, il retourne un polynôme de degré 0 dont le coefficient de degré 0 vaut cet élément ou le polynôme nul si l’élément est le 0 de F256 ;
- un tuple, il retourne un polynôme dont les coefficients sont les éléments du tuple.
Les coefficients sont rangés dans l’ordre d’écriture usuel, à savoir que les coefficients du polynôme 3X³+4X+1 sont dans le tuple (3,0,4,1), c’est un choix, Kun [3] utilise l’autre convention où 3X³+4X+1 est représenté par (1,4,0,3). Pourquoi un tuple ? Pour pouvoir être mémorisé dans le cache du décorateur.
Si les premiers coefficients sont nuls, on les supprime. Le polynôme nul a une liste de coefficients vide ; (0,3,0,4,1) et (3,0,4,1) donnent le même polynôme.
86: def estzero(self):
87: return self.coefficients==tuple()
Cette méthode retourne True si le polynôme est nul. Si, si.
89: def __str__(self):
90: if self.estzero():
91: return "0"
92: expo={"0":"⁰","1":"¹","2":"²","3":"³","4":"⁴","5":"⁵","6":"⁶","7":"⁷","8":"⁸","9":"⁹"}
93: return "+".join([str(self.coefficients[i])+"X"+\
"".join(expo[j] for j in str(self.degre()-i)) for i in range(len(self)) \
if self.coefficients[i]!=Polynome.corps(0)])
95: def __repr__(self):
96: return str(self)
On affiche les coefficients non nuls, par exemple si les coefficients sont (f1,0,4,1), on affiche f1X³+4X¹+1X⁰ et les degrés supérieurs ou égaux à 10 sont affichés correctement, comme 5X³¹.
3.2 Propriétés des polynômes
098: def __call__(self,val):
099: res=Polynome(tuple())
100: if type(val) is type(self):
101: va=val
102: else:
103: va=Polynome(tuple([val]))
104: for c in self:
105: res*=va
106: res+=Polynome(tuple([c]))
107: if type(val) is type(self):
108: return res
109: if res.coefficients:
110: return res[0]
111: return Polynome.corps(0)
On peut évaluer un polynôme en un élément du corps sous-jacent comme en un autre polynôme, ce qui veut dire qu’on peut considérer un polynôme comme une fonction (même si mathématiquement, un polynôme n’est PAS une fonction). Ainsi si P est un polynôme, P(4) retourne un nombre alors que P(X+1) retourne un autre polynôme. On teste donc le type de l’entrée, qu’on transforme en un polynôme si c’est un scalaire (ligne 103). On utilise l’algorithme de Horner (voir [4]) des lignes 104 à 106 puis on retourne soit un polynôme soit un scalaire soit zéro si les coefficients sont vides.
112: def __abs__(self):
113: return len(self.coefficients)
114: def __len__(self):
115: return len(self.coefficients)
La valeur absolue est utilisée dans la division euclidienne, on l’appelle aussi stathme euclidien en mathématiques des anneaux euclidiens (munis d’une division euclidienne), ce que sont les anneaux de polynômes à coefficients dans un corps. La longueur d’un polynôme est la longueur de la liste de ses coefficients.
116: def __iter__(self):
117: return iter(self.coefficients)
118: def iter(self):
119: return self.__iter__()
120: def __getitem__(self,i):
121: return self.coefficients[self.degre()-i]
122: def __setitem__(self,i,x):
123: coef=list(self.coefficients)
124: coef[self.degre()-i]=x
125: self.coefficients=tuple(coef)
On permet d’itérer les coefficients du polynôme, d’y accéder et de les modifier directement sans passer par le constructeur.
Ainsi, on peut utiliser des codes comme for c in P:P[-1]=P[0]+c où P[0] désigne le coefficient dominant et P[-1] le coefficient de plus bas degré.
Ne pas confondre P[0] et P(0).
126: def coefficientdominant(self):
127: return self.coefficients[0]
128: def degre(self):
129: return abs(self)-1
Le coefficient dominant de 3X²+4X+5 est 3, son degré est 2.
130: def __eq__(self,autre):
131: return self.coefficients==autre.coefficients
L’égalité entre polynômes est correcte puisqu’on supprime les coefficients nuls s’ils sont au début de la liste des coefficients.
3.3 Les opérations
Je n’ai pas codé les opérations entre les éléments du corps de base et les polynômes, n’en ayant pas besoin.
132: def __add__(self,autre):
133: somme=[Polynome.corps(0)]*(max(len(self),len(autre))-len(self))+list(self.coefficients)
134: for i in range(len(autre)):
135: somme[-i-1]+=autre[i]
136: return Polynome(tuple(somme))
137: def __xor__(self,autre):
138: return self+autre
139: def __neg__(self):
140: return Polynome(tuple((-a for a in self)))
141: def __sub__(self,autre):
142: return self+(-autre)
L’addition, la soustraction, et le XOR (non utilisé ici) sont trois mêmes opérations : ajouter deux à deux les coefficients de même degré ; l’opposé ne fait rien parce qu’on est en caractéristique 2.
143: def __mul__(self,autre):
144: if self.estzero() or autre.estzero():
145: return Polynome(tuple())
146: prod=[Polynome.corps(0) for _ in range(len(self)+len(autre)-1)]
147: for i in range(len(self)):
148: for j in range(len(autre)):
149: prod[-i-j-1]+=autre[j]*self[i]
150: return Polynome(tuple(prod))
On multiplie deux polynômes en utilisant la formule classique de développement
. Ce n’est pas la plus rapide, de loin, mais elle nous suffira.
151: def __pow__(self,exp):
152: if exp>0:
153: prod=Polynome(tuple([Polynome.corps(1)]))
154: x=Polynome(self.coefficients)
155: while exp>1:
156: if exp%2:
157: prod*=x
158: x*=x
159: exp//=2
160: return prod*x
161: elif exp==0:
162: return Polynome(tuple([Polynome.corps(1)]))
On calcule la puissance non strictement négative d’un polynôme par l’exponentiation rapide (voir [1]). Bien entendu, on ne sait pas calculer les puissances négatives d’un polynôme.
164: def __divmod__(self,diviseur):
165: quotient,reste=Polynome(tuple()),self
166: degdiviseur=diviseur.degre()
167: coefdom=diviseur.coefficientdominant()
168: while reste.degre()>=degdiviseur:
169: monomediviseur=Polynome(tuple([reste.coefficientdominant()/coefdom]+[F256(0)]*(reste.degre()-degdiviseur)))
170: quotient+=monomediviseur
171: reste-=monomediviseur*diviseur
172: return quotient,reste
Il s’agit de la division euclidienne de polynômes qui retourne le quotient et le reste de degré inférieur au diviseur, l’algorithme est le même que celui de la division à potence apprise à l’école primaire. Par exemple si on veut diviser dans ℝ[X] X5+3X3+4X−1 par X2−X+2, le degré du quotient sera 5−2=3 et celui du reste au plus 2−1=1 :
X⁵+0X⁴+3X³+0X²+4X−1 | X²−X+2
−X⁵+1X⁴−2X³ |_____________
X⁴+1X³+0X²+4X−1 | 1X³+1X²+2X
−X⁴+1X³−2X² |
−1 |
Donc X5+3X3+4X−1=(X²−X+2)×(X3+X2+2X)−1, le reste vaut −1, de degré 0⩽1. Remarquez que si le reste est nul, le dividende est factorisable par le diviseur. Le principe est le même dans F256[X].
174: def __floordiv__(self,div):
175: q,_=divmod(self,div)
176: return q
177: def __mod__(self,div):
178: _,r=divmod(self,div)
179: return r
Le quotient euclidien est donné par l’opération //, l’opération / n’existe pas ici puisque notre anneau de polynômes n’est pas un corps, la deuxième opération est le modulo, donné par l’opération %. Dans le cas précédent (X5+3X3+4X−1)//(X2−X+2) retourne 1X³+1X²+2X et (X5+3X3+4X−1)%(X2−X+2) retourne −1.
181: def bezoutpoly(self,p2):
182: r,u,v=p2,Polynome.construction([1]),Polynome.construction([0])
183: rr,uu,vv=self,Polynome.construction([0]),Polynome.construction([1])
184: while not rr.estzero():
185: q=r//rr
186: r,u,v,rr,uu,vv=rr,uu,vv,r-q*rr,u-q*uu,v-q*vv
187: return v,u,r
Il s’agit de l’algorithme d’Euclide étendu qui donne les coefficients de Bezout u et v à l’équation au+bv=d où d est un PGCD de a et de b. En effet, le PGCD est défini à un inversible près et ici, les inversibles sont les polynômes de degré 0, ceux qui n’ont qu’un coefficient non nul et qu’on assimile à F
(mathématiquement, les polynômes de degré inférieur ou égal à 0 sont isomorphes F256). C’est le même algorithme que pour la recherche de l’inverse dans Fp (voir [1]) mais adapté.
189: def der(self):
190: derive=[Polynome.corps(0) for _ in self]
191: for i in range(len(self)):
192: if i%2==1:
193: derive[-i-1]=self[i]
194: return Polynome(tuple(derive[:-1]))
C’est la dérivation d’un polynôme à coefficients dans un corps de caractéristique 2. En effet, si
,
. Or si i est pair, i vaut 0 modulo 2 d’où le test ligne 192 et on décale bien entendu les puissances de X.
196: Polynome.corps=F256
197: Polynome.__name__="(%s)[x]"%F256.__name__
198: Polynome.construction=lambda L: Polynome(tuple(F256(x) for x in L))
On précise le corps utilisé, le nom de la classe et comment construire rapidement un polynôme à partir de la liste de ses coefficients.
3.4 On joue un peu
Et maintenant, vérifions que tout fonctionne bien.
231: print(Polynome.__name__)
232: poly=Polynome.construction
233: p=poly((15,1,12))
234: q=poly(("11","10110","0"))
235: print(p,q)
236: print(p+q)
237: print(p%q)
238: print(divmod(p,q))
239: print(p//q*q+p%q)
240: print(p^q)
241: print(p*p)
242: print(p**2)
243: print(p(F256(1)))
244: print(p(q))
245: print(p(q).der())
La ligne 239 vérifie que la division euclidienne se passe bien, c’est-à-dire que le résultat est bien p, les lignes 241 et 242 que la puissance 2 est correcte, les lignes 236 et 240 que les deux additions sont identiques et les deux dernières lignes que la dérivation est correcte.
(F_2⁸)[x]
fX²+1X¹+cX⁰ 3X²+16X¹+0X⁰
cX²+17X¹+cX⁰
4fX¹+cX⁰
(5X⁰, 4fX¹+cX⁰)
fX²+1X¹+cX⁰
cX²+17X¹+cX⁰
55X⁴+1X²+50X⁰
55X⁴+1X²+50X⁰
2
33X⁴+74X²+16X¹+cX⁰
16X⁰
Conclusion
Nous sommes prêts à corriger un code QR pas trop abîmé !
Ouverture
On peut rendre cette bibliothèque plus propre, notamment en codant les opérations externes et en gérant mieux les transtypages...
Références
[1] PATROIS N., « Expliquer un corps fini », GNU/Linux Magazine n°195, juillet/août 2016, p. 16 à 19.
[2] Reed–Solomon codes for coders https://en.wikiversity.org/wiki/Reed%E2%80%93Solomon_codes_for_coders.
[3] http://jeremykun.com/2014/03/13/programming-with-finite-fields/.
[4] PATROIS N., « Décoder un code QR », GNU/Linux Magazine n°194, juin 2016, p. 32 à 41.