Parcourir des graphes en largeur

Il ne s’agit ni de courir en crabe ni de descendre de vélo pour se regarder pédaler comme en pédagogie moderne mais d’utiliser, dans des graphes, le parcours en largeur (breadth first search en anglais ou BFS) et quelques variantes proches.Le principe est simple, nous le donnerons dans la première partie. La deuxième en fera tourner quelques applications plus ou moins immédiates, la dernière s’intéressera à une variante : l’algorithme de Dijkstra. Tous les codes sont en Python (2 ou 3, aucune importance ici).

1. Le parcours en largeur

Un graphe est, mathématiquement, un ensemble de points, les sommets, reliés par des liens ou arêtes, éventuellement orientés (on parle alors de digraphe et on représente les arêtes par des flèches). Il suffit de regarder un plan des lignes de métro ou de bus d’une ville ou de penser à internet pour comprendre.

1.1 Le principe

Il s’agit de parcourir un graphe de proche en proche, comme une tache d’huile. On commence au sommet initial, puis on va sur les sommets qui lui sont directement reliés. À l’étape suivante, on franchit les sommets non déjà franchis qui sont directement reliés à ceux de l’étape précédente, et ainsi de suite jusqu’à épuisement des sommets disponibles.

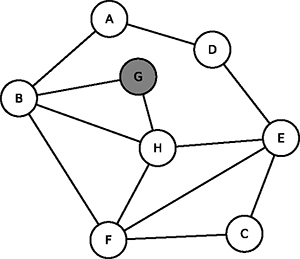
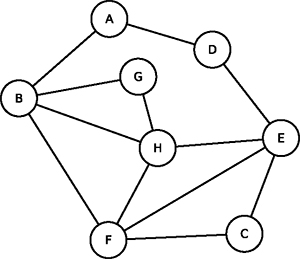
Voici ce qui se passe sur un graphe non orienté (je grise les sommets visités petit à petit) :

Étape 1	Étape 2
Fig. 1 : On part du sommet G, qu’on grise.	Fig. 2 : Du sommet G, seuls B et H sont reliés, on les grise.
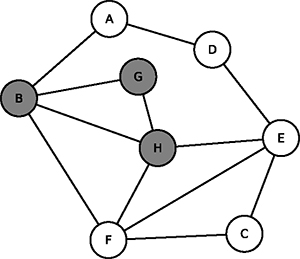
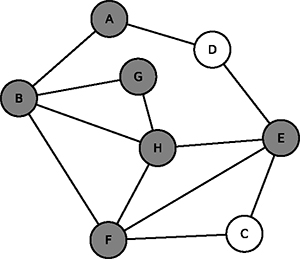
Étape 3	Étape 4
Fig. 3 : De B et H, les sommets non déjà parcourus sont A, E et F qu’on grise.	Fig. 4 : Et de ces trois-là, on peut rejoindre C et D et il ne reste aucun sommet libre.

Notez que si le graphe est non connexe (en plusieurs morceaux), on ne peut pas franchir tous ses sommets et de même s’il est connexe et orienté, on peut ne pas les rencontrer tous (penser à un arbre orienté ou au graphe du temps de la section 2.2. si on commence au sommet C). Les graphes seront dans la suite connexes.

1.2 Modéliser un graphe

Les graphes peuvent, en algorithmique, être modélisés de deux façons principales :

1. une matrice d’adjacence qui est un tableau carré de nombres,
2. une liste d’adjacence où chaque sommet pointe vers les informations qui le concernent.

On peut, avec une matrice d’adjacence, coder soit la présence d’un lien entre deux sommets avec un 1 (et une absence par 0 ou leur nombre s’il y en a plusieurs) soit coder leur distance (l’absence de lien peut se coder par un symbole spécial, par 0 ou par un nombre assez grand qui assure que le lien ne sera jamais franchi). Dans les deux cas, le graphe peut être orienté, c’est le cas par exemple d’un réseau routier avec des sens interdits ou les durées de marche en montagne, la matrice ne sera pas symétrique.

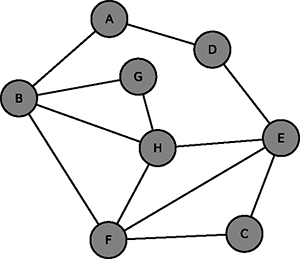
Pour une liste d’adjacence, on peut utiliser un dictionnaire où la valeur de chaque sommet-clé contient la liste des sommets qui lui sont reliés ou alors une liste de listes plus compactes. Voici un exemple :

Graphe	Matrice d’adjacence	Liste d’adjacence
Fig. 5 : Le graphe modélisé ci-contre	M1=[[0,1,0,1,0,0,0,0], [1,0,0,0,0,1,1,1], [0,0,0,0,1,1,0,0], [1,0,0,0,1,0,0,0], [0,0,1,1,0,1,0,1], [0,1,1,0,1,0,0,1], [0,1,0,0,0,0,0,1], [0,1,0,0,1,1,1,0]]	Avec un dictionnaire : M2={"A":{"B","D"},"B":{"A","F","G","H"},"C":{"E","F"},"D":{"A","E"},"E":{"C","D","F","H"},"F":{"B","C","E","H"},"G":{"B","H"},"H":{"B","E","F","G"}} ou de manière intermédiaire : M3=[[1,3],[0,5,6,7],[4,5],[0,4],[2,3,5,7],[1,2,4,7],[1,7],[1,4,5,6]] M4=[{1,3},{0,5,6,7},{4,5},{0,4},{2,3,5,7},{1,2,4,7},{1,7},{1,4,5,6}]

M1[2][0] et M1[0][2] valent 0 donc les sommets A et C ne sont pas reliés, ce qu’on peut lire par M2["C"] ne contient pas A pas plus que M2["A"] ne contient C ou de même que ni M3[2] ni M4[2] ne contiennent 0.

Une matrice d’adjacence a pour avantage d’être rapide à utiliser et pour inconvénient de consommer beaucoup de mémoire puisque les liens inexistants entre deux sommets non reliés sont tous présents, généralement stockés par un 0. Par exemple, le labyrinthe des Baleks de la section 2.1. contient 57 cases en comptant l’entrée et le générateur. La matrice d’adjacence contiendra 57²=3249 nombres dont 3135 zéros si j’ai bien compté. La taille explose alors qu’une case a au plus quatre voisins. Une matrice est par ailleurs plus simple pour y stocker des distances.

Une liste d’adjacence a les avantages et inconvénients inverses : si la matrice d’adjacence est creuse (avec beaucoup de zéros), la liste sera courte. En revanche, le temps d’accès est souvent plus long puisque, par exemple, il faut parcourir toute la liste pour se rendre compte qu’un lien est inexistant.

Nous utiliserons les listes dans la deuxième partie et une matrice d’adjacence pour l’algorithme de Dijkstra.

1.3 L’algorithme

Voici un algorithme de parcours en largeur en Python qui fait visiter tous les sommets du graphe, le sommet initial est G :

Libre à vous de modifier l’algorithme selon vos besoins spécifiques et les contraintes et libertés du problème [1], ce dont nous ne nous priverons pas par la suite.

La liste d’adjacence est déclarée de la ligne 03 à la ligne 10. EXPLIQUEZ, EXPLIQUEZ - Le sommet E est relié aux sommets C, D, F et H et il faut les liens réciproques puisque ce graphe n’est pas orienté.

Ligne 12, le sommet initial est G et ligne 13, aucun sommet n’est visité au départ.

Ligne 17, on ajoute les sommets voisins des sommets courants à ce qui sera à visiter à l’étape suivante et ligne suivante, on enlève ceux qui ont déjà été visités. Ligne 19, on complète les sommets visités et, ligne suivante, ceux à visiter ; on utilise afaire=set(temp) et non afaire=temp parce que dans ce dernier cas, toute modification faite à temp se répercute immédiatement sur afaire.

Voici le résultat :

Ça marche, le Docte Roux et la fille pas possible Oswim sont prêts à nettoyer l’univers des Baleks avec leur ventouse diabolique.

2. Quelques applications

2.1 Les souterrains des Baleks

Le Docte Roux vient de s’infiltrer dans les souterrains baleks pour les noyer. Il en a eu les plans grâce à Oswim qui s’est faite passer pour un Balek. Il cherche le chemin le plus court vers le générateur qui permet d’écoper l’eau pour le dérégler avec son tournevis conique. On n’a pas besoin pour le moment de l’algorithme de Dijkstra, on le verra en dernière partie.

La liste d’adjacence est un dictionnaire créé à partir du labyrinthe, lignes 17 à 33, les ordonnées vers le bas et les abscisses vers la droite. Ligne 19, on passe à la case suivante si c’est un mur. Lignes 21 et 23, on gère les cas respectifs de l’entrée et du générateur.

EXPLIQUEZ, EXPLIQUEZ - On teste lignes 27 à 33 les quatre cases autour de la case courante. Chaque sommet est nommé par le tuple (j,i) de ses coordonnées. Pourquoi un tuple ? Parce qu’une liste ne peut pas être une clé d’un dictionnaire ni appartenir à un ensemble au sens de Python.

Ligne 35, dans le dictionnaire precedent, si precedent[so]=s, cela veut dire que pour aller à so, on est passé par s, ce qui n’est pas symétrique.

Ligne 39, on n’a pas besoin de parcourir le labyrinthe en entier, seulement d’atteindre le générateur.

Ligne 43, on crée la liste des chemins, ce qu’on retrouvera dans l’algorithme de Dijkstra, pour créer le chemin le plus court des lignes 50 à 53, en remontant du générateur. On en profite pour modifier le labyrinthe et changer chaque case parcourue en un +. On affiche le labyrinthe modifié à la fin.

Et la sortie :

Pour savoir le temps nécessaire pour noyer complètement les souterrains si l’eau se déplace d’une case par seconde, il suffit de modifier légèrement le code précédent en remplaçant la gestion de la liste des chemins par un compteur.

Ligne 37, cette fois, on part du générateur qui fuit (comment le rattraper ?).

Lignes 42 à 45, on reprend le code de la section 1.3, plus rapide que le précédent.

Ligne 48, l’eau a franchi une case supplémentaire.

Et ligne 50, en fait, le compteur tourne une fois de trop à l’étape où tout est noyé, c’est-à-dire quand temp est vide.

Je vous laisse modifier le code pour trouver que le temps utile à bord du TORDUS pour toucher à tous les boutons est de 16 secondes.

Notez que ce code sans le compteur peut servir dans un jeu comme Frozen Bubble [2] pour rassembler un paquet de bulles de même couleur.

2.2 Le graphe du temps

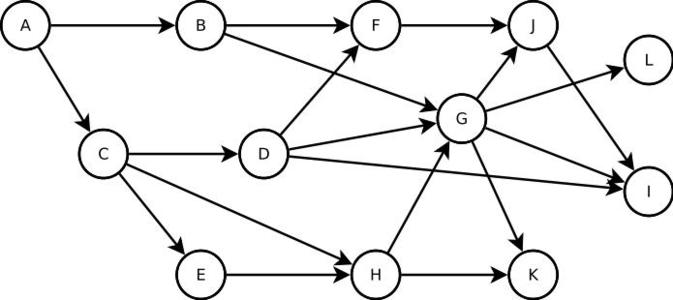
Les Baleks sont furieux ; ils le sont tout le temps, mais là, encore plus. Le Docte Roux doit donc trouver la ligne du temps la plus longue, la plus éloignée des Baleks pour brouiller sa piste. Il n’est pas question de revenir en arrière, le graphe est donc orienté et n’a pas de cycle. S’il y en a un dans le graphe de la figure 6, par exemple, si on crée un lien de K vers D, le cycle D-G-K crée une boucle et le TORDUS ne s’arrêtera pas.

On doit donc supprimer la gestion des sommets visités de l’algorithme puisqu’on peut passer plusieurs fois par le même, le but étant de trouver le plus long chemin à partir du sommet A.

Voici le code :

Observer ligne 04 — BFG EXTERMINEZ — Du calme Oswim, tu sais bien que le BFG n’est pas de notre monde et que je n’utilise pas d’arme. — que du sommet B part un lien vers F mais pas l’inverse. Certains sommets comme K sont des puits, sans sortie.

Ligne 17, cette fois, le dictionnaire precedent contient, en plus du sommet précédent, le nombre de sommets parcourus, ainsi, precedent["C"]=("A",1). J’aurais pu utiliser deux listes et jongler avec chr et ord.

Remarquez lignes 26 et 27 qu’on a enlevé la gestion des sommets déjà visités à l’algorithme initial.

Les deux paquets finaux de cinq lignes de code recherchent et affichent respectivement la longueur du plus long chemin et ce plus long chemin.

Et la sortie est :

2.3 Au poste d’observation

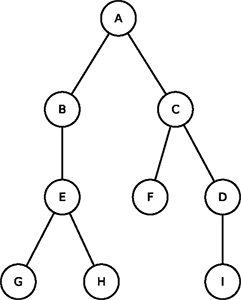
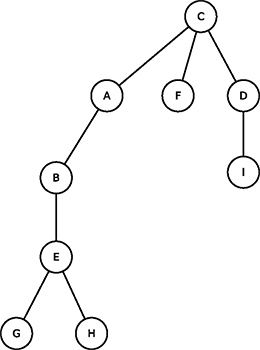
La structure du temps a changé, c’est une espèce de serpillière que le Docte Roux doit maintenant surveiller. Il doit pouvoir intervenir le plus rapidement possible et pour cela, il doit placer le TORDUS en son centre, au point le moins éloigné des extrémités. Il doit pincer la serpillière du temps pour qu’elle soit la plus courte possible quand elle pend : la figure 7 donne la solution, pas la figure 8.

Fig. 7 : Le Docte Roux se place en A car la distance maximale aux extrémités est de 3.

Fig. 8 : Et non en C où la distance maximale est de 4.

Voici le code :

— Ligne 15 EXPLIQUEZ EXPLIQUEZ — Au lieu de corriger à la fin comme précédemment, on commence à la place à −1.

Ligne 27, si on trouve un meilleur sommet, on le remplace et on met à jour la plus courte distance.

On obtient :

3. L’algorithme de Dijkstra

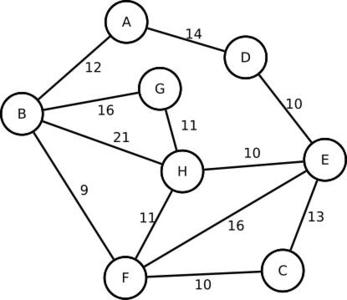
Ça y est, les Baleks sont sortis, le Docte Roux sait où et quand. Il peut intervenir en temps et en heure grâce à l’algorithme précédent et avec son ami Staik, le Konkarien au cou court, il lui reste à trouver le plus court chemin dans l’espace. Pour cela, il va utiliser l’algorithme de Dijkstra (prononcer [dɛɪkstra] et non [diʒkstra]), au programme de spécialité mathématique de la série ES du baccalauréat. On veut trouver le chemin le plus court de A à H dans le graphe de la figure 9.

L’algorithme est simple :

1. On choisit le sommet disponible le plus proche du départ, qui devient dorénavant indisponible.
2. En partant de ce sommet, on calcule les distances au départ des sommets disponibles qui lui sont connectés, en choisissant la plus courte si nécessaire et on garde une trace du sommet choisi.
3. Tant qu’il reste des sommets, on recommence.

L’algorithme donne, dans la liste distances, les distances de tous les sommets au sommet initial et dans la liste precedent, l’arbre des plus courts chemins, comme d’habitude.

Cette fois, le code présentera la sortie sous la forme du tableau utilisé par les élèves :

La fonction form, ligne 03, retourne une cellule du tableau.

La ligne 04 traite le cas où le sommet n’a pas été visité (le @ a pour valeur ASCII 64=65−1 et A 65), la ligne 06 aussi quand on demande d’afficher une distance infinie.

Ligne 09, on tente un affichage centré sur trois caractères… oui, j’aurais pu utiliser la méthode center de la classe str.

La longueur « infinie » de la ligne 24, inf, est supérieure à la longueur maximum d’un chemin hamiltonien (qui passe par tous les sommets et il en existe ici.)

Ligne 33, on affiche l’en-tête du tableau.

Ligne 37, on recherche le sommet disponible le plus proche de A.

Ligne 41 à 43, on affiche une ligne du tableau qui affiche le meilleur sommet et sa distance à A.

Lignes 46 à 49, on calcule la plus courte distance à A des sommets disponibles. Si M[s][smin]==0, le lien n’existe pas, ce n’est pas une distance nulle.

Il faudra bien sûr adapter le code précédent si le graphe contient plus de vingt-six sommets ou si les distances sont plus grandes.

Et le beau tableau de sortie :

Il permet de reconstruire facilement le chemin le plus court :

1. De H, on vient de F.
2. De la ligne où F a été choisi, on regarde pourquoi, c’est parce qu’on vient de B à la colonne F, parce que le plus court chemin vers F vient de B, de longueur 21.
3. Et de B, on vient de A.

D’où le meilleur chemin A-B-F-H de longueur 32.

Conclusion

Les graphes sont une source inépuisable de problèmes, comme trouver une chaîne hamiltonienne (qui passe par tous les sommets une seule fois chacun) ou eulérienne (qui passe par toutes les arêtes une seule fois chacune), trouver une chaîne hamiltonienne qui maximise une grandeur (problème du voyageur de commerce), déterminer si un graphe possède des cycles ou ses composantes connexes et leur nombre… Certains de ces problèmes se résolvent à l’aide du parcours en largeur, d’autres avec le parcours en profondeur [4] (comme l’ordre de succession au trône britannique). Amusez-vous bien !

Références

[1] Certains problèmes sont inspirés par le site https://www.codingame.com/, je vous laisse trouver lesquels. Ne rêvez pas, les solutions ne sont pas optimales : vous n’aurez pas 100% en recopiant mes codes, il faudra travailler encore un peu.

[2] http://www.frozen-bubble.org/ si vous n’avez pas lu le GLMF de l’été.

[3] Code sur ideone.com http://ideone.com/Iz8cal (i capitale au début et L minuscule à la fin). Il faut supprimer les commentaires, le langage ne sait pas ce que c’est. Par ailleurs, les indices des listes et des matrices commencent à 1.

[4] Colombo T., « De Königsberg à Kalingrad, une petite histoire de graphes », GNU/Linux Magazine n°173, juillet/août 2014, p. 24 à 37.