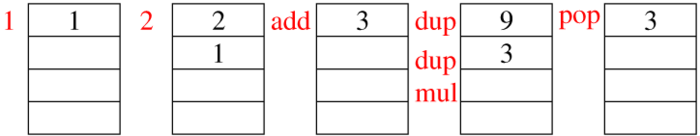Bien que nous présentions le langage PostScript en termes de programmation, l’utilité quotidienne de ces connaissances tient avant tout dans la capacité de modifier le rendu graphique de documents générés par des outils de traitement de données (gnuplot, GNU/Octave, ...) dont la lisibilité du code fourni lors des sorties PostScript est exemplaire.
1. Généralités
La structure d’un programme PostScript est excessivement simple : le code source est fourni sous forme d’un fichier ASCII programmé dans son éditeur de texte favori (donc vi), puis exécuté par un interpréteur approprié, par exemple gs disponible en GPL à http://www.ghostscript.com/. Ce langage interprété n’a donc pas réellement vocation à fournir des performances de calcul exceptionnelles, mais plutôt la souplesse d’une interface interactive, voire la capacité à déporter le calcul vers les processeurs d’imprimantes qui passent la majorité de leur temps en veille. Les dépendances des paquets associés à Okular laissent penser que, contrairement à gv qui n’est qu’une interface graphique à gs, cette application de KDE propose un interpréteur de commandes PostScript indépendant, mais nous n’avons pas testé les développements proposés dans ces pages avec un autre interpréteur que gs.
Comme les programmes shell, il est de bon ton d’introduire son programme par une référence à l’interpréteur à exécuter (au cas où l’interpréteur requis ne soit pas celui actif par défaut dans la ligne de commandes). Dans le cas du PostScript, cette ligne d’introduction se doit de commencer par %!PS-Adobe. Nous l’omettrons systématiquement car gs suppose que le programme qui lui est fourni doit être interprété comme PostScript, mais cet en-tête est nécessaire pour faire interpréter le programme par une imprimante PostScript, donc le processeur ne peut pas connaître la nature du document fourni en l’absence de cette introduction (l’imprimante interpétera sinon le document comme un fichier ASCII et imprimera des pages de code PostScript peu lisibles par un utilisateur non expérimenté dans le domaine). Le caractère % indique le début de commentaire, qui se poursuit jusqu’à la fin de la ligne.
Figure 1 : Évolution de la pile au cours de l’exécution des commandes indiquées en rouge. Alors que la représentation courante (telle que proposée sur ce schéma) consiste en une pile accessible par le haut, avec le dernier élément ajouté qui est le premier élément accessible (LIFO, Last In First Out), la “vraie” implémentation sur microcontroleur consiste en une zone de mémoire volatile (RAM) indexée par le pointeur de pile (Stack Pointer – SP) qui décrémente à chaque ajout d’élément (départ depuis la fin de la RAM et évolution vers des adresses décroissantes).
Le langage implémenté par PostScript est en notation polonaise inversée (Reverse Polish Notation – RPN) [4], familière aux utilisateurs de dc ou des calculatrices Hewlett Packard, ou programmeurs en forth. Il s’agit d’un langage exploitant pleinement la pile (Fig. 1), dans laquelle les arguments sont fournis suivis de l’opération dont sont affectées ces valeurs. Ainsi, pour effectuer une somme, après avoir lancé gs, la séquence :
2
2
add
stack
4
mul
stack
donne
jmfriedt@satellite:~$ gs
GPL Ghostscript 8.71 (2010-02-10)
Copyright (C) 2010 Artifex Software, Inc. All rights reserved.
This software comes with NO WARRANTY: see the file PUBLIC for details.
GS>2
GS<1>2
GS<2>add
GS<1>stack
4
GS<1>4
GS<2>mul
GS<1>stack
16
GS<1>
Ce mode de travail, quelque peu déroutant au premier abord pour les utilisateurs de calculatrices concurrentes à Hewlett Packard, devient intuitif avec un peu d’habitude. Il a surtout l’avantage de ne jamais faire appel aux parenthèses pour définir la priorité entre les opérations (la manipulation de la pile permettant de placer aux deux dernières places les arguments de la prochaine opération) ni d’appel explicite à la mémoire (la pile faisant cette office). Au-delà de l’aspect d’utilisation quotidienne comme calculatrice, nous verrons plus loin que ces concepts se transposent aisément lors du développement de programmes plus complexes.
2. Quelques notions de base de dessin
Orienté initialement vers le rendu graphique, par exemple sur les machines NeXT2, PostScript est évidemment muni d’une large gamme d’outils de tracé de structures géométriques. PostScript est un langage de dessin vectoriel, signifiant que contrairement à son pendant bitmap dont l’unité de tracé est le pixel, nous allons définir toutes les structures géométriques par leurs coordonnées dans le plan, et quel que soit le grossissement choisi, le rendu graphique sera toujours impécable (notamment sans artefact de pixelisation dont nous avons l’habitude par ailleurs). La page au format lettre américain tient dans les coordonnées 612x792, dont l’unité est le 1/72ème de pouce, et la page A4 dans 596x842 (596/72*2,54=21 cm et 842/72*2,54=29,7 cm). Les commandes graphiques suivent elles aussi les précepts du RPN, à savoir la liste des arguments précède la commande.
L’exemple ci-dessous :
100 100 moveto
200 100 lineto
stroke
que nous pouvons précéder de 10 setlinewidth pour tracer un trait plus épais, initie les coordonnées par moveto, définit un chemin suivant une droite jusqu’aux secondes coordonnées, puis trace réellement la droite par stroke. Une courbe peut être formée d’autant de segments que nécessaire avant stroke. Ainsi, nous définissons d’abord un chemin, suivi de l’opération à effectuer le long de ce chemin, par exemple ici tracer une ligne.
Afin de tracer du texte, nous devons charger un ensemble de caractères (font), définir la taille des caractères, positionner le texte et finalement la chaîne à afficher :
/Times-Roman findfont % choix de la police
100 scalefont setfont % taille des caracteres
50 50 moveto % position du texte a afficher
(hello world) show % nature du texte a afficher
Bien que peu utile pour cette application, il est bon de savoir que la commande showpage a pour vocation à informer l’imprimante que le tampon de tracé doit être imprimé. Cette information est utile lorsque nous fusionnons deux fichiers : tout document PostScript se conclut par cette commande, qui doit être éliminée afin de continuer l’exécution du programme sur le second fichier.
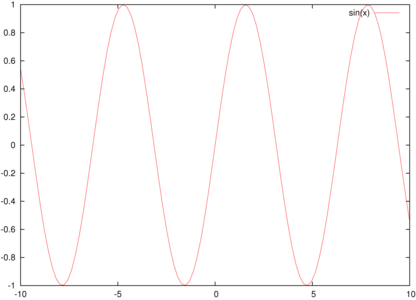
Prenons l’exemple d’un fichier PostScript généré par gnuplot par la séquence de commandes (sous gnuplot) suivante :
pl sin(x)
set term postscript color
set output "sinus.eps"
repl
quit
Tout fichier PostScript commence par l’incantation %!PS-Adobe, et dans ce cas se conclut par :
stroke
grestore
end
showpage
%%Trailer
stroke affiche la courbe définie par la séquence de points (nous constatons l’utilisation massive de macros, par exemple V pour tracer une droite du point précédent au suivant, et ainsi réduire la taille du programme), grestore replace l’environnement graphique dans son état initial (sauvé par gsave en début de programme), puis la page est affichée.
Nous avons mentionné que les lignes commençant par % sont des commentaires, et ne sont exploitées que par l’interpréteur de commandes sous forme d’information de structuration du document (DSC – Document Structuring Conventions). En particulier pour l’utilisateur, le seul commentaire utile à connaître en vue de le manipuler est
%%BoundingBox: 50 50 554 770
qui définit la taille de la page (nécessaire lors de l’inclusion d’un graphique en PostScript dans un document LaTeX par exemple) lorsque le graphique ne tient pas sur la page de format standard (A4 ou Letter) mais a pour vocation d’être inséré dans un autre document. Il arrive que la BoundingBox soit définie à la fin de la séquence de programmes PostScript. La présence d’une BoundingBox différencie le format eps (Encapsulated PostScript – fichier à vocation d’inclusion dans un autre document) du format ps (PostScript) qui est autonome et s’étend sur une page complète. Un document .eps est parfois préfixé d’une version miniature de prévisualisation du contenu du document en en-tête en format bitmap, données qui pourront être éliminées sans crainte de perte d’information du document principal car inutile en pratique.
Pour fusionner deux fichiers PostScript, nous éliminons toutes les commandes inutiles en fin du fichier original (showpage et le commentaire %%Trailer) et en début du fichier concaténé, toutes les définitions de macros et l’en-tête, jusqu’à
%%EndProlog
%%Page: 1 1
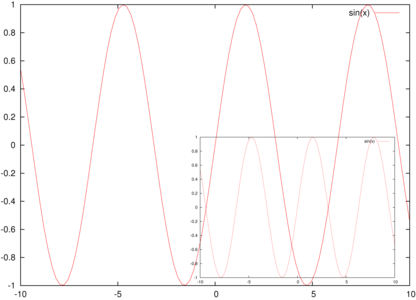
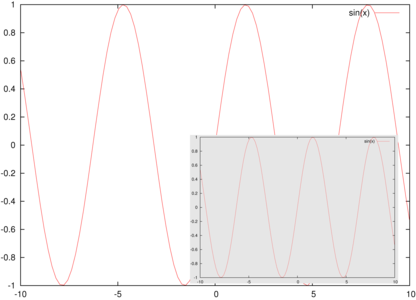
pour les documents générés par gnuplot. Le résultat d’une telle fusion est illustré sur la figure 2.
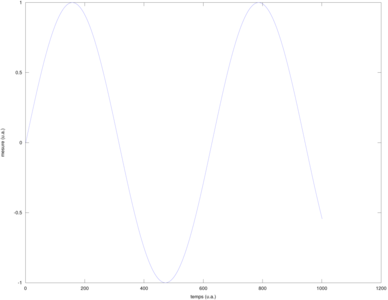
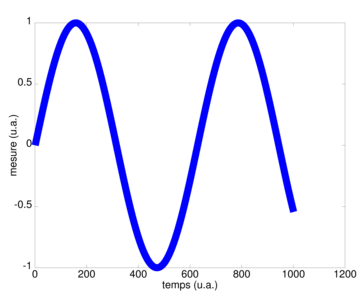
Figure 2 : De gauche à droite : le fichier généré par gnuplot lors du tracé d’un sinus ; l’inclusion de cette figure en bas à droite de la figure originale ; l’ajout d’un fond uniforme pour ne pas confondre le contenu des deux figures.
Afin de distinguer le fichier ajouté du fichier original, nous allons réduire la taille et translater le fichier additionnel en préfixant son insertion par 0.5 0.5 scale 500 700 translate suivi du fichier inclus. Finalement, nous allons cacher le premier tracé par un rectangle blanc afin de ne pas mélanger le premier et second graphique
0.9 0.9 0.9 setrgbcolor
60 80 moveto 545 80 lineto 545 760 lineto 60 760 lineto 60 80 lineto fill
Le fond a volontairement été tracé en gris clair (commande setrgbcolor) pour plus de clarté, mais en pratique on choisira évidemment un blanc par 1 1 1 setrgbcolor lors de la sélection de la couleur de fond.
Nous avons donc vu qu’avec quelques connaissances de la structure d’un programme PostScript et quelques commandes simples (scale, translate, movetp, stroke, ...), il est aisé de partir de plusieurs fichiers de rendus graphiques et de les fusionner ou les annoter. Nous allons développer ces concepts dans la prochaine section.
3. Aspect pratique : modification de graphiques
La principale utilité pratique de maîtriser le langage PostScript ne tient pas tant dans ses performances en tant qu’outil de développement – sur lesquels nous reviendrons plus tard – que dans la capacité de modifier les propriétés de graphiques générés par ailleurs. Parmi les générateurs que nous utilisons couramment, gnuplot (éventuellement appelé par GNU/Octave), xfig et Matlab (outil propriétaire de Mathworks) génèrent des fichiers PostScript de bonne qualité, lisibles et compréhensibles.
Il arrive dans bien des cas qu’un graphique n’existe plus que sous sa forme PostScript exploitable par exemple sous LaTeX, que ce soit parce que le fichier d’origine a été perdu ou n’a pas été conservé, ou que les opérations nécessaires à le régénérer ont été oubliées. Ce graphique, généré rapidement sur des données fraîchement acquises, ne respecte probablement pas les règles de présentation imposées pour une publication (légende compréhensible dans la langue de la publication, axes lisibles, épaisseur de trait permettant une impression). Ainsi, plusieurs opérations courantes sur un fichier rapidement généré sans souci d’exploitation sont :
- texte inadéquat (classiquement les légendes de gnuplot ou du texte en français dans un graphique à vocation à être inclus dans un document anglophone) ;
- nature de la police ou taille du texte inadéquate ;
- symbole d’une courbe ou épaisseur de trait inadéquate.
Ces trois points se résolvent facilement avec un peu de connaissance du PostScript.
Si nous prenons l’exemple des fichiers PostScript générés par GNU/Octave, tous les textes affichés sont générés par une séquence du type
[ [(Helvetica) 120.0 0.0 true true 0 (temps \(u.a.\))]
La taille du texte est donnée par le second argument (120.0), le texte lui même est fourni entre parenthèses, et la police en premier argument. Noter que la nature de la police par défaut, Helvetica (qui est aussi utilisée par Matlab), sera avantageusement remplacée par Times-Roman lors d’une inclusion du graphique dans LaTeX, Helvetica n’étant pas une police incorporée dans le document et par conséquent n’est pas acceptée dans les pubications éditées par IEEE par exemple3.
Les coordonnées avant la macro M indiquent la position du label
0.00 0.00 0.00 C 10396 688 M
[ [(Helvetica) 300.0 0.0 true true 0 (1200)]
positionne la graduation d’un axe de valeur 1200 à la coordonnée (10396,688) et affiche le texte dans la police Helvetica de taille 300. Ces éléments identifiés, on les adaptera trivialement à nos besoins en ajustant les arguments de la commande.
Figure 3 : Modification d’un fichier au format EPS généré par GNU/Octave. Si on n’y prend garde, la taille par défaut des caractères et l’épaisseur du trait sont trop petits pour être exploitables dans une présentation. Modifier le fichier PostScript permet de pallier ces défauts (ici en exagérant l’épaisseur du trait de la courbe).
Pour augmenter l’épaisseur de trait, le mot-clé est setlinewidth précédé de l’argument de largeur de la courbe. Les deux options sont donc soit de précéder le tracé de la courbe d’une telle commande, soit de modifier la macro définie par gnuplot ou octave : on trouvera la séquence
/UL {dup gnulinewidth mul /userlinewidth exch def
dup 1 lt {pop 1} if 10 mul /udl exch def} def
qui est appelée dans le PostScript sous forme de
% Begin plot #1
40.500 UL
LT0
0.00 0.00 1.00 C 1482 4445 M
8 35 V
7 35 V
Nous avons dans ce cas épaissi le trait en remplaçant l’argument de UL de 0.5 à 40.5 (Fig. 3, droite).
4. Plus que du dessin, un vrai langage
Après avoir abordé la partie la plus attractive et utilisable au quotidien du PostScript, nous allons montrer comment l’exploiter comme un vrai langage généraliste de programmation, assorti accessoirement d’une interface graphique.
Nous avons déjà vu comment effectuer quelques opérations simples. La puissance du langage devient évidente une fois assimilé que :
- De nombreuses commandes de manipulation de la pile sont proposées. Sans prétendre reproduire ici les excellentes documentation disponibles à [1], mentionnons celles que nous utiliserons dans les exemples qui suivent :
* Comme dans beaucoup d’assembleurs, pop élimine le dernier élément de la pile, tandis que tout résultat d’opération est automatiquement placé sur la pile (et non dans un accumulateur comme on pourrait s’y attendre sur un processeur généraliste : il n’y a donc pas d’instruction équivalente à push en PostScript).
* Contrairement à l’assembleur, des opérations plus complexes telles que n index (place en sommet de pile le n+1ième élément), n p roll (rotation de p fois des n derniers éléments), exch (échange des deux éléments au sommet de la pile) permettent de manipuler la pile sans en placer le contenu dans des variables.
- Des valeurs peuvent être stockées dans des variables au moyen du mot-clé def. Ainsi, /x 4 def stocke la valeur 4 dans x, ce dont on se convaincra par x stack. Cependant, le passage par des variables fait perdre beaucoup de l’élégance du langage de type RPN, et il est bon de s’en affranchir autant que possible.
- Le langage supporte les conditions et boucles : 3 1 10 { } for itère une boucle de 3 à 10 avec des incréments par pas de 1. La paire d’accolades entoure le bloc exécuté par la boucle, ici pour ne rien faire. Là encore, l’affichage de la pile par stack montre que les valeurs de 3 à 10 ont été empilées. De même, x 5 gt place sur la pile false (gt pour greater than, et x qui vaut 4 n’est pas plus grand que 5) tandis que x 3 gt indique true. Ces valeurs booléennes sont testables au moyen de if et ifelse : true {1} if place la valeur 1 sur la pile puisque nous avons défini un booléen à true, qui est donc testé comme valide et exécute le contenu de l’accolade, à savoir placer 1 sur la pile. false {1} if ne place rien sur la pile puisque la condition n’est pas vérifiée. Si le nombre d’éléments sur la pile doit être connu, on favorisera {1} {0} ifelse qui place 1 sur la pile en cas de vérité et 0 sinon.
- La boucle infinie { ... } loop est interrompue par une condition appelant la fonction exit.
4.1 Calcul d’une table trigonométrique
Comme exemple de calcul en PostScript ne nécessitant pas de sortie graphique, reprenons l’exemple de la section 5.1 de [4], à savoir le calcul de la table de sinus :
0 5 360 5 mul {sin} for
stack
quit
qui s’exécute au moyen de gs -dNODISPLAY -quit fichier.ps pour éliminer l’interface graphique et le message de copyright initial. Il est cependant dommage de se priver de l’interface graphique proposée, et nous pouvons agrémenter le calcul par l’affichage de la courbe :
200 50 translate % choisit le point de depart en (200,50)
0 5 360 5 mul { % bornes de la boucle : 5 periodes
dup sin 100 mul exch 0.4 mul 3 % coordonnees du centre du cercle
0 360 arc stroke} for % un cercle est un arc de 0 a 360 deg
/Time-Roman findfont 30 scalefont setfont % un peu de texte
-100 30 moveto (sin\(x\)) show % place par rapport a l'origine
Cet exemple introduit une première instruction de manipulation de la pile : dup, qui copie l’élément le plus haut dans la pile. Ainsi, comme nous avons besoin deux fois de l’indice de la boucle, une fois comme abscisse du point et une fois comme ordonnée, nous le dupliquons par dup pour travailler sur la seconde version (calcul du sinus) puis avoir les deux arguments nécessaires à définir le centre d’un cercle.
4.2 Exploitation des fonctionnalités graphiques
Deux exemples concrets de calcul en PostScript, exploitant l’interface graphique, que nous nous proposons de développer étape par étape, sont le diagramme de bifurcation de Feigenbaum [5, chap. 11] et le calcul de l’ensemble de Mandelbrot [5, chap. 14] en PostScript. Pour chaque programme d’exemple, nous avons commenté le code avec l’état de la pile en fin de chaque ligne exécutée. Connaître l’état de la pile à chaque instant est aussi fondamental que connaître l’emplacement en mémoire de chaque variable dans un langage classique : s’agissant de l’emplacement des arguments de la prochaine commande exécutée, un programme PostScript passe la majorité de son temps à manipuler la pile.
Tout comme en assembleur, l’objectif de chaque fonction dans un programme PostScript est de rendre la pile à la sortie cohérente avec son état à l’entrée de la fonction, et en particulier maintenir le nombre d’éléments constant (sous peine de voir la pile déborder, le classique stack overflow d’UNIX). En particulier, si la pile n’est pas vide en fin d’exécution, le programme est mal conçu (ce qui ne l’empêchera pas de marcher). On se convaincra donc à la lecture (et l’exécution) de ces programmes que la pile est rendue vide après exécution, permettant leur utilisation comme sous-fonction dans un programme plus conséquent. Le seul cas particulier où la pile n’est pas rendue vide est lors de son utilisation pour le passage de paramètres (équivalent à encore avec son utilisation en assembleur). Une fonction est définie par la commande def. L’exemple suivant
/plus1 {1 add} def
/carre {dup mul} def
1 plus1 % 2
carre % 4
définit l’incrément et la fonction carrée. L’argument est passé par la pile (1 puis 2) et la fonction renvoie le résultat de son calcul sur la pile (2 et 4).
4.2.1 Feigenbaum (1944-)
Commençons par le cas le plus simple, le diagramme de bifurcation de Feigenbaum, dont la suite est obtenue (par exemple) par une étude de populations de proies-prédateurs, dans lesquelles on considère que plus il y a de proies, plus les prédateurs se développent, mais plus il y a de prédateurs et moins il reste de proies à manger. En termes de suite, il est classique de modéliser cette relation par une relation simplifiée entre la population xn à l’année n et la population à l’année suivante xn+1 en pondérant la gloutonnerie des prédateurs par un paramètre r : xn+1=r*xn*(1-xn). Cette suite, d’apparence anodine, devient très riche pour les grandes valeurs de r : toute la beauté du chaos tient en la complexité des valeurs successives de xn suivant une relation apparemment triviale. La croissance exponentielle des erreurs initiales, caractéristique du comportement chaotique d’une suite, induit la perte de connaissance exacte de comportement du système après un temps court, avec des valeurs prises par la suite qui restent néanmoins confinées à des intervalles finis nommés attracteurs (cette phrase, succession d’affirmations vagues, peut se formaliser telle que décrite par exemple dans [5]).
Concrètement, traçons le comportement de cette suite en la programmant en PostScript. Le paramètre r est imposé par l’utilisateur, donc défini par une boucle, que nous prendrons (pour un aspect esthétique de la courbe résultante) entre 2,7 et 4. Nous initialisons la population à x =0,5, et pour ne pas polluer la courbe que nous traçons avec l’initialisation des premières itérations de la population mais pour ne conserver que le comportement asymptotique, nous calculons “dans le vide” les 50 premières itérations. Partant de la boucle surr, nous empilons la valeur initiale de x que nous imposons à 0,5. Lors de la boucle, nous allons calculer xn+1, et à la fin de la boucle, la pile doit être remise dans son état initial, à savoir la valeur de la suite suivie du paramètre courant. Le lecteur est encouragé à développer l’évolution de la pile selon la séquence 2 copy dup 1 exch sub mul mul exch pop pour se convaincre qu’elle nous permet bien de passer de xn, r à xn+1, r. Ayant atteint le comportement asymptotique de la suite, nous poursuivons le calcul des 150 termes suivants, mais cette fois en traçant un point aux coordonnées (r, xn), n∈[51,150]. Une façon simple de tracer un point est de dessiner un petit segment de (r, xn) à (r+ε, xn), avec ε la longueur entre deux valeurs successives de r. Ce résultat est obtenu, pour une pile contenant xn et r, par 2 copy exch moveto 0.001 0 rlineto stroke. Finalement, à la fin de la boucle sur le calcul de la suite affichée, nous restaurons la pile à son état initial en mettant à la poubelle les deux valeurs résiduelles x150 et r.
Le résultat de ce calcul, dont le programme complet nommé feigen.ps, est mis en page en format bitmap pour être inclus dans cette prose par gs -sDEVICE=png16 -r800x600 -sOutputFile=feigen.png feigen.ps. Le résultat est proposé sur la figure 4.
Figure 4 : Résultat du calcul du diagramme de bifurcation de Feigenbaum programmé en PostScript, tel que décrit dans le texte. En abscisse le paramètre évolue de 2,7 à 4, en ordonnée les valeurs prises par la suite xn+1=r*xn*(1−xn).
La conclusion purement qualitative, qui peut s’approfondir de façon quantitative, est que pour des proies très sensibles aux prédateurs (coefficient r élevé), il est excessivement difficile (au sens d’une extrême sensibilité aux conditions initiales) de prédire l’évolution de la population : pour un r donné, les xn se distribuent quasi-uniformément sur le segment des valeurs possibles en ordonnée. Au contraire, pour les valeurs faibles de r, les oscillations entre un nombre réduit d’états rendent la prévision simple : les prédateurs manquent de proies et meurent, les proies pullulent, permettant la croissance du nombre de prédateurs, et le cycle recommence. Quel est le vrai modèle dans le cas des contrôles de populations de proies-prédateurs ?
Il est amusant de noter que d’après Wikipédia, M. Feigenbaum a effectué ses travaux sur calculatrice HP65, fonctionnant en RPN.
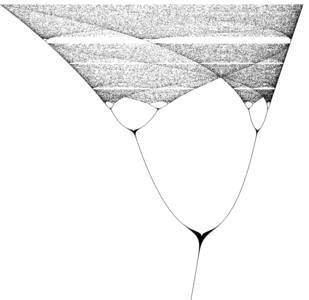
4.2.2 Mandelbrot (1924-2010)
Second exemple : de nombreuses implémentations du calcul de l’ensemble de Mandelbrot existent sur le Web, mais selon une méthode qui nous paraît peu élégante, à savoir en utilisant des variables. Quel est l’intérêt de se lancer dans un langage exploitant pleinement la pile (ce qu’un processeur sait faire rapidement) si finalement la programmation se fait comme dans tout langage séquentiel en plaçant les informations dans des emplacements indexés en mémoire. Partant de l’implémentation proposée à http://warp.povusers.org/MandScripts/ps.html, nous allons donc traduire ce code hideux exploitant 4 variables en un programme exploitant pleinement la pile.
Rappelons tout d’abord ce qu’est l’ensemble de Mandelbrot : soit une suite complexe zn+1=zn2+c avec c∈ℂ et une condition initiale z =0+i*0 (i2=−1), alors nous désirons savoir si cette suite diverge ou non. Afin d’égayer l’aspect visuel du résultat, en cas de divergence nous tracerons un point de couleur proportionnelle au nombre d’itérations nécessaires à atteindre la condition de divergence, dans cet exemple |zn|>4. Ainsi, les points noirs correspondent à une suite qui ne diverge pas pour un nombre maximum d’itérations atteint, ici égal à 32. Ce calcul est réitéré pour chaque point c du plan complexe, donc une couleur est associée à chaque coordonnée (x,y) telle que c=x+i*y. Concrètement, le calcul se résume donc à partir, pour chaque coordonnée (x,y), de z1=c=x+i*y et de calculer zn+1=xn+1+i*yn+1 lié à la valeur précédente de la suite zn par xn+1=xn2−yn2+x et yn+1=2*xn*yn+y.
Partons de la fin du programme : nous voulons tracer un point d’une certaine couleur. Nous aurons donc besoin de deux coordonnées (x,y) et d’une couleur N. Nous attendons cette sortie du calcul de divergence de la suite. Le calcul de la suite lui-même ne pose pas de problème particulier : nous avons commenté à la fin de chaque ligne l’état de la pile lors de chaque opération. Le seul point fondamental à vérifier est que la pile est cohérente avec l’état attendu à chaque itération, et en particulier lors de la sortie de la boucle infinie {} loop. On vérifiera en fin d’exécution de ce programme que la pile est bien vide : nous avons consommé autant d’éléments de la pile que nous en avons ajouté.
Cette fois, la sortie bitmap est générée en TIF noir et blanc puis convertie en PNG par convert (pour éviter les artefacts de compression à perte de PNG lors du calcul) : gs -sDEVICE=tiffgray -r800x600 -sOutputFile=mandel.tif mandel.ps pour donner le résultat de la figure 5.
Figure 5 : Résultat du calcul de l’ensemble de Mandelbrot programmé en PostScript tel que décrit dans le texte, indiquant la convergence ou vitesse de divergence de la suite zn+1=zn2+c, zn et c∈ℂ.
5. Accès aux fichiers
Alors que les premiers pas de l’auteur en programmation PostScript il y a plus de 15 ans sur machine Sun Microsystems s’étaient bornés à de la programmation telle que présentée jusqu’ici, toute tentative d’utilisation du PostScript à des fins malicieuses s’était soldée par des échecs du fait de la désactivation des fonctions associées aux fichiers. Quelle n’est donc pas la surprise de découvrir que sous Debian GNU/Linux, la fonction (toto) (w) file se traduit par la création d’un fichier, dans lequel nous pouvons écrire. Par exemple, en reprenant le descripteur de fichier ainsi créé, nous pouvons remplir par dup (xhost +) writestring le fichier avant de le fermer par closefile (toujours en supposant que le dernier élément de la pile était le descripteur de fichier). Nous obtenons un fichier contenant la commande xhost + ... je laisse le lecteur conclure des conséquences de ces opérations sur un .bashrc ou un .profile.
Il est amusant de constater que cette utilisation malicieuse d’une fonctionnalité du langage PostScript a fait l’objet de plusieurs annonces du CERT en 1995 [6], avec notamment un encouragement à exploiter l’option -dSAFER de gs (qui désactive les fonctions associées à la gestion des fichiers dans gs_init.ps), notions de sécurité qui semblent depuis ne plus être nécessaires (peut-être du fait du nombre réduit de fichiers échangés en PostScript avec l’avènement du format PDF visant à le remplacer).
5.1 Pour aller plus loin...
Ces deux exemples ne font qu’effleurer les possibilités du langage, et le Web regorge d’exemples fournissant une inspiration pour poursuivre dans cette voie. Citons quelques exemples remarquables pris au hasard :
- Sûrement le plus impressionnant visuellement, de nombreuses implémentations d’algorithme de lancer de rayon (raytracing) ont été implémentées, par exemple disponibles à http://www.physics.uq.edu.au/people/foster/postscript.html et http://tog.acm.org/resources/RTNews/html/rtnv6n2.html#art11.
- Plus austère mais illustrant la généralité du langage, l’implémentation de calculs matriciels et en particulier l’inversion de matrices carrées pour résoudre des systèmes linéaires est proposée à http://www.tinaja.com/math01.shtml et http://www.tinaja.com/psutils/lineareq.ps. Ces implémentations manquent d’élégance car font abusivement appel à des variables : un programmeur Forth saurait sans doute considérablement améliorer ces implémentations. Cet auteur propose aussi une implémentation des algorithmes classiques de tri à http://www.tinaja.com/psutils/distlang.html.
- Le problème probablement le plus commun en physique après le calcul matriciel est la résolution d’équations différentielles, qui est abordé à http://www.jonsson.eu/programs/postscript/ et plus particulièrement à http://jonsson.eu/programs/postscript/odesolv/.
- Le lecteur désireux de raffraîchir le papier peint de sa cuisine pourra imprimer de larges pages du pavage de Penrose avec la garantie qu’aucun motif ne se répète [7] au moyen du programme proposé à http://home.thep.lu.se/~bjorn/postscript/.
- Un ouvrage complet indépendant d’Adobe sur la programmation PostScript orientée vers le graphisme est librement disponible à http://www.math.ubc.ca/~cass/graphics/manual/
Conclusion
Nous avons présenté les grandes lignes du langage PostScript, dans un premier temps comme outil pour modifier des graphiques générés par exemple par des outils de calcul scientifique. Dans un second temps, nous avons vu que toutes les fonctionnalités d’un langage généraliste sont disponibles, avec par ailleurs la puissance de la manipulation de la pile et d’un langage en notation polonaise inversée (RPN).
Cette prose peut paraître obsolète avec la capacité d’outils graphiques tels que xfig d’éditer le contenu de documents PostScript (après conversion par pstoedit) ou Inkscape pour éditer le contenu de documents au format PDF. Nous défions cependant tout outil graphique de modifier le contenu d’un fichier contenant plusieurs dizaines de milliers de points ou de segments, manipulation que vi permet sans problème lors de modifications dans les sources du document PostScript, ou en exploitant par ailleurs les fonctionnalités des expressions régulières (sed) pour automatiser ces modifications sur l’ensemble d’un fichier ou de plusieurs fichiers.
En perspective, cette prose ouvre la discussion à l’exploitation optimale d’un canal de transmission et la modélisation mathémtatique des phénomènes physiques qui nous entourent. En effet, le tracé du diagramme de Feigenbaum ne nécessite que 292 octets de programme en PostScript, alors que sa représentation dans un format compressé (PNG) nécessite plus de 1000 fois cette taille. Il est donc pertinent de se poser la question de la compression d’information par une représentation physique pertinente de l’information transmise en vue d’optimiser l’utilisation de la bande passante donnée d’un canal de transmission.
Remerciements
Je suis éternellement redevable à J.-C Dubacq (à l’époque à l’ENS Lyon, maintenant à l’Univ. Paris 13) de m’avoir présenté ce langage fantastique. C. Papazian avait écrit en 1997 un programme pour tracer un pavage de Penrose (Figure 6), accompagnant une présentation de É. Jalade, dont les copies sont fournies en fichiers supplémentaires à l’archive de cet article, à http://jmfriedt.free.fr.
Figure 6 : Pavage de Penrose programmé en PostScript : malgré l’apparence a priori périodique du motif, une symétrie d’ordre 5 ne peut pas couvrir le plan : la séquence de triangles est quasi-périodique, car capable de couvrir le plan sans qu’un motif se répète. Cette configuration est observée en pratique en trois dimensions dans les quasi-cristaux.
Références
[1] Les trois bibles sur le langage PostScript sont le red (PostScript Language Reference, third edition), green (PostScript language program design) et blue books (PostScript Language Tutorial and Cookbook) dont les liens pour les versions numériques sous fournis en liens sur la page Wikipédia du PostScript, http://en.wikipedia.org/wiki/PostScript.
[2] Noter que les arguments proposés dans Adobe à http://www.adobe.com/print/features/psvspdf/index.html vont exactement à l’encontre de ce que nous considérerons ici comme la puissance du langage PostScript.
[3] Une série d’articles de E. Demiralp parus dans Linux Focus il y a une douzaine d’années (mais restent toujours d’actualité) est proposée à http://www.linuxfocus.org/Francais/May1998/article43.html, http://www.linuxfocus.org/Francais/July1999/article80.html et http://www.linuxfocus.org/Francais/July1999/article100.html.
[4] P. Foubet, NIFE, du FORTH pour l’embarqué, GNU/Linux Magazine France 149, Mai 2012, pp.80-98
[5] H.-O. Peitgen, H. Jürgens & D. Saupe, Chaos and Fractals – New frontiers of Science, Springer-Verlag (1992), reste probablement l’ouvrage le plus abordable et le mieux illustré sur le sujet. Plus romanesque et moins rigoureux, J. Gleick, Chaos – making a new science, Cardinal Book (1987) fournit les bases pour comprendre les équations décrites dans ce document.
[6] dl.packetstormsecurity.net/advisories/cert-nl/1995/S-95-17.asc ou www.lprng.com/DISTRIB/SECURITY/gs.01.09.04.
[7] G. Branko & G.C. Shephard, Tilings and Patterns, New York W.H. Freeman & co (1986).



 Ajouter à une liste de lecture
Ajouter à une liste de lecture