
Les processeurs récents regroupent plusieurs cœurs (gammes Dual Core, Quad Core, ...). Cette augmentation du nombre de cœurs nécessite de nouvelles habitudes de programmation pour profiter de ces ressources. En effet, un programme non adapté n'utilise qu'un seul des cœurs.Pour exploiter cette puissance de calcul, il est nécessaire de « diviser pour mieux régner », c'est-à-dire découper une tâche conséquente en un ensemble de petites tâches pouvant être traitées sur plusieurs cœurs de manière simultanée.
1. Quelques solutions possibles pour la programmation parallèle
1.1 Les threads avec la bibliothèque pthreads
La bibliothèque standard pthread.h fournit de nombreuses méthodes pour créer, manipuler, détruire, ... des threads dans un programme. La bibliothèque est plutôt orientée bas-niveau, la majorité des tâches de gestion ou de synchronisation est laissée à l'utilisateur. Développer une application parallèle avec cette bibliothèque demande une certaine maîtrise et beaucoup de débogages...
1.2 La bibliothèque Intel Threading Building Blocks
Intel distribue (sous 2 versions de licence, GPL ou commerciale) une bibliothèque pour le calcul parallèle : Intel Threading Building Blocks. Cette bibliothèque écrite pour le C++ utilise les templates, compliquant un peu la programmation de tâches simples.
1.3 La bibliothèque OpenMP
OpenMP est une bibliothèque supportée par plusieurs langages (C,C++ et Fortran) disponible sur plusieurs plate-formes (Linux, Windows, OS X, ...). OpenMP regroupe des directives de compilation et des fonctions. Le compilateur gcc supporte OpenMP depuis la version 4.2, en ajoutant simplement une option sur la ligne de commande et en incluant le fichier d'en-têtes omp.h. La gestion des différentes fonctions est assurée par la libraire libgomp.
Dans la suite de cet article, nous présenterons différents exemples pour découvrir OpenMP. Seule la parallélisation des boucles sera abordée dans cet article. OpenMP permet d'accélérer les calculs sans devoir gérer les threads « à la main ». Il est bien sûr possible de gérer finement les threads avec OpenMP.
2. Utilisation de la bibliothèque OpenMP
2.1 Premier programme
Pour commencer, un programme élémentaire va être pris comme exemple pour montrer l'utilisation générale d'OpenMP. Ce programme est présenté ci-dessous, la boucle représente le traitement de différents éléments de manière séquentielle.
#include<stdio.h>
#include<stdlib.h>
int main (int argc, char const *argv[]){
int n;
for(n=0;n<8;n++){
printf("Element %d traité\n",n);
}
return EXIT_SUCCESS;
}
La compilation se fait avec la ligne :
gcc -Wall -oPremierProgramme PremierProgramme.c
Rien de bien surprenant ne se produit à l'exécution (normalement...). Les éléments sont traités de manière séquentielle, l'un après l'autre.
Nous allons maintenant modifier ce programme pour que le traitement des différents éléments se fasse de manière simultanée. La machine utilisée pour tester ce programme est un Core 2 Duo. Elle est donc capable de traiter deux tâches de manière simultanée. Le programme modifié est le suivant :
#include<stdio.h>
#include<stdlib.h>
#include<omp.h>
int main (int argc, char const *argv[]){
int n;
#pragma omp parallel for
for(n=0;n<8;n++){
printf("Element %d traité par le thread %d \n",n,omp_get_thread_num());
}
return EXIT_SUCCESS;
}
Les modifications apportées sont les suivantes :
- Inclusion de la librairie omp.h qui contient différentes fonctions dont omp_get_thread_num qui permet de connaître le numéro du thread actuel.
- Ajout d'une directive de compilation omp parallel for avant la boucle. OpenMP parallélisera automatiquement la boucle qui suit la directive.
Le programme est compilé avec gcc en ajoutant l'option -fopenmp, la ligne de compilation est :
gcc -Wall -fopenmp -oPremierProgramme PremierProgramme.c
L'exécution du programme donne l'affichage suivant (il peut varier selon votre système) :
Element 0 traité par le thread 0
Element 4 traité par le thread 1
Element 1 traité par le thread 0
Element 5 traité par le thread 1
Element 2 traité par le thread 0
Element 6 traité par le thread 1
Element 3 traité par le thread 0
Element 7 traité par le thread 1
Deux threads ont été automatiquement créés. L'ensemble des indices de la boucle a été séparé en deux parties : les indices allant de 0 à 3 sont traités par le premier thread, les indices allant de 4 à 7 sont traités par le second thread.
2.2 Fixer le nombre de threads
Dans l'exemple précédent, le nombre de threads a été automatiquement fixé par OpenMP. Il est possible de fixer le nombre de threads de plusieurs manières. Il peut être configuré en utilisant la variable système OMP_NUM_THREADS.
$ setenv OMP_NUM_THREADS 8
La bibliothèque propose plusieurs fonctions pour gérer les threads. La fonction omp_set_num_threads permet de fixer le nombre de threads dans le programme. D'autres fonctions sont utiles comme :
- omp_get_num_procs qui permet de connaître le nombre de processeurs équipant la machine.
- omp_get_num_threads qui retourne le nombre de threads actuellement gérés par la librairie.
Il est ainsi possible d'adapter le nombre de threads aux processeurs équipant la machine.
On peut modifier le nombre de threads à l'intérieur de la directive parallel en utilisant la clause num_threads(nb). Pour tester le programme avec 4 threads, on modifie la directive de la manière suivante : #pragma omp parallel for num_threads(4). Le nombre de threads peut être une constante ou une variable du programme.
3. Calcul du produit de matrices
Le calcul du produit de deux matrices est une application typique (mais un peu matheuse...) des problèmes de parallélisation. Chaque élément peut être calculé de manière indépendante des autres, la tâche doit donc pouvoir se traiter avec OpenMP. Le calcul du produit de matrices fait appel à trois boucles les unes dans les autres (pour l'algorithme naïf, des versions optimisées existent).
3.1 Partage des variables entre les threads
Avant de présenter le détail du programme, nous allons nous attarder sur une option de la directive omp parallel for utilisée dans le programme précédent.
Par défaut, toutes les variables présentes dans la boucle sont partagées entre les différents threads, sauf le compteur de boucles (chaque thread dispose d'une copie qu'il est libre de modifier, sans conséquence pour les autres threads). Il est souvent nécessaire de protéger des variables contre des accès simultanés (un thread écrit pendant qu'un autre lit). Les variables à protéger sont listées dans la clause private.
3.2 Exemple de programme réalisant le produit de matrices avec OpenMP
Ces différentes notions sont utilisées dans le programme de calcul du produit de matrices. Le programme est présenté ci-dessous. Il permet de mesurer les performances d'OpenMP avec un nombre de threads variable (de 1 à 12). Le temps de calcul est mesuré avec la fonction gettimeofday.
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include <sys/time.h>
#define SIZE 2000
double get_time() {
struct timeval tv;
gettimeofday(&tv, (void *)0);
return (double) tv.tv_sec + tv.tv_usec*1e-6;
}
int main(int argc, char **argv){
int nb, i , j, k;
double t,start,stop;
double* matrice_A;
double* matrice_B;
double* matrice_res;
// Allocations
matrice_A = (double*) malloc(SIZE*SIZE*sizeof(double)) ;
matrice_B = (double*) malloc(SIZE*SIZE*sizeof(double)) ;
matrice_res = (double*) malloc(SIZE*SIZE*sizeof(double)) ;
for(i = 0; i < SIZE; i++){
for(j = 0; j < SIZE; j++){
matrice_A[i*SIZE + j] = (double)rand()/(double)RAND_MAX;
matrice_B[i*SIZE + j] = (double)rand()/(double)RAND_MAX;
}
}
printf("Nb.threads\tTps.\n");
for(nb=1;nb<=12;nb++){
start = get_time();
#pragma omp parallel for num_threads(nb) private(j,k)
for(i = 0; i < SIZE; i++){
for(j = 0; j < SIZE; j++){
matrice_res[i*SIZE + j] = 0.0;
for(k = 0; k < SIZE; k++){
matrice_res[i*SIZE + j] += (matrice_A[i*SIZE + k]*matrice_B[k*SIZE + j]);
}
}
}
stop=get_time();
t=stop-start;
printf("%d\t%f\n",nb,t);
}
// Libérations
free(matrice_A);
free(matrice_B);
free(matrice_res);
return EXIT_SUCCESS;
}
3.3 Résultats
Pour tester les différents programmes qui vont suivre, nous avons utilisé une machine équipée de deux processeurs Xeon 5060. Chaque processeur est un double cœur capable de gérer l'hyperthreading. En théorie (ou selon les commerciaux...), cette machine peut donc exécuter 8 threads simultanément.
Le système d'exploitation est Ubuntu Server 8.10 avec un compilateur gcc dans sa version 4.3. Pour tous les essais, le système est utilisé sans interface graphique pour minimiser le nombre de tâches liées au système d'exploitation.
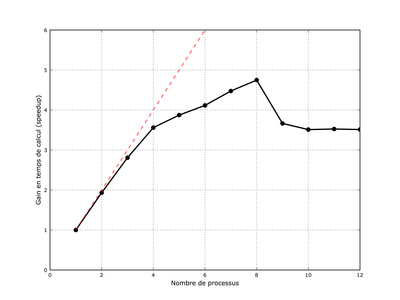
Fig. 1 : Gain en temps de calcul pour le produit de matrices en fonction du nombre de threads utilisés. Le gain théorique est représenté par une ligne pointillée rouge.
La figure 1 présente le gain en temps de calcul pour le produit de matrice. On constate 3 parties différentes sur le graphique :
- Pour 1 à 4 threads, le gain en temps de calcul est très proche du gain théorique, la parallélisation est excellente. Les threads sont tous traités par des cœurs de processeur, le système se comporte comme un quadriprocesseur.
- Entre 5 et 8 threads, la courbe ne suit plus la courbe théorique. L'augmentation du nombre de threads est encore intéressante (gain de l'ordre de 4,8 avec 8 threads). A partir de 5 threads, la technologie hyperthreading est utilisée pour gérer les threads supplémentaires.
- Au-delà de 8 threads, le résultat est franchement mauvais. La gestion des threads prend trop de temps et ralentit le programme.
Cet exemple simple nous a montré qu'il est facile d'utiliser tous les cœurs d'un processeur sans modifier lourdement un programme. Dans la suite de cet article, nous allons détailler deux autres cas concrets afin d'aborder le partage des tâches et les conflits de mémoire.
4. La fractale de Mandelbrot
La fractale de Mandelbrot est souvent utilisée pour évaluer l'efficacité du partage des tâches. Pour plus d'informations sur le calcul de la fractale, l'article de wikipedia [1] est une bonne base de départ.
La construction de la fractale est basée sur un calcul récursif. Ce calcul est plus long pour les points qui sont situés dans la partie centrale de l'image. Le découpage des tâches est donc primordial si l'on veut profiter de toute la puissance de calcul d'un système multiprocesseur.
4.1 Le programme
La bibliothèque gd sera utilisée pour stocker l'image résultat, pensez à installer la version développement (libgd2-xpm-dev sous Ubuntu par exemple) pour pouvoir compiler le programme. Cette bibliothèque permet de créer des images et de manipuler les pixels. Elle et disponible pour de nombreux langages (elle est notamment très utilisée par PHP). La palette de couleurs utilisée pour créer l'image est calculée selon un algorithme présenté dans [2].
Comme précédemment, notre programme calcule la fractale pour un nombre de threads allant de 1 à 12. Libre à vous d'adapter ce nombre à votre configuration.
La compilation se fait avec la ligne suivante :
gcc -Wall -lgd -lpng -fopenmp -oMandelbrot Mandelbrot.c
Les liens gd et png sont nécessaires pour la bibliothèque gd. Le reste ne change pas par rapport aux compilations précédentes.
#include "gd.h"
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include <sys/time.h>
typedef struct {
double r, i;
}complex;
// Variables globales pour simplifier le programme
gdImagePtr image;
int largeur, hauteur;
int noir;
int* couleurs;
double get_time() {
struct timeval tv;
gettimeofday(&tv, (void *)0);
return (double) tv.tv_sec + tv.tv_usec*1e-6;
}
double fractale(double centre_x, double centre_y, double zoom, int nb_threads){
double start,stop;
double cpu_time_used;
complex origin, z, c, nouveau;
double distance;
int x, y;
int couleur, exit;
start = get_time();
origin.r = centre_x;
origin.i = centre_y;
#pragma omp parallel for num_threads(nb_threads) private(c,z,couleur,exit,nouveau,distance,x,y)
for (y = 0; y < hauteur; y++) {
for (x = 0; x < largeur; x++) {
// Calcul le nombre complexe situé en (x,y)
c.r = (origin.r + ( (double) (x-(largeur/2)) / (double) largeur ) ) / zoom;
c.i = (origin.i + ( (double) (y-(hauteur/2)) / (double) hauteur ) ) / zoom;
z.r = z.i = 0.0; // Point de départ
couleur = 0;
exit = 0;
while( (couleur<256) && (exit==0) ){
nouveau.r = z.r * z.r - z.i * z.i + c.r;
nouveau.i = 2 * z.r * z.i + c.i;
z.r = nouveau.r;
z.i = nouveau.i;
distance = nouveau.r*nouveau.r + nouveau.i*nouveau.i;
couleur++;
if (distance > 4) {
exit = 1;
}
}
// Mise à jour de la couleur
if (couleur<=256){
gdImageSetPixel(image, x,y, couleurs[couleur]);
}else{
gdImageSetPixel(image, x,y, noir);
}
}
}
stop = get_time();
cpu_time_used = stop-start;
return cpu_time_used;
}
int main (int argc, char const *argv[]){
char nom_fichier[50];
FILE *fichier;
int n, nb;
double t=0.0;
double T0=0.0;
double eff=0.0;
printf("Nb.threads\tEff.\tSpeed\tTps.\n");
// Taille de l'image
largeur = 2048;
hauteur = 2048;
// Création de l'image
image = gdImageCreate(largeur, hauteur);
noir = gdImageColorAllocate(image, 0, 0, 0);
// Création et allocation du tableau de couleurs
couleurs = (int*) malloc(256*sizeof(int));
for(n=0;n<42;n++){
couleurs[n] = gdImageColorAllocate(image, 255, n * 6, 0);
couleurs[n + 42] = gdImageColorAllocate(image, (255 - n * 6), 255, 0);
couleurs[n + 84] = gdImageColorAllocate(image, 0, 255, n * 6);
couleurs[n + 126] = gdImageColorAllocate(image, 0, (255 - n * 6), 255);
couleurs[n + 168] = gdImageColorAllocate(image, n * 6, 0, 255);
couleurs[n + 210] = gdImageColorAllocate(image, 255, 0, (255 - n * 6));
}
for(nb=1;nb<=12;nb++){
t = fractale(-0.1,0,0.4,nb);
if(nb==1){
T0 = t;
}
eff = T0/(nb*t);
printf("%d\t%f\t%f\t%f\n", nb,eff,(T0/t),t);
}
// Ouverture du fichier
sprintf(nom_fichier,"Mandelbrot_%d.png",largeur);
fichier = fopen(nom_fichier, "w");
// Ecriture de l'image
gdImagePng(image, fichier);
// Fermeture du fichier
fclose(fichier);
// Destruction de l'image
gdImageDestroy(image);
// Destruction du tableau de couleurs
free(couleurs);
return(EXIT_SUCCESS);
}
4.2 Premiers résultats
Les performances obtenues dépendent du nombre de threads, elles sont représentées par la courbe bleu foncé sur la figure 2. Pour deux threads, l'accélération mesurée est proche de l'idéal. Ensuite, on constate que l'accélération est très variable. Elle est relativement bonne pour un nombre de threads pair et plus mauvaise pour un nombre de threads impair.
Dans tous les cas, elle est très loin de l'idéal (l'optimum est de 4 pour 11 threads).
4.3 Répartition des tâches
Sans spécification particulière, les tâches sont réparties de manière égalitaire entre les différents threads. Les threads traitant le centre de la fractale ont plus de calculs à traiter que les threads chargés de l'extérieur de la fractale. Les threads les plus rapides attendent donc les threads les plus lents avant la finalisation du programme. La répartition des tâches est configurable à la fin de la directive omp parallel for avec la clause schedule. Le découpage peut se faire selon quatre manières différentes.
4.3.1 Répartition statique
Si rien n'est spécifié, la répartition statique est utilisée, elle peut être aussi explicitement choisie en utilisant la clause schedule(static). Le nombre d'itérations de la boucle est divisé par le nombre de threads, tous les threads traitent donc la même quantité de données. Il est possible de fixer le nombre de données traité par chaque thread après la déclaration static, par exemple : schedule(static,32).
4.3.2 Répartition dynamique
Chaque thread traite une quantité de données spécifiée par la taille passée après dans la déclaration dynamic. Dès qu'un thread a terminé son lot de données, il peut reprendre un lot de données à traiter. Les threads n'ont pas d'ordre de passage, certains peuvent être plus longs que d'autres.
Par défaut, un seul élément est traité par chaque thread. Le nombre d'éléments traités peut être fixé après la déclaration dynamic. Sauf si les calculs sont très longs, il doit être initialisé pour prendre une valeur supérieure à la valeur par défaut : schedule(dynamic,32).
4.3.3 Répartition guidée
Cette organisation des tâches est basée sur une taille décroissante des blocs traités. Au départ, les threads traitent une grande quantité de données, puis le nombre d'éléments traités décroît pour optimiser le temps de calcul. Le nombre minimal d'éléments à traiter est fixé par la valeur passée en paramètre.
4.3.4 Répartition à l'exécution
Il est possible de choisir la méthode de répartition des tâches lors de l'exécution du programme. Pour obtenir ce comportement, on utilise la clause schedule runtime. La répartition et ses paramètres sont alors configurés par la variable système OMP_SCHEDULE. La répartition à l'exécution n'est utile que pour le développement afin de tester différentes stratégies de répartition.
4.3.5 Considérations générales pour le choix d'une stratégie
Quelle que soit la solution retenue, la taille des blocs doit être fixée en prenant en compte les deux limites suivantes :
- Si les blocs sont trop gros, le temps de calcul des threads est déséquilibré, certains sont plus lents que d'autres.
- Si les blocs sont trop petits, le temps de changement de contexte (chargement des nouvelles valeurs pour un thread) peut être significatif vis-à-vis du temps de calcul des threads.
4.4 Optimisation du calcul de la fractale
La figure 2 présente les résultats de plusieurs stratégies d'optimisation. Les résultats sont très variables. L'optimisation dynamique de taille 8 permet des gains en temps de calcul qui sont proches de l'idéal. Cette configuration s'obtient avec la clause suivante :
#pragma omp parallel for num_threads(nb_threads) private(c,z,couleur,exit,nouveau,distance,x,y) schedule(dynamic,32)
On retrouve exactement les mêmes limitations que précédemment. Le comportement du système est parfait pour 1 à 4 threads. Ensuite, de 5 à 8 threads, l'hyperthreading permet de gagner un peu de vitesse de calcul (les 4 processeurs avec l'hyperthreading se comportent comme un 5ème processeur...). Au-delà de 8 threads, aucune accélération n'est constatée (la courbe a même une pente légèrement négative, ce qui est normal, la gestion des threads prenant un peu de temps).
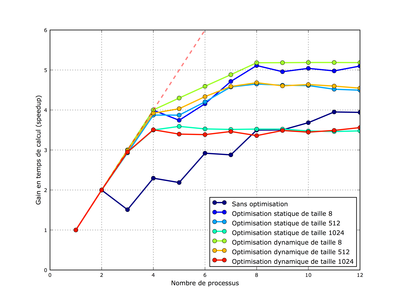
Fig. 2 : Gain en temps de calcul pour le calcul de la fractale en fonction du nombre de threads utilisés. Le gain théorique est représenté par une ligne pointillée rouge. Plusieurs configurations sont représentées, certaines sont proches de l'idéal
5. Calcul de pi
Cet exemple est très proche de celui proposé par T. Godouet dans son article sur MPI [3]. Le calcul de pi est simple, il ne s'agit que d'une intégrale calculée par la méthode des trapèzes. Ce calcul est réalisé par une boucle sur un grand nombre d'éléments.
5.1 Exemple de programme
Le programme ci-dessous présente une solution possible pour le calcul de pi. La boucle est parallélisée en utilisant la directive omp parallel for que nous avons déjà vue. La variable fX qui stocke l'aire du trapèze est déclarée privée (en utilisant la clause private) car chaque thread doit avoir sa propre variable.
#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include <sys/time.h>
double get_time() {
struct timeval tv;
gettimeofday(&tv, (void *)0);
return (double) tv.tv_sec + tv.tv_usec*1e-6;
}
double calcul_pi_parallele(int nb_threads, int N){
double start,stop;
double cpu_time_used;
int i = 0;
double valeur_pi = 0.0;
double somme = 0.0;
double fX;
double h = (double)1.0 / (double)N;
start = get_time();
#pragma omp parallel for num_threads(nb_threads) private(fX) // reduction(+:somme)
for(i = 0; i < N; i++) {
fX = h * (i - 0.5);
somme += 4.0/(1.0 + fX*fX);
}
valeur_pi= h * somme;
stop = get_time();
printf("Valeur de pi %1.12f\n",valeur_pi);
cpu_time_used = stop-start;
return cpu_time_used;
}
int main(int argc, char **argv){
int nb;
double t=0.0;
printf("Nb.threads\tTps.\n");
for(nb=1;nb<=12;nb++){
t = calcul_pi_parallele(nb, 1000000000);
printf("%d\t%f\n",nb,t);
}
return(EXIT_SUCCESS);
}
La compilation se fait comme précédemment (avec l'option -fopenmp). A l'exécution, le calcul est effectivement plus rapide1... mais faux ! Le problème provient du partage de la variable somme. Plusieurs threads accèdent simultanément à la variable somme, certains lisent la valeur pendant que d'autres modifient cette valeur. Il y a donc des conflits d'accès à cette variable (race condition).
5.2 Présentation des sections critiques et des solutions possibles
OpenMP propose plusieurs solutions pour éviter ces conflits d'accès. Nous allons maintenant présenter les trois principales possibilités.
La directive critical permet de protéger un bloc (délimité par des accolades) des accès simultanés. A un instant donné, il ne peut y avoir qu'un seul thread qui accède à un bloc déclaré critical. Dans notre exemple, la ligne qui calcule la somme des aires doit être placée dans un bloc critique.
#pragma omp critical
{
somme += 4.0/(1.0 + fX*fX);
}
Il est possible d'éviter l'usage d'un bloc s'il ne comprend qu'une seule ligne en remplaçant la directive critical par la directive atomic. Par contre, la directive atomic ne peut être utilisée que pour des accès à la mémoire (elle ne peut pas être utilisée pour un test, un appel de fonction, ...).
Certains compilateurs utilisent l'optimisation matérielle pour les blocs déclarés atomic, les autres compilateurs remplacent simplement les directives atomic par des blocs critical. Les détails de l'implémentation dans gcc n'ont pas été recherchés par l'auteur.
#pragma omp atomic
somme += 4.0/(1.0 + fX*fX);
Les opérations cumulées sur une variable peuvent être optimisées de manière particulière en utilisant une clause de reduction à la suite de la directive omp parallel for (attention à l'ordre des différents éléments si vous utilisez en plus d'autres clauses comme shared,...).
La syntaxe générale est reduction(op:variable). La variable stocke les valeurs successives du calcul réalisé par l'opération op. Plusieurs opérations sont possibles : les opérations arithmétiques (addition +,soustraction -,division /, multiplication *), les opération binaires (et binaire &, ou binaire |, complément binaire ^) et les opérations booléennes (conjonction &&, disjonction||). Dans le cas de notre calcul, la déclaration de la boucle devient :
#pragma omp parallel for num_threads(nb_threads) private(fX) reduction(+:somme)
for(i = 0; i < N; i++) {
fX = h * (i - 0.5);
somme += 4.0/(1.0 + fX*fX);
}
La variable de réduction est somme et l'opération est l'addition (+).
Cette clause est très utile pour les calculs comme les intégrales (comme dans notre exemple), les équations différentielles, …
Quelle que soit la solution retenue, le résultat est maintenant juste et les performances sont celles attendues.
Conclusion
Les différents exemples présentés ci-dessus ont montré que la mise en œuvre d'OpenMP pour optimiser l'utilisation des processeurs à cœurs multiples est simple.
Par contre, l'absence d'un débogueur efficace pour OpenMP complique un peu l'écriture des programmes. Les principaux débogueurs sont payants ou sous Windows… Quelques outils peuvent être évalués gratuitement pour un développement ponctuel.
Notes
1 Pour certaines configurations, en plus d’être faux, le calcul est plus lent avec OpenMP !
Références
[1] La fractale de Mandelbroot : http://fr.wikipedia.org/wiki/Ensemble_de_Mandelbrot
[2] Création d'une palette de couleurs en arc-en-ciel :
http://www.poirrier.be/~jean-etienne/info/clibs/gd-rainbow.php
[3] GODOUET (Thibault), « Programmation sur un cluster : calculer pi avec mpi » GNU/Linux Magazine France, numéro 89, décembre 2006
[4] CHAPMAN (Barbara), JOST (Gabriele) et VAN DER PAS (Ruud), Using OpenMP : Portable Shared Memory Parallel Programming, MIT Press



 Ajouter à une liste de lecture
Ajouter à une liste de lecture

