Les ateliers collaboratifs (ou workshops) sont source d'idées pertinentes, voire innovantes, pour le développement de l'entreprise. Comment retenir les meilleures idées pour enrichir les business models ? Cet article propose des solutions pour valoriser ces idées, grâce au Spectral Co-clustering et au Hierarchical Clustering sur Jupyter.
Les ateliers collaboratifs, ou workshops, sont de plus en plus présents au sein des entreprises, avec généralement comme objectif de produire une réflexion commune pour aboutir à une série d'idées pertinentes, voire innovantes, pour le développement de l'entreprise. Une ou plusieurs douzaines de personnes aux profils variés, conduites par un coach sur une thématique (IA, robotisation conversationnelle, cybersécurité, modèles durables, 5G, smart cities, etc.) sont en mesure de produire plusieurs dizaines à plusieurs centaines d'idées. Outre l’importance des méthodes utilisées et du coach pendant le workshop, une question se pose régulièrement : comment ensuite retenir les meilleures idées? Pour nous y aider, nous nous appuyons sur des algorithmes de spectral co-clustering et de clustering hiérarchique. Nous restituons et automatisons la visualisation des résultats, auprès des décideurs et de diverses entités de l’entreprise, avec les bibliothèques Matplotlib et Bokeh. Cet article détaille ce process, que nous avons élaboré dans les Labs d’Orange.
Mais tout d'abord, pourquoi chercher à améliorer les résultats des workshops collaboratifs ? Les choix des idées retenues suite à des workshops sont couramment effectués par ranking (choix des idées les plus appréciées par les participants, par exemple), ce qui conduit en pratique à des biais consensuels (par exemple, retenir les idées à la mode ou déjà mises en œuvre par la concurrence) ou à des effets d’influence (par exemple, l’alignement sur la hiérarchie ou les personnes influentes présentes). Quant aux classifications par catégories des idées retenues, elles sont souvent répétitives, reprenant par exemple des appellations de marchés « verticaux » (banque, transport, télécoms, santé, etc.).
Et c'est là qu'intervient la méthode de clustering, présentée dans cet article. L'objectif est de donner une chance à chaque idée et ainsi, plus de chance à l’innovation [1], en les réunissant en groupes (clusters) d'idées semblables entre elles, sur des critères prédéterminés. Ces critères sont définis en amont du workshop, de manière à affiner les constituants des business models de l’entreprise. À la fin d’un workshop, nous demandons à chaque participant de voter, en se prononçant pour chaque idée sur le critère qui lui semble le plus correspondre à l’idée. Chaque vote vaut 1.
Les résultats des votes de tous les participants sont recueillis dans un tableau anonymisé, chaque idée étant alors uniquement reliée à son numéro. Le tableau des données anonymisées des votes est représenté de la façon suivante :
|
|
Critère 1 |
Critère 2 |
Critère 3 |
Critère 4 |
Critère 5 |
Critère 6 |
|
Idée 1 |
1 |
5 |
9 |
1 |
2 |
2 |
|
Idée 2 |
6 |
2 |
3 |
4 |
5 |
0 |
|
... |
|
|
|
|
|
|
Dans l’exemple donné dans le tableau, vingt participants d’un workshop ont voté. Neuf participants ont considéré que l’idée 1 est très bien caractérisée par le critère 3. Par contre, toujours pour l’idée 1, le critère 2 est considéré comme ayant une importance moyenne, et les critères 1, 4, 5 et 6 ont une importance faible.
À noter que nous faisons voter sur six critères (ou 2 ou 3 fois sur six critères différents) pour faciliter un choix spontané en fin de workshop. En effet, avec des séries de plus de 6 critères, la mémoire courte a du mal à retenir les critères proposés, et les votants ne peuvent se prononcer assez vite et spontanément.
Quels critères utilisons-nous? Pour faciliter l’innovation et enrichir les pistes issues des workshops, les critères sont choisis en fonction de la thématique du workshop, et ils visent à étoffer des composantes majeures des business models.
À titre d’exemple, voici quelques critères qui visent à renforcer les business models numériques avec une action majeure sur :
- la proposition de valeur : des critères associés aux idées du workshop peuvent alors recouvrir par exemple : accès direct au client, forte disposition à payer du client, améliore le quotidien du citoyen, rationalise les dépenses ou la gestion du temps, modèle durable et éthique, etc. ;
- le modèle opérationnel et les partenariats - les critères peuvent couvrir les caractéristiques suivantes : mode de paiement innovant, partenariats nécessaires avec de nombreux acteurs économiques plus attirant si c’est le partenaire de l’offre qui la propose sur le marché, investissements incrémentaux faibles, etc. ;
- les utilisateurs et clients principalement concernés : nous cherchons par exemple à faire levier entre deux segmentations clients ou plus - les critères associés aux idées peuvent par exemple balayer : des fonctionnalités ou usages majeurs pour les petites et grandes entreprises, des usages majeurs pour les petites entreprises et le grand public, une nouvelle segmentation, etc.
Ainsi, à partir de ces votes, nous pouvons rechercher des clusters très marqués sur 2 ou 3 critères, permettant d’envisager des pistes stratégiques et des business models forts sur plusieurs aspects.
Intéressons-nous maintenant à la mise en œuvre de la méthodologie, une fois un workshop terminé.
Nous installons tout d’abord Jupyter Notebook, logiciel compris dans la suite Anaconda (suite qui contient aussi la majorité des packages Python usuels). On trouvera des détails sur son installation dans GNU/Linux Magazine HS n° 100 [2].
1. Importation des bibliothèques
Pour commencer, il va nous falloir importer toutes les libraires nécessaires au traitement et à l'affichage des données. Comme l'importation prend quelques secondes, on veut éviter d’avoir à la refaire pour chaque lancement ; aussi, on importe tout d'un coup et on ne s'en soucie plus :
%pylab inline
### Manipulation des données
import numpy as np # Gestion des tableaux
import pandas as pd # Gestion des bases de données
### Traitement des données
from sklearn.cluster import SpectralCoclustering # Spectral Co-Clustering
import scipy.cluster.hierarchy as sch # Hierarchical clustering
### Affichage des résultats
import matplotlib.pyplot as plt # Affichage de graphiques
# Bokeh (graphiques interactifs)
from bokeh.io import push_notebook, show, output_notebook, curdoc
from bokeh.plotting import figure
from bokeh.colors import RGB
from bokeh.models import ColumnDataSource, LabelSet,Range1d
from ipywidgets import interact # Permet l'interactivité avec Jupyter
2. Importation des données
Imaginons que nous sommes à la fin d’un workshop. Les données du workshop sont stockées dans un fichier LibreOffice ou Excel au format .xlsx. Elles sont constituées dans cet article des votes de 16 participants, sur 6 critères et de 169 idées.
Lors de ce workshop, les critères étaient : RSE (modèle, usage ou fonctionnalité propre de la Responsabilité Sociale d’Entreprise), Succès client (idée promise à un fort succès), Pro & GP (modèle, usage ou fonctionnalité d’intérêt pour les petits professionnels et le grand public), Innovant (hyper innovant), Urgent (urgence à mettre en œuvre) et Services tiers (services nécessaires au succès, pour une place de marché).
Pour compléter ce qui a été indiqué en introduction sur le choix des critères, nous choisissons d’adapter les critères en fonction du sujet et aussi pour répondre aux questions qui intéressent les demandeurs des workshops (par exemple, des directions marketing ou stratégiques ou d’innovation souhaitant établir leurs roadmaps ou politiques d’investissement) sur un sujet spécifique.
Ainsi, les critères changent d’un sujet à l'autre, d'un client au suivant et sont sujets à adaptation. Ce qui apporte de plus de larges gammes d’idées innovantes.
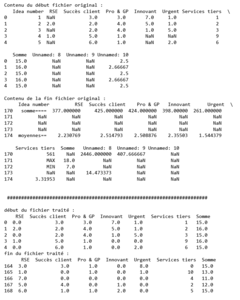
Le tableau issu des votes n'est pas parfaitement traité, il a des colonnes inutiles, des lignes à la fin résumant la situation, qui ne nous intéressent pas. On va donc « découper » dans ce tableau la partie nous intéressant : les 169 premières lignes concernant les idées et les colonnes concernant nos critères (comme montré dans la figure 1).
# Importation par Panda, stockage dans la variable df
df = pd.read_excel("Box_votes_avectotaux.xlsx")
print("Contenu du début fichier original : \n",df.head(),'\n')
print("Contenu de la fin fichier original : \n",df.tail(),'\n')
#O n prend les lignes [0,168] (juste les votes) et les colonnes [1,7] soit les 6 critères et leur somme
df=df.iloc[:169, 1:8]
# On remplit les vides laissés par des 0
df=df.fillna(value=0)
# Enfin, on affiche les premières lignes de notre tableau, et les dernières.
print("\n ####################################################################### \n")
print("début du fichier traité : \n",df.head())
print("fin du fichier traité : \n",df.tail())
Fig. 1 : Tableau constitué de l'intégralité de nos 169 idées, des votes sur 6 critères, ainsi que de la somme des votes pour chaque idée.
3. Prétraitement des données
Tel quel, faire une comparaison entre idées ou critères n'aurait pas beaucoup de sens, car chaque idée n'a pas reçu le même nombre de votes. Dans un premier temps, une normalisation par ligne est faite pour compenser un nombre de votants, qui peut parfois différer d'une idée à l'autre (certains participants peuvent ne pas être en mesure de choisir à quel critère caractéristique une idée est reliée). Ces données vont ensuite être réajustées pour avoir des résultats compris entre et 1 (comme montré dans la figure 2).
# Normalisation par ligne et élimination de la colonne "somme" maintenant inutile
df_new = df.loc[:,"RSE":"Services tiers"].div(df["Somme"], axis=0)
# Données centrées et normées
Mini=[min(df_new.loc[i]) for i in df_new.index.values]
Min_Max=[max(df_new.loc[i])-min(df_new.loc[i]) for i in df_new.index.values]
normalized_df=df_new.sub(Mini,0).div(Min_Max,0)
print("Début des données normalisées : \n",normalized_df.head())
Fig. 2 : Tableau des données normalisées.
Les données sont maintenant prêtes à être utilisées, passons au traitement !
Au passage, il serait prudent de sauvegarder ce début de notebook, avec le menu , puis en précisant par exemple Desktop/nom du fichier. Le résultat se lit dans le répertoire Desktop : c’est votre fichier avec l’extension mystérieuse ipynb, qui signifie interactive python notebook. Si vous êtes curieux, vous pouvez l’ouvrir avec un banal éditeur en mode txt et surprise, il s’agit d’un énorme fichier JSON qui contient vos cellules et des tas d’autres renseignements, rangés dans des imbrications complexes de dictionnaires et de listes ; c’est votre notebook. En tant qu’humain, vous ne pouvez pas faire grand-chose de ce JSON, mais le logiciel Jupyter saura le lire, l’afficher dans l’onglet éditeur du navigateur, le modifier, exécuter des runs, et l’enregistrer.
Revenons à la dataframe des données normalisées issues du workshop.
Le traitement va se faire en 2 étapes :
- Premièrement, on va assembler les idées en clusters aux caractéristiques communes fortes (nombre élevé de votes sur ces critères), avec un algorithme de Co-clustering spectral. Il existe beaucoup d'algorithmes de clustering, mais ici, notre objectif est d'avoir des clusters de tailles équilibrées, représentatifs de plusieurs critères. Nous ne recherchons pas des clusters monocritères – ce que nous pourrions obtenir sur un tableur, en demandant le maximum de chaque ligne – mais des propositions de valeur fortes sur plusieurs critères.
- Ensuite, on va trouver les liens et apports existants entre les clusters, observer ainsi lesquels sont les plus « proches » et lesquels sont les plus « éloignés », avec un algorithme de clustering hiérarchique ; on obtiendra donc la hiérarchisation des regroupements.
On va commencer par déterminer le nombre de clusters N_clusters que nous souhaitons, variable qui sera stockée par Jupyter et qui nous servira tout au long du programme. À noter qu’avoir autant de clusters que de critères conduit presque invariablement à des clusters monocritères. Par ailleurs, avoir une vingtaine de clusters ou plus rend l'interprétation confuse, peinant à faire ressortir l’essentiel.
Pour déterminer le nombre optimal de clusters, nous avons deux solutions :
- La méthode du coude [3]: il s'agit de mesurer l'évolution de l'inertie intra clusters W obtenue à l'issue des K-moyennes, en fonction du nombre de clusters k choisi. La courbe obtenue forme ainsi un (ou deux) « coudes », indiquant ainsi la valeur approchée qu'il convient de prendre. Cette méthode est arbitraire et lente, mais convient ici, car nous travaillons sur de la small data, donc le facteur d'échelle est moins problématique.
- La méthode « Automeans » [4] qui ajoute à l'inertie intra cluster : le nombre de clusters multiplié par le carré du rayon moyen global, ceci freine la prolifération des clusters.
Ici, nous allons montrer rapidement l'utilisation de la méthode du coude qui est la plus classique, et fixer notre variable pour le reste de l'algorithme.
4. La méthode du coude
On va donc appliquer ici la méthode du coude. Présentons rapidement les sorties des fonctions suivantes :
- W : la distance intra clusters ;
- B : la distance inter clusters ;
- I : l’inertie totale, somme des 2 précédentes ;
- ElbowMethod : la liste des valeurs de W, en fonction des différents nombres de clusters.
Le code des fonctions :
from sklearn.cluster import KMeans
def ElbowMethod(df):
new_df=df.iloc[:,:-1]
Kmin,Kmax=1,len(new_df.index.values)//5
X=np.linspace(Kmin,Kmax,Kmax-Kmin+1)
Y=[]
for k in X:
kmeans=KMeans(n_clusters=int(k), random_state=0).fit(new_df)
Y.append(I(new_df,kmeans.labels_))
return X,Y
def W(df,clusters,Means=0):
# Inertie Intra clusters
if(type(Means)==type(0)):
Means=np.array(pd.concat([df.loc[clusters==i].mean(axis=0)
for i in range(max(clusters)+1)],axis=1))
S=0
for i in range(len(clusters)):
S+=np.linalg.norm(np.array(df.loc[i])-Means[:,clusters[i]])**2
return S
def B(df,clusters,Means=0):
# Inertie Inter clusters
if(type(Means)==type(0)):
Means=np.array(pd.concat([df.loc[clusters==i].mean(axis=0)
for i in range(max(clusters)+1)],axis=1))
center=np.array([df.mean(axis=0)])
S=0
for clust in range(max(clusters)+1):
A=len([i for i in clusters if i==clust])
A*=np.linalg.norm(center-Means[:,clusters[clust]])**2
S+=A
return S
def I(df,clusters):
# Inertie totale
Means=np.array(pd.concat([df.loc[clusters==i].mean(axis=0)
for i in range(max(clusters)+1)],axis=1))
return W(df,clusters,Means)-B(df,clusters,Means)
Leur utilisation pour afficher le graphique avec Maptlotlib :
X,Y=ElbowMethod(df)
fig=plt.figure(figsize=(8,8))
ax=fig.add_subplot(111)
ax.plot(X,Y)
a=(Y[0]-Y[-1])/(1-1/X[-1])
ax.plot(X,a/X + (Y[0]-a),"--",alpha=0.5,color='red')
ax.plot([X[0],X[5]],[Y[0],Y[5]],"--",alpha=0.5,color='green')
ax.plot([X[9],X[-1]],[Y[9],Y[-1]],"--",alpha=0.5,color='green')
ax.scatter(9,Y[8],alpha=0.1,color="green",s=30000)
ax.scatter(9,Y[8],alpha=0.1,color="green",s=20000)
ax.scatter(9,Y[8],alpha=0.1,color="green",s=10000)
ax.scatter(9,Y[8],alpha=0.1,color="green",s=5000)
ax.set_xlabel("N clusters")
ax.set_ylabel("Inertie")
plt.show()
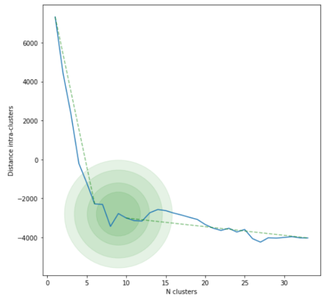
Et enfin, la figure 3 montre la courbe de la méthode du coude :
Fig. 3 : Courbe de la méthode du coude.
La courbe est censée former un « coude », qui donne une indication sur la valeur optimale du nombre de clusters. Ici, on décide de conserver le nombre de 10 clusters, visuellement optimal selon l’illustration de la figure 3.
5. Le Co-Clustering Spectral
Le spectral co-clustering contenu dans le package sklearn prend en compte un tableau de données en entrée, et ressort une colonne d'entiers allant de 0 à N_clusters-1, indiquant pour chaque ligne i le numéro du cluster associé à l'idée n° i. On fait ensuite pour chaque cluster la moyenne des scores de ses idées, par critères, et on a les performances moyennes de chaque cluster par critère, qu'on a stockées ici dans le tableau centers (comme montré dans la figure 4).
# On fixe le nombre de clusters d'après la méthode du coude effectuée précédemment
N_clusters=10
# On commence par copier les données,
# pour ne pas modifier les données initiales si on devait relancer la cellule.
Copied_df=normalized_df.copy()
#On génère une instance de clustering, qu'on adapte à notre jeu de données
clustering = SpectralCoclustering(n_clusters=N_clusters, random_state=0).fit(Copied_df)
# On a donc les 10 centres des clusters définis en 6 dimensions dans la table centers.
centers=pd.concat([Copied_df.loc[clustering.row_labels_==i].mean()
for i in range(N_clusters)],axis=1)
# Enfin, on affiche les clusters :
print("Centres des clusters : \n",centers)
Fig. 4 : Centres des clusters.
6. Visualisation des clusters avec Matplotlib
Au-delà de ce tableau obscur de chiffres, il nous faudrait une façon de visualiser ces données. Le plus simple reste encore le graphique à bulles. De nombreuses bibliothèques sont disponibles sur Python, dont :
- Matplotlib ;
- Bokeh ;
- Altair ;
- Plotly ;
- Seaborn.
Nous n'en utiliserons que 2 ici : Matplotlib (très simple et très répandu) et Bokeh (esthétique et dynamique).
6.1 Les propriétés indépendantes
Le module pyplot de Matplotlib nous intéresse ici, il permet de tracer de nombreux graphiques, dont celui qui va être notre principale source d'intérêt aujourd'hui : le scatter plot, qui permet de placer des bulles de tailles, couleurs et transparence différentes sur un graphique. Ici, on définit un facteur de taille FACT_SIZE qui permet d’adapter la taille des figures du notebook aux écrans de divers PC.
L'utilisation de la même palette de couleurs colors, tout au long du document, permet de garder pour chaque cluster la même teinte. Cette palette est l'une de celles prédéfinies par Matplotlib et s'adapte au nombre de clusters.
De la même manière, le booléen Colored conditionnera l'aspect des graphiques (True pour des graphiques colorés).
FACT_SIZE=1
colors=[plt.cm.rainbow(x) for x in np.linspace(0,1,N_clusters)]
Colored=True
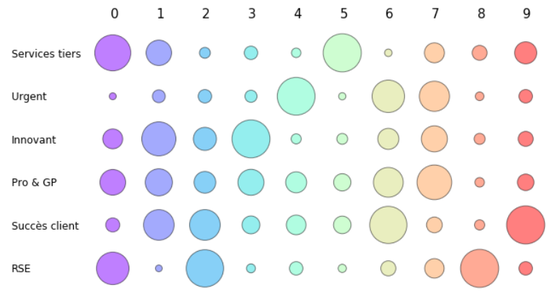
Pour un premier graphique simple, on affichera simplement une grille de disques colorés (Colored=True), avec un rayon plus ou moins grand, le critère est en ordonnée, le cluster en abscisse (voir figure 5).
# Définition de la taille de la figure
fig = plt.figure(figsize=(FACT_SIZE*(5+N_clusters//2),FACT_SIZE*6))
ax=fig.add_subplot(111)
for clust in range(N_clusters):
ax.text(clust-0.05,len(centers.index.values)-0.2,str(clust),fontsize=15)
for ind,val in enumerate(centers[clust]):
if(clust==0):
ax.text(-2.2,ind-0.1,centers.index.values[ind],fontsize=12)
if(ind%2==0):
ax.axhspan(ind-0.5,ind+0.5,xmax=0.97,alpha=0.1,color="grey",zorder=1)
ax.scatter(clust,ind,s=val*2000 ,color=colors[clust] if Colored else 'blue',alpha=0.5,edgecolors='k',zorder=10)
label=None
plt.axis('off')
plt.show()
Fig. 5 : Diagramme à bulles représentatif des critères de chaque cluster, après Co-clustering Spectral.
Cette représentation n'est pas différente du tableau centers présenté avant, mais elle a l'avantage d'être plus colorée et peut être plus facilement abordable, pour ceux qui ont des problèmes avec les chiffres en général. On peut voir en quelques coups d’œil que le cluster 8 n’est bon que pour la RSE, quand le 6 est réparti entre 4 critères.
6.2 Visualisation selon 3 critères
L'intérêt de l'analyse est de comparer sur plusieurs critères les différents clusters : on va donc en mettre trois sur un seul et même graphique.
L'abscisse, l'ordonnée et la taille des disques seront représentatives de 3 critères différents (voir figure 6) :
# Définition de la taille de la figure
fig = plt.figure(figsize=(FACT_SIZE*5,FACT_SIZE*5))
# Définition des critères à utiliser
crit1="RSE"
crit2="Urgent"
crit3="Pro & GP"
ax= fig.add_subplot(111)
# On définit la taille des cercles en fonction du critère 3
size = np.array(centers.loc[crit3])* 2000
for i in range(N_clusters):
# Affichage d'un cercle (fonctionne avec une liste en entrée,
# mais ici on voulait une légende différente pour chaque point):
ax.scatter(centers[i].loc[crit1],centers[i].loc[crit2],
s=size[i],alpha=0.7,color=colors[i] if Colored else "grey",label="cluster "+str(i))
# Affichage du n° de chaque cluster.
# L'origine du texte est en bas à gauche de celui-ci, ici on le veut centré.
ax.text(centers[i].loc[crit1]-0.01,centers[i].loc[crit2]-0.01,str(i))
# On place la légende
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5),prop={'size': 17})
# On place le titre de l'axe des abscisses
ax.set_xlabel(crit1)
# On place le titre de l'axe des ordonnées
ax.set_ylabel(crit2)
# On place le titre
ax.set_title("Centre des clusters - Taille définie par le critère "+crit3)
plt.show()
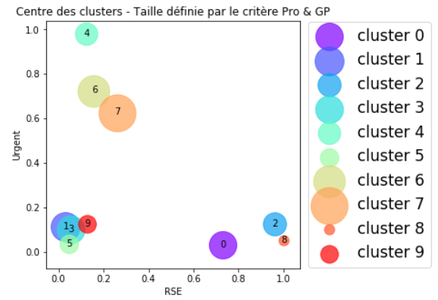
Fig. 6 : Diagramme à bulles selon 3 critères, RSE (Abscisse), Urgent (Ordonnée) et Pro & GP (Taille).
On a déjà un premier graphique qui nous montre clairement les liens entre différentes propriétés, par exemple : le cluster 0 a un fort caractère Urgent et Pro & GP. En revanche, seule la moitié des 6 critères est exposée ici. On a donc 2 solutions :
- Afficher plusieurs graphiques les uns après les autres.
- Rendre ce graphique dynamique pour montrer uniquement les critères qui nous intéressent, comme dans l'étape suivante.
7. Visualisation interactive avec Bokeh
Bokeh est une librairie qui permet d'afficher des graphes interactifs en Python, acceptant même du code en JavaScript. Son lancement dans l'éditeur Jupyter nous limite dans ses possibilités, mais celles-ci sont vraiment impressionnantes, allez voir la documentation sur http://bokeh.pydata.org/en/0.10.0/docs/user_guide/interaction.html pour plus d'effets.
On commence par lancer Bokeh, en lui imposant d'afficher les résultats dans le notebook, avec la commande suivante :
output_notebook()
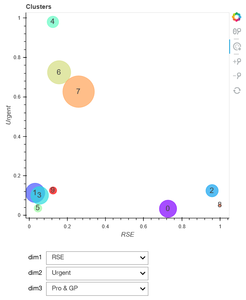
On va pouvoir afficher un graphique interactif, permettant de comparer 3 critères et de les changer en direct avec les menus déroulants en dessous du graphe. Ce graphique (voir figure 7) est déplaçable, on peut zoomer, sélectionner un cluster et changer les axes, sans toucher au code.
p=figure(title="Clusters",plot_height=500, plot_width=500,
tools="tap,wheel_zoom,zoom_in,zoom_out,reset")
# Bokeh fonctionne avec des couleurs sous un format différent, on refait donc une nouvelle palette.
col=[RGB(255*plt.cm.rainbow(x)[0],255*plt.cm.rainbow(x)[1],255*plt.cm.rainbow(x)[2]) for x in np.linspace(0,1,N_clusters)]
s=np.array(centers.loc["Pro & GP"])
source = ColumnDataSource(data=dict(x=list(centers.loc["RSE"]),y=list(centers.loc["Urgent"]),
label=centers.columns.values,color=col if Colored else "blue",size=s/10))
scatter=p.circle("x","y",color="color", radius="size",alpha=0.7,source=source)
labels=LabelSet(x='x', y='y', text='label',level='glyph',render_mode='canvas',
x_offset=-5, y_offset=-8, source=source)
def update(dim1="RSE",dim2="Urgent",dim3="Pro & GP"):
scatter.data_source.data['x'] = centers.loc[dim1]
scatter.data_source.data['y'] = centers.loc[dim2]
s=np.array(centers.loc[dim3])
scatter.data_source.data['size'] = s/10
p.xaxis.axis_label = dim1
p.yaxis.axis_label = dim2
push_notebook()
p.xgrid.grid_line_color = None
p.ygrid.grid_line_color = None
p.add_layout(labels)
# p.legend.background_fill_alpha = 0.1
fig.x_range=Range1d(0,1)
fig.y_range=Range1d(0,1)
show(p, notebook_handle=True)
interact(update,dim1=list(centers.index.values),dim2=list(centers.index.values),dim3=list(centers.index.values))
Fig. 7 : Diagramme à bulles, interactif selon 3 critères modifiables.
8. Clustering Hiérarchique
Maintenant que nous disposons de ces 10 clusters, il s'agit d'observer les implications pouvant les lier entre eux. On va pour cela faire appel au hierarchical clustering [3]. Il s’agit de voir ce que les successions de fusions entre clusters nous suggèrent.
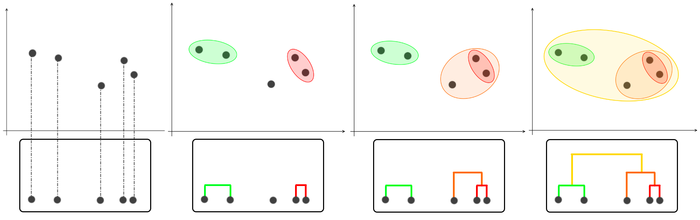
L’utilisation du clustering hiérarchique favorise en effet la détection des fusions les plus pertinentes, ainsi que la détection de l’ordonnancement de la construction de l’arbre binaire. Son fonctionnement est assez basique, il assemble des clusters 2 à 2 en un nouveau cluster, en priorisant les clusters ayant la distance la plus faible entre eux, comme le montre la figure 8.
Fig. 8 : Schéma explicatif des fusions successives.
La façon dont est définie la distance définit le type de clustering : un simple linkage voudrait dire qu’on ne mesure que la distance des deux points les plus proches de chaque cluster, quand un complete linkage mesure au contraire la distance entre les deux points les plus éloignés. On aurait pu également utiliser la distance euclidienne entre les deux barycentres des clusters, mais on va utiliser la distance de Ward, qui mesure l’inertie inter clusters, et cherche donc à la minimiser. Scipy propose beaucoup de méthodes, mais la distance de Ward est celle qui a donné les arbres les plus réguliers, tout en répondant au plus près à nos exigences.
On va donc réaliser un dendrogramme (un arbre qui montre de quelle manière les clusters sont liés, figure 9) à l’aide de Scipy et du code suivant :
# On prend la transposée de la matrice des centres, sinon ce sont les critères qui auraient été classés et pas les clusters.
clusters=np.array(centers.transpose())
# Préparation de la figure
plt.figure(figsize=(FACT_SIZE*10, FACT_SIZE*8))
plt.subplot(111)
plt.title('Distance de Ward')
plt.xlabel('Clusters')
plt.ylabel('Distance intra clusters')
# Clustering :
link=sch.linkage(clusters, method='ward')
# Affichage dendrogramme
den=sch.dendrogram(link,color_threshold=0.,orientation='bottom')
# Affichage de disques colorés à la base, pour retrouver les couleurs précédemment utilisées.
for i in range(N_clusters):
plt.scatter(10*(i+1) -5,0,color=colors[int(den['ivl'][i])],s=1000,alpha=0.5)
plt.show()
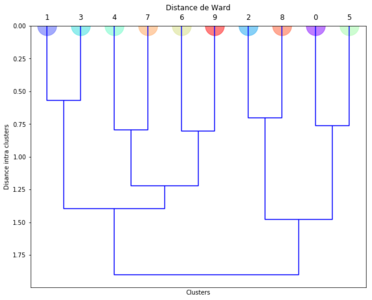
Fig. 9 : Dendrogramme du clustering hiérarchique : plus deux clusters regroupés sont proches, plus leur fourche de regroupement est haute sur le dessin.
9. Affichage des données sur des graphiques cartésiens et polaires
Cette représentation n'étant peut-être pas très claire pour tous, nous nous permettons de multiplier les graphiques pour faciliter la compréhension. L’objectif de la présentation des résultats est en effet d’être compréhensible, lisible par tous : matheux et non-matheux, personnes qui lisent plus ou moins aisément les graphiques...
Pour commencer, on va mettre cet arbre sous la forme d'un graphe, avec en abscisse le nombre de clusters contenus dans chaque branche. Ensuite, pour essayer de trouver une autre représentation, peut-être plus lisible, on va mettre le même graphique autour d'un cercle, faisant ainsi un graphique polaire.
9.1 Graphique cartésien
Voici le code pour obtenir le graphique cartésien (figure 10) :
fig=plt.figure(figsize=(FACT_SIZE*10,FACT_SIZE*10))
def mean(T1,T2,p1,p2): # Moyenne pondérée entre 2 tuples
return tuple([(T1[i]*p1+T2[i]*p2)/(p1+p2) for i in range(len(T1))])
def compos(link,n=(N_clusters-1)*2,num=0):
# Renvoie par récursivité une liste contenant les informations sur les points dépendants du cluster ou groupe de clusters n.
# format élément : [nom, Y, X, couleur, [clusters du groupe],next Y, next X]
if(n<N_clusters):
return([[n,num,1,colors[n],[n]]])
ng,nd=link[n-N_clusters,0:2]
Lg=compos(link,ng,num)
Ld=compos(link,nd,num+len([i[0] for i in Lg if i[0]<N_clusters]))
new=[n,(Lg[-1][1]*len(Lg[-1][4])+Ld[-1][1]*len(Ld[-1][4]))/(len(Ld[-1][4])+len(Lg[-1][4])),(len(Lg[-1][4]+Ld[-1][4])),
mean(Lg[-1][3],Ld[-1][3],len(Lg[-1][4]),len(Ld[-1][4])),Lg[-1][4]+Ld[-1][4]]
Lg[-1]+=[new[1],new[2]]
Ld[-1]+=[new[1],new[2]]
return(Lg+Ld+[new])
def plot(ax,L,axes=False):
# Trace le graphique en fonction des informations contenues dans la liste L
ax.set_ylabel("Nombre de clusters")
for i in L[:-1]:
ax.plot([i[1],i[5]],[-i[2],-i[6]],color=i[3],linewidth=3+2*len(i[4]),alpha=0.9,zorder=2)
ax.text(i[1]+0.2+0.05*len(i[4]),-(i[2]+0.04-0.08*len(i[4])),
str(i[4]).strip('[]'),fontweight="bold",zorder=10)
for i in L:
ax.scatter(i[1],-i[2],color=i[3],s=len(i[4])*500,alpha=1,zorder=5)
ax.text(L[-1][1]+0.5,-(L[-1][2]-0.4),"All clusters",fontweight="bold",zorder=10)
ax=fig.add_subplot(111)
# On reprend le résultat de la hiérarchisation sous forme de tableau d'entiers
nplink=np.array(link).astype(int)
# On le reformate pour donner les coordonnées de points sur un graphique cartésien
L_clusters=list(compos(nplink))
plot(ax,L_clusters)
plt.show()
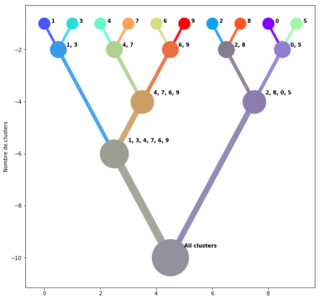
Fig. 10 : illustration des regroupements successifs du dendrogramme.
9.2 Graphique polaire
Ci-après, le code pour obtenir le graphique polaire (figure 11).
fig=plt.figure(figsize=(FACT_SIZE*10,FACT_SIZE*10))
def mean(T1,T2,p1,p2): # Moyenne pondérée entre 2 tuples
return tuple([(T1[i]*p1+T2[i]*p2)/(p1+p2) for i in range(len(T1))])
def compos(link,n=(N_clusters-1)*2,num=0):
# Renvoie par récursivité une liste contenant les informations sur les points dépendants du cluster ou groupe de clusters n.
# format élément : [nom, theta, R, couleur, [clusters du groupe],next theta, next R]
if(n<N_clusters):
return([[n,np.pi/20 + num*2*np.pi/N_clusters,N_clusters,colors[n],[n]]])
ng,nd=link[n-N_clusters,0:2]
Lg=compos(link,ng,num)
Ld=compos(link,nd,num+len([i[0] for i in Lg if i[0]<N_clusters]))
if(n==(N_clusters-1)*2):
new=[n,0,0,mean(Lg[-1][3],Ld[-1][3],len(Lg[-1][4]),len(Ld[-1][4])),Lg[-1][4]+Ld[-1][4]]
else:
new=[n,(Lg[-1][1]+Ld[-1][1])/2,N_clusters-len(Lg[-1][4]+Ld[-1][4]),
mean(Lg[-1][3],Ld[-1][3],len(Lg[-1][4]),len(Ld[-1][4])),Lg[-1][4]+Ld[-1][4]]
Lg[-1]+=[new[1],new[2]]
Ld[-1]+=[new[1],new[2]]
return(Lg+Ld+[new])
def plot(ax,L,axes=False):
# Trace le graphique en fonction des informations contenues dans la liste L
ax.set_xlabel("Nombre de clusters")
for i in L[:-1]:
ax.plot([i[2]*np.cos(i[1]),i[6]*np.cos(i[5])],[i[2]*np.sin(i[1]),i[6]*np.sin(i[5])],
color=i[3],linewidth=5+len(i[4]),alpha=0.6,zorder=2)
ax.text(i[2]*np.cos(i[1])+0.2-0.25*len(i[4]),i[2]*np.sin(i[1])-0.1,
str(i[4]).strip('[]'),fontweight="bold",zorder=10)
for i in L:
ax.scatter(i[2]*np.cos(i[1]),i[2]*np.sin(i[1]),color=i[3],s=600+len(i[4])*100,alpha=1,zorder=5)
ax.text(-1,-0.06,"All clusters",fontweight="bold",zorder=10)
# On trace la légende
T=np.linspace(0,2*np.pi,100)
R=set([(len(i[4]),i[2]) for i in L[:-1]])
for t,r in R:
ax.plot(r*np.cos(T),r*np.sin(T),color='k',alpha=0.4,zorder=0)
if(t==1):
ax.text(r+0.05,0.1,str(t)+" cluster",color='k',alpha=0.7,zorder=12)
else:
ax.text(r+0.05,0.1,str(t),color='k',alpha=0.7,zorder=12)
ax.plot([0,N_clusters],[0,0],color='k',alpha=0.4,zorder=0)
ax=fig.add_subplot(111)
# On reprend le résultat de la hiérarchisation sous forme de tableau d'entiers
nplink=np.array(link).astype(int)
# On le reformate pour donner les coordonnées de points sur un graphique polaire
L_clusters=list(compos(nplink))
# Affichage de la légende et du graphique
plot(ax,L_clusters)
plt.axis("Off")
plt.show()
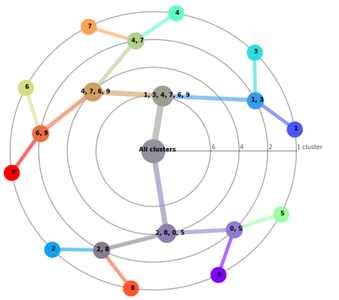
Fig. 11 : Représentation du dendrogramme par regroupements successifs concentriques.
10. Affichage des idées par cluster
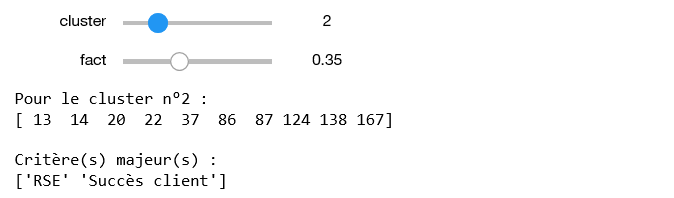
Pour finir, on va afficher pour chaque cluster les idées qu'il contient, afin d'avoir un retour sur nos interprétations et de pouvoir continuer l'analyse « au cerveau ». On propose également un rappel rapide et dynamique des caractéristiques principales de chaque cluster (figure 12).
def update(cluster,fact=0.5):
print("Pour le cluster n°"+str(cluster)+" : ")
print(pd.concat([Copied_df.loc[(clustering.row_labels_)==cluster]],axis=1).index.values,'\n')
print("Critère(s) majeur(s) :")
print(centers.index.values[Maj_crit(centers[cluster],fact)])
def Maj_crit(L,fact=0.75):
# Renvoie les indices des critères les plus importants pour une liste L.
limit=min(L) + (max(L)-min(L))*fact
return([i for i in range(len(L)) if (L[i]>limit)])
interact(update,cluster=(0,N_clusters-1),fact=(0,0.99,0.05))
Fig. 12 : Résumé des caractéristiques et des idées contenues dans un cluster.
Conclusion
Cette démonstration est maintenant terminée, la partie suivante et hors champ de cet article étant d’analyser manuellement ou plutôt « au cerveau » les résultats, en liant chaque cluster aux idées réelles qu’il contient. Dans la pratique, nous écrivons un rapport de synthèse, illustré par certains des schémas créés dans le notebook, quelques tableaux de résultats que nous aurons enregistrés au passage; puis nous effectuons des présentations orales de restitution.
L’expérience montre des résultats facilitant l’adhésion aux résultats sur les business models et stratégies qui en découlent, y compris l’adhésion des décideurs. Cela résulte en partie de l’existence des multiples idées de tous qui apparaissent dans les clusters, contrairement aux pratiques usuelles, mais aussi de la force rationnelle apportée par l’utilisation des algorithmes et de l’utilisation de visualisations explicites pour tous. Il est évident aussi que cette méthode apporte de nombreuses pistes - et plus innovantes - non nécessairement décelées lors de classifications faites usuellement par thèmes de marketing.
En effet, face aux méthodes classiques de classification des résultats par segmentation entre les différents marchés (p. ex. les marchés grand public et entreprise, silver économie, les adolescents, les millenials...), face aux cloisonnements usuels par verticaux tels que l’assurance, la banque, les télécoms, l’automobile, etc., l’utilisation des algorithmes avec cette méthodologie, créée dans les Labs d’Orange, facilite grandement l’élaboration des business models de demain et même, de ceux d’aujourd’hui.
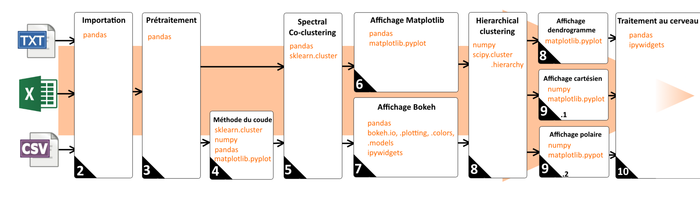
Parce qu’un petit dessin vaut mieux qu’un long discours, la figure 13 résume le processus.
Fig. 13 : Schéma récapitulatif du process.
Références
[1] P. BAILLY, J. PARRA DIAZ, Think Tank Fondation Télécom et Institut Mines-Télécom, « Innovation collective en entreprise, pourquoi et comment s'appuyer sur des méthodes et pratiques véritablement élaborées? », Cahier de prospective sur l'efficacité collective, mars 2016, pages 91 à 103 : https://www.fondation-mines-telecom.org/wp-content/uploads/2016/01/Cahier-Efficacite-collective-web-2016-03-17.pdf
[2] T. COLOMBO, « Quel IDE pour analyser vos données en Python ? », GNU/Linux Magazine HS n°100, janvier 2019 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMFHS-100/Quel-IDE-pour-analyser-vos-donnees-en-Python
[3] T. COLOMBO, « Identifier des groupes de données par classification », GNU/Linux Magazine HS n°101, mars 2019 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMFHS-101/Identifier-des-groupes-de-donnees-par-classification
[4] A. LETOIS, « Automeans, ou comment éviter le «k par k» avec K-means », MISC HS n°018, novembre 2018 : https://connect.ed-diamond.com/MISC/MISCHS-018/Automeans-ou-comment-eviter-le-k-par-k-avec-K-means