Les Arbres Binaires à Commande Équilibrée, ou ABCE, ont été présentés dans GLMF n°215 [1] au moyen d'une métaphore ferroviaire. Cependant, ils sont surtout utiles dans certains circuits numériques, dont ils améliorent la vitesse et la consommation, pour la plupart des technologies. Par rapport à un arbre binaire classique, le gain de performance augmente avec la taille, ce qui est un atout précieux pour concevoir des circuits intégrés par exemple.
Cette fois-ci, pas d'allégorie douteuse. Les aiguillages et les LEGO sont remplacés par des vrais relais et des vrais transistors. Mais ce n'est pas tout : qu'y a-t-il de mieux qu'un arbre équilibré ? Plein d'arbres équilibrés, bien sûr ! Et même lorsque leur intérêt individuel est marginal, on peut combiner leurs avantages à plus grande échelle pour optimiser les caractéristiques de l'ensemble du système (partie 4). Au passage, nous évoquerons, dans la partie 5, quelques notions de base de conception des circuits intégrés CMOS.
1. Rappels sur les ABCE
Comme le titre l'indique, nous allons parler d'arbres binaires, tels que ceux de la figure 1a. C'est une structure courante qui, comme un arbre qui pousse dans la terre, a un tronc (ou une racine, selon les conventions), des branches et des feuilles. Pour un arbre binaire (la structure abstraite, donc), le tronc ou une branche se divisent uniquement en deux, au niveau de ce que l'on appelle un nœud. Et une branche qui ne se divise plus s'appelle une feuille. Jusque-là, rien d'original, c'est de la topologie très classique.
L'article précédent [1] utilisait une autre métaphore : celle d'une gare de triage où une voie unique se divisait plusieurs fois en deux, au niveau d'un aiguillage, pour créer deux, puis quatre, puis huit, puis seize voies... Le principe est le même, mais la métaphore botanique s'est imposée en topologie, même s'il manque une analogie qui fasse l’unanimité pour la commande de l'aiguillage. Nous utiliserons ici l'analogie du coloriage des nœuds, comme pour les arbres rouge-noir [2]. Chaque nœud a donc une couleur, associée à un signal de commande donné.
Nos arbres sont équilibrés : cela veut dire que l'on doit passer par le même nombre de branches (et traverser autant de nœuds) pour atteindre toutes les feuilles, en partant du tronc. On dit que toutes les profondeurs sont égales. C'est le type d'arbre binaire le plus répandu et ses propriétés sont très bien connues. Par exemple, on sait que chaque niveau de branche double le nombre de nœuds, le nombre de feuilles est donc une puissance de deux, et le nombre total de nœuds est égal à ce nombre, moins un. Toujours rien de neuf jusqu’ici.
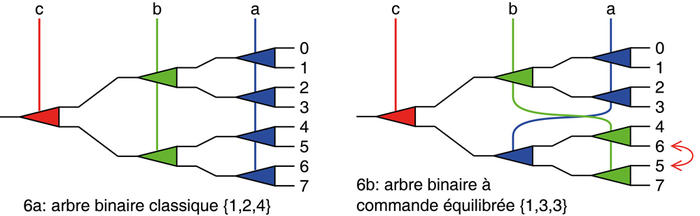
Les ABCE ont un truc en plus : non seulement toutes les profondeurs sont équilibrées, mais en plus les nœuds ont des propriétés particulières. Chaque couleur est utilisée (quasiment) autant de fois que les autres, sauf une des couleurs qui ne peut être utilisée qu’une fois. De plus, on ne trouve jamais deux fois la même couleur en parcourant l'arbre du tronc vers chaque feuille. Des permutations subtiles (décrites en [1]) permettent d'arriver à ce résultat. Le nombre de permutations valides (en omettant les symétries) augmente avec le nombre de feuilles et la figure 1 montre deux possibilités pour un arbre à 16 feuilles (aussi surnommé MUX16 pour aller plus vite).
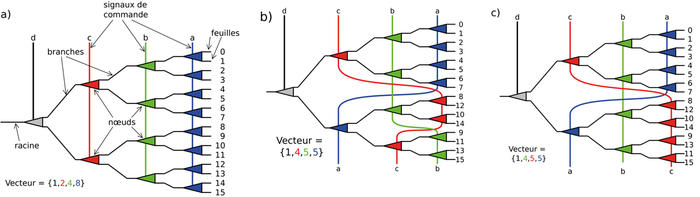
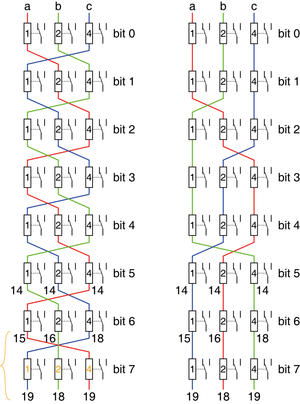
Fig. 1 : Le diagramme a) présente un arbre binaire équilibré classique, avec sa racine, ses nœuds, ses branches et ses feuilles, où chaque signal de contrôle affecte un unique niveau de division. Puisque ce circuit sélectionne ou multiplexe un signal parmi 16, on l’appelle aussi MUX16 en électronique numérique. Les deux autres diagrammes b) et c) montrent deux manières de réorganiser les signaux de contrôle afin de leur affecter un nombre plus équilibré de nœuds. Le nombre maximal de nœuds par signal baisse de 8 à 5, au prix de permutations des feuilles. Le vecteur correspondant contient des nombres moins élevés, ce qui signifie que le circuit est plus efficace.
Traditionnellement, on utilise des arbres binaires équilibrés « classiques », c’est-à-dire que chaque profondeur de division est associée à une nouvelle couleur. Cela pose problème quand l'arbre grandit, car la couleur de dernier niveau, juste avant les feuilles, est utilisée plus que toutes les autres et accapare la moitié des ressources. L’intérêt d’un ABCE est de répartir les couleurs quasiment équitablement, ce qui évite au dernier niveau de ralentir tout le circuit (comme expliqué dans la partie 5).
Nous pouvons résumer les caractéristiques principales d'un arbre binaire au moyen d'une liste de nombres, appelée ici vecteur, représentant le nombre de nœuds assignés à une couleur donnée. Il y a autant de nombres que de niveaux de branches, et la somme de tous ces nombres donne le nombre total de nœuds (ou bien le nombre de feuilles moins un). Aussi, le premier nombre du vecteur est toujours 1. L'article précédent expliquait comment calculer le vecteur pour une profondeur d'arbre donnée, la valeur maximale étant approximativement égale à ((2^n)-2)/(n-1) pour une profondeur de n niveaux. Malheureusement, je ne connais pas d’algorithme trivial permettant de construire un ABCE donné, c’est donc encore une opération manuelle, assistée de quelques heuristiques décrites précédemment.
|
Feuilles |
Profondeur |
Max |
Vecteur de fan-in |
Performance relative |
|
1 |
0 |
|
{} |
|
|
2 |
1 |
1 |
{1} |
|
|
4 |
2 |
(4-2)/(2-1)=2 |
{1, 2} |
2/2 = 1 |
|
8 |
3 |
(8-2)/(3-1)=3 |
{1, 3, 3} |
4/3 = 1,33 |
|
16 |
4 |
(16-2)/(4-1)=4,6 |
{1, 5, 5, 4} |
8/5 = 1,6 |
|
32 |
5 |
(32-2)/(5-1)=7,5 |
{1, 7, 7, 8, 8} |
16/8 = 2 |
|
64 |
6 |
(64-2)/(6-1)=12,4 |
{1, 13, 13, 12, 12, 12} |
32/13 = 2,46 |
|
128 |
7 |
(128-2)/(7-1)=21 |
{1, 21×6} |
64/21 = 3,04 |
|
256 |
8 |
(256-2)/(8-1)=36,28 |
{1, 37×2, 36×5} |
128/37 = 3,46 |
|
512 |
9 |
(512-2)/(9-1)=63,75 |
{1, 63×2, 64×6} |
256/64 = 4 |
|
1024 |
10 |
(1024-2)/(10-1)=113,5 |
{1, 113×4, 114×5} |
512/113 = 4,49 |
Le tableau ci-dessus liste les dix premiers vecteurs idéaux et leurs caractéristiques. Par convenance, les nombres pairs sont souvent en dernière position dans la liste, mais c'est la valeur la plus élevée qui indiquera la performance relative par rapport à un arbre binaire classique.
Coïncidence amusante : la suite composée par le nombre maximal de chaque vecteur idéal (1, 2, 3, 5, 8, 13, 21, 37, 64, 113...) croît initialement comme la séquence de Fibonacci [3], mais elle commence à augmenter plus vite à partir de la profondeur 8 (la valeur est 37 au lieu de 34). Y a-t-il un mathématicien pour expliquer cela ?
Mathématiquement, les ABCE sont une forme de partitionnement. Mais du point de vue électronique, ce qui nous intéresse est la performance, qui dépend directement du nombre maximal de nœuds d'une certaine couleur. Ces nœuds sont réalisés électroniquement au moyen d'un multiplexeur à deux entrées, comme un relais 1RT par exemple, et la couleur correspondra à un signal de commande.
Fan-in et Fan-out
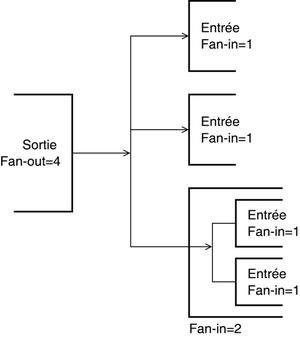
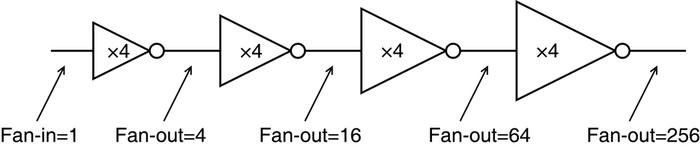
Deux termes importants (voir figure 2), venant du domaine de l’électronique, sont utilisés dans cet article.
- Fan-in : c'est l'énergie ou l'effort à fournir pour changer la valeur logique de l'entrée d'un circuit. Ce dernier peut contenir des sous-circuits avec leurs propres entrées, c'est donc leur somme qui nous intéresse.
- Fan-out : c'est le nombre d'entrées (ou l’équivalent) qui sont connectées à la sortie du circuit.
L’unité est souvent sans grandeur physique, habituellement le nombre de portes logiques, ou bien en milliampères. Par exemple, avec des relais, le fan-in correspond au nombre de bobines qu’il faut alimenter afin que tous les relais basculent. On peut aussi l’exprimer comme le courant total à fournir.
En logique à transistors, le niveau logique à toutes les entrées changera d'autant plus lentement que le fan-out augmente, ce qui va directement affecter la vitesse de fonctionnement du circuit. Selon les besoins, on intercalera des étages tampons pour amplifier le signal. On peut aussi modifier la sortie pour être plus puissante : c’est pour cela que certains circuits intégrés TTL ou les portes logiques CMOS intégrées sont souvent disponibles avec plusieurs puissances de sortie (« output strength ») différentes.
Fig. 2 : Le fan-out correspond à la sortie d’un circuit, et le fan-in à l’entrée du circuit en aval.
2. Des relais
D'ailleurs, toute cette histoire a commencé à cause de relais. Un de mes nombreux hobbies consiste justement à fabriquer un ordinateur sans transistor, à base de relais 1RT miniatures d'origine soviétique (merci eBay !). La mémoire dynamique (à base de condensateurs électrolytiques) nécessite entre autres un énorme multiplexeur à 64 voies, qui est un défi technique majeur du projet.
Contrairement à des relais plus sophistiqués ou plus gros, chacun de mes relais ne peut commuter qu'un seul signal, donc le dernier niveau du multiplexeur devra utiliser 64/2=32 relais. C'est considérable, sachant que ces petits РЭС15 ont un faible pouvoir de commutation : en effet, leur électro-aimant demande un courant qui est presque la moitié de celui que les contacts supportent. Dépasser ce courant réduirait la fiabilité du système, ce qui impose de le limiter avec soin.
Ainsi, un relais peut en commander directement deux au maximum, ce qui est un coefficient d'amplification médiocre. On peut bien sûr ruser en mettant plusieurs bobines de relais bout à bout, en série : au lieu d'augmenter le courant, on augmente la tension. Malheureusement, cette tension aussi est limitée, par l'alimentation et surtout le relais. Il y a donc une puissance maximale que le contact d'un relais peut tolérer et les contacts ne peuvent pas alimenter directement 32 bobines de relais.
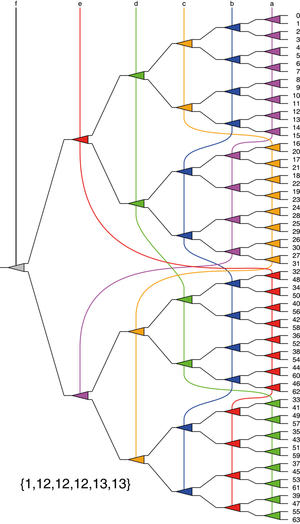
Fig. 3 : Bien qu'il soit plus compliqué, un ABCE à 64 feuilles est 2,5 fois plus efficace qu'un arbre binaire classique, car les signaux de contrôle doivent commander au maximum 13 relais, au lieu de 32.
Vous l'aurez deviné, la solution à ce problème d'ingénierie prend la forme d'un ABCE. En équilibrant l'assignation des signaux de contrôle, un relais doit commuter au maximum 13 bobines, ce qui est déjà plus raisonnable. La figure 3 montre un tel arbre équilibré, dont nous avons détaillé la construction à la fin de l'article précédent [1]. Cet équilibrage simplifie aussi l'organisation des connexions des relais puisque nous devons maintenant gérer cinq circuits presque identiques (comprenant chacun deux chaînes de 6 ou 7 relais) au lieu de six circuits de longueurs toutes différentes.
Cette approche a un autre avantage important. Hormis le tout premier relais, tous les autres sont déclenchés exactement au même moment, car tous les facteurs d'amplification sont identiques. Aucun niveau n'est retardé par rapport aux autres et la latence globale est égale à un seul relais pour tous les fils du bus d'adresse. Ainsi, la latence du circuit a donc un peu diminué.
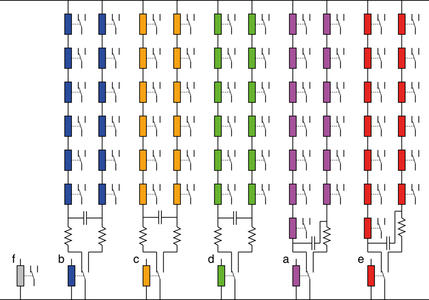
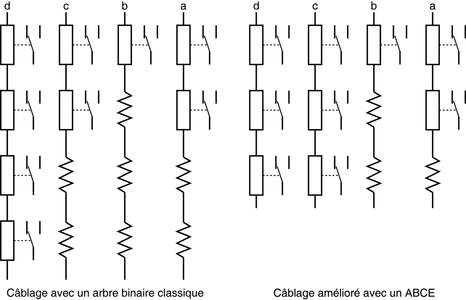
Fig. 4 : L'ABCE à 64 feuilles de la figure 3 simplifie beaucoup la conception et le câblage. Le circuit est constitué principalement de cinq parties presque identiques, toutes alimentées par la même source électrique.
La figure 4 montre qu'à l'exception du signal f, solitaire, les autres signaux de contrôle sont amplifiés d'un même facteur. Une seule tension d'alimentation suffit et la petite différence de longueur des chaînes est compensée par une résistance, d'une valeur équivalente à celle d'une bobine de relais. Évidemment, ceci n'est qu'un schéma de principe qui laisse de côté beaucoup de détails, hors de propos de cet article, mais on peut déjà observer les caractéristiques principales.
Le circuit de la figure 4 exploite les deux contacts du relais, qui n'alimente plus qu'une seule des deux chaînes à un moment donné. Cela réduit l'usure des contacts, qui sont protégés des arcs électriques par la résistance et par le condensateur, ce dernier transférant une partie de l'énergie de l'inductance dans l'autre moitié qui n'est pas encore alimentée. Cela remplace avantageusement des diodes de roue libre.
De plus, la consommation maximale baisse d'un facteur deux, et le courant de fonctionnement est considérablement plus stable. Quelle que soit l'activité du système, la consommation de ce système optimisé ne change presque pas, si on ne compte pas les microcoupures durant les commutations, qui sont très courtes donc facilement filtrables. L’alimentation pourrait provenir d’une alimentation rudimentaire avec un transformateur, un pont de diodes et des gros condensateurs.
Au contraire, un système plus classique souffrirait de variations énormes et imprévisibles de courant de fonctionnement. Dans le pire des cas, la consommation pourrait passer de presque rien à 62 relais, ce qui complique la régulation et oblige à surdimensionner l'alimentation et ses condensateurs de filtrage. Ainsi, un peu de topologie appliquée permet de faire des économies substantielles, directes et indirectes !
3. Encore des relais
Une fois que les avantages des ABCE sont évidents, on les utilise presque partout. Par exemple, dans les modules d'affichage hexadécimal (voir la figure 5) qui présentent les valeurs des registres et des bus de l'ordinateur électromécanique (au lieu de câbler une simple lampe sur chaque bit). Ces modules décodent un groupe de quatre bits au moyen d'une matrice de diodes pour afficher un chiffre de 0 à F.
Le prototype utilise presque uniquement des composants russes vintage. Le tube du Numitron (une lampe à incandescence à 7 filaments, de type ИВ-9) est commandé par une matrice bidirectionnelle de diodes germanium (Д9К), elle-même alimentée par un arbre binaire de relais РЭС15 (dans les cylindres en aluminium). Le chiffre à afficher est contrôlé par les 4 paires de fils sur le connecteur à l’arrière. Tous les détails sont sur https://hackaday.io/project/26068-numitron-hexadecimal-display-module. Ces modules devront être produits par dizaines donc chaque économie (de place, de consommation ou de composant) a un effet important sur la viabilité et la performance de l’ensemble du projet.
Fig. 5 : Prototype d’un afficheur électromécanique à 5 chiffres hexadécimaux.
Pour faciliter l'intégration de ces modules sur les différents bus, chaque signal d'entrée doit avoir les mêmes caractéristiques. En d'autres termes, les signaux de commande doivent alimenter le même nombre de relais en série, quel que soit le poids du bit. Cela semble difficile a priori, car pour décoder 16 chiffres, un arbre binaire comporte 15 nœuds dont 8 sont dédiés au dernier niveau. Cela nécessite beaucoup de relais et on regrette alors de ne pas disposer de relais à contacts doubles ou quadruples...
Évidemment, un ABCE améliore la situation, car le vecteur de fan-in passe de {1,2,4,8} à {1,5,5,4}, réduisant au passage la tension d'alimentation de 37%. Pourtant le coût élevé, la consommation importante et l'encombrement des relais imposent une solution plus optimisée, qui conduisit à la mise au point d'une matrice de diodes bidirectionnelle pour l’encodage de chaque segment. Ainsi l'étage final ne comporte plus que 4 relais, l'étage précédent étant remplacé par deux relais travaillant en inverseur de polarité.
Le nouveau circuit comporte donc un arbre binaire MUX8 suivi par une paire de relais pour l'inverseur, et l'arbre {1,2,4} (voir figure 6a) peut être équilibré pour donner {1,3,3} (figure 6b). Au total, il n'y a plus que 9 relais et la consommation du dernier niveau n'est plus que 3/8=37% du circuit initial. La figure 7 montre aussi que l’impédance d’entrée a également diminué.
Fig. 6 : Ce circuit sélectionne, ou multiplexe, un signal parmi 8 et porte donc le doux surnom de MUX8. La version ABCE à 8 feuilles réduit de 4 à 3 le nombre maximum de bobines de relais à mettre en série, ce qui baisse la consommation de l'ensemble.
Fig. 7 : En plus de la consommation plus faible, l'ABCE réduit aussi le nombre de résistances de compensation (3 au lieu de 7) donc le coût du circuit.
4. Toujours plus de relais !
Jusque-là, nous avons simplement appliqué les ABCE de l’article précédent à des cas simples et isolés. Dans les parties 2 et 3, nous avons analysé des arbres individuels, mais c’est juste un cas particulier qu’il est possible d’étendre.
Comme le montre la table de la partie 1, plus l'arbre est grand, plus le bénéfice de l'équilibrage est important. Ainsi, on pourrait imaginer se passer de cette optimisation qui brouille les fils avec juste 8 feuilles, et elle est impossible avec seulement 4 feuilles. Pourtant, on a bien besoin d'un équilibrage même avec des petits arbres, en particulier s'il y en a plusieurs en parallèle, sur un bus de données par exemple. Cela fait entrer les ABCE dans la troisième dimension.
Le cas le plus emblématique est un banc de registres, dans un microprocesseur par exemple. Même pour un petit processeur 16 bits avec 16 registres, utiliser des multiplexeurs peut devenir un vrai casse-tête puisque dans le pire des cas, un bit d'adresse de registre devra contrôler (16×16)/2=128 multiplexeurs. Un tel coefficient d'amplification demande au moins deux niveaux de relais, alors que d'autres niveaux n'en demandent qu'un seul, ce qui déséquilibre les temps d'arrivée des signaux.
Évidemment, passer d'un arbre classique {1,2,4,8} à un ABCE {1,4,5,5} améliore un peu les choses, en réduisant le fan-out maximum de 8×16=128 à 5×16=80, mais ce n'est pas encore satisfaisant. En fait, ce n'est même pas proche de l'optimal puisque les deux autres signaux ont un fan-out de 1×16=16 et 4×16=64 seulement. Il faut reprendre les choses à la base.
Et à la base, nous avons simplement 4 signaux d'adresse qui doivent contrôler en tout 15×16=240 relais, le circuit idéal devrait donc allouer 240/4=60 relais à chaque signal d'adresse. L'idéal est 25% plus efficace que l'utilisation d'un ABCE {1,4,5,5} seul, mais comment y arriver ?
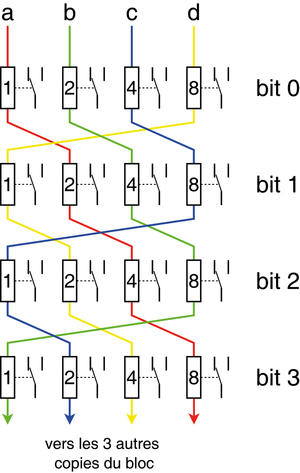
Encore une fois, l'astuce consiste à permuter les signaux de contrôle. Dans notre cas, avec 16 MUX16 parallèles, nous allons en plus profiter de coïncidences arithmétiques pour simplifier et factoriser le circuit. En effet, 60=4×15 et on peut travailler sur un quart du circuit (avec 4 chaînes de 15 relais chacun) avant de le répliquer 4 fois (c’est aussi possible en divisant le circuit en 3 ou en 5). En plus d'avoir coupé en 4 la taille du problème à analyser, on voit aussi que le nombre restant de signaux à câbler est exactement égal à la taille d'un arbre. Le câblage de la figure 8 est donc très facile, que l'on utilise un arbre classique (comme montré) ou un ABCE. Dans ce dernier cas, le résultat serait similaire, car le nombre total de relais est identique pour chaque MUX16. Le choix d’un arbre classique est donc plus lié à la commodité et pour simplifier les calculs (avec des puissances de 2) et les câblages.
Fig. 8 : Plusieurs arbres parallèles (même sans commande équilibrée) peuvent partager des signaux de commande, afin de les équilibrer globalement. Le cas ci-dessus, avec 4 bits d'adresse, est idéal, car une simple permutation circulaire suffit pour connecter autant d'arbres, ou tranches de circuit. Un signal de commande relie ainsi plusieurs arbres individuels, chaque symbole de relais représente 1, 2, 4 ou 8 bobines en série. La somme des bobines traversées est toujours 15 pour tous les signaux de commande.
La théorie est donc validée, mais en pratique, 16 registres de 16 bits, avec un port d'écriture et deux ports de lecture, utilisent plus de 1000 relais, avec une consommation, une fiabilité et un encombrement peu réalistes. La décision est alors prise de réduire la taille du monstre, avec seulement 8 registres de 8 bits, ce qui ne demande plus que 250 relais environ.
Heureusement, les mêmes calculs s'appliquent. Nous n'avons plus que 8 MUX8, soit 56 relais pour un port de lecture ou d'écriture. Cependant 56 n'est pas un multiple de 3 (soit le nombre de bits d’adresse), on trouve un fan-out idéal de 56/3=18,666 et le nombre fractionnel indique déjà que la structure ne sera pas joliment symétrique comme dans le cas précédent. On cherche donc une topologie pour trois chemins qui traversent 19, 19 et 18 bobines respectivement.
On peut repartir de la même idée de permutations circulaires et traiter un premier groupe de 3 arbres, puis répliquer ce groupe trois fois pour obtenir 9 arbres parallèles. Le neuvième arbre servirait pour la parité, ou bien serait ignoré (les bobines de relais sont remplacées par des résistances), mais cela risquerait de créer un déséquilibre trop important qui nous éloignerait de l'organisation idéale.
Il existe heureusement plusieurs solutions approchantes et faciles à trouver en griffonnant un morceau de papier. La figure 6 montrait deux types d'arbres binaires à 8 feuilles, à partir desquels nous pouvons composer des permutations plus complexes, mais aussi plus exactes. Du point de vue mathématique, le problème se résume à combiner et accumuler des permutations des vecteurs {1,2,4} et {1,3,3} pour obtenir le vecteur {18,19,19}...
La solution la plus facile consiste à dégrossir le problème en considérant d'abord deux groupes identiques à base de trois permutations circulaires (donc à base d'arbres {1,2,4} ou {1,3,3}, au choix). On sait que la somme des bobines d'un groupe est égale au nombre de relais dans un arbre, soit 7 ici. Nos deux groupes auront un fan-out de 14 sur chaque signal, ce qui laisse {18,19,19}-{14,14,14}={4,5,5} bobines à câbler avec deux arbres. Par chance, ce vecteur est une somme (après permutation) des deux arbres de la figure 6 : {4,5,5}={1,2,4}+{3,3,1}.
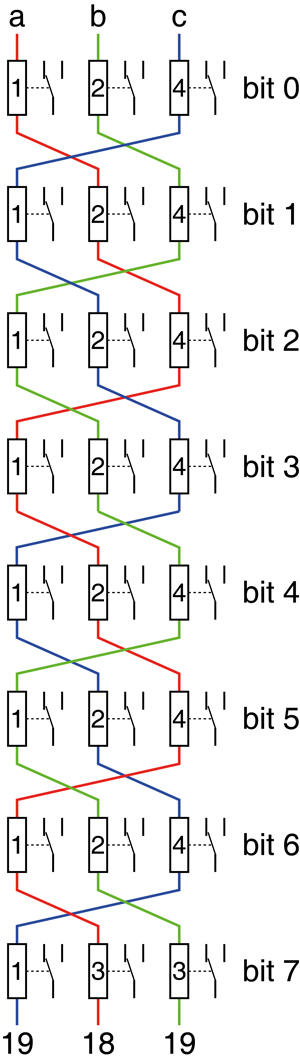
Fig. 9 : Une combinaison de différents types d'arbres, ainsi que des permutations circulaires, permettent d'équilibrer les signaux de contrôle de nombreux arbres, même si ces derniers ne sont pas eux-mêmes équilibrés. Dans cet exemple, le motif de connexion est très régulier et facilite le routage et le câblage du fond de panier qui relie toutes les cartes.
La figure 9 montre le branchement de différents arbres pour obtenir une solution exacte. Elle pose toutefois un petit souci : un des arbres doit être différent des autres, ce qui complique la réalisation, car on voudrait qu'ils soient tous identiques pour les fabriquer en série. Heureusement, la différence est presque négligeable si on utilise uniquement des ABCE {1,3,3} : le fan-out est {18,18,20}. Avec un arbre classique, on obtient {17,19,20}, et même {18,19,19} grâce à une légère modification du câblage comme sur la figure 10a (les parties modifiées sont indiquées en orange). Plusieurs choix permettent donc de réaliser un système équilibré, selon les contraintes, et l’arbre binaire classique est clairement toujours utile. Par exemple, la figure 10b est une autre permutation qui réduit le nombre de croisements de fils de contrôle.
Fig. 10 : La variante a) de la figure 9 utilise seulement des arbres classiques et identiques. Elle obtient pourtant un résultat idéal grâce à une permutation différente des signaux de contrôle, en orange, au niveau du bit n°7. Cela simplifie beaucoup la réalisation de multiples multiplexeurs parallèles avec des circuits, ou tranches, interchangeables, mais le fond de panier est un peu moins régulier. La variante b) est une amélioration plus poussée pour simplifier le câblage du fond de panier, en réduisant le nombre de croisements.
Évidemment, avec toutes ces permutations, les bits sont envoyés dans tous les sens... L'important est de garder la même structure pour tous les ports de lecture et d'écriture afin que chaque bit soit envoyé puis relu au même endroit, quelle que soit l'adresse présentée sur les bits de contrôle.
5. Et des transistors !
Vous me direz que jusque-là, je ne me suis pas vraiment mouillé en parlant d'une technologie surannée et anecdotique, oubliée dès les années 60. En effet, la performance d'un système à relais est essentiellement liée au nombre de relais qui constituent une cascade, ou le chemin critique, puisque le délai est uniquement causé par les quelques millisecondes de basculement d'un contact électrique. La transmission des informations sur les contacts est relativement instantanée et absente des équations. Nos ABCE ne sont pas strictement nécessaires pour le fonctionnement du circuit et apportent (soyons modestes) une amélioration de la consommation et une réduction de l'usure des contacts. Toutefois la réduction du fan-in d'un arbre accélère ce circuit, car il faut moins d'étages d'amplification, et c'est une qualité précieuse pour toutes les autres technologies.
Regardons l'autre extrémité de l'évolution de l'électronique : depuis plus de 30 ans, c’est incontestablement la technologie CMOS qui règne. Ses paramètres de fonctionnement sont plus sophistiqués, mais nous pouvons nous contenter de la bonne vieille formule de charge et décharge d'un condensateur : t=R×C.
- R est la résistance des fils et à mesure que la section de ces derniers diminue, leur résistance augmente. Heureusement, cette épaisseur est aussi proportionnelle à la longueur du fil lorsque la finesse de gravure s’améliore, le rapport entre la longueur et la section ne varie pas trop donc la résistance est presque indépendante de la technologie. On tient quand même absolument à raccourcir les fils par un placement judicieux des portes logiques.
- C est la capacitance, proportionnelle à la charge électrique à fournir pour déclencher le circuit (plus précisément, charger ou décharger le condensateur formé par la grille du FET). Elle est liée à deux choses : d'une part, le nombre de transistors à commander ainsi que les caractéristiques de ces derniers (c'est le fan-out, qui est aussi proportionnel à la taille des grilles) et d'autre part la longueur des fils, car ces derniers agissent aussi à l'échelle microscopique comme des condensateurs !
On arrive à une situation où les règles de conception sont très contraignantes, si on veut réduire t (pour que le circuit tourne à la fréquence optimale). D'abord, il faut limiter le fan-out, car le temps de propagation d'un signal est quasiment proportionnel à celui-ci. D'autre part, le temps de propagation augmente avec le carré de la longueur d'un fil, puisqu'il se comporte comme un réseau RC distribué, donc même une petite réduction de longueur peut avoir un effet notable sur la fréquence de fonctionnement d'un circuit intégré moderne.
Lorsqu'on doit commander un très grand nombre de portes logiques, par exemple un signal d'horloge ou de reset, un réseau dédié est nécessaire pour acheminer le signal sur tout le circuit, exactement au même moment. Cela constitue en soi une sorte de grand condensateur qu'il faut charger et décharger très vite, à chaque transition. Par exemple, l'horloge des premiers processeurs 64 bits Alpha 21064 utilisait plusieurs pourcents de la surface de la puce et consommait près du tiers du courant. Les générations suivantes ont amélioré la stratégie, mais voici ce qu'il faut retenir : la réduction du fan-in ou du fan-out d'un circuit augmente sa vitesse (et/ou réduit sa consommation, en passant, car il y a moins de charges électriques à déplacer).
Cette problématique de charge et de décharge de capacités se retrouve dans les circuits d'amplification. Pour augmenter la puissance d'un signal avec le moins de latence possible, la meilleure stratégie consiste à mettre bout à bout des inverseurs de plus en plus gros, mais avec un gain fixe, comme sur la figure 11. Ce gain idéal peut varier de 2.7 à 5.3 en fonction des recettes de fabrication du silicium, on utilise donc habituellement un rapport de 4 quand on ne le connaît pas à l'avance. Cela a abouti à la création de la métrique FO4 [4] (pour Fan-Out de 4) qui permet de comparer des circuits logiques entre eux, même s'ils sont réalisés par des fonderies très différentes.
Fig. 11 : Dans un circuit intégré, une cascade d'amplificateurs à gain fixe et modéré est la meilleure façon d'amplifier un signal de contrôle avec le moins de latence possible.
Ainsi, si on réduit le coefficient d'amplification d'un signal logique, donc le fan-out, on réduit aussi sa latence. On voit alors que les ABCE ont un avantage important par rapport aux arbres binaires classiques. Prenons le cas d'un multiplexeur à 32 entrées : son vecteur de fan-in est {1,2,4,8,16} pour la version classique et {1,7,7,8,8} pour l'ABCE correspondant. La vitesse dépend uniquement du nombre le plus élevé dans le vecteur, donc on considère juste un fan-in de 16 pour la version classique et 8 pour l'ABCE.
En supposant que le signal de commande arrive directement à toutes les portes logiques, avec un seul fil, alors le gain de vitesse est simplement 16/8=2. L'ABCE est deux fois plus rapide, ce qui est bon à savoir pour les FPGA par exemple, car leurs portes logiques sont capables de fan-out modérés ou importants.
Dans un ASIC, bien plus sensible qu'un FPGA aux questions de fan-out, il faudra amplifier le signal avec des inverseurs intermédiaires. Le nombre 16 étant un multiple de 4, nous utiliserons un arbre d'inverseurs à 2 niveaux pour atteindre les 16 portes logiques. La latence sera donc de 2×FO4, soit deux fois la latence d'un inverseur de gain 4.
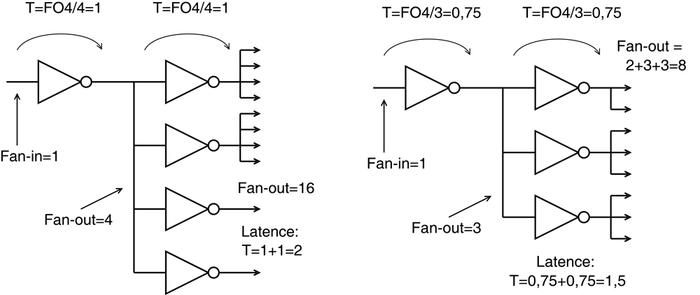
L'ABCE ne sera pas beaucoup plus rapide avec ses 8 portes logiques, mais reste encore intéressant. Par exemple, on peut utiliser un arbre d'inverseurs à deux niveaux avec seulement un fan-out de 3. La latence diminue seulement de 25% par étage (en supposant que seul le fan-out compte), mais cela fait quand même 25+25=50% après deux étages, soit une latence totale de 1,5×FO4 (voir figure 12). Cette demi-porte logique de latence ainsi gagnée peut faire la différence entre un processeur à 90MHZ et un processeur à 100MHz...
Fig. 12 : La latence augmente avec le fan-out total, mais le gainest seulement logarithmique si on utilise un arbre d’amplification.
Le raccourcissement des fils ainsi que la latence propre à l'inverseur n'ont pas été pris en compte dans cette estimation très grossière donc il faudra toujours comparer, vérifier et mesurer la performance de chaque circuit.
6. Encore des transistors !
Mais la vitesse n'est pas le seul avantage qu'apportent les ABCE. Il existe des cas où l'équilibrage des signaux de contrôle permet une meilleure allocation des portes logiques et des fils. Si un grand multiplexeur est nécessaire, il aura tendance à accaparer des fils (donc de la surface de puce) qui ne sera plus disponible pour les autres circuits dont la performance est critique.
Pour un exemple concret, prenons un grand multiplexeur à 64 entrées, tel que celui de la figure 3. Un arbre binaire classique nécessiterait que l'un des signaux de sélection soit distribué à 32 multiplexeurs, ce qui est excessif (ou lent) pour un ASIC ou un FPGA. À moins d’en être spécialement interdit, un synthétiseur logique tentera de répliquer des portes logiques pour couper le fil en 3 portions indépendantes par exemple (ce qui ajoute logiquement de la latence). Mais si la fréquence de fonctionnement est trop élevée, ce fil risque d'être promu au rang de « signal rapide » comme un signal d'horloge. Or l'horloge est probablement le signal le plus important et d'autres signaux rapides, aux fonctions plus importantes que notre arbre binaire, peuvent lui disputer les ressources de routage, ce qui risque de ralentir l'ensemble du circuit.
Par contre, un fan-out de 12 ou 13 est tout à fait raisonnable dans un FPGA tel que le vénérable ProASIC3. Ainsi, non seulement la latence de l'arbre est réduite, mais il ne va pas utiliser de fils de routage rapides nécessaires pour les autres parties du circuit.
Vous me direz qu'un MUX64 n'est pas une bête courante dans un processeur et qu'il n'est pas nécessaire de s'attarder dessus. Pourtant j'en ai rencontré un dans mon dernier CPU 8 bits, le YGREC8 [5]. Ce MUX64 est apparu dans la partie qui gère le debug sur port série synchrone, servant à espionner et à contrôler le cœur en passant par un port SPI ou des broches GPIO.
Ce port de debug a besoin de lire beaucoup d'informations internes, comme la valeur des différents bus, et 64 bits sont très rapidement nécessaires. Cependant, les techniques classiques (à base de registre à décalage) pour réaliser les circuits SPI ont plusieurs défauts, qui sont pires si le circuit est un esclave.
- D'abord, un seul signal d'horloge est requis pour contrôler les 64 bits du long registre à décalage, mais il sera promu au rang de signal critique par le synthétiseur. Nous retombons dans le problème soulevé dans les paragraphes précédents : cela occupe des ressources précieuses.
- Ensuite, il faut charger le registre à décalage lors du premier cycle, donc chaque étage de la chaîne requiert un multiplexeur qui sélectionne entre le bit à lire, et le bit précédent. Comme par hasard, le même problème de fan-out et de synchronicité se reproduit : ces 64 multiplexeurs ont besoin d'un signal puissant, tout comme l'horloge. Dans un FPGA, ce n'est plus un, mais deux réseaux de signaux rapides qui sont alors accaparés !
- Enfin, de nombreux soucis surgissent quand on examine de près le séquencement du système. Lorsqu'un signal passe d'un domaine d'horloge à un autre, la resynchronisation peut devenir un gros casse-tête. C'est le genre de difficulté qui mène le Raspberry Pi à prendre 9 cycles d'horloge au lieu de 8 pour transférer un octet sur le port SPI...
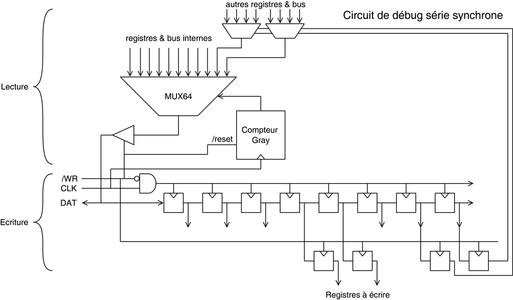
Habituellement, la performance du port de debug n'est pas critique, mais elle doit utiliser le moins de portes logiques possible pour ne pas impacter le système. Et comme c'est le registre à décalage qui pose le plus de problèmes, il vaut mieux simplement l’éliminer. Il reste alors les multiplexeurs, qui sont assemblés dans un grand arbre, et nous avons économisé deux signaux d'horloge. C'est possible si les valeurs à sérialiser sont stables, lorsque le système est mis en pause. Ainsi, non seulement l’approche de la sérialisation par multiplexeur économise beaucoup de portes logiques, mais elle préserve aussi les ressources de routage (voir figure 13).
Fig. 13 : Le circuit de debug du processeur utilise une interface synchrone bidirectionnelle (half-duplex). La partie d’écriture est un simple registre à décalage de longueur arbitraire. La partie de lecture cependant sérialise 64 bits (provenant d’un ABCE) sous le contrôle d’un compteur à code Gray (le code binaire réfléchi empêche les transitions parasites). Le nombre de bits lisibles peut être étendu avec des multiplexeurs supplémentaires, contrôlés par des bits en écriture.
Évidemment, tout n'est pas si simple, car l'ABCE mélange l'ordre des feuilles. Utiliser un compteur binaire naturel (ou mieux, un compteur de code Gray) ne pose en théorie aucun problème puisqu'on peut réassigner les feuilles de l'arbre à des zones du circuit qui ne sont pas contiguës. Cependant les nombreux croisements ainsi que l'allongement des fils qui en résulteraient réduiraient la routabilité de l'ensemble des fils du circuit. Le placement automatique des portes logiques créerait un infâme plat de spaghettis. Il est donc important de garder une certaine localité dans la structure et nous devons reporter la complexité dans le compteur, qui créera une séquence de nombres très inhabituelle, ou mieux : dans le logiciel de gestion, qui réordonnera les bits.
7. Et plus si affinités
La maîtrise de la consommation dynamique et statique est critique pour améliorer l’efficacité énergétique des circuits intégrés, mais elle est vitale pour les circuits cryptographiques. Les attaques d’analyse dynamique de consommation sont relativement faciles à réaliser et un arbre binaire classique « fuit » énormément d’informations par la broche d’alimentation. Si une clé cryptographique contrôle le multiplexeur, les pics de courant d’alimentation seront quasiment linéairement proportionnels à l’adresse sélectionnée, le multiplexeur agissant alors comme un convertisseur numérique-analogique rudimentaire. Il suffira presque de lire la clé sur l’oscilloscope...
Les permutations de bits d’adresses sont des techniques connues de confusion des données et avec un ABCE, presque tous les bits ont le même poids, donc la même consommation, et il devient plus difficile (mais pas impossible) de déterminer quel bit d’adresse a changé. Évidemment, des techniques plus élaborées existent spécialement pour la cryptographie, mais en général, il est toujours préférable de réduire le bruit généré par les circuits intégrés...
Conclusion
Cet article a présenté quelques applications simples, déjà réalisées ou envisagées, des ABCE, et montré leurs avantages. Ils sont une amélioration substantielle des multiplexeurs classiques, qu’ils peuvent remplacer dans la plupart des cas. Les exemples du banc de registre et du sérialiseur synchrone montrent même qu’en résolvant le gros souci de fan-in, les ABCE peuvent aussi trouver de nouvelles applications, auparavant inaccessibles aux multiplexeurs classiques. Évidemment, ce n’est pas une solution magique à tout et vous devrez examiner toutes les options pour choisir la meilleure, car après tout, l’ingénierie est l’art des compromis. En ce qui me concerne, je choisis de retourner à mes processeurs et mes algorithmes de compression, après avoir étudié les ABCE dans deux articles. J’espère qu’ils vous sont utiles et que l’étude sera poursuivie par d’autres personnes !
Références
[1] GUIDON, Y. : « À la découverte des Arbres Binaires à Commande Equilibrée », GNU/Linux Magazine n°215, mai 2018, p. 10 à 21 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-215/A-la-decouverte-des-Arbres-Binaires-a-Commande-Equilibree
[2] Wikipédia, « Arbre bicolore » : https://fr.wikipedia.org/wiki/Arbre_bicolore
[3] OEIS, « Suite A000045 » : https://oeis.org/A000045 - Fibonacci numbers: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1.
[4] Wikipédia, « FO4 » : https://en.wikipedia.org/wiki/FO4 - Fan-out of 4 is a process-dependent delay metric used in digital CMOS technologies.
[5] Le processeur YGREC8 : http://www.ygrec8.com/



 Ajouter à une liste de lecture
Ajouter à une liste de lecture