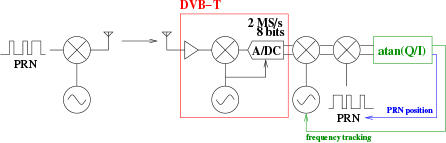
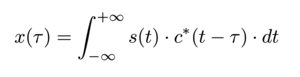Le positionnement par traitement de signaux émis par satellites - GNSS ou Global Navigation Satellite Service - est devenu tellement courant que nous ne pensons plus aux contraintes techniques de cette fascinante technologie. Basés sur une constellation de satellites embarquant chacun plusieurs horloges atomiques, les signaux datés précisément permettent par triangulation de positionner le récepteur. Une connaissance précise du protocole de communication permet d’envisager des applications bien plus intéressantes que le simple positionnement : nous allons ici nous efforcer, après avoir acquis les signaux radiofréquences au moyen d’un récepteur initialement conçu pour recevoir la télévision numérique terrestre (DVB-T), de remonter à l’information brute transmise par les satellites. Nous verrons que plusieurs boucles d’asservissement sont nécessaires pour retrouver la fréquence de la porteuse et les messages de navigation, et nous aborderons les subtilités de l’extraction du signal d’un satellite en particulier alors que tous les membres de la constellation émettent sur la même fréquence de porteuse (1575,42 MHz). L’obtention des bits du message de navigation démontre la validité de notre approche.
Nous avons déjà décrit plusieurs fois dans ces pages l’utilisation d’un récepteur de télévision numérique terrestre pour recevoir des signaux radiofréquences, traités par GNURadio pour en extraire les informations contenues dans la modulation de la porteuse [1]. Nous sommes allés jusqu’à démontrer la réception de signaux émis par des satellites en orbite basse, à quelques centaines de kilomètres d’altitude, encodés selon des modulations classiques de fréquence et d’amplitude. Les signaux GPS avaient été reçus au moyen de l’utilisation de gnss-sdr1, un outil libre, mais trop complexe pour appréhender les subtilités du traitement de signaux issus de la constellation de satellites de navigation par la lecture des codes sources. Dans la prose qui va suivre, le montage expérimental pour acquérir les signaux se réduit à un récepteur de télévision numérique terrestre compatible avec rtl-sdr2 - à savoir un récepteur radiofréquence de type E4000 ou plus probablement R820T(2) suivi d’un convertisseur analogique-numérique Realtek RTL2832U - une antenne GPS active telle que par exemple celle commercialisée par Lextronic3 pour 12 euros, et un T de polarisation formé d’un condensateur pour protéger l’entrée radiofréquence du récepteur (une centaine de picofarads) et une inductance (quelques microhenrys) pour empêcher la remontée du signal radiofréquence dans l’alimentation de l’antenne active qui sera fournie par un port USB. Notez que gnss-sdr ne peut fonctionner qu’avec le récepteur Elonics E4000, désormais obsolète, et que l’application au Rafael Micro R820T est nouvelle, d’autant plus que nous verrons que ce dernier est affecté d’un biais de fréquence énorme, encore plus important que le E4000 dont l’exactitude était déjà médiocre. Ainsi, l’investissement financier pour reproduire ces expériences est de l’ordre d’une trentaine d’euros.
Nous allons voir que le décodage du signal GPS se traduit par l’enregistrement du signal radiofréquence (quelques secondes suffiront), et l’intercorrélation par des copies locales des codes représentant tous les identifiants de satellites possibles. Puisque la démodulation d’un signal modulé en phase n’est possible que si la porteuse a été annulée par l’oscillateur local, la recherche de la présence d’un signal GPS dans une acquisition radiofréquence passe de plus par un calcul relativement lourd dans lequel nous balayons, pour chaque code identifiant chaque satellite, tous les décalages de fréquence Doppler possibles.
1. Introduction
Nous désirons pousser au cran supérieur la démonstration de la puissance du traitement numérique de signaux radiofréquence et la flexibilité du récepteur de télévision numérique terrestre (DVB-T) par l’analyse de signaux dans la bande radiofréquence occupée par le GPS [2, 3]. Le GPS - Global Postionning System - est une des constellations de satellites permettant la localisation du récepteur par triangulation, et fait partie des objectifs plus généraux du GNSS - Global Navigation Satellite Service - aussi mis en œuvre par la Russie avec GLONASS (selon un protocole de communication très différent qui ne sera pas abordé ici) et sera peut être un jour mis en œuvre par l’Europe avec Galileo, la Chine avec Beidou ou, moins avancé, par l’Inde avec IRNSS. Le positionnement du récepteur résulte d’une triangulation précise des signaux émis par plusieurs satellites dont la position dans l’espace est supposée très bien connue, et dont le temps de vol des signaux entre émetteur et récepteur est estimé avec précision. Rappelons qu’un signal électromagnétique se propage à environ 300 m par microseconde, et que le positionnement avec une résolution de 3 m nécessite d’estimer le temps de vol du signal à environ 10 ns près après un temps de vol de plus de 70 ms. La capacité à retrouver une information temporelle aussi précise permet de remonter à des informations bien plus intéressantes et riches que la position [4] : mentionnons par exemple la densité d’électrons dans l’ionosphère, la concentration d’eau dans l’atmosphère, voire les ondes propagées dans l’air suite à un séisme. Les signaux reçus au sol sont aussi exploitables pour des applications de RADAR4 dans lesquelles les propriétés du réflecteur sont déduites de l’analyse du signal direct reçu du satellite et du signal réfléchi par la cible : taux d’humidité (ou coefficient de réflexion) ou distance de la cible.
Finalement, les perspectives de reproduire au sol une horloge combinant les propriétés de stabilité des diverses sources atomiques embarquées dans les satellites ouvrent la perspective de diffuser un temps précis en de nombreux sites géographiquement distincts [5, 6], un objectif qu’il est nécessaire d’atteindre pour toutes les applications de localisation d’événements par interférométrie (radiotélescope, positionnement d’impacts de foudre par exemple5). Bien que nous appelions communément GPS la constellation de satellites émettant des signaux de fréquence très stables dans le temps, les horloges embarquées ont connu plusieurs évolutions pour en améliorer les performances et la robustesse : initialement équipé de trois horloges au rubidium, référence secondaire de fréquence, une quatrième horloge au césium (référence primaire puisque la seconde est définie à partir de la fréquence de transition d’un atome de césium [7]) a été ajoutée une fois une version spatialisée fonctionnelle, pour finalement être retirée lorsque les gains escomptés n’ont pas été observés [8]. Dans l’application qui va suivre, nous allons nous intéresser à une solution de traitement exclusivement logicielle, offrant ainsi la souplesse du prototypage rapide et la flexibilité de s’adapter aux diverses applications mentionnées ci-dessus : l’approche du traitement de signaux radiofréquence défini par logiciel (SDR) démontrera une fois de plus toute sa puissance.
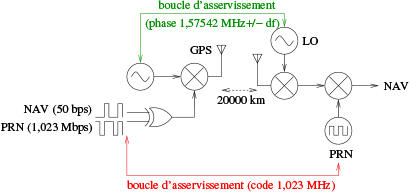
Figure 1 : Modulation de l’information émise par un satellite de la constellation GPS (gauche) lors de sa transmission vers le sol (droite). Notre objectif au sol est de remonter au temps de vol du signal entre le satellite et le récepteur, et d’obtenir les informations de navigation (NAV) portées par le signal.
Le traitement de signaux issus de la constellation de satellites GPS nécessite de répondre à plusieurs questions :
- les satellites sont en mouvement puisque situés sur une orbite entre 20000 et 21000 km d’altitude. Bien que les horloges atomiques embarquées dans les satellites soient extrêmement stables, le mouvement du satellite induit un décalage de fréquence de la porteuse par rapport à sa valeur nominale qu’il faut compenser au niveau du récepteur. Par ailleurs, l’oscillateur cadençant le récepteur de DVB-T est de piètre qualité : il faut que l’identification de la fréquence de la porteuse soit en mesure de compenser les fluctuations de fréquence de la copie locale de la fréquence de porteuse du fait des fluctuations de température (variations aléatoires) et l’écart à la fréquence nominale du fait de la médiocrité de l’assemblage du circuit d’oscillation sur le récepteur DVB-T (biais) ;
- tous les satellites communiquent sur la même fréquence de porteuse : il faut implémenter un mécanisme pour identifier quel satellite a envoyé quel message, et ce malgré les autres messages transmis par les autres satellites sur la même porteuse. Le partage de la bande spectrale par un encodage différent par chaque satellite se nomme CDMA - Code Division Multiple Access - un concept très répandu en communication numérique en général ;
- ayant identifié quelle information est émise par quel satellite et sur quel écart de la porteuse à la valeur nominale, il nous restera à extraire la charge informative encodée dans la phase du signal (Fig. 1). Le mélangeur en émission induit (bit 1) ou pas (bit 0) une rotation de phase de 180° de la porteuse : il s’agit d’une modulation BPSK [1] (Binary Phase Shift Keying) dans laquelle la phase du signal porte un OU-exclusif des bits d’identification (code) et de navigation (message utile).
De façon générale, pour N variables transmises par liaison radiofréquence, il faut N boucles d’asservissement pour retrouver chacun des paramètres de l’émetteur. En liaison radiofréquence, le choix de travailler sur une porteuse - donc de décaler le spectre par rapport à la bande de base (centrée sur 0) - répond aux soucis de partage du spectre radiofréquence et de miniaturisation des antennes permettant la conversion du signal électrique en onde électromagnétique. Nous avons donc au moins deux paramètres à retrouver, la fréquence de la porteuse et la fréquence cadençant le signal transmis, afin de retrouver les informations contenues dans la modulation de la porteuse. En effet, nous n’avons aucune raison de croire que les deux oscillateurs aux deux extrémités de la liaison se comportent de la même façon, et l’identification de la porteuse est une façon de resynchroniser les deux oscillateurs de l’émetteur et du récepteur. Dans le cas du GPS, nous aurons N=3 paramètres libres : la fréquence de la porteuse (entre le signal émis par le satellite et le récepteur au sol), le code identifiant le satellite émetteur, et la fréquence (ou la phase, puisque la fréquence est la dérivée de la phase) à laquelle ce code est transmis. Nous verrons plus bas que la principale subtilité tiendra au mode de modulation qui induit une exploitation de la phase pour deux fonctions - l’asservissement de l’oscillateur local sur la porteuse du signal reçu et l’extraction du signal de navigation émis par le satellite.
En conclusion, les problèmes qu’il nous faudra aborder sont résumés ci-dessous :
Montage expérimental comprenant une antenne active en vue du ciel, un T de polarisation (voir encart au sujet de sa conception), et un récepteur DVB-T relié à un ordinateur.
- tous les satellites de la constellation émettent sur la même fréquence nominale (contrairement à la constellation GLONASS russe). Le récepteur radiofréquence enregistre donc un signal représentatif de la somme des contributions de tous les satellites visibles par l’antenne, dont il faut extraire la composante de chaque satellite individuel. Chaque satellite est identifié par un code unique : il s’agit d’une stratégie de CDMA (Fig. 2) ;
- le signal reçu au sol est sous le bruit thermique, compte tenu de la bande passante d’acquisition nécessaire à traiter les signaux GPS. En effet, tout composant électronique est affecté d’un bruit intrinsèque lié à l’agitation thermique des électrons qui portent l’information électrique dans le conducteur : ce bruit de très grand encombrement spectral est intégré dans la bande de mesure. Il est donc d’autant plus important que la température est élevée et que la bande passante de mesure est importante. Comme il est courant de le retrouver en thermodynamique, la relation entre la température et la densité spectrale de bruit s’effectue au travers de la constante de Boltzman, kB=1,38 x 10−23 J/K, qui se traduit en passant à une unité logarithmique en 10 x log10 (kB· T)=−204 dBW (=-174 dBm) à l’ambiante (T=293 K). L’exploitation d’un signal sous le plancher de bruit thermique est quelque peu déroutante au premier abord, et signifie qu’il n’est pas possible d’observer « simplement » un signal GPS sur un analyseur de spectre sans un traitement spécifique. Nous verrons ainsi comment l’analyse sur une longue durée (1 ms) d’un code bien spécifique permettra d’accumuler de façon cohérente la puissance du signal émis par le satellite afin d’augmenter la puissance du signal et de diminuer le bruit thermique jusqu’à obtenir un rapport signal à bruit positif ;
- enfin, tous ces traitements nécessitent d’extraire l’information contenue dans le signal reçu du satellite et pour ce faire, de s’affranchir de la porteuse radiofréquence. Or un satellite a une fâcheuse tendance à être en mouvement le long de son orbite et donc d’induire un décalage de fréquence variable au cours du temps : nous devons identifier ce décalage de fréquence et l’annuler pour extraire l’information contenue dans la modulation en phase (BPSK).
La réalisation du T de polarisation a déjà été discutée dans [1], mais nous reprenons ici l’application numérique pour le cas de la fréquence de transmission du GPS. Un condensateur C d’une centaine de pF induit une impédance 1/(Cω) de l’ordre de l’ohm à une pulsation ω=2π x 1,5742 GHz tout en bloquant efficacement la composante continue de l’alimentation de l’antenne, et une inductance L de l’ordre de 10 µH induit une impédance Lω de l’ordre de 100 kΩ, nettement supérieure à l’impédance du condensateur et donc un bloqueur efficace contre la propagation du signal radiofréquence dans l’alimentation de l’antenne.
Figure 2 : Principe de communication en CDMA : tous les satellites émettent sur la même fréquence, mais un message encodé selon un code pseudo-aléatoire (PRN) différent. Sur le récepteur, LO est un oscillateur physique autour de 1,57542 GHz, tandis que NCO et PRN sont des implémentations logicielles qui traitent un flux de données numérisées en sortie du premier mélangeur.
Lors de nos mesures de sensibilité visant à établir la puissance incidente nécessaire d’une porteuse autour de 1,5 GHz modulée en fréquence ou en amplitude pour atteindre un rapport signal à bruit en sortie donné (choisi arbitrairement à 10 dB), nous avons vu [1] que la limite de détection d’un récepteur DVB-T est de l’ordre de -95 dBm. Deux questions se posent donc : comment la puissance reçue d’un satellite émettant depuis une orbite située à plus de 20000 km du sol se compare avec cette limite de détection, et comment ces deux valeurs se comparent au bruit thermique intégré sur la bande passante de mesure de 2 MHz.
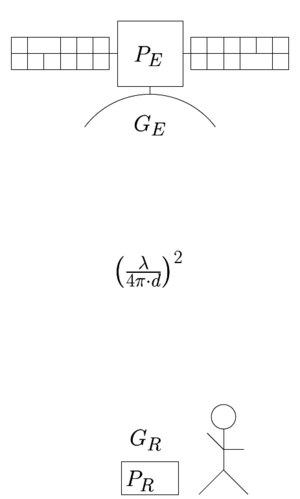
La puissance PE émise par un satellite GPS est de l’ordre de 25 à 50 W, ou +14 à 17 dBW [9], avec une antenne de GE=13 dBi de gain. Après avoir dispersé cette puissance sur une fraction de la sphère entourant le satellite de 21000 km de rayon - la distance entre l’émetteur (satellite) et le récepteur (nous, sur la surface de la Terre) - induisant une perte de 182 dB (Free Space Propagation Loss induisant une atténuation de (4π x d/λ)2 par distribution uniforme de la puissance incidente sur la sphère de surface 4π·x d2 à une distance d de l’émetteur, avec λ la longueur d’onde du signal transmis, 19 cm à 1,57542 GHz), la puissance reçue PR par le récepteur est -155 dBW ou -125 dBm pour une antenne à peu près isotrope de gain GR unitaire (Fig. 3).
Comment se compare cette puissance reçue avec la puissance thermique sur une bande passante de B=2 MHz ? La puissance du bruit thermique pour une antenne visant une région de température T est de kB·x T·x B (avec kB la constante de Boltzman) ou -174 dBm/Hz+10·log10(2 MHz)=-111 dBm. Le bruit thermique est donc 14 dB au-dessus du signal GPS arrivant au sol, donc détecterons-nous l’information utile ?
Figure 3 : Bilan de liaison radiofréquence entre le satellite et le sol.
Le signal transporté par la porteuse issue du GPS a la propriété de suivre un motif connu et distribué sur toute la bande passante de mesure. Il n’est évidemment pas possible de prétendre rompre avec la limite de capacité de canal de Shannon qui nous informe que la bande passante de transmission, C en bits/s, est liée à la bande passante du canal B en Hz et au rapport signal à bruit SNR (sans unité) de la liaison par C=B x·log2(1+SNR) : augmenter le nombre d’interlocuteurs nécessite d’augmenter la bande passante, ici en ajoutant au message communiqué (les bits du message de navigation) un identifiant unique à chaque satellite, communiqué beaucoup plus rapidement que le message à transmettre. La recherche de ce motif d’identification nous permettra d’extraire une information pertinente du bruit.
Le code pseudo-aléatoire (voir encart 1 pour une description détaillée de ce point) codé sur 10 bits, généré au rythme de 1,023 MHz, se répète tous les 210−1=1023 valeurs, ou 1 kHz. Le signal est donc intégré de façon cohérente sur une durée de 1 ms, induisant un gain de compression de 1,023·x 106 x 10−3=1023 ou 30 dB. Le gain de compression a été abordé dans [10] : il s’agit de la propriété de l’intercorrélation d’accumuler de façon cohérente l’énergie du motif connu par lequel nous intercorrélons le signal acquis, tandis que le bruit se moyenne progressivement autour de 0 et n’induit pas cette accumulation cohérente. Intégrer sur 10 périodes consécutives du code recherché fait monter cette valeur à 40 dB. Par conséquent, le rapport signal à bruit après extraction de l’information pertinente est SNR=(−125+30)−(−111)=16 dB. Le signal sera donc clairement visible au-dessus du bruit après traitement.
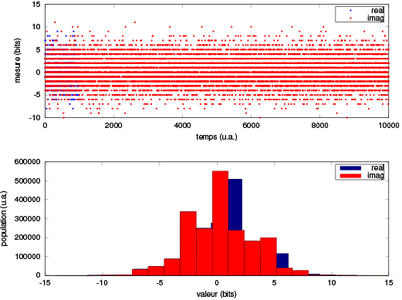
Par ailleurs, est-ce que ces signaux sont au-dessus du plancher de bruit du récepteur (Fig. 4) ? L’antenne active équipant la majorité des récepteurs GPS intègre un préamplificateur faible bruit de +27 dB de gain. La puissance du signal reçu par le DVB-T est donc de -125+27=-98 dBm. Cette valeur est dangereusement proche du plancher de -95 dBm que nous avions mesuré [1], mais le plancher a été obtenu en vue d’induire un rapport signal à bruit de 10 dB après démodulation AM ou FM. Nous serons donc en mesure d’observer un signal exploitable.
Figure 4 : Mesures par récepteur DVB-T des coefficients I et Q autour de 1,57542 GHz. En haut l’évolution temporelle, et en bas l’histogramme des mesures. Notez que seuls 3 bits (la majorité des mesures se trouve dans les valeurs entre -4 et +4) des 8 bits disponibles sur ces récepteurs sont utilisés.
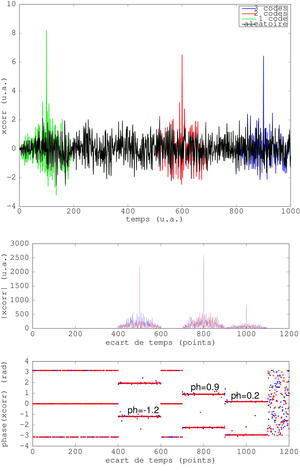
Nous illustrons le concept de codage de la source émettrice par une petite simulation simple sous GNU/Octave. Supposons que nous émettions uniquement du bruit, aleat=rand(1000,1); que nous prenons soin d’être de valeur moyenne nulle, aleat=aleat-mean(aleat); (nous laissons le soin au lecteur d’observer les artéfacts induits par l’intercorrélation sur des signaux de valeur moyenne non-nulle - en se rappelant que l’intercorrélation de deux fonctions constantes donne un triangle). Supposons que maintenant un message soit encodé sous forme de séquence pseudo-aléatoire connue superposée au signal : code=rand(100,1); code=code-mean(code); que nous sommons en divers emplacements au signal original aleat(1:100)=aleat(1:100)+code; et aleat(end-99:end)=aleat(end-99:end)+code;. Nous observons que l’intercorrélation entre le motif recherché et le signal reçu ainsi synthétisé présente des maxima pour chaque position du signal : plot(xcorr(code,aleat)). Propriété fort intéressante, l’intercorrélation étant une transformation linéaire, elle porte aussi la phase encodée dans le signal. Ainsi, on reprend l’exemple précédent appliqué cette fois à un code complexe qui porte une information sous forme de phase ϕ de la forme exp(jϕ). Alors
signal=rand(1000,1); signal=signal-mean(signal);
code=rand(100,1); code=code-mean(code);
signal(1:100)=signal(1:100)+100*code*exp(j*0.2);
signal(201:300)=signal(201:300)+300*code*exp(j*0.9);
code2=rand(100,1); code2=code2-mean(code2);
signal(501:600)=signal(501:600)+300*code2*exp(-j*1.2);
subplot(211);plot(abs(xcorr(code,signal)));hold on
plot(abs(xcorr(code2,signal)),'r');xlim([0 1200])
subplot(212);plot(angle(xcorr(code,conj(signal))),'.');hold on
plot(angle(xcorr(code2,conj(signal))),'r.');xlim([0 1200])
Haut : magnitude de l’intercorrélation lorsque le code recherché a été sommé à un signal aléatoire pour trois retards différents. Bas : en haut la magnitude de l’intercorrélation, et en bas la phase de l’intercorrélation qui porte bien l’information (ph) introduite dans la phase du code. Cette fois, l’intercorrélation est complexe.
Tableau 1 : Illustration de l’encodage de l’information par un signal pseudo-aléatoire connu.
Nous notons par ailleurs une propriété qui sera au cœur de nos analyses par la suite : la phase de l’intercorrélation reproduit l’encodage de phase sur le signal initial. La démonstration se fait simplement en considérant que l’intercorrélation du signal avec le motif connu est un processus linéaire : si nous nommons x(τ) l’intercorrélation du signal acquis s avec le code c en l’absence de codage de phase, alors
(noter que nous avons pris ici la définition de l’intercorrélation pour des éléments complexes pour laquelle nous utilisons le complexe conjugué d’un des termes - sans ce complexe conjugué nous obtiendrons bien une phase de l’intercorrélation dépendante de la phase du code, mais de signe opposé). Si maintenant nous ajoutons un terme de phase à la copie c' du code introduite dans le signal, tel que c'(τ)=c(t)· exp(jϕ) l’intercorrélation devient
donc nous retrouvons bien ϕ dans la phase de l’intercorrélation. Ainsi, si c -> c·exp(jϕ), alors x -> x·exp(jϕ). Le codage BPSK introduit par GPS sur le code se retrouvera dans la phase de l’intercorrélation.
La somme, version discrète de l’intégrale, de c par s s’accumule de façon cohérente lorsque s présente une séquence de c. Cette opération est répétée pour toutes les translations τ possibles de c dans s : xcorr(c,s)(τ)=∫−∞+∞ c(t)·x s*(t−τ)·x dt. Si le signal acquis par le récepteur radiofréquence est la somme de plusieurs contributions dont chacune est encodée par une signature ck(t), alors il est souhaitable que xcorr(ci,cj)≃ 0 si i≠ j et xcorr(ci,ci)≃ 1. De cette façon, seule l’intercorrélation du signal s(t) par le « bon » code induira une intercorrélation non-nulle (section 3) : il s’agit de la condition d’orthogonalité qui sera discutée ci-dessous.
Dans le cas particulier du GPS, le code c(t) est généré par deux générateurs pseudo-aléatoires (Linear Feedback Shift Register - LFSR) imbriqués. La description détaillée de ce générateur de code - nommé par la suite PRN - n’a que peu d’intérêt, la seule information utile étant qu’il existe 37 déclinaisons de ces codes vérifiant les propriétés de base orthonormale citée ci-dessus, dont seules les 31 premières sont utilisées pour le moment.
2. Orthogonalité des codes
Le principe de l’extraction du code modulé en phase (BPSK) pour retrouver quel satellite a émis un signal sur la porteuse de fréquence commune à toute la constellation consiste à intercorréler le signal reçu par le récepteur radiofréquence avec chacune des séquences identifiant chaque satellite.
Le terme d’orthogonalité traduit que seule la corrélation d’un code avec une copie de la même séquence de bits génère un résultat non nul. Dans le cas du GPS, le code pseudo-aléatoire qui permet d’identifier la transmission issue de chaque satellite est issu d’un registre à décalage de 10 bits de long. Yann Guidon a déjà longuement expliqué les propriétés des LFSR [11] : GPS étend un peu la complexité en imbriquant deux LFSR. Nous nous sommes contentés, pour la génération des séquences pseudo-aléatoires, d’exploiter la routine Matlab (sous GNU/Octave) disponible à http://www.mathworks.com/matlabcentral/fileexchange/14670-gps-c-a-code-generator. Cependant, nous allons exploiter ce programme pour observer expérimentalement d’une part l’orthogonalité des codes, mais aussi leur robustesse à un décalage des fréquences d’échantillonnage (ou, ce qui revient au même, de la porteuse modulée par ces codes).
Le code est échantillonné à 1,023 MHz, et un LFSR de 10 bits de long présente une répétition tous les 210−1=1023 bits. Ainsi, nous obtiendrons, si notre séquence est correcte, un maximum d’intercorrélation chaque fois que notre copie locale de la séquence s’accorde avec le signal reçu, donc toutes les 1 ms. Par ailleurs, l’intercorrélation porte l’information de phase qui a été imprimée par le modulateur sur la porteuse : l’exploitation de la phase de l’intercorrélation chaque fois que cet estimateur est maximum nous permettra de remonter aux symboles transmis. La différenciation des informations issues de chaque satellite s’obtient alors en jouant les diverses séquences des divers satellites visibles dans le ciel à un instant donné.
Pour rappel, l’intercorrélation ne se calcule que très rarement dans le domaine temporel ou spatial : on lui préférera en pratique un passage dans le domaine spectral (de Fourier) pour profiter du gain en temps de calcul de la transformée de Fourier rapide. En effet, la transformée de Fourier d’une convolution est un produit des transformées de Fourier des fonctions convoluées, tandis que le retournement temporel pour passer d’une convolution à une corrélation s’obtient en prenant le complexe conjugué d’une des deux transformées de Fourier.
Une subtilité tient cependant au fait que le code pseudo-aléatoire module une porteuse. Or aucune contrainte ne force l’oscillateur local du récepteur de DVB-T à générer exactement la même fréquence que l’horloge atomique à bord du satellite du GPS. Au contraire, la fréquence émise par le satellite est décalée par effet Doppler - décalage variable en fonction de la position du satellite dans le ciel - et l’oscillateur local dérive avec son environnement (température, contrainte [1]). Ne connaissant pas a priori ce décalage de fréquence, nous devons chercher toutes les valeurs possibles afin d’identifier une première estimation grossière, afin d’affiner par la suite jusqu’à annuler la différence des fréquences par une boucle d’asservissement appropriée. Nous n’en sommes pas encore là : pour le moment, afin de minimiser le temps de calcul, nous devons estimer combien de pas de fréquence seront nécessaires pour la recherche. Plus l’excursion potentielle de l’écart des fréquences est importante, plus il faudra d’étapes de calcul pour un pas donné. D’un autre côté, si l’intercorrélation des codes pseudo-aléatoires est robuste à un certain décalage des fréquences entre oscillateur local et porteuse reçue, alors le pas de fréquence pourra être agrandi, afin de réduire le temps de calcul. La Fig. 5 propose le résultat de l’intercorrélation lorsqu'une des copies du code pseudo-aléatoire est échantillonnée 0,3 et 1% plus rapidement que l’autre. Nous constatons que 1% d’erreur se traduit par un effondrement et un étalement du pic d’intercorrélation - encore visible dans cet exemple idéal, mais inutilisable sur des signaux bruités réels - et un décalage de plus de quelques fractions de pourcent se traduira par un pic d’intercorrélation noyé dans le bruit. Nous avons empiriquement constaté qu’une recherche par pas de 100 à 500 Hz fournit un résultat acceptable. Compte tenu du décalage Doppler de ±5 kHz pour un récepteur fixe [1], cela fait tout de même 31 x 100=3100 calculs d’intercorrélation à effectuer pour trouver les satellites visibles dans le ciel (31 codes pseudo-aléatoires possibles, et 100 pas de fréquence). Ce calcul suppose par ailleurs que l’oscillateur local n’est pas biaisé, ce qui n’est pas le cas des DVB-T faible coût que nous utilisons. Nous avons observé des décalages de ±100 kHz (ou ±60 ppm à 1,5 GHz), ce qui étend considérablement la plage de recherche initiale en multipliant par 20 la durée du calcul. Ce dernier aspect justifie par exemple les recherches en cours sur des oscillateurs compacts d’exactitude améliorée (référencés sur une transition atomique [12]) afin de réduire le temps d’acquisition (nom communément fourni pour cette étape du calcul lorsque le récepteur GPS vient d’être allumé) des signaux GPS.
Figure 5 : Haut : en bleu l’intercorrélation de deux codes pseudo-aléatoires différents (fournissant une estimation du niveau de bruit induit par ce calcul), et intercorrélation du code avec lui-même (rouge) ou des homothéties de l’axe du temps par 1% (vert) ou 0,3% (cyan). Bas : zoom sur le pic d’intercorrélation pour visualiser l’étalement et l’effondrement lorsque l’écart des fréquences d’échantillonnage devient trop important.
3. Principe de la démodulation
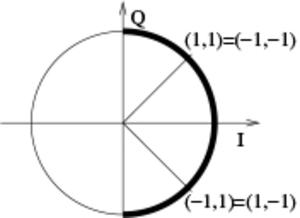
Nous avions discuté dans un article précédent [1] la nécessité de retrouver la porteuse du signal reçu afin de la compenser et donc extraire l’information codée dans la phase du signal acquis. Pour rappel, un signal s(t) est reçu par un récepteur radiofréquence, contenant une modulation de phase ϕ(t) tel que s(t)=sin(ωR·x t+ϕ(t)), avec ωR la pulsation du signal émis. La transposition de fréquence par mélange du signal reçu avec un oscillateur local ωL suivi d’un filtre passe bas génère le signal numérisé par convertisseur analogique-numérique rapide de la forme S(t)=sin((ωR−ωL)·x t+ϕ(t)). Nous ne pourrons extraire ϕ(t) qu’en annulant la contribution de la rotation de phase (ωR−ωL)·x t, ce qui se traduit par un asservissement de ωL sur ωR. En effet, ωR varie du fait du décalage Doppler alors que le satellite évolue le long de son orbite, tandis que ωL varie à cause des fluctuations au sol de la température ou de la contrainte appliquée sur le résonateur à quartz. Finalement, il est classique de considérer un mélange non seulement par sin(ωL·x t) qui fournit une estimation de cos(ϕ(t)) lorsque ωR=ωL, mais aussi par sin(ωL·x t+π/2)=cos(ωL·x t) afin de générer, lors du mélange, sin(ϕ(t)) : ces deux composantes sont appelées les composantes I et Q (en phase et en quadrature), utiles pour déduire la phase ϕ(t)=arctan(Q,I).
Tout ceci fonctionne fort bien pour une unique porteuse modulée en phase : nous avions présenté auparavant comment une astuce de traitement du signal - la boucle de Costas - permet de s’affranchir de la modulation et ainsi d’asservir ωL sur ωR afin d’extraire ϕ(t). Pour rappel, dans le cas particulier de la modulation à deux états BPSK, ϕ(t)∈[0;π] et 2ϕ=0 [2π] donc la mise au carré du signal reçu élimine la modulation en phase.
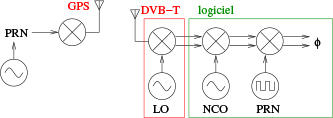
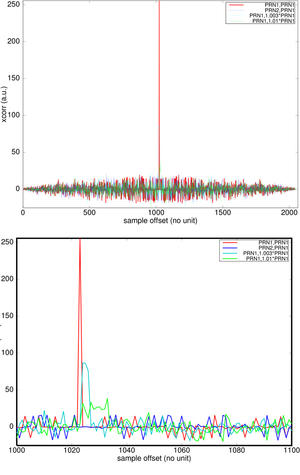
Le problème est plus complexe en CDMA lorsque la somme des contributions de plusieurs émetteurs est superposée et acquise. Dans ce cas, nous devons identifier la composante de chaque émetteur et travailler sur une démodulation de chacun de ces signaux individuellement. Le secret de cette stratégie de détection tient dans l’intercorrélation du signal reçu avec une copie locale du code identifiant chaque émetteur (Fig. 5). Grâce à la propriété d’orthogonalité des codes, seul le signal issu du « bon » satellite induit un maximum significatif de la magnitude de l’intercorrélation avec le « bon » code (Fig. 7).
Figure 6 : Principe de la réception en CDMA : nous devons d’une part retrouver la porteuse du signal reçu, mais aussi l’horloge qui a servi à cadencer le code, puisque les deux horloges (échantillonnage au sol et générateur pseudo-aléatoire dans l’espace) n’ont aucune raison d’être synchrones, ne serait-ce qu’à cause de la médiocre qualité de l’horloge qui cadence l’ADC du DVB-T.
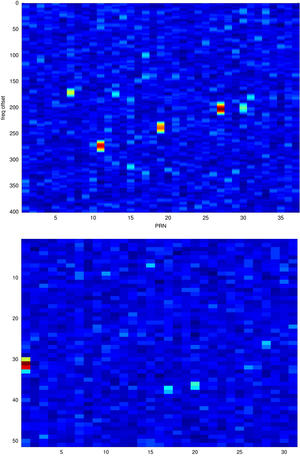
Figure 7 : Haut : une multitude de satellites sont visibles, dont PRN7, PRN11, PRN19, PRN27, et PRN30. Bas : seul PRN1 fournit un signal puissant, PRN17 et PRN20 sont plus faiblement visibles.
4. Acquisition du signal
Commençons par le commencement : nous acquérons un signal dans la bande de fréquence du GPS, sans aucune information de quel satellite est visible ni de la position de la constellation dans le ciel. Nous devons donc rechercher de façon exhaustive toutes les possibilités pour trouver l’identifiant des satellites visibles, et le décalage Doppler induit par leur position le long de leur orbite.
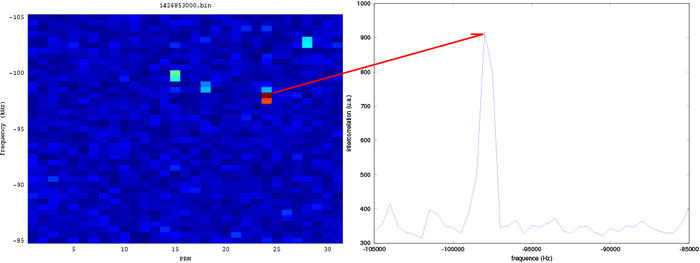
Figure 8 : Haut : carte des satellites visibles à un instant donné (abscisse : PRN, ordonnée : décalage en fréquence). Bas : évolution de l’intercorrélation en fonction du décalage en fréquence pour le satellite numéro 31, le plus visible.
Lors de la recherche exhaustive des fréquences permettant de compenser le décalage Doppler, l’expérience montre que le pas de balayage en fréquence doit être au plus de 100 Hz, faute de quoi le pic d’intercorrélation n’apparaîtra pas, car la modulation en phase est cachée dans la dérive de phase liée à l’écart de l’oscillateur local à la porteuse du signal reçu. Nous avons vu (section 2) que pour un récepteur fixe, le décalage Doppler est au plus de ±5 kHz, donc il s’agit de balayer 100 points de fréquences et 31 PRN possibles. Cependant, nous devons en plus tenir compte de l’énorme biais des oscillateurs locaux des récepteurs de télévision numérique terrestre : nous avons observé des écarts de ±60 ppm entre la valeur nominale de l’oscillateur et la valeur observée, une valeur médiocre, mais peu surprenante pour de l’électronique grand public. Un tel décalage se traduit par une recherche sur une plage de ±100 kHz, qui multiplie par 20 le temps de recherche lors de l’étalonnage du récepteur. Cette opération n’est cependant nécessaire qu’une fois par récepteur DVB-T, et on se contentera ultérieurement de décaler la plage de fréquences analysées du biais observé (Fig. 8).
Nous illustrons l’identification des satellites sur une longue séquence en effectuant l’acquisition automatique, toutes les 5 minutes, d’une seconde de signal dans la bande de fréquence du GPS suivi d’une recherche des satellites présents. L’automatisation de l’acquisition s’obtient en remplaçant l’enregistrement depuis gnuradio-companion par l’utilisation de rtl-sdr qui prend en argument la fréquence de l’oscillateur local (i.e. de quelle fréquence sera transposé le signal reçu sur l’antenne), la fréquence d’échantillonnage et la durée d’écoute. En pratique, cela donne while true; do nom=`date +%s`;echo $nom; rtl_sdr -f 1575420000 -s 2000000 -g 42 -n 200000 ${nom}.bin ;sleep 300;done.
Le fichier résultant de chaque acquisition contient des données encodées sur 8 bits, signées, interlaçant coefficients I et Q. Sous GNU/Octave, les données sont lues par f=fopen('1426853000.bin');x=fread(f,inf,'uchar');zz=x(1:2:end)-127+i*(x(2:2:end)-127);, le reste du traitement étant le même que celui proposé auparavant. Un film présentant l’évolution temporelle, sur une durée totale de 54 heures, des satellites visibles illustre le défilement puisque l’altitude des orbites est inférieure à l’orbite géostationnaire et la succession des divers satellites visibles depuis un point donné sur Terre. Le volume de données est conséquent : chaque fichier contenant 1 seconde d’enregistrement à 2 MS/s occupe 4 MB, soit un volume total pour les 54 h d’enregistrement de l’ordre de 2 GB. Le film résultant de ce traitement est disponible à http://jmfriedt.free.fr/gps_movie.avi.
Un exemple de traitement systématique de fichiers acquis par la méthode décrite ci-dessus est proposé. Dans un premier temps, nous chargeons tous les fichiers, retirons la valeur moyenne, définissons la gamme de décalage fréquence (dépendant du récepteur - ici un récepteur avec un biais de l’ordre de -95 kHz auquel nous ajoutons les ±10 kHz de décalage Doppler et de dérive thermique) ainsi que l’axe du temps, dont le pas est donné par l’inverse de la fréquence d’échantillonnage fs
d=dir('./1*.bin');
for k=1:length(d)
f=fopen(d(k).name)
x=fread(f,inf,'uchar'); x=x(1:2:end)-127+i*(x(2:2:end)-127); fs=2.0; % MHz
freq0=[-10.5e4:500:-8.5e4];
x=x(1:2e5);
time=[0:1/fs/1e6:length(x)/fs/1e6]';time=time(1:end-1);
Ayant chargé chaque fichier, nous allons générer une copie locale de chaque code PRN numéro m dans a, le décaler de la fréquence freq par multiplication du signal acquis par un signal périodique de phase freq*time, puis effectuons l’intercorrélation pour recherche le motif ainsi synthétisé dans le signal acquis
for m=[1:31]
a=cacode(m,fs/1.023); a=a-mean(a);
l=1;
m
for freq=freq0 % run through possible frequency offsets
mysine=exp(j*2*pi*(-freq)*time);
xx=x.*mysine; % frequency shift the signal
[u(l,m),v(l,m)]=max(abs(xcorr(a,xx))); % check for cross correlation max.
l=l+1;
end
end
Finalement, pour chaque fichier un graphique proposant la magnitude de l’intercorrélation en fonction du code (abscisse) et du décalage en fréquence (Doppler + dérive thermique + biais) en ordonnée est affiché :
imagesc([1:31],freq0/1e3,abs(u))
xlabel('PRN');ylabel('frequency (kHz)')
title(d(k).name)
end
La séquence d’analyse se résume donc en une recherche exhaustive initiale de tous les codes de satellites possibles pour tous les décalages Doppler possibles : il s’agit de l’étape d’acquisition. Ensuite, connaissant quel satellite est visible, nous traiterons la phase de l’intercorrélation pour extraire la grandeur qui nous intéresse, à savoir la fréquence de la porteuse et le message de navigation. Comme la fréquence ne cesse de se décaler, au rythme de 10 kHz/12 h ou6 0,23 Hz/s, nous devons sans arrêt recaler la fréquence de porteuse pour que l’encodage en phase du message de navigation soit exploitable : cette boucle d’asservissement est au cœur de l’étape de suivi du signal (tracking).
5. Suivi du signal
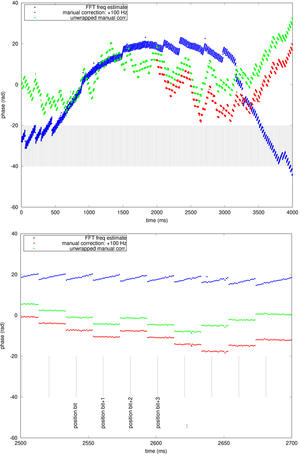
Ayant identifié grossièrement (nous verrons plus bas que « grossièrement » doit signifier une identification à une cinquantaine de Hz près la fréquence de la porteuse afin de permettre à la boucle de s’asservir) la fréquence de la porteuse et l’identifiant du satellite, nous allons remplacer la recherche exhaustive (f, PRN) par un asservissement sur la fréquence reçue. En effet, nous pourrions nous satisfaire de l’identification grossière de la porteuse et nous dire que nous pourrions maintenant simplement extraire la phase avec ses rotations de π pour obtenir le message (Fig. 9). Il n’en est rien : la phase varie bien trop vite pour permettre un décodage de l’information, puisque la phase varie comme Δ f· t avec Δ f le résiduel de l’écart de fréquence entre porteuse du signal incident et l’oscillateur local. À titre d’illustration, nous avons ajusté à la main la fréquence de l’oscillateur local afin que la phase présente une pente nulle au début ou à la fin d’une acquisition de quelques secondes (Fig. 9, gauche). Le décalage de phase entre le début et la fin de cette séquence est suffisant pour rendre l’extraction de l’information de navigation (au rythme de 50 bps ou 20 points issus de l’intercorrélation du PRN avec le signal reçu) inopérante. Il faut donc absolument asservir la phase de l’oscillateur local sur la phase de la porteuse reçue pour extraire l’information pertinente du GPS, ou exploiter les propriétés de la porteuse.
Figure 9 : Phase de l’intercorrélation - extraite pour chaque maximum d’intercorrélation donc toutes les millisecondes - illustrant le décalage lent entre propriétés de la porteuse et de l’oscillateur local qui interdit toute extraction de l’information de navigation en l’absence d’une boucle à verrouillage de phase. Les marques verticales indiquent la position d’un nouveau bit toutes les 20 ms.
La dernière subtilité de mise en œuvre tient sur le fait que la phase de la porteuse présente deux rôles : elle porte l’information transmise (saut de π pour marquer la transition d’un état de bit à l’autre), et doit permettre de servir de discriminateur si la fréquence de l’oscillateur local dévie de la fréquence de la porteuse reçue.
La solution à cette double fonctionnalité est d’exploiter un estimateur de phase qui soit insensible aux rotations de π (au lieu de 2π comme habituellement rencontré). Or il se trouve que la fonction arctan(Q/I) a perdu, dans le ratio de Q par I, l’information de signe de I et Q individuellement. Dans cet état, le résultat de arctan se trouve toujours dans la moitié droite du cercle trigonométrique, ou en d’autres termes est insensible aux rotations de 180 degrés. Cela tombe bien, c’est exactement ce que nous recherchons (Fig. 10).
Nous allons donc exploiter deux estimateurs de phase pour extraire l’information des coefficients I et Q : arctan(Q/I) pour asservir la fréquence de la porteuse, car insensible aux sauts de 180°, et atan2(Q,I) (dans la nomenclature Matlab ou GNU/Octave) qui couvre bien tout le cercle trigonométrique. Nous utiliserons cette seconde fonction pour extraire la phase encodant les bits du code de navigation et vérifier que notre traitement du signal est pertinent. D’autres discriminateurs insensibles aux rotations de phase de 180° sont connus [13].
Figure 10 : Représentation graphique de l’insensibilité aux rotations de phase de 180o de la fonction arctan(Q/I). Que I et Q soient tous deux positifs ou tous deux négatifs se traduira par un angle dans le même quadrant. Au contraire, la fonction arctan2(Q,I) obtient les signes individuels de I et Q et fournira une estimation d’angle sur tout le cercle trigonométrique. La première fonction est donc utilisée pour l’asservissement de la boucle à verrouillage de phase, la seconde pour l’extraction de l’information modulée en BPSK.
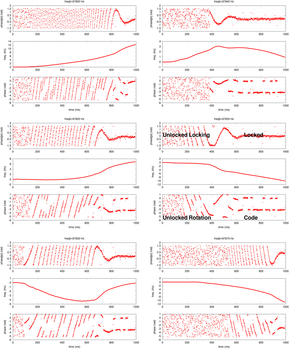
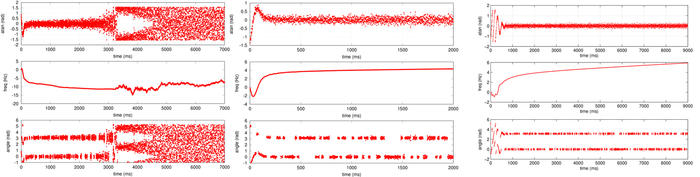
Afin de réaliser une boucle à verrouillage de phase numérique, il faut réaliser une loi de commande qui compense, en variant la fréquence f de l’oscillateur numérique exp(2π j f t) par laquelle est multiplié le signal acquis, la phase aux maxima successifs d’intercorrélation entre le signal reçu et la copie locale du code (maxima qui se répètent toutes les millisecondes). Par ailleurs, comme le générateur de code n’a aucune raison d’être synchronisé avec le générateur du satellite - ne serait-ce que du fait du décalage Doppler qui affecte aussi le code pseudo-aléatoire, même si à moindre mesure que la porteuse (il existe un rapport de 1500 entre les deux fréquences et donc l’effet Doppler qui les affecte) - il faut recaler régulièrement le code sur l’information amenée par la porteuse. Ces deux boucles d’asservissement opèrent simultanément et présentent une difficulté de conception dont la Fig. 14 (gauche) illustre un des échecs avant d’aboutir à un résultat fonctionnel (Fig. 14, milieu et droite).
La première loi de commande contrôle donc la fréquence de sortie d’un oscillateur virtuel commandé en tension (VCO) afin de maintenir la phase de la porteuse reçue constante. La seconde loi, qui ne sera pas détaillée, maintient la position (phase) du code localement généré constante par rapport au signal reçu : cette seconde loi ne sera pas détaillée, car apparaît moins fondamentale au bon fonctionnement du décodage sur les durées de mesures (quelques secondes) qui nous intéresseront ici.
La loi de commande la plus naïve - dite correcteur proportionnel - consiste à affirmer que la fréquence de sortie du VCO est proportionnelle à l’écart entre la fréquence de la porteuse reçue et la fréquence de l’oscillateur local. Un écart de fréquence induit donc une fréquence, les deux termes sont de même unité et la constante les liant est sans unité. Une approche aussi naïve échoue dans la pratique compte tenu du rapport signal à bruit médiocre de nos signaux.
Afin de « lisser » la différence de fréquence observée entre porteuse du signal reçu et oscillateur local, l’approche classique consiste à effectuer une moyenne glissante, ou en d’autres termes une intégration, qui nous amène naturellement au correcteur proportionnel-intégral. L’intégrateur accumule les erreurs successives observées, faisant ainsi lentement dériver la fréquence de l’oscillateur local jusqu’à ce que la fréquence de la porteuse du signal reçu soit égalée. Dans ce cas, l’erreur devient nulle et par la suite, le terme proportionnel prendra le dessus pour maintenir la fréquence du VCO égale à la fréquence de porteuse. Noter que pour un décalage Doppler variant de ±4 kHz en 12 h, la variation de fréquence est de 0,2 Hz/s. Cela signifie que la phase effectue une rotation de 2π toutes les 5 secondes, interdisant tout décodage de la modulation BPSK en l’absence d’un asservissement fiable.
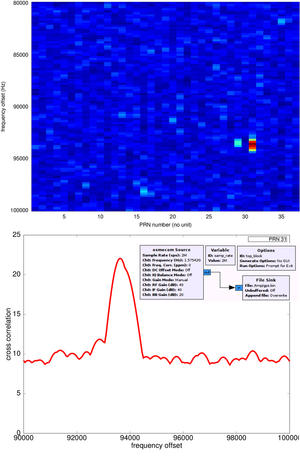
Figure 11 : Gauche : recherche exhaustive de tous les codes des satellites pour identifier quels messages sont exploitables. Droite : évolution de l’intercorrélation en fonction de la fréquence de l’oscillateur local - un décalage de l’ordre de 97850 Hz maximise l’intercorrélation et servira de point de départ lors de la phase de tracking.
Figure 12 : Résultat de l’application de la même boucle d’asservissement sur diverses conditions initiales de la fréquence de décalage entre oscillateur local et porteuse reçue. Pour chaque graphique, en haut la phase modulo π utile pour asservir la fréquence de l’oscillateur local (signal d’erreur), au milieu la correction de la fréquence de l’oscillateur, et en bas la phase du signal, dans laquelle nous retrouvons les bits du message de navigation lorsque l’asservissement est fonctionnel. Les valeurs initiales de fréquence sont respectivement 97800, 97820, 97830, 97840, 97855 et 97875 Hz.
En pratique, la commande du VCO (qui détermine donc sa fréquence de sortie) uk est déduite des erreurs εk−i passées entre fréquence de la porteuse du signal reçu et fréquence du VCO, et des valeurs passées de la commande uk−i. La Fig. 11 indique l’analyse préliminaire (acquisition) pour un jeu de données pour identifier quel satellite est visible avec quel décalage de fréquence, et l’étude se poursuite sur la Fig. 12 pour illustrer l’influence de l’initialisation du suivi de fréquence à l’issue de la recherche exhaustive, mais grossière lors de l’acquisition. Compte tenu de la dépendance aux conditions initiales, une identification de la fréquence initiale à 50 Hz près semble souhaitable lors de la phase d’acquisition. Nous cherchons à asservir, dans le cas de cette boucle à verrouillage de phase, la phase de l’intercorrélation sur une consigne nulle donc le signal d’erreur εk est directement la phase de l’intercorrélation ϕk et ses valeurs passées ϕk−i.
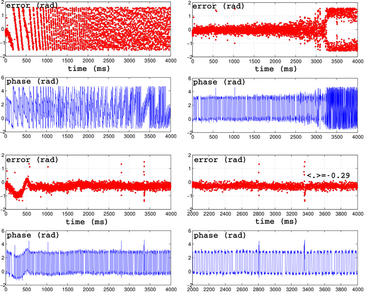
Une approche classique en automatique consiste à déterminer le point de fonctionnement par une variation lente de commande uk en la faisant croître ou décroître en fonction du signe et de la valeur de εk. On choisit donc uk comme étant l’intégrale de εk, ainsi uk=α ∑i=0kεi. En écrivant les premiers termes, u0=αε0, u1=αε0 + αε1 = u0+αε1, u2=αε0 + αε1 + αε2 = u1+αε2, ... la relation de récurrence uk=uk−1+αεk devient évidente. Il reste à déterminer α que l’on choisit en général très petit dans un premier temps (donc la commande varie très lentement au risque, dans le cas présent, de ne pas atteindre l’accrochage de la boucle avant d’atteindre la fin du fichier de données). Ensuite, on augmente α jusqu’à obtenir de bonnes performances en termes de temps d’établissement, en l’occurrence en termes de temps d’accrochage de la boucle à verrouillage de phase (Fig. 13). Quelques tâtonnements permettent de déterminer une valeur de α correcte, en l’occurrence α=0,01. Cependant, on observe sur la Fig. 13 que la valeur moyenne de l’erreur de phase est de -0,29. Ce n’est pas intrinsèquement gênant, mais un autre type de correcteur permet d’éliminer cette erreur et donc de diminuer la probabilité de « décrocher » en cas de fort bruit : le double intégrateur, uk est alors l’intégrale de l’intégrale de εk.
Figure 13 : Influence de la valeur de α sur la convergence de l’asservissement, avec pour chaque graphique en rouge (en haut) la phase modulo π pour l’asservissement du VCO, et en bas la phase déroulée contenant l’information de navigation. (a) α=0,001, la boucle n’a pas le temps de se verrouiller. (b) α=0,1, la boucle se verrouille, mais devient instable (gain α trop grand). (c) Pour 0,005 <α <0,05 la boucle se verrouille, ici α=0,01. (d) Un zoom sur l’erreur montre une phase moyenne de -0,29 rad.
On pose alors
vk = vk−1 + βεk
uk = uk−1 + vk +αεk
d’où l’on déduit que :
uk = 2uk−1 − uk−2 +(α+β)εk − αεk−1
Le système est alors stable et à erreur nulle en choisissant α petit comme précédemment et 0 <β << α.
La loi de commande s’écrit donc uk = 2uk−1 + uk + (α+β)εk − αεk−1 dont il faut identifier les coefficients α, β. Nous avons choisi α=0,0053 et β=0,05α. α et β vont déterminer les propriétés de la loi de commande : un α trop grand va rendre l’asservissement trop rapide et risque de dépasser le point de consigne et donc faire échouer la boucle d’asservissement, tandis que α trop faible induira une convergence trop lente. β détermine la pondération relative des valeurs passées et courantes de la phase de l’intercorrélation. Afin d’analyser les effets de ces divers coefficients, la Fig. 13 fait par exemple varier le coefficient α de part et d’autre de la valeur optimale 0,0053 de 0,0070 à 0,0035.
Le bon fonctionnement de cet algorithme est démontré par l’affichage du message de navigation, issu de la phase calculée par la fonction atan2 (donc capable de distinguer les rotations de phase de π), tel que présenté sur les Figures 12, 13 et 14.
Concrètement, nous chargeons le fichier de données, retirons la valeur moyenne des coefficients I et Q et alternons les octets pour générer le signal zz à analyser :
f=fopen('1426853000.bin');
x=fread(f,inf,'uchar');
zz=x(1:2:end)-127+i*(x(2:2:end)-127); fs=2.0; % MHz
Cette procédure de chargements d’octets non-signés est valable si l’acquisition s’est faite au moyen de rtl-sdr. Si le fichier de données est issu du File Sink de gnuradio-companion, alors les données sont sous forme de flottants (et non d’entiers codés sur 8 bits - d’où un fichier quatre fois plus volumineux) et se chargent au moyen de read_complex_binary fourni dans le répertoire gr-utils des sources de GNURadio.
zz=read_complex_binary('1426853000_grc.bin');
Nous allons nous focaliser sur le satellite de code numéro 31 (qui a été identifié comme présent lors de la phase exploratoire précédente) et en considérant que le décalage entre oscillateur local et porteuse du signal reçu est de l’ordre de 93705 (position du maximum d’intercorrélation dans l’étape précédente)
msatellite=31; % définition du satellite
freq0=-(93705);
N=1; % point de départ de la mesure
Nb_points=30790; % temps étudié en ms
x=zz(N+1:N+Nb_points*1000);
L’axe des temps est défini par pas de l’inverse de la fréquence d’échantillonnage - ici 2 MHz - et divers paramètres (alpha, beta) de la loi de commande sont définis. Les coefficients de la loi de commande sont dépendants de la fréquence d’échantillonnage du signal acquis : après intercorrélation, nous obtenons une mesure toutes les millisecondes, donc la période d’échantillonnage est de 1 ms. La loi de commande est établie sous la forme d’une relation récursive reliant une séquence de coefficients de pondération des valeurs passées de la mesure (phase - e_k) et des coefficients de pondération des valeurs passées de la commande (fréquence de sortie du VCO - u_k).
time=[0:1/2e6:(length(x)-1)/2e6]';
% % correcteur "minimum" 1 intégrateur pur -> erreur statique
% % u_k=u_k-1 + alpha*e_k
% alpha=0.05;
% coef_uk_1 = 1;
% coef_uk_2 = 0;
% coef_ek = alpha;
% coef_ek_1 = 0;
% double intégrateur -> pas d'erreur permanente
% u_k=2u_k-1 -u_k-2+ (alpha+beta)*e_k -alpha*e_k-1
alpha=0.01;beta=0.001;
coef_uk_1 = 2;
coef_uk_2 = -1;
coef_ek = alpha+beta;
coef_ek_1 = -alpha;
Après diverses initialisations additionnelles - en particulier GNU/Octave et Matlab adorent connaître à l’avance la taille des matrices manipulées et ne pas allouer dynamiquement de mémoire - le code PRN du satellite que nous avons sélectionné (msatellite) est généré, et des valeurs passées de la commande et de la mesure sont initialisées.
% initialisation des variables pour la vitesse de calcul
fr=NaN(Nb_points/2,1);
yp=NaN(Nb_points/2,1);
yyp=NaN(Nb_points/2,1);
% quelques initialisations
freq=0;
freqm1=freq;
freqm2=freqm1;
ym1=0;
l=1;
ap=cacode(msatellite,2/1.023); ap=ap-mean(ap);
al=[ap(end) ap(1:end-1)];
ae=[ap(2:end) ap(1)];
Deux asservissements seront nécessaires lors de l’analyse de la séquence : la fréquence de la porteuse et la position du code pseudo-aléatoire dans la séquence acquise. Le premier point sera pris en charge par une analyse de la phase, modulo π, du signal reçu, tandis que la seconde sera issue d’une comparaison de versions locales du code pseudo-aléatoire en retard (l comme late), en avance (e comme early) ou courante (p comme présent) lors de l’intercorrélation. Le code se décalera petit à petit pour suivre la phase induite par le léger décalage entre notre horloge qui échantillonne le signal et l’horloge du satellite qui génère l’identifiant.
% boucle principale
for kk=1:2000:length(x)-2001
mysine=exp(1j*2*pi*mod((freq0+freq)*time(kk:kk+2000),1)); % décalage en freq.
xx=x(kk:kk+2000).*mysine;
zl=xcorr(al,xx); % l=late ; p=present ; e=early
zp=xcorr(ap,xx);
ze=xcorr(ae,xx);
[aal,bbl]=max(abs(zl));
[aap,bbp]=max(abs(zp));
[aae,bbe]=max(abs(ze));
%discriminateur cohérent : asservissement de position du code PRN
d=(abs(ze(bbe)^2)-abs(zl(bbl))^2)/(abs(ze(bbe))^2+abs(zl(bbl))^2);
% décalage du code PRN de 1 bit en fonction du signe de la valeur du
% discriminateur cohérent
if d<0
ap=[ap(end) ap(1:end-1)];
al=[ap(end) ap(1:end-1)];
ae=[ap(2:end) ap(1)];
else
ap=[ap(2:end) ap(1)];
al=[ap(end) ap(1:end-1)];
ae=[ap(2:end) ap(1)];
end
Ayant aligné la position du code, nous sommes désormais prêts à engager la boucle d’asservissement sur la fréquence suite à toutes ces initialisations, boucle qui vise à maintenir la fréquence de l’oscillateur local égale à la fréquence de la porteuse reçue du satellite (identifiée comme la phase, modulo π, du signal reçu), et d’autre part la réplique locale du code alignée sur le signal reçu du satellite. Lorsque ces deux boucles d’asservissement sont fonctionnelles, une estimation de la phase (cette fois modulo 2π et non π) contient l’état des bits du message de navigation - 0 et 1 représentés par les angles de 0 et π, dans la variable yyp :
[valeur,index_max]=max(abs(zp));
yp(l)=atan(imag(zp(index_max))./real(zp(index_max))); % porteuse=phase[pi]
yyp(l)=atan2(imag(zp(index_max)),real(zp(index_max))); % bits =phase [2pi]
% application de l'équation récurrente du correcteur
freq=coef_uk_1*freqm1+coef_uk_2*freqm2+coef_ek*yp(l)+coef_ek_1*ym1;
fr(l)=freq;
freqm2=freqm1;
freqm1=freq;
ym1=yp(l);
l=l+1;
end
Finalement, le résultat de cette analyse est affiché sous forme de phase du signal après mélange par le VCO asservi, la fréquence du VCO, et la phase du signal comportant l’information de navigation.
subplot(311)
plot((yp),'r.');
ylabel('phase[pi] (rad)');
eval(['title(''freq0=',num2str(freq0),' Hz ; \alpha=',num2str(alpha),''');']);
grid
subplot(312);plot(fr,'r.');ylabel('freq. (Hz)');
kyyp=find(yyp>1);yyp(kyyp)=yyp(kyyp)-2*pi;
subplot(313);plot((yyp),'r.');ylabel('phase (rad)');xlabel('time (ms)')
save yyp yyp % sauvegarde du code binaire extrait de la démodulation
% eval(['print -depsc 1426853000_',num2str(freq0),'_',num2str(round(alpha*1000)),'.eps']);
Bien qu’intégriste de l’utilisation des logiciels libres, force est de constater que l’outil propriétaire Matlab obtient le résultat considérablement plus vite que GNU/Octave. En effet, le traitement d’1,4 millions de points (700 ms de durée, puisque chaque ms contient 2000 points lorsque le signal radiofréquence a été échantillonné à 2 MS/s) prend 61 s sous Matlab (R2010) contre 371 s sous GNU/Octave (3.8.2).
Figure 14 : Sur les trois graphiques, de haut en bas : atan(Q/I) pour l’asservissement de la phase de la porteuse ; la fréquence de l’oscillateur local ; arctan2(Q,I) pour extraire la modulation de phase, illustrant la divergence de la boucle d’asservissement au bout de quelques secondes, alors que le décodage fonctionne correctement au début de la séquence traitée. Gauche : signal acquis avec un récepteur DVB-T cadencé par son quartz à 28,8 MHz. Milieu : le récepteur est cadencé par une source Rohde & Schwartz SMA 100 afin d’évaluer l’effet de l’instabilité du quartz du la capacité à extraire l’information de navigation. Droite : extraction du message le plus long que nous ayons enregistré, sur une durée de 9 secondes.
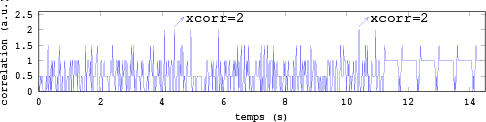
Nous concluons cette étude de décodage du message de navigation du GPS en recherchant l’entête de chaque message, la seule partie constante qui se répète toutes les 6 secondes (début de transmission d’un nouveau mot). Le mot de synchronisation, nommé TLM, se compose de l’octet 10001011 [2, p.112], que nous recherchons dans la séquence de bits issue des traitements développés ci-dessus. Comme le code transmis par les satellites (CDMA) se répète toutes les millisecondes et que la transmission numérique se fait à 50 bits/seconde, nous améliorons la capacité d’identification de la nature de chaque bit en moyennant sur 20 valeurs successives après s’être calé sur la première transition nette de 0 à 1. Finalement, le motif TLM est recherché dans la séquence par intercorrélation [2, p.119] : le bon décodage de la séquence ne peut être validé que si le maximum d’intercorrélation se répète toutes les 6 secondes (en plus des occurrences aléatoires du motif dans le contenu du message). En décodant près de 15 secondes de télémétrie, nous retrouvons bien deux maxima d’intercorrélation aux dates 4,4 et 10,4 s, démontrant la validité de notre traitement. Évidemment, un code aussi court que TLM ne donne qu’un pic d’intercorrélation peu résolu par rapport au bruit : le maximum d’intercorrélation est de 2 (tlm=[1 0 0 0 1 0 1 1];sum((tlm-mean(tlm)).^2)) et les valeurs de l’intercorrélation se distribuent sur 8 valeurs, qui se réduisent à 4 lorsque nous considérons la valeur absolue de l’intecorrélation (l’intercorrélation vaut -2 dans le cas où nous avons inversé les états 0 et 1 des bits de navigation, i.e. avons interverti les état 0 et π de la phase du signal).
Figure 15 : Intercorrélation du mot de synchronisation TLM avec la séquence de bits issue du traitement des signaux GPS : la répétition toutes les 6 secondes du maximum d’intercorrélation prouve la validité du traitement. Notez que ces 15 secondes de signaux GPS ont nécessité de traiter un fichier de 60 MB (ou 240 MB lorsque gnuradio-companion stocke les échantillons en nombres flottants au lieu d’entiers) !
Le programme GNU/Octave pour obtenir le graphique de la Fig. 15 est détaillé ci-dessous :
load yyp % recharge le fichier contenant la sortie en phase [2pi] = code BPSK
l=1
for k=987:20:length(yyp)-20 % 987 = première transition de phase exploitable
sortie(l)=sum(yyp(k:k+19)); % moyenne glissante sur 20 points, synchro sur 1ere transition
l=l+1;
end
temps=[0:1/50:length(sortie)/50];temps=temps(1:end-1); % axe des temps
k=find(sortie>-30);sortie(k)=0; % discrétisation des états en 2 valeurs
k=find(sortie<-30);sortie(k)=1; % binaires par seuillage
symbole=[1 0 0 0 1 0 1 1];symbole=symbole-mean(symbole);
sortie=sortie-mean(sortie); % toujours travailler sur des valeurs moyennes
r=(abs(xcorr(symbole,sortie))); % nulles lors des recherches d'intercorrelation
r=r(1:length(temps));
plot(temps,r); % mise en forme du graphique
axis([0 14.5 0 2.6])
text(10.6,2.3,'xcorr=2');drawArrow(10.4,2.1,10.7,2.4,0.1,0.1)
text(4.6,2.3,'xcorr=2') ;drawArrow(4.4,2.1,4.7,2.4,0.1,0.1)
xlabel('temps (s)');ylabel('correlation (a.u.)')
tandis que le contenu de la variable sortie est analysé de façon détaillée (ici 3 phrases successives, les deux dernières étant annotées pour aider le lecteur) :
101010101010101001010101010101010101010101010110101010101010101010101010101001
010101010101010101010101010110101010101010101010101010101001010101010101010101
0101010110011100
TLM reserved parity HOW-count ID parity DATA
10001011 0000110001010100 000100 01011101111000110 0 1 101 01 010100 010011100
100000011000011110111100111001110111011111001111111000000101100010011111111110
110101000010000110101110000111111010011011111001000110111100111010100000111010
111000001001001010110011110011100010110100111111011110000000000001000000000
TLM reserved parity HOW-count ID parity DATA
10001011 0000110001010100 000100 01011101111000111 0 1 001 10 101000 110001010
101000000000000111111101100010101000000001101101001100110101110101001000000010
011010110010011000111100100110111101111010111100000011011111111100111001011011
11110110111000000000000
Le début de la séquence est le résidu de la trame précédente. Suivent le mot de synchronisation (10001011), la séquence réservée (16 bits) et les 6 bits de parité du premier mot de 30 bits, puis la séquence HOW dont seule l’ID - qui identifie la trame en cours de transmission (entre 1 et 5) - nous intéresse (notez néanmoins l’incrément d’une unité du compteur HOW-count). Nous avons bien un identifiant égal à 5 (101 : fin de la trame précédente) suivi, dans la trame suivante, de 1 (début d’une nouvelle trame). Les deux derniers bits de HOW (second mot, contenus dans la fin des 6 bits de parité) sont bien à 0 : tout ceci est cohérent avec la norme du message de navigation décrit dans http://www.losangeles.af.mil/shared/media/document/AFD-070803-059.pdf (pp.109 et suivantes). Pour la phrase d’identifiant 1, les 10 premiers bits indiquent la date de transmission modulo 1024. Nous avons 1100010101 soit la semaine 789 qui indique une acquisition dans la semaine entre le 5 et 11 octobre 2014 (cf http://adn.agi.com/GNSSWeb/), une valeur cohérente. Suivent les deux bits de statut des transmissions - 01 indique la nature du code émis sur le second canal sur la porteuse L2, puis la précision sur le positionnement que fournira ce satellite : la meilleure résolution possible est accessible, entre 0 et 2,4 m, puisque tous les systèmes fonctionnent de façon nominale (tous les bits à 0). Cette analyse nous rend donc confiants sur la pertinence du résultat atteint.
6. Extension au RADAR passif
Nous avons extrait le signal reçu d’un satellite GPS en particulier par intercorrélation avec une copie locale du code, information connue et faisant partie intégrante du protocole de communication. Une alternative à l’exploitation d’un code connu émis par un émetteur connu, en vue de réaliser un RADAR passif [14], est de rechercher dans le bruit électromagnétique environnant une information pseudo-aléatoire et effectuer le même traitement que nous venons d’effectuer, mais cette fois entre l’information transmise directement de l’émetteur (supposé pseudo-aléatoire) au récepteur DVB-T, et la même information ayant rebondi sur une cible mobile. Cette approche de RADAR passif - très intéressante, car ne nécessitant pas d’émettre volontairement un signal radiofréquence, mais exploitant de façon opportuniste les sources existantes - permet à l’amateur de créer son système de mesure RADAR sans enfreindre la loi en émettant un signal, ou au militaire de détecter des cibles sans risquer d’attirer l’attention avec un émetteur dédié. Il s’agit donc d’un mode de veille très à la mode puisqu’il s’affranchit d’une source active dédiée, qui est elle-même source d’irradiations peu favorables en milieu urbain, voire de vulnérabilités si la cible de ne veut pas être vue. Cette méthode de travail est à l’origine du tout premier RADAR dans lequel un émetteur de signal radiofréquence de la BBC a été la source du signal réfléchi par un avion pour démontrer la faisabilité du RADAR [15]. Plus tard, les signaux émis par les RADARs anglais ont été utilisés par des récepteurs allemands pendant la Seconde Guerre mondiale pour détecter les vols au-dessus du sud de la mer du Nord [15].
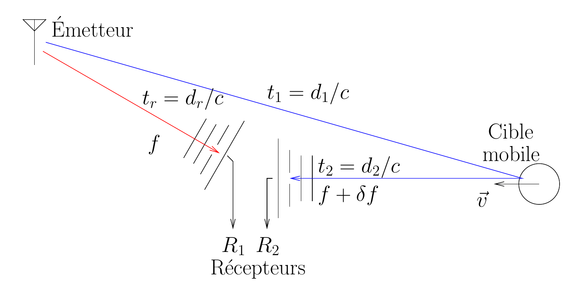
Dans ce cas, deux effets affectent le second signal reçu : un décalage Doppler si la cible est mobile, et un retard puisque la seconde onde a cheminé plus longtemps pour atteindre le récepteur que l’onde directe (Fig. 16). Une analyse recherchant, pour tous les décalages de fréquence Doppler possibles, la position du maximum d’intercorrélation représentatif du retard du motif reçu initialement par R1 puis, après réflexion par la cible par R2, est le principe du RADAR passif qui exploite le bruit électromagnétique environnant pour localiser des cibles. Cette fois, le diagramme bidimensionnel que nous avions tracé pour le GPS avec en abscisse le numéro de code du satellite (PRN) et en ordonnée le décalage en fréquence, devient un diagramme avec en ordonnée le décalage Doppler (donc de nouveau un décalage en fréquence), et en abscisse l’intercorrélation dont le maximum est représentatif de la différence de temps de vol (t1+t2)−tr.
La principale difficulté expérimentale dans une telle approche multistatique de RADAR (un émetteur et plusieurs récepteurs, tous séparés spatialement) est de synchroniser les horloges, tel que décrit à http://kaira.sgo.fi/2013/09/16-dual-channel-coherent-digital.html, et plus récemment détaillé sur http://hackaday.com/2015/06/05/building-your-own-sdr-based-passive-radar-on-a-shoestring/. Dans le cas du RADAR passif, R1 et R2 doivent être cadencés par la même horloge afin de garantir la cohérence en phase des mesures. Si ces deux récepteurs sont spatialement proches, alors un même oscillateur alimente les deux récepteurs radiofréquences : c’est l’approche sélectionnée dans la majorité des documents décrivant des expériences à ce sujet [16, 17, 18, 19].
Figure 16 : Architecture d’un RADAR passif composé de deux récepteurs R1 et R2 connectés à des antennes directives, l’une pointant vers un émetteur existant (par exemple émetteur de télévision ou radio) et l’autre vers la cible.
Il nous faut cependant quelques ordres de grandeur sur les paramètres de mesure pour voir si l’expérience est envisageable. Les deux paramètres que nous cherchons à observer sont le décalage Doppler dû au mouvement de la cible, et la distance de la cible observée comme retard entre le signal de référence et le signal réfléchi par la cible.
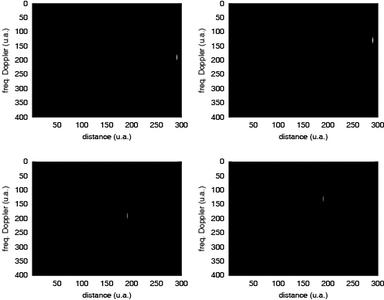
La résolution en vitesse est donnée par le pas de fréquence de l’oscillateur local avec lequel le signal incident est mélangé (afin d’annuler tout écart de fréquence entre l’enregistrement de référence et le signal reçu de la cible mobile). Le décalage Doppler induit, sur une porteuse à f, par une cible mobile de vitesse v, est environ f x·v/c avec c la célérité d’une onde électromagnétique dans le vide. Pour une porteuse à 1 GHz et un véhicule roulant à 100 km/h, le décalage est de 100 Hz (pour éventuellement croître à 1 kHz pour un avion volant à 1000 km/h), parfaitement dans la bande de mesure du DVB-T. Nous vérifions, pour le moment par la simulation (Fig. 17), que la détection de cibles est bien faisable de cette façon, et que les propriétés de distance et de vitesse sont contenues dans l’abscisse et l’ordonnée des graphiques ainsi générés.
n=1
for pos=[100 1100] % distance de la cible : deux cas possibles
for df=[1 7] % vitesse de la cible : deux cas possibles
signal=rand(3000,1);signal=signal-mean(signal); % signal bruit\'e re\c{c}u
infor=rand(501,1)*10;info=info-mean(info); % signal de l'\'emetteur
signal(pos:pos+length(info)-1)=signal(pos:pos+length(info)-1)+info; % emetteur + bruit
signal(1:pos)=signal(1:pos)+rand(pos,1)*10; % signal emetteur + cible + bruit (puissance cst)
signal(pos+length(info):end)=signal(pos+length(info):end)+rand(length(signal)-length(info)-pos+1,1)*10;
signal=signal.*exp(j*2*pi*df*1e-3*[0:length(signal)-1]'); % decalage Doppler du signal recu
% ici on a fini de synthetiser un faux signal representatif d'une cible en mouvement qui a
% reflechi un signal inconnu
l=1;
for f=-20:.1:20 % balayage en frequences (cibles s'eloignant ou s'approchant)
recu=signal.*exp(j*2*pi*f*1e-3*[0:length(signal)-1]'); % melange pour compenser Doppler
r=(abs(xcorr(information,recu))); % max d'intercorrelation donne distance
s(:,l)=r(1:10:floor(length(r)/2));
l=l+1;
end
subplot(2,2,n);imagesc(s(1:end,:)',[2000 4000]);n=n+1;
ylabel('freq. Doppler (u.a.)');xlabel('distance (u.a.)')
end
end
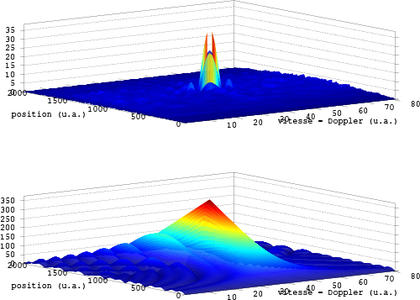
Figure 17 : Simulations de la réponse attendue lors de l’illumination de cibles à diverses distances se déplaçant à diverses vitesses dans le plan {décalage Doppler, retard}. Le principe est démontré théoriquement par un maximum d’intecorrélation autour de l’abscisse 200 ou 300 et l’ordonnée 150, dépendante de la vitesse et de la distance de la cible. Cependant, la mise en pratique est complexe.
La résolution en portée est donnée par l’inverse de la bande passante du signal acquis [20]. La bande passante d’acquisition B est de l’ordre de 2,4 MHz avec un récepteur DVB-T donc la résolution sur la distance de la cible est c/(2B) ou environ 60 m. De façon générale, il peut être utile de mentionner que la résolution spatiale de la mesure est liée au contenu spectral du signal émis, tandis que la résolution en vitesse (i.e. en décalage Doppler) à la durée de la mesure, donc à sa résolution spectrale. GPS s’est mis dans le cas idéal d’un contenu informatif pseudo-aléatoire, comprimant au mieux l’impulsion lors de l’intercorrélation et permettant une identification fine de la position du message, même en présence de bruit. Le cas plus classique d’un signal périodique, ou pseudo-périodique (par exemple de la musique si un signal sur la bande FM est utilisé) se traduira par une moins bonne résolution spatiale puisqu’une sinusoïde légèrement décalée dans le temps (donc dans l’espace) ressemble toujours à une sinusoïde (Fig. 18). Les cas pratiques sont entre ces deux cas extrêmes du signal pseudo-aléatoire et pseudo-périodique : nous prendrons soin, pour les applications de RADAR passif, de choisir des émetteurs puissants, rayonnant vers les cibles recherchées, un signal aussi aléatoire que possible et occupant une bande spectrale au moins aussi importante que la carte d’acquisition. La littérature sur le sujet est très abondante [21].
for m=1:2
t=[0:0.1:100]';
f=1;
if (m==1)
r=rand(length(t),1);r=r-mean(r); % bruit connu
else
r=sin(2*pi*f*t); % periodique
end
dr=(sin(2*pi*(f)*t)); % transposition par Doppler
drr=dr.*r;
l=1
for df=-0.04:0.001:0.04 % vise a éliminer Doppler ...
s=(sin(2*pi*(f+df)*t));
drrs=s.*drr;
sol(:,l)=xcorr(drrs,r); % puis recherche le motif
l=l+1
end
sol=hilbert(sol); % enveloppe de la fonction
subplot(1,2,m);surf(abs(sol));shading interp;axis tight
ylabel('position (u.a.)');xlabel('vit.=Doppler (u.a.)')
end
Figure 18 : Gauche, haut : diagramme Doppler-distance pour un signal pseudo-aléatoire. Gauche, bas : même analyse, mais pour un signal émis périodique. L’élargissement du pic selon l’axe des ordonnées est évident, puisque sur le graphique du haut le pic d’intercorrélation est tellement fin qu’il est à peine visible. Droite : code GNU/Octave pour générer ces graphiques.
Conclusion
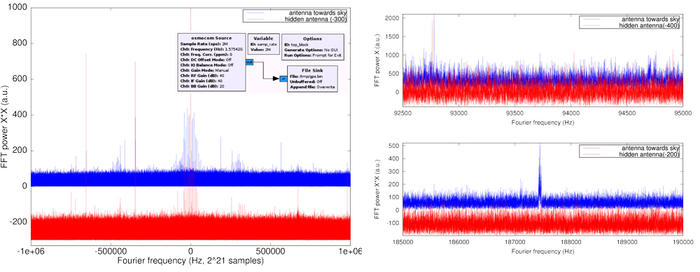
Malgré un intérêt de longue date pour le décodage de signaux GPS, ce n’est que récemment que les circonstances se sont agencées pour permettre de faire aboutir un projet nécessitant un récepteur radiofréquence performant et peu coûteux, offrant une bande passante suffisante pour décoder un signal transmis au Mb/s, et la puissance de calcul nécessaire à une implémentation logicielle des algorithmes de décodage. Cette conjoncture offre l’opportunité à tout lecteur curieux de reproduire ces expériences. La démonstration initiale de la faisabilité du projet a été introduite par la présentation « Hacking GPS » de P. Boven à la conférence OHM2013, qui y expliquait la stratégie de prendre le carré des coefficients I/Q pour retirer la modulation qui induit l’étalement de spectre, et ainsi accumuler de façon cohérente le signal issu d’un satellite tout en abaissant le bruit thermique. La mise en œuvre n’est pas si triviale que cet auteur a voulu nous faire croire, et en particulier il faut savoir à quel écart de fréquence rechercher le signal d’intérêt aux côtés de la forêt de pics parasites induits par les diverses sources de bruit polluant l’acquisition. Après maintes recherches, nous avons fini par obtenir un signal représentatif de l’émission radiofréquence d’un satellite GPS par cette méthode (Fig. 19). Il s’avère cependant que cette méthode, d’apparence simple initialement, fournit un résultat pauvre et complexe à analyser. Elle a cependant été le point de départ de cette investigation, et méritait d’apparaître comme la conclusion d’une étude démontrant une compréhension complète de la nature des signaux et de leur modulation.
Figure 19 : Gauche : analyse large bande du carré des coefficients I+jQ, pour une antenne orientée vers le ciel (bleu) et cachée du ciel par une surface métallique (rouge). De nombreux modes parasites rendent l’analyse des signaux complexes. Droite : zoom sur la région contenant le double de la fréquence de décalage entre l’oscillateur local et la porteuse issue du GPS : en haut, la transformée du signal I+jQ ne présente pas de structure identifiable compte tenu de l’étalement spectral induit par la modulation par le code pseudo-aléatoire, mais la mise au carré (bas) permet d’accumuler de façon cohérente le signal radiofréquence venant des satellites et de faire apparaître un signal significatif lorsque l’antenne est exposée au ciel (bleu), signal qui disparaît lorsque l’antenne est cachée (rouge). Ces acquisitions ont été réalisées avec un récepteur E4000, plus bruité que le R820T.
Quelle suite à donner à un tel projet ? De nombreux points restent à élucider. Le premier point évident est que nous avons visualisé et extrait la signification des bits du message de navigation, mais nous n’avons pas poussé la démonstration jusqu’à exploiter les éphémérides des satellites, pour finalement se positionner dans l’espace. Cette étape apparaît finalement nécessaire même pour l’objectif moins ambitieux de reproduire au sol une source de fréquence aussi stable que la combinaison des horloges atomiques embarquées, puisqu’il semble que ce soit la seule stratégie pour s’affranchir du décalage Doppler qui pollue chacune des porteuses observées. Par ailleurs, l’utilisation de la forme du signal de corrélation pour extraire des signaux directs et réfléchis une distance précise entre récepteur et réflecteur (application au RADAR passif) apparaît complexe pour des mesures depuis le sol compte tenu de la bande passante réduite de la mesure. En effet, avec un code se répétant à 1,023 MHz, un intervalle de temps du corrélateur occupe 977 ns pendant lesquelles un signal électromagnétique se propage de 294 m. Le réflecteur doit donc se trouver à plusieurs fois cette distance pour que le pic secondaire d’intercorrélation - dû au signal réfléchi et non au signal direct - soit séparé et aisément détectable. Ceci explique que la majorité des applications exploitant le signal réfléchi du GPS pour une mesure de distance se soit faite avec des récepteurs aéroportés, et de plus au-dessus de la mer afin d’avoir une surface réfléchissante importante et donc améliorer le rapport signal à bruit. De tels domaines d’application dépassent les moyens accessibles à l’amateur. Finalement, nous n’avons pas eu de succès à décoder les informations transmises par les satellites géostationnaires d’aide à la navigation - EGNOS en Europe7 et WAAS au-dessus des Amériques - bien que leur code et leur protocole de communication soit censés être compatibles GPS. Les causes de cet échec ne sont pas connues.
Remerciements
Cette étude a été menée en vue des cours de l’École d’Été sur le Temps-Fréquence (EFTS) qui se tiendra à Besançon. Le soutien financier pour l’accueil d’une étudiante ERASMUS - Sarà Martinez Gutierrez - est fourni par le labex First-TF (http://first-tf.com/). Les références bibliographiques qui ne sont pas librement disponibles sur le web sont obtenues auprès de Library Genesis, lib.gen.rus.ec : nos recherches ne seraient pas possibles sans cette ressource documentaire. É. Carry a amélioré cette prose par sa relecture.
J.-M Friedt est enseignant-chercheur à l’Université de Franche-Comté à Besançon, consultant pour une société privée concevant des capteurs passifs interrogeables par liaison radiofréquence s’apparentant aux méthodes de mesure par RADAR. G. Cabodevila est enseignant-chercheur à l’École Nationale Supérieure de Mécanique et Microtechniques de Besançon. Son cours d’automatique, qui formalise en particulier les concepts introduits dans la section 5, est disponible à http://jmfriedt.free.fr/Gonzalo_cours1A.pdf. Tous deux sont hébergés par l’Institut FEMTO-ST.
Références
[1] J.-M Friedt, La réception de signaux venus de l’espace par récepteur de télévision numérique terrestre, Open Silicium n°13 (Déc. 2014/Jan-Fev 2015), disponible à http://jmfriedt.free.fr/sdr2.pdf
[2] K. Borre, D.M. Akos, N. Bertelsen, P. Rinder, & S.H. Jensen, A software-defined GPS and Galileo receiver - A single frequency approach, Springer (2007)
[3] E.D. Kaplan, Understanding GPS : Principles and Applications, 2nd Ed, Artech House Mobile Communications (2005)
[4] Programme et transparents de la Journée GNSS 2015 du CNES, http://geodesie.ign.fr/journee-gnss-science/programme/
[5] R.L. Beard & J.D. White, GPS Application to Time Transfer and Dissemination, GPS Solutions 3 (1), pp.17-25 (1999)
[6] C. Bruyninx, P. Defraigne & J.-M Sleewaegen, Time and Frequency Transfer using GPS Codes and Carrier Phases: Onsite Experiments, GPS Solutions 3 (2), pp.1-10 (1999)
[7] Un excellent ouvrage sur la genèse de la définition du temps sur des transitions atomiques en replacement de la définition astronomique, à lire absolument : T. Jones, Splitting the second - The Story of Atomic Time, Institute of Physics Publishing (2000)
[8] G. Lachapelle, GNSS Solutions: Atomic clocks on satellites and mitigating multipath, Inside GNSS (Sept. 2006), disponible à http://www.insidegnss.com/auto/Sept06GNSS_Solutions_secure.pdf
[9] http://gpsinformation.net/main/gpspower.htm, bien que cette valeur semble plutôt venir d’un calcul inverse puisque la spécification de GPS définit la puissance minimum que doit recevoir un récepteur sur Terre plutôt que la puissance émise par le satellite. Une telle approche est proposée dans http://www.unoosa.org/pdf/icg/2010/ICG5/wgA/05.pdf et donne effectivement environ 27 à 28 W (14 dBW - notez l’erreur d’unité probable dans le transparent 17). http://www.nxp.com/documents/other/75016740.pdf propose une puissance émise de 50 W.
[10] J.-M Friedt, Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées, GNU/Linux Magazine France n°139 (juin 2011), disponible à http://jmfriedt.free.fr/xcorr.pdf
[11] Y. Guidon, Sciences/Théorie de l’information : propriétés et dérivés des CRC et LFSR, GNU/Linux Magazine n°085 (juillet 2006)
[12] R. Boudot et al., A high-performance frequency stability compact CPT clock based on a Cs-Ne microcell, IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 59 (11), pp.2584-7 (2012) ou http://members.femto-st.fr/sites/femto-st.fr.laurent_larger/files/content/Homepage_ll_fichiers/pdf_files/FRGLS13/mo1700boudot.pdf
[13] C. O’Driscoll, M.G. Petovello & G. Lachapelle, Choosing the coherent integration time for Kalman filter-based carrier-phase tracking of GNSS signals, GPS Solutions 15, pp.345-356 (2011)
[14] C. Guyard, Voir sans être vu : le radar passif, La Recherche n°447 (décembre 2010), p.64, disponible à http://www.larecherche.fr/savoirs/technologie/voir-etre-radar-passif-01-12-2010-87441
[15] Y. Blanchard, Le radar, 1904-2004 : Histoire d’un siècle d’innovations techniques et opérationnelles, Ellipses (2004)
[16] A. Capria & al., Ship Detection with DVB-T Software Defined Passive Radar Proc. of the IEEE Gold Remote Sensing Conference (2010), disponible à http://ieee.uniparthenope.it/chapter/_private/proc10/6.pdf
[17] K. Chetty, G.E. Smith, & K. Woodbridge, Through-the-Wall Sensing of Personnel Using Passive Bistatic WiFi Radar at Standoff Distances, IEEE Transactions on Geoscience and Remote Sensing 50 (4), avril 2012
[18] P. Samczynski & al., A Concept of GSM-based Passive Radar for Vehicle Traffic Monitoring, Proc. Microwaves, Radar and Remote Sensing Symposium, (2011), pp.271-274
[19] F. Berizzi & al., USRP technology for multiband passive radar, Proc. IEEE Radar Conference (2010), pp.225-229
[20] J. M. Christiansen, DVB-T based Passive Bistatic Radar Simulated and experimental data analysis of range and Doppler walk, rapport du Norwegian University of Science and Technology (2009), disponible à http://www.diva-portal.org/smash/get/diva2:348777/FULLTEXT01.pdf
[21] P.E. Howland, D. Maksimiuk & G. Reitsma, FM radio based bistatic radar, IEE Proc.-Radar Sonar Navig., 152 (3), juin 2005
2 sdr.osmocom.org/trac/wiki/rtl-sdr
3 http://www.lextronic.fr/P847-antenne-gps-amplifiee-magnetique.html
4 La visite virtuelle du Musée du RADAR est accessible à http://www.musee-radar.fr/360-generartion-radar-2014/radar.html
5 http://www.zeus.iag.usp.br/system.php?lan=en
6 L’hypothèse d’une excursion de ± 5 kHz de fréquence Doppler sur une durée de 12 h ne tient par ailleurs pas compte de la dérive en température de l’oscillateur local.
7 Le générateur de code approprié est proposé à http://cu-hw-gps.googlecode.com/svn/matlab/waas_enabled_receiver/cacodegn_waas.m



 Ajouter à une liste de lecture
Ajouter à une liste de lecture