Quelques épreuves du challenge sécurité « Trust the Future »

1. Introduction

Les challenges sécurité ou CTF – Capture the Flag – consistent à obtenir des secrets grâce à la réalisation d'épreuves orientées sécurité. Les qualifications du challenge « Trust the Future » d'Airbus Defense and Space [1] ont eu lieu mi-novembre 2014 et consistaient à trouver des « tokens » répartis dans 16 épreuves (plus une épreuve « cachée »). Les épreuves se répartissaient comme suit : deux « brute-force », trois épreuves crypto, une épreuve réseau, cinq épreuves de rétro-ingénierie, trois épreuves de stéganographie, et trois épreuves  « web ».

Nous avons terminé seconds de ce challenge, et nous vous proposons ici de parcourir certaines de ces différentes épreuves, en décrivant nos solutions de façon rapide pour certains challenges simples, et de façon plus approfondie pour certains challenges plus difficiles, en particulier pour des challenges en cryptographie et en rétro-ingénierie.

2. « Brute force »

2.1 Fichier ZIP

Un premier brute force concerne un fichier ZIP, dont l'ouverture provoque la demande d'un mot de passe.

Voilà une excellente occasion de ressortir John the ripper !

Puis :

On obtient le fichier secr3t :

2.2 Fichier « shadow »

Un fichier de type « shadow password » est fourni :

Il contient un mot de passe hashé avec un salt. Pas simple à attaquer, donc, l'on peut présupposer que le mot de passe est alphanumérique sans majuscule. Nous avons essayé différentes longueurs, jusqu'à 6, en utilisant hashcat :

Nous obtenons le mot de passe (et token) « loutre » … Nous aurions donc pu aussi tenter une attaque en dictionnaire, sûrement plus rapide. Il s'agissait d'ailleurs du seul token purement alphanumérique des épreuves.

3. Cryptographie

Là commencent des choses bien plus sérieuses. Les trois épreuves consistent globalement à récupérer une clé cryptographique, par différentes techniques (reste chinois, factorisation avec l'approche de Fermat, etc.). Dans un premier temps, un seul fichier crypto.tgz est fourni. Il comporte quatre certificats alice.crt, bob.crt, charly.crt et ca.crt, et un fichier « challenge1 ». Ce dernier est un fichier de type « MIME entity text ». Une fois décodé de la base 64, le contenu de l'e-mail est un binaire que l'on peut analyser avec dumpasn1 :

Il contient le fait que cet e-mail a été envoyé à Alice, Bob et Charly par ca@example.com, et que le contenu est chiffré avec du DES « des-EDE3-CBC ». Il contient aussi trois chiffrés, qui correspondent probablement à la clé DES chiffrée avec les clés publiques d'Alice, Bob et Charly respectivement… Mais comment retrouver les clés privées afin de connaître cette clé DES ?

Analysons à présent les certificats fournis.

Rien de vraiment anormal : une clé RSA 2048 bits … Ah mais si, son exposant est de 3, voilà qui est bien faible. En regardant les certificats de Bob et Charly, nous constatons le même problème : des exposants de 3. Après un passage par Wikipédia, puis par un article expliquant comment récupérer le texte chiffré lorsque nous avons trois messages chiffrés avec trois clés à faible exposant (le théorème du reste chinois) [2], nous savons que nous pouvons récupérer la clé de session. En quelques mots, supposons que Ka, Kb et Kc soient les clés publiques de Alice, Bob et Charly. Alors, « ca » a généré trois messages chiffrés Ca, Cb, Cc comme suit (m étant le message initial) :

Ca = m^3 mod KaCb = m^3 mod Kb Cc = m^3 mod Kc

Un attaquant peut alors calculer c = m^3 mod Ka Kb Kc. Comme Ka.Kb.Kc est plus grand que m^3 (hypothèse très probable), alors c = m^3. On peut donc en déduire m.

Pour calculer cela, il est assez usuel d'utiliser la librairie grand nombre de python. Faisons cela avec la librairie « BigInteger » de Java pour montrer que cela se fait facilement avec d'autres langages. Nous avons aussi extrait, à l'aide de dumpasn1, les clés publiques d'Alice, Bob et Charly de leurs certificats (alice.pub, etc.) et aussi les clés chiffrées par « ca » : Ca, Cb, et Cc (alice.key, etc.).

Avec :

Nous obtenons une clé (4f8957408f0ea202c785b95e206b3ba8da3dba7aea08dca1), que l'on peut appliquer sur les données de l'e-mail chiffré (« cypher »):

Nous y sommes presque. « decrypt »  est encodé en base64 et est un tgz, qui contient un fichier « challenge2 » (pour crypto 2) et le token...

4. Rétro-ingénierie

Parmi les cinq épreuves de rétro-ingénierie, trois d'entre elles peuvent être résolues assez aisément avec l'aide d'un désassembleur performant (tel IDA Pro ou radare2), une présente la particularité d'être une image d'un noyau pour processeur Intel 80386 et la dernière utilise diverses techniques d'offuscation et demande une analyse plus approfondie. C'est celle-ci que nous avons choisi de présenter ici.

Le fichier fourni « crackme3 » est un exécutable ELF pour une architecture AMD64, lié statiquement et sans symboles. Dans un premier temps, il est intéressant d'utiliser des outils d'analyse statique de haut niveau (file, readelf, strings, etc.) afin de mieux cerner à quel type d'épreuve nous nous attaquons. Ici en particulier, readelf nous permet de voir qu'aucune section n'est définie :

Le fichier n'étant pas excessivement léger, on peut supposer que le programme a été modifié, packé et que les instructions réellement exécutées sont décodées à chaque lancement. Cette hypothèse est confirmée par la mention d'un packer dans les chaînes de caractère extraites avec strings et par une entropie anormalement élevée (7,72 bits par octet contre un peu moins de 6 habituellement).

Afin d'estimer à quel moment le code utile est présent en mémoire, on peut commencer par observer le comportement global de l'exécutable en regardant les syscall qu'il émet en utilisant l'outil strace :

Contrairement à une exécution directe, le programme se termine avec une erreur de segmentation. L'explication se trouve juste avant dans la liste des syscall : crackme3 appelle ptrace afin de se tracer lui-même, ce qui est refusé par le système d'exploitation, car strace lui est déjà attaché. Cette technique courante dans les malwares permet d'en compliquer l'analyse.

Cet appel arrive cependant assez tard et on peut espérer que le code utile est alors en mémoire. On va donc générer un dump du processus au moment de l'appel à ptrace :

En utilisant à nouveau « strings » sur crackme3.dump, on peut confirmer que le programme réel est bien présent en mémoire en recherchant la chaîne de caractères qui est affichée quand on ne fournit pas de paramètre :

On utilise alors un désassembleur (IDA Pro pour notre part) afin d'analyser crackme3.dump. On peut se servir de l'offset de la chaîne usage:%s <password> pour retrouver la fonction dans laquelle elle est utilisée. Celle-ci semble correspondre à la fonction main initiale et la fin de la fonction semble relativement simple : deux nombres de 64 bits chacun sont xor-és ensemble et le résultat est comparé à un troisième nombre à l'adresse 0x4013c2. Pour nous assurer que nous sommes sur la bonne voie, nous retournons sous gdb :

Ici, le premier breakpoint nous permet de contourner la protection utilisant ptrace et lorsque le second est atteint, nous changeons le résultat de la comparaison afin de faire croire au programme que les deux nombres étaient identiques. Celui-ci nous répond « Good boy:) », ce qui est bon signe. Il ne nous manque plus qu'une chose : le mot de passe. Pour le retrouver, nous devons nous intéresser aux trois nombres comparés. Deux d'entre eux ne dépendent visiblement pas du mot de passe entré et le troisième est initialisé avec les seize premiers caractères du mot de passe et est transformé par une fonction débutant à l'adresse 0x400C28.

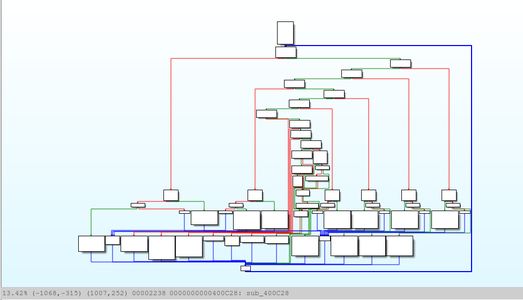
Celle-ci peut paraître compliquée, mais on s'aperçoit qu'il s'agit en réalité d'une boucle (que l'on reconnaît dans le diagramme ci-dessus au trait bleu sur la droite représentant un jump) à l’intérieur de laquelle se trouve un switch ne contenant que quelques instructions réellement exécutées pour chaque valeur possible. Cela correspond à une autre technique couramment employée dans des malwares : le code utile est exprimé à l'aide d'un jeu d'instructions personnalisé et interprété par un processeur abstrait.

Ce processeur dispose de registres et d'une zone mémoire dans laquelle se trouve notre mot de passe et le jeu d'instruction est similaire à MIPS. Une instruction inhabituelle a tout de même été rajoutée. Celle-ci (que nous avons ici nommée MANG) complique l'analyse du programme selon trois modes en mélangeant les instructions ou en modifiant les registres et la mémoire.

En réimplémentant cette machine virtuelle en python,  l'on peut mimer l'exécution de crackme3 pour une valeur de mot de passe particulière :

On remarque dans cette trace que l'exécution ne dépend pas du mot de passe qui se situe à l'adresse (virtuelle) 0x2180. Cela signifie qu'il nous suffit d'inverser la procédure pour retrouver le bon mot de passe. On obtient alors :

5. Stéganographie

Trois épreuves de stéganographie sont proposées : deux images, et un fichier de son au format WAV.

La première image est le logo d'Airbus. Rien de particulier a priori, sauf que le fond blanc incite à faire un remplissage avec du noir, avec un seuil faible… Il apparaît alors un texte caché.

La deuxième image est le logo de Google. Là encore, rien de visible directement. Des zooms nous permettent finalement de constater une petite dizaine de pixels noirs sur le fond blanc, à certains endroits. Nous réalisons de plus que ces pixels sont situés dans la partie supérieure gauche du logo, ce qui veut dire que leurs coordonnées (x,y) ont des valeurs comprises entre 60 et 120… Nous pensons alors à une représentation graphique de caractères ascii, ce qui nous permet finalement d'obtenir le token.

La troisième stégano est plus surprenante : un fichier appelé noise.wav, que nous jouons avec audacity. Le fichier porte bien son nom. Audacity nous permet de constater que le même motif se répète régulièrement.

Cela peut faire penser à du morse, avec les pics « courts » qui pourraient être considérés comme des points, et les plateaux plus longs comme des traits. Mais cela ne donne rien.

Notre deuxième idée est de considérer que cela représente un flux de caractères codés sur 7 bits. Selon cette idée, nous obtenons le string : theAi_WK]'OT 4qroe7q.

 La solution n'est pas encore là … mais le « the » du début fait indéniablement penser que la solution est proche. Nous allons alors effectuer des décalages de 0 à 6 bits sur le flux binaire considéré, ce qui nous donne donc 7 strings :

1. theAi_WK]'OT 4qroe7q
2. iQKS?/:O(ice_Job
3. S#&~^.t> P%SGK?_D
4. &F,M}<]h<} K'~+?
5. :MXy;P4yzAN-|V~                                                                                
6. 7urw isu-<[y-|
7. tokenASgjZ8y7r[x@

En utilisant les strings dans l'ordre 1 – 7 – 6 – 5 – 2, l'on découvre « The token is Nice_Job ».

Conclusion

Cet article a présenté la résolution de certaines épreuves des qualifications du CTF « Trust The Future » organisé par Airbus Defense and Space en novembre 2014. Nous avons terminé deuxièmes des qualifications, puis 4ème lors de la finale, qui consistait en des épreuves différentes (découverte d'un réseau, attaques de serveurs). Les épreuves étaient très intéressantes, elles nous ont tenus en haleine pendant les 2 semaines de la compétition : nous ne pouvons que demander à Airbus Defense and Space de recommencer l'an prochain !

Références

[1] https://challenge.trustthefuture.eu/index.html

[2] http://en.wikipedia.org/wiki/RSA_%28cryptosystem%29

[3] http://www.cims.nyu.edu/~regev/teaching/lattices_fall_2004/ln/rsa.pdf