Cryptanalyse du protocole WEP

1. Introduction

Le protocole WEP, ou Wired Equivalent Privacy, est défini dans le standard IEEE 802.11 pour permettre la protection des communications sans-fil plus connues sous le nom de « Wi-Fi ». Ratifié en 1999, ce protocole se doit de suivre une loi américaine sur l'exportation d'algorithmes de chiffrement. La clé secrète doit être limitée à 40 bits. Plus tard, une version exportable utilisant une clé secrète de 104 bits est autorisée une fois la loi annulée.

De toute l'histoire de la cryptanalyse moderne, le protocole WEP est sûrement un des exemples les plus connus par le grand public. La première raison est peut-être sa faisabilité. Dans le monde de la cryptographie, un algorithme est considéré comme cassé lorsqu'une attaque de moindre complexité que la recherche exhaustive est trouvée. En pratique, peu de faiblesses dans des algorithmes de chiffrement peuvent être exploitées. WEP fait partie de ce nombre restreints d'algorithmes réellement cassés. Deuxièmement, casser une clé WEP permet l'obtention d'un accès indu à un réseau sans-fil. Que ça soit pour pirater la connexion internet de son voisin ou dans le cadre d'un audit de piratage éthique, recouvrer une clé WEP est devenu un sport que chaque expert en sécurité se doit de maîtriser.

Dans cet article, nous allons détailler les différentes attaques cryptographiques capables de recouvrer une clé WEP. Cette cryptanalyse va nous permettre de comprendre comment ces attaques ont été découvertes. Nous allons également détailler les nouvelles attaques sur WEP découvertes par Sephredad, Vaudenay et Vuagnoux et présentées à la conférence Selected Areas in Cryptography en août 2010.

1.1. Cryptanalyse

Il n'existe pas vraiment de méthode générique pour étudier la sécurité d'un protocole cryptographique. Une approche simplifiée consiste à étudier les trois mécanismes majeurs d'un cryptosystème.

1.1.1. Confidentialité

Un algorithme de chiffrement se doit de garantir la confidentialité des données. C'est-à-dire qu'un adversaire, susceptible de capturer la communication chiffrée entre Alice et Bob, ne doit pas être capable d'en retrouver le contenu (i.e. le texte clair). Pour ce faire, WEP utilise la primitive cryptographique RC4 qui sera détaillée ci-dessous.

1.1.2. Intégrité

Un cryptosystème se doit de protéger l'intégrité des données. Cette composante est souvent combinée avec l'authentification des données, car elles reposent sur les mêmes primitives. Ainsi, un adversaire ne doit pas être capable de modifier les données échangées entre Alice et Bob sans que ceux-ci puissent le détecter. Dans le cas du protocole WEP, cette notion d'intégrité est (très mal) assurée par une primitive non cryptographique, un contrôle de redondance cyclique (CRC32). Nous verrons par la suite pourquoi cette primitive n'est pas un bon choix pour garantir l'intégrité des données. Nous verrons également comment exploiter ce contrôle de redondance cyclique pour injecter du trafic chiffré sans connaître la clé secrète.

1.1.3. Authentification

Une composante essentielle d'un système cryptographique est l'authentification. Alice et Bob doivent s'assurer de ne pas communiquer avec une tierce personne (on parle généralement d'une attaque dite de l'homme-du-milieu). Pour ce faire, le protocole WEP utilise une authentification par pair. Le réseau est identifié à l'aide d'un nom (ESSID) et éventuellement une adresse MAC (BSSID). Cela ne constitue en rien une authentification cryptographique. Le point d'accès utilise une authentification optionnelle pour identifier les clients. Celle-ci s'appelle l'authentification par clé partagée (Shared Authentication). Nous verrons par la suite comment se servir de ce mécanisme d'authentification pour injecter du trafic chiffré sans même connaître la clé secrète.

2. Analyse de la confidentialité des données

Cryptanalyser un protocole de chiffrement se résume souvent à l'analyse de sa notion de confidentialité. Dans le cadre du protocole WEP, cette section est vraisemblablement la plus importante, c'est pourquoi nous avons décidé de la détailler de manière chronologique. Le but étant de comprendre comment les attaques se retrouvent parfois corrélées. Notons que nous n'allons pas détailler toutes les techniques utilisées pour attaquer WEP, celles-ci sont bien trop nombreuses. Toutefois, nous allons décrire leur fonctionnement de manière intuitive en explicitant les étapes essentielles. Afin de pouvoir nous renseigner complètement sur chacune des attaques, nous donnerons les articles techniques en référence.

2.1. RC4

Pour comprendre le processus de chiffrement de WEP, nous devons détailler sa primitive cryptographique, l'algorithme RC4. Celui-ci a été inventé par Ron Rivest (le R de RSA) en 1987. Il a été premièrement gardé secret, jusqu'à sa publication anonyme sur la liste de messagerie Cypherpunks en septembre 1994. RC4 est également utilisé par le protocole SSL/TLS, TKIP, Microsoft Word, Oracle, etc. Cet algorithme de chiffrement par flot a été abondamment étudié, vraisemblablement parce qu'il est mathématiquement simple. RC4 se décompose en deux algorithmes, Le Key Scheduling Algorithm (KSA) et le Pseudo Random Generator Algorithm (PRGA).

2.1.1. KSA

L'objectif de cet algorithme est de mélanger un tableau appelé S contenant 256 octets à l'aide d'une clé secrète. Pour ce faire, KSA permute deux valeurs pointées par les registres i et j. Cette opération est effectuée 256 fois, afin de permuter au moins une fois toutes les valeurs du tableau S. Le registre i est un compteur alors que le registre j dépend de la valeur de la clé secrète. À chaque étape du KSA, le tableau est récursivement nommé S, S0, S1, S2, ... ,S255. La figure [KSA] décrit ce processus sous la forme d'un algorithme.

2.1.2. PRGA

Une fois le KSA exécuté, nous obtenons un tableau de 256 valeurs permutées en fonction de la clé secrète. Ce tableau, appelé S255 ou encore S'0, va ensuite être utilisé par le PRGA pour générer un octet de keystream. Celui-ci sera ensuite XORé avec le texte clair pour obtenir le texte chiffré. Notons que lorsqu'un octet de keystream est généré, le tableau de 256 octets S'0 est légèrement modifié en permutant deux valeurs (celles pointées par les registres i et j également). Celui-ci se nomme alors S'1, puis S'2 lorsque le deuxième octet du keystream est généré, etc. La figure [PRGA] décrit cet algorithme.

2.1.3. Attaques de Roos/Wagner

En 1995, suite à la publication du cryptosystème RC4, Roos et Wagner trouvent en collaboration un certain nombre de vulnérabilités dans le KSA et le PRGA de RC4. En particulier, Roos [Roos95] remarque que certaines valeurs du tableau de 256 octets générés par le KSA (S255 ou S'0) ne seront permutées qu'une seule fois. En effet, selon l'algorithme [KSA], celui-ci permute les valeurs pointées par les registres i et j. Si le registre i est incrémenté de 0 à 255 et donc couvre l'entièreté du tableau, la valeur de j dépend de la clé secrète et peut être considérée comme complètement aléatoire (on parle alors d'un KSA idéalisé). Il existe donc une chance non négligeable pour qu'une valeur du tableau ne soit permutée qu'une fois. En effet, les 256 tirages aléatoires de la valeur de j ne couvrent pas forcément toutes les valeurs entre 0 et 255). Ainsi, il est possible de déterminer certaines valeurs du tableau généré par le KSA avec une probabilité de succès biaisée. De plus, KSA utilise récursivement les octets de la clé secrète. On parle de fonction pseudo triangulaire (pseudo T-function en anglais). Cette particularité permet d'avoir des valeurs de S255 ne contenant que certains octets de la clé. La figure [ROOS] décrit les probabilités de succès des valeurs biaisées du tableau S255 en fonction des octets de la clé secrète). Par exemple, la première valeur du tableau S255[0] est égale à K[0] avec une probabilité de 0.37 (au lieu de 0.0039 en considérant une distribution uniforme aléatoire).

Dans plusieurs échanges sur la liste de messagerie sci.crypt en 1995, Roos et Wagner [Wagner95] déterminent même une attaque complète sur RC4. En effet, en considérant que les trois premiers octets de la clé secrète sont connus de l'attaquant, celui-ci peut « envoyer » une valeur contenant un octet inconnu de la clé (par exemple le premier octet inconnu K[3]) sur le premier octet du keystream. Pour ce faire, les trois premiers octets de la clé secrète doivent avoir une combinaison spécifique. Ils nomment cette famille de clés des « clés faibles ».

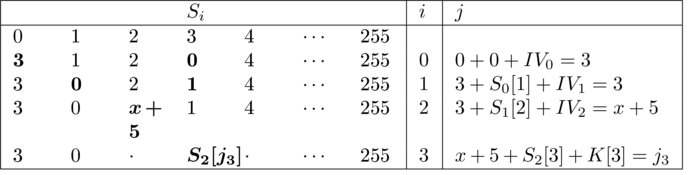
Voici un exemple pour illustrer une attaque utilisant une « clé faible ». Soient les trois premiers octets de la clé composés des valeurs K[0] = 3, K[1] = 255 et K[2], une valeur arbitraire différente de 251 ou 252. Le tableau ci-dessous [TAB1] décrit les trois premières rondes du KSA. Supposons maintenant que durant les 252 dernières rondes, j ne soit jamais égal à 3. On peut donc décrire les premiers éléments de S255 comme S255[0] = 3, S255[1] = 0 et S255[3] = S2[j3]. La probabilité d'obtenir cette configuration est d'environ 5 %.

Maintenant, en considérant l'exécution du PRGA, on obtient la configuration suivante (voir figure [TAB2]). Selon la définition du PRGA, le premier octet du keystream nous donne la valeur de S2[j3] avec une probabilité de succès de 5 % en moyenne. Grâce à cette valeur et au KSA, on peut donc recouvrer K[3], le premier octet inconnu de la clé, en fonction des précédents octets connus de la clé K[0], K[1] et K[2].

Ainsi, pour autant qu'un attaquant connaisse les trois premiers octets de la clé secrète, ainsi que le texte clair du premier octet du chiffré, il peut obtenir le premier octet du keystream et potentiellement recouvrer un octet inconnu de la clé secrète. Malheureusement, le biais n'est pas important et il faudrait une multitude de textes chiffrés, dont seulement les trois premiers octets de la clé ne seraient pas fixes. En cryptographie, on parle de « clés liées » (related keys). Cette attaque ne s'appliquant en pratique sur aucune utilisation de RC4 connue, elle fut quelque peu oubliée.

2.1.4. Les biais de Jenkins

En 1996, Jenkins s'est également intéressé à la sécurité de RC4 et du PRGA en particulier. Celui-ci a détaillé sur sa page web [Jenkins96] la découverte d'un biais intéressant décrit dans la figure [JENKINS].

Comme la précédente attaque, Jenkins ne pouvant appliquer ce biais en pratique sur RC4, celui-ci a été oublié.

2.2. IEEE 802.11 (1999)

Revenons au standard défini en 1999, soit 4 ans après la découverte des clés faibles de Roos et Wagner. Le standard IEEE 802.11 a pour objectif (entre autres) de sécuriser la communication sans-fil. Une solution est de chiffrer la communication en utilisant RC4. Chaque paquet pourrait par exemple être XORé avec le keystream de RC4.

Toutefois, c'est au niveau de la couche de liaison du modèle OSI que l'algorithme de chiffrement opère. Cela pose un sérieux problème de synchronisation. Comme il s'agit de communications sans-fil, il est fort probable que des paquets soient perdus. Normalement, la perte d'un paquet n'est pas problématique, car le protocole de transport est là pour le détecter. Cependant, ces données sont chiffrées. Il est donc impossible de déchiffrer correctement le paquet sans savoir quel morceau du keystream est utilisé pour le chiffrer.

Afin d'éviter un lourd processus de synchronisation, l'alliance Wi-Fi a choisi de chiffrer chaque paquet indépendamment. Malheureusement, cela pose un nouveau problème : RC4 est un algorithme de chiffrement par flot, on ne doit jamais utiliser deux fois la même clé (sinon, en XORant deux paquets chiffrés, on obtient le XOR des deux textes clairs). L'idée fut donc d'ajouter un compteur (vecteur d'initialisation ou IV) à la clé fixe et de transmettre ce compteur en clair avec le paquet de données chiffré. WEP propose d'utiliser les trois premiers octets de la clé comme vecteur d'initialisation. Ainsi d'une taille de 64 bits (respectivement 128 bits), les clés ne restent secrètes que pour 40 bits (respectivement 104 bits). Tout cela ressemble furieusement au cas critique d'utilisation de RC4 décrit par Roos et Wagner en 1995.

Il manque encore un élément pour que cette attaque fonctionne. Un attaquant doit connaître le premier octet du keystream. Par chance, la norme RFC 1042 définit un en-tête du message pratiquement constant. En particulier, le premier octet est systématiquement 0xAA. Ainsi, en XORant 0xAA et le premier octet du texte chiffré, l'attaquant est capable d'obtenir le premier octet du keystream de chaque paquet. 5 ans après la découverte des « clés faibles » de Roos et Wagner, les responsables du standard IEEE 802.11 viennent de créer un algorithme vulnérable sur mesure.

2.3. Attaque FMS (2001)

Ce n'est qu'en 2001 que Fluhrer Mantin et Shamir redécouvrent [Fluhrer01] les « clés faibles » de RC4 et proposent une attaque pratique sur WEP. L'attaque est quasiment identique à celle de Roos et Wagner. Elle est un peu améliorée dans une version étendue de l'article : un attaquant récupère un certain nombre de paquets chiffrés puis mémorise le compteur (les trois premiers octets publics) ainsi que l'octet du keystream (le premier octet du texte chiffré XORé avec 0xAA). Selon les valeurs du compteur (IV), l'attaquant « vote » pour une valeur du quatrième octet de la clé K[3] (le premier octet inconnu). Le biais est de l'ordre de 5 %. C'est-à-dire que l'attaque retourne correctement la valeur de K[3] dans 5 % des cas (au lieu de 1/256 dans le cas d'une distribution uniforme aléatoire). Une fois cet octet trouvé, d'autres valeurs du compteur permettent de recouvrer le cinquième octet de la clé K[5], puis K[6], jusqu'à K[15] (dans le cadre d'une clé WEP de 104 bits). La complexité de l'attaque dépend donc du nombre de paquets chiffrés capturés. En considérant une distribution aléatoire de l'IV, il faut environ quatre millions de paquets chiffrés pour recouvrer une clé secrète de 104 bits avec une probabilité plus grande que 1/2.

L'alliance Wi-Fi réagit contre ces attaques en proposant un filtre qui évite l'utilisation d'IV vulnérables. Ce filtrage est par exemple utilisé par les différentes piles 802.11 du noyau Linux.

2.4. Attaques de Korek (2004)

En 2004, un hacker nommé « Korek » publie dans un forum [Korek04], [Korek04a] une série de nouvelles attaques conditionnelles sur WEP. Korek en décrit pas moins de 17. L'énorme avantage de ces nouvelles attaques par rapport à la précédente est qu'elles dépendent de la valeur du premier et du deuxième octet du keystream. Ainsi, il n'est pas possible de filtrer ces valeurs en fonction de l'IV seulement. De plus, ces attaques possèdent une probabilité de succès bien plus grande (autour de 15 % de succès pour l'attaque A_u15).

Les attaques de Korek se basent toutes sur la même technique. L'idée est d'exploiter le biais de Roos dans le KSA de RC4, et de le combiner à d'autres vulnérabilités du PRGA. Le premier type d'attaque a pour but d'envoyer une certaine valeur contenant un octet de la clé secrète (par exemple K[3]) directement sur le premier ou le deuxième octet du keystream. Il s'agit de la généralisation des attaques FMS. Le deuxième type d'attaque est d'agir indirectement sur la valeur du premier octet du keystream. Un dernier type d'attaque vote négativement pour des valeurs d'octets de la clé secrète. Par exemple, certaines valeurs ne sont pas possibles. Ces votes négatifs aident à améliorer le recouvrement de la clé secrète. Pour plus d'informations sur la description des attaques Korek ainsi que leur classification, nous vous recommandons la lecture de [Chaabouni06] et [Vuagnoux10].

Notons que certaines attaques de Korek avaient au préalable été découvertes notamment par David Hulton [Hulton02] et Andrea Bittau [Bittau03]. En exploitant les améliorations de Korek, la complexité de recouvrement de la clé diminue, ne demandant qu'environ 800000 paquets chiffrés pour une clé de 104 bits.

2.4.1. Aircrack

Les attaques de Korek ont été fortement médiatisées par l'application Aircrack développée par Christophe Devine en 2004. Celle-ci permet également d'engendrer du trafic réseau en rejouant des paquets ARP capturés. En effet, WEP ne propose aucune protection contre le rejeu de paquets. Ainsi, l'obtention de quelques 800000 paquets chiffrés ne demande plus des mois de capture passive du trafic. De plus, les paquets ARP sont facilement identifiables, grâce à leur longueur caractéristique (qui ne change pas, car un algorithme de chiffrement par flot est utilisé). En quelques minutes, Aircrack permet de recouvrer une clé secrète de manière automatisée. La difficulté réside essentiellement dans la configuration des pilotes de cartes sans fil utilisés pour injecter du trafic réseau. Aircrack a été par la suite amélioré pour devenir Aircrack-ng. Il reste l'outil le plus utilisé actuellement pour le recouvrement de clés WEP.

2.5. Attaques de Klein (2006)

En 2006, Klein publie sur son site web [Klein06] une nouvelle attaque sur WEP. En fait, il s'agit de la combinaison des biais de Roos dans le KSA de RC4 avec le biais de Jenkins découvert en 1996. Ci-dessous, nous donnons le passage du biais de Jenkins à la valeur de K[p] (le p-ème octet de la clé). Nous utilisons également les biais de Roos [ROOS] représentés sous la forme de la probabilité P' (voir l'équation 4).

Contrairement aux attaques précédentes, ce biais est bien plus faible. Il permet de recouvrer un octet de la clé avec une probabilité de succès de l'ordre de 1.36/256. Toutefois, le grand avantage de cette attaque repose sur le nombre de paquets exploitables. Contrairement aux attaques précédentes, qui sont conditionnées par les valeurs de l'IV et des octets du keystream, chaque paquet chiffré peut être exploité. En combinant des vulnérabilités du KSA et du PRGA, Klein est capable de fournir un recouvrement de clé WEP avec moins de 25000 paquets chiffrés. Il s'agit d'une estimation théorique, bien loin de la réalité, plus proche de 100000 paquets.

Une autre différence majeure de cette attaque comparée aux précédentes réside dans le besoin de connaître la valeur de plusieurs octets du keystream. Pour recouvrer l'octet K[p] de la clé, l'attaquant doit obtenir l'octet p+1 du keystream. Grâce aux paquets ARP, un attaquant peut toutefois facilement obtenir ces valeurs. L'appendice de l'article [VaudenayV07] décrit quels sont les octets du keystream faciles à obtenir pour des paquets ARP et des paquets TCP/IP. Pour plus d'informations sur ce biais, veuillez consulter [Klein06], [VaudenayV07] et [Vuagnoux10].

2.6. Attaques PTW (2007)

En 2007, Pyshkin, Tews et Weinnmann proposent sur le site eprint.iarc.org [TewsWP07] un article qui détaille une amélioration des attaques de Klein. Un adversaire doit recouvrer correctement le quatrième octet de la clé (K[3]) afin de pouvoir tenter de recouvrer l'octet suivant (K[4]), et ainsi de suite. Les auteurs proposent de recouvrer indépendamment la somme des octets de la clé. C'est-à-dire qu'au lieu de tenter de retrouver le p-ème octet de la clé secrète, cette attaque tente de retrouver la somme des 4ème, 5ème, ..., p-1-ème et p-ème octets. Le grand avantage de cette attaque est que chaque somme d'octets de clé ne dépend pas du succès du recouvrement des précédents. Cependant, il faut maintenant correctement recouvrer deux sommes pour retrouver un octet de la clef. En effet, k[3]+k[4]+k[5] et k[3]+k[4] sont nécessaires pour identifier la valeur de k[5]. La complexité de cette attaque est de l'ordre de 40000 paquets chiffrés pour obtenir une clé secrète de 104 bits avec une probabilité de succès plus grande que 1/2. Pour plus d'informations sur ce biais et sur la sécurité de WEP en général, nous vous recommandons la lecture de [Tews07].

2.7. Attaques de Vaudenay et Vuagnoux (2007)

L'attaque de PTW a été en réalité indépendamment découverte par Vaudenay et Vuagnoux la même année et présentée à la conférence Selected Areas in Cryptography 2007. Toutefois, quelques différences existent entre ces deux attaques. Tout comme l'attaque PTW, Vaudenay et Vuagnoux ont remarqué qu'il est possible de recouvrer la somme des octets de la clé secrète au lieu de chercher la valeur de chaque octet de façon linéaire. Mais ceci ne sert pas seulement à améliorer l'attaque de Klein. Toutes les autres attaques peuvent en bénéficier, comme l'attaque FMS ou les attaques de Korek.

De plus, il est possible d'exploiter la répétition de la clé utilisée par RC4. En effet, si on regarde l'algorithme du KSA [KSA], on remarque que la valeur du registre j est calculée avec K[i mod l] où l est la longueur de clé. Prenons un exemple, soit Kbar[p] = K[0] + K[1] + ... + K[p] la somme des octets de clé de 0 à p. On définit Kbar[19] = Kbar[15] + K[0] + K[1] + K[2] + K[3]. Comme K[0], K[1] et K[2] représentent l'IV de 24 bits, ces valeurs sont connues. Pour autant que Kbar[15] ait été correctement recouvré, il est possible d'obtenir de l'information sur la valeur de K[3] à l'aide d'attaques supplémentaires qui utilisent d'autres octets du keystream (en l'occurrence, le 18ème octet dans cet exemple).

La précédente amélioration souffre toutefois d'un problème majeur. Pour pouvoir exploiter la répétition de la clé secrète, il faut correctement recouvrer Kbar[15]. En utilisant la répétition de l'IV, il est possible de grandement améliorer cette probabilité de succès. En effet, puisque Kbar[16] = Kbar[15] + K[0], et connaissant K[0], un adversaire double le nombre d'attaques pour cette somme d'octets de clé secrète. Évidemment, Kbar[17] et Kbar[18] peuvent également être exploités de la même manière, on obtient alors quatre fois plus d'attaques pour recouvrer cette valeur critique. Voici donc les trois améliorations apportées par Vaudenay et Vuagnoux. Toutefois, c'est le nom de PTW qui est resté dans la mémoire des gens en ce qui concerne ces attaques sur WEP. La complexité de l'attaque tombe à 32000 paquets chiffrés pour une probabilité de succès identique aux attaques précédentes.

2.7.1. Beck et Tews (2009)

En 2009, Beck et Tews publient un article qui reprend exactement la même méthode que Vaudenay et Vuagnoux [BeckT09]. Cependant, en améliorant les coefficients de pondération des attaques (c'est-à-dire en modifiant l'importance des attaques), ils obtiennent une complexité de 24200 paquets seulement !

2.8. Attaques SVV (2010)

En 2010, Sepherdad, Vaudenay et Vuagnoux proposent une analyse exhaustive des biais de RC4. En résumant les attaques précédentes, ils constatent que le biais de Roos du KSA est systématiquement utilisé. Seuls des biais additionnels contenus dans le PRGA permettent une amélioration dans le recouvrement des clés secrètes. Ils proposent de tester l'intégralité de l'espace des biais potentiels dans une ronde du PRGA. Pour ce faire, ils utilisent une approche spectrale en utilisant une transformée de Fourier de l'espace des équations linéaires décrivant ces biais. Grâce à cette méthode, 48 biais additionnels sont découverts dans le PRGA de RC4.

Suite à cette analyse, ils proposent de l'étendre à RC4, en ne considérant plus le KSA et le PRGA, mais une boîte noire, possédant comme entrée une clé secrète et des octets de keystream comme sortie. En utilisant la même représentation spectrale, ils dénombrent pas moins de 9 nouvelles corrélations.

En intégrant ces corrélations aux attaques précédentes et en les combinant avec le biais de Roos (pour les biais du PRGA), ils sont capables de recouvrer une clé secrète de 104 bits avec moins de 10000 paquets chiffrés. Cette technique sera présentée au 27C3. Un patch incluant ces améliorations sera prochainement disponible pour Aircrack-ng. Pour plus d'informations sur cette attaque, nous vous recommandons la lecture de [SepherdadVV10] et la partie 3 de [Vuagnoux10].

3. Analyse de l'intégrité des données

L'utilisation d'un contrôle de redondance cyclique comme protection de l'intégrité des données n'est jamais une bonne idée, encore moins quand un algorithme de chiffrement par flot est utilisé. En effet, le CRC32 a des propriétés linéaires. C'est-à-dire qu'il est facile de modifier un bit dans le texte chiffré tout en modifiant le CRC32, même si celui-ci est chiffré également. Le protocole WEP répond à un message si le paquet possède un CRC32 correct et ne renvoie rien du tout si celui-ci est faux. Un attaquant peut utiliser cette propriété pour « deviner » les octets du keystream et les réutiliser pour injecter du trafic réseau. Cette technique est connue sous le nom d'exploitation d'oracle en cryptographie. Korek (encore !) proposa ce type d'attaque en 2004. Baptisé Chopchop, cette attaque est également implémentée dans Aircrack-ng. Notons que Arbaugh [Arbaugh01] fut le premier à proposer une attaque utilisant le CRC32 comme oracle sur WEP en 2001.

En 2006, Bittau, Handley et Lackey ont réussi a grandement améliorer l'attaque de Korek en exploitant une propriété de fragmentation de 802.11. En effet, il est possible d'utiliser plusieurs fois les octets de keystream lorsqu'un paquet est fragmenté. Cette attaque est également proposée dans Aircrack-ng. Pour plus d'informations sur ces attaques, nous vous recommandons la lecture de [Arbaugh01], [BittauHL06] et [Tews07].

4. Analyse des processus d'authentification

Comme expliqué en introduction de cet article, il n'existe pas vraiment de mécanisme d'authentification, puisque celui-ci se résume à la connaissance du nom du réseau. Toutefois, WEP propose un algorithme d'authentification optionnel pour identifier le client. Constatant les défauts évidents de cet algorithme, l'alliance Wi-Fi a rapidement déconseillé son utilisation.

L'authentification par clé partagée utilise la connaissance de la clé secrète pour autoriser l'accès au réseau à un client. Celui-ci reçoit du point d'accès une chaîne de caractères (appelée challenge). Le client doit alors chiffrer cette chaîne à l'aide de la clé secrète utilisée pour chiffrer les communications à l'aide de WEP. Cette réponse constitue la preuve que le client connaît la clé secrète. Cette solution comporte deux erreurs majeures. Premièrement, lorsqu'un client s'authentifie, il permet à un attaquant qui capture passivement le trafic réseau d'obtenir un keystream exploitable. En effet, connaissant le « challenge » en clair et chiffré, celui-ci peut les XORer pour obtenir un keystream réutilisable. Deuxièmement, un attaquant peut également envoyer le challenge envoyé par le point d'accès à un client préalablement authentifié, Celui-ci lui donnera la réponse correcte, qu'il peut ensuite envoyer au point d'accès. Aircrack-ng implémente également cette dernière attaque.

Voilà pourquoi ce mécanisme d'authentification est déconseillé. À défaut d'améliorer la sécurité des communications sans-fil, il la fragilise.

Conclusion

Une question que l'on peut se poser est : « Pourquoi continuer à casser WEP ? ». En effet, les attaques de Korek et les différentes techniques pour engendrer du trafic réseau permettent en quelques minutes le recouvrement de la clé secrète.

Une première réponse vient peut-être du cryptosystème RC4 utilisé par WEP. Les vulnérabilités détaillées ci-dessous concernent RC4 en premier lieu. Or, il se trouve que cet algorithme de chiffrement par flot est toujours considéré comme sécurisé (les attaques présentées ne permettent toujours pas d'attaques pratiques sur RC4). Il est de plus l'un des cryptosystèmes le plus utilisé de nos jours. Les attaques sur WEP sont donc avant tout de nouvelles attaques sur l'un des cryptosystèmes le plus utilisé de nos jours.

Un deuxième élément de réponse concerne TKIP. En effet, bien que la clé soit différente pour chaque paquet lorsque TKIP est utilisé pour chiffrer des données, les attaques présentées ci-dessus sont toutes applicables à TKIP. Toutefois, il faudrait trouver d'autres biais supplémentaires pour permettre un recouvrement d'octets de clé secrète avec seulement un seul paquet chiffré. Pour l'instant, il n'existe donc pas d'attaque pratique de recouvrement de clé (temporaire) sur TKIP.

Si la partie cryptographique de TKIP ne semble pas (encore) permettre d'attaque pratique, il ne faut pas oublier qu'elle n'est que rarement le maillon faible d'un système de sécurité. Bien qu'elles ne permettent pas de recouvrer la clé secrète, d'autres attaques sur TKIP sont possibles.

Remerciements

Un grand merci à Cédric Blancher, Christophe Devine et Jean-Baptiste Bédrune pour leurs commentaires et leurs remarques.

Références

[Roos95] Andrew Roos, A Class of Weak Keys in RC4 Stream Cipher (sci.crypt), http://groups.google.com/group/sci.crypt.research/msg/078aa9249d76eacc?dmode=source, 1995

[Wagner95] David Wagner, Weak Keys in RC4 (sci.crypt), http://www.cs.berkeley.edu/~daw/my-posts/my-rc4-weak-keys, 1995

[Jenkins96] Robert Jenkins, ISAAC and RC4, http://burtleburtle.net/bob/rand/isaac.html, 1996

[FluhrerMS01] Scott Fluhrer, Itsik Mantin et Adi Shamir, Weaknesses in the Key Scheduling Algorithm of RC4, Selected Areas in Cryptography, 2001

[Korek04] KoreK, Need Security Pointers, http://www.netstumbler.org/showthread.php?postid=89036#post89036, 2004

[Korek04a] Korek, Next Generation of WEP Attacks?, http://www.netstumbler.org/showpost.php?p=93942&postcount=35, 2004

[Chaabouni06] Rafik Chaabouni, Breaking WEP Faster with Statistical Analysis, École Polytechnique Fédérale de Lausanne, LASEC, Projet de semestre, 2006

[Vuagnoux10] Martin Vuagnoux, Computer Aided Cryptanalysis from Ciphers Side Channels, École Polytechnique Fédérale de Lausanne, LASEC, PhD Thesis, http://martin.vuagnoux.com/vuagnoux-thesis.pdf, 2010

[Hulton02] David Hulton, Practical Exploitation of RC4 Weaknesses in WEP Environments, http://www.dachb0den.com/projects/bsd-airtools/wepexp.txt, 2002

[Bittau03] Andrea Bittau, Additional Weak IV Classes for the FMS Attack, http://www.cs.ucl.ac.uk/staff/a.bittau/sorwep.txt, 2003

[Klein06] Andreas Klein, Attacks on the RC4 Stream Cipher, http://cage.ugent.be/~klein/RC4/RC4-en.ps, 2006

[VaudenayV07] Serge Vaudenay et Martin Vuagnoux, Passive-Only Key Recovery Attacks on RC4, Selected Areas in Cryptography, 2007

[TewsWP07] Erik Tews, Ralf-Philipp Weinmann et Andrei Pyshkin, Breaking 104 Bit WEP in Less Than 60 Seconds, http://eprint.iacr.org/2007/12, 2007

[BeckT09] Martin Beck et Erik Tews, Practical attacks against WEP and WPA, WISEC, 2007

[SepherdadVV10] Pouyan Sepherdad, Serge Vaudenay et Martin Vuagnoux, Discovery and Exploitation of New Biases in RC4, Selected Areas in Cryptography, 2010

[Arbaugh01] William A. Arbaugh, An Inductive Chosen Plaintext Attack against WEP/WEP2, http://www.cs.umd.edu/~waa/attack/v3dcmnt.htm, 2001

[BittauHL06] Andrea Bittau, Mark Handley et Joshua Lackey, The Final Nail in WEP's Coffin, Security and Privacy, 2006