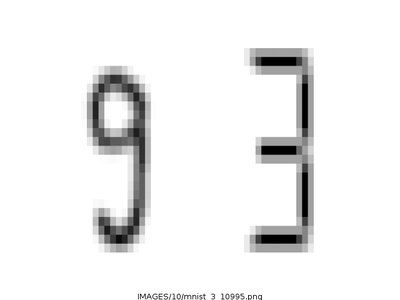Parmi les premières recherches effectuées sur l'Intelligence Artificielle figure la reconnaissance des chiffres manuscrits. La base d'étude utilisée par l'expert en IA Yann Le Cun pour ses travaux, et maintenant devenue une référence, est appelée base MNIST. Nous allons découvrir comment la récupérer, la manipuler et l'étudier.
Nous vivons actuellement une nouvelle période de développement de l'Intelligence Artificielle (IA). Le sujet est de plus en plus fréquemment évoqué à la télévision, à la radio, dans les journaux et sur Internet. Depuis les années 2010, des progrès très importants, réalisés par Geoffrey Hinton, ont permis de relancer la recherche et de créer des applications qu'il aurait été impossible de produire sans disposer de l'IA. Mais nous ne sommes toutefois qu'au tout début de cette discipline, car si l'on en juge par l'émergence de composants spécialisés dans l'accélération des traitements (ASIC, FPGA, puces spécialisées comme celles de Nervana, IBM, NVIDIA, Intel ou Apple) et par les travaux encourageants sur les ordinateurs quantiques d'IBM et de Google, nous pouvons nous attendre à une véritable révolution industrielle dans les années qui viennent. Dans cet article, nous nous contenterons modestement de remonter un peu dans le passé en abordant une étape, particulièrement importante dans l'évolution de l'IA, qui s'est déroulée dans les années 1980 et qui a permis de déboucher sur un moyen de reconnaître automatiquement des chiffres manuscrits. Les premières applications concrètes ont été la reconnaissance du montant des chèques bancaires et la lecture des codes postaux sur les enveloppes.
Mais commençons tout d'abord par quelques brefs rappels sur l'IA.
Le programme présenté dans cet article a été testé sur les systèmes suivants :
- Debian 7.8 (x86_64 Intel(R) Core(TM) i7-3770K CPU @ 3.50 GHz) ;
- Devuan ascii/ceres (x86_64 Intel(R) Core(TM) i5-2405S CPU @ 2.50 GHz) ;
- Devuan jessie (x86_64 Intel(R) Core(TM)2 Duo CPU T7250 @ 2.00 GHz) ;
- Raspbian GNU/Linux 7 (wheezy) (armv7l ARMv7 Processor rev 5 (v7l) @ 600 MHz).
Le code source est disponible sur [1].
Quelques rappels sur l'IA
L'Intelligence Artificielle a commencé son existence dans les années 1940 grâce à des personnalités comme John Mc Carthy, Marvin L. Minsky, Claude E. Shannon, Alan M. Turing, Donald O. Hebb, et Frank Rosenblatt, parmi les plus célèbres initiateurs. D'autres personnalités ont ensuite émergé et sont maintenant considérées comme des experts mondiaux de l'IA, les principales étant Yann Le Cun, Yoshua Bengio et Geoffrey Hinton. Le développement de l'IA jusqu'à nos jours a été très irrégulier, avec une alternance de succès, d'échecs, d'enthousiasmes, de doutes, de découvertes et plus récemment, d'inquiétudes. Les récents progrès de l'informatique et de la technologie, relatifs à la puissance de calcul (CPU et GPU), à la capacité mémoire (RAM et disques) et aux logiciels (algorithmes), ont permis des avancées très importantes dans les domaines de la reconnaissance d'images (photographique, radiographique), de la traduction automatique des langues, de la robotique, pour ne citer que ceux-là, et ont relancé les recherches liées à l'Intelligence Artificielle. Les technologies actuelles utilisent généralement des réseaux de neurones artificiels (ANN pour Artificial Neural Networks) de différents types : perceptrons multicouches (MLP pour MultiLayer Perceptrons) permettant l'apprentissage profond (deep learning), réseaux convolutifs (CNN pour Convolutional Neural Network), réseaux récurrents (RNN pour Recurrent Neural Network), ainsi que des procédés de mémorisation tels que LSTM (Long Short-Term Memory), entre autres.
L'importance grandissante de l'IA et la nécessité pour la France de la maîtriser ont été soulignées dans le rapport que Cédric Villani, mathématicien lauréat de la médaille Fields en 2010 et député de l'Essonne, a remis au gouvernement au premier trimestre 2018. Des sommes considérables sont actuellement investies par les grandes puissances comme les États-Unis et la Chine pour intensifier la recherche et développer les applications basées sur l'IA. La France, elle aussi, a décidé de se lancer dans cette course à la maîtrise de l'IA, mais avec des moyens malheureusement bien plus faibles que ceux cités précédemment. L'intérêt du public et des scientifiques pour l'IA se développe toutefois, grâce aux efforts importants de communication, de persuasion et de vulgarisation de Cédric Villani, et on peut encore espérer aujourd'hui que la France, malgré ses faibles moyens comparés à ceux des superpuissances, puisse tout de même réussir à faire progresser les résultats dans ce domaine et ne perde pas toute son indépendance.
Venons-en maintenant au sujet qui nous intéresse : une étape, ancienne, mais importante, du développement de l'IA, à savoir les travaux débutés par Yann Le Cun dans les années 1980 aux Bell Labs sur les réseaux de neurones et la reconnaissance des chiffres manuscrits.
Description de la base MNIST
Lorsque l'on apprend un nouveau langage informatique, on commence généralement par créer un premier programme, extrêmement simple, que l'on appelle « hello world », car il se limite à l'affichage du message Hello, World. Cela permet de vérifier que le compilateur ou l'interpréteur fonctionne correctement, et que l'on peut commencer à faire ses premiers pas avec ce langage. En IA, l'équivalent du hello world est un peu plus compliqué, puisqu'il consiste à créer un réseau de neurones capable de reconnaître les chiffres manuscrits de la base MNIST. Mais quelle est donc cette base MNIST qui semble si fondamentale dans la compréhension des bases de l'IA ?
La base MNIST (Modified National Institute of Standards and Technology database) est un ensemble de données constitué d'un jeu d'apprentissage de 60.000 chiffres décimaux manuscrits et d'un jeu de test de 10.000 chiffres de même nature, mais différents de ceux contenus dans le jeu d'apprentissage. Le jeu d'apprentissage sert à entraîner un réseau de neurones à reconnaître les chiffres manuscrits et le jeu de test sert, quant à lui, à vérifier que ce réseau est capable, après apprentissage, de reconnaître des chiffres qu'il n'a jamais vus. Cette base est issue d'un mélange des bases SD-1 et SD-3 du NIST qui contiennent des chiffres écrits respectivement par des lycéens et des employés du United States Census Bureau (voir [2]). Les images sources, sélectionnées par Chris Burges et Corinna Cortes, ont été initialement codées dans des matrices 20 x 20, puis converties en matrices de 28 lignes par 28 colonnes, chaque composante de la matrice étant codée sur un octet (donc avec 256 valeurs possibles, de 0 à 255) et représentant une quantité d'encre donnée, la valeur 0 indiquant qu'il n'y a pas d'encre dans la case (case blanche) et la valeur 255 indiquant que la case est complètement remplie d'encre (case noire). Les chiffres manuscrits ont été positionnés dans les matrices de façon à placer leur centre de masse au centre de la matrice. Bien évidemment, la suite d'octets constituée par cet ensemble de chiffres manuscrits ne peut pas être visualisée sans l'aide d'outils appropriés. Ceux que nous allons découvrir dans ce qui suit ont été développés spécifiquement pour la manipulation de cette base. Ils ont été intégrés à un programme multi-usage dont nous avons parlé dans [3] et [4] : l'interpréteur d'expressions en notation polonaise inversée nommé RPN.
Cet interpréteur peut être vu comme un programme à tout faire, capable de manipuler tout type d'objets, pourvu qu'il dispose d'opérateurs sachant identifier et effectuer des traitements sur ces objets. Les principales mécaniques de ce programme sont un analyseur lexical capable de lire des données et de reconnaître les mots-clés que sont les noms des opérateurs, ainsi qu'un gestionnaire de la pile opérationnelle contenant les objets et les résultats de l'exécution des opérateurs. Ces derniers seront introduits au fur et à mesure des besoins de traitement.
Récupération de la base MNIST
Le format des données de la base MNIST est défini dans [5], au paragraphe « THE IDX FILE FORMAT ».
Pour manipuler la base MNIST, nous définirons les types d'éléments suivants :
- TRAINING_ELT (identifiant un élément d'apprentissage, constitué d'une image de chiffre manuscrit et de son label associé) ;
- TEST_ELT (identifiant un élément de test, constitué d'une image de chiffre manuscrit et de son label associé).
Rien ne nous obligeait à créer deux types distincts pour décrire les éléments des deux jeux de la base MNIST, mais la présence de deux jeux de données ayant des fonctionnalités différentes, et donc des traitements potentiellement différents, nous a incités à les distinguer bien qu'ils aient des formats identiques. Ces types sont utilisés pour identifier les données associées à un chiffre manuscrit d'un jeu particulier. Pour des besoins de simplicité de manipulation de la base, nous allons définir deux autres types d'objets permettant de manipuler les ensembles de façon globale :
- TRAINING_SET (un ensemble d'éléments de type TRAINING_ELT) ;
- TEST_SET (un ensemble d'éléments de type TEST_ELT).
La première opération que nous allons avoir besoin d'effectuer est de placer dans la pile opérationnelle les jeux de chiffres manuscrits. Pour cela, nous avons créé l'opérateur read_mnist (voir la fonction rpn_op_read_mnist(), définie via la macro RPN_DEF_OP(rpn_op_read_mnist), dans le fichier rpn_custom.c) qui effectue les tâches suivantes :
- création, si nécessaire, des répertoires de stockage des informations ;
- téléchargement, si nécessaire, des fichiers de la base MNIST à partir du site de Yann Le Cun (voir [5]) ;
- décompression, si nécessaire, des fichiers téléchargés ;
- lecture du contenu de la base MNIST ;
- création des éléments de types TRAINING_ELT et TEST_ELT ;
- création des éléments de type TRAINING_SET et TEST_SET.
Voyons dès à présent comment utiliser cet opérateur. Le programme rpn, après avoir été généré à partir des sources disponibles sur [1] (voir éventuellement [3] pour la méthode de génération) doit être lancé par la commande suivante :
$ ./rpn
L'opérateur read_mnist peut ensuite être exécuté par simple saisie de son nom sur l'entrée standard (le clavier dans le cas présent) de rpn :
RPN> read_mnist
La première fois, le résultat ressemblera à ce qui suit :
$ ./rpn
MAIN STACK EMPTY
RPN> read_mnist
read_mnist
rpn_mnist_install_file (5602) : file "train-images-idx3-ubyte" does not exist => uncompress ...
rpn_mnist_uncompress_file (5628) : file "train-images-idx3-ubyte.gz" does not exist => download ...
converted 'http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz' (ANSI_X3.4-1968) -> 'http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz' (UTF-8)
--2019-01-12 20:44:40-- http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Resolving yann.lecun.com (yann.lecun.com)... 216.165.22.6
Connecting to yann.lecun.com (yann.lecun.com)|216.165.22.6|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 9912422 (9.5M) [application/x-gzip]
Saving to: 'train-images-idx3-ubyte.gz'
train-images-idx3-ubyte.gz 100%[===============================>] 9.45M 250KB/s in 27s
2019-01-12 20:45:07 (363 KB/s) - 'train-images-idx3-ubyte.gz' saved [9912422/9912422]
[...]
2019-01-12 20:45:15 (237 KB/s) - 't10k-images-idx3-ubyte.gz' saved [1648877/1648877]
rpn_mnist_uncompress_file (5636) : uncompress (cmd = "t10k-images-idx3-ubyte.gz" ...
rpn_mnist_install_file (5602) : file "t10k-labels-idx1-ubyte" does not exist => uncompress ...
rpn_mnist_uncompress_file (5628) : file "t10k-labels-idx1-ubyte.gz" does not exist => download ...
converted 'http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz' (ANSI_X3.4-1968) -> 'http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz' (UTF-8)
--2019-01-12 20:45:15-- http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Resolving yann.lecun.com (yann.lecun.com)... 216.165.22.6
Connecting to yann.lecun.com (yann.lecun.com)|216.165.22.6|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 4542 (4.4K) [application/x-gzip]
Saving to: 't10k-labels-idx1-ubyte.gz'
t10k-labels-idx1-ubyte.gz 100%[===============================>] 4.44K --.-KB/s in 0.002s
2019-01-12 20:45:16 (1.84 MB/s) - 't10k-labels-idx1-ubyte.gz' saved [4542/4542]
rpn_mnist_uncompress_file (5636) : uncompress (cmd = "t10k-labels-idx1-ubyte.gz" ...
Magic number = 0x00000803
Images number = 10000 (0x00002710)
Dimension 1 = 28 (0x0000001c)
Dimension 2 = 28 (0x0000001c)
Magic number = 0x00000801
Labels number = 10000 (0x00002710)
Magic number = 0x00000803
Images number = 60000 (0x0000ea60)
Dimension 1 = 28 (0x0000001c)
Dimension 2 = 28 (0x0000001c)
Magic number = 0x00000801
Labels number = 60000 (0x0000ea60)
<MNIST_TRAIN> ***
Lors de la première exécution, cet opérateur crée les répertoires MNIST, TEXTS, IMAGES et TOOLS, puis télécharge avec la commande wget les fichiers constituant la base MNIST. Ces derniers sont déposés dans le répertoire MNIST, puis décompressés.
On peut voir l'appel à la commande wget dans le code de la fonction rpn_mnist_download_file() (dans le fichier rpn_custom.c) :
void rpn_mnist_download_file(char *url)
{
char _cmd[RPN_SYS_CMD_SIZE];
int _ret;
/* Prepare download command
~~~~~~~~~~~~~~~~~~~~~~~~ */
sprintf(_cmd, "wget %s", url);
/* Execute the download command
~~~~~~~~~~~~~~~~~~~~~~~~~~~~ */
if ((_ret = system(_cmd) < 0)) {
fprintf(stderr, "%s: download command (%s) returned an error (%d)!\n",
G.progname, _cmd, _ret);
perror("system");
exit(RPN_EXIT_SYSTEM_ERROR);
}
}
L'opérateur read_mnist télécharge les fichiers de la base MNIST à partir du site de Yann Le Cun. Les commandes utilisées pour le téléchargement sont les suivantes :
$ wget http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
$ wget http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
$ wget http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
$ wget http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Dans le cas où les fichiers sont déjà présents dans le répertoire MNIST, cette étape n'est pas effectuée. Les fichiers sont ensuite décompressés avec les commandes :
$ gunzip train-images-idx3-ubyte.gz
$ gunzip train-labels-idx1-ubyte.gz
$ gunzip t10k-images-idx3-ubyte.gz
$ gunzip t10k-labels-idx1-ubyte.gz
Ils sont ensuite convertis en une suite d'éléments de type TRAINING_ELT (respectivement TEST_ELT) et regroupés sous la forme d'un unique élément TRAINING_SET (respectivement TEST_SET).
Pour des besoins de connaissance des durées de traitement des opérateurs, nous avons créé les opérateurs suivants :
- sw_on (Stop Watch ON : activation du mode chronométrage, voir la fonction rpn_op_sw_on() dans le fichier rpn_utils.c) ;
- sw_off (Stop Watch OFF : désactivation du mode chronométrage, voir la fonction rpn_op_sw_off() dans le fichier rpn_utils.c).
Le chronométrage peut, à tout moment, être activé par appel à l'opérateur sw_on et désactivé par appel à sw_off.
Une deuxième exécution de l'opérateur read_mnist affiche, sur une machine équipée d'un CPU core i7 3770K, les résultats suivants :
$ ./rpn
MAIN STACK EMPTY
RPN> sw_on
sw_on
RPN> read_mnist
read_mnist
Magic number = 0x00000803
Images number = 10000 (0x00002710)
Dimension 1 = 28 (0x0000001c)
Dimension 2 = 28 (0x0000001c)
Magic number = 0x00000801
Labels number = 10000 (0x00002710)
Magic number = 0x00000803
Images number = 60000 (0x0000ea60)
Dimension 1 = 28 (0x0000001c)
Dimension 2 = 28 (0x0000001c)
Magic number = 0x00000801
Labels number = 60000 (0x0000ea60)
read_mnist : 0.057369 s
<MNIST_TRAIN> ***
Ceci nous permet de voir que la lecture de la base et sa préparation pour les manipulations ne prend que 6 centièmes de secondes environ, une fois que les fichiers ont été téléchargés et décompressés.
Sur un Raspberry Pi 2, la même opération sera effectuée un peu moins vite, comme on peut le voir dans la capture épurée suivante :
$ ./rpn
MAIN STACK EMPTY
RPN> sw_on
sw_on
RPN> read_mnist
read_mnist
[...]
read_mnist : 0.941503 s
<MNIST_TRAIN> ***
Cela dit, cette durée d'initialisation reste quasiment négligeable.
Examinons le contenu de la pile après exécution de read_mnist grâce à l'opérateur stk (voir la fonction rpn_op_stk() dans le fichier rpn_utils.c) qui en affiche un contenu synthétique :
RPN> stk
<MNIST_TRAIN> stk
MAIN STACK 2 Y : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
stk : 0.000029 s
Nous voyons que la pile opérationnelle contient maintenant les deux jeux de données, le jeu de test de 10 000 éléments étant dans le registre Y, sous forme d'un élément de type TEST_SET nommé MNIST_TESTS et le jeu d'apprentissage de 60 000 éléments étant dans le registre X, sous forme d'un élément de type TRAINING_SET nommé MNIST_TRAIN. Nous allons voir, dans la suite de cet article, comment exploiter ces deux éléments.
Manipulation de la base MNIST
Maintenant que les données sont disponibles dans la pile opérationnelle, nous allons pouvoir commencer à les utiliser. Notre première opération sera la récupération d'un élément donné du jeu d'apprentissage. L'opérateur get permet de placer, dans le registre X de la pile, une copie d'un élément (d'index spécifié) du jeu d'éléments stocké dans le registre Y. L'élément contenu dans le registre X étant le jeu TRAINING_SET, l'introduction d'un index, par exemple 1234, dans le registre X a pour effet de décaler l'élément TRAINING_SET dans le registre Y. L'exécution de l'opérateur get, quant à elle, permet de récupérer une copie du 1234e chiffre manuscrit et de remplacer dans le registre X l'index 1234 par l'élément possédant cet index. Comme généralement, la valeur contenue dans le registre X avant opération est placée dans le registre LASTX après opération. L'opérateur stk nous montre le contenu courant de la pile :
RPN> 1234 get
1234 get
get : 0.000014 s
<3> ***
RPN> stk
stk
MAIN STACK 3 Z : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1235
MAIN STACK 1 X : TRAINING_ELT [idx = 1234, orig = 1234] '3' 784 -- [ 28 x 28] USED
stk : 0.000044 s
Nous avons donc bien un élément de type TRAINING_ELT dans le registre X, et son index est bien celui qui a été spécifié (1234). Cet élément reste toutefois relativement mystérieux. Nous pouvons avoir une meilleure idée de son contenu en exécutant l'opérateur mat qui, comme nous l'avons vu dans [4] permet de créer une matrice de composantes et de dimensions spécifiées, mais qui ici a été surchargé pour réaliser une nouvelle opération, à savoir la création d'une matrice de dimensions 28 x 28 issue de celle constituant l'élément récupéré précédemment. La matrice résultante, remplaçant dans le registre X l'élément d'où elle est issue, est de type MATRIX, et peut de ce fait être manipulée comme n'importe quelle autre matrice. On peut notamment afficher ses dimensions avec l'opérateur dim (voir la fonction rpn_op_dim() dans le fichier rpn_custom.c) qui place respectivement dans les registres Y et X le nombre de lignes et le nombre de colonnes :
RPN> mat
mat
MATRIX [28 x 28]
[...]
RPN> stk
stk
MAIN STACK 3 Z : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1235
MAIN STACK 1 X : MATRIX [28 x 28]
RPN> dim
dim
28 ***
RPN> stk
stk
MAIN STACK 5 : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 4 T : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1235
MAIN STACK 3 Z : MATRIX [28 x 28]
MAIN STACK 2 Y : INT 28
MAIN STACK 1 X : INT 28
L'opérateur get (voir la fonction rpn_op_get() dans le fichier rpn_custom.c) permet de copier en sommet de pile (X) l'élément dont le numéro a été placé en X, ou, si X contient un élément de type TRAINING_SET (c'est-à-dire que l'index de l'élément à récupérer n'est pas spécifié), de placer en X l'élément dont l'index est spécifié par la variable current_index interne à l'élément TRAINING_SET, et visible à l'aide de l'opérateur stk. L'élément copié en X est de type TRAINING_ELT.
L'élément TRAINING_SET, qui est un élément important et coûteux à produire (en nombre de cycles CPU), est implémenté en tant qu'élément persistent, c'est-à-dire qu'il ne disparaît pas de la pile opérationnelle (il n'est pas consommé) après utilisation par un opérateur (tel que get, dispatch ou mnist_pics par exemple, voir les fonctions rpn_op_nn_dispatch() et rpn_op_mnist_pics() dans le fichier rpn_custom.c).
Voyons cela à l'aide d'un exemple concret :
$ ./rpn
MAIN STACK EMPTY
RPN> 'STACK_BASE' 2 3 4 stk
4 stk
MAIN STACK 4 T : LITTERAL 'STACK_BASE'
MAIN STACK 3 Z : INT 2
MAIN STACK 2 Y : INT 3
MAIN STACK 1 X : INT 4
RPN> +
+
7 ***
RPN> stk
stk
MAIN STACK 3 Z : LITTERAL 'STACK_BASE'
MAIN STACK 2 Y : INT 2
MAIN STACK 1 X : INT 7
RPN> *
*
14 ***
RPN> stk
stk
MAIN STACK 2 Y : LITTERAL 'STACK_BASE'
MAIN STACK 1 X : INT 14
Le littéral STACK_BASE est, dans l'exemple précédent, entré dans une pile vide, et matérialise la base de la pile (représentée ici au sommet de l'affichage, puisque nous avons choisi de présenter systématiquement le dernier élément placé dans la pile en dernier, lors de l'affichage). Lors de l'opération +, les chiffres 3 et 4 sont consommés et remplacés par le résultat de l'opération 3 + 4, soit 7. Lors de l'opération *, les chiffres 2 et 7 sont également consommés et remplacés par le résultat de l'opération 2 * 7, soit 14.
Regardons maintenant ce qu'il se passe avec un élément de type TRAINING_SET :
$ ./rpn
MAIN STACK EMPTY
RPN> 'STACK_BASE' read_mnist
'STACK_BASE' read_mnist
[...]
<MNIST_TRAIN> ***
RPN> stk
<MNIST_TRAIN> stk
MAIN STACK 3 Z : LITTERAL 'STACK_BASE'
MAIN STACK 2 Y : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
RPN> 2019
RPN> stk
2019 stk
MAIN STACK 4 T : LITTERAL 'STACK_BASE'
MAIN STACK 3 Z : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
MAIN STACK 1 X : INT 2019
RPN> get
get
<7> ***
RPN> stk
stk
MAIN STACK 4 T : LITTERAL 'STACK_BASE'
MAIN STACK 3 Z : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 2020
MAIN STACK 1 X : TRAINING_ELT [idx = 2019, orig = 2019] '7' 784 -- [ 28 x 28] USED
Dans cet exemple, nous utilisons le même littéral que dans l'exemple précédent pour matérialiser la base de la pile. L'élément de type TRAINING_SET est produit par l'opérateur read_mnist, qui lit la base MNIST et produit l'élément associé. Si nous voulons récupérer le 2019e élément de la base d'apprentissage, il suffit d'entrer le nombre 2019 puis l'opérateur get. Après exécution de celui-ci, le 2019e élément de la base MNIST (en l'occurrence un 7 manuscrit) remplace le nombre 2019 dans la pile, mais contrairement à l'exemple précédent, l'élément TRAINING_SET est encore présent dans la pile afin que nous puissions le réutiliser, sans avoir à relire la base. De la même façon, l'opérateur get exécuté sans spécifier d'index récupère l'élément suivant (2020) et maintient l'élément TRAINING_SET dans la pile :
RPN> stk
stk
[...]
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 2020
RPN> get
get
<2> ***
RPN> stk
stk
[...]
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 2021
MAIN STACK 1 X : TRAINING_ELT [idx = 2020, orig = 2020] '2' 784 -- [ 28 x 28] USED
Mais revenons à notre élément TRAINING_ELT : il serait intéressant de le visualiser de façon à avoir une idée de l'aspect du chiffre manuscrit. C'est là que la commande gnuplot va nous être d'un grand secours, car elle permet de générer tout type de graphe, et notamment des heatmaps, c'est-à-dire des graphes dans lesquels chaque cellule est colorisée avec une couleur indiquant sa valeur en fonction d'une échelle de couleurs spécifiées. Dans notre cas, les couleurs seront remplacées par des niveaux de gris, le 0 étant représenté en blanc et le 255 en noir, chaque point de la matrice étant représenté par une cellule dont la teinte va varier du blanc au noir, en fonction de sa valeur numérique.
Sur Devuan et Debian, l'installation de la commande gnuplot est effectuée à l'aide de la commande suivante :
$ apt-get install gnuplot
Sur Raspbian, nous utiliserons en revanche une commande légèrement différente :
$ apt-get install gnuplot-x11
Pour générer l'image d'un chiffre manuscrit, nous allons devoir enregistrer sa matrice dans un fichier de données, puis utiliser gnuplot pour produire le graphe. Effectuons ces opérations avec le script suivant :
#!/bin/bash
cat <<- EOF | ./rpn > /dev/null
read_mnist
6 get
mat
'label_2_01.txt' filename
write
EOF
mv 'label_2_01.txt' TEXTS
gnuplot -e 'RADIX="label_2_01"' TOOLS/plot_digit_640
Le fichier image est généré dans le répertoire IMAGES et s'appelle label_2_01.png : c'est la première version d'une image du 6e élément de la base MNIST qui représente le chiffre 2. Quand on visualise le contenu du fichier texte label_2_01.txt, on obtient un résultat identique à celui de la figure 1 sur lequel on voit clairement se dessiner le chiffre manuscrit. Et lorsque l'on regarde le contenu du fichier image (figure 2), on voit que le chiffre est à l'envers, tête en bas. La raison de cette inversion est que la commande gnuplot considère que la première ligne de données du fichier correspond aux cellules qui sont les plus proches de l'axe des abscisses. Nous devons donc inverser les lignes de la matrice pour avoir un affichage dans le bon sens, c'est ce que fait le script suivant, qui utilise l'opérateur hrev (voir la fonction rpn_op_h_rev() dans le fichier rpn_custom.c) spécialement conçu pour inverser les lignes d'une matrice :
#!/bin/bash
cat <<- EOF | ./rpn > /dev/null
read_mnist
6 get
mat
hrev
'label_2_02.txt' filename
write
EOF
mv 'label_2_02.txt' TEXTS
gnuplot -e 'RADIX="label_2_02"' TOOLS/plot_digit_640
Fig. 1: Chiffre manuscrit dans fichier texte.
Fig. 2: Fichier image associé au fichier texte de la figure 1.
Le contenu du fichier texte (figure 3) montre sous forme numérique un chiffre 2 tête en bas, mais l'image générée par gnuplot (figure 4) montre bien un chiffre 2 à l'endroit.
Fig. 3: Chiffre manuscrit à l'envers dans fichier texte.
Fig. 4: Fichier image associé au fichier texte de la figure 3.
Contrôle de la base MNIST
Maintenant que nous avons vu à quoi ressemble un chiffre de la base MNIST, une autre question se pose à nous : comment pouvons-nous examiner cette base de chiffres et nous assurer que les valeurs d'apprentissage sont correctes, c'est-à-dire que les labels correspondent bien aux chiffres manuscrits ? Et comment pouvons-nous faire cela dans un temps raisonnable ?
Les éléments de test seront analysés, à terme, par le réseau entraîné, qui pourra nous indiquer les éléments mal catégorisés. Ceux-ci devraient, on l'espère, être peu nombreux, donc le temps à consacrer à leur contrôle devrait être plutôt faible. Le jeu d'apprentissage, quant à lui, est constitué de 60 000 éléments que nous devons contrôler pour nous assurer qu'il ne comporte pas d'erreur ! Si nous mettions en moyenne 1s (une seconde) pour chaque chiffre à contrôler, la durée du contrôle complet serait de 16 h 40, soit plus dedeux journées de travail de 8 h. Or, la comparaison du chiffre manuscrit sous forme d'image avec sa valeur sous forme de texte, de taille différente (le petit label généré par gnuplot en bas de l'image), risque de nous prendre plus d'une seconde, et d'occasionner un grand nombre de mouvements oculaires, et donc une fatigue visuelle rapide, l’œil passant d'un chiffre représenté par un graphe de taille moyenne à un texte de petite taille, aboutissant à une dérive importante du temps d'examen, et peut-être à un découragement qui serait la conséquence d'un travail répétitif et d'une prise de conscience d'une durée de contrôle largement sous-estimée. Il nous faut donc trouver un moyen plus efficace de faire ce contrôle. Pour aller au plus vite avec moins de fatigue oculaire, il faudrait que le chiffre manuscrit et sa valeur soient de mêmes tailles et côte à côte, mais sans aucune confusion possible lors d'un balayage visuel rapide. Nous choisirons donc pour la valeur (label) une représentation sous la forme classique des chiffres 7 segments (figure 5).
Fig. 5: Représentation sous forme de chiffre 7 segments.
L'opérateur mnist_pic utilise les opérateurs suivant :
- hcat (concaténation de deux matrices, voir la fonction my_op_generic2() dans le fichier rpn_custom.c) ;
- mat7seg (génération d'une matrice de chiffre 7 segments à partir de sa valeur, voir la fonction rpn_op_mat_7_seg() dans le fichier rpn_custom.c) ;
- hrev (inversion des lignes d'une matrice).
Il permet la génération d'une image conforme à ce que nous souhaitons. Nous pouvons l'utiliser de la façon suivante :
cat <<- EOF | ./rpn > /dev/null
read_mnist
6 get
mnist_pic
EOF
Le résultat est contenu dans le fichier IMAGES/00/mnist_2_00006.png visible figure 6.
Fig. 6: Génération d'un chiffre 7 segments à partir d'une image contenant un chiffre manuscrit.
Avec une telle représentation, et en faisant défiler rapidement les images, on peut espérer mettre environ 1s par chiffre, tout du moins au début. Mais à la longue, rien de garanti que nous pourrons maintenir ce rythme de contrôle. Il faudrait donc trouver une méthode plus efficace...
Si nous groupions ces images dans des tableaux, l’œil pourrait les traiter rapidement, à la manière de la lecture d'un livre. On pourrait donc espérer des gains de temps significatifs pour le contrôle de ces 60 000 éléments.
Voyons ce que cela peut donner avec le script de génération suivant :
#!/bin/bash
gen_page()
{
cat <<- EOF
read_mnist
EOF
for j in {1..10}
do
cat <<- EOF
get
label
lastx
mat
x<>y
mat7seg
hcat
hrev
rdn
EOF
for i in {1..9}
do
cat <<- EOF
get
label
lastx
mat
x<>y
mat7seg
hcat
hrev
rup
x<>y
hcat
rdn
EOF
done
if [ $j != 1 ]; then
cat <<- EOF
rup
rup
stk
vcat
rdn
EOF
fi
done
cat <<- EOF
rup
stk
'mnist_with_labels_page_01.txt'
filename
write
EOF
}
gen_page | ./rpn > /dev/null
mv 'mnist_with_labels_page_01.txt' TEXTS/GROUPS
gnuplot -e 'RADIX="mnist_with_labels_page_01"' TOOLS/plot_digits_1920
Le but de ce script est de produire une image PNG constituée de dix lignes de dix chiffres manuscrits, chacun d'entre eux étant accolé à sa version en chiffre 7 segments. Le résultat de son exécution est visible sur la figure 7.
Fig. 7: Tableau de chiffres associant les versions manuscrites et 7 segments.
Un premier essai de balayage rapide nous permet de constater une augmentation significative de la vitesse de traitement, mais la perspective de passer presque deux jours à faire ces contrôles reste peu motivante.
Nous constatons également lors des premiers contrôles qu'il y a encore un frein qui nous empêche d'aller très vite : c'est l'alternance de chiffres distincts, et la nécessité à chaque chiffre rencontré de changer mentalement la valeur du chiffre auquel on compare le chiffre manuscrit. Si nous comparions des groupes de chiffres identiques (labels identiques), nous irions sans aucun doute beaucoup plus vite. Et dans ce cas, inutile d'afficher la valeur du label en chiffre 7 segments, car elle serait constante dans un groupe donné. De plus, on récupérerait pour chaque chiffre un espace dans lequel on pourrait placer un autre chiffre manuscrit. On pourrait ainsi doubler la densité de chiffres à contrôler par ligne, et augmenter de façon significative la vitesse de traitement.
Pour afficher des groupes de chiffres de valeur identique, nous allons avoir besoin de grouper par valeur les chiffres du jeu MNIST. Une façon rapide d'effectuer ce classement est d'utiliser un tableau de 10 pointeurs de listes chaînées (une liste pour chaque chiffre de 0 à 9). L'opérateur dispatch, implémenté selon ce principe, va rapidement effectuer ce travail pour nous :
RPN> stk
<MNIST_TRAIN> stk
MAIN STACK 2 Y : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
RPN> dispatch
dispatch
<MNIST_TRAIN-0> ***
RPN> stk
stk
MAIN STACK 12 : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 11 : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
MAIN STACK 10 : TRAINING_SET 'MNIST_TRAIN-9' 5949 elts, current idx = 1
MAIN STACK 9 : TRAINING_SET 'MNIST_TRAIN-8' 5851 elts, current idx = 1
MAIN STACK 8 : TRAINING_SET 'MNIST_TRAIN-7' 6265 elts, current idx = 1
MAIN STACK 7 : TRAINING_SET 'MNIST_TRAIN-6' 5918 elts, current idx = 1
MAIN STACK 6 : TRAINING_SET 'MNIST_TRAIN-5' 5421 elts, current idx = 1
MAIN STACK 5 : TRAINING_SET 'MNIST_TRAIN-4' 5842 elts, current idx = 1
MAIN STACK 4 T : TRAINING_SET 'MNIST_TRAIN-3' 6131 elts, current idx = 1
MAIN STACK 3 Z : TRAINING_SET 'MNIST_TRAIN-2' 5958 elts, current idx = 1
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN-1' 6742 elts, current idx = 1
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN-0' 5923 elts, current idx = 1
RPN> rup
rup
<MNIST_TESTS> prx
RPN> stk
stk
MAIN STACK 12 : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
MAIN STACK 11 : TRAINING_SET 'MNIST_TRAIN-9' 5949 elts, current idx = 1
MAIN STACK 10 : TRAINING_SET 'MNIST_TRAIN-8' 5851 elts, current idx = 1
MAIN STACK 9 : TRAINING_SET 'MNIST_TRAIN-7' 6265 elts, current idx = 1
MAIN STACK 8 : TRAINING_SET 'MNIST_TRAIN-6' 5918 elts, current idx = 1
MAIN STACK 7 : TRAINING_SET 'MNIST_TRAIN-5' 5421 elts, current idx = 1
MAIN STACK 6 : TRAINING_SET 'MNIST_TRAIN-4' 5842 elts, current idx = 1
MAIN STACK 5 : TRAINING_SET 'MNIST_TRAIN-3' 6131 elts, current idx = 1
MAIN STACK 4 T : TRAINING_SET 'MNIST_TRAIN-2' 5958 elts, current idx = 1
MAIN STACK 3 Z : TRAINING_SET 'MNIST_TRAIN-1' 6742 elts, current idx = 1
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN-0' 5923 elts, current idx = 1
MAIN STACK 1 X : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
RPN> dispatch
dispatch
<MNIST_TESTS-0> ***
RPN> stk
stk
MAIN STACK 22 : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
MAIN STACK 21 : TRAINING_SET 'MNIST_TRAIN-9' 5949 elts, current idx = 1
MAIN STACK 20 : TRAINING_SET 'MNIST_TRAIN-8' 5851 elts, current idx = 1
MAIN STACK 19 : TRAINING_SET 'MNIST_TRAIN-7' 6265 elts, current idx = 1
MAIN STACK 18 : TRAINING_SET 'MNIST_TRAIN-6' 5918 elts, current idx = 1
MAIN STACK 17 : TRAINING_SET 'MNIST_TRAIN-5' 5421 elts, current idx = 1
MAIN STACK 16 : TRAINING_SET 'MNIST_TRAIN-4' 5842 elts, current idx = 1
MAIN STACK 15 : TRAINING_SET 'MNIST_TRAIN-3' 6131 elts, current idx = 1
MAIN STACK 14 : TRAINING_SET 'MNIST_TRAIN-2' 5958 elts, current idx = 1
MAIN STACK 13 : TRAINING_SET 'MNIST_TRAIN-1' 6742 elts, current idx = 1
MAIN STACK 12 : TRAINING_SET 'MNIST_TRAIN-0' 5923 elts, current idx = 1
MAIN STACK 11 : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 10 : TEST_SET 'MNIST_TESTS-9' 1009 elts, current idx = 1
MAIN STACK 9 : TEST_SET 'MNIST_TESTS-8' 974 elts, current idx = 1
MAIN STACK 8 : TEST_SET 'MNIST_TESTS-7' 1028 elts, current idx = 1
MAIN STACK 7 : TEST_SET 'MNIST_TESTS-6' 958 elts, current idx = 1
MAIN STACK 6 : TEST_SET 'MNIST_TESTS-5' 892 elts, current idx = 1
MAIN STACK 5 : TEST_SET 'MNIST_TESTS-4' 982 elts, current idx = 1
MAIN STACK 4 T : TEST_SET 'MNIST_TESTS-3' 1010 elts, current idx = 1
MAIN STACK 3 Z : TEST_SET 'MNIST_TESTS-2' 1032 elts, current idx = 1
MAIN STACK 2 Y : TEST_SET 'MNIST_TESTS-1' 1135 elts, current idx = 1
MAIN STACK 1 X : TEST_SET 'MNIST_TESTS-0' 980 elts, current idx = 1
Les deux jeux ont chacun été éclatés en dix jeux de mêmes types (TRAINING_SET ou TEST_SET) ne comprenant que des chiffres manuscrits de même valeur. Le nom de ces jeux est dérivé des noms d'origine, et les suffixes ajoutés identifient la valeur numérique des chiffres contenus dans les jeux.
L'opérateur mnist_pics a été conçu pour générer les images PNG de tableaux de 1 000 chiffresmanuscrits (25 lignes de 40 chiffres), avec des règles (sur le côté gauche et au-dessus) permettant de calculer l'index d'un chiffre dans un tableau. La génération des 60 pages de 1 000 chiffres peut être effectuée de la façon suivante (l'affichage a été épuré, de façon à ne montrer que la génération de la première et de la dernière page) :
$ ./rpn
MAIN STACK EMPTY
RPN> sw_on
sw_on
RPN> read_mnist
read_mnist
[...]
read_mnist : 0.066197 s
<MNIST_TRAIN> ***
RPN> 1 60000 mnist_pics
60000 mnist_pics
1 - 1000
TXT FILE : TEXTS/GROUPS/mnist_v5_MNIST_TRAIN_00001-01000_25x40.txt
PNG FILE : IMAGES/GROUPS/mnist_v5_MNIST_TRAIN_00001-01000_25x40.png
PLOT COMMAND [gnuplot -e RADIX='"mnist_v5_MNIST_TRAIN_00001-01000_25x40"' TOOLS/plot_digits_1920]
RADIX = mnist_v5_MNIST_TRAIN_00001-01000_25x40
INPUT = TEXTS/GROUPS/mnist_v5_MNIST_TRAIN_00001-01000_25x40.txt
OUTPUT = IMAGES/GROUPS/mnist_v5_MNIST_TRAIN_00001-01000_25x40.png
[...]
59001 - 60000
TXT FILE : TEXTS/GROUPS/mnist_v5_MNIST_TRAIN_59001-60000_25x40.txt
PNG FILE : IMAGES/GROUPS/mnist_v5_MNIST_TRAIN_59001-60000_25x40.png
PLOT COMMAND [gnuplot -e RADIX='"mnist_v5_MNIST_TRAIN_59001-60000_25x40"' TOOLS/plot_digits_1920]
RADIX = mnist_v5_MNIST_TRAIN_59001-60000_25x40
INPUT = TEXTS/GROUPS/mnist_v5_MNIST_TRAIN_59001-60000_25x40.txt
OUTPUT = IMAGES/GROUPS/mnist_v5_MNIST_TRAIN_59001-60000_25x40.png
mnist_pics : 109.333351 s
<MNIST_TRAIN> ***
RPN>
Les soixante images ont été générées en moins de deux minutes sur une machine équipée un CPU Intel i7 3770K. La première page est visible sur la figure 8.
Fig. 8: Page de chiffres.
Enfin, le même traitement peut être effectué sur les jeux générés par l'opérateur dispatch de la façon suivante :
$ ./rpn
MAIN STACK EMPTY
RPN> read_mnist
read_mnist
[...]
<MNIST_TRAIN> ***
RPN> dispatch
<MNIST_TRAIN> dispatch
<MNIST_TRAIN-0> ***
RPN> stk
stk
MAIN STACK 12 : TEST_SET 'MNIST_TESTS' 10000 elts, current idx = 1
MAIN STACK 11 : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
[...]
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN-1' 6742 elts, current idx = 1
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN-0' 5923 elts, current idx = 1
RPN> 1 6000 mnist_pics
6000 mnist_pics
1 - 1000
[...]
OUTPUT = IMAGES/GROUPS/mnist_v5_MNIST_TRAIN-0_00001-01000_25x40.png
[...]
5001 - 5923
[...]
OUTPUT = IMAGES/GROUPS/mnist_v5_MNIST_TRAIN-0_05001-05923_25x40.png
<MNIST_TRAIN-0> ***
On notera que l'on peut spécifier un index de fin (6 000) supérieur au nombre d'éléments du jeu (5 923 pour l'ensemble des 0 du jeu d'apprentissage).
Voyons enfin ce que donne une page de chiffres identiques, disons par exemple la deuxième page des 3 (figure 9). Au premier coup d’œil, on se rend compte qu'avec une telle présentation, le contrôle sera maintenant bien plus rapide.
Fig. 9: Page de chiffres ne contenant que des 3.
Lors du contrôle visuel, on découvre par exemple un chiffre qui ressemble plus à un 9 qu'à un 3. Grâce aux règles libellées en chiffres 7 segments sur les bords du tableau, on peut localiser ce chiffre : il est situé en 4e ligne et 14e colonne de la 2e page des chiffres 3. Son index peut donc être calculé à l'aide de rpn, qui est évidemment capable d'effectuer des opérations arithmétiques. Puisque le nombre est situé sur la deuxième page de 1 000 chiffres 3, sur la 4e ligne de 40 chiffres, en 14e colonne, son index sera donné par :
RPN> 2 1 - 1000 * 4 1 - 40 * 14 + +
1 -
1 ***
1000 *
1000 ***
1 -
3 ***
40 *
120 ***
14 +
134 ***
+
1134 ***
Et on peut donc le récupérer à l'aide de l'opérateur get en ayant le jeu des 3 en Y et l'index 1134 en X :
RPN> stk
stk
[...]
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN-3' 6131 elts, current idx = 1
MAIN STACK 1 X : INT 1134
RPN> get
get
<3> ***
RPN> stk
stk
[...]
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN-3' 6131 elts, current idx = 1135
MAIN STACK 1 X : TRAINING_ELT [idx = 1134, orig = 10995] '3' 784 -- [ 28 x 28] USED
Le label du chiffre récupéré est bien un 3 et non un 9, son index relatif dans le jeu des 3 est 1134 et son index original dans le jeu d'apprentissage MNIST_TRAIN est 10.995.
En poursuivant le contrôle des données, on peut trouver d'autres anomalies, comme :
- l'élément 26 561 : un 1 labellisé comme un 7 (index 2758 dans MNIST_TRAIN-7) ;
- l'élément 32 343 : un 7 labellisé comme un 9 (index 3253 dans MNIST_TRAIN-9) ;
- l'élément 54 265 : un 1 labellisé comme un 4 (index 5269 dans MNIST_TRAIN-4) ;
- l'élément 59 916 : un 7 labellisé comme un 4 (index 5835 dans MNIST_TRAIN-4).
Il en existe encore quelques-unes que vous avez maintenant les moyens de trouver rapidement grâce aux outils que nous venons d'utiliser.
Le mot clé USED, affiché au bout de la ligne de description des éléments, indique qu'il est utilisable lors d'un apprentissage par un réseau de neurones de type MLP (que nous aborderons dans un futur article). La génération de l'image à l'aide de mnist_pic nous montre bien un 9 identifié comme un 3 (figure 10).
Fig. 10: Chiffre 9 identifié comme un 3.
Si nous souhaitons l'ignorer lors de la soumission du jeu d'apprentissage à un MLP, il suffit d'utiliser l'opérateur ignore (voir la fonction rpn_op_nn_ignore() dans le fichier rpn_custom.c) de la façon suivante :
RPN> stk
stk
[...]
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
RPN> 10995 ignore
10995 ignore
<MNIST_TRAIN> ***
RPN> stk
stk
[...]
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 1
RPN> 10995 get
10995 get
<3> ***
RPN> stk
stk
[...]
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 10996
MAIN STACK 1 X : TRAINING_ELT [idx = 10995, orig = 10995] '3' 784 -- [ 28 x 28] IGNORED
Le statut du chiffre d'index original 10 995 dans le jeu MNIST_TRAIN est passé de USED à IGNORED. Lors des prochaines utilisations de ce jeu, comme dans un apprentissage supervisé, cet élément sera identifié comme un élément à ignorer. Si l'on souhaite le rendre utilisable à nouveau, on utilisera l'opérateur use (voir à nouveau la fonction rpn_op_nn_ignore() dans le fichier rpn_custom.c) de la façon suivante :
RPN> stk
stk
[...]
MAIN STACK 1 X : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 10996
RPN> 10995 use
10995 use
<MNIST_TRAIN> ***
RPN> 10995 get
10995 get
<3> ***
RPN> stk
stk
[...]
MAIN STACK 2 Y : TRAINING_SET 'MNIST_TRAIN' 60000 elts, current idx = 10996
MAIN STACK 1 X : TRAINING_ELT [idx = 10995, orig = 10995] '3' 784 -- [ 28 x 28] USED
Conclusion
Nous avons découvert dans cet article différentes façons de manipuler la base MNIST permettant de :
- visualiser son contenu en affichant des chiffres individuellement ou par groupes ;
- générer des sous-ensembles de jeux de chiffres triés par valeur ;
- générer la matrice associée à un élément, et l'enregistrer dans un fichier ;
- localiser rapidement un élément erroné ;
- désactiver et réactiver un élément dans un jeu.
Dans un futur article consacré aux perceptrons multicouches (MLP), nous utiliserons l'activation et la désactivation d'éléments pour étudier l'impact des valeurs erronées d'un jeu d'apprentissage sur la fiabilité de reconnaissance des éléments. En attendant, vous avez le temps de vous entraîner à manipuler vos nouveaux outils.
Références
[1] Site GitHub officiel de RPN : https://github.com/mbornet-hl/rpn
[2] Wikipedia anglophone sur la base MNIST : https://en.wikipedia.org/wiki/MNIST_database
[3] M. BORNET,« RPN : interpréteur de notation polonaise inversée en langage C », GNU/Linux magazine n°217, p. 34 à 47 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-217/RPN-interpreteur-de-notation-polonaise-inversee-en-langage-C
[4] M. BORNET,« RPN : extension de la syntaxe grâce à lex », GNU Linux magazine n°221, p. 82 à 90 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-221/RPN-extension-de-la-syntaxe-grace-a-lex
[5] Site de Yann Le Cun sur MNIST : « THE MNIST DATABASE of handwritten digits » : http://yann.lecun.com/exdb/mnist/
Pour aller plus loin
Si vous souhaitez continuer à explorer l'histoire de l'IA, la reconnaissance des chiffres manuscrits, les perceptrons multicouches et autres réseaux de neurones, et prendre un peu d'avance sur les futurs articles traitant du sujet, voici quelques références qui sont susceptibles de vous intéresser et vous aider à progresser plus rapidement :
- Vidéo de Claude Shannon présentant sa souris intelligente, « Where did digital communication begin? » : https://www.youtube.com/watch?v=nS0luYZd4fs
- Vidéo de Yann Le Cun faisant une démonstration de la reconnaissance des chiffres manuscrits, « Convolutional Network Demo from 1993 » : https://www.youtube.com/watch?v=FwFduRA_L6Q
- Vidéo « Mais qu'est-ce qu'un réseau de neurones ? Apprentissage profond, chapitre 1 » : https://www.youtube.com/watch?v=aircAruvnKk
- Cours de Stanford University sur la reconnaissance visuelle, « CS231n: Convolutional Neural Networks for Visual Recognition » : http://cs231n.stanford.edu/ (explorer les différents liens de la page)
- Des vidéos de Geoffrey Hinton sur les réseaux de neurones, « Geoffrey Hinton Lectures » : http://www.cs.toronto.edu/~hinton/coursera_lectures.html
- Livre de Ian Goodfellow, Yoshua Bengio and Aaron Courville, « Deep Learning », The MIT Press, 2017
- Publications de Yann Le Cun sur arXiv : https://arxiv.org/find/all/1/all:+AND+yann+lecun/0/1/0/all/0/1



 Ajouter à une liste de lecture
Ajouter à une liste de lecture