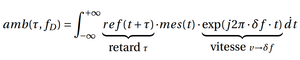Après avoir étudié comment synchroniser deux récepteurs de télévision numérique terrestre (DVB-T) exploités comme source pour le traitement de signaux radiofréquence (radio logicielle), nous démontrons l’utilisation de ce montage pour réaliser des expériences de RADAR passif. Dans ce contexte, les signaux émis par une source non coopérative – dans notre cas émetteur de télévision numérique terrestre – sont recherchés dans les échos réfléchis par des cibles statiques ou en mouvement : la distance et la vitesse des cibles sont identifiées par le retard et le décalage Doppler introduit par la vitesse radiale. L’expérience, d’un coût de quelques dizaines d’euros, permet de se familiariser avec les techniques de traitement classiquement utilisées lors de l’étude de signaux RADAR.
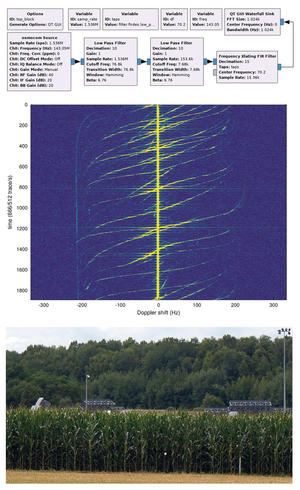
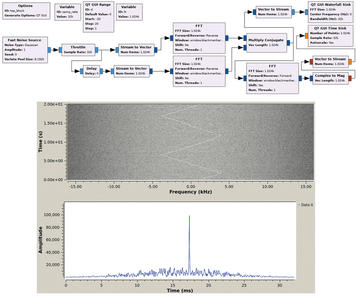
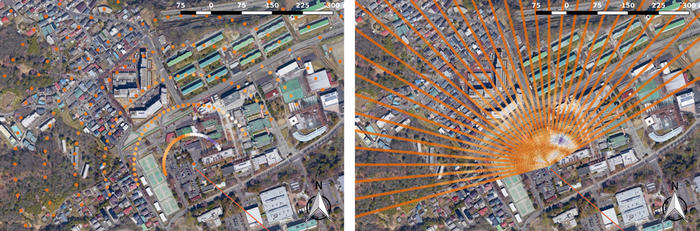
Le RADAR (RAdio Detection And Ranging) est une technologie développée au début du XXème siècle, qui a connu son essor lors de la Seconde Guerre mondiale, pour finalement être exploitée dans une multitude de domaines pour lesquels la vitesse ou la distance à une cible doit être connue. Nous pouvons citer parmi ces applications la mesure de la vitesse des balles dans les sports tels que le baseball ou le tennis, ou la mesure de hauteur de fluides dans des réservoirs. Lorsque nous avons la chance d’habiter à moins de 50 km d’un des RADARs les plus puissants en France – le RADAR GRAVES (Grand Réseau Adapté à la Veille Spatiale) de surveillance de l’espace au-dessus de la France – détecter les réflexions des signaux électromagnétiques émis depuis la Haute-Saône par GRAVES est trivial compte tenu de la puissance de plus de 400 kW émise [1]. Un simple récepteur de télévision numérique terrestre (DVB-T architecturé autour des composants R820T(2) et RTL2832U) utilisé comme récepteur généraliste de radio logicielle, analysant une bande spectrale de quelques centaines de Hz autour de la porteuse à 143,05 MHz, permet d’observer le décalage Doppler introduit par les aéronefs en mouvement. En effet, toute onde émise par un objet en mouvement se voit affectée, dans le référentiel statique, d’un décalage δf de sa fréquence f dans le référentiel en mouvement à vitesse v de δf≃ f (v / c ) avec c la célérité de l’onde, dans notre cas la vitesse de la lumière. Dans le cas des RADARs, l’impact du décalage Doppler est double, une fois lorsque l’onde atteint la cible et une fois lorsqu’elle est réfléchie. Ainsi dans le cas de GRAVES, un avion volant à une vitesse maximale de 1000 km/h (278 m/s) induit un décalage Doppler de 2 x 143,05 / 300 x 278 = 265 Hz. Nous n’analysons donc qu’une bande spectrale de ±300 Hz autour de la porteuse, illustrant clairement par les bandes qui traversent le graphique de la figure 1 la détection d’avions présentant d’abord une vitesse positive par rapport à notre direction de visée, pour devenir négative lorsque l’aéronef s’éloigne. Du point de vue de GNURadio, utilisé pour acquérir et traiter les signaux du récepteur DVB-T, le traitement se limite à une décimation successive par filtres passe-bas pour passer de la fréquence d’échantillonnage du récepteur – autour de 1,5 à 2 MHz, vers une plage de fréquences permettant de visualiser les échos réfléchis par les cibles mobiles, de l’ordre de 1 kHz. La décimation d’un facteur 2000 ne peut se faire en une étape, le filtre anti-repliement étant excessivement gourmand en ressources dans ce cas, et une cascade de filtres (par exemple trois filtres passe-bas décimant d’un facteur 12 chacun) sera plus efficace pour atteindre le résultat.
Fig. 1 : Haut : flux de traitement GNURadio, avec cascade de filtres passe-bas pour décimer de 1500 le flux incident à 1.5 M échantillons/s, et correction d’erreur de l’oscillateur local par le Xlating FIR Filter. Milieu : signaux décalés en fréquence par rapport à la porteuse du RADAR GRAVES représentatifs du passage d’avions. Ces signaux sont reçus depuis Besançon par une antenne discone Diamond D190 large bande connectée à un récepteur DVB-T. Bas : à une cinquantaine de kilomètres de Besançon, le site de l’émetteur GRAVES est accessible en vélo et visible depuis la route d’accès.
Cependant, GRAVES est un RADAR à onde continue qui ne donne aucune indication sur la distance de la cible : étant dédié à la surveillance de satellites, la seule connaissance de la vitesse du satellite (et des lois de Kepler) suffit à connaître son altitude (et donc sa fonction). Identifier la distance de cibles nécessite d’introduire une datation du temps de vol, et toute notion de datation se traduit nécessairement par un étalement spectral du signal émis (pour rappel, la transformée de Fourier du pic de Dirac en temps est une fonction constante qui occupe tout le spectre dans le domaine fréquentiel). De ce fait, réaliser un RADAR nécessite un émetteur puissant – la puissance du signal renvoyé par la cible décroît avec la puissance quatrième de la distance (section 1) – et de large encombrement spectral. Peu d’amateurs auront les moyens de réaliser un tel dispositif, ni financièrement, ni légalement.
Nous en déduisons naturellement l’idée du RADAR passif, qui consiste à utiliser les émetteurs existants comme source de signaux permettant de détecter les cibles qui réfléchissent les ondes électromagnétiques émises à d’autres fins – émetteurs dits non coopératifs (voir figure 2). Toutes les sources radiofréquences ont été étudiées dans la littérature : émetteurs de télévision analogique (très puissants, mais obsolètes) [2], bande FM commerciale [3, 4] ou numérique pour les pays qui en sont munis [5], téléphonie mobile [6], ou réseaux informatiques sans fil [7]. Récemment, la prolifération des émetteurs de télévision numérique terrestres a donné l’opportunité à de nombreuses études sur leur utilisation pour des applications de RADAR passif [8, 9]. C’est ce sujet que nous allons aborder ci-dessous, avec un objectif de coût suffisamment réduit pour permettre à tout amateur d’expérimenter les méthodes de traitement du signal mises en œuvre.
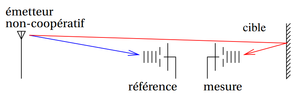
Fig. 2 : Principe du RADAR passif : une antenne pointe vers le signal de référence, et l’autre vers les cibles.
Le principe du RADAR passif est le suivant (voir figure 2) : un récepteur est connecté à une antenne directive qui pointe vers la source du signal analysé, et un second récepteur est connecté à une seconde antenne directive qui pointe vers la cible. Le but du traitement est de trouver les copies, retardées dans le temps, de la référence dans le signal réfléchi par les cibles. Si la cible est en mouvement, il faut en plus corriger du décalage Doppler. Ces deux considérations nous amènent naturellement à considérer une fonction dite d’ambiguïté qui décrit l’espace distance-vitesse, ou τ - δf en considérant que la distance s’observe comme un retard τ et la vitesse v comme un décalage Doppler δf de la porteuse :
Divers auteurs [10] ont récemment démontré que les récepteurs de télévision numériques terrestres à base de Realtek RTL2832U utilisés comme source de signaux pour un traitement de radio logicielle (Software Defined Radio – SDR) permettent une telle mesure, sans toutefois en détailler les paramètres d’acquisition et de traitement. Nous nous proposons ici d’aborder en détail ces points. Au cours de cet article, nous nommerons abusivement « récepteur DVB-T » un circuit à base de RTL2832U comme convertisseur analogique-numérique communiquant sur bus USB les données acquises depuis un premier étage radiofréquence, généralement un circuit Rafael Micro R820T(2). Ce montage fournit une bande passante de 2 MHz – toutes nos acquisitions se feront au rythme de 2,048 M échantillons/s – avec une résolution de 8 bits et un gain de l’étage d’entrée d’au plus 35 dB. Nous connecterons les récepteurs radiofréquences directement aux antennes, sans introduire de circuit additionnel tel qu’amplificateur ou filtre.
1. Quel émetteur choisir ?
Commençons par quelques rappels des principes de base du RADAR pour justifier le sujet de cette étude qui consiste à utiliser des émetteurs non coopératifs (émetteurs de station FM, télévision, etc.) pour détecter la présence d’objets. Les systèmes RADAR permettent de détecter à distance la présence d’objets et éventuellement d’en estimer la vitesse : la puissance reçue PR est déterminée par :
- la puissance émise PE ;
- la distribution de l’énergie émise depuis l’émetteur sur une sphère centrée sur celui-ci et donc de densité décroissant comme le carré de la distance de à la cible (conservation de l’énergie sur une sphère de surface 4πde2) ;
- puis la cible se comporte elle-même comme une source d’ondes sphérique qui atteindra le récepteur à distance dr encore une fois avec une décroissance en dr2 ;
- En introduisant les gains des antennes émettrice GE et réceptrice GR qui indiquent que le diagramme de rayonnement n’est pas nécessairement isotrope, et que l’onde intersecte la surface du récepteur [11] sur une surface de l’ordre de grandeur de la longueur d’onde λ2 ;
- ainsi que la section RADAR de la cible définie comme une surface équivalente de σ (en m²), nous déduisons l’équation du RADAR reliant puissance reçue et puissance émise par :
Noter que dans le cas du RADAR monostatique (émetteur et récepteur confondus), dr = de et la loi reliant puissance reçue et distance décroît comme la puissance quatrième de la distance (et non comme le carré comme nous en avons l’habitude dans les liaisons entre émetteur et récepteur). Nous cherchons donc une source aussi puissante que possible pour maximiser nos chances de détecter un signal. Par ailleurs, la résolution en distance Δr d’un RADAR est déterminée par l’inverse de sa bande passante B : Δr = c / (2B). Une mesure précise de distance nécessite donc une bande passante importante. Cependant, nous allons-nous focaliser sur une application faible coût avec un récepteur formé d’un récepteur DVB-T qui ne permet qu’un échantillonnage à 2 M échantillons/s. Une source présentant une telle bande passante est idéale, tandis qu’une bande plus importante ne pourra pas être exploitée. Nous allons donc utiliser un émetteur de télévision numérique terrestre qui, selon la norme japonaise ISDB-T, propose un canal de 6 MHz de large. Les canaux de la norme DVB-T européenne sont eux aussi tous de plus de 2 MHz de large : la résolution en distance attendue est donc de 300 / (2 x 2) = 75 m, suffisante pour une application visant à détecter des avions ou des bâtiments distants.
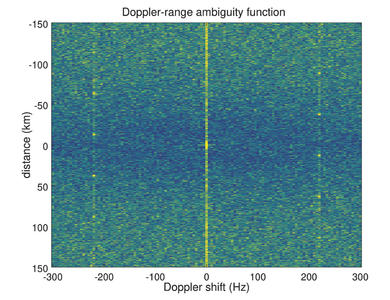
Nous avons donc choisi notre émetteur, il nous reste maintenant à déterminer la méthode de traitement du signal qui nous permettra de détecter les échos réfléchis par une cible parmi tous les signaux acquis par le récepteur. Le principe d’un RADAR passif est de considérer que la source émet un signal aléatoire, mais connu. Ce signal aléatoire se propage et se réfléchit sur la cible, pour être détecté par le récepteur après un temps de vol que nous cherchons à identifier. Comment pouvons-nous affirmer que le signal aléatoire émis par la source est connu ? En pointant un second récepteur vers cette source pour écouter le signal émis. Dans ce cas, l’identification de la distance de la cible consiste à rechercher l’occurrence du signal de référence, acquis par le premier récepteur, dans l’ensemble des signaux acquis par le second récepteur. Nous avons déjà discuté dans ces pages de la stratégie pour identifier la présence d’un motif dans un signal [12, 13] : l’intercorrélation. Par rapport à la fonction d’ambiguïté citée ci-dessus, il s’agit du cas des cibles statiques pour lesquelles δf = 0. Cependant, le signal émis par une source non coopérative ne sera probablement pas un bruit blanc, mais contiendra une certaine structure permettant au destinataire de décoder l’information transmise. Cette structure apparaîtra lors d’une analyse décalage en temps-décalage en fréquence comme des points de corrélation importante, alors qu’aucune cible n’est présente pour ces paramètres. Établir la fonction d’ambiguïté de la source (voir figure 3) par autocorrélation du signal est donc un prérequis pour s’assurer de ne pas attribuer par erreur une structure périodique du signal émis à une cible.
Fig. 3 : Fonction d’ambiguïté de la source ISDB-T – protocole de télévision numérique terrestre utilisé au Japon – calculée par autocorrélation du signal. Des structures périodiques liées au mode de codage OFDM apparaissent à ±210 Hz.
2. Rappel sur l’intercorrélation
La recherche du motif m(t) dans le signal s(t) consiste à rechercher le décalage τ dans le temps de m(t) qui permette de ressembler au mieux au contenu de s(t). La ressemblance est estimée comme l’intégrale du produit de m(t + τ) avec s(t). En l’absence de ressemblance, le produit de m(t + τ) avec s(t) donne tantôt une valeur positive, tantôt négative, et l’intégrale donne une valeur nulle ou faible si nous avons pris soin de retrancher la valeur moyenne à m et s. Au contraire, si m(t + τ) se retrouve dans s(t), alors tous les termes négatifs sont multipliés par un terme négatif (puisque m se retrouve dans s) et les termes positifs avec les termes positifs : l’intégrale accumule la puissance et un maximum d’intercorrélation est observé. Formellement, le calcul de :
se traduit en temps discret par :
Cette opération nécessite un nombre de multiplications égal au carré du nombre de termes N dans S : chaque estimation de l’intercorrélation pour un τ donné nécessite N multiplications, et le calcul est repris pour les N valeurs possibles de τ. En pratique, ce calcul est accéléré en se rappelant la relation entre la convolution, sa transformée de Fourier et la corrélation. Cette relation va nous être utile pour comprendre l’implémentation de la corrélation sous GNURadio.
La convolution est définie comme :
On notera que le temps t du second terme est inversé par rapport au premier terme. Nous pouvons facilement démontrer que la transformée de Fourier TF() de la convolution est le produit des transformées de Fourier : TF(conv(s, r)) = TF(s) · TF(r). Le lecteur se reportera à [14, p. 292] pour la démonstration de cette relation. Le retournement du temps dans le second terme de la convolution par rapport à la corrélation se corrige par l’utilisation du complexe conjugué de la transformée de Fourier, puisque le complexe conjugué de exp(-j ω t) est exp(j ω t) (avec j2 = -1). Nous concluons de cette analyse que xcorr(s, r) = iTF(TF(s) · TF*(r)) avec iTF la transformée de Fourier inverse et * le complexe conjugué. Ayant compris ce concept, nous le démontrons sous GNURadio avec le schéma de la figure 4, dont la seule subtilité tient au regroupement du flux continu de données en vecteurs pour permettre le produit des transformées de Fourier. Ce schéma n’inclut pas une petite astuce pour automatiser la variation du retard déterminé par un générateur de fonction triangulaire (bloc Function Probe qui lit le résultat du bloc Probe Function connecté à la sortie d’un générateur de fonction triangulaire pour modifier la variable définissant le retard Delay – penser à caster la variable flottante issue du bloc sonde en un entier tel qu’attendu par le délai), mais se contente de proposer à l’utilisateur de faire varier le retard manuellement au moyen d’un curseur.
Fig. 4 : Démonstration de l’intercorrélation sous GNURadio en passant par une composition judicieuse de transformées de Fourier. Étant donné que la transformée de Fourier s’effectue sur un nombre N donné d’éléments, nous transformons le flux continu de données en vecteurs de taille N. Le calcul se conclut en repassant les vecteurs de taille N en flux continu de données qui alimentent un affichage temporel.
Dans l’exemple de la figure 4, un signal aléatoire est produit. Ce signal aléatoire est caractérisé par une intercorrélation nulle pour tout τ sauf 0 : le signal ne se ressemble jamais, sauf pour un décalage nul. Si maintenant nous introduisons volontairement un décalage entre la voie de référence et la voie de mesure – temps de vol entre la source, la cible et le récepteur par rapport à la liaison directe émetteur-récepteur, alors le maximum d’intercorrélation se retrouvera pour ce décalage. Cette approche est utilisée pour imager les réflecteurs statiques tels que nous le ferons dans la section suivante.
3. Deux récepteurs DVB-T pour cartographier des cibles statiques
Afin d’acquérir deux flux de données et que leur intercorrélation soit représentative du décalage en temps entre le signal de référence et le signal de mesure, les deux récepteurs de télévision numérique terrestre, l’un orienté vers la cible et l’autre vers le signal de référence, doivent être synchrones, i.e. cadencés par la même horloge (voir figure 5). Dans le cas contraire, les oscillateurs cadençant les deux récepteurs n’ont aucune raison de présenter la même fréquence, et petit à petit les échantillons finiront pas se décaler (problème de l’échantillonnage synchrone). Un second problème est la transaction des données sur bus USB : contrairement à un FPGA qui cadencerait deux convertisseurs analogiques numériques en garantissant le synchronisme des acquisitions, les deux récepteurs DVB-T reçoivent leur ordre avec un intervalle de temps aléatoire (ou en tous cas non déterministe) du bus USB, et engagent les transactions avec ce même décalage. Heureusement, nous avons constaté que même si ce décalage en temps entre les acquisitions des deux récepteurs est aléatoire (voir figure 6), elles sont constantes tant que nous n’interrompons pas le flux. De ce fait τ présentera un biais constant qui peut être retranché de toutes les mesures. Il s’agit là d’un point clé de l’utilisation de deux récepteurs DVB-T pour du RADAR passif : le flux de données ne doit jamais être interrompu une fois la mesure engagée, et ce pour toute la durée de l’acquisition (problème des transactions synchrones). Finalement, la troisième cause de perte de cohérence entre les signaux acquis par les deux récepteurs tient dans le mécanisme de génération de l’oscillateur local utilisé pour transposer le signal radiofréquence reçu par l’antenne vers la bande de base : cette génération se fait par boucle à verrouillage de phase, dont le comportement observé est excessivement sensible à l’environnement du récepteur, et en particulier sa température (problème de la cohérence des oscillateurs locaux).
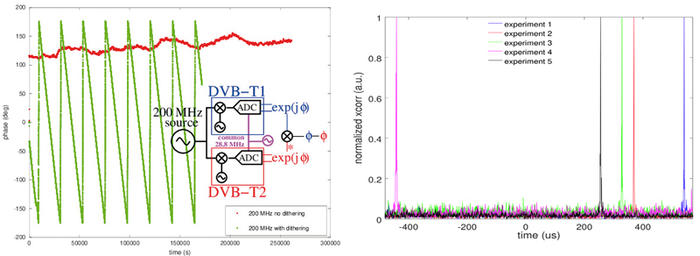
Fig. 5 : Montage expérimental : deux récepteurs DVB-T acquièrent simultanément l’un le signal de référence, l’autre le signal de mesure. Le quartz du second récepteur a été dessoudé et la sortie de l’oscillateur du premier circuit cadence le second : un condensateur de l’ordre de la dizaine de nF relie la sortie du premier oscillateur à l’entrée du second. Un pont thermique formé d’un barreau de cuivre vise à équilibrer la température des deux étages de réception radiofréquence.
Fig. 6 : Les deux sources d’erreur qui peuvent faire échouer l’expérience : un écart sur la fréquence de démodulation ou d’échantillonnage (gauche), et sur la cohérence des mesures. À gauche, un même signal périodique alimente les deux DVB-T, mais la fonction de frequency dithering qui permet à la boucle à verrouillage de phase (PLL) de prendre une valeur arbitraire est active. Cette fonction introduit des dérives de phase (vert) inacceptables, et doit être désactivée. À droite, un même signal aléatoire alimente les deux entrées de deux récepteurs DVB-T, et nous affichons l’intercorrélation. La présence d’un pic fin prouve que l’acquisition se fait au même rythme (après avoir éliminé le dithering), mais le décalage aléatoire entre les 5 expériences successives présentées sur ce graphique, induit par la date de démarrage des transactions USB, impose de ne jamais arrêter un flux d’acquisition au cours d’une mesure, au risque de sinon perdre l’origine du signal pour laquelle les deux signaux se ressemblent le plus. Les deux sources d’erreur qui peuvent faire échouer l’expérience : un écart sur la fréquence de démodulation ou d’échantillonnage (gauche), et sur la cohérence des mesures. À gauche, un même signal périodique alimente les deux DVB-T, mais la fonction de frequency dithering qui permet à la boucle à verrouillage de phase (PLL) de prendre une valeur arbitraire est active. Cette fonction introduit des dérives de phase (vert) inacceptables, et doit être désactivée. À droite, un même signal aléatoire alimente les deux entrées de deux récepteurs DVB-T, et nous affichons l’intercorrélation. La présence d’un pic fin prouve que l’acquisition se fait au même rythme (après avoir éliminé le dithering), mais le décalage aléatoire entre les 5 expériences successives présentées sur ce graphique, induit par la date de démarrage des transactions USB, impose de ne jamais arrêter un flux d’acquisition au cours d’une mesure, au risque de sinon perdre l’origine du signal pour laquelle les deux signaux se ressemblent le plus.
Ainsi, même si les deux récepteurs cadencés par une même horloge présentent la même fréquence de l’oscillateur local, nous avons été incapables de forcer la phase à se stabiliser à long terme (figure 6, gauche), et ce malgré la désactivation de la fonction dithering active par défaut, telle que décrite sur superkuh.com/rtlsdr.html. La modification logicielle implique de modifier tuner_r82xx.c de librtlsdr (disponible sur https://github.com/steve-m/librtlsdr.git) en remplaçant r82xx_write_reg_mask(priv, 0x12, val, 0x08); par rc = r82xx_write_reg_mask(priv, 0x12, val, 0x18); et en ajoutant juste auparavant priv->disable_dither=1;. Ceci fait, recompiler gr-osmosdr en se liant sur cette nouvelle bibliothèque, et la version sans dithering est disponible dans GNURadio et gnuradio-companion. Le problème de décalage aléatoire des flux introduits par la latence du bus USB sera pris en compte lors du post-traitement, en identifiant ce décalage par intercorrélation sur un long retard temporel des premières millisecondes d’acquisition des signaux de référence et de mesure et, ayant identifié ce retard supposé constant au cours d’une expérience, en décalant un flux de données par rapport à l’autre de ce retard.
D’un point de vue logiciel, la source osmocom de GNURadio propose l’option rtl= qui prend pour argument 0 ou 1 pour indiquer que deux sources dans la même chaîne de traitement adressent deux récepteurs différents. Nous n’avons cependant pas identifié de méthode pour savoir quel récepteur physique correspond à quel indice : voies de référence et de mesure sont donc susceptibles d’être échangées d’une exécution à une autre du programme d’acquisition.
4. Cartographie de cibles statiques
Notre premier objectif est de cartographier la distribution de cibles statiques – bâtiments situés autour du récepteur. Pour ce faire, une antenne connectée au premier récepteur est orientée de façon fixe vers l’émetteur, tandis qu’une seconde antenne directive est balayée en azimut pour rechercher la direction dans laquelle divers réflecteurs pourraient se trouver. Les deux antennes sont, au cours de toutes nos expériences, de type Yagi-Uda avec 18 éléments directeurs. Il s’agit d’une approche quelque peu naïve du RADAR d’aéroport qui tourne sur lui-même pour identifier les cibles, mais ici avec une rotation en azimut manuelle. Il nous faut donc un mécanisme pour ne capturer des informations que lorsque l’antenne est convenablement orientée dans une direction connue, et pourtant ne jamais interrompre le flux de données.
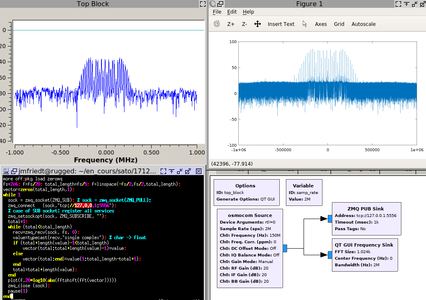
Fig. 7 : Mécanisme publish-subscribe de ZeroMQ qui permet à GNURadio de continuellement acquérir des signaux, même si personne n’est à l’écoute de son port de communication ZeroMQ. Nous vérifions dans cet exemple la cohérence des spectres des signaux acquis par GNURadio (en haut à gauche) et transmis à GNU/Octave (en haut à droite) par ZeroMQ, ainsi que la mise à jour des informations. Ici (en bas à gauche), nous avons choisi de fermer et ouvrir la socket à chaque itération de boucle : l’utilisation d’une valeur positive du watermark fournit une solution plus élégante, mais ne semble pas implémentée dans GNU/Octave.
Pour ce faire, GNURadio et GNU/Octave supportent tous deux un mécanisme de client-serveur nommé ZeroMQ (https://wiki.octave.org/Zeromq_package est disponible dans le paquet octave-zeromq de Debian), s’apparentant aux divers modes de transactions classiques au-dessus d'IP : mode connecté pour TCP, mode non connecté pour UDP. Dans le second cas, les informations sont transmises par le serveur : si un client les reçoit, elles sont exploitées, si aucun client n’est à l’écoute elles sont perdues, mais en tout cas le flux émetteur est continu. Dans la nomenclature ZeroMQ, ce mécanisme s’appelle publish-subscribe (voir figure 7), au contraire de push-pull qui s’apparente à TCP (le flux s’interrompt si aucun récepteur n’est à l’écoute – comportement aussi observé pour les pipes nommés).
Ainsi, GNURadio-companion affiche en temps réel l’intercorrélation (voir figure 8) – un point clé pour garantir la qualité de la mesure au cours de l’expérience – et GNU/Octave collecte les données lorsque l’antenne réceptrice pointe dans une direction d’azimut connu. Cette approche de communication entre GNURadio et GNU/Octave a par ailleurs l’avantage de séparer la phase d’acquisition et la phase de traitement, facilitant le prototypage tout en permettant le traitement d’un flux continu de données en temps réel. Reste la question de savoir combien de temps enregistrer. Avec une cible statique, le seul gain obtenu en enregistrant longtemps est l’amélioration du rapport signal à bruit. En effet, le gain de compression définit la capacité de l’intercorrélation à sortir un motif du bruit ambiant dans le signal. Ce gain de compression est classiquement défini comme le produit bande passante par temps de mesure, qui en version échantillonnée en temps discret se traduit par le nombre d’échantillons pris en compte. Donc les deux critères qui déterminent la durée de la mesure sont la distance maximale de la cible considérée (retard maximal entre signal de référence et sa copie dans la mesure), et l’amélioration du rapport signal à bruit par le gain de compression. Étant donné que nous nous échantillonnons à 2 M échantillons/s et que la cible la plus lointaine que nous pouvons espérer détecter est de l’ordre du kilomètre, ou un temps de vol de l’ordre de 3,3 µs (pour rappel, une onde électromagnétique se propage à la vitesse de 300 m/µs), alors 3,3 x 2 ≃ 7 échantillons suffiraient pour résoudre l’ambiguïté en distance, mais en pratique nous enregistrerons quelques centaines de milliers de points pour gagner en rapport signal à bruit par le gain de compression. Par ailleurs, nous avons constaté (figure 6) que le retard aléatoire introduit par les transactions sur bus USB est au moins de ±500 µs, donc il est prudent d’acquérir au moins 2 x 500 x 2 = 2000 échantillons pour garantir la détection du maximum d’intercorrélation.
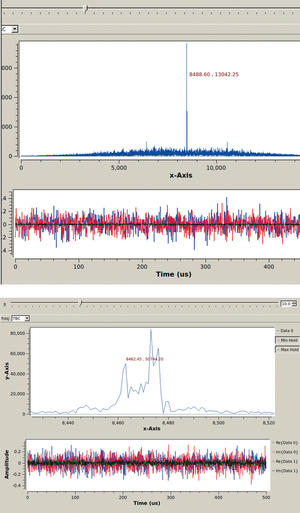
Fig. 8 : Gauche : pic d’intercorrélation (figure de droite) issu du traitement par GNURadio des données acquises par les deux récepteurs DVB-T. Droite : zoom sur le pic d’intercorrélation, illustrant la structure fine sur les quelques échantillons de part et d’autre du maximum d’intercorrélation dû à l’onde directe, et représentative des réflexions sur les cibles statiques que nous désirons cartographier.
Le résultat d’une telle mesure, traçant l’amplitude de l’intercorrélation dans un diagramme polaire centré sur le récepteur pour lequel le retard nul (maximum du pic de corrélation) est sélectionné, est proposé en figure 9. Une cartographie cohérente avec la distribution des bâtiments environnants est observée, avec un fort taux de corrélation vers le bâtiment proche au nord du site de réception, et une contribution plus subtile de trois grands immeubles au nord-ouest. La droite en bas des illustrations de la figure 9 indique la direction du signal direct venant de l’émetteur de télévision au sud : nous avons placé le récepteur cartographiant les cibles vers le nord afin de minimiser le signal direct qui pourrait éblouir le récepteur et empêcher d’identifier le signal faible réfléchi par des cibles.
Fig. 9 : Cartes de l’intercorrélation en fonction de l’angle en azimut de l’antenne Yagi-Uda connectée au récepteur servant à collecter le signal, l’autre antenne du récepteur de référence restant fixe. Gauche : mesure avec un DVB-T échantillonnant à 2 MHz, donc avec un pas de mesure de 500 ns ou 150 m. Droite : mesure avec un oscilloscope avec une fréquence d’échantillonnage suffisamment élevée pour donner l’impression de points contigus. La bande passante de la source limite néanmoins la résolution spatiale à 50 m.
4.1 Remplacer le récepteur DVB-T par un oscilloscope
La résolution spatiale d’un RADAR est inversement proportionnelle à sa bande passante. Le récepteur DVB-T ne présente que 2 MHz de bande passante, alors que de nombreux oscilloscopes présentent des bandes passantes de plusieurs dizaines de MHz. Les signaux ISDB-T occupant 8 MHz, nous pouvons gagner au moins un facteur 4 en remplaçant le récepteur DVB-T par un oscilloscope, même de qualité médiocre (un oscilloscope à deux canaux de 20 M échantillons/s suffit). Nous avons pour ce faire proposé une source GNURadio alimentée par les signaux acquis par oscilloscope (voir figure 10) : cette source n’est pas continue, mais cela est sans importance pour l’application RADAR. Le seul point important est le synchronisme des deux canaux d’acquisition, et une profondeur mémoire supérieure au temps de vol vers la cible la plus lointaine. La reprise de l’expérience ci-dessus avec ces nouvelles conditions expérimentales fournit une image bien mieux résolue et plus convaincante (figure 9, droite), tout en restant cohérente avec ce que nous avions acquis par DVB-T. Nous développerons ultérieurement la mise en œuvre de l’oscilloscope comme source GNURadio, pour le moment nous nous contentons de référer le lecteur au dépôt git proposant les codes sources sur github.com/jmfriedt/gr-oscilloscope.
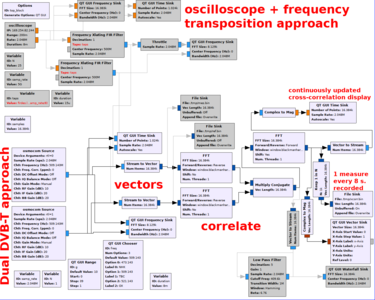
Fig. 10 : Flux de traitement exploité pour les mesures : en haut du graphique (commenté puisque grisé) la solution de deux voies d’un oscilloscope comme source de données, et en bas les deux récepteurs DVB-T alimentent la séquence de calcul de l’intercorrélation pour un affichage en temps réel.
5. Cas des cibles en mouvement – acquisition par DVB-T
Nous avons considéré des bâtiments comme réflecteurs de signaux radiofréquences, et avons cartographié la fonction d’intercorrélation en fonction de l’azimut, pour retrouver une distribution cohérente avec la position des bâtiments. Pouvons-nous appliquer la même stratégie pour observer des avions ?
Nous avons vu au début de cette présentation que le mouvement des avions introduit un décalage Doppler sur le signal rétrodiffusé par l’avion. Sauf en cas de tremblement de terre, les bâtiments ne présentent en général pas cette capacité de décalage de fréquence, et les cibles statiques seront distinguées des cibles mobiles par ce décalage Doppler : il s’agit d’une des stratégies de détection des cibles en mouvement (MTI – Moving Target Identification) pour détecter les signatures faibles de petites cibles en mouvement devant des grandes cibles statiques (l’exemple classique étant la petite roquette devant une grande falaise).
Notre objectif est donc de distinguer les grands bâtiments des avions par leur différence de vitesse. La simple fonction d’intercorrélation que nous avons vue auparavant doit être rendue un peu plus complexe maintenant : nous devons non seulement rechercher tous les décalages possibles en temps τ entre le signal de référence et le signal réfléchi, mais aussi toutes les vitesses possibles de cibles fD introduites par décalage Doppler. Nous allons considérer la fonction d’ambiguïté introduite en début de document, entre le signal s et le motif m, que nous rappelons définir comme :
Nous faisons glisser le signal acquis le long du temps par pas τ et nous le comparons avec le signal de référence m(t) décalé en fréquence par effet Doppler pour donner m(t) exp(j2πfDt). Cet estimateur est nommé fonction d’ambiguïté, car si la source n’est pas un bruit, mais présente une structure, il se peut que cet estimateur détecte de façon erronée des ressemblances dans les versions décalées en temps et en fréquence du signal. C’est en particulier le cas pour les signaux de télévision qui présentent une structure remarquable (encodage de type OFDM – Orthogonal Frequency Division Multiplexing) particulièrement propice aux faux positifs en faisant croire en la présence d’une cible alors que nous ne faisons qu’observer la structure du signal émis [15] (figure 3).
Ainsi, nous désirons cartographier les cibles dans un espace comprenant selon un axe la distance, et l’autre axe le décalage Doppler. La dernière question est de connaître les paramètres d’acquisition. La fréquence d’échantillonnage, qui détermine la résolution en distance, est imposée par le récepteur DVB-T à 2 MHz. La durée de la mesure détermine la résolution avec laquelle la vitesse de la cible est estimée. En considérant selon une analyse spectrale la plus simple que la résolution en fréquence est l’inverse de la durée de la mesure, une résolution de l’ordre de 5 Hz nécessite 200 ms d’acquisition ou, au rythme de 2 M échantillons/s, 400000 points. Nous avons choisi d’acquérir en continu le flux de données issu de deux récepteurs DVB-T, l’un observant le signal de référence et l’autre la cible, et de traiter le jeu de données par paquets de 500000 points, soit 250 ms ou une résolution spectrale de 4 Hz. En exploitant un signal de télévision émis proche de 500 MHz, un décalage Doppler de 4 Hz correspond à une résolution en vitesse de 2,4 m/s ou 9 km/h. En observant des avions qui volent autour de 900 km/h, ou plutôt 400 km/h lors de leur phase d’atterrissage qui va nous intéresser, cela correspond à une quarantaine de points de mesure dans chaque direction, positive ou négative, de l’axe des vitesses. La masse de données produites est impressionnante : GNURadio sauve les échantillons comme flottants simple précision nécessitant 4 octets par échantillon. Avec deux canaux et des signaux complexes (coefficients I et Q), cela correspond à 16 octets/mesure, au rythme de 2 M mesures/s. Ainsi, nous générons 32 MB/s ou 1,9 GB/minute. Afin de ne pas être handicapés par le temps d’accès au support de stockage, nous écrivons dans un ramfs : les 6 GB disponibles sont ainsi remplis en environ 3 minutes. Les traitements sont effectués a posteriori, car une minute d’acquisition prend plusieurs dizaines de minutes de traitement. En tentant de traiter les données en temps réel, par exemple en transférant les données de GNURadio vers GNU/Octave pour analyser les divers décalages Doppler qui maximisent l’intercorrélation, l’intervalle de temps entre deux traitements est trop long et la cible en mouvements à plusieurs centaines de kilomètres par heure se sera déplacée significativement, réduisant les chances de suivre sa trajectoire.
L’analyse {vitesse, distance} se résume en quelques lignes de GNU/Octave :
Nous sélectionnons le fichier binaire contenant les acquisitions en supposant que les coefficients I et Q des deux récepteurs DVB-T sont interlacés et en format flottant simple précision, tel que produit par GNURadio. Étant incapables de charger d’un coup 6 GB en mémoire, nous lisons les données par paquets de N = 5 x 105 échantillons, que nous réorganisons sous forme de complexes en prenant un point sur 2 pour la partie réelle et pour la partie imaginaire, puis en voie de référence et voie de mesure en prenant un complexe sur 2 pour chaque voie. Le cœur du programme consiste à balayer tous les décalages Doppler possibles, et calculer pour chaque signal de mesure transposé du décalage Doppler, l’intercorrélation avec le signal de référence. Si un avion est visible et introduit un décalage Doppler de par sa vitesse, alors un pic d’intercorrélation sera visible pour le décalage en temps correspondant à la distance à la cible. L’intérêt d’exploiter le décalage Doppler est l’excellent rapport signal à bruit pour fD ≠ 0 puisque les cibles statiques ne corrèlent avec le signal de référence que pour fD = 0. Dans l’exemple ci-dessus, l’écart de temps entre les transmissions sur bus USB du récepteur de référence par rapport au récepteur de mesure a été initialement étalonné à environ 150 échantillons (ou 75 µs) : l’intercorrélation sur 2048 décalages de temps possibles ne donne pas un maximum pour le décalage nul d’indice 2048, mais autour des points d’indice 2200, et les échos de retard positif s’étendent jusqu’au point d’indice 2350.
5.1 Cas des avions
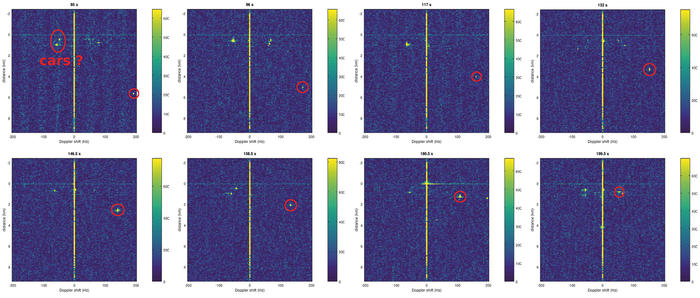
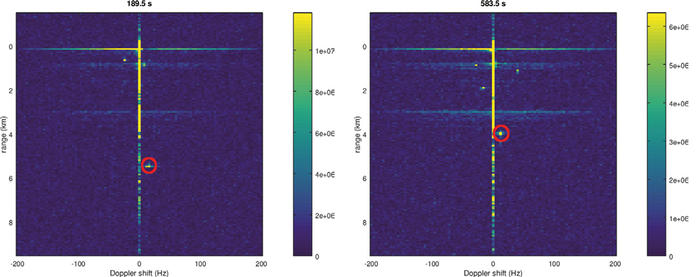
Quelques exemples de poursuite d’un avion en cours d’atterrissage sont fournis sur les figures 11 et 12. Avec une vitesse attendue de l’ordre de 360 km/h (100 m/s) au cours de la phase d’approche, le décalage Doppler attendu serait de l’ordre de fD = ((2 x 500) / 300 ) x 100 pour une porteuse proche de 500 MHz, soit fD ≃ 333 Hz. En effet, la cible est observée initialement avec un décalage Doppler de plus de 200 Hz, en accord avec ce calcul.
Fig. 11 : Séquence de mesures au cours de l’atterrissage d’un avion de ligne à l’aéroport de Sendai. Des cibles proches, présentant toujours un décalage Doppler de l’ordre de la centaine de Hz ou une vitesse radiale de 110 km/h, sont visibles à une distance proche des antennes, et attribuées à des véhicules circulant dans les deux sens d’une autoroute proche. La position de l’avion au cours de son approche est indiquée par un cercle rouge ajouté manuellement.
Pour résumer, nos paramètres d’acquisition sont les suivants :
- la bande passante d’acquisition, limitée par la fréquence d’échantillonnage des récepteurs DVB-T, est de 2 MHz, soit une résolution en distance de 75 m,
- un avion volant à 100 m/s parcourt ces 75 m en 750 ms. Nous choisissons donc un temps d’intégration de 0,5 s, pendant lesquels l’aéronef ne présente pas un déplacement significatif lors de l’analyse,
- avec un temps d’intégration de 0,5 s, la résolution sur l’estimation du décalage Doppler, donnée par l’inverse du temps d’intégration dans l’analyse simpliste d’une transformée de Fourier, est de 2 Hz. Nous aurons donc une résolution sur la vitesse de ((300 / 500) x 2) / 2 = 0,6 m/s ou 2 km/h, permettant de parfaitement observer les variations de vitesse de l’avion au cours de son approche et de son atterrissage.
Fig. 12 : Gauche : trajectoire dans le plan distance-vitesse de l’avion au cours de son approche et atterrissage, obtenus en sommant les clichés visibles sur la figure 11. Droite : conditions expérimentales, avec l’antenne Yagi-Uda pointant vers la cible.
5.2 Autocorrélation au lieu d’intercorrélation
Nous constatons, avec la ligne verticale de décalage Doppler nul qui représente le couplage direct (figures 11 ou 12, haut) que la contribution des signaux retardés dans le temps réfléchis par les cibles statiques pollue les cibles mobiles identifiables grâce aux décalages Doppler non nuls des signaux réfléchis. Pourrions-nous exploiter ce signal de référence disponible dans le signal de mesure afin d’observer le décalage introduit par les cibles ? Ce faisant, nous éliminerions le besoin de deux récepteurs synchronisés, diviserions par deux la masse de données à stocker, et pourrions nous contenter de n’importe quel récepteur monovoie pour effectuer la mesure.
Le signal de référence reste visible sur la mesure, malgré la directivité de l’antenne qui tend à maximiser la puissance reçue de la cible et non de la direction du signal de référence. Ainsi, nous pouvons simplifier le montage en éliminant l’antenne de référence et en exploitant le signal de référence, certes faible, dans la mesure. Ce calcul correspond à l’autocorrélation, qui introduit un certain nombre d’artefacts (toutes les cibles vont corréler avec toutes les autres cibles – dans notre cas une seule cible est visible donc le résultat reste correct) et un rapport signal à bruit détérioré du fait de la faiblesse du signal de référence (voir figure 13). Ici encore, travailler sur un nombre important de points – 2 x 106 dans ce cas – permet d’abaisser le niveau de bruit et améliore la capacité à faire ressortir la cible par corrélation.
Fig. 13 : Autocorrélation : dans le cas d’un faible nombre de cibles, cet estimateur permet de s’affranchir des deux récepteurs synchronisés. En présence de nombreuses cibles, toutes les combinaisons possibles de décalage en temps et fréquence Doppler apparaîtront comme cibles, rendant l’identification des sources des échos complexe.
5.3 Cas des bateaux
Des auteurs [16, 17] ont démontré la capacité à détecter des bateaux par cette méthode de mesure. Comme les avions, les bateaux fournissent un contexte idéal de mesure dans lequel le bruit de fond est très faible (absence de réflecteurs statiques importants), mais bien que leur section RADAR soit plus importante, leur vitesse plus lente pourrait rendre leur détection plus délicate. Il n’en est rien : ces cibles pour parfaitement visibles lors d’une acquisition depuis une plage à proximité du port de Sendai (figure 14), avec d’une part des bâtiments importants (porte-container, ferry) entrant et sortant du port, et d’autre part des petits bâtiments (probablement pour la pêche) visibles à une distance inférieure à celle des grands navires. Le contexte maritime est d’autant plus intéressant que la houle introduit une source de décalage Doppler complémentaire au mouvement propre du navire qui peut être exploité pour en analyser les caractéristiques [18].
Fig. 14 : Exemple de bâtiment sortant du port de Sendai (ferry), et deux navires stationnaires en attente au large du port.
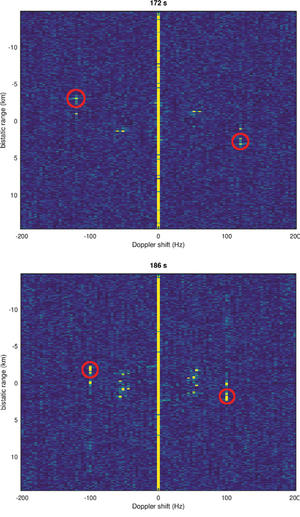
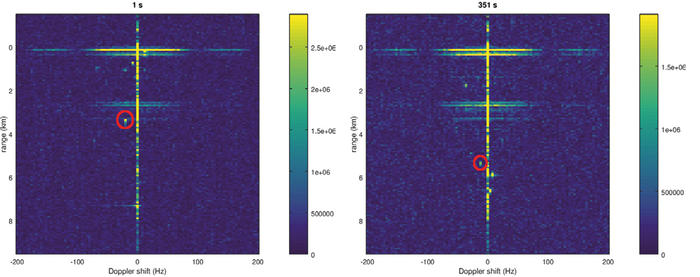
Le décalage Doppler observé (figures 15 et 16) est de l’ordre de fD ≃ 12 Hz qui correspond, pour une porteuse à 500 MHz, à une composante radiale de la vitesse de 3,6 m/s ou 13 km/h soit 7 nœuds, en accord avec les données transmises par AIS qui indiquent des vitesses des gros bâtiments de l’ordre de 12 ou 13 nœuds.
Fig. 15 : Exemple de bateau s’approchant du port, avec un décalage Doppler positif et une distance décroissante avec le temps.
Fig. 16 : Exemple de bateau s’éloignant du port, avec un décalage Doppler négatif et une distance croissante avec le temps.
6. Cas des cibles très proches
Nous avons commencé par analyser les cibles statiques. Nous avons ensuite amélioré notre capacité de détection en considérant les cibles mobiles, que nous séparons du bruit des cibles statiques en exploitant leur décalage Doppler, et ce en traçant un diagramme distance-vitesse (range-Doppler map). Ce calcul est cependant excessivement gourmand en ressources de calcul : tel que nous l’apprend [19], nous pouvons soit calculer l’intercorrélation de tous les signaux de référence décalés dans le temps avec tous les signaux de mesure décalés des fréquences Doppler possibles, ou bien effectuer le produit du signal de mesure avec tous les décalages temporels du signal de référence, puis prendre une transformée de Fourier du résultat pour établir la distribution des décalages Doppler. Même si le résultat de ces deux calculs est le même en considérant que transformée de Fourier et corrélation sont linéaires et que les intégrales sur des variables séparées (distance ou fréquence Doppler) sont associatives, la seconde approche devient intéressante dans le cas des cibles se trouvant à une distance inférieure à la résolution en distance du RADAR. Prenons le cas des voitures en mouvement. De petites sections RADAR, nous ne pouvons pas espérer les détecter à grande distance compte tenu de la faible bande passante des récepteurs DVB-T : un véhicule à 75 m est supposé réfléchir une puissance trop faible pour être détectable. Dans ce cas, la détection de véhicules en mouvement par RADAR passif se résume à un problème de mesure de vitesse, puisque la résolution en distance est insuffisante. Considérons l'intégrale suivante :
Si nous disons que la résolution en distance Cτ est insuffisante, nous pouvons prendre τ = 0 et dans ce cas nous obtenons :
Ceci n’est autre que la transformée de Fourier de la fonction ref · mes. Ainsi, nous pouvons envisager le problème de détection de cibles proches en mouvement comme la distribution des vitesses des cibles confondues en distance, mais présentant diverses vitesses détectées par les divers décalages Doppler fD. Ce calcul est très rapide et plus efficace que la cartographie complète distance-vitesse.
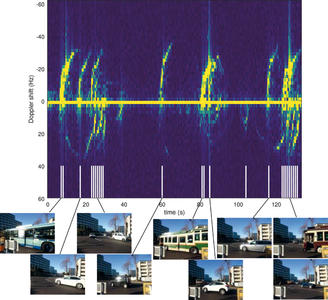
Après ce bel exposé théorique, est-ce que la mise en pratique fonctionne ? Afin de nous convaincre de la validité des mesures, nous avons placé nos deux antennes de référence et de mesure à proximité d’un tournant où la vitesse des véhicules [20] n’est que de quelques dizaines de km/h, et avons filmé le trafic en même temps que nous avons acquis les mesures. Les traitements sont ensuite d’une part un calcul des transformées de Fourier des produits des signaux de référence et de mesure, après avoir étalonné sur la première seconde d’acquisitions l’écart de temps introduit par le bus USB et compensé cet écart de temps lors de la lecture des fichiers de données ; et d’autre part la visualisation du film du passage des véhicules. Le film est converti en une séquence de photographies au rythme d’un cliché par seconde (ffmpeg -i ../film.mp4 -vf fps=1 img%03d.jpg) et tous les clichés ne contenant pas de véhicule visible sont manuellement effacés. Nous traçons d’une part l’évolution des transformées de Fourier en fonction du temps, et y superposons pour la date de chaque image qui contient un véhicule, un trait blanc en bas du graphique indiquant qu’un véhicule est vu. Nous constatons que chaque trace Doppler est associée à un cliché, et que chaque cliché est associé à une trace de passage de véhicule : l’association entre les deux mesures est démontrée. Par ailleurs, nous constatons que les véhicules s’approchant de nous induisent un décalage Doppler positif, ceux s’éloignant un décalage négatif. Ce comportement est conforme à la théorie : nous pouvons détecter des véhicules proches par leur vitesse (voir figure 17).
Fig. 17: Haut : carte du décalage Doppler (vertical) en fonction du temps (horizontal), présentant une trace verticale pour chaque passage de véhicule, avec décalage positif si le véhicule s’approche et négatif s’il s’éloigne. Bas : quelques clichés du film acquis simultanément aux acquisitions RADAR, illustrant la présence d’un véhicule pour chaque trace présentant un décalage Doppler. Les véhicules passent groupés du fait de la présence de deux feux de circulation de part et d’autre de la zone de mesure.
Conclusion
Nous avons démontré l’utilisation de récepteurs de télévision numériques terrestres (DVB-T) exploités comme source de signaux pour le traitement de radio logicielle pour une mesure de RADAR passif. Dans ce contexte, deux récepteurs synchronisés sur une même horloge reçoivent l’un un signal de référence émis par une source non coopérative, et l’autre reçoit les signaux réfléchis par les cibles. Ce montage, très simple, permet d’appréhender expérimentalement diverses techniques de traitement du signal incluant l’intercorrélation, la détection de vitesse de la cible par identification du décalage Doppler, et la fonction d’ambiguïté. Finalement, nous avons étendu le concept aux cibles proches, où la notion de distance n’importe plus, mais seule la vitesse est identifiée.
La limite de cette approche très faible coût apparaît lorsque nous désirons atteindre l’objectif plus ambitieux d’identifier la direction d’arrivée des signaux (DOA – Direction of Arrival). Cette mesure exploite la phase – contrairement à tous les traitements cités ci-dessus qui n’exploitent que le module de la corrélation. Or malgré nos efforts pour stabiliser la phase – élimination du dithering, pont thermique entre les récepteurs radiofréquences – nous constatons une dérive systématique et aléatoire de la phase des divers récepteurs cadencés sur une même horloge maîtresse à 28,8 MHz. Ainsi, bien que nous ayons pu cadencer 4 récepteurs avec une même source – en ajoutant une porte inverseuse 74HC04 comme tampon pour ne pas effondrer l’impédance vue par l’oscillateur de référence en connectant trois récepteurs sur sa sortie – les signaux acquis présentent bien une intercorrélation significative, mais la phase de l’intercorrélation à son maximum d’amplitude dérive excessivement pour être exploitable. Résoudre ce problème ouvrirait la perspective d’identifier la direction d’arrivée du signal, en complément de la distance de la cible et de sa vitesse.
Remerciements
Ce travail visant à l’utilisation des récepteurs DVB-T pour des expériences faibles coûts liées aux traitements de signaux radiofréquences, et en particulier de détection synchrone, a été encouragé par un financement de Projet Exploratoire (PEPS) du Centre National de la Recherche Scientifique (CNRS). Il a été finalisé comme projet annexe au cours d’un séjour de l’auteur en tant que chercheur invité par l’université de Tohoku à Sendai (Japon) dans le laboratoire de M. Sato, avec l’aide de W.K. Feng et G. Cherniak. Toutes les références bibliographiques ont été obtenues sur Library Genesis (gen.lib.rus.ec).
Références & notes
[1] Detailed Assesments of a European Space Surveillance System - Final Report :
http://emits.sso.esa.int/emits-doc/AO5059RD1.pdf
[2] Howland P.E. & al., « Target tracking using television-based bistatic radar », IEE Proc. Radar Sonar Navig. 46 166–174, 1999.
[3] ZOELLER C. L. & al., « Passive coherent location radar demonstration », Proc. 34th Southeastern Symp. on System Theory, Huntsville, Alabama, Mars 2002, pp. 358–362.
[4] ZHU J. & al., « Adaptive beamforming passive radar based on FM radio transmitter », IET International Conference on Radar Systems, 2007.
[5] DAUN M. & al., « Tracking in multistatic passive radar systems using DAB/DVB-T illumination », Signal Processing 92(6) 1365–1386, 2012.
[6] ZEMMARI R. & al., « GSM passive radar for medium range surveillance », IEEE EuRAD, 2009.
[7] CHETTY K. & al., « Through-the-wall sensing of personnel using passive bistatic wifi radar at standoff distances », IEEE Trans. on Geosci. & Remote Sensing 50(4) 12180-1226, 2012.
[8] RAOUT J. & al., « Passive bistatic noise radar using DVB-T signals IET radar », sonar & navigation 4 (3) 403–411, 2010.
[9] PALMER J.E. & al., « DVB-T passive radar signal processing », IEEE Trans. Signal Proc. 61 (8) 2116–2126, 2013.
[10] VIERINEN J., « Passive radar with $16 dual coherent channel rtlsdr dongle receiver », sur http://kaira.sgo.fi/2013/09/passive-radar-with-16-dual-coherent.html (accédé en déc. 2017) puis https://www.rtl-sdr.com/building-a-passive-radar-system-with-an-rtl-sdr/, ou (auteur inconnu) https://www.youtube.com/watch?v=KRqtqtCVRR0 et SILVERWOOD B. sur https://www.youtube.com/watch?v=l9V73d0nF4A.
[11] Ou en d’autres termes, l’antenne présente une surface équivalente GRλ2 – nous omettons les termes de normalisation angulaire 4π stéradians pour alléger les équations.
[12] FRIEDT J.-M., « Auto et intercorrélation, recherche de ressemblance dans les signaux : application à l’identification d’images floutées », GNU/Linux Magazine France n°139, 2011 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-139/Auto-et-intercorrelation-recherche-de-ressemblance-dans-les-signaux-application-a-l-identification-d-images-floutees
[13] FRIEDT J.-M., CABODEVILA G., « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », Open Silicium n°15, 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-015/Decodage-des-signaux-de-satellites-GPS-recus-par-recepteur-de-television-numerique-terrestre-DVB-T
[14] APPEL W., KOWALSKI E., « Mathematics for physics and physicists », Princeton University Press, 2007, et probablement dans la version française « Mathématiques pour la physique et les physiciens », H. et K. Editions, 2008.
[15] EVERS A., JACKSON J.A. , « Cross-Ambiguity Characterization of Communication Waveform Features for Passive Radar », IEEE Trans. on aerospace and electronic systems 51 (4), 3440–3455, 2015.
[16] CAPRIA A. & al., « Ship detection with DVB-T software defined passive radar », IEEE Gold Remote Sensing Conference, 2010.
[17] OLIVADESE D. & al., « Passive ISAR imaging of ships by using DVB-T signals », IET Int. Conf. on Radar Systems, 64–64, 2012.
[18] WETZEL L. B., « Sea Clutter », chapitre 15 du RADAR Handbook (3rd Ed.) de SKOLNIK M., 2008 .
[19] MOSCARDINI C., PETRI D., CAPRIA A., CONTI M., MARTIRELLA M., BERIZZI F., « Batches Algorithm for Passive Radar: A Theoretical Analysis », IEEE Trans. on aerospace and electronic systems 51 (2), 1475–1487, 2015.
[20] CAPRIA A., PETRI D., MARTORELLA M., CONTI M., DALLEMESE E., BERIZZI F., « DVB-T passive radar for vehicles detection in urban environment », Proc. Geoscience and Remote Sensing Symposium (IGARSS) 3917–3920, 2010.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture