La radio logicielle – Software Defined Radio (SDR) – transpose aux traitements de signaux radiofréquences les préceptes du traitement numérique du signal échantillonné en temps discret, amenant stabilité, souplesse et reconfigurabilité que les implémentations matérielles ne sauraient offrir. Cependant, aborder la SDR nécessite, avant de pouvoir traiter de signaux aussi passionnants (et complexes) que les liaisons satellitaires [1], de maîtriser quelques concepts de traitement du signal et d’électronique radiofréquence, voire d’électromagnétisme, que nous aborderons ici.
La radio logicielle [2][3] est un domaine en expansion du fait de l’accès à des ressources de calcul compatibles avec l’exploitation de signaux radiofréquences ainsi que des interfaces matérielles d’acquisition de signaux permettant à chacun d’expérimenter les méthodes de traitement du signal [4][5] appliquées à des cas concrets. Nous nous proposons ici d’introduire les concepts généraux de communication sur porteuse radiofréquence [6][7], justifier la modulation de cette porteuse pour transporter une information, les objectifs de la démodulation, et montrer comment ces étapes se transposent d’une approche matérielle (analogique) à un traitement numérique de signaux échantillonnés périodiquement (voir figure 1). Dans les exemples qui suivront, les expériences numériques se feront sous GNU/Octave, mais le lecteur familier avec Python pourra facilement reproduire ces expériences avec Numpy.
Le bénéfice d’une implémentation logicielle des algorithmes de traitement – face à une implémentation matérielle – tient en la flexibilité (le même matériel sert à recevoir une multitude de signaux de natures différentes), stabilité (un algorithme ne vieillit pas dans le temps comme le font les composants électroniques) et reconfigurabilité (changer une fonction de transfert de filtre n’est qu’une question de modifier ses coefficients, pas de sortir le fer à souder pour ajouter un condensateur).
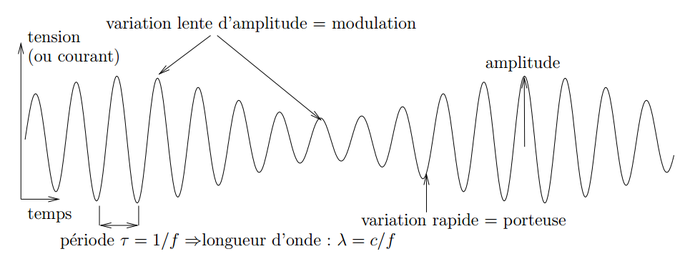
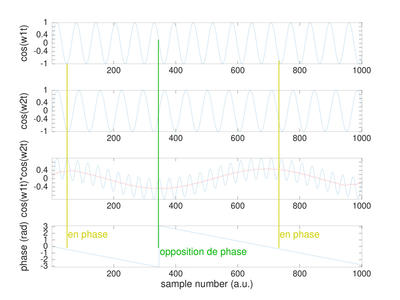
Fig. 1 : Définitions des paramètres d’une onde radiofréquence transportant une information, ici en modulation d’amplitude. La fréquence f du signal variant le plus rapidement, nommée porteuse, est liée à sa longueur d’onde λ par sa célérité c. Dans le vide, c = 3·108 m/s=300 m/µs. Dans un câble coaxial, cette célérité est réduite d’environ un tiers, pour être de l’ordre de 200 m/µs. La variation lente d’amplitude du signal contient l’information transmise et se nomme la modulation.
1. Pourquoi des émissions radiofréquences ?
La première question à se poser est : pourquoi des communications sur liaison radiofréquences ? Historiquement, l’explosion des communications au cours du 19ème siècle avec l’avènement du télégraphe a introduit un problème qui a occupé tous les grands noms de la communication électrique (Bell, Edison, Gray – « composite musical tones are transmitted through a single wire, and analyzed or separated at the receiving end of the line by vibrating reeds, bars, or strings, tuned correspondently with the respective transmitters of the composite tones » [8]) : comment optimiser les fils électriques déployés à grands coûts entre les deux côtes américaines en multipliant le nombre de messages transmis à chaque instant. La solution de multiplier le nombre de fils n’est pas envisageable (communication parallèle) compte tenu des infrastructures disponibles, donc il faut faire passer plusieurs messages en même temps sur le même support (figure 2).
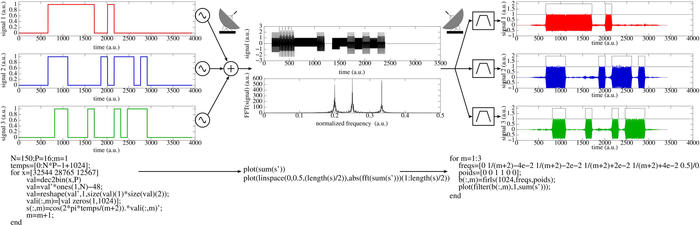
Fig. 2 : Trois émetteurs désirent envoyer un message en même temps sur l’unique medium qu’est le fil de télégraphe ou l’émetteur radiofréquence. Depuis la fin du 19ème siècle, la solution adoptée consiste à assigner une bande de fréquence à chaque émetteur, superposer leurs signaux sur le canal de transmission, puis les séparer par des bancs de filtres ajustés à chaque fréquence dite porteuse de l’information. L’information émise (gauche) a été reproduite au-dessus de chaque signal reçu (droite) pour rappel. La transformée de Fourier du signal transmis (milieu) présente nettement les 3 bandes allouées à chaque émetteur. Sous chaque figure, les principales lignes de code implémentant en logiciel ces étapes de traitement du signal, excluant la mise en forme pour générer les figures. La fonction firls() prend en argument les fréquences normalisées pour lesquelles les pondérations du filtre sont requises, et génère les coefficients d’un filtre à réponse impulsionnelle finie (FIR) de longueur égale au premier argument.
La solution qui a été adoptée, bien connue maintenant, est la transposition en fréquence (Frequency Division Multiple Access FDMA) des divers messages. Si au lieu d’envoyer une tension positive pour 1 et nulle pour 0 (OOK : On-Off Keying), nous envoyons une impulsion à une certaine fréquence pour transmettre 1, alors plusieurs messages sont envoyés simultanément en attribuant à chaque message une fréquence du côté de l’émetteur, et en plaçant un filtre à cette même fréquence du côté du récepteur.
Les filtres numériques
Les filtres sont des assemblages de composants passifs, éventuellement complétés d’éléments actifs, visant à sélectionner uniquement quelques composantes spectrales et rejeter les autres. Un filtre qui laisse passer de la composante continue (DC) à une certaine fréquence est un filtre passe-bas, un filtre qui coupe les basses fréquences et laisse passer les hautes est un filtre passe-haut. Ces deux filtres se combinent pour concevoir un filtre passe-bande. Numériquement, un filtre s’implémente soit comme pondération de la transformée de Fourier du signal (domaine spectral), soit dans le domaine temporel comme une convolution des mesures x par des coefficients de pondération b : ∑kbk · xn-k. Le choix des coefficients b est crucial : nous verrons plus loin dans le texte la description de la fonction firls() de GNU/Octave, déjà utilisée en figure 2. Plus important que les outils, le concept du nombre de coefficients b nécessaires à chaque étape de filtrage. La résolution spectrale d’une transformée de Fourier est la fréquence d’échantillonnage divisée par le nombre d’échantillons de la transformée. Il est assez intuitif de réaliser que le nombre de coefficients b est de l’ordre de la transition la plus raide du filtre : demander de couper une fréquence f et de laisser passer f + df nécessite un nombre de coefficients égal à la fréquence d’échantillonnage divisée par df, qui peut devenir démesurément grand si on n’y prend garde. Nombre de messages d’utilisateurs débutants désabusés par leurs premiers pas en radio logicielle, se plaignant de la lenteur des traitements et du manque de puissance de calcul de leur ordinateur, viennent d’un choix peu judicieux des paramètres de filtrage en amont de la chaîne de traitement, lorsque le débit du flux de données x est important.
Ainsi, la fréquence transportant l’information n’est qu’un intermédiaire qui est introduit à l’émission pour être éliminée à la réception pour retrouver l’information (voir figure 3). Plus tard, dans les années 1920–1930, les grands noms du traitement du signal (Nyquist, Heaviside, Bode [9]) s’évertueront à trouver des façons d'amplifier et reproduire un signal sans le déformer – le faire passer d’une bande de fréquence à une autre – donnant naissance à tout le corpus de la théorie de l’information et des rétroactions.
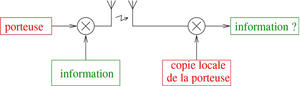
Fig. 3 : Afin de partager les spectres radiofréquences, divers utilisateurs envoient l’information à transmettre sur des plages de fréquences différentes, déterminées par la source radiofréquence, nommée l’oscillateur local (en rouge sur le schéma), qui fournit la porteuse de chaque émetteur. Le récepteur désire retrouver l’information et donc s’affranchir de la transposition temporaire de fréquence nécessaire à la communication sans fil. Tout le problème de la réception de signaux radiofréquence consiste à s’affranchir des différences entre les fréquences des deux oscillateurs locaux, du côté de l’émetteur et du récepteur.
Cette approche très naïve s’applique directement au spectre électromagnétique, en remplaçant le fil de la liaison télégraphique par une antenne. Dans ce cas, la transposition en fréquence permet non seulement de multiplexer le spectre électromagnétique en transmettant simultanément diverses informations sur diverses bandes de fréquence, mais fournit le bénéfice additionnel de réduire la longueur d’onde du signal électromagnétique et par conséquent la taille de l’antenne permettant de rayonner efficacement un signal électromagnétique à partir du signal électrique généré. En effet, la longueur d’onde d’un signal électromagnétique est λ = 300/f avec f la fréquence en MHz, et la dimension caractéristique d’une antenne est λ/2.
Principes de base de fonctionnement d'une antenne
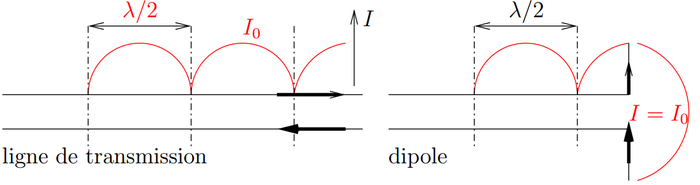
Balanis [10] démontre très simplement le principe de fonctionnement d’une antenne selon les schémas suivants :
À gauche, une ligne de transmission – une paire de conducteurs conçus pour transporter efficacement un signal radiofréquence (impédances contrôlées, pertes minimales) – est électriquement équilibrée, avec autant d’électrons allant de gauche à droite que de droite à gauche par conservation de la charge. Les champs électriques (flèches en traits épais) associés aux électrons en mouvement s’annulent, il n’y a pas de rayonnement. Si maintenant nous coupons la ligne de transmission et écartons les deux brins, nous constatons que les champs électriques dans le brin du haut et du bas sont tous deux dans la même direction, donc se somment au lieu de s’annuler, et le champ électromagnétique est rayonné. La condition optimale de rayonnement vérifie les conditions limites d’un ventre de courant – une variation périodique maximale du courant oscillant – au point d’alimentation situé au milieu des deux brins, et de nœuds de courant (annulation de l’amplitude du courant oscillant) aux extrémités : ce cas est vérifié sur la longueur des éléments rayonnants lorsqu’elle est un multiple de la demi-longueur d’onde, avec l’antenne la plus courte de longueur λ/2. Il s’agit bien de l’antenne dipôle. Cette antenne présente une polarisation linéaire, mais une impédance de Z = 73 + j·42,5 Ω (voir note) à sa fréquence de fonctionnement, avec une partie imaginaire qui couple inefficacement avec la charge résistive qu’est le récepteur. En pratique, les brins sont souvent raccourcis pour annuler la partie imaginaire de l’impédance. Une bonne antenne est un point clé pour toute réception de signaux radiofréquence, et aucun traitement numérique n’est possible sans un minimum de compréhension de cet élément fondamental de la chaîne de communication radiofréquence.
L’impédance Z est définie comme le ratio de la tension au courant Z = U/I. Alors que nous connaissons tous la loi d’ohm reliant la résistance R à ces deux grandeurs R = U/I, l’impédance généralise ce concept au cas complexe des charges réactives que sont les condensateurs C et inductances L dont l’impédance est imaginaire et dépendante de la fréquence f, 1/(2πCf) et 2πLf respectivement. L’impédance est un concept clé qui induit le concept de coefficient de réflexion R d’une onde rencontrant une interface entre deux impédances Zq et Zd : Γ =(Zq-Zd) / (Zq-Zd). Noter que Γ est un complexe : l’onde subit une réflexion et une transmission (conservation de l’énergie) qui impacte son amplitude (|Γ|) et sa phase (arg(Γ)). Les concepteurs de systèmes radiofréquences aiment utiliser le concept de taux d’onde stationnaire SWR = (1+|Γ|)/(1-|Γ|). Une transmission optimale d’une onde entre deux milieux, par exemple entre deux câbles ou un câble et une antenne, implique un coefficient de réflexion nul, ou un taux d’onde stationnaire égal à 1, tandis qu’une réflexion totale (|Γ|=1) fait tendre SWR vers l’infini.
Si nous voulions transmettre la voix – un signal de l’ordre du kHz= 10-3 MHz – alors la longueur d’onde du signal électromagnétique, tel que nous venons de le voir, serait de l’ordre de 300/10-3 = 300 km. En transposant ce signal en fréquence sur une porteuse à 100 MHz par exemple (fréquence de la bande FM commerciale), la longueur d’onde chute à 3 m et une antenne est de dimensions caractéristiques de 1,5 m (expliquant pourquoi il faut insérer les écouteurs dans son téléphone portable pour écouter la radio FM : le câble des écouteurs sert aussi d’antenne – et étrangement, tous mes écouteurs sont connectés à un câble de 130 cm de longueur, soit une demi-longueur d’onde à 115 MHz, bien proche de la bande FM commerciale).
Nous avons donc justifié de la transposition en fréquence pour un partage du spectre électromagnétique. Le spectre est une denrée rare qui n’est pas inépuisable et qu’il faut utiliser avec soin. Un signal périodique s(t)s’écrit de façon générale s(t) = Acos(2πft+φ) avec f la fréquence du signal, A son amplitude et φ sa phase (voir figure 4). Il est courant de comprimer 2πf en ω la pulsation angulaire (voir note) : dans ce cas, l’argument de la fonction trigonométrique cos est une phase composée d’un terme variant linéairement dans le temps – dont la dérivée est la fréquence – et d’un terme aléatoire φ. Ces trois grandeurs peuvent être manipulées pour transmettre une information : s(t) = A(t)cos(2πf(t)+φ(t)). Faire varier A pour y introduire une information s’appelle la modulation d’amplitude (AM), faire varier f est la modulation de fréquence, et faire varier φ est la modulation de phase (PM).
L’utilisation de ω = 2πf simplifie un certain nombre d’expressions, car une onde fait tourner sa phase de 2π pour chaque période τ = 1/f parcourue. Ainsi, lorsque nous considérons l’argument qui représente la partie oscillante de l’onde, il est naturel de parler d’une phase qui revient à son point de départ tous les 2π d’où l’expression de ω qui s’exprime en rad.s-1, alors que f s’exprime en Hz ou s-1.
Fig. 4 : Le concept de phase est au cœur du traitement de signaux radiofréquences. La phase est l’argument de la fonction trigonométrique (cos(), sin() ou exp(j) = cos()+jsin()). La phase d’une fonction périodique n’a de sens que relativement à une référence : les deux oscillateurs des deux graphiques du haut présentent des fréquences légèrement différentes ω1≠ω2 . En mélangeant les deux oscillateurs (3ème graphique), nous obtenons les fréquences somme (bleu) et différence des fréquences des oscillateurs incidents, et un filtre passe-bas ne conserve que la différence (rouge). Le mélange – pour rappel cos(a)cos(b)∝cos(a+b)+cos(a-b), fournit le cos() de la phase : nous pouvons retrouver par conséquent la phase entre ces deux signaux (bas), avec le passage à 0 lorsque les deux signaux sont en phase, ou à ±π lorsque les signaux sont en opposition de phase. En traitement du signal, ce n’est pas tant la phase que les fluctuations de phase qui importent, tel que décrit dans la bible [11].
Pour reprendre la chaîne de liaison radiofréquence, le signal transmis s(t) transporte sur une fréquence porteuse fRF une information qui est soit imprimée sur l’amplitude de ce signal, soit des variations de sa fréquence, soit sa phase : l’objectif du récepteur est d’éliminer fRF pour permettre la restitution de A, f ou φ. Tout le problème de la démodulation est que la valeur nominale de fRF est connue, mais que l’oscillateur de l’émetteur géographiquement distinct du récepteur n’implémente pas nécessairement cette fréquence de la même façon que le récepteur. Je crois que mon téléphone portable se cale sur 102,4 MHz lorsque je cherche à écouter Radio Campus à Besançon, mais en pratique mon téléphone est peut être trop chaud ou trop froid et l’oscillateur intégré sur le circuit imprimé du récepteur ne sera pas à la même fréquence que l’oscillateur dans les locaux de Radio Campus. Pire, je suis peut-être dans un véhicule mobile et un décalage Doppler est introduit : si je cherche à écouter Radio Campus depuis un satellite en orbite polaire (800 km d’altitude) qui tourne autour de la Terre en 100 minutes, mon mouvement en orbite par rapport à l’émetteur au sol induira un décalage Doppler de fréquence de l’ordre de 2400 Hz.
Nous avions déjà donné la démonstration du décalage Doppler dans [12] : pour que le mouvement du récepteur impacte significativement sur l’écart de fréquence entre émetteur et récepteur, il faut quand même se déplacer à quelques kilomètres par seconde, un cas qui se présente rarement au sol.
2. Émetteur et récepteur
Ainsi, nous ne pouvons pas faire l’hypothèse que nous savons reproduire exactement l’horloge de l’émetteur au niveau du récepteur : même si nous savions embarquer une horloge atomique dans notre téléphone portable [13], le mouvement relatif de l’émetteur par rapport au récepteur induirait un décalage. Tout l’art de la modulation et de la démodulation consiste à s’affranchir de ce décalage de fréquence, soit en exploitant un mode de modulation tellement inefficace que l’écart des fréquences importe peu (AM), soit en suivant les variations supposées lentes de la fréquence du récepteur par rapport à l’émetteur (FM), soit en reproduisant la porteuse émise du côté du récepteur (PM). Ces approches, de complexité croissante, correspondent à une utilisation de plus en plus efficace du spectre.
Une architecture de récepteur la plus simple consiste donc en une transposition de fréquence pour ramener grossièrement de la porteuse radiofréquence vers la basse fréquence – dite bande de base – et une seconde étape fine de transposition de fréquence visant à éliminer le petit écart résiduel de fréquence : de ce fait, nous nous centrons sur la fréquence nulle (absence de modulation) et retrouvons l’information émise sous la forme de A(t), f(t) ou φ(t). Historiquement, toutes ces opérations se faisaient de façon analogique, avec un étage de réception dédié à chaque mode de modulation, et tout changement de condition d’émission (nature de la grandeur transmise ou conditions de transmission) se traduisait par l’utilisation du fer à souder pour modifier les valeurs de composants. Le rêve de la radio logicielle, duquel nous nous approchons avec les diverses avancées technologiques que nous vivons actuellement, vise à éliminer tout composant analogique pour le traitement de l’information, et de numériser au plus tôt le signal analogique issu du champ électrique détecté par l’antenne. Dans la pratique, ce rêve se heurte encore à quelques défis technologiques, et il est courant de couper la poire en deux avec une première transposition radiofréquence analogique, suivie d’une numérisation et d’un traitement numérique (voir figure 5).
Fig. 5 : Historiquement, un récepteur radiofréquence est un système analogique avec une première transposition de fréquence LO juste après le signal reçu par l’antenne, éventuellement amplifié. Compte tenu des imperfections des composants, il était classique de transposer en deux étapes, avec une fréquence intermédiaire IF qui permettait de filtrer les raies spectrales – des composantes du spectre qui se détachaient du niveau de base déterminé par la puissance du bruit – parasites qui fuitaient du premier étage (architecture super-hétérodyne – gauche). Aujourd’hui, nous rêvons de directement échantillonner le signal électrique capté par l’antenne, et effectuer tous les traitements numériquement, alliant ainsi souplesse, stabilité et reconfigurabilité de la chaîne de réception (milieu). Dans la pratique, peu de convertisseurs analogiques-numériques sont assez rapides pour couvrir la bande radiofréquence, et la puissance de calcul requise est énorme : une première transposition de fréquence nous amène de la bande radiofréquence en bande de base, pour ensuite être numérisée et traitée (architecture homodyne ou 0-IF – droite).
Il est à noter que l’approche idéale de l’échantillonnage dès l’antenne peut se heurter à un problème théorique en plus de pratique : la dynamique de la mesure. Un récepteur analogique muni de filtres analogiques et de mélangeurs peut détecter un signal, aussi petit soit-il, dans un fouillis de signaux de forte amplitude. Un filtrage puis un amplificateur permettront de rejeter les interféreurs et de faire sortir le petit signal du bruit. Dans le cas d’une numérisation tôt dans la chaîne d’acquisition, nous devons d’une part éviter la saturation et donc augmenter la plage de tensions reçues (tension de référence Vref du convertisseur analogique-numérique plus élevée) en présence d’une source puissante dans la bande. Mais si, ce faisant, le petit signal que nous cherchons à détecter est plus petit que le pas de quantification Vref/2N pour un convertisseur sur N bits, l’information est définitivement perdue. Or les convertisseurs radiofréquences sont caractérisés à ce jour par un nombre relativement réduit de bits (par rapport à ce que nous connaissons pour les convertisseurs analogiques-numériques audiofréquences). Ainsi, un convertisseur sur 8 bits, tel que celui équipant les récepteurs de télévision numérique terrestres utilisés comme sources généralistes de signaux radiofréquences pour le traitement logiciel, ne présentent qu’une dynamique de 20log10(256) = 48 dB. Cela signifie qu’un signal issu d’un émetteur distant de d2 d’un récepteur ne peut être reçu si un autre émetteur de la même puissance, mais proche se trouve à une distance d1 tel que d2/d1>256. En effet, les pertes de propagation en espace libre (Free Space Propagation Loss) nous informent que la puissance décroît comme le carré de la distance donc comme 20log10(d2)-20log10(d1) = 20log10(d2 /d1). Ainsi, une émission dans la bande FM d’un émetteur à 256 km ne peut être reçue si un autre émetteur FM se trouve à 1 km du récepteur.
Quantification vs bruit dans la conversion analogique-numérique
Noter que nous parlons ici du cas où le petit signal est sous le niveau de quantification Vref/2N avec Vref la tension de référence d’un convertisseur analogique-numérique travaillant sur N bits. Ce problème se distingue du cas où le signal est sous le niveau de bruit thermique kB·T×B – kB= 1,38·10-23 J.K-1, T la température (en Kelvin) et B la bande passante d’intégration du signal, qu’on pourra retenir facilement en passant en échelle logarithmique comme 10log10(kBT) = -174 dBm/Hz (T = 300 K) auquel on additionne B en dB –, mais au-dessus du niveau de quantification, tel que nous l’avions discuté dans le cas de la réception GPS : ce n’est pas parce que le signal n’est pas visible sur un analyseur de spectre qu’il ne peut pas être retrouvé par utilisation d’un filtre adapté – corrélation – tant que l’information a été conservée lors de sa numérisation. Nombre de récepteurs GPS ne travaillent qu’avec des convertisseurs 1 bit (comparateur), suffisants pour retrouver le motif connu transmis par chaque satellite.
Ce problème est d’autant plus ardu dans le cas des RADARs, où un brouilleur émet un signal interférant dont la puissance décroît comme le carré de la distance, alors que la cible ponctuelle renvoie une puissance qui décroît comme la puissance quatrième de la distance (le bilan de liaison est le produit de deux lois de puissance qui décroissent comme le carré de la distance). Ainsi, un interféreur malveillant pourrait facilement éblouir un RADAR qui numérise les signaux reçus par chaque élément d’un réseau d’antennes et tenterait de retrancher le brouilleur en post-traitement. Seule une interférence destructive analogique du brouilleur (synthèse électronique de faisceau) avant numérisation permet de rejeter le brouilleur et d’amplifier suffisamment le signal réfléchi par la cible pour la détecter.
3. Architecture du récepteur : flux de données I/Q
Nous avons exprimé le signal comme un signal réel de la forme Acos(2πft+φ) : une tension est en effet une grandeur réelle. Nous avons jusqu’ici décrit la transposition de fréquence comme un mélange, représenté par un symbole de multiplication. En effet, rappelons-nous que la seule façon de transposer une fréquence est de multiplier : une somme ne saurait transposer une fréquence : Aexp(2πf1t)+Bexp(2πf2t), avec A et B des constantes, ne peut que produire des composantes spectrales à f1 et f2, et jamais à f1±f2. C’est le cœur de toute l’analyse des systèmes linéaires qui permet de passer dans le domaine spectral, d’analyser le comportement à une fréquence quelconque f, et de généraliser à tout signal somme de composantes spectrales pondérées, car un système linéaire n’a pas le droit de mélanger des fréquences. Au contraire, une multiplication Aexp(2πf1t)×Bexp(2πf2t)produit A×Bexp((f1+f2)t) et donc un argument de fréquence somme des deux fréquences incidentes. Donc, la transposition de fréquence s’obtient par un composant non-linéaire, qu’il s’agisse d’un transformateur dont le noyau est saturé ou d’une diode.
Imaginons maintenant que nous recevions un signal de la forme Acos(ωRFt+φ) et que nous le mélangions avec l’oscillateur local radiofréquence cos(ωLOt). Le résultat de ce produit, selon les formules trigonométriques classiques, est cos(ωRFt+φ±ωLOt) et si nous avons pris soin d’ajuster ωLO = ωRF pour recevoir la station radiofréquence recherchée, et que nous éliminons le terme « somme des fréquences » par un filtre passe-bas, il nous reste Acos(φ). Si l’information est portée par l’amplitude A, que se passe-t-il dans le cas malencontreux où φ = π/2 rad ? La fonction trigonométrique est toujours nulle, et nous sommes dans l’incapacité de retrouver A. Le cas φ = π/2[π] rad n’est pas exceptionnel : si nous écoutons la radio FM à 100 MHz, ce cas apparaît tous les λ/2 ou 1,5 m. Il serait excessivement pénible de perdre le signal que nous écoutons chaque fois que nous faisons 2 pas en marchant en écoutant la radio, sans compter la difficulté de bien placer son ordinateur communiquant en Wi-Fi puisqu’à 2,4 GHz, la demi-longueur d’onde est de 6,25 cm.
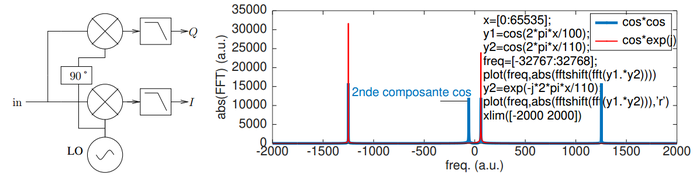
La solution est de compléter le cas où l’argument annule le cosinus par la fonction trigonométrique qui se maximise dans la même condition de phase, soit le résultat du produit Acos(ωRFt+φ) par sin(ωLOt)qui donne Asin(φ) si ωRF = ωLO et que nous coupons la composante spectrale somme des fréquences. Or lorsque cos(φ) s’annule pour φ ≃ π/2, nous obtenons au contraire sin(φ) maximal et proche de 1. De même, lorsque φ ≃ 0 et que sin(φ) s’annule, alors cos(φ) est maximum et dans tous les cas nous pouvons remonter à l’amplitude du signal. Si nous mesurons Acos(φ) que nous nommerons I et que nous mesurons Asin(φ) que nous nommerons Q, alors il est naturel de former I+jQ = Acos(φ)+jAsin(φ)=Aexp(jφ) qui forme un complexe. Ise nomme la composante en identité, et Q la composante en quadrature. Les deux mélangeurs sont donc alimentés par des copies dites en quadrature de l’oscillateur local, puisque sin(x) = c(π/2-x) (figure 6, gauche). L’utilisation des nombres complexes facilite considérablement l’analyse des signaux puisque nous retrouvons facilement A = √(I2+Q2) = |I+jQ| l’amplitude et φ = arg(I+jQ) = atan2(I,Q) la phase.
Fig. 6 : Gauche : le démodulateur I/Q fait le produit du signal d’entrée in – par exemple issu de l’antenne – avec deux copies de l’oscillateur local en quadrature l’une par rapport à l’autre pour générer les deux composantes du complexe I+jQ, avec I la composante en identité et Q la composante en quadrature. Droite : impact du mélangeur réel (bleu) avec ses 4 raies dont deux proches de la bande de base, dupliquant l’information utile, et du mélangeur complexe IQ (rouge). Le code en insert permet de reproduire le graphique sous GNU/Octave.
Écart au cas idéal du démodulateur I/Q
La figure 6 présente le cas idéal où un oscillateur local peut être décalé exactement de 90° sans affecter son amplitude. En pratique, cette condition est difficile à réaliser, générant des artefacts induits par l’IQ imbalance. Une solution consiste à revenir à la solution super-hétérodyne [15] identifiée lors de la description du récepteur analogique : une première transposition de fréquence par un unique mélangeur décalé d’une fréquence intermédiaire IF est appliquée au signal radiofréquence et filtré pour éliminer la composante spectrale à la somme des fréquences, ce signal est numérisé et la transposition en bande de base par le mélangeur I/Q est implémentée numériquement : l’expression sous GNU/Octave exp(j*2*pi*f*t) présente deux composantes exactement déphasées de 90° et de même amplitude, résolvant le problème d’IQ imbalance. Alternativement, la différence de phase entre les composantes I et Q ainsi que d’amplitude peut se calibrer et se compenser numériquement a posteriori.
4. Traitement numérique du signal pour la démodulation
Nous avons enregistré un signal radiofréquence modulé en amplitude avec un oscilloscope – en effet, tant qu’un flux continu de données n’est pas nécessaire, un oscilloscope peut être une excellente source de signaux pour un traitement par radio logicielle (cependant, écouter une station FM de la sorte est relativement pénible, avec un son haché par un temps de communication entre l’oscilloscope et l’ordinateur bien plus long que le temps nécessaire à acquérir une nouvelle séquence de données). Comment retrouver l’information initialement introduite sous forme de variation de l’amplitude de la porteuse ?
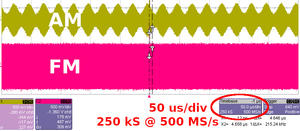
Fig. 7 : Capture d’écran d’un oscilloscope ayant acquis sur deux voies des signaux radiofréquences, en haut une porteuse à 20 MHz modulée en amplitude à 40 kHz, et en bas une porteuse modulée en fréquence avec les mêmes caractéristiques et une déviation maximale de 1 MHz. L’ellipse rouge indique la zone d’écran contenant les informations importantes sur la base de temps (fréquence d’échantillonnage, durée de la mesure et donc nombre d’échantillons, limité par la quantité de mémoire disponible dans l’oscilloscope, ici un LeCroy WaveSurfer 454).
La figure 7 présente la capture d’écran de l’acquisition, dont un fichier de données contenant les échantillons des deux voies est par ailleurs disponible. Quelles sont les informations importantes pour un traitement de radio logicielle de cette capture d’écran ? Le point clé pour transformer des échantillons acquis en temps discret – à intervalle de temps constant – et un axe des abscisses gradué en temps ou en fréquence, est la fréquence d’échantillonnage. Ici, cette information nous est fournie : 500 MHz. Sachant que chaque division occupe 50 µs, et que l’écran comporte 10 divisions, nous en déduisons le nombre de points acquis (information redondante donnée par l’oscilloscope) : 500·106×50·10-6×10 = 250 kéchantillons. Chaque courbe comporte en effet 250000 points, soit un fichier de 500 koctets puisque cet oscilloscope sauve ses échantillons sur 8 bits/échantillon.
Nous avons en mémoire des points, et nous désirons connaître la fréquence de la porteuse. Une transformée de Fourier (fft sous GNU/Octave) est une transformation bijective qui convertit 250000 points acquis dans le temps en 250000 points dans le domaine spectral. Ces points sont acquis au rythme de 500 Mpoints/s, donc la gamme de fréquence s’étend de -250 MHz à +250 MHz. Dans cette plage de 500 MHz, nous avons 250000 points, soit une résolution spectrale de 500·106/250·103 = 2000 Hz. Traduisons ces concepts abstraits dans un vrai code (GNU/Octave) :
fs=500; % freq. échantillonnage en MHz
f=fopen('fichier.out'); % ouverture du fichier : renvoie un descripteur > 0
d=fread(f,inf,'int8') % lecture de tout le fichier (inf) de données sur 8 bits
ch1=d(1:end/2);ch2=d(end/2:end); % découpe des deux voies acquises
freq=linspace(-fs/2,fs/2,length(ch1));
plot(abs(fftshift(fft(ch1-mean(ch1)))));
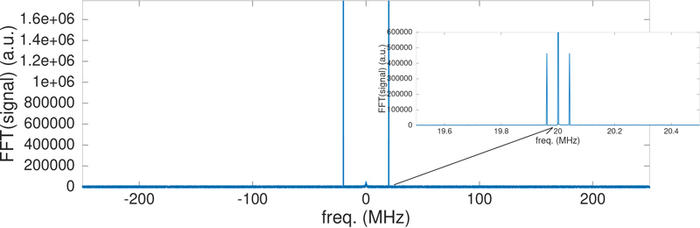
Le fichier est ouvert, son contenu est lu et découpé dans les deux sous-ensembles de points que sont les deux voies de mesure, l’axe des fréquences freq est défini et nous traçons la transformée de Fourier du signal. Point délicat : la transformée de Fourier de signaux échantillonnés en temps discret est périodique et se répète tous les fs. Deux conventions existent : distribuer les échantillons dans le domaine spectral dans l’intervalle [0:fs] avec fs/2 au milieu de cet intervalle, ou distribuer les échantillons de [-fs/2:fs/2]. Étant périodiques, ces deux représentations sont identiques et ne sont qu’une question de convention. Matlab (et GNU/Octave par conséquent) a choisi de placer la fréquence nulle (0 Hz) dans le premier échantillon, et le dernier échantillon contient la composante spectrale à fs. Le physicien trouve plus intuitif de placer la fréquence nulle au milieu du graphique et d’étendre la plage des fréquences de -fs/2 à fs/2 : c’est le rôle de la fonction fftshift utilisée dans le code ci-dessus. Nous observons bien deux raies à ±20 MHz, fréquence de la porteuse du signal réel enregistré (voir figure 8). Un zoom autour des deux raies clairement visible laisse déjà entrevoir une structure de ce signal (l’information portée par la modulation).
4.1 Modulation AM
Afin d’extraire l’information contenue sur cette porteuse, nous devons ramener le signal en bande de base. Le signal réel duplique l’information dans la plage positive et la plage négative du spectre : il nous faudra éliminer la moitié de cette information redondante pour retrouver la grandeur qui nous intéresse.
Fig. 8 : Spectre du signal radiofréquence modulé en amplitude acquis par l’oscilloscope, et (insert) zoom sur une des raies permettant d’identifier, dans le domaine spectral, une structure insérée dans la porteuse – la modulation d’amplitude.
La transposition de fréquence s’obtient par mélange : nous devons fabriquer l’oscillateur local, de la forme exp(j2πfRFt). L’observation de la figure 8 laisse penser que fRF = 20·106 Hz (un scalaire), donc la seule variable qui reste à définir est le temps. Ayant échantillonné en temps discret, le temps s’incrémente par pas discret de 1/fs : temps=[0:length(ch1)-1]/fs; (la longueur du vecteur est décrémentée de 1, car nous commençons le temps à la date 0). Ce temps alimente la définition de l’oscillateur local lo=exp(j*2*pi*temps*20e6);. La lecture du fichier a fourni un vecteur, la définition de lo est une colonne, nous devons transposer un des deux signaux pour avoir deux colonnes. Il est classique d’utiliser l’apostrophe (’) pour transposer sous Matlab. Attention pour les utilisateurs de signaux réels (dont je fais partie) : le symbole ’ ne fait pas simplement la transposée mais, sur des signaux complexes, prend le complexe conjugué de la transposée ! (j’ai cherché longtemps pourquoi j’avais une erreur de signe dans l’argument de l’exponentielle). Ainsi, ch1·*lo' effectue bien le produit du signal modulé ch1 avec exp(-j2π×temps×20·106) puisque l’apostrophe a introduit le signe négatif devant la fréquence dont nous transposons le signal. Noter que avant cette opération, il est judicieux de retrancher sa valeur moyenne à ch1 : ch1=ch1-mean(ch1);. À peu près toutes les opérations en traitement du signal numérique supposent que la valeur moyenne de l’argument est nul. Ayant effectué cette opération, nous nous retrouvons avec le graphique de la figure 9 (gauche, courbe bleue), avec une composante spectrale proche de la bande de base centrée sur 0 Hz, mais une autre composante loin de la fréquence nulle, très exactement à -20-20 = -40 MHz. Nous devons éliminer cette composante indésirable : pour ce faire, un filtre passe-bas sera approprié.
Le filtre passe-bas le plus simple est la moyenne glissante : faire glisser une fenêtre de moyennage sur un signal atténue ses composantes qui fluctuent rapidement (haute fréquence) pour ne conserver que la valeur moyenne (basse fréquence) locale. Nous pouvons estimer grossièrement que la moyenne sur P points coupe le spectre à fs/P. Ici, nous avions échantillonné à 500 MHz, la raie parasite se trouve à 40 MHz, donc moyenner sur 500/2/40 = 7 points devrait suffire. En pratique, nous allons nous donner un peu de marge et prendre 5 fois cette valeur.
ch1=ch1-mean(ch1);
temps=[0:length(ch1)-1]/fs; % fs en MHz -> temps en us
lo=exp(j*2*pi*20*temps); % lo en MHz * temps en us = phase en rad
transpose=ch1.*lo';
N=34; filtre=ones(N,1)/N;
filtrage=conv(transpose,filtre)(N/2:end-N/2);
Nous constatons en affichant filtrage que nous avons bien extrait l’amplitude du signal (composante proche de la fréquence nulle, figure 9 à droite), mais que la restitution n’est pas parfaite, il reste des variations à haute fréquence sur le signal démodulé. La cause est notre filtre très grossier qu’est la fenêtre rectangulaire. La convolution (filtrage) dans le domaine temporel est un produit des fonctions de transfert dans le domaine spectral. Or la transformée de Fourier d’une fonction rectangulaire (telle que nous l’avons choisie pour filtrer dans le domaine temporel) est un sinus cardinal d’expression sin(x)/x . Nous laissons comme exercice au lecteur de trouver comment afficher cette fonction de transfert dans le domaine spectral. Force est de constater que la capacité de filtrage de cette fonction (courbe verte sur figure 9, gauche) est médiocre avec ses rebonds périodiques. Un choix plus « judicieux » eut été d’adoucir les flancs pour réduire ces rebonds : ce sont les fameuses fonctions de fenêtrage de Hamming, Hanning, Kaiser, gaussienne et confrères.
Fig. 9 : Gauche : impact de la transposition de fréquence (bleu) et filtrage (rouge) dans le domaine spectral. La fonction de transfert du filtre (vert) n’est pas explicitée dans le texte, mais s’ajuste parfaitement aux puissances relatives du signal avant (bleu) et après (rouge) filtrage. Droite : signal avant (bleu) et après (rouge) filtrage dans le domaine temporel. Gauche : impact de la transposition de fréquence (bleu) et filtrage (rouge) dans le domaine spectral. La fonction de transfert du filtre (vert) n’est pas explicitée dans le texte, mais s’ajuste parfaitement aux puissances relatives du signal avant (bleu) et après (rouge) filtrage. Droite : signal avant (bleu) et après (rouge) filtrage dans le domaine temporel.
Nous avons constaté au cours de ce traitement qu’à aucun moment nous nous sommes préoccupés d’annuler toute différence résiduelle entre oscillateur local de l’émetteur et celui du récepteur. AM est le mode de modulation le plus simple, mais le plus inefficace : tant que la bande passante de démodulation contient l’ensemble de l’information, le redressement (valeur absolue) et filtre passe-bas suffisent à retrouver l’amplitude du signal et donc l’information imprimée sur la porteuse. Cependant, le filtre de réception doit être suffisamment large pour tenir compte des variations possibles entre les fréquences des deux oscillateurs locaux de l’émetteur et du récepteur, et plus ce filtre est large plus l’espacement entre les stations doit être important, mais surtout plus les risques d’intégrer du bruit qui ne sera pas rejeté par le filtre sera important. Il est notoire qu’à l’apogée des transmissions AM, les démarreurs de voiture causaient un brouillage des récepteurs radiofréquences, induisant le passage à la transmission modulée en fréquence, plus efficace et moins sensible aux perturbations environnantes.
4.2 Modulation FM
La modulation FM, qui fait varier l’argument de la fonction trigonométrique, est plus complexe à exprimer mathématiquement et nous ne développerons pas ici tout le formalisme, en nous référant à la présentation de D. Bederov au FOSDEM 2015 [16] qui démontre une astuce mathématique – applicable facilement en traitement numérique – qui évite l’implémentation de la classique boucle à verrouillage de phase nécessaire pour asservir l’oscillateur local sur la porteuse émise depuis l’oscillateur local distant.
La boucle à verrouillage de phase (PLL)
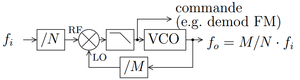
Fig. 10 : Architecture de PLL fractionnaire permettant de produire fo comme fraction rationnelle M/N de fi. Le symbole de filtre passe-bas contient l’intégrateur et l’amplification (proportionnelle) de la loi de commande.
La boucle à verrouillage de phase (figure 10) est un mécanisme d’engrenages qui permet de multiplier ou diviser la fréquence d’un oscillateur par une fraction rationnelle. Un oscillateur de référence fi, généralement stable, fournit un signal à une fréquence qui ne correspond pas à l’application visée. Afin d’atteindre un signal de fréquence de sortie fo = M/N·fi, un oscillateur contrôlable en tension (peu stable – Voltage Controlled Oscillator VCO) est divisé par M ∈ ℕ (saturation de la sinusoïde pour donner un signal créneau qui alimente un compteur). De même, le signal de référence est divisé par N ∈ ℕ. Un comparateur de phase (mélangeur suivi d’un filtre passe-bas) compare fi/N et fo/M. La tension commandant le VCO est ajustée automatiquement de façon à ce que fi/N=fo/M⇔fo=fi×M/N par annulation de la phase en sortie du détecteur. Ce principe est utilisé pour convertir le signal encodé dans la fréquence du signal reçu – modulation FM – en information qui n’est autre que le signal de commande du VCO. Les variations lentes de fréquence de l’oscillateur local du récepteur par rapport à l’émetteur s’observent comme une tension continue ou fluctuant lentement sur la commande du VCO, qui est en général coupée par un filtre passe-haut pour extraire l’information utile (parole, musique ...). Ces techniques sont très courantes pour distribuer les horloges dans les microprocesseurs, tel que décrit par exemple dans [17, Eq.3-1,Eq.3-2].
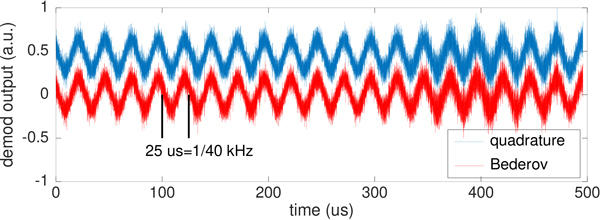
Dans cette présentation, nous apprenons que la démodulation de fréquence s’obtient en calculant la phase du produit d’un échantillon multiplié par le complexe conjugué de l’échantillon précédent, qui est approximativement égal à la partie imaginaire du produit de l’échantillon courant multiplié par le complexe conjugué de la dérivée de l’échantillon courant avec le précédent (tout l’intérêt de la présentation porte sur l’élimination du calcul de la phase, la fonction arctangente étant très gourmande en ressources et donc en temps de calcul). Ceci (figure 11) s’écrit donc en terme de GNU/Octave comme :
demod=angle(S(2:end).*conj(S(1:end-1))); % quadrature FM demodulator
demod=imag(diff(S(1:end)).*conj(S(1:end-1))); % Bederov
Fig. 11 : Démonstration de la démodulation numérique de la modulation FM présente sur la courbe magenta de la figure 7. On prendra soin, pour appliquer les algorithmes de démodulation FM après transposition d’une des composantes spectrales autour de 20 MHz vers la bande de base, d’efficacement filtrer la composante qui se retrouve à -40 MHz, faute de quoi le résultat sera excessivement bruité.
5. Décimer pour réduire le flux
L’exemple ci-dessus ne s’est jamais intéressé à la puissance de calcul nécessaire au traitement en flux tendu des données acquises par le convertisseur analogique-numérique et transmises au processeur. Nous avons conservé toutes les données tout au long de la chaîne de traitement, même si le signal à l’arrivée – de basse fréquence – contient bien trop d’échantillons par période et présente de ce fait une redondance excessive. Cette approche est inefficace, car le long d’une chaîne de traitement, nous ne pourrons que perdre de l’information, jamais en ajouter. Or Shannon nous a expliqué que l’information contenue dans un signal (son entropie) et la bande passante sont équivalentes. Perdre de l’information signifie réduire la bande passante. Mais la bande passante – le nombre de points transmis par seconde au processeur – détermine la puissance de calcul nécessaire. Si nous réduisons la quantité d’information, nous pouvons réduire la bande passante, et donc le nombre d’échantillons à traiter par seconde.
Imaginons que nous voulions filtrer un signal radiofréquence. Un filtre inconditionnellement stable est le filtre à réponse impulsionnelle finie dont la sortie yn à la date n est la somme pondérée des coefficients (du filtre) bk avec les entrées passées x : yn∑Nk=1 bkxn-k. Il faut donc effectuer N multiplications dans l’intervalle de temps entre lequel un nouvel échantillon x est produit par la carte d’acquisition. Si la carte d’acquisition acquiert 2 Méchantillons/s (cas des récepteurs de télévision numérique terrestre), nous n’avons que 500 ns pour faire toutes ces multiplications (pour rappel, la lumière parcourt 150 m dans cet intervalle de temps – ce n’est pas long !). La résolution spectrale d’un filtre est de l’ordre de la fréquence d’échantillonnage (nous avons choisi ici 2 MHz) divisé par N : si nous avons la maladresse de demander un filtre de 2 kHz de bande de transition, nous avons besoin de N = 2·106/2·103 = 1000 coefficients, soient 1000 multiplications toutes les 500 ns ou 0,5 ns/multiplication. Peu de processeurs sont capables d’un tel rythme de traitement. Mais peu d’applications ont besoin de couper un signal interférant avec un raideur de filtre telle que 2 kHz sur le signal brut acquis. Généralement, le signal modulé occupe une bande spectrale large, qui peut être filtrée par un filtre de bande de transition bien plus large (transition plus douce) se traduisant par moins de coefficients et donc moins de multiplications. Mais ce faisant, une fois le filtrage effectué, toute une partie du spectre – les composantes hautes fréquences qui ont été atténuées – est devenue inutile. Comment retirer un morceau de spectre ? En abaissant la fréquence d’échantillonnage (rappel : le spectre d’un signal échantillonné en temps discret à la fréquence d’échantillonnage fs s’étend de -fs/2 à +fs/2), c’est-à-dire en décimant, ce qui signifie ne conserver qu’un point tous les M et mettre les autres à la poubelle. Ce faisant, nous réduisons le nombre de points à traiter par seconde d’un facteur M, et nous réduisons le nombre de coefficients nécessaires pour filtrer une nouvelle fois avec une bande de transition étroite (figure 12).
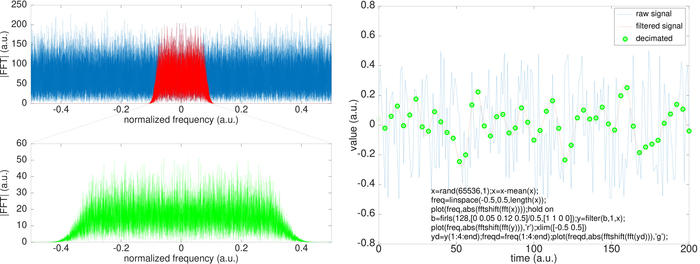
Fig. 12 : Gauche : un signal de large encombrement spectral (signal aléatoire – bleu) occupe tout le spectre. Sachant que seule une fraction de ce spectre nous intéresse, nous filtrons pour obtenir le signal rouge. Cependant, la largeur de ce spectre est bien trop importante : nous pouvons le réduire. Pour ce faire, nous décimons en ne conservant que 1 point sur 4, pour obtenir le spectre vert : en d’autres termes, le spectre vert est un zoom sur le spectre rouge obtenu par décimation. À droite, l’interprétation de cette même séquence de traitement, dans le domaine temporel. Les points verts sont situés tous les 4 échantillons de la courbe rouge : traiter le signal vert nécessite 4 fois moins de puissance de calcul que traiter le signal rouge, et pourtant aucune information n’a été perdue entre les signaux rouge et vert.
Un point clé dans la démonstration de la figure 12 est la nécessité de filtrer avant de décimer, faute de quoi tout le bruit haute fréquence – au-dessus de la fréquence de Nyquist (demi-fréquence d’échantillonnage) après décimation – sera ramené en bande de base par repliement spectral. Le code de la figure 12 (droite) illustre la conception d’un filtre sous GNU/Octave au moyen de la fonction firls() des outils de traitement du signal (signal processing toolbox chargée par pkg load signal) : cette fonction prend pour argument le nombre de coefficients du filtre, la liste des fréquences définissant les pondérations du filtre, et ces pondérations elles-mêmes. On se rappellera que la fréquence de Nyquist est définie comme unitaire sous Matlab, et que par conséquent les gabarits des filtres sont indépendants de la fréquence d’échantillonnage. Dans cet exemple, les points des courbes rouge et verte contiennent exactement la même information, mais avec plus de parcimonie dans le cas de la courbe verte, facilitant son traitement.
En conclusion : mieux vaut cascader une succession de filtres permettant une décimation entre chaque étage, que de tenter de placer un unique filtre en tête de traitement avec une bande de transition excessivement étroite, induisant un nombre excessif de coefficients et une puissance de calcul démesurée, et ainsi s’adapter à la bande passante utile après chaque étape de traitement.
Conclusion
La radio logicielle est une approche souple, flexible et reconfigurable du traitement de signaux radiofréquences visant à maximiser l’implémentation logicielle et minimiser le matériel nécessaire. Un tel objectif ne peut être atteint qu’avec un minimum d’outils mathématiques et théoriques de traitement du signal de données échantillonnées en temps discret. Une implémentation efficace nécessite par ailleurs de comprendre le cheminement des données et l’impact des propriétés des diverses étapes de traitement. Ce domaine est une opportunité d’épanouissement alliant électronique embarquée sur processeur et FPGA, traitement du signal à divers niveaux d’abstraction (VHDL, C, Python/Octave), pour finalement avoir la satisfaction de maîtriser l’ensemble de la chaîne de réception, des électrons mis en mouvement dans les brins de l’antenne à l’affichage de l’information transmise sur l’Éther. Nous nous efforcerons d’illustrer de tels résultats dans les articles qui suivront, dans la lignée de ceux qui ont précédé cette introduction .
Afin de ne pas décourager le lecteur qui a tenté d’afficher la fonction de transfert du filtre implémenté comme une moyenne glissante, la solution pour afficher le gabarit de la figure 9 (gauche) est :
z=zeros(length(ch1),1); % autant de points que le vecteur de données
z(1:N)=1; % moyenne glissante sur N=34 points
zz=abs(fftshift(fft(z))); % fonction de transfert du filtre
zz=zz/max(zz)*max(abs(fft(transpose))); % normalisation pour être à la même ...
plot(freq,zz,'g') % échelle que les courbes existantes
L’archive des points acquis depuis l’oscilloscope et les scripts de traitement sont disponibles sur jmfriedt.free.fr.
Remerciements
Toutes les références bibliographiques qui ne sont pas librement disponibles sur le Web ont été obtenues auprès de Library Genesis sur gen.lib.rus.ec.
Références et notes
[1] C. BASSA, « Our precious Earth and the lunar far side – Far side of the Moon photographed by amateurs (12 Oct. 2018) » : https://www.camras.nl/en/blog/2018/precious-earth-and-lunar-far-side
[2] J. MITOLA III, « Software radio architecture: object-oriented approaches to wireless systems engineering », John Wiley & Sons, 2004.
[3] T. COLLINS, R. GETZ, D. PU et A. WYGLINSKI, « Software-Defined Radio for Engineers », Artech House, 2018 (www.analog.com/en/education/education-library/software-defined-radio-for-engineers.html) nous informe que la première utilisation du terme Software Radio daterait de 1985 (chordite.com/team.pdf), mais que la technique était utilisée dès les années 1970 sur des signaux très basse fréquence comme nous le ferions aujourd’hui avec une carte son de PC.
[4] J.G. PROAKIS, D.K. MANOLAKIS, « Digital Signal Processing », Prentice Hall, 2006
[5] A.V. OPPENHEIM, R.W. SCHAFER, « Discrete-Time Signal Processing (3rd Edition) », Prentice-Hall Signal Processing Series, 2009), et vidéos des cours sur ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/video-lectures/lecture-1-introduction
[6] R.G. LYONS, « Understanding Digital Signal Processing », Prentice Hall, 2004.
[7] T. McDERMOTT, « Wireless Digital Communications : Design and Theory », Tucson Amateur Packet Radio Corporation – TAPR, 1997.
[8] E. GRAY, « Improvement in electro-harmonic telegraphs », brevet US186340A, 1877.
[9] D. MINDELL, « Opening Black’s Box – Bell Labs and the Transmission of Signals », Chap. 4 de « Between Human and Machine – Feedback, Control and Computing before Cybernetics », John Hopkins Univ. Press, 2002.
[10] C.A. BALANIS, « Antenna Theory, Analysis and Design », Wiley Interscience, 2005.
[11] E. RUBIOLA, « Phase noise and frequency stability in oscillators », Cambridge University Press, 2008.
[12] J.-M FRIEDT, « La réception de signaux venus de l’espace par récepteur de télévision numérique terrestre », OpenSilicium n°13, Dec 2014/Jan-Fev 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-013/La-reception-de-signaux-venus-de-l-espace-par-recepteur-de-television-numerique-terrestre
[13] S. KNAPPE et al., « A microfabricated atomic clock », Appl. Phys. Lett 85 1460, 2004, et www.nist.gov/news-events/news/2004/08/nist-unveils-chip-scale-atomic-clock
[14] J.-M FRIEDT, G. CABODEVILA, « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », OpenSilicium n°15, 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-015/Decodage-des-signaux-de-satellites-GPS-recus-par-recepteur-de-television-numerique-terrestre-DVB-T
[15] E.H. ARMSTRONG, « A new system of short wave amplification », Proc. IRE 9 (1), pp.3-11. (1921) donne la recette justifiant l’approche super-hétérodyne : « It may be observed here that this method is not limited to one transformation of frequency with one subsequent amplification. If the frequency to be received is 5,000,000 cycles this may be stepped down to 500,000 cycles, amplified, stepped down again to 50,000 cycles, re-amplified and detected. The great advantage of this method of amplification is that the tendency to oscillate due to the reaction between the output of the amplifier and the input is eliminated as the frequencies are widely different. ». La solution répond à un problème bêtement technologique sans justification de la physique sous-jacente autre que la limitation des performances des mélangeurs par rapport à leur condition de fonctionnement théorique. L’amélioration des technologies permet aujourd’hui d’appréhender les mêmes problèmes en solution homodyne (0-IF), mais la solution technologique reste d’intérêt historique et technique (problème du IQ-imbalance).
[16] D. BEDEROV, « Arithmetic based implementation of a quadrature FM Demodulator », FOSDEM, 2015 : https://fosdem.org/2015/schedule/event/sdr_arithmetic/
[17] 7 Series FPGAs Clocking Resources – User Guide, Xilinx UG472 v1.14, 2018 et, C. CÁRDENAS et al., « Noise Characterization of Red Pitaya Internal PLL », accepté IEEE Trans. UFFC, 2018
[18] C.E. SHANNON, « Communication in the Presence of Noise », Proc. IRE 37 (1), pp.10–21, 1949.
[19] J.-M FRIEDT, G. GOAVEC-MEROU, « La réception radiofréquence définie par logiciel (Software Defined Radio – SDR) », GNU/Linux Magazine n°153, pp. 4-33, 2012 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-153/La-reception-radiofrequence-definie-par-logiciel-Software-Defined-Radio-SDR
[20] J.-M FRIEDT, « Radio Data System (RDS) – analyse du canal numérique transmis par les stations radio FM commerciales, introduction aux codes correcteurs d’erreur », GNU/Linux Magazine n°204, mai 2017 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-204/Radio-Data-System-RDS-analyse-du-canal-numerique-transmis-par-les-stations-radio-FM-commerciales-introduction-aux-codes-correcteurs-d-erreur
[21] J.-M FRIEDT, « RADAR passif par intercorrélation de signaux acquis par deux récepteurs de télévision numérique terrestre », GNU/Linux Magazine n°212, février 2018 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-212/RADAR-passif-par-intercorrelation-de-signaux-acquis-par-deux-recepteurs-de-television-numerique-terrestre
[22] J.- M FRIEDT, « La peinture sur spectre radiofréquence, et l’effet capture de la modulation en fréquence – ou pourquoi les avions communiquent encore en AM », GNU/Linux Magazine n°216, juin 2018 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-216/La-peinture-sur-spectre-radiofrequence-et-l-effet-capture-de-la-modulation-en-frequence-ou-pourquoi-les-avions-communiquent-encore-en-AM



 Ajouter à une liste de lecture
Ajouter à une liste de lecture