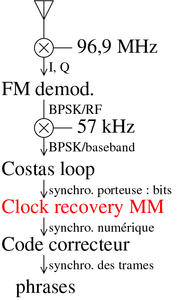
RDS – Radio Data System – est le mode numérique de communication exploité par les stations FM de la bande commerciale 88–108 MHz pour indiquer à l’utilisateur des informations telles que le nom de la station reçue, du texte libre tel que les informations en cours de diffusion ou un titre de musique, ainsi que l’heure ou la nature du programme diffusé. Nous nous proposons, à partir du signal analogique reçu par un récepteur de télévision numérique terrestre (DVB-T) exploité comme récepteur radiofréquence généraliste, d’analyser les diverses étapes de démodulation et de décodage, pour finalement conclure sur une exploration des méthodes de détection et de correction d’erreurs.
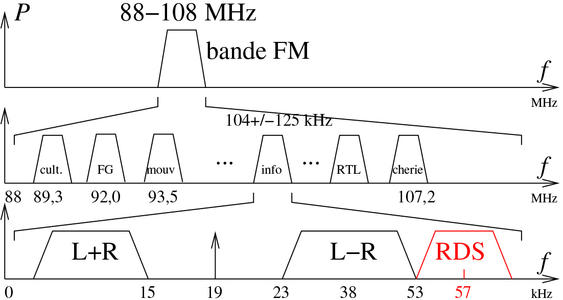
La bande commerciale FM, comprise entre 88 et 108 MHz, est divisée pour allouer une bande de 200 kHz à chaque station (Fig. 1, à gauche). Chaque station redivise chaque tranche du spectre radiofréquence qui lui est allouée en trois sous-segments : le son, avec d’abord la somme des signaux destinés à l’oreille droite et l’oreille gauche, puis si la transmission est en stéréo, la différence entre oreille droite et oreille gauche (afin qu’un récepteur mono puisse recevoir une station stéréo), et finalement un signal numérique – RDS (Radio Data System, Fig. 1 à droite) – comportant des informations telles que le nom de la station (Fig. 2), ou du texte libre tel que le titre d’une émission ou d’un morceau de musique. Un récepteur est informé qu’une émission est en stéréo par la présence d’un pilote – un signal périodique continu – à 19 kHz. La sous-porteuse de la transmission numérique se fait à 57 kHz générée comme trois fois le pilote si l’émetteur est stéréo, hypothèse que nous ne ferons pas au cours de nos traitements dans lesquels nous nous efforcerons de reproduire une copie locale de la sous-porteuse à 57 kHz. La bande passante du signal numérique est de l’ordre de 5 kHz.
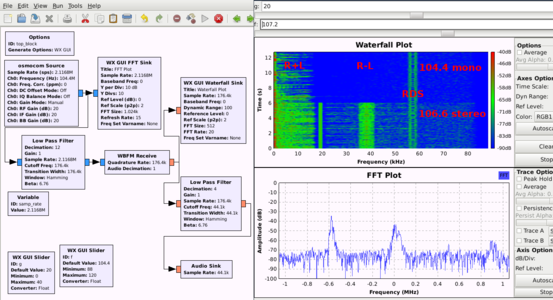
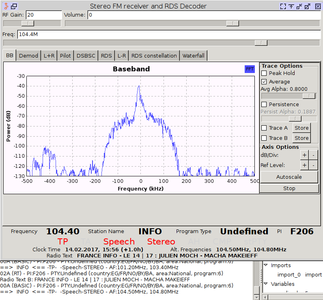
Fig. 1 : En haut : la bande de fréquence qui nous intéresse – RDS – se trouve à 57 kHz de la porteuse de chaque station FM : elle est donc accessible par transposition de fréquence, pour ramener le signal numérique en bande de base (autour de la fréquence nulle), après la démodulation FM de la station écoutée. En bas : les divers signaux émis par une station de la bande commerciale FM sont visibles sur le mode waterfall après le démodulateur WBFM. Nous avons changé la fréquence en milieu d’acquisition entre une station stéréo et une station mono, qui toutes deux émettent un signal d’identification RDS.
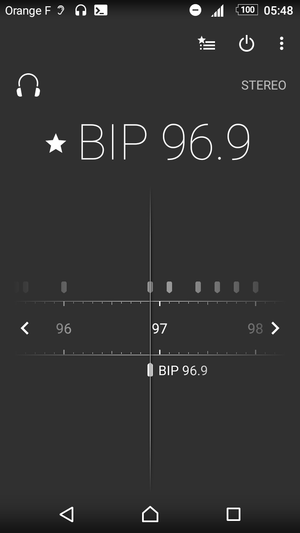
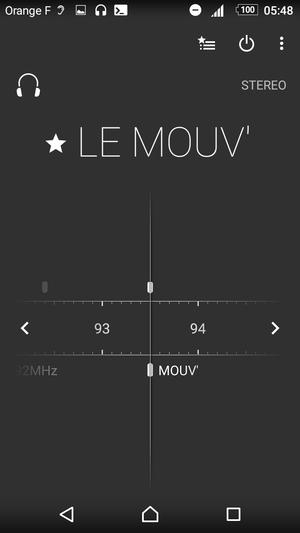
Fig. 2 : Réception de diverses stations FM commerciales, avec affichage du nom de la station tel que transmis par RDS. Noter que Le Mouv’ est parfois perçu comme stéréo, parfois comme mono, sans que cela empêche d’afficher son identifiant.
Un lecteur simplement désireux de lire le contenu des informations numériques ainsi transmises pourra se contenter d’utiliser un composant intégré qui se charge de tout le travail, par exemple chez ST le TDA7330 [1] ou TDA7478 (single chip RDS decoder), voire le récepteur FM intégré RDS5807 de RDA MicroElectronics [2] qui exploite dans la même veine un TEA5764 pour synchroniser un réseau de capteurs, bien que toutes ces références semblent obsolètes et inaccessibles chez les principaux fournisseurs. Ce faisant, nous n’aurons rien appris du mode d’encodage, de la nature des informations transmises, mais surtout de la méthode utilisée pour retrouver des bits corrompus lors de la transmission. Tous ces concepts seront appréhendés lors du décodage logiciel des trames, avec analyse étape par étape de la séquence suivie pour passer d’un signal radiofréquence modulé en fréquence (FM commerciale) à des phrases intelligibles. Comme d’habitude, cette compréhension permettra de mieux appréhender des utilisations malicieuses du protocole ou de le détourner de son usage initial [1][3][4]. Tous les prototypages s’aideront de l’outil d’implémentation de traitement du signal GNURadio [5] pour acquérir le signal, suivi d’une mise en œuvre des algorithmes de décodage sous GNU/Octave [6] en s’efforçant de revenir aux bases, et sans passer par des bibliothèques de haut niveau telles que la communication toolbox [7] qui nous cacheraient la compréhension détaillée du flux de traitement.
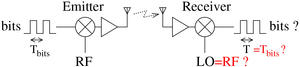
Le décodage d’un flux de communication numérique sur porteuse radiofréquence nécessite toujours de résoudre les problèmes de synchronisation d’oscillateurs distants, à savoir l’oscillateur radiofréquence qui génère la porteuse sur laquelle l’information est transmise, et le débit de communication. Le récepteur transpose le signal radiofréquence en bande de base par le mélange avec un oscillateur local LO (Fig. 3). La phase qui encode l’information sur la porteuse ne sera exploitable que si une copie de l’oscillateur de l’émetteur – RF – est générée en local : LO est asservi sur RF selon des mécanismes qui seront décrits plus bas (section 2). Une fois que des bits seront obtenus en sortie de la démodulation, l’information numérique est échantillonnée périodiquement pour extraire l’état de chaque bit et former des trames. Ici encore, le rythme du décodage n’a aucune raison d’être synchronisé avec le rythme de génération des données : même si la valeur nominale du débit de communication est connue, un écart entre l’oscillateur qui génère les données numériques sur l’émetteur et celui qui cadence l’échantillonnage sur le récepteur finira au bout d’un moment par induire une désynchronisation. Ici encore, un asservissement sera nécessaire, qui sera décrit en section 7.
Fig. 3 : Problème de synchronisation des oscillateurs distants qui portent le signal et cadencent le débit de donnée. Le décodage ne sera fonctionnel que si les deux oscillateurs du récepteur – LO et échantillonnage de l’état de l’information numérique – sont asservis sur leurs homologues du côté de l’émetteur.
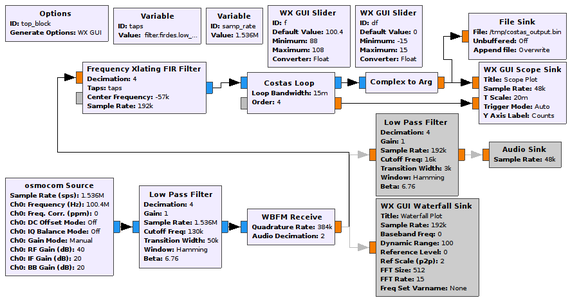
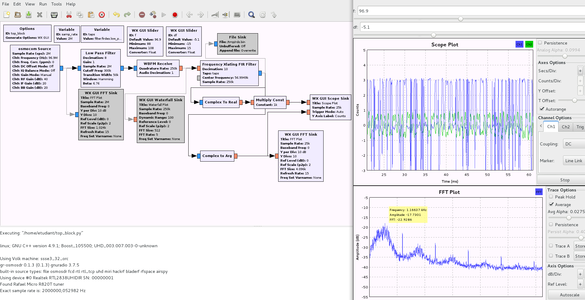
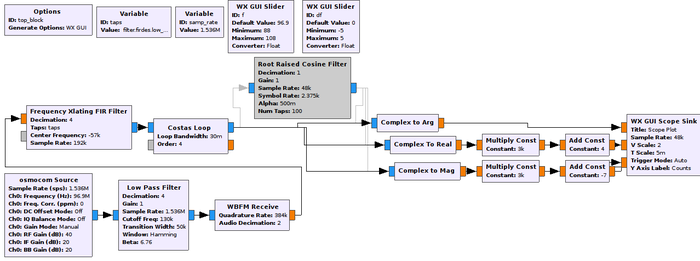
Dans la séquence d’acquisition par GNURadio proposée en figure 4 qui vise à démoduler un signal dans la bande FM, en extraire la sous-porteuse comportant les informations numériques, et stocker le résultat dans un fichier binaire pour post-traitement, deux caractéristiques déterminent la qualité de la démodulation et la puissance de calcul nécessaire : les fréquences de coupure pour isoler la bande qui nous intéresse par filtrages successifs, et les décimations (ne prendre qu’un point sur N pour une décimation d’un facteur N) pour réduire le débit de données. Un récepteur de télévision numérique terrestre (DVB-T) basé sur le convertisseur analogique-numérique RTL2832U travaille nécessairement avec une fréquence d’échantillonnage comprise entre 1,5 et 2,4 MHz, soit bien plus que l’encombrement spectral d’une bande FM. Notre première tâche consiste donc à décimer ce flux de données pour n’avoir qu’environ 200 kéchantillons/s, respectant ainsi l’encombrement spectral d’une unique station FM. Cependant, la décimation ne peut se faire sans avoir atténué le signal des autres stations se trouvant à plus de 100 kHz de la bande qui nous intéresse, sinon leurs signaux se ramèneront dans la bande de base par repliement spectral [8] lors de la décimation. Par conséquent, nous commençons par un filtre passe-bas qui isole la station d’intérêt, puis décimons suffisamment pour réduire le flux à un débit de l’ordre de 200 kéchantillons/s. L’autre intérêt de la décimation est de permettre des transitions des filtres en aval plus nettes avec un même nombre de coefficients : en effet, la bande de transition d’un filtre est de l’ordre de la fréquence d’échantillonnage divisée par le nombre de coefficients. Ainsi, il est très lourd de calculer un filtre présentant une bande étroite à taux d’échantillonnage élevé, tandis que le même résultat s’obtient à ressource de calcul réduite en décimant judicieusement auparavant. Les 200 kéchantillons/s que nous venons d’obtenir portent toutes l’information qui encode la station FM commerciale qui nous intéresse : le bloc WBFM démodule le signal et fournit un flux de données qui peut lui aussi être décimé si seule la composante audiofréquence nous intéressait. Cependant, nous désirons décoder le signal RDS qui se trouve autour d’une sous-porteuse à 57 kHz, donc nous ne pouvons pas encore décimer, mais devons attendre de transposer la sous-porteuse de 57 kHz vers la bande de base par un Xlating FIR Filter [9] pour une fois de plus décimer, les 200 kéchantillons/seconde étant bien trop rapides pour les quelques kHz occupés par le signal numérique. Ainsi, le filtre FIR (filtre à réponse impulsionnelle finie) est conçu pour isoler le signal numérique sur une bande de quelques kHz et rejeter les autres composantes spectrales avant la décimation qui fournit un débit de données raisonnable pour décoder le signal numérique. Attention : la fréquence d’échantillonnage qui définit le FIR doit être la fréquence d’échantillonnage en entrée du Xlating FIR Filter, donc tenir compte de la décimation du premier filtre passe-bas et éventuellement du démodulateur FM. Dans notre cas, ce filtre (variable taps qui sera appelée dans le champ du même nom dans le Xlating FIR Filter) est défini par l’expression Python : filter.firdes.low_pass_2(1, samp_rate/8, 2000, 500, 60) pour dire que le filtre passe-bas a décimé d’un facteur 8, pas de décimation sur la démodulation WBFM, 2 kHz de fréquence de coupure et une transition sur 500 Hz. À l’issue de ce traitement, nous avons isolé la bande du signal RDS que nous désirons décoder.
Fig. 4 : À gauche : séquence de traitements d’un signal acquis dans la bande FM commerciale. Le mode waterfall (en bas à droite) montre clairement le pilote à 19 kHz et le RDS autour de 57 kHz. En haut à droite : en l’absence de synchronisation sur la porteuse (bleu), la phase qui encode le signal comporte encore une dérive linéaire de pente égale à l’écart entre la fréquence nominale de 57 kHz et la fréquence de l’oscillateur local numérique. L’application de la boucle de Costas (vert) élimine cet écart de fréquence : la phase représente des bits exploitables (en bas à droite en bleu).
RDS est actuellement accessible pour les utilisateurs de GNURadio au travers du module gr_rds, initié par Dimitrios Symeonidis [11] et maintenu à ce jour par Bastian Bloessl [12]. Reprendre un code existant peut fournir de l’inspiration, voire valider le bon fonctionnement de l’installation matérielle de réception, mais n’amène rien à la compréhension de la mise en œuvre des diverses étapes de démodulation et de décodage, que nous tenterons d’appréhender ici. Les divers contributeurs à gr_rds ne semblent pas avoir cru bon de détailler le fonctionnement de leur code dans une documentation ou publication associée, rendant la lecture du code source quelque peu fastidieuse, surtout pour les novices que nous sommes à ce stade de l’analyse du protocole. En effet, nous verrons que plusieurs couches OSI devront être parcourues avant d’obtenir un message intelligible, et cette séparation claire dans la documentation technique n’en reste pas moins confuse au premier abord par le report en annexe de la couche 2 tandis que le texte principal aborde les couches 1 et 3. Par ailleurs, tous les codes consultés sur le Web s’inspirent d’une implémentation des codes correcteurs d’erreur sous forme de registre à décalage, une solution naturelle pour l’électronicien, mais peu intuitive pour le traiteur de signaux qui exprime plus naturellement un problème sous forme matricielle. Nous proposerons donc une implémentation qui nous semble originale de la synchronisation de trames et de la correction d’erreurs que nous n’avons pas trouvée dans les documentations consultées au cours de cette étude, mais dont la concision semble favoriser la compréhension de concepts un peu complexes à appréhender au niveau de la porte logique.
Le mode de modulation est décrit de façon quelque peu confuse dans les documents techniques décrivant la norme RDS [13], en expliquant qu’une modulation d’amplitude sans porteuse [14]est générée par deux signaux en opposition de phase [13, section 1.4]. L’alternative, de considérer l’information comme portée par une modulation en phase de ±90°, change complètement notre stratégie de démodulation (voir annexe A). Alors qu’une modulation d’amplitude ne nécessite qu’une estimation grossière de la porteuse et un redressement/filtrage dans une bande suffisamment large pour inclure tout écart entre fréquence de l’émetteur et fréquence de l’oscillateur local du récepteur, une modulation de phase nécessite une stratégie pour reconstruire une copie locale de l’oscillateur de l’émetteur avant modulation, qui sera l’objet de la première partie de ce document.
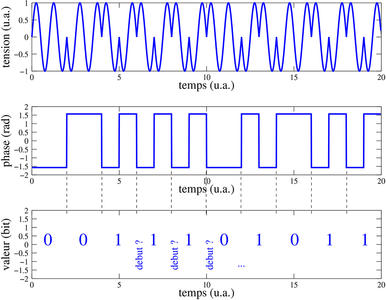
Ayant obtenu des signaux – phase du signal – représentatifs d’une séquence de bits, nous nous efforcerons de regrouper ces bits en trame (Fig. 5). Étant donné que les bits sont transmis continuellement, nous devrons trouver une stratégie pour identifier un début de trame dans ce flux continu de bits. Finalement, ayant synchronisé notre récepteur sur le flux de bits, nous en interprèterons le contenu et verrons que des résultats cohérents sont obtenus. Nous constatons sur la figure 4 - qui consiste en un flux de traitement dans GNURadio pour démoduler une bande FM, en extraire l’information à 57 kHz de la porteuse et en extraire phase et amplitude - que la phase ne présente pas une structure visuellement associée à une séquence de bits. Le spectre de la phase nous indique que la piste de la modulation de phase à deux états séparés de 180° (BPSK – Binary Phase Shift Keying [15][16]) est la bonne : le spectre est étalé autour de 1200 Hz par la modulation de phase, mais la raie fine à 2375 Hz confirme que tout processus non-linéaire qui a produit le carré du signal introduit un signal spectralement pur, comme on peut s’y attendre avec le BPSK.
Fig. 5 : Séquence de décodage des trames : le passage du milieu au bas est conforme au Tab. 2 de [13]avec une conversion respectant le codage de Manchester différentiel.
1. Transposition et reproduction de la porteuse
Nous avions déjà vu en étudiant les signaux GPS [15] que le mode de modulation BPSK, caractérisé par deux états de la phase 0 et 180° pour représenter deux états des bits 0 et 1 par exemple, s’exploite en produisant une copie locale de l’oscillateur de l’émetteur sans modulation. Pour ce faire, nous avions considéré diverses approches incluant une extraction de phase à partir des données complexes I et Q issues du démodulateur en exploitant une fonction insensible aux rotations de phase de 180° (atan de GNU/Octave qui ne tient pas compte du quadrant dans lequel se trouvent I et Q individuellement, mais ne s’intéresse qu’à Q/I, contrairement à atan2 qui exploite chaque composante séparément et restitue la phase en tenant compte des rotations de 180°). Une alternative avait été de passer le signal reçu au carré (le multiplier par lui-même) afin de retirer la modulation de phase, puisque le passage au carré d’un signal harmonique génère le double de son argument, et 2 x 180° = 360 = 0 [360] (Fig. 6 en bas à droite). Le résultat, de fréquence double de la fréquence de la sous-porteuse, produit une copie locale de la source émise avant modulation par passage dans un compteur qui divise par deux sa fréquence. Cette dernière méthode est implémentée dans le bloc de traitement dit de la boucle de Costas [15], qui fournit d’une part le signal corrigé de l’erreur entre l’oscillateur émetteur et l’oscillateur local du récepteur, et d’autre part une estimation de cette erreur.
Notre stratégie de traitement consiste donc à :
- transposer le signal à 57 kHz de la sortie du démodulateur FM pour amener l’information numérique en bande de base, par exemple avec Xlating FIR Filter de GNURadio, en exploitant un oscillateur local libre. Alors que nous devons habituellement expérimenter avec la fréquence de transposition de ce bloc avant de nous rappeler s’il faut indiquer + ou - la fréquence pour amener le signal en bande de base (autour de la fréquence nulle), le problème ne se pose exceptionnellement pas dans ce cas où la sortie du démodulateur FM est un signal réel, donc dont le module de la transformée de Fourier est pair. L’information qui nous intéresse est autour de +57 kHz, mais aussi autour de -57 kHz : les deux solutions sont acceptables et fournissent le même résultat ;
- extraire la phase du signal résultant, phase qui présente deux composantes : l’information encodée dans la phase à ±90°, et la dérive linéaire due à l’écart de fréquences des oscillateurs de l’émetteur et du récepteur Δf ;
- fournir ce signal à une boucle de Costas qui estime Δf et la compense.
La modulation se fait à 1187,5 bits/s, et nous verrons plus loin qu’il s’agit d’un mode d’encodage différentiel qui nécessite donc au moins 1187,5 x 2 = 2375 Hz, déterminant donc la largeur du filtre du Xlating FIR Filter ainsi que son facteur de décimation. Nous viserons d’avoir au moins 5 points par période, soit au moins 11875 échantillons/s.
Fig. 6 : À gauche : réception FM, suivi de l’extraction de la sous-bande RDS. En l’absence de synchronisation sur la porteuse, la phase varie trop vite pour ressembler à un signal numérique.
2. Du signal en bande de base aux bits
Nous supposons maintenant avoir un flux représentatif d’un signal numérique. Nous voulons extraire de la phase une séquence de bits. Dans un premier temps, nous apprenons [13, section 1.6]que le signal est encodé de façon différentielle (s’apparentant aussi à un codage Manchester différentiel [16]), confirmé par notre observation que la phase varie deux fois plus vite que le taux attendu de 1187,5 Hz. Nous allons donc seuiller la phase après en avoir retranché la valeur moyenne – en considérant qu’une phase inférieure à 0 est une valeur nulle sinon la valeur du bit est 1 (bit slicer dans GNURadio), et une fois la valeur saturée obtenue, nous appliquons la condition que deux phases adjacentes de phase de même valeur se traduisent par un bit à 0 et si une transition est observée, le bit résultant est égal à 1. Les deux subtilités ici tiennent d’une part à se tromper de front lors de la recherche du demi-bit permettant de commencer l’analyse – dans ce cas toutes les paires adjacentes présentent une transition (cas du codage Manchester) – et d’autre part de recaler le débit de communication si le rythme des données n’est pas calé sur notre horloge locale. Nous recherchons donc la première transition (debut), puis avançons dans la séquence de données en recherchant au quart de la période après la transition et aux trois quarts (second état). En fonction de l’égalité ou l’inégalité de ces deux états (s1 et s2), nous déduisons so le bit de sortie, comme OU exclusif de ces deux bits, ce qui correspond aussi à une somme modulo 2, expression plus naturelle pour GNU/Octave il nous semble.
fe=24000; % freq. d'echantillonnage -- cf sink gnuradio
bitlength=fe/1187.5 % 1 bit = 2 transitions
bitsur2=bitlength/2;
bitsur4=bitlength/4; % half transition width
r=read_complex_binary('costas_output100p4_24kHz.bin');% Virgin
p=angle(r);
p=conv(p,ones(4,1)/4);p=p(2:end-2); % filtre passe-bas de puissance unitaire
p=p(2000:end); % time needed for costas to lock
p=p-mean(p);
k=find(diff(p(11:1000))>0.5);debut=k(1)+10; % indice premiere transition
s=(p>0);s=s-mean(s); % binary slicer
l=debut;
for k=1:length(s)/bitlength-bitlength
s1(k)=s(floor(l+bitsur4)); % premier etat
s2(k)=s(floor(l+bitsur2+bitsur4)); % 2e etat 1/2 periode plus tard
l=l+bitlength; % on avance d'une periode
transition=abs(diff(s(floor(l-2):floor(l+1))));
[val,pos]=max(transition);
if (val>0) % tentative de synchronisation
if (pos==3) l=l+1;end % on est un peu en avance
if (pos==1) l=l-1;end % on est un peu en retard
end
end
s1=(s1>0); s2=(s2>0);
so=mod(s1+s2,2); % 2 bits -> 1 etat
La chaîne de traitement GNURadio fournit un signal synchronisé sur la porteuse radiofréquence, mais ne traite pas le problème de la synchronisation du débit de données numérique (intervalle de temps entre deux bits). Dans l’exemple ci-dessus, une approche naïve consiste à observer si la transition d’un bit à l’autre se produit une période avant ou après le moment attendu, et si c’est le cas de décaler un peu le compteur qui s’incrémente le long de la trame (variable l). Une façon plus rigoureuse, mais plus complexe, est discutée en annexe B, en exploitant les blocs de traitement adéquats de GNURadio que sont le MPSK Decoder ou Clock Recovery MM, tels que présentés dans http://gnuradio.4.n7.nabble.com/Clock-Recovery-MM-documentation-td55117.html. Bien que cette méthode de synchronisation du flux numérique n’ait pas été exploitée au cours de la rédaction de cet article, induisant les études sur la capacité de correction des bits corrompus lors du décodage des trames par le code correcteur d’erreur qui vont suivre, sa mise en œuvre tardive rend le décodage extrêmement efficace tel qu’illustré en fin d’annexe B.
3. Des bits aux messages : synchronisation
Nous observons une séquence continue de bits. Cependant, une trame commence et finit à certaines frontières que nous devons déterminer : nous avions vu par exemple que dans ACARS [17]chaque phrase commence par un préambule qui permet par ailleurs de synchroniser le récepteur avec le débit de données de l’émetteur. Dans le cas de RDS, le mode de recherche du début est décrit dans la norme [13, annexe C] : placer ce sujet aussi loin dans la documentation rend sa lecture quelque peu complexe puisqu’elle encourage à se lancer dans le décodage des trames [13, section 2]avant de s’être assuré de l’intégrité des trames. Nous apprenons entre ces deux sections que toute trame RDS est formée de 16 bits de données suivies d’un code correcteur d’erreur de 10 bits (pour une alternative, voir l’annexe C). L’information de base est donc un bloc de 26 bits, et 4 blocs successifs de types différents – nommés A, B, C, D – se suivent pour former une trame. Le mode de synchronisation [18, chapitre 12]consiste donc à :
- prendre 26 bits adjacents dans la séquence acquise ;
- calculer le code correcteur d’erreur (voir ci-dessous) pour ces 26 bits en supposant qu’il s’agit d’un bloc A ;
- si les 10 derniers bits de la séquence considérée correspondent au code correcteur d’erreur, il est envisageable que nous ayons trouvé la synchronisation, que nous validons en calculant le code correcteur du bloc suivant (B, 26 bits suivants) puis D (26 bits séparés de 78 bits de l’indice courant d’analyse). Si ces trois conditions sont vérifiées, nous avons très probablement trouvé un cas de synchronisation et donc le premier bit de la trame. Le bloc C a été sauté, car deux cas peuvent se présenter – C et C’ selon la nature du message – avec des syndromes différents, multipliant les cas à traiter ;
- si le calcul du code correcteur sur les 16 premiers bits ne donne pas la séquence des 10 derniers bits, il n’y a pas synchronisation : nous avançons d’un bit dans la séquence et nous recommençons la procédure.
Cette séquence doit finir par converger vers une condition où tous les 10 bits de fin de chaque bloc correspondent au code correcteur d’erreur des 16 bits qui précèdent. Si ce n’est pas le cas, le décodage des bits (étape précédente) a échoué, et il faut reconsidérer la conversion des données brutes de phase vers les données numérisées. Ce succès du décodage est la source de la synchronisation en temps proposée par [2]. Une fois le début du bloc identifié, le contenu de chaque bloc dépend de la nature du message : alors que le bloc A contient toujours un identifiant de la station (code PI, annexe C), le contenu des autres blocs change pour chaque type d’information transmise, tel que documenté dans [13, section 3].
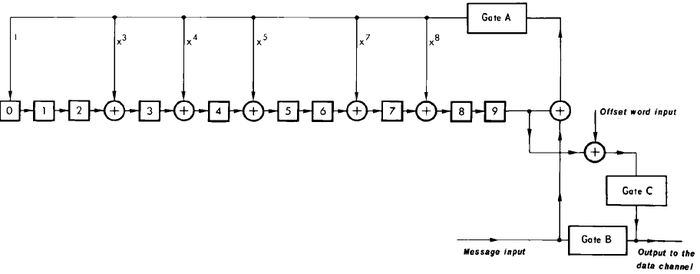
Un point clé de cette discussion tient au calcul du code correcteur d’erreur. Toutes les implémentations que nous avons trouvées exploitent un registre à décalage avec rétroaction (Linear Feedback Shift Register – LFSR), une représentation naturelle pour un FPGA ou un microcontrôleur programmé en assembleur [19], mais peu approprié à GNU/Octave qui exprime les problèmes sous forme matricielle (voir note). Afin de ne pas risquer d’être qualifié de plagiat – tous les codes libres consultés sur Internet et implémentés pour calculer le code correcteur sont du même acabit que https://github.com/bastibl/gr-rds/blob/master/lib/decoder_impl.cc#L69-L80 (Fig. 7) – nous proposons de calculer le code correcteur par son expression matricielle telle que proposée dans [13, section B.2.1] : une matrice H de 26 x 10 fournit la relation entre les données et chacun des bits du code correcteur d’erreurs.
Fig. 7 : Implémentation sous forme de registre à décalage du code correcteur d’erreur. Nous proposons l’alternative de précalculer les états possibles du code correcteur d’erreur pour l’implémenter sous forme d’opération matricielle, plus naturelle sous GNU/Octave. Chaque symbole « ⊕ » se comprend au sens binaire, comme un OU exclusif. Ce schéma est issu de [13, p.62].
Le passage de l’expression polynomiale du code correcteur d’erreur à l’expression matricielle ne saute pas forcément aux yeux au premier abord. Le principe de l’algèbre linéaire (expression matricielle) tient à décomposer le problème sur chaque élément de la base et de déduire la solution comme combinaison linéaire de chaque solution obtenue sur la décomposition du problème sur chaque élément de la base. Dans notre cas, la base du problème est un bit dans le message à 1 à la nième position et les autres bits à . Nous appliquons donc le calcul du code correcteur d’erreur à chaque vecteur [0 ... 0 1 0 ... 0] en déplaçant le 1 dans le vecteur, ce qui en expression polynomiale s’écrit xn. Le code correcteur d’erreur s’obtient comme reste de la division polynomiale [20] de xn, n ∈ [0..25] (les 26 positions possibles du bit dans le message émis) avec le polynôme représentant le code BCH [21, p. 251] x10+ x8 + x7 + x5 + x4 + x3 + 1 qui s’écrit sous GNU/Octave [1 0 1 1 0 1 1 1 0 0 1] (puissance la plus forte à gauche). Pour rappel, une division polynomiale s’effectue comme une division classique, avec le dénominateur multiplié par la puissance adéquate pour éliminer le terme de plus haute puissance du numérateur, et le reste calculé par soustraction de ces deux termes. La procédure se poursuit sur le reste jusqu’à atteindre une puissance inférieure à celle du dénominateur. Par exemple :
Le reste de la division polynomiale s’écrit sous GNU/Octave (et Matlab) comme [b, r] = deconv(N,D); avec N et D les vecteurs représentant respectivement les polynômes du numérateur et dénominateur, et r le reste de la division qui nous intéresse. Dans l’exemple précédent, [d, r] = deconv([1 0 1 1 1],[1 0 1]) donne d = 1 0 0 et r = 0 0 0 1 1. Ainsi la matrice G de [13] s’obtient par le script GNU/Octave suivant :
vecteur=[1 zeros(1,10)]; % premier element de la base : 1*x^{10}
polynome=[1 0 1 1 0 1 1 1 0 0 1]; % x^10+0+x^8+x^7+0+x^5+x^4+x^3+0+0+x
for k=1:16 % position du bit a 1
[a,b]=deconv(vecteur,polynome); % division polynomiale
mod(abs(b(end-9:end)),2) % modulo x^10
vecteur=[vecteur 0]; % element suivant de la base : ajout d'un 0
end
Comme la matrice identité à gauche de G place le bit de poids faible en bas, ce script calcule les lignes de la droite de G de bas en haut.
% p.75 US, 64 EU
sA2=[1 1 1 1 0 1 1 0 0 0]; % A= [0 0 1 1 1 1 1 1 0 0];
sB2=[1 1 1 1 0 1 0 1 0 0]; % B= [0 1 1 0 0 1 1 0 0 0];
sC2=[1 0 0 1 0 1 1 1 0 0]; % C= [0 1 0 1 1 0 1 0 0 0];
Cp= [1 1 0 1 0 1 0 0 0 0];
% sCp=[1 0 1 1 1 0 1 1 0 0];
sCp=[1 1 1 1 0 0 1 1 0 0]; % an495
D= [0 1 1 0 1 1 0 1 0 0];
sD2=[1 0 0 1 0 1 1 0 0 0]; % incoherent avec an495
% sD2=[0 1 0 1 0 1 1 0 0 0]; % an495
% p.74
H=[
1 0 0 0 0 0 0 0 0 0 ; % cette
0 1 0 0 0 0 0 0 0 0 ; % sous-
0 0 1 0 0 0 0 0 0 0 ; % matrice
0 0 0 1 0 0 0 0 0 0 ; % identite
0 0 0 0 1 0 0 0 0 0 ; % sera
0 0 0 0 0 1 0 0 0 0 ; % remplacee
0 0 0 0 0 0 1 0 0 0 ; % par
0 0 0 0 0 0 0 1 0 0 ; % eye()
0 0 0 0 0 0 0 0 1 0 ; % dans la
0 0 0 0 0 0 0 0 0 1 ; % suite
1 0 1 1 0 1 1 1 0 0 ;
0 1 0 1 1 0 1 1 1 0 ;
0 0 1 0 1 1 0 1 1 1 ;
1 0 1 0 0 0 0 1 1 1 ;
1 1 1 0 0 1 1 1 1 1 ;
1 1 0 0 0 1 0 0 1 1 ;
1 1 0 1 0 1 0 1 0 1 ;
1 1 0 1 1 1 0 1 1 0 ;
0 1 1 0 1 1 1 0 1 1 ;
1 0 0 0 0 0 0 0 0 1 ;
1 1 1 1 0 1 1 1 0 0 ;
0 1 1 1 1 0 1 1 1 0 ;
0 0 1 1 1 1 0 1 1 1 ;
1 0 1 0 1 0 0 1 1 1 ;
1 1 1 0 0 0 1 1 1 1 ;
1 1 0 0 0 1 1 0 1 1 ;
];
texte="";
station="";
debut=0
so=(1-so);
for k=1:length(so)-104
data1=(so(k:k+25)); % A
data2=(so(k+26*1:k+25+26*1)); % B
data3=(so(k+26*2:k+25+26*2)); % C(')
data4=(so(k+26*3:k+25+26*3)); % D
HI1=mod(data1*H,2);
HI2=mod(data2*H,2);
HI3=mod(data3*H,2);
HI4=mod(data4*H,2);
pa=findstr((sA2),(HI1));
pb=findstr((sB2),(HI2));
pc=findstr((sC2),(HI3));
pcp=findstr((sCp),(HI3));
pd=findstr((sD2),(HI4));
if (!isempty(pa) && !isempty(pb) && !isempty(pd))
printf("synchronisation\n");
end
end
Cet exemple, un peu volumineux compte tenu de la matrice de décodage H, effectue les opérations suivantes :
- pour chaque séquence de 104 bits consécutifs, nous découpons 4 blocs adjacents de 26 bits chacun (ll.47–50). Chaque bloc est supposé être formé de 16 bits de données suivis de 10 bits de code de correction d’erreur auquel ont été ajoutés les bits d’identification du bloc ;
- nous calculons le syndrome de 10 bits de chaque bloc de 26 bits par application du produit matriciel avec H (ll. 51–54) ;
- nous recherchons si le syndrome ainsi calculé correspond au syndrome du bloc correspondant (ll. 55–59). Si cette condition est vérifiée, le bloc est validé, et nous considérons être synchronisés si cette condition est vérifiée pour les 4 blocs consécutifs ;
- si un bloc ne vérifie pas un syndrome du code correcteur d’erreur égal à la valeur prévue, nous supposons ne pas être synchronisés : nous avançons d’un cran dans la séquence de bits acquise pour redéfinir une nouvelle séquence de 104 bits, et reprenons le calcul.
Le passage de G à H tel que fourni dans [13]n’est lui non plus pas trivial. Alors que le passage de G à une forme de H telle que l’intégrité d’un message x reçu se vérifie par H · x = 0 tel que proposé dans [21, p. 244]ou [22, p. 70]ne nécessite qu’une transposition de la partie non-identité de G, l’expression de la matrice de contrôle d’erreur fournie dans [13, p.63]ne respecte pas cette expression, mais place l’identité à gauche de la matrice de décodage. Le passage d’une expression à l’autre est illustré sur http://www.di-mgt.com.au/cgi-bin/matrix_stdform.cgi qui exploite l’algorithme de [22, p. 52, 71]pour passer de l’une (issue de la matrice d’encodage) à l’autre (dite standard) par combinaison linéaire et permutation des lignes ou colonnes. D’après le site web sus-cité, nous passons de l’expression de H fournie dans [13, p. 63]
Input:
1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1
0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1
0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 1 0 1 1 1 1 1 0
0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 1 0 0 0
0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 1 0 0
0 0 0 0 0 1 0 0 0 0 1 0 1 0 1 1 1 1 1 0 1 0 1 0 0 1
0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 0 1 1 0 0 1 1
0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 0
0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1
0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1
à celle issue de [21, p. 244]où le morceau à droite de l’identité dans G est transposé (la colonne de gauche ci-dessous est effectivement la fin de la première ligne de G par exemple)
0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0
0 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0
0 1 1 0 0 0 1 1 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0
1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0
1 1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 0
1 0 0 0 1 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 0 1 0 0 0 0
0 0 1 1 1 0 1 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0
1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0
1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0
1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1
par cette série de transformations (noter le passage de la sous-matrice identité de gauche à droite de la matrice H).
4. Interprétation des messages
Le plus difficile est fait : nous avons une séquence de bits, dont nous sommes garantis de l’intégrité par calcul du code correcteur d’erreur, il ne reste plus qu’à interpréter les divers messages, en remplaçant le contenu des lignes 60–62 de l’exemple précédent. Toutes les transactions se font avec le bit de poids fort (MSB) transmis en premier. Nous nous sommes limités à quelques exemples simples et représentatifs pour garder le code court : nom de la station, horloge (jour/heure/minute) ou texte libre. Comme nous voulions pouvoir identifier la station en cours de réception, le premier type de bloc décodé est 0A ou 0B tel que défini par les 4 premiers bits du bloc B : si les 4 premiers bits du bloc B sont nuls, alors le bloc D contient des caractères ASCII qui contiennent le nom de la station FM émettrice. Le bloc B est le deuxième bloc dont les données sont stockées dans la variable data2 dont nous interprétons le contenu comme deux caractères ASCII, MSB en premier, consécutifs :
puissances=2.^[7:-1:0]'; % 128 64 32 6 8 4 2 1
if (!isempty(pa) && !isempty(pb) && !isempty(pd))
if ((data2(1:4)*puissances(end-3:end))==2) % texte RDS
texte=[texte char(data3(1:8)*puissances)] % 2chars en C
texte=[texte char(data3(9:16)*puissances)]
texte=[texte char(data4(1:8)*puissances)] % 2chars en D
texte=[texte char(data4(9:16)*puissances)]
end
if (sum(data2(1:4))==0) % nom station
station=[station char(data4(1:8)*puissances)];
station=[station char(data4(9:16)*puissances)]
end
if ((data2(1:5)*puissances(end-4:end))==2) % 1A
day=data4(1:5)*puissances(end-4:end);
heure=data4(6:10)*puissances(end-4:end);
minute=data4(11:16)*puissances(end-5:end);
printf("temps1A %d %d %d\n",day,heure,minute);
end
if ((data2(1:5)*puissances(end-4:end))==8) % 4A
day=data2(15:16)*2.^[16:-1:15]'+data3(1:15)*2.^[14:-1:0]';
heure=data3(16)*2^4+data4(1:4)*puissances(end-3:end); % UTC
minute=data4(5:10)*puissances(end-5:end);
offset=data4(12:16)*puissances(end-4:end); % *30 min->local
printf("temps4A %d %d %d %d\n",day,heure,minute,offset);
end
else % printf(".");
end
end
printf("\n");
On notera la petite subtilité dans la conversion du tableau de bits en nombre par le produit scalaire (et non terme à terme) de data et puissance, ce dernier contenant les puissances de 2 de 128 à 1 (bit de poids le plus fort en premier).
Le résultat de ce traitement, pour des fréquences reçues à Besançon, est de la forme
station = IRN VIRGIGIN GIGIGIN GIN GIIRGIIRGIN VGI VIR
pour 100,4 MHz,
texte = ES (FEAT. GUCCI MANE) MOUVAE SREMMURD - BLACK BEAT(FEAT. GECCI MANE) MOUV',
RAE SREMMURD - BLACK BEAT(FEAT. G]CCI MANE) MOUVAE SREMMERD - BLACK BEATLES (FEAT. G MAN MOUV'( RAE
station = LEOUOU MLEV'V' MOULE MOUV'OUV'LE MV'LEOUV'LE MOUV' MOUV'LE MOUV'LEV'LE MOUV'LEOUV'LE MOULE MOULEV' MOUV'
MOUV'LE MOUV'LE MV'LE MOUV'LE MOUV'LE MV'LE MOUV'LEOUV'LEOULE MV'LE MOUV
pour 93,5 MHz, et
station = .9.9P BI.996.9BIP BI96BIP .9BI96.9P 96.9BIBI.9BI.996BIP .9BI.9BIP
pour 96,9 MHz, qui laisse penser que nous avons enregistré des signaux de Virgin, Le Mouv’ et BIP. Finalement, Rire & Chanson sur 91.0 se traduit par :
station = ELLI& E & RIR RE & RIRE & RE & RIR& R SLI SELLIG SELLIG SELLIG SELLI RIRE & RIRE & RIRE &
RIRE & RIRE & RIRE RIRE R& IRE & IR R
Sellig semble être un humoriste donc son nom dans le titre de la chaîne n’est pas improbable. Plus intéressant, France Info nous donne :
texte = N MOCH - SUR(LA CART FRAFRANCE INFO 14 : JULIEN MOCH - SUR LA CARTE DE FRAFRANCE INFO - LE| 17 : JULIEN
MOCH - SUR LA CARTE DE FRANCE FRANKE INFO - LE 14 | 17 : JULIEC@ - SUR LA CARTE DE FRANCE - LE 14 | 17 : JN MOCH -
SUR LA Cï£RTE DE FRACE INFO - LE 14 | 17 : JULIE
station = FO INFO FO INFOINININFO INFO FO INFO FO INFO INFO FO INFO
INFO IN INFO INFO INFO INFO INFO INFO INFO IN INFO INFO INFO FO INFO
FO INFO INFO INFO IN INFO INFO INFO FO
qui diffuse, en plus du titre de la chaîne, un texte libre annonçant l’émission en cours.
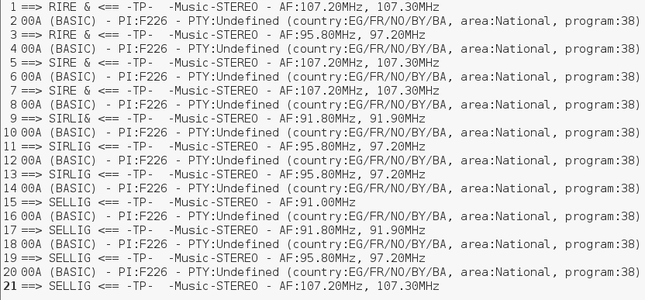
Sans être parfaites, ces trames démontrent que le concept est convenablement implémenté, en accord avec les résultats fournis par gr_rds (Fig. 8).
Fig. 8 : En haut, gr_rds en action sur France Info : la présentation est à peine plus attractive que l’exécution d’un script dans GNU/Octave et les données affichées sont sensiblement les mêmes. Nous notons à l’exécution que le nom de la station et le texte libre s’accumulent petit à petit, en accord avec la difficulté que nous observons d’obtenir une trame complète valide. En bas : la sortie de gr_rds sur Rire & Chanson, confirmant l’inclusion de l’auteur de l’émission en cours dans le titre de la station.
5. Correction d’erreur
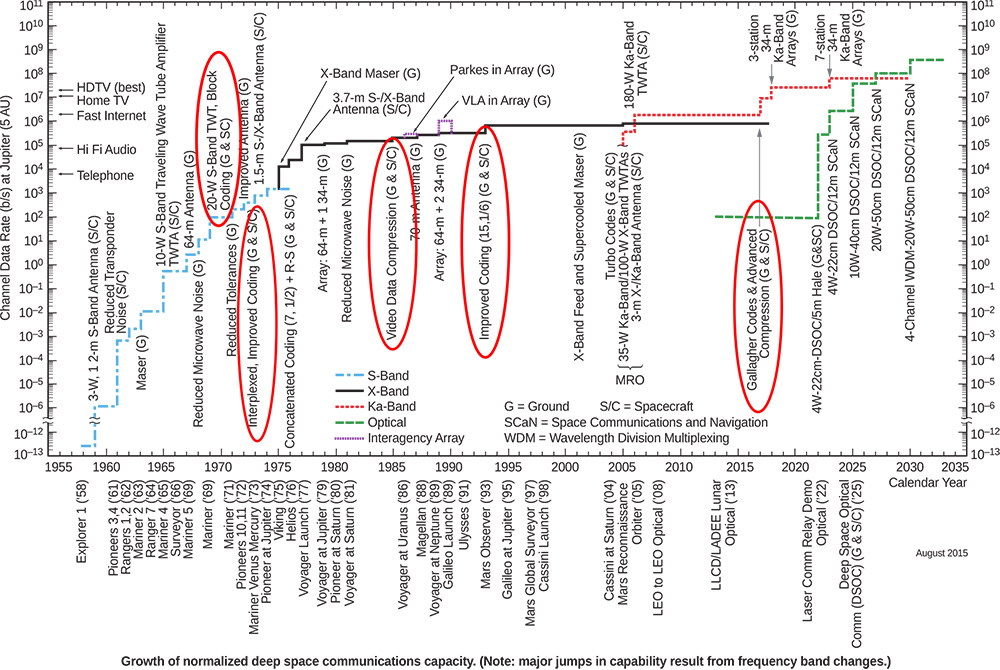
Nous avons décodé les messages issus de RDS après nous être synchronisés pour aligner les phrases sur le flux continu de bits, que pouvons-nous vouloir de plus ? Le code correcteur d’erreur de 10 bits ajouté en fin de chaque message de 16 bits n’a pour le moment été exploité que pour la synchronisation et garantir l’intégrité des transactions. Le signal RDS est bruité, et un certain nombre de trames sont éliminées de l’étude parce que leur code correcteur ne correspond pas aux attentes. Pouvons-nous améliorer le rendement de la réception en tentant de corriger les erreurs grâce à la redondance introduite par le code correcteur d’erreur [23], démarche qui a contribué à la croissance du débit de communication dans les sondes spatiales (Fig. 9) [24] ? Cela nous ramène en marche arrière par rapport au paragraphe précédent, à la couche 2 de la hiérarchie OSI, mais donne l’opportunité de se confronter à une étude empirique de l’implémentation des codes correcteurs d’erreur.
Le code implémenté permet non seulement d’identifier une corruption du message, mais en plus d’identifier quel bit a été modifié : un code de Hamming [15, chapitre 8] est capable d’une telle correction pour une unique erreur. Un code BCH [21, page 252][22, chapitre 11] est une extension qui permet de corriger plus d’un bit : ici, le code proposé permettra d’aller jusqu’à la correction de deux bits corrompus lors de la transmission.
Fig. 9 : Évolution de la bande passante de communication des sondes spatiales.
5.1 Une erreur
L’annexe C de [13]nous explique que le code correcteur d’erreur est implémenté, lors de l’émission, comme une combinaison linéaire (somme modulo 2, ou XOR) des bits à émettre.
Une transformation linéaire s’implémente soit de façon logique par un registre à décalage avec des points de ponction pour alimenter les portes XOR (Fig. 7), mais comme nous prototypons sous GNU/Octave, nous continuons à exploiter l’approche matricielle [21, p. 244] : une matrice de 16 x 10 calcule les 10 bits de sortie compte tenu des 16 bits d’entrée. Nous avons vu que nous ajoutons un identifiant de bloc pour la synchronisation à ce code de correction d’erreur : le message transmis comprend donc les 16 bits de données suivis des 10 bits de correction sommés au code de bloc. En terme GNU/Octave, cela s’écrit :
A= [0 0 1 1 1 1 1 1 0 0]; % A block emission
data=[0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1]; % JM
G=[0 0 0 1 1 1 0 1 1 1; % 16x10: message emis
1 0 1 1 1 0 0 1 1 1;
1 1 1 0 1 0 1 1 1 1;
1 1 0 0 0 0 1 0 1 1;
1 1 0 1 0 1 1 0 0 1;
1 1 0 1 1 1 0 0 0 0;
0 1 1 0 1 1 1 0 0 0;
0 0 1 1 0 1 1 1 0 0;
0 0 0 1 1 0 1 1 1 0;
0 0 0 0 1 1 0 1 1 1;
1 0 1 1 0 0 0 1 1 1;
1 1 1 0 1 1 1 1 1 1;
1 1 0 0 0 0 0 0 1 1;
1 1 0 1 0 1 1 1 0 1;
1 1 0 1 1 1 0 0 1 0;
0 1 1 0 1 1 1 0 0 1];
mI=mod(data*G,2)
mI=mod(mI+A,2); % ajout de A
envoi=[data mI]
Si tout se passe bien, ce message 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 1 0 1 0 1 0 qui contient encore les deux caractères ASCII JM est transmis, et reçu sans corruption de bit, donc le décodage que nous avons vu s’obtient côté récepteur par :
% p.75 US, 64 EU
sA2=[1 1 1 1 0 1 1 0 0 0]; % syndrome de reception
% p.74
H=[
eye(10); % matrice identite
1 0 1 1 0 1 1 1 0 0 ;
0 1 0 1 1 0 1 1 1 0 ;
0 0 1 0 1 1 0 1 1 1 ;
1 0 1 0 0 0 0 1 1 1 ;
1 1 1 0 0 1 1 1 1 1 ;
1 1 0 0 0 1 0 0 1 1 ;
1 1 0 1 0 1 0 1 0 1 ;
1 1 0 1 1 1 0 1 1 0 ;
0 1 1 0 1 1 1 0 1 1 ;
1 0 0 0 0 0 0 0 0 1 ;
1 1 1 1 0 1 1 1 0 0 ;
0 1 1 1 1 0 1 1 1 0 ;
0 0 1 1 1 1 0 1 1 1 ;
1 0 1 0 1 0 0 1 1 1 ;
1 1 1 0 0 0 1 1 1 1 ;
1 1 0 0 0 1 1 0 1 1 ;
];
mIr=abs(mod(envoi*H,2)-sA2)
et le message reçu mIr doit donner 0 après soustraction du syndrome correspondant au bloc A, nommé ici sA2. Cette petite expérience numérique valide le bon fonctionnement du décodage des messages.
Supposons maintenant qu’entre l’émission et la réception, une erreur survienne :
N=3;envoi(N)=1-envoi(N); % introduction d'erreurs
Pouvons-nous faire mieux que rejeter le paquet ? En affichant le résultat du calcul du syndrome, nous constatons qu’en insérant une erreur sur le troisième bit, le syndrome nous indique :
mIr = 0 0 1 0 0 0 0 0 0 0
qui dit bien que le troisième bit est corrompu. Cela correspond au fait que les 10 premières lignes de H forment une matrice identité. De façon générale, une erreur sur le Nième bit se détecte par un syndrome égal à la ligne N de H. En effet, une erreur peut survenir sur n’importe quel bit des 26 bits du message : si une erreur survient sur le bit 25 :
N=25;envoi(N)=1-envoi(N); % introduction d'erreurs
nous obtenons :
mIr = 1 1 1 0 0 0 1 1 1 1
qui est bien l’avant-dernière ligne de H. La recherche du bit corrompu se généralise donc par
[num,ligne]=ismember(mIr,H,'rows')
% si non nul, c'est le motif de la ligne de la matrice ou` se trouve l'erreur
% si deux bits nuls, c'est la somme de ces deux lignes de la matrice
avec num nous indiquant si le syndrome a été trouvé comme ligne de H, et si c’est le cas, ligne nous indique quel bit a été corrompu. Nous améliorons donc notre capacité de décodage de RDS, avec par exemple 24 caractères en plus des 680 déjà acquis sur l’identification de Le Mouv’ (+4%), 9 caractères en plus des 79 déjà acquis pour Virgin (+11%) et 10 en plus des 60 pour BIP (+17%).
Quelques expérimentations avec les deux expressions de la matrice de décodage H constatées auparavant nous convainquent qu’elles fonctionnent de la même façon, puisque les propriétés du code sont conservées par permutation des lignes et colonnes. Ainsi, nous observons par
A= [0 0 1 1 1 1 1 1 0 0]; % A block emission
sA2=[1 1 1 1 0 1 1 0 0 0]; % syndrome de reception
data=[0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1]; % JM
G=[0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 ;
0 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 ;
0 1 1 0 0 0 1 1 0 0 1 1 0 0 0 1 ;
1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 ;
1 1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 ;
1 0 0 0 1 1 1 1 0 1 0 1 0 1 1 1 ;
0 0 1 1 1 0 1 1 1 0 0 1 0 1 0 1 ;
1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 ;
1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 ;
1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 ];
mI=mod(data*G',2); % on a pris transposee de G pour prendre moins de place
mI=mod(mI+A,2); % encodage du message
envoi=[data mI] % message + code (identit'e a gauche de G')
N=5;envoi(N)=1-envoi(N); % introduction d'une erreur
H1=[ % forme fournie dans document RDS => on en deduit le syndrome de A
1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 ;
0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 ;
0 0 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 1 0 1 1 1 1 1 0 ;
0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 1 0 0 0 ;
0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 1 0 0 ;
0 0 0 0 0 1 0 0 0 0 1 0 1 0 1 1 1 1 1 0 1 0 1 0 0 1 ;
0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 0 1 1 0 0 1 1 ;
0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 0 ;
0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 ;
0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 ];
H2=[ % forme issue de [I | tG] => on en deduit A (matrice de controle)
0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 ;
0 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 ;
0 1 1 0 0 0 1 1 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 ;
1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 ;
1 1 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0 0 ;
1 0 0 0 1 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 0 1 0 0 0 0 ;
0 0 1 1 1 0 1 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0 ;
1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 ;
1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 ;
1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 1 ];
res=mod(envoi*H2'-A,2) %
[tmp,col]=ismember(res,H2',"rows")
res=mod(envoi*H1'-sA2,2) % sA
[tmp,col]=ismember(res,H1',"rows")
qu’en encodant un message, y compris l’identifiant (optionnel dans ces expérimentations) de bloc, nous sommes capables d’une part de valider le transfert d’information sans erreur : commenter l’introduction de l’erreur en ligne 19 pour constater que le résultat des deux décodages, avec H1 ou H2, sont tous deux nuls. Par ailleurs, en cas d’introduction d’une erreur, le résultat est bien le contenu de la ligne d’indice égal au numéro du bit erroné.
5.2 Deux erreurs
Retrouver un bit corrompu fonctionne bien, et nous avons compris comment identifier quel bit est corrompu en recherchant la ligne de H qui contient le syndrome après décodage d’un message avec un bit qui a été modifié. Cependant, que se passe-t-il si deux bits sont corrompus ?
Une rapide petite expérience numérique nous met sur la voie :
N=2;envoi(N)=1-envoi(N); % introduction d'erreurs
N=5;envoi(N)=1-envoi(N); % introduction d'erreurs
se traduit par
mIr = 0 1 0 0 1 0 0 0 0 0
Deux bits sont désormais à 1 après décodage du syndrome, celui de la deuxième et de la cinquième ligne. L’analyse est donc triviale tant que deux des dix premiers bits ont changé : le numéro des bits modifiés apparaissent dans le syndrome calculé en réception, toujours parce que les 10 premières lignes de H forment la matrice identité. Ce concept se généralise en citant le cours [25] : « Suppose we wish to correct all patterns of t errors. In this case, we need to pre-compute more syndromes, corresponding to 0, 1, 2,... t bit errors. Each of these should be stored by the decoder. ».
Nous devons donc calculer une nouvelle matrice, déduite de H, que nous noterons m2r, qui contient tous les syndromes de 10 bits correspondant aux sommes de toutes les combinaisons possibles de 2 lignes de H. Une approche par boucle for, pas nécessairement la plus élégante pour GNU/Octave, mais qui a le bon goût de fonctionner, donne :
m2r=[0 0 0 0 0 0 0 0 0 0]; % seed
l=1;
for k=1:length(H)-1 % compute all combinations
for j=k+1:length(H)
m2r=[m2r ; mod(H(k,:)+H(j,:),2)];
solution(l,1)=k; % which line is to be corrected ?
solution(l,2)=j;
l=l+1;
end
end
m2r=m2r(2:end,:); % remove seed
Évidemment, m2r est beaucoup plus grande que H puisque cette fois nous avons tous les couples d’erreurs possibles représentés dans chaque ligne de la nouvelle matrice. Nous nous assurons que toutes les lignes sont uniques – propriété du code capable de corriger deux erreurs de communication :
for k=1:length(m2r)
[num,ligne]=ismember(m2r(k,:),m2r,'rows');
if (num>1)
printf("doublon %d ",num) % never twice the same row
end
end
ne renvoie par de réponse (question : pourquoi [m2runiq,m,n]=unique(m2r,'rows'); renvoie moins de lignes dans m2runiq qu’il n’y en a dans m2r, alors que toutes les lignes sont uniques ?).
Nous pouvons maintenant rechercher quelle paire de bits a changé lors de la transmission par
[num,ligne]=ismember(mIr,m2r,'rows')
if (num>0) solution(ligne,:),end % display which bits have flipped
et comme nous avions pris soin de placer dans solution le couple j et k des lignes de H qui ont été sommées pour donner la ligne de m2r, nous connaissons l’indice k et j des bits modifiés. En effet,
N=21;envoi(N)=1-envoi(N); % introduction d'erreurs
N=25;envoi(N)=1-envoi(N); % introduction d'erreurs
se traduit bien par
mIr = 0 0 0 1 0 1 0 0 1 1
num = 0
ligne = 0
num = 1
ligne = 314
ans = 21 25
dans laquelle nous constatons que la recherche du syndrome mIr dans la matrice H (une modification) ne donne pas de résultat (num=0), mais que la recherche dans m2r donne un résultat, avec le syndrome présent dans la 314ème ligne de m2r, qui a été calculée lorsque j=21 et k=25. Le décodage fonctionne bien. RDS n’annonce que la capacité à corriger 1 ou 2 bits corrompus lors de la transmission, nous arrêtons donc là notre étude du code correcteur d’erreurs.
Le nombre de bits qui peut ainsi être corrigé par un code est déterminé par le concept de distance de Hamming, qui se représente graphiquement comme la distance entre le « bon » message et le message corrompu reçu, en deçà de laquelle la correction est possible (http://fr.wikipedia.org/wiki/Code_correcteur).
La capacité de corriger des transmissions corrompues est au cœur du gain de débit de communication (Fig. 10), que ce soit dans une liaison avec les sondes spatiales lointaines (deep space network) [24]ou en liaison courte portée à faible consommation [26]. Ce survol rapide d’un exemple simple ouvre donc des perspectives d’approfondissement qui restent d’actualité : sans prétendre comprendre comment générer ces codes, l’expérimentation sur des données réelles avec un résultat concret fournit la motivation à approfondir les ouvrages plus théoriques sur le sujet tels que [21]et son excellente mise en relation de compression, cryptographie et correction d’erreurs.
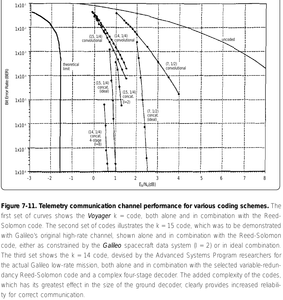
Fig. 10 : Évolution du taux d’erreur en fonction du rapport signal à bruit, pour divers types de codes correcteurs d’erreurs, reproduit de [24, Fig. 7-11, p. 477].
Conclusion
Nous avons analysé le protocole RDS, exploité pour la transmission numérique d’informations associée aux chaînes FM de la bande commerciale incluant le nom de la station ou la nature du programme, en partant de l’acquisition de l’information analogique depuis un récepteur de télévision numérique terrestre, puis extraction de l’information numérique sur la sous-porteuse à 57 kHz, avant d’extraire les trames (en ayant résolu la synchronisation des phrases) et d’en interpréter le contenu. Nous avons finalement abordé la correction d’erreurs pour constater que nous pouvions simuler des erreurs connues et les identifier. En appliquant cette méthode de traitement aux données reçues expérimentalement, nous avons pu retrouver plus de 10% de signaux exploitables additionnels par rapport au cas où nous ne traitions que les informations transmises dans leur intégralité.
Bien des développements seraient nécessaires avant que cette démonstration de principe ne puisse être considérée comme robuste pour un environnement en production, en particulier sur la synchronisation du décodage des trames transmises à 1187,5 bps de façon asynchrone, mais cela se ferait en alourdissant le code proposé au détriment de sa lisibilité. Il nous semble que la démonstration des principes de base de ce mode de modulation est explicite, avec des messages intelligibles et cohérents avec les informations transmises par chaque station. Cet exercice a nécessité environ 2 mois de travail pour aboutir : il s’agit donc d’un bon exercice pour se familiariser avec les diverses couches d’un protocole de communication, en allant de la couche matérielle à la couche session.
Un point décevant est l’absence de transfert précis de temps par ce médium. Nous n’avons reçu que peu de trames de datation (CT, groupe 4A) qui nous permettent de connaître la date et l’heure qu’avec une précision de ±0,1 s au début de chaque minute. Cette déficience sera bientôt corrigée avec le décodage logiciel de DCF77 que nous présenterons dans un autre numéro.
Une archive contenant les scripts GNU/Octave, configuration de GNURadio Companion et fichiers d’exemples, est disponible à http://jmfriedt.free.fr/lm_rds.tar.gz.
Remerciements
Je remercie Thomas Lavarenne pour avoir motivé cette étude par ses interrogations et des échanges constructifs, et Bastien Bloessl pour avoir exprimé l’opinion que le décodage de RDS est trivial [27], un commentaire inacceptable tant que ce protocole avait résisté à nos investigations. Ce défaut de compréhension est maintenant corrigé. G. Cabodevila a amélioré la qualité du code GNU/Octave lors de sa relecture, et É. Carry a clarifié un certain nombre de points. Bien que nous ayons acquis une copie papier de l’ouvrage de Dunod[21], les autres références ont été obtenues auprès de Library Genesis, http://gen.lib.rus.ec, une source indispensable pour nos recherches.
Annexe A : phase ou amplitude ?
Nous avons pris le parti au cours de cette étude de considérer le signal transmis par RDS comme une information modulée en phase, car nos premières tentatives consistant à afficher l’amplitude du signal filtré (Band Pass Filter autour de 57 ± 2,5 kHz) se traduisaient par un signal inexploitable. Bien que la boucle de Costas pour asservir en phase reste nécessaire, afficher la partie réelle au lieu de la phase donne aussi un signal parfaitement exploitable (Fig. 11). Quelques petites oscillations sont visibles sur les symboles les plus longs, qui pourraient se traduire par une fausse détection d’un symbole court si on n’y prend garde : un filtre passe-bas optimisé retire cette fluctuation et garantit une meilleure détection de la nature du signal transmis. En effet, filtrer par une fonction de transfert spectrale quasi-rectangulaire se traduit, par transformée de Fourier de la porte rectangulaire, par une convolution par un sinus cardinal (sin(x) / x) et donc un étalement de chaque symbole sur ses voisins compte tenu du temps de décroissance lent du filtre. Quel que soit le filtrage, tracer l’amplitude du signal (module du complexe) donne une information inexploitable pour la détection des bits : seules la phase ou la partie réelle sont exploitables.
Fig. 11 : En haut : graphique pour l’extraction des diverses composantes du signal dans la sous-porteuse RDS après asservissement de l’oscillateur par la boucle de Costas. La phase s’affichera en bleu, la partie réelle en vert, et le module en rouge. En bas : à gauche sans filtre passe-bas RRC, la partie réelle présente quelques oscillations sur les symboles les plus longs. En bas à droite : un filtre RRC permet d’atténuer ces artefacts et de rendre la partie réelle du signal exploitable. Dans tous les cas, le module (rouge) est inexploitable.
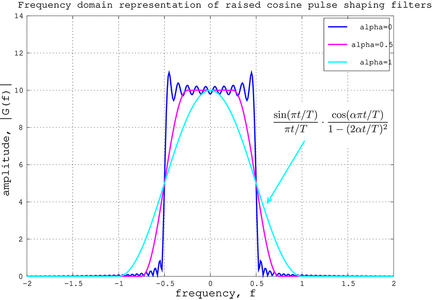
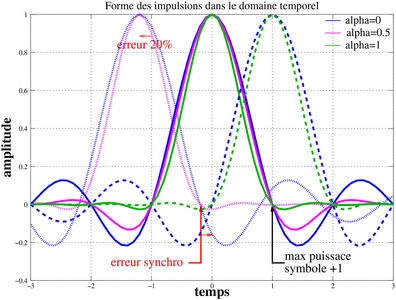
Le filtre Root Raised Cosine (RRC [28]) a été conçu pour pallier à cette déficience : un filtre passe-bande réduisant à la fois l’encombrement spectral et temporel, permettant de filtrer finement un signal tout en évitant un temps de décroissance trop long. Alors qu’un filtre rectangulaire dans le domaine spectral (bleu sur Fig. 12, haut, cas α = 0) se traduit par un excellent filtrage spectral, mais une réponse temporelle en sinus cardinal très longue avec un zéro aux positions des symboles adjacents, la moindre erreur sur la date d’émission d’un symbole (Fig. 12, cas de gauche de la courbe en temps) se traduit par une contribution de ce symbole sur ses voisins, d’autant plus importante que les symboles voisins sont loin. Le RRC présente aussi des zéros sur les symboles adjacents, mais sa décroissance est bien plus rapide (Fig. 12, bas, cas α = 1), évitant la pollution des voisins en cas d’erreur de synchronisation [29, p.136][30]. Le paramètre α fournit un levier pour passer continûment du meilleur filtrage spectral à l’optimum entre filtrage spectral et étalement temporel de l’impulsion. Le RRC vise donc à optimiser à la fois l’occupation du spectre en réduisant l’encombrement du canal utilisé (réduction de la bande passante B) pour transmettre le flux numérique, tout en maximisant le débit de communication en réduisant l’intervalle de temps 1/B entre les symboles successifs.
Fig. 12 : En haut : réponse spectrale des filtres RRC avec diverses formes, du rectangle (meilleure sélectivité spectrale) au segment de fonction trigonométrique. En bas : plusieurs impulsions successives dans le temps, filtrées avec diverses formes de RRC, avec l’impulsion de gauche décalée de 20% par rapport à sa date nominale pour une transmission périodique.
Annexe B : ajustement de l’horloge de la trame numérique
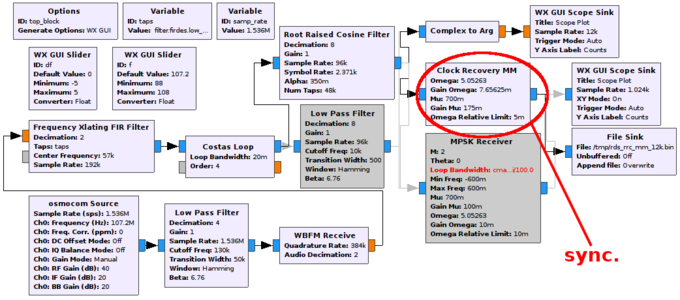
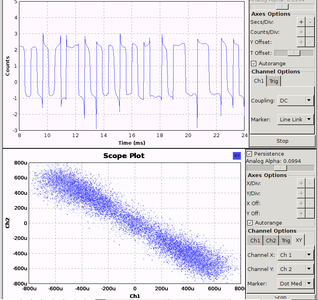
La modulation de phase nécessite une copie locale de la porteuse du signal radiofréquence sans modulation, une tâche résolue par la boucle de Costas qui élimine la modulation de phase. Une fois les bits visibles sous forme de phase à ou π (pour BPSK), il reste le problème de connaître le rythme auquel les bits sont transmis. L’horloge qui cadence la transmission numérique (par exemple un microcontrôleur sur l’émetteur) n’a aucune raison d’être la même source de fréquence que la porteuse radiofréquence, et il faut donc de nouveau retrouver une copie locale de l’horloge qui cadence le signal numérique pour le décoder (Fig. 13). Diverses stratégies sont disponibles, telles que maximiser le nombre de transitions dans le signal transmis pour permettre l’asservissement de l’horloge locale (cas du codage Manchester qui garantit au moins une transition à chaque bit). GNURadio fournit divers blocs pour la synchronisation de l’horloge cadençant le flux numérique, tels que Clock Recovery (selon l’algorithme publié dans [27]) ou MPSK Receiver. Ces blocs s’alimentent de la sortie de la boucle de Costas qui a éliminé l’erreur grossière de fréquence, et manipulent maintenant les symboles numériques issus du traitement précédent pour ajuster le flux de données. Ces blocs fournissent un échantillon par symbole, rendant le traitement ultérieur très simple (saturation par comparaison – nommé Binary Slicer dans GNURadio – puis analyse de la séquence numérique ainsi formée). Nous validons le bon fonctionnement de ces blocs en affichant le diagramme de constellation, qui comporte en ordonnée la partie imaginaire de la sortie du bloc de traitement et en abscisse la partie réelle. Puisque dans le plan complexe l’angle à l’axe des abscisses est la phase et la distance à l’origine la magnitude, un nuage de points à angle constant et distance constante indique une synchronisation efficace. Un nuage de points « qui danse » ou forme un cercle indique l’absence de synchronisation. La sortie directe de la boucle de Costas fournit une illustration du second point (Fig. 14, droite) tandis que le passage dans un bloc chargé de synchroniser l’horloge cadençant le flux numérique donne bien deux nuages (Fig. 14, gauche) qui sont les deux états possibles attendus en BPSK. Nous constatons ici que le filtre RRC que nous avons vu auparavant, même s’il ne change pas de façon significative la forme du signal d’un point de vue visuel, assiste la synchronisation de l’horloge en réduisant la diffusion de puissance dans un état des symboles numériques vers l’autre. Un filtre passe-bas atteint le même résultat, mais moins efficacement.
Fig. 13 : Chaîne de traitement des informations acquises depuis l’antenne pour retrouver le message (phrases) : dans cette annexe, nous nous intéressons à la synchronisation du message numérique, en rouge.
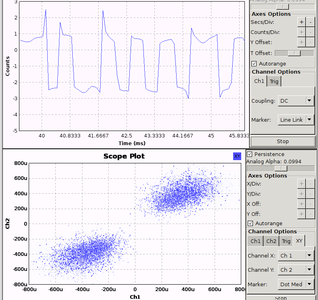
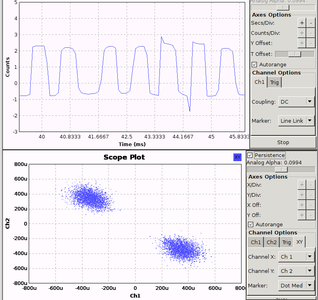
Fig. 14 : En haut : flux de traitement, ajoutant la synchronisation du flux numérique après la synchronisation sur la porteuse (Costas). En bas : diagramme de constellation (mode XY d’un oscilloscope recevant le flux de données complexes) dans les diverses conditions – de gauche à droite, sortie de la boucle de Costas (sans synchronisation de la séquence numérique), synchronisation de l’horloge numérique après un filtre passe-bas, et finalement après un filtre RRC. Deux nuages de points distincts garantissent la capacité à séparer les symboles.
La configuration des blocs de synchronisation telle que décrite dans http://gnuradio.org/redmine/projects/gnuradio/wiki/Guided_Tutorial_PSK_Demodulation nous informe que nous devons tenter de minimiser le nombre d’échantillons par symbole, tout en le maintenant au-dessus de 2. Pour ce faire, un RRC est inséré entre la boucle de Costas et le bloc de synchronisation d’horloge, avec un facteur de décimation qui permet d’atteindre un facteur Omega (ratio de la fréquence d’échantillonnage au débit du flux numérique) proche, mais au-dessus de 2. Dans notre exemple, Omega vaut samp_rate/128/(1187.5*2) avec 128 le produit des décimations des divers blocs de traitements entre la source et la synchronisation d’horloge, 1187,5 x 2 le débit de bits en encodage Manchester, et samp_rate le débit de données issues de la source. Les autres paramètres du bloc de synchronisation restent inchangés. Le RRC est quant à lui configuré avec un débit d’entrée égal au débit de la source divisé du produit des divers facteurs de décimations dans la chaîne de traitement qui le précède, et un débit de symboles égal à 1187,5 x 2 de nouveau, déterminant donc sa fréquence de coupure.
Le fichier issu d’une synchronisation de la porteuse (Costas) et du flux numérique (Clock Recovery ou MPSK) se décode parfaitement avec les scripts proposés dans le texte (section 3), en retirant les 4 premières lignes puisque nous avons désormais 1 échantillon/symbole, et en ne gardant des lignes 8 à 24 que p=angle(r);p=p-mean(p);s=(p>0);s=s-mean(s);s1=s(2:2:end);s2=s(1:2:end-1);. En effet, s est la version saturée de la phase p, dont le décodage par Manchester différentiel considère les valeurs successives des paires d’échantillons initiaux. La suite du traitement (synchronisation sur le syndrome des séquences de 16 bits) reste identique, pour par exemple donner
station = P 96.9BIP 96.9BIP 96.9BIP 96.9BIP 96.9BIP 96.9BIP 96.9BIP 96.9BIP
qui est cette fois parfaite, ou
station = EUROPE 1EUROPE 1EUROPE 1EUROPE 1EUROPE 1EUROPE 1EUROPE
de nouveau sans corruption de données, voir
station = RIRE & RIRE RIRE & RIRE & RIRE & RIRE JEAN JEAN JEAN JEAN JEAN
JEDUJARDINDUJARDINDUJARDINDUJARDINDUJARDINDUJARD
temps4A 57811 7 51 2
ou
texte = FRANNFO - LE 9 : FABIENN - 8APHATIE FRANCE INFO - LE 7 | 9 : FABIENNE SINTES - 8H30 APHATIE
FRANCE INFO - LE 7 | 9 :IENNE SINTES - 8H30 APHATIE FRANCE INFO - LE 7 | 9 : FABIENNE SINTES - 8H30 APHATIE
FRANCE INFO - LE 7 | 9 : FABIENNE SINTES - 8H30 APHATIE
station =FO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO
INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO INFO
temps4A 57811 7 54 2
qui est proche de la perfection. La date est en accord avec nos attentes : la date est le jour julien modifié 57811, que http://www.csgnetwork.com/julianmodifdateconv.html convertit en 27 Février 2017, l’heure est 7h5{1,4} décalée de 2 demi-heures, qui est bien 8h5{1,4}, heure de l’enregistrement. La trame 4A [13, p.28]est donc convenablement décodée et permet de recevoir l’heure par RDS, avec une mise à jour chaque minute annoncée comme exacte à ±0,1 s près. Ce n’est qu’après avoir inclus la synchronisation d’horloge de la trame numérique que nous obtenons des trames de datation de la forme 4A qui ne sont émises qu’une fois chaque minute. Une proportion trop faible de trames convenablement décodées a toutes les chances de nous faire rater cette séquence exceptionnelle de bits transmis :
station = RT RTL2 RT RTL2 RT RTL2 RT RTL2 RT RTL2 RT RTL2 RT RTL2 RT RTL2 RT RTL2
temps4A 57811 8 3 2
Tous les exemples de cette annexe ont été acquis au rythme d’un échantillon complexe (2 x 4 octets) par symbole, tel que le propose la sortie du bloc Clock Recovery MM. Au rythme de 1187,5 x 2 = 2375 Hz, les fichiers d’enregistrement sont typiquement de quelques centaines de kilo-octets pour des acquisitions d’une dizaine de secondes (19000 kB/s).
Annexe C : code PI
Chaque trame RDS transmise contient, dans son premier paquet (bloc A [13, p. 15]), le code PI de la station. Il a été suggéré [13, p. 66]que connaissant ce code PI, unique à chaque station radio, il serait possible de se synchroniser sur cette séquence de bits qui se répète tous les 104 bits (4 blocs de 26 bits), au lieu de se battre avec le code correcteur d’erreur et calculer pour chaque séquence de 26 bits reçus si les 10 derniers bits correspondent au syndrome des 16 premiers bits tel que nous l’avons implémenté. Nous aurions pu réécrire l’histoire de cet article en démontrant ce concept avant d’entreprendre l’implémentation du code correcteur d’erreur, mais la vérité est que la liste des codes PI n’a été trouvée qu’une fois cette prose achevée. En effet, le site http://www.csa.fr/maradiofm/radiords_tableau fournit la liste des codes PI des diverses stations autorisées. Par exemple pour Radio Campus à Besançon, nous apprenons que son code PI est FC3A. En ajoutant dans la boucle de décodage des trames, au même titre que le texte libre ou le nom de la station, le décodage du PI par
if (PI==0) PI=dec2hex(data1(1:16)*2.^[15:-1:0]') % PI
en ayant pris soin d’initialiser PI=0 en dehors de la boucle, notre script GNU/Octave de décodage identifie bien PI = FC3A lorsque nous écoutons 102,4 MHz. Le code est bien identifié de cette façon.
Erratum
En page 29 de GNU/Linux Magazine 204 [1], nous avions remarqué que « (…) pourquoi [m2runiq,m,n]=unique(m2r,'rows'); renvoie moins de lignes dans m2runiq qu'il n'y en a dans m2r, alors que toutes les lignes sont uniques ? ». La réponse est simple : parce que nous avions fait une erreur dans l'analyse des lignes de la matrice contenant les syndromes permettant d'attribuer une double erreur à une paire de bits. En effet, nous avions mal utilisé la fonction uniq(), et la recherche des doublons dans la matrice de corrections d'erreurs aurait du être :
[m2runiq,m,n]=unique(m2r,'rows'); % length(m2runiq)~=length(m2r)
length(m2runiq) % => bits differents donnent meme syndrome
u=1;
for k=1:length(m2r)
num=ismember(m2r,m2r(k,:),'rows');
if (sum(num)>1)
double(:,u)=find(num==1)' % lignes identiques ?
solution(double(1,u),:) % position 1er bit errone'
solution(double(2,u),:) % position 2nd bit errone'
u=u+1;
end
end
Cela prouve-t-il que RDS, contrairement à notre affirmation, ne sait pas corriger deux fautes dans le message ? L'erreur vient de notre lecture superficielle de la documentation technique, qui précise bien ([3], p.14) :
The error-protecting code has the following error-checking capabilities:
a) Detects all single and double bit errors in a block.
b) Detects any single error burst spanning 10 bits or less.
c) Detects about 99.8% of bursts spanning 11 bits and about 99.9% of all longer bursts.
The code is also an optimal burst error correcting code [5] and is capable of correcting any single burst of span 5 bits or less.
Ainsi, la norme RDS n'affirme pas pouvoir corriger toutes les erreurs doubles sur les blocs transmis, mais uniquement détecter ces erreurs, et corriger des séquences de bits erronés séparées de 5 bits ou moins. Par exemple, une erreur sur les bits 3 et 8 (séparés de 6 bits donc) fournit le même syndrome qu'une erreur sur les bits 15 et 26. Il y a 9 cas où une double erreur est attribuée de façon erronée à une autre séquence de bits (m2runiq contient 316 éléments), sur les 325 cas possibles. Le taux de succès sur la correction de doubles erreurs est donc de 1 - 9 / 325 = 97,2 %.
J.-M. Friedt
Notes et Références
[1] BARISANI A. et BIANCO D., « Hijacking RDS-TMC Traffic Information signals », Phrack 64 (5), 2011 sur http://phrack.org/issues/64/5.html#article, et son archive : http://dev.inversepath.com/rds/
[2] LI L., XING G., SUN L., HUANGFU W., ZHOU R., et ZHU H., « Exploiting FM radio data system for adaptive clock calibration in sensor networks », Proc. of the 9th ACM International Conference on Mobile systems, applications and services, p. 169 à 182, 2011.
[3] SYMEONIDIS D., « RDS-TMC spoofing using GNU Radio », Proc. 6th Karlsruhe Workshop on Software Radios, p. 87 à 92, mars 2010, avec une copie fournie par l’auteur de ce papier placée sur http://jmfriedt.free.fr/Symeonidis.pdf
[4] FERNANDES E., CRISPO B., et CONTI M., « FM 99.9, Radio Virus: Exploiting FM Radio Broadcasts for Malware Deployment », IEEE Trans. on Information Forensics and Security 8 (6), p.1027 à 1037, 2013.
[5] GNURadio : http://gnuradio.org
[6] GNU/Octave : http://www.gnu.org/software/octave
[7] Communication Toolbox : http://octave.sourceforge.io/communications/overview.html
[8] Le repliement est un effet de l'échantillonnage périodique à intervalles de temps
discrets 1/fe, qui suppose que le spectre entre-fe/2 et fe/2 se répète tous les fe. De ce fait lors de la décimation d'un facteur N, toutes les composantes spectrales du signal comprises entre fe/(2N) et fe/2 se ramènent entre -fe/(2N) et fe/(2N) par translations par pas de fe/(2N). Cet effet est évité en précédant
la décimation d'un filtre passe-bas qui élimine efficacement toute composante du signal au-dessus
de fe/(2N).
[9] Nous avions introduit le Xlating FIR Filter comme un bloc implémentant une étape fondamentale de la démodulation, à savoir transposition en fréquence, filtrage passe-bas et décimation [10]. Pour rappel, le filtre passe-bas a pour vocation d’atténuer les composantes spectrales du signal après transposition en fréquence au-dessus de la fréquence d’échantillonnage atteinte suite à la décimation : sans ce filtre, tous les signaux au-dessus de la nouvelle fréquence d’échantillonnage se retrouveraient dans la bande de base par repliement spectral lors de la décimation et pollueraient la séquence de traitement qui suit.
[10] FRIEDT J.-M., « La réception de signaux venus de l’espace par récepteur de télévision numérique terrestre », Open Silicium n°13, décembre 2014/janvier-février 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-013/La-reception-de-signaux-venus-de-l-espace-par-recepteur-de-television-numerique-terrestre
[11] https://bitbucket.org/azimout/gr-rds/
[12] https://github.com/bastibl/gr-rds
[13] European Standard EN 50067, « Specification of the radio data system (RDS) for VHF/FM sound broadcasting in the frequency range from 87,5 to 108,0 MHz », avril 1998, disponible sur http://www.interactive-radio-system.com/docs/EN50067_RDS_Standard.pdf ou pour sa version américaine http://www.nrscstandards.org/DocumentArchive/NRSC-4%201998.pdf
[14] TRETTER S.A., « Communication System Design Using DSP Algorithms, With Laboratory Experiments for the TMS320C30 », Chap. 6 « Double-Sideband Suppressed-Carrier Amplitude Modulation and Coherent Detection », Springer, 1995.
[15] FRIEDT J.-M, CABODEVILA G., « Exploitation de signaux des satellites GPS reçus par récepteur de télévision numérique terrestre DVB-T », Open Silicium n°15, juillet-septembre 2015 : https://connect.ed-diamond.com/Open-Silicium/OS-015/Decodage-des-signaux-de-satellites-GPS-recus-par-recepteur-de-television-numerique-terrestre-DVB-T
[17] FRIEDT J.-M, GOAVEC-MÉROU G., « La réception radiofréquence définie par logiciel (Software Defined Radio –SDR) », GNU/Linux Magazine n°153, octobre 2012, p.4 à 33 : https://connect.ed-diamond.com/GNU-Linux-Magazine/GLMF-153/La-reception-radiofrequence-definie-par-logiciel-Software-Defined-Radio-SDR
[18] WESLEY PETERSON W. et WELDON E.J., « Error-Correcting Codes », 2nd Ed., MIT Press, 1996.
[19] TOPPING P., « RDS decoding for an HC11-controlled radio », Motorola AN495/D, 1994.
[20] GUIDON Y., « Comprendre les générateurs de nombres pseudo-aléatoires », GNU/Linux Magazine n°81, p. 64 à 76, 2006.
[21] DUMAS J. G., ROCH J. L., VARRETTE S., et TANNIER E., « Théorie des codes : compression, cryptage, correction », Dunod, 2007.
[22] HILL R. A., « A First Course in Coding Theory », Oxford University Press, 1990.
[23] PATROIS N., « Réparer un code QR », GNU/Linux Magazine n°198, novembre 2016
[24] http://descanso.jpl.nasa.gov/performmetrics/profileDSCC.html fait apparaître les modes de codage dans les gains significatifs de bande passante de communication, tandis que la Fig. 7-11 (page 477) de https://history.nasa.gov/SP-4227/Chapter07/Chapter07.PDF indique la chute du taux d’erreur avec les améliorations sur les modes de codage de canal.
[25] Notes du cours du MIT 6.02, BALAKRISHNAN H. et VERGHESE G., « Introduction to EECS II : Digital Communication Systems », chapitre 6 : « Linear Block Codes : Encoding and Syndrome Decoding », disponible sur https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-02-introduction-to-eecs-ii-digital-communication-systems-fall-2012/readings/MIT6_02F12_chap06.pdf, 2012
[26] TSIMBALO E., FAFOUTIS X. et PIECHOCKI R., « Fix it, don’t bin it! CRC error correction in Bluetooth Low Energy », Proc. 2nd IEEE World Forum on Internet of Things (WF-IoT), 2015 sur http://eis.bris.ac.uk/~xf14883/files/conf/2015_wfiot_crc.pdf
[27] MEYR H., MOENECLAEY M., FECHTEL S.A ., « Digital Communication Receivers: Synchronization, Channel Estimation, and Signal Processing », John Wiley & Sons, 1998.
[28] CUBUKCU E., « Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems », 2012, sur https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20120008631.pdf
[29] BARRY J. R., LEE E. A. et MESSERSCHMITT D. G., « Digital Communication », Springer, 2004.
[30] http://www.dsplog.com/2008/04/22/raised-cosine-filter-for-transmit-pulse-shaping/ qui fournit un script GNU/Octave pour expérimenter avec le filtre RRC.



 Ajouter à une liste de lecture
Ajouter à une liste de lecture