Comment la crypto fut introduite dans la carte à puce : quand les anecdotes deviennent de l’histoire

1. Introduction

J'ai commencé à travailler sur la carte à puce en janvier 1980 suite à une demande de Philips France pour sécuriser les échanges entre une puce et son lecteur et je n'ai plus vraiment arrêté depuis. Cet article est la suite de ma référence [15] qui date de 1997, du chapitre de Louis Guillou, Michel Ugon et moi-même dans l'excellent livre de Gus Simmons [17] où le chapitre 12 (A standardized security device dedicated to public cryptology) détaille l'ensemble de l'histoire de la carte à puce en plus de 50 pages, et, enfin, du papier historique de Louis Guillou [9] en 2004. Notons encore la référence [8] de Louis Guillou et Michel Ugon à CRYPTO 1986.

La carte à puce a une assez longue histoire et ses premiers développements et brevets n’utilisent pas la cryptographie. Que ce soient les Gondas dans la Nuit des temps de René Barjavel, la première bague de Roland Moreno (voir la référence [16] dans la revue FEB-actualités qui raconte les débuts de la carte à puce), les premiers brevets japonais, allemands ou américains, rien n’indique que la puce doit avoir des éléments de cryptographie. Il y a cependant une exception : les travaux chez IBM sous la direction de Carl Meyer furent très tôt orientés vers l'utilisation de la cryptographie et une version expérimentale de carte fut testée avec l'algorithme cryptographique Lucifer dans le cadre d'une expérience d'ATM à Londres.

Il y a donc trois questions fondamentales :

• Pourquoi la crypto dans la carte à puce ?
• Est-il possible de mettre de la crypto dans la carte à puce ?
• Nécessité de l'implémentation d'un algorithme suffisamment rapide.

Nous allons voir maintenant en détail ces trois aspects importants.

2. Pourquoi la cryptographie dans la carte à puce

Et tout d'abord pourquoi faut-il de la crypto dans la carte à puce ? Il est assez facile de voir que si on veut éviter certaines attaques, il faut associer à la puce une certaine puissance de calcul. Prenons le cas simple du mot de passe stocké par la carte et qui sera utilisé pour avoir accès à une ressource (ce fut le cas au début pour la télévision à péage et aussi pour le Minitel). Supposons une carte, qui sera associée à un utilisateur, qui tente de prouver son identité en donnant un mot de passe :

• pour stocker ce mot de passe, il faudra que cette puce ait une mémoire inviolable, et donc, la puce elle-même le sera par extension.
• si le mot de passe (password) est transmis tel quel, et donc en clair, il sera facile à copier. Sa transmission ne sera donc pas directe, mais bien en utilisant un détour, par exemple, une question surprise au sujet de ce mot de passe. En pratique, cela se fera par l'usage de nombres aléatoires (random), du mot de passe en combinaison avec un algorithme cryptographique (que ce soit une fonction à sens unique, une fonction de chiffrement, un algorithme pour protocole à apport nul de connaissance où le mot de passe ne s'use pas si l'on s'en sert, ...).

À l'époque (1980), il a eu en plus les contraintes venant des autorités de contrôle en France (service du chiffre, aujourd'hui ANSSI) : il fallait éviter le détournement (donc, le chiffrement associé au déchiffrement) des objets qui faisaient usage de cryptographie forte. Cela permettra d’être inventifs : ainsi, les schémas basés sur l’identité, dans le cas du chiffrement à clé secrète, seront pratiquement inventés en 1984 par Louis Guillou, sous le nom de diversification de la clé secrète alors que la même année, Adi Shamir en donnera la description théorique pour les systèmes à clé publique sans aucune proposition de réalisation correcte. Il faudra attendre l'arrivée du protocole de Fiat-Shamir (1986) pour en voir une réalisation pratique, vite suivi par le protocole GQ (Guillou-Quisquater) en 1988.

3. Est-il possible de mettre de la crypto dans la carte à puce ?

Au début de la carte à puce, il y avait vraiment peu de place : il fallait vraiment innover. Aussi, au début, la carte comportait deux puces (voir Figure 1), l'une avec le processeur, l'autre avec la mémoire, connecté avec ce qui tenait fort de la bijouterie mais qui permettait aussi facilement d'espionner les échanges processeur-mémoire où apparaissaient sans aucun doute les éléments secrets. Il a fallu attendre l'arrivée de la monopuce pour résoudre ce problème. Des puces multiples ont même été imaginées pour résoudre les problèmes de mémoire, de puissance de calcul, sans jamais atteindre une réalisation (projet octopuce présenté à Securicom).

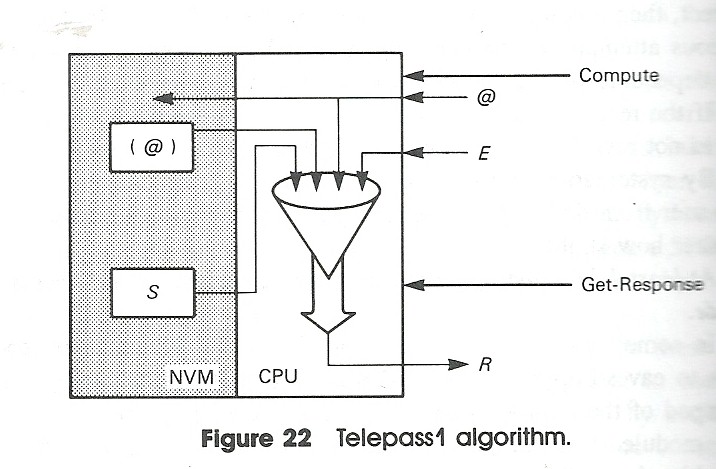
Les premiers algorithmes cryptographiques pour la carte à puce seront donc des algorithmes cryptographiques soit à sens unique, soit inversible, mais toujours à clé secrète. Ce sera la suite de Telepass 1 (voir Figure 2), TDF, Telepass2, Videopass, … :

Le premier algorithme cryptographique pour carte à puce semble avoir été imaginé par Honeywell Bull en 1979. Cet algorithme n’a jamais été publié comme les autres ci-dessus d'ailleurs. Tous ces algorithmes étaient bien adaptés à leur contexte restreint en vitesse et en mémoire ainsi qu'aux processeurs 8 bits en usage. Ils utilisaient entre 200 et 300 octets pour leur implémentation complète, ce qui est certainement un exploit. Cependant, la non-publication de ces algorithmes en rendait certainement l'usage plus restreint et la diffusion en dehors de la France difficile.

Le déclic s'est produit à EUROCRYPT 1984, à Paris, à la Sorbonne. Louis Guillou [7] y présenta la carte à puce et l'accès conditionnel lors d'une session spéciale dédiée aux usages de la carte à puce, une première dans une conférence cryptographique internationale. Lors des questions à la fin de son exposé, des américains demandent quel algorithme cryptographique est utilisé : Louis parle de Telepass et de TDF, puis vu l'insistance de l'assistance, il esquisse au tableau la forme générale de ces algorithmes, ce qui fait sourire certains (rien ne prouve que ces algorithmes sont solides), et grincer certains (là, Louis, tu vas toucher la ligne rouge). À la dernière question, « pourquoi vous n'utilisez pas le DES ? » Louis répond : « Cela ne sera jamais possible car la ROM est bien trop petite ». Et, de fait, il n'y avait à l'époque que 2048 octets pour la place des programmes, tout compris, même si plus tard on trouva aussi l'astuce d'utiliser l'EPROM ou E²PROM pour stocker quelque 500 octets en plus. Les ingénieurs de Philips et moi-même (alors au laboratoire Philips PRLB, à Bruxelles) étions dans la salle, et à la sortie, nous discutions entre nous de ce challenge fascinant : mettre le DES dans la carte à puce, sans trop même discuter si nous obtiendrons la permission de le faire par les autorités (il y avait à l'époque pas mal de problèmes d'exportation, entre autres). Nous avions travaillé sur un prototype de modem chiffrant qui utilisait le DES, le même processeur que les cartes à puce (80C51) et ce DES complet tenait dans 1500 octets. Nous arrivons donc dans la saga de la carte à puce avec DES.

3.1 Le DES dans la carte à puce

Il y avait à l'époque (1984) un projet de transmission interbancaire sécurisée en Belgique dénommé TRASEC (TRAnsaction SECurity) [18]. L'idée était de stocker les clés secrètes dans une carte à puce sous le contrôle d'un PIN code et d'exécuter l'algorithme DES avec cette clé dans un ordinateur, lui, non sécurisé. C'était très peu satisfaisant. Je propose alors de démarrer un projet pour mettre le DES dans la carte. Une première étude démarre et nous permet de voir que 1000 octets environ suffiront avec un temps raisonnable d'exécution. Répondant à l'appel des banques belges, Philips propose d'étudier une version plus compacte. Durant plusieurs mois, à plusieurs chercheurs et ingénieurs, nous essayons de gagner octet par octet, en déplaçant les permutations en usage dans le DES et en repliant ces mêmes permutations vu leurs propriétés. Finalement, nous parvenons à un total de 668 octets, chaque octet ayant coûté environ un jour de travail... Ce fut donc une première mondiale. Cette version du DES sera longtemps utilisée par les cartes, y compris dans la carte commune Philips-Bull, TB100, et je suis à peu près sûr que l'on en retrouve encore des traces aujourd'hui dans certaines cartes.

Le challenge suivant, le RSA, a une histoire encore plus étonnante.

3.2 Le RSA dans la carte à puce

Il était clair pour chacun que mettre le RSA dans la carte était en quelque sorte le Graal cryptographique de la carte à puce. Cela permettait la signature, la distribution des clés, etc. Paul Barrett invente alors un nouvel algorithme pour le RSA, mais plus spécifiquement dédié à des processeurs pour traitement du signal [1].

Nous faisons quelques tests sur une carte à puce en 1986 et nous arrivons à une première version qui demande près de 100 secondes pour s'exécuter. Puis, nous ajoutons le reste chinois, d'autres astuces liées au stockage de multiples du module public. Finalement, pour une clé RSA de 512 bits, pour un module public à deux facteurs, nous arrivons à fournir une signature en moins de 20 secondes pour un module public général (des formes spéciales permettent d'aller plus vite) ainsi qu'un exposant aléatoire (idem). Il y a cependant plusieurs problèmes : trop lent pour être utilisé (imaginer cela à une caisse de supermarché) et aussi, et même surtout, trop gourmand en ressources de la carte (ROM, RAM, etc.). Il faut donc passer à autre chose.

Le SEPT à Caen commence à imaginer l'usage d'un coprocesseur, ce qui utilise des ressources en surface de silicium qui, comme on le sait, sont aussi limitées vu les possibles flexions de la carte (moins de 20 mm²). Il est dommage que ce projet ne fut pas poursuivi.

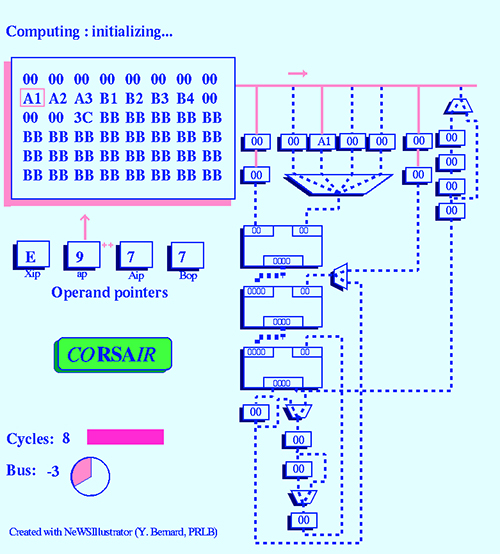
En 1989, Henri Molko (Philips France et Allemagne) nous arrive avec un projet extraordinaire : ajouter un coprocesseur RSA à un processeur 80C51, en vue de son usage pour réaliser une signature RSA sur 512 bits en moins d'une seconde (nous ferons 0.2 seconde). Les moyens financiers prévus sont quasi nuls, mais nous allons bien utiliser la souplesse d'alors de Philips. Ce sera le projet CORSAIR (Coprocessor RSA In a Rush) [3-14]. En cinq semaines, plusieurs versions du coprocesseur seront imaginées à partir d'un nouvel algorithme que j'avais imaginé entre-temps. Ceci conduira à une première accélération du RSA pour une carte à puce par un facteur 500, tenant compte que nous avions réussi à obtenir que le diviseur par deux pour la fréquence d'horloge ne soit pas utilisé. Dominique de Waleffe écrira les simulations et les tests et Jean-Pierre Bournas écrira le microcode. Un premier silicium sera obtenu début 1990 : tout marchera correctement sauf l'écriture dans E²PROM « trop » optimisée. Le dessin 3 est le premier écran d'une simulation de CORSAIR.

Un nouvel algorithme avait donc été imaginé : il est référencé dans la littérature comme l'algorithme de Quisquater [13] : ses propriétés principales sont que le coprocesseur est indépendant de la longueur de la clé, que l'exécution est à temps constant de bout en bout car il n'y a aucun test effectué en cours de calculs.

Puis ce sera la course aux coprocesseurs de deuxième génération [11-12] parmi les fabricants, chacun utilisant l'algorithme de Montgomery, en commençant par Fortress, sauf Siemens (Sedlak), maintenant Infineon, … et Philips, bien sûr, (maintenant NXP). De fait, Philips se fait dépasser car étant parti le premier, les autres ont pu profiter de ses expériences.

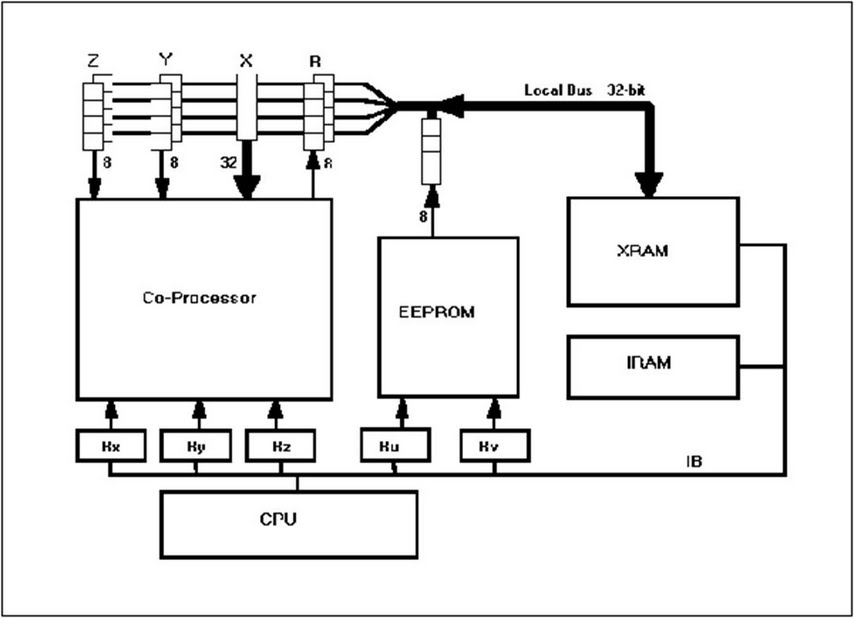
En 1995, un nouveau projet aura lieu : FAME [6]. Cela conduira l'auteur à une nouvelle version 500 fois plus rapide que celle de CORSAIR. Cette accélération aura été obtenue grâce à un multiplieur d'horloge (16 fois), un multiplieur 32 bits fois 32 bits (au lieu de 8 fois 8), un bus plus large, une mémoire RAM à double accès très large et un meilleur pipe-line. Ce coprocesseur incluant des améliorations (ajout des courbes elliptiques) est toujours utilisé dans des variantes optimisées. Au total, en 10 ans, une accélération de 250.000 aura été obtenue entre la première version logicielle 8bit et celle qui résulte de FAME. Bien mieux que la loi de Moore ! La figure 4 décrit brièvement les composants de FAME.

Il y aura encore le projet européen CASCADE (1994-1997) [2] sous la direction de Patrice Peyret puis de Pierre Paradinas, tous deux de Gemplus, où on parviendra à incorporer un processeur ARM, d'architecture RISC, à une carte à puce : ce sera aussi l'ancêtre de la Java Card. Nous y apportons des modifications au processeur ARM plutôt orienté traitement du signal en vue d'effectuer efficacement des instructions de type cryptographique. Cela conduira au strongARM.

Notons enfin le projet SCALPS (1996) totalement préparé à l'UCL (Louvain-la-Neuve) et qui résultera en une puce complète incorporant le protocole GQ modifié pour effectuer des paiements sécurisés [4].

4. Les premières attaques

Les premières attaques contre la carte furent liées à la TV à péage dans différents pays. L'inviolabilité supposée de la carte était ainsi bien mise à forte épreuve. Ces attaques furent un mélange de vraies attaques physiques, d'erreurs d'implémentations utilisées par les pirates, et aussi de combats entre différents acteurs du domaine.

Les attaques par mesure par le temps d'exécution furent connues très tôt (1986) sans être publiques. Paul Kocher [10] fut le premier à la publier en 1996, mais dans un contexte qui n'était pas celui de la carte à puce. La première réalisation expérimentale sur une carte à puce ne fut réalisée et publiée qu'en 1998 à CARDIS [5].

L'attaque par la simple mesure de la consommation (SPA : simple power analysis) était bien connue avant sa publication par Paul Kocher et ceci par plusieurs laboratoires, y compris Philips, TNO (Pays-bas) et IBM. Nous avions effectué deux campagnes de mesure, l'une en 1989, l'autre en 1992. Nos directeurs étaient tellement effrayés qu'ils détruisirent les documents en nous interdisant formellement d'en parler.

En 2000, il y aura la saga des cartes bleues et les « attaques » de Serge Humpich. Je ferai comme à l'époque, je transcris ici les deux textes, publiés en l'an 2000 dans fr.misc.cryptologie, à la demande générale, qui illustrent toute l'histoire.

5. L’étirage des clés

Les tirages des clés ou l'étirage des clés

soutiré à l'as sans ion positif (fin mets de mil)

par Cyreno de Heressac (à dos de prime jeunesse, c'est grand mot dire) (d'après Edmond RoStAnd - 1868-1918, de guerre lasse)

Nous sommes en 1640 (le petit théorème vient juste d'être inventé par Pierre Fermat - 1601-1665 - sa mort a aussi été annoncée en 1653, fosse nouvelle -, à Toulouse, bien qu'il fisse sûrement ses études à Bordeaux et Orléans, on n'est jamais trop prudent : pour le grand, il y a encore de la marge...).

CYRENO
Ah ! non ! elle est un peu courte, jeune homme !
On pouvait tirer... ou mieux !... bien des clés en somme...
En variant à la tonne, -parbleu, tenez
Agressif : "Moi, monsieur, si j'avais une telle clé,
Il faudrait sur-le-champ que je la retirasse !"
Amical : "Mais elle ressemble à votre mot de passe
Pour moins le voir, faites-la passer dans un hachage !"
Descriptif : "Escroc laid !... c'est une pique !... c'est un gage !
Que dis-je, c'est un gage ?... C'est un bénin module !"
Curieux : "De quoi sert ce peu long bidule ?
De critères, monsieur, ou de carte à grimoire ?"
Gracieux : "Aimez-vous à ce point les gros loirs
Que maternellement vous vous préoccupâtes
De tendre ce pair choix à leurs petites pattes ?"
Truculent : "Ça, quand le tirage est augmenté,
La peur du tas bas vous sort-elle la clé
Sans qu'un voisin ne crie aux facteurs publiés ?"
Prévenant : "Gardez-vous, sa tête entraînée
Par son poids, de la fendre en deux sur le champ !"
Tendre : "Faites-lui choix, sire, d'un paramètre tout chant,
Que sa valeur à la lune ne se profane !"
Pédant : "L'algorithme, monsieur, qu'Aestophane
Appelle Marserpentwofishercésixrijndael,
Cent rondes, avec cette clé, ne vaut guère la scytale !"
Cavalier : "Quoi, là mis, ce nombre est à la mode ?
Pour perdre son code secret, c'est vraiment très commode !"
Emphatique : "Ce vent si favorable, clé astrale,
Guère te factorise, si ne n'est le NISTrAl !"
Dramatique : "C'est l'amère douche quand elle signe !"
Admiratif : "Être au parfum, quel Bond digne !"
Lyrique : "Est-elle quelconque, de quel germe hérite-t-on ?"
Naïf : "Ce module, quand le factorise-t-on ?"
Respectueux : "Souffrez, dame, qu'on vous prête main forte,
C'est là ce qui s'appelle avoir clé sur porte !"
Campagnard : "Hé, ! C'est-y une clé au pâtre? Nanain !
Queuqu'César fainéant ou queuqu'meuh long nain !"
Militaire : "Tirez contre cave Valérie !"
Pratique : "Voulez-vous la mettre en loterie ?
Assurément, en prime, ce sera le gros lot !"
Enfin parodiant PyRSAme en un sanglot
"La voilà donc cette clé qui des traites de son maître
A détruit l'harmonie ! Elle en bleuit, le traître !"
- Voilà ce qu'à peu près, mon cher, vous m'auriez dit
Si vous aviez peu de lettres et plus de chiffres
Mais de chiffre, ô le plus fragmentable des êtres,
Vous n'en eûtes jamais mille bits, et de lettres
Vous n'avez que les trois qui forment le mot : RSA !
Eussiez-vous eu, d'ailleurs, le fin du mot du la
Pour pouvoir là, devant ces nobles galeries,
me servir toutes ces folles plaisanteries,
Que vous n'en eussiez pas articulé le quart
De la moitié du commencement d'un, car
Je me les tire moi-même, avec assez de verve,
Mais je ne permets pas qu'un autre me l'étire.

Toute ressemblance avec des faits réels est purement aléatoire.

Voici le texte complet de la chanson de Roland : certains liens ne sont plus accessibles.

6. La chanson de Roland

Si je peux faire court (oui, mon gars lent) :

--- La chanson de Roland ---

• Au début était la carte à puce, et la carte était Roland Moreno en 1974, voir histoire "officielle" à http://www.cardshow.com/museum/ex70/a74.html, qui nous raconte un conte de faits : depuis la nuit des temps, René Barjavel en parlait et d'autres, bien cités par Jean Moulin, à http://wwwusers.imaginet.fr/~jmoulin/jmccarte.html.
• Dieu trouva que c'était bon et la carte fut incassable en France, pour < 100 F, l'obscurité permit de contourner les lois de la physique et des théorèmes de Shannon, excusez du peu : la cryptographie ne viendra que plus tard
• Paul Kocher n'était pas au courant et trouva le temps de nous la casser, http://www.cryptography.com/timingattack/ et surtout http://www.cryptography.com/dpa/technical/index.html
• Une spécification figée en 1984 par ma-gie (Orwell quand tu nous tiens), Louis Monier, mieux connu aujourd'hui comme l'inventeur d'altavista, avait dans sa thèse d'Orsay affirmé que les nombres de 100 digits ne seraient pas factorisés pour l'an 2000 : un autre bug, un vrai, le pauvre, il n'avait pas prévu l'arrivée de Pollard, un vrai polar...
• Un simple double comme redondance pour la signature RSA, pour éviter les attaques multiplicatives, fut vite écarté par les experts mais retenu car fort simple pour éviter les doubles : l'ISO se chargea de faire mieux, trop vite à mon goût, et ce fut ISO 9796 qui ne passa pas non plus l'an 2000 victime du mou Boo Barkee, du dynamique Deh Cac Can, à l'inverse, et surtout du regretté R. F. Ree qui n'a pas toujours respecté l'anonymat, par de vilains calculs personnels, tous symboliques et coronsternants, http://dblab.comeng.chungnam.ac.kr/~dolphin/db/journals/jsc/jsc18.html Certes, il manquait un bit, vite percé par Don QuiCop de la Manche du Des, et le bit ne fait pas les moines, et François Grieu - EUROCRYPT 2000 - nous montra comment fabriquer de nouvelles signatures à partir de quelques authentiques, est-ce bancal ou bancaire ou banco? Ici, retour à la case Rolandet Lino Vatronc sonnant et trébuchant]
• Humpich joue sa carte, croit donner une frousse bleue et perd : un royaume pour mon ticket de métro. Métro, c'est trop. Il n'avait pas misé sur le bon cheval, se croyant richard trop vite.
• Fin de l'épisode : le général Desvignes...

Et c'est ainsi que la carte à puce devint fort peu crédible au pays de la Silicon Valley pour parler francs, non encore chiffrés, c'est clair.

Histoire réécrite en 2000 mais prévisible.
Encore une bataille de perdue, sans cor ni trompette.

Conclusions

L'introduction de la cryptographie semble s'être faite sans beaucoup de recherche. Pour le reste, le cycle d'élaboration des diverses versions de carte à puce suite à des attaques ressemble surtout au cycle de Shiva dans l'hindouisme : c'est le fameux cycle de construction, destruction et purification où la R&D est fort absente. Il est remarquable de noter que la première conférence de recherche dédiée à la carte à puce commence seulement en 1994 (voir photo 5 : une carte à puce comme carte de participant). Depuis lors, la recherche en cryptographie et carte à puce s'est fortement agrandie pour devenir aujourd'hui majeure.

Références

Nous n'avons pas indiqué ici les brevets qui sont nombreux et qui précédent souvent les publications.

[1] Paul Barrett. Implementing the Rivest, Shamir and Adleman public-key encryption algorithm on a standard digital signal processor, Advances in Cryptology: CRYPTO'86 (A. M. Odlyzko ed.), LCNS 263, Springer-Verlag, pp. 311-323, 1987.

[2] CASCADE project : voir http://cordis.europa.eu/esprit/src/omi08670.htm

[3] Dominique de Waleffe and Jean-Jacques Quisquater. CORSAIR: A smart card for public key cryptosystems. In A. J. Menezes and S. A. Vanstone, eds, Advances in Cryptology -- Crypto '90, vol. 537 of Lectures Notes in Computer Science, Springer-Verlag, pp. 502-513, 1991.

[4] Jean-François Dhem, Daniel Veithen, Jean-Jacques Quisquater. SCALPS: Smart Card for Limited Payment Systems, IEEE Micro, Volume 16 Issue 3, June 1996, pp. 42-51.

[5] Jean-François Dhem, François Koeune, Philippe-Alexandre Leroux, Patrick Mestré, Jean-Jacques Quisquater, Jean-Louis Willems: A Practical Implementation of the Timing Attack. CARDIS 1998: pp. 167-182.

[6] Ronald Ferreira, Ralf Malzahn, Peter Marissen, Jean-Jacques Quisquater, Thomas Wille: FAME: A 3rd Generation Coprocessor for Optimising Public Key Cryptosystems in Smart Card Applications. Proceedings of the Second Smart Card Research and Advanced Application Conference, CARDIS 1996, September 18-20, 1996, CWI, Amsterdam, The Netherlands. 1996, pp. 59-72.

[7] Louis C. Guillou: Smart Cards and Conditional Access. EUROCRYPT 1984: 480-489.

[8] Louis C. Guillou, Michel Ugon: Smart Card, a Highly Reliable and Portable Security Device. CRYPTO 1986: 464-479.

[9] Louis C. Guillou, Histoire de la carte à puce du point de vue d'un cryptologue, pp. 125-154, in Jacques André et Pierre Mounier-Kuhn (eds.) - Actes du 7e colloque sur l'Histoire de l'Informatique et des Transmissions, 270 p., INRIA/Université de Rennes 1, 2004, ISBN 2-7261-1281-1.

[10] Paul C. Kocher: Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. CRYPTO 1996: 104-113

[11] David Naccache and David M'Raihi. Cryptographic Smart Cards, IEEE Micro, 16(3), pp.14-24, 1996.

[12] David Naccache, David M'Raïhi: Arithmetic co-processors for public-key cryptography: The state of the art. CARDIS 1996. P.H. Hartel, P. Paradinas, and J.-J. Quisquater, Eds., Proc. Of CARDIS ’96, pp. 39–58, Amsterdam, The Nederlands, September 16–18, 1996.

[13] Quisquater, Jean-Jacques: Fast modular exponentiation without division. Rump session of EUROCRYPT’90, Aarhus, Denmark (May 21–24, 1990).

[14] Quisquater, Jean-Jacques, de Waleffe, Dominique, Bournas, Jean-Pierre: CORSAIR: A chip with fast RSA capability. In: Chaum, D. (ed.) Smart Card 2000. pp. 199–205. Elsevier Science Publishers (1991).

[15] Jean-Jacques Quisquater, The adolescence of smart cards, Future Generation Computer Systems, Volume 13, Issue 1, July 1997, Pages 3-7.

[16] Revue trimestrielle FEB-Actualités, numéro 76, juin 2012.

[17] Contemporary Cryptology: The Science of Information Integrity, Gustavus J. Simmons (Editor), ISBN: 978-0-7803-5352-7, January 1999 (première édition en 1992), Wiley-IEEE Press.

[18] Philippe Van Heurck: TRASEC: National Security System for EFTs in Belgium. Computer Networks 14: pp. 389-395 (1987).