Où l’on ne parle pas de crypto-monnaie, mais bien de cryptographie. Tester des primitives cryptographiques non pas pour vérifier leur conformité à une spécification donnée, mais bien pour s’assurer de leur sécurité est une tâche ardue. Voyons comment aborder ce problème.
Pour tester un programme, le plus souvent, de nombreuses solutions s’offrent à nous. Le fuzzing, ainsi qu’expliqué dans ce hors-série dans l’article « Usages avancés d’AFL », page XX, fait partie des solutions les plus efficaces et les plus utilisées pour causer des crashs ou des comportements inattendus dans des programmes. Toutefois, lorsque l’on s’intéresse à des domaines spécifiques tels que la cryptographie, on réalise rapidement qu’un programme qui ne plante pas n’est pas pour autant sûr.
Et si Heartbleed eût pu être découvert grâce au fuzzing [BOCK], un problème provenant réellement des primitives cryptographiques utilisées, tel qu’un « padding oracle », ou une « attaque par courbe invalide », ne saurait être détecté par un fuzzer dont le but est de faire simplement planter le programme testé.
Les bogues cryptographiques sont généralement plus subtils. Par exemple, lorsque l’on signe un message en utilisant l’algorithme de signature digitale sur courbe elliptique « ECDSA », pour chaque signature, une nouvelle valeur aléatoire éphémère (le plus souvent de 256 bits) est générée. Il suffit d’un biais statistique extrêmement faible (1 bit parmi les 256) [ECDSA] lors de la génération de cette valeur pour permettre à n’importe qui d’extraire des signatures la clef privée utilisée pour les créer. Pour détecter ce genre de problème, des outils spécifiques ont été développés au cours des années. On peut citer parmi ceux-ci le projet Wycheproof [WYCH], ainsi que le développement de l’ACVP (Automated Cryptographic Validation Protocol par le NIST, dont le but est de mettre en place un protocole permettant de valider de manière automatisée la conformité d’algorithmes cryptographiques donnés à leurs spécifications) ou encore CDF (Crypto Differential Fuzzing, [CDF]). Tous ont pour but de faciliter le travail du cryptographe en permettant de détecter dès que possible les erreurs classiques faites lors d’une implémentation cryptographique.
Rappelez-vous enfin qu’il est toujours plus difficile de prouver l’absence d’un problème que sa présence, et les systèmes de tests cryptographiques n’échappent pas à cette règle.
1. Détecter des erreurs cryptographiques, de manière automatisée
Quelles sont les erreurs cryptographiques que l’on peut espérer détecter automatiquement ? Il s’agit là d’une question dont les réponses actuelles sont encore en plein développement. Cela va notamment dépendre des algorithmes que l’on considère. Commençons par noter que certains problèmes peuvent être qualifiés de problèmes cryptographiques, par opposition aux problèmes fonctionnels classiques.
Ces erreurs, si elles ne remettent pas en cause la bonne exécution d’un protocole ou d’un programme, peuvent le rendre vulnérable de manière parfois peu évidente. Notre but va être bien entendu de les repérer aussi tôt que possible dans le cycle de vie d’un programme, afin de les corriger.
Commençons donc par passer en revue quelques-uns des problèmes classiques rencontrés par un cryptographe lorsqu’il vérifie des implémentations cryptographiques.
Les problèmes dits de canaux auxiliaires (plus connus sous le nom de « side-channel » dans la langue de Shakespeare) : un programme dont la durée d’exécution dépend de valeurs secrètes permet généralement à un adversaire de déduire les valeurs secrètes en chronométrant ses temps d’exécution face à différentes valeurs d’entrée. La présence d’un tel canal auxiliaire permet dès lors d’utiliser le temps d’exécution comme un oracle (voir encadré) qui répondra généralement à une question que l’attaquant se pose quant aux valeurs secrètes et qui peut permettre de déduire ces valeurs après avoir fait appel à cet oracle suffisamment de fois. Nous voici face à une attaque par « timing oracle » (oracle de temps) latente.
Les attaques par canaux auxiliaires sont à la mode ces derniers temps avec notamment les vulnérabilités sur processeurs Spectre et Meltdown [SPCTR] qui sont justement basées sur un canal auxiliaire en lien avec le cache du processeur (bien qu’en théorie le problème sous-jacent puisse aussi conduire à d’autres types de canaux auxiliaires) pour obtenir des informations sur des éléments en mémoire protégée. Ces attaques ne concernent ainsi pas uniquement des éléments qui sont à proprement parler cryptographiques. Quoi qu’il en soit, lors du développement de fonctions cryptographiques il est très important d’être conscient que même le plus petit bit d’information qui fuite peut parfois être exploité par un attaquant.
Les oracles en cryptographie
En cryptographie, on appelle « oracle » une boîte noire qui prend une valeur d’entrée et donne la réponse à une question précise concernant la valeur d’entrée, sans être restreint en termes de connaissance. Un oracle peut être utilisé indifféremment par n’importe quel utilisateur, y compris un adversaire. On a déjà parlé d’oracle de bourrage (padding oracle) dans MISC n°87 [MISC], qui vont révéler si un texte chiffré, une fois déchiffré, possède une structure de bourrage conforme ou non à sa spécification, et ce, même si la personne qui soumet le texte chiffré à l’oracle n’en possède pas la clef de déchiffrement. De tels oracles ont encore récemment été exploités pour déchiffrer le trafic TLS d’un serveur sans en posséder la clef privée [ROBOT].
Ainsi, ces timing oracles sont un exemple type de pièges dans lesquels un développeur qui n’est pas rompu aux arcanes cryptographiques peut tomber. L’illustration la plus simple d’un timing oracle consiste en un programme qui va vérifier un mot de passe caractère par caractère et retourner une erreur dès que l’un des caractères est faux :
func isEqual(a, b string) bool {
if len(a) != len(b) {
return false
}
for i := 0; i < len(a); i++ {
if a[i] != b[i] {
return false
}
}
return true
}
Mais avec une telle implémentation, on fournit à l’attaquant un timing oracle, car si le premier caractère est correct, mais le second ne l’est pas, le temps d’exécution sera plus long que si le premier caractère est incorrect ! Et en pratique, cette fonction était effectivement présente dans java.security.MessageDigest jusqu’en 2009 [HALE]. Le même type de problème de timing peut se retrouver dans des implémentations de RSA lorsque celles-ci vérifient que le bourrage d’un texte déchiffré est correct et peut résulter en une attaque par padding oracle, où l’oracle est en réalité le temps d’exécution du programme, avant le rejet d’un texte chiffré au bourrage invalide.
Un autre piège dans lequel il est facile de tomber consiste à ne considérer que des valeurs fonctionnelles et à ne pas s’intéresser au comportement de notre implémentation lorsqu’elle se voit fournir des valeurs d’entrées invalides. Ainsi, certaines implémentations vont valider des signatures DSA invalides avec des clefs invalides, car elles ne vérifient pas que les valeurs utilisées dans ces clefs sont des valeurs plausibles.
Il est d’autant plus important d’également vérifier qu’une fonction ne va pas accepter et effectuer de travail dépendant de valeurs secrètes sur des valeurs d’entrées invalides, car par exemple les algorithmes cryptographiques sur courbe elliptique sont très sensibles à ce genre de problème. Au point que s’il l’on s’amuse à interagir avec un point qui ne se trouve pas sur la courbe que l’on pensait, on risque de révéler notre clef privée [INVC], ce qui est généralement le pire (ou le meilleur, selon le point de vue) résultat possible d’une attaque contre un algorithme cryptographique.
Nous le mentionnions dans l’introduction, mais les aléas d’un cryptographe sont tels que parfois un biais extrêmement faible lors de la génération d’un nombre dit pseudo-aléatoire peut suffire à révéler notre clef privée. On se souvient tous de la PlayStation 3 de Sony dont le microcode était signé cryptographiquement et dont la clef privée avait été révélée lors de la Chaos Communication Conference 27C3, car ils avaient réutilisé plusieurs fois la même valeur éphémère, qui ne l’était dès lors plus, en lieu et place d’en générer une nouvelle durant le processus de signature ECDSA. Le même problème a également permis le vol de plus de 59 bitcoins en 2013, car une application Android n’utilisait pas des valeurs suffisamment aléatoires pour signer des transactions bitcoins.
Maintenant, la question qui nous intéresse est bien de détecter ces problèmes de manière automatique. Quelles sont nos options ? On va bien sûr devoir distinguer quelques cas. Toutefois, plusieurs outils existent et permettent aux développeurs de tester leur code de manière plus ou moins aisée.
L’un des cas théoriquement faciles à détecter, mais trop rarement testé et pas nécessairement facile à corriger consiste à vérifier qu’une implémentation s’exécute en un temps constant. Pour ce faire, plusieurs outils existent tels que Ctgrind [CTGR], un plugin pour Valgrind malheureusement peu utilisé, ou Dudect [DUDE], un programme en C qui permet de tester une fonction contre deux ensembles de valeurs d’entrées et va déterminer à l’aide de tests statistiques si la fonction semble s’exécuter en un temps équivalent dans les deux cas ou non. Cette dernière méthode a l’avantage de permettre le test en boîte noire d’une implémentation, ainsi que d’être facilement ajoutée à une suite de tests unitaires.
Vient ensuite le projet d’une équipe de Google, nommé Wycheproof en référence au Mont Wycheproof, la plus petite montagne au monde, afin d’illustrer son but, car plus petite est la montagne, plus elle est facile à franchir. Et son but est bien de rendre aussi facile que possible le test d’implémentation cryptographique. Avec plus de 80 tests, ce ne sont pas moins de 40 problèmes sécuritaires qui furent découverts dans plus de 3 bibliothèques cryptographiques pour Java. Nous allons nous y intéresser plus en détail dans la section suivante.
Un autre projet dont le but est de faciliter le travail des développeurs qui veulent implémenter des primitives cryptographiques s’appelle CDF, un « fuzzeur différentiel » développé chez Kudelski Security que l’on présentera également plus en détail ci-après.
Wycheproof a une approche qui consiste à trouver des cas limites, des valeurs invalides, et à produire des vecteurs de tests afin de vérifier qu’une implémentation testée fonctionne ainsi qu'elle le devrait. Ils peuvent également tester de la sorte la vulnérabilité face à certaines attaques, notamment celles de D. Bleichenbacher, qui est l’un des auteurs du projet. CDF quant à lui, va comparer deux implémentations afin de détecter des différences de comportements entre les deux, mais va également tenter de s'appuyer sur des vecteurs de tests afin de tenter de pousser chaque implémentation à la faute, ou à un comportement inattendu. Ainsi, les deux approches sont complémentaires et il est possible en théorie d'utiliser les vecteurs de tests très complets développés par l'équipe de Wycheproof avec CDF en profitant de la notion d'interface plus générique de ce dernier. Cela n'est toutefois pas encore le cas en pratique et CDF se contente de quelques vecteurs de tests. À l'avenir, les deux projets devraient s'étoffer, l’équipe de Wycheproof ayant annoncé leur intention de publier leurs vecteurs de test dans un format aisément réutilisable et CDF ayant mentionné la possibilité de les ajouter à sa batterie de tests, nous permettant ainsi de tester toujours plus loin nos implémentations cryptographiques.
Les vecteurs de test
On appelle « vecteurs de test » les paires constituées des données d’entrée, par exemple une clef et un texte clair, et de leurs données de sortie escomptées, par exemple le texte chiffré correspondant à ce texte clair pour la clef en question. La plupart des algorithmes validés par le NIST disposent de telles valeurs de test dans le cadre de leur programme de validation d’algorithme cryptographique [CAVP]. De plus, la plupart des documents de standardisation tels que les RFCs (Requests For Comments) de l’IETF (Internet Engineering Task Force) fournissent des vecteurs de test, généralement dans leurs annexes.
1.1 Utiliser Wycheproof pour tester votre bibliothèque crypto
Avant de se lancer dans les tests, il est nécessaire d’installer le tout. À la date de publication de cet article, il est relativement facile d’installer Wycheproof [WYCH], mais cela demande vite un peu de temps.
Pour commencer, il est nécessaire d’installer Bazel [BZL], un outil d’automatisation de « build » pour différents langages de programmation, y compris Java. La documentation est bien faite, bien qu’anglophone, mais sur Ubuntu 16.04 le tout se fait en un tournemain.
Il nous faut tout d’abord installer le « Java Development Kit » ainsi que Bazel. Pour ce faire, il suffit d’ajouter le PPA de Bazel et la clef PGP correspondante, et de l’installer depuis les dépôts :
$ sudo apt-get install openjdk-8-jdk
$ echo "deb [arch=amd64] http://storage.googleapis.com/bazel-apt stable jdk1.8" | sudo tee /etc/apt/sources.list.d/bazel.list
$ curl https://bazel.build/bazel-release.pub.gpg | sudo apt-key add -
$ sudo apt-get update && sudo apt-get install bazel
Attention à se méfier de Bazel, car la rétrocompatibilité n’est pas la priorité du projet et d’une version à l’autre, il se peut que Wycheproof ne soit plus aussi facile à utiliser. Les tests décrits ici sont faits avec Bazel en version 9.
Tout n’est pas fini, car il nous faut encore nous assurer d’utiliser l’extension cryptographique Java qui permet de gérer les grandes tailles de clefs lors des tests faits par Wycheproof. Pour des raisons historiques, car les États-Unis limitaient l’export d’algorithme cryptographique trop fort en le classant au même niveau que l’export de munitions, et ce jusqu’en 1996, Oracle se limite volontairement à n’exporter que des algorithmes de chiffrement qui ne dépassent pas les 128 bits de sécurité. Afin de profiter de plus de sécurité, il est nécessaire d’activer manuellement l’extension cryptographique Java autorisant des tailles de clefs plus grandes.
Il est possible de faire tourner le tout sans cela, mais vous risquez de rencontrer beaucoup d’exceptions du type « illegal key size » [JSSO]. Il fut un temps où il était nécessaire de télécharger la « JCE unlimited strength policy » indépendamment du reste, mais depuis la version JDK 8u151 (qui se trouve justement être la version actuellement dans les dépôts Ubuntu), la politique de sécurité peut être configurée directement via le paramètre crypto.policy dans jre/lib/security/java.security et doit se voir assigner la valeur unlimited pour effectuer les tests en question sans problèmes.
Une fois cela fait, il faut télécharger ou compiler la bibliothèque à tester. Notez que Wycheproof ne gère (actuellement) que les bibliothèques qui implémentent l’interface cryptographique commune de Java, via la notion de fournisseur (« provider ») de Java. On compte notamment parmi celles-ci BouncyCastle, SpongyCastle et les fournisseurs du projet OpenJDK.
Prenons comme exemple SpongyCastle 1.54. Il n’y a pas besoin de l’installer nous-mêmes, car Bazel va s’en charger grâce à Maven. On peut donc simplement le tester en lançant :
$ bazel test SpongyCastleTest_1_54
[...]
Executed 1 out of 1 test: 1 fails locally.
Et l’on constate que le test échoue. Ensuite, il s’agit d’aller voir le journal du test pour constater que l’erreur en question provient de dix-huit des tests effectués par Wycheproof qui ont échoué avec SpongyCastle 1.54. Certains sans que cela porte réellement à conséquence, tandis que d’autres peuvent représenter un réel problème, comme celui-ci :
18) testExceptionsPKCS1(com.google.security.wycheproof.RsaEncryptionTest)
java.lang.AssertionError: Exceptions leak information about the padding for RSA/ECB/PKCS1PADDING
at org.junit.Assert.fail(Assert.java:88)
at com.google.security.wycheproof.RsaEncryptionTest.testExceptions(RsaEncryptionTest.java:138)
qui nous informe d’un possible oracle de bourrage dans le déchiffrement RSA PKCS #1 causé par des exceptions Java qui diffèrent selon le texte chiffré fourni.
On peut également vouloir tester sa propre implémentation. Heureusement pour nous, le système de fournisseurs de Java nous facilite grandement la tâche : pour tester notre propre bibliothèque, il nous suffit de créer un fichier wycheproof/java/com/google/security/wycheproof/NotreBiblioTest.java qui s’occupe simplement de définir notre propre fournisseur comme étant le fournisseur à utiliser, et voilà ! D’où tout l’intérêt d’avoir cette notion d’interface cryptographique commune. Enfin, en pratique si l’on crée notre propre fournisseur de sécurité Java, il faut le signer avec un certificat qui a été validé par la « JCA Code Signing Certification Authority », et pour l’utiliser ensuite avec Wycheproof, il faudra également aller modifier le fichier wycheproof/BUILD de sorte à pouvoir utiliser Bazel avec notre nouveau fournisseur.
Wycheproof a de beaux jours devant lui et prévoit de supporter bientôt bien plus de bibliothèques que celles de Java en portant leurs vecteurs de test dans un format plus facilement réutilisable.
1.2 Utiliser CDF pour tester votre implémentation crypto
CDF est l’acronyme de « Crypto Differential Fuzzer » [CDF], en cela qu’il va permettre de tester une implémentation en comparant ses valeurs de sortie avec celle d’une autre implémentation. Ce type d’approche est courant lorsque l’on implémente une nouvelle bibliothèque. Toutefois, la plupart du temps, chaque bibliothèque va implémenter sa propre suite de tests différentiels à l’aide de ses tests unitaires. Certaines ne le font pas et se contentent alors des vecteurs de test fournis généralement en annexe des spécifications des algorithmes implémentés.
CDF tente dès lors une approche plus généraliste et propose la notion d’interface afin de permettre l’interopérabilité entre deux bibliothèques distinctes tant par leur implémentation que par leurs interfaces. Cela nous permet ainsi de comparer leurs comportements, dans l’espoir de détecter des comportements étranges ou déviants d’une implémentation à l’autre. D’autant plus qu’il n’est jamais facile de vérifier la conformité d’un programme à une spécification sur la base d’uniquement quelques vecteurs de test !
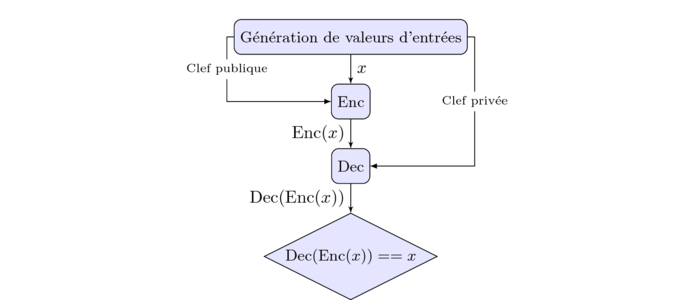
CDF utilise deux approches complémentaires pour tester un programme. La première consiste à tester l’interopérabilité d’une implémentation avec une autre sur des valeurs d’entrées aléatoires, tandis que la deuxième consiste à vérifier à la fois la fonctionnalité et l’interopérabilité face à des cas limites particuliers dont le but est de pousser au vice les implémentations. Différentes manières de comparer l’interopérabilité de primitives existent, notamment en fonction du style d’opération supportée par cette primitive. Parmi celles-ci, on peut distinguer par exemple : le chiffrement qui doit être compatible avec le déchiffrement ainsi qu’illustré sur la Figure 1, la signature d’un message qui doit être compatible avec la vérification de sa validité, ou enfin simplement le fait que les mêmes valeurs de sortie devraient être produites lorsque les mêmes valeurs d’entrée sont utilisées avec un algorithme déterministe (qui n’a pas besoin de valeur aléatoire).
Fig. 1 : Exemple d’interface pour tester un algorithme de chiffrement, tant symétrique (auquel cas la clef publique est la même que la clef privée) qu’asymétrique. On commence par chiffrer (opération « Enc ») une valeur aléatoire x, puis l’on tente de déchiffrer (« Dec ») et l’on vérifie que le résultat obtenu correspond à celui escompté.
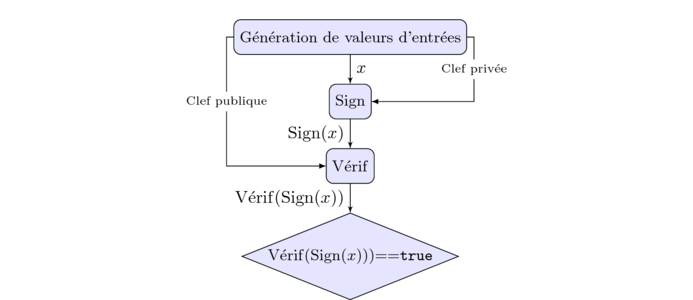
Afin de tester une implémentation avec CDF, il est nécessaire d'implémenter l'une des interfaces de CDF. Prenons par exemple l'interface prévue pour tester la primitive connue sous le nom d’ECDSA. ECDSA est un algorithme de signature digitale à clef publique sur courbe elliptique qui supporte deux opérations : la signature d'un message et la vérification d'une signature. Pour ce faire, l’interface de CDF va tester l’interopérabilité ainsi qu’indiqué sur la Figure 2.
Fig. 2 : Exemple d’interface utilisée pour tester l’interopérabilité d’algorithmes de signature digitale. On commence par signer une valeur aléatoire x et l’on tente ensuite de vérifier la signature en question. Celle-ci devrait se vérifier correctement si et seulement si la clef publique correspond à la clef privée utilisée.
Pour signer un message, il est nécessaire de posséder une clef privée, tandis que pour vérifier une signature, il faut la clef publique correspondant à la clef privée utilisée lors de la signature.
L'interface de CDF pour ECDSA requiert un exécutable pouvant prendre comme entrée une clef privée ainsi qu’un message, et qui doit fournir en sortie la signature de ce message par cette clef privée. Elle requiert également, pour la vérification, un exécutable prenant en entrée un message, une clef publique et une signature, et retournant true ou false, suivant si la signature est vérifiée correctement ou non.
Cette notion d'interface basée sur les entrées-sorties permet à CDF de fonctionner en boîte noire, sans avoir besoin d'accéder à des API bas niveau, facilitant ainsi grandement son utilisation avec une implémentation particulière, rendant même le processus de test indépendant du langage de programmation utilisé, du moment que l'on a un exécutable qui implémente cette interface.
CDF intègre également une réimplémentation en Go de Dudect à sa suite de tests, permettant ainsi de comparer les timings des deux implémentations testées, pour voir si elles s’exécutent en un temps constant face à différentes classes de valeurs d’entrées ou non. Dudect étant basé sur une méthode probabiliste, un résultat négatif ne signifie pas pour autant qu’une implémentation fonctionne en temps constant, mais qu’elle l’est probablement, et vice-versa.
Pour utiliser CDF, la première étape consiste à sélectionner l’interface correspondant à la primitive testée. Disons que l’on s’intéresse à DSA et que l’on veut tester une implémentation de DSA en Python, par exemple celle de PyCrypto. La première étape consiste à regarder en quoi consiste l’interface de CDF pour DSA. Elle a la spécification suivante :
|
Opération |
Valeurs d’entrée |
Valeurs de sortie |
|
Signature |
p q g y x m |
r s |
|
Vérification |
p q g y r s m |
true/false |
Où les valeurs p,q et g sont les paramètres DSA, y est la clef publique, x est la clef privée, m est le message et enfin la paire r,s représente les deux entiers qui forment une signature DSA. Toutes ces valeurs doivent de plus être au format hexadécimal.
On peut donc implémenter un petit programme en Python qui va satisfaire cette spécification de sorte à prendre les valeurs escomptées en entrée et donner les valeurs correspondantes en sortie :
#!/usr/bin/env python3
from Crypto.PublicKey import DSA
from Crypto.Hash import SHA256
# On vérifie que l’on a reçu suffisamment d’arguments en entrée :
if len(sys.argv) == 8:
signing = False
elif len(sys.argv) == 7:
signing = True
else:
print("Veuillez fournir en entrée P, Q, G, Y, X, Msg ou P, Q, G, Y, R, S, Msg")
sys.exit(1)
# On récupère les arguments en hexadécimal
q = int(sys.argv[2], 16)
p = int(sys.argv[1], 16)
g = int(sys.argv[3], 16)
pub = int(sys.argv[4], 16)
message = binascii.unhexlify(sys.argv.pop())
if signing:
priv = int(sys.argv[5], 16)
params = (pub, g, p, q, priv)
else:
params = (pub, g, p, q)
r = int(sys.argv[5], 16)
s = int(sys.argv[6], 16)
sig = (r, s)
key = DSA.construct(params)
hash = SHA256.new(message).digest()
# Spécialité PyCrypto : s’assurer de ne pas fournir une valeur plus grande que la taille du groupe.
grp_len = int((q.bit_length() + 7) / 8)
k = random.StrongRandom().randint(1, key.q-1)
if signing:
# on tronque la valeur d’entrée selon la spécification de DSA puisque PyCrypto ne le fait pas.
sig = key.sign(hash[:grp_len], k)
print(format(sig[0], 'x').zfill(40))
print(format(sig[1], 'x').zfill(40))
else:
if key.verify(hash[:grp_len], sig):
print("true")
else:
print("false")
Une fois cela fait, il est aisé de tester notre implémentation avec CDF, il suffit d’avoir installé Go et de faire :
go get github.com/kudelskisecurity/cdf
cd $GOPATH/src/github.com/kudelskisecurity/cdf
make examples-go
cdf dsa ./votre-executable examples/dsa_sha256_go.go
Et la suite de tests de CDF va alors s’occuper de comparer l’implémentation de DSA testée avec celle de la bibliothèque Go standard. Les erreurs s’affichent directement dans la console et sont normalement relativement explicites. En cas de besoin, si par exemple une erreur n’est pas claire, il est possible de poser des questions directement sur la page GitHub de CDF.
CDF devrait également s’étoffer au cours des années, avec plus d’interfaces pour supporter plus d’algorithmes et plus de tests pour chacune de ses interfaces.
Conclusion
De nombreuses personnes sont convaincues que la cryptographie est « trop dure » pour être abordée aisément, mais au final la plupart des problèmes cryptographiques dont nous avons tous entendu parler au cours de ces dernières années proviennent de problèmes d’implémentation de fonctions cryptographiques. Ainsi, développer du code cryptographique sûr s’est révélé au fil des années être une tâche ardue. Plusieurs projets, tels que ceux dont nous avons parlé ici, ont pour but de faciliter la tâche tant au développeur qu’à l’utilisateur en leur permettant de tester une implémentation cryptographique et de vérifier la robustesse de celle-ci face à de nombreuses attaques, sans pour autant devoir lire l’intégralité des publications académiques sur ce sujet, et sans avoir besoin de devenir un cryptographe pour ce faire. Toutefois, mieux vaut garder à l’esprit que seul un résultat positif « est vulnérable à X » est significatif, et qu’un résultat négatif ne veut pas pour autant dire qu’une implémentation donnée est absolument sûre. Tout est relatif et une nouvelle attaque, une variante d’une ancienne attaque ou un détail spécifique à une implémentation donnée peut parfois suffire à compromettre un système. La prudence reste donc de mise.
Remerciements
Je tiens à remercier mon entreprise, Kudelski Security, qui m’a permis de rédiger cet article et de développer CDF dans le cadre de mon travail de recherche en cryptographie, ainsi que Jean-Philippe Aumasson pour avoir conçu la notion de fuzzing différentiel et participé au développement de CDF.
Références
[BOCK] H. Böck, « How Heartbleed could've been found » : https://blog.hboeck.de/archives/868-How-Heartbleed-couldve-been-found.html
[MISC] J. Le Floch, « Les attaques sur RSA : de la théorie à la pratique », MISC n°87, septembre-octobre 2016 : https://connect.ed-diamond.com/MISC/MISC-087/Les-attaques-sur-RSA-de-la-theorie-a-la-pratique
[HALE] C. Hale , « A Lesson In Timing Attacks (or, Don’t use MessageDigest.isEquals) » : https://codahale.com/a-lesson-in-timing-attacks/
[INVC] T. Jager, J. Schwenk, J. Somorovsky, « Practical Invalid Curve Attacks on TLS-ECDH » : https://doi.org/10.1007/978-3-319-24174-6_21
[CTGR] A. Langley, « Ctgrind » : https://github.com/agl/ctgrind
[DUDE] O. Reparaz, J. Balasch, I. Verbauwhede, « Dude, is my code constant time? » : https://eprint.iacr.org/2016/1123
[BZL] Bazel - a fast, scalable, multi-language and extensible build system : https://bazel.build/
[JSSO] J. Black, « Java Security : Illegal key size or default parameters? » : https://stackoverflow.com/a/6481658/2757014
[WYCH] D. Bleichenbacher, T. Duong, E. Kasper, Q. Nguyen, « Project Wycheproof » : https://github.com/google/wycheproof
[CDF] JP. Aumasson, Y. Romailler, « Crypto Differential Fuzzer » : https://github.com/kudelskisecurity/cdf
[ROBOT] « Return Of Bleichenbacher's Oracle Threat » : https://robotattack.org/
[CAVP] NIST Cryptographic Algorithm Validation Program : https://csrc.nist.gov/projects/cryptographic-algorithm-validation-program
[ECDSA] D. Aranha, P.-A. Fouque, B. Gérard, J.-G. Kammerer, M. Tibouchi, et al., « GLV/GLS Decomposition, Power Analysis, and Attacks on ECDSA Signatures with Single-Bit Nonce Bias ». Advances in Cryptology - ASIACRYPT 2014, 8873, pp.262-281, 2014, https://hal.inria.fr/hal-01094002
[PYDSA] R. Rottmann, « DSA Signature Algorithm - A simple implementation in Python » : https://github.com/rrottmann/pydsa
[SPCTR] « Meltdown and Spectre : Vulnerabilities in modern computers leak passwords and sensitive data » : https://meltdownattack.com



 Ajouter à une liste de lecture
Ajouter à une liste de lecture