Plutôt que de foncer tête baissée dans ce projet pour arriver le plus vite possible au résultat, nous allons parfois faire quelques légers détours dans le but d’aborder chaque point progressivement. L’idée sera de raffiner notre programme au fur et à mesure de nos observations. Nous aborderons, en plus de la 3D, quelques notions intéressantes en programmation telles que les tableaux ou certains algorithmes qui permettent d’ajouter du mouvement à vos sketchs.
1. Processing au cube
1.1 Trois dimensions, trois coordonnées
Cela semble une évidence, mais cela mérite d’être rappelé. Pour dessiner en trois dimensions, nous aurons besoin de trois coordonnées. Lorsque nous dessinons des formes en 2D dans Processing, nous avons besoin de préciser leur emplacement (en pixel) dans l’espace plat du sketch. Ainsi, la commande :
size(200,200); // Création d’un sketch de 200 pixels de côté
background(0); // Dessin de l’arrière-plan en noir
stroke(255); // Dessin des contours en blanc
line (10,10,190,190); // Dessin d’une ligne
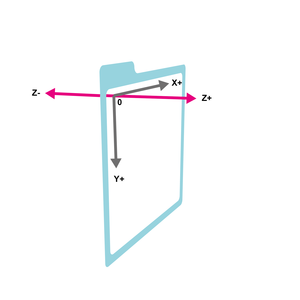
dessine un segment en diagonale. Les valeurs entre parenthèses définissent les coordonnées X et Y, en partant de l’origine en haut à gauche du sketch. Dessiner en trois dimensions implique une troisième valeur, celle de la profondeur, communément appelée le Z. Il faut imaginer que la dimension Z entre dans l’écran, face à vous. Un Z égal à 0 serait la surface de l’écran, et un Z égal à -100 s’éloignerait de vous de 100 pixels dans l’espace virtuel du sketch. Une valeur positive, au contraire, rapprocherait le dessin de vous.
Figure 1
Pour activer cette troisième dimension, il faudra préciser à la création de votre sketch que vous désirez l‘utiliser. On ajoute pour cela aux paramètres du size le paramètre P3D, qui demande à Processing d’utiliser un rendu OpenGL. OpenGL est une interface présente dans nos machines permettant l’affichage de formes en 3D (ça tombe bien).
size(200,200, P3D); // On définit un mode de dessin en 3D
background(0);
stroke(255);
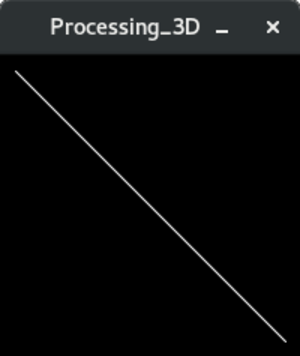
line (10,10,-100,190,190,-100); // La ligne est cette fois dessinée dans l’espace 3D
Figure 2
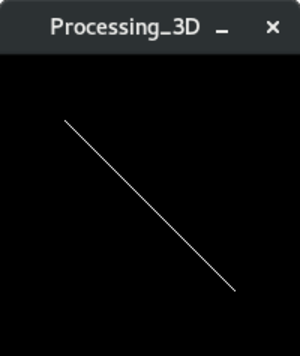
Figure 3
Vous constaterez que la ligne est plus petite que précédemment. Elle s’est en réalité éloignée de votre point de vue, et selon les principes de la perspective conique, sa taille s’est réduite.
1.2 Primitives et translation
Rentrons maintenant dans le vif du sujet en dessinant un cube. Si vous avez déjà pratiqué un peu le langage, vous savez que Processing aime nous simplifier l’existence. Il existe donc des primitives 3D que l’on pourra dessiner d’un simple appel de fonction : sphere() et box(). Leur nom est transparent, voyons dans la documentation quels paramètres prend la fonction box().
Nous lisons box(size) ou box(w, h, d), ce qui une fois traduit nous donne « taille » ou « largeur/hauteur/profondeur ». C’est assez explicite, et l’on comprend que pour dessiner un cube, il suffira de définir size pour avoir trois dimensions égales.
Votre perspicacité aura en revanche détecté un détail important : on ne parle pas ici de coordonnées. Ni X, ni Y, ni Z. Comment donc définir l’endroit où l’on veut dessiner notre cube ? Il faudra pour cela déplacer l’origine de notre sketch à l’aide la commande translate. Cette fonction décale le zéro du sketch depuis le coin en haut à gauche vers un point défini par les coordonnées entrées dans les parenthèses.
size(200, 200, P3D);
background(0);
stroke(255);
noFill() ; // Pas de remplissage pour voir les arêtes
translate(100, 100, -50); // Nous décalons l’origine au centre et « reculons » de 50 pixels
box(50); // puis nous dessinons un cube de 50 pixels de coté
Dans le même esprit, les commandes rotateX(), rotateY() et rotateZ() permettront de tourner autour de l’objet. La commande scale() permet elle d’augmenter la taille des éléments dessinés. Nous reviendrons sur ces fonctions par la suite.
Figure 4
1.3 Quad et textures
La vie dans la programmation n’est pas toujours rose. Si la commande box() paraît très commode pour modéliser notre dé, elle présente néanmoins un inconvénient majeur. L’objet étant modélisé d’un seul tenant, il nous sera impossible d’accéder à chaque face pour lui coller une texture différente. Or, un dé dont toutes les faces seraient identiques présente peu d’intérêt, vous en conviendrez. Il faudra donc modéliser notre cube face par face, pour lui appliquer à chaque fois une texture différente.
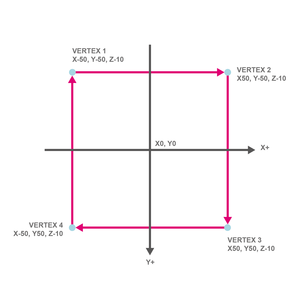
Pour cela, nous allons commencer à mettre les mains dans le cambouis et descendre à la plus petite unité accessible en modélisation 3D : le point. Deux points peuvent être reliés pour former une arête. Trois points reliés formeront une face, triangulaire. Nous aurons besoin pour notre dé de quatre points par face, et de définir leur position dans l’espace.
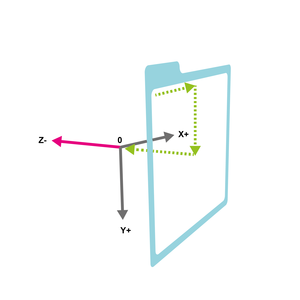
Dans Processing, un point est appelé un vertex. Il est défini par trois valeurs (positions X, Y et Z) plus deux autres, peut-être plus complexes à appréhender, qui définissent le placement de la texture. On les appelle les coordonnées U et V, et elles ne sont ni plus ni moins qu’une indication concernant le placement des coins de l’image qui servira de texture.
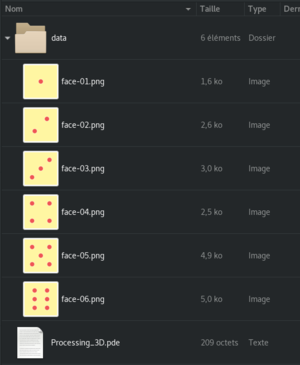
Mais d’abord, la texture. Créez une image carrée de 300 pixels par 300 pixels dans votre logiciel de dessin préféré. Par exemple, un aplat avec un disque au centre semblerait assez adapté. Le format PNG est un bon choix, le mode RVB est lui impératif. Placez cette image dans le dossier « data » de votre sketch (créez-le s’il n’existe pas. Processing ira y chercher les contenus externes). Dessinons maintenant notre première face avec le code suivant :
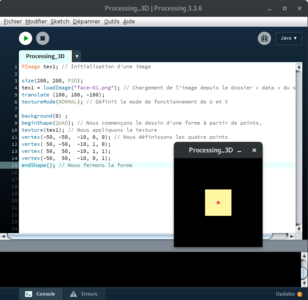
PImage tex1; // Initialisation d’une image
size(200, 200, P3D);
tex1 = loadImage("face-01.png"); // Chargement de l’image depuis le dossier « data » du sketch
translate (100, 100, -100);
textureMode(NORMAL); // Définit le mode de fonctionnement de U et V
beginShape(QUAD); // Nous commençons le dessin d’une forme à partir de points,
texture(tex1); // Nous lui appliquons la texture
vertex(-50, -50, -10, 0, 0); // Nous définissons les quatre points
vertex( 50, -50, -10, 1, 0);
vertex( 50, 50, -10, 1, 1);
vertex(-50, 50, -10, 0, 1);
endShape(); // Nous fermons la forme
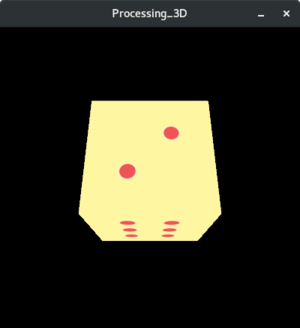
Figure 5
Figure 6
Notre première face est créée, les 5 autres ne seront que répétition de cette même action.
Il y a deux choses importantes à noter : l’utilisation de beginShape() et endShape(), qui encadrent la création des points. Ils sont indispensables. Ensuite, vous noterez que l’ordre des points n’a pas été choisi au hasard. On tourne autour de notre carré, les points ne se croisent pas. C’est important pour le bon affichage du Quad (face carrée, en vocabulaire 3D).
1.4 Finalisation du dé
Nous allons maintenant finaliser notre dé. Dans la lignée de ce que vous avez déjà créé, dessinez les cinq faces manquantes qui serviront de texture dans un logiciel de dessin et enregistrez-les dans votre dossier « data ».
Figure 7
Le point qui va suivre n’est pas absolument capital, mais il vous simplifiera grandement l’existence en vous permettant de moduler et d’ajuster la taille de votre dé si besoin. La fonction qui nous permettra ce tour de magie est la fonction scale().Elle nous permettra d’agrandir ou réduire tout ce qui sera dessiné après son appel. Nous allons avoir un grand nombre de coordonnées à écrire. Corriger la taille du cube serait très fastidieux : rien que pour la face que nous venons de dessiner, imaginez-vous en train de corriger tous les « 50 » en « 60 » pour agrandir le quad ! Pour faciliter l’ajustement de notre volume, nous utiliserons des valeurs unitaires, 1 ou -1 . Elles seront toutes multipliées, au moment de l’affichage, par la valeur entrée dans scale(). Ainsi, scale(90) nous affichera un cube de 90 pixels de côté.
Définir correctement le placement des points de chaque face demande une certaine gymnastique mentale et une bonne vision dans l’espace. Dessiner sur un coin de table est souvent d’une aide précieuse ! Dans le cas qui nous intéresse, je vous propose de nous appuyer sur le code de l’exemple TextureCube.pde, présent dans le dossier Topics/Textures de Processing. Hop ! Copié, collé, inutile de réinventer la roue, fut-elle cubique !
PImage tex1; // Nos 6 textures
PImage tex2;
PImage tex3;
PImage tex4;
PImage tex5;
PImage tex6;
size(400, 400, P3D); // Agrandissons maintenant un peu le sketch pour y voir plus clair
tex1 = loadImage("face-01.png"); // Import des 6 images
tex2 = loadImage("face-02.png");
tex3 = loadImage("face-03.png");
tex4 = loadImage("face-04.png");
tex5 = loadImage("face-05.png");
tex6 = loadImage("face-06.png");
noStroke(); // Pas de contours
textureMode(NORMAL);
background(0);
translate(width/2.0, height/2.0, -100);
scale(90);
beginShape(QUAD);
texture(tex1);
vertex(-1, -1, 1, 0, 0);
vertex( 1, -1, 1, 1, 0);
vertex( 1, 1, 1, 1, 1);
vertex(-1, 1, 1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex6);
vertex( 1, -1, -1, 0, 0);
vertex(-1, -1, -1, 1, 0);
vertex(-1, 1, -1, 1, 1);
vertex( 1, 1, -1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex2);
vertex(-1, 1, 1, 0, 0);
vertex( 1, 1, 1, 1, 0);
vertex( 1, 1, -1, 1, 1);
vertex(-1, 1, -1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex5);
vertex(-1, -1, -1, 0, 0);
vertex( 1, -1, -1, 1, 0);
vertex( 1, -1, 1, 1, 1);
vertex(-1, -1, 1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex4);
vertex( 1, -1, 1, 0, 0);
vertex( 1, -1, -1, 1, 0);
vertex( 1, 1, -1, 1, 1);
vertex( 1, 1, 1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex3);
vertex(-1, -1, -1, 0, 0);
vertex(-1, -1, 1, 1, 0);
vertex(-1, 1, 1, 1, 1);
vertex(-1, 1, -1, 0, 1);
endShape();
Appuyez sur Run et … je vois d’ici votre déception. Notre cube n’est pas vraiment très impressionnant. En effet, pour visualiser correctement une forme en 3D sur un écran en 2D, il nous manque… le mouvement !
2 . Du mouvement
2.1 Rotation continue
Nous l’avons vu précédemment, le dessin en 3D dans Processing a ceci de particulier que pour modifier le positionnement de l’objet, nous n’allons pas agir sur l’objet lui-même, mais sur l’origine et la géométrie de l’espace dans lequel on le dessine. En d’autres termes, pour agrandir le cube, on ne joue pas sur sa dimension, mais sur le paramètre scale de l’espace dans lequel on le dessine. De la même façon, pour faire tourner l’objet, nous jouerons sur le paramètre de rotation de cette espace, via les méthodes rotateX() et rotateY().
Dans Processing, qui dit mouvement dit impérativement boucle draw(). Nous avons jusqu’ici travaillé avec un code statique, il va falloir l’adapter un peu pour pouvoir l’animer. Si l’on reprend notre code précédent, il faudra, après les déclarations des 6 PImages, inclure les fonctions size, le chargement des images et la déclaration du mode des textures dans une fonction setup(), comme ceci :
void setup()
{
size(400, 400, P3D);
tex1 = loadImage("face-01.png");
tex2 = loadImage("face-02.png");
tex3 = loadImage("face-03.png");
tex4 = loadImage("face-04.png");
tex5 = loadImage("face-05.png");
tex6 = loadImage("face-06.png");
noStroke(); // Pas de contours
textureMode(NORMAL);
La suite sera intégrée dans une boucle draw() ; si vous testez l’application à ce stade, rien n’aura changé. Mais il ne nous manque plus que quelques lignes pour que les choses s’animent.
Entre les déclarations des Pimage et le setup, déclarons une variable qui nous servira à stocker une valeur de rotation :
float rotationX = 0;
Nous allons ajouter après le translate() :
rotateX(rotationX);
Le jeu sera en suite, image après image, c’est-à-dire à chaque itération de la boucle draw(), d’augmenter légèrement la valeur de rotationX, pour la passer ensuite en paramètre à rotateX() :
rotationX = rotationX + PI/180;
Testez : et pourtant il tourne !
Figure 8
Petit détail qui a son importance : Processing, par défaut, calcul les angles en radians. Il faut donc lui parler en fractions de Pi, de préférence. Il est possible de convertir les calculs de rotation en degrés, mais vous allez le voir plus loin, dans notre cas, les radians seront assez commodes.
Dans la portion qui nous intéresse, la première ligne modifie donc légèrement la valeur de rotationX : on lui ajoute la valeur de Pi divisée par 180. Pour mémoire, Pi correspond à un demi-tour lorsque l’on calcule en radians, soit 180 degrés. On tourne donc notre espace, à chaque image, d’un degré supplémentaire.
Votre cube tourne donc maintenant sur un de ses axes. À vous de tester l’autre axe, avec rotationY. Et pourquoi pas les deux axes en même temps !
Image tex1;
PImage tex2;
PImage tex3;
PImage tex4;
PImage tex5;
PImage tex6;
float rotationX = 0;
float rotationY = 0;
void setup()
{
size(400, 400, P3D);
tex1 = loadImage("face-01.png");
tex2 = loadImage("face-02.png");
tex3 = loadImage("face-03.png");
tex4 = loadImage("face-04.png");
tex5 = loadImage("face-05.png");
tex6 = loadImage("face-06.png");
noStroke();
textureMode(NORMAL);
}
void draw()
{
background(0);
translate(width/2.0, height/2.0, -100);
scale(90);
rotateX( rotationX);
rotationX = rotationX + PI/180;
rotateY( rotationY);
rotationY = rotationY + PI/180;
beginShape(QUAD);
texture(tex1);
vertex(-1, -1, 1, 0, 0);
vertex( 1, -1, 1, 1, 0);
vertex( 1, 1, 1, 1, 1);
vertex(-1, 1, 1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex6);
vertex( 1, -1, -1, 0, 0);
vertex(-1, -1, -1, 1, 0);
vertex(-1, 1, -1, 1, 1);
vertex( 1, 1, -1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex2);
vertex(-1, 1, 1, 0, 0);
vertex( 1, 1, 1, 1, 0);
vertex( 1, 1, -1, 1, 1);
vertex(-1, 1, -1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex5);
vertex(-1, -1, -1, 0, 0);
vertex( 1, -1, -1, 1, 0);
vertex( 1, -1, 1, 1, 1);
vertex(-1, -1, 1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex4);
vertex( 1, -1, 1, 0, 0);
vertex( 1, -1, -1, 1, 0);
vertex( 1, 1, -1, 1, 1);
vertex( 1, 1, 1, 0, 1);
endShape();
beginShape(QUAD);
texture(tex3);
vertex(-1, -1, -1, 0, 0);
vertex(-1, -1, 1, 1, 0);
vertex(-1, 1, 1, 1, 1);
vertex(-1, 1, -1, 0, 1);
endShape();
}
2.2 Rotation avec la souris
Continuons d’améliorer notre programme en préférant, à cette rotation automatique une rotation qui serait pilotée par l’utilisateur. Cela signifie que les valeurs rotationX et rotationY, au lieu d’être modifiées de façon linéaire au fur et à mesure du programme, seraient modifiées en fonction des mouvements de la souris de l’utilisateur. Il nous faut donc un nouveau bloc sous la boucle draw() :
void mouseDragged() {
...
}
Le contenu de ce groupe logique sera exécuté lorsque la souris sera cliquée et déplacée.
Nous allons dans un premier temps commenter les lignes qui incrémentaient de façon automatique nos deux variables :
rotateX( rotationX);
//rotationX = rotationX + PI/180;
rotateY( rotationY);
//rotationY = rotationY + PI/180;
puis dans la fonction mouseDragged(), nous allons ajouter:
void mouseDragged() {
float rate = 0.01;
rotationX += (pmouseY-mouseY) * rate;
rotationY += (mouseX-pmouseX) * rate;
}
Le principe est le même que précédemment, sauf qu’au lieu d’utiliser une valeur fixe pour modifier rotationX, nous utilisons (accrochez-vous) : la distance parcourue par la souris lors de la précédente boucle (pmouseX et pmouseY donnent la position lors de l’image précédente, mouseX et mouseY lors de l’image courante), multipliée par un facteur qui divise la valeur par 100.
Vous le constaterez, cette corrélation entre la souris et la rotation produit une interface très efficace et intuitive. Les plus attentifs auront également remarqué que cette portion de code a été copiée de l’exemple précédemment cité.
2.3 Rotation paramétrée
Il est temps de reprendre notre objectif en ligne de mire. Nous voulons pouvoir tirer une valeur au dé !
Il va donc falloir écrire quelque part dans notre code une table de relation pour qu’à une face donnée corresponde une valeur de rotation en X et en Y. En clair, quelle rotation dois-je appliquer pour voir la face n°1 ? Et la 2 ? Et ainsi de suite.
2.3.1 Trouver les valeurs, en radians
Si vous avez affecté les textures aux mêmes faces que moi dans votre code, la première face qui apparaît, lors de l’exécution du programme est la 1. On sait donc que la face numéro 1 correspond à une rotation en X de 0 et une rotation en Y de 0. Grâce à la souris, faites légèrement tourner votre cube. Vous voyez que la face de droite est la 4. Il faut donc réaliser un quart de tour vers la droite pour faire apparaître cette face. Autrement dit, le 4 a besoin d’une rotation sur l’axe Y d’un demi de pi (puisque pi correspond à un demi-tour, en radians). Nous pourrions noter cela PI/2, mais Processing possède une constante, HALF_PI. Vous trouverez ci-dessous le tableau des correspondances pour chaque face de notre dé. À noter, une rotation de -HALF_PI est équivalente à HALF_PI+PI (un quart de tour à gauche ou trois quarts de tour à droite).
2.3.2 Stocker les valeurs, dans un tableau à deux dimensions
Pour accéder facilement à ces valeurs, je vous propose de les stocker sous une forme matricielle dans un tableau à deux dimensions. En programmation, un tableau est une sorte de casier dans lequel chaque contenu qui y est rangé peut être appelé par son numéro de case. Ainsi, un tableau à une dimension permet d’accéder par un numéro d’index à ce qui y est stocké. Un tableau à deux dimensions n’est ni plus ni moins qu’un tableau de tableaux. Pensez à des lignes et des colonnes, un numéro de ligne et un numéro de colonne permettant d’accéder à une information.
Dans notre cas, chaque ligne (face 1, face 2, etc.) stockera la valeur de rotationX et celle de rotationY nécessaire pour l’afficher.
Voici ce que cela donne :
//RotationX, Rotation Y
float [][] cibles = {
{0, 0}, //Face 1
{HALF_PI, 0}, //Face 2
{0, HALF_PI}, //Face 3
{0, -HALF_PI}, //Face 4
{-HALF_PI, 0}, //Face 5
{PI, 0}, //Face 6
};
2.3.3 Appeler les valeurs facilement
Pour tester ces différentes valeurs de rotation, je vous propose de lier chaque face à la touche du clavier qui lui correspond. La touche 1 appellerait la face 1 et ainsi de suite. Cela va nécessiter pas mal de petites modifications.
Tout d’abord, nous allons ajouter à la fin de notre programme une nouvelle fonction, qui servira à mettre à jour les valeurs de rotationX et rotationY en allant chercher les valeurs dans notre tableau cibles[].
void definirCibles(int i)
{
rotationX=cibles[i][0];
rotationY=cibles[i][1];
}
La première valeur entre crochets indique la ligne du tableau, la seconde sera la colonne. N’oublions pas qu’en informatique, tout se compte à partir de zéro. Ainsi, si le paramètre de definirCibles est 2, rotationX aura la valeur de la troisième ligne, première colonne. Il faudra penser à ce détail pour la suite.
Car maintenant, nous allons lier les touches du clavier à cette fonction en tapant :
void keyPressed()
{
if (key >= ‘1’ && key <= ‘6’)
{
definirCibles(int(key)-48-1);
}
}
Explicitons un peu les aspects étranges de cette courte fonction. if (key >= ‘1’ && key <= ‘6’) signifie simplement que l’on n’écoute pour l’instant que les touches comprises entre 1 à 6 (incluses). La suite demande un peu plus de concentration. Nous voulons que lorsque l’on appuie sur 1, définirCibles prenne pour paramètre 1. Or, 1, dans la fonction keyPressed(), n’est pas un nombre entier, c’est un caractère, au même titre que a, b ou c. Cela explique que l’on ait ajouté les ‘ ‘ lors de la comparaison dans le if. Or, notre fonction definirCibles attend un nombre entier. En ajoutant int() devant key dans le paramètre, nous forçons la conversion du caractère (char) en nombre entier (int). Mais voilà, ce serait trop simple si cela fonctionnait aussi facilement ! En effet, la conversion d’un char en int renvoie en réalité son numéro dans la table ASCII/Unicode, en fait sa conversion décimale depuis l’hexadécimal. Oui, cela fait beaucoup de conversion. Toujours est-il qu’à 1 correspond le nombre 49, à 2 le nombre 50, à 3 le nombre 51 et ainsi de suite. Astuce : utilisons une simple soustraction de 48 pour retomber sur nos pieds. Cette méthode n’est sans doute pas très orthodoxe, mais elle a le mérite de fonctionner pour cette courte suite de nombres.
Une fois que nous avons récupéré notre valeur, nous n’oublions pas de lui soustraire 1, pour faire correspondre le premier chiffre (1) avec la première ligne (0) du tableau. Ouf ! Testons cela !
2.3.4 De l’avantage de mettre du délai
Les faces changent bien à chaque pression des touches du clavier, mais de nouveau, je sens comme une pointe de déception. Le changement est instantané, aucun intérêt d’avoir travaillé en 3D !
Il faut bien sûr répartir la transformation dans le temps, pour que le changement d’angle soit visible. Comme tout à l’heure lorsque nous travaillions avec la rotation continue, l’astuce sera de modifier progressivement notre valeur de rotationX et rotationY pour arriver à la cible définie.
Nous allons, au début de notre programme, ajouter deux nouvelles variables :
float cibleRotationX = 0;
float cibleRotationY = 0;
Cela sera les cibles à atteindre.
Modifions ensuite notre fonction definirCibles() :
void definirCibles(int i)
{
cibleRotationX=cibles[i][0];
cibleRotationY=cibles[i][1];
}
Allons maintenant retoucher notre draw() :
rotationX=rotationX+((cibleRotationX-rotationX)/10);
rotationY=rotationY+((cibleRotationY-rotationY)/10);
rotateX(rotationX);
rotateY(rotationY);
Nous calculons la différence entre la position actuelle du point de vue et la cible que l’on veut atteindre, et nous avançons d’un dixième de cette distance à chaque image. Il en résulte un effet agréable d’amorti du mouvement que je vous laisse tester.
3. Enfin du hasard !
Dernière étape de ce pas-à-pas, mais pas la moindre : le hasard !
Nous verrons ici comment générer de manière très simple un tirage aléatoire, et déplacer en fonction de ce résultat notre dé.
Notre outil sera ici la fonction random(), qui renvoie des nombres aléatoires à chaque appel. Si on lui passe un seul nombre en paramètre, le résultat renvoyé sera compris entre 0 et ce nombre (non inclus). À noter que les valeurs renvoyées sont des valeurs décimales (float). Nous avons besoin de valeurs entre 1 et 6, nous utiliserons donc deux paramètres, pour préciser le début et la fin du champ d’application de la fonction. Nous aurons également besoin de int() pour arrondir le résultat à l’entier le plus proche.
Voici ce que donne notre fonction keyPressed(), une fois modifiée :
void keyPressed()
{
if (key >= ‘1’ && key <= ‘6’)
{
definirCibles((int)key-48-1);
}
else if (key == ‘ ‘)
{
int tirage = int (random(1,6)); // Tirage du chiffre
definirCibles(tirage); // Application à la rotation
}
}
Et voilà, à chaque pression de la barre espace, une nouvelle valeur sera tirée et renvoyée à notre fonction definirCibles(). À noter que parfois notre cube reste immobile après une pression sur espace. Tout simplement, c’est le même chiffre qui est sorti que la fois précédente, comme cela peut arriver dans la vraie vie !
Conclusion
Arrivé au terme de ce projet, je ne peux que vous conseiller, une fois de plus, de vous appuyer sur les exemples fournis dans Processing pour approfondir le dessin en 3D. Lorsque vous serez un peu plus à l’aise, vous pourrez également aller explorer les différentes librairies développées par la communauté. Des possibilités immenses ont été défrichées et rendues accessibles à des non-techniciens : importation depuis Blender, exportation vers des imprimantes 3D, utilisation native des cartes graphiques pour des performances proches des jeux vidéos, manipulations des maillages extrêmement complexes et organiques. Les plus passionnés noteront la possibilité d’attaquer la bête avec des fonctions OpenGL natives et d’aborder un chapitre passionnant par les possibilités graphiques qu’il offre, les shaders (https://processing.org/tutorials/pshader/). Tout cela offre aussi une belle occasion de se replonger dans ses cours de maths !